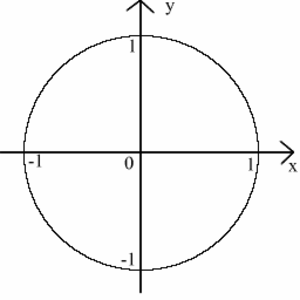
$y$-akseli (engl. y axis, y-axis)
Karteesisen koordinaattijärjestelmän toinen akseli. $y$-akseli on kohtisuorassa $x$-akselia vastaan.
Katso myös $z$-akseli, $y$-akselin suunta, $x$-akseli, Ordinaatta, Karteesinen koordinaatisto, Koordinaattiakseli, Akseli.
$y$-akselin suunta (engl. y direction)
Suunta, johon kuljetaan, jos lähdetään liikkeelle origosta ja liikutaan $y$-akselin suuntaisesti kohti $y$-koordinaatin positiivisia arvoja.
Katso myös $y$-akseli.
Ydin (engl. Kernel, Null space)
Matemaattisten struktuurien välisen kuvauksen ydin on niiden määrittelyjoukon alkioiden joukko, jotka kuvautuvat neutraalialkiolle. Vektoriavaruuksien välisen lineaarikuvauksen ydin on nollalle kuvautuvien vektorien joukko. Matriisin ydin on niiden vektoreiden joukko, joiden tulo matriisin kanssa on nolla.
Katso myös Nollakohtien joukko, Lineaarimuunnos, Vektoriavaruus, Homomorfismin ydin, Matriisin dimensio, Lineaarikuvaus.
Yhdeksän, 9 (engl. 9, Nine)
Yhdeksän on kolmas neliöluku. Se on kahden kuution summa: $9 = 1^{3} + 2^{3}$. Se on ainoa neliöluku, joka on kahden peräkkäisen kuution summa. Se on pienin pariton yhdistetty luku.
(8, 9) on ainoa alkulukupotenssien pari, jonka erotus on 1 ((2, 3):n ohella).
Se on neljäs onnenluku. Se on ykkösen jälkeen pienin onnenluku, joka on neliö.
Se on ykkösen jälkeen pienin Kaprekarin luku.
Yhdeksän on neljäs alikertomaluku.
$\phi(9) = 6$, $d(9) = 3$, $\sigma(9) = 13$.

Katso myös Kaprekarin luku, Onnekkaat luvut.
Yhdeksän pisteen ympyrä, Feuerbachin ympyrä (engl. Nine point circle, Nine-point circle, Feuerbach circle)
Kolmion sivujen keskipisteet, korkeusjanojen kantapisteet ja Eulerin pisteet sijaitsevat saman ympyrän kehällä. Tätä ympyrää kutsutaan Feuerbachin ympyräksi tai yhdeksän pisteen ympyräksi.
Katso myös Kolmion korkeusjana, Ympyrä, Kolmioon liittyvät ympyrät, Eulerin pisteet, Keskipiste.
Yhdeksänkymmentäluku (engl. Nineties)
Vuodet 1990--1999.
Yhden kerran, Kerran (engl. Once)
Yksi kerta.
Katso myös Frekvenssi.
Yhdenmuotoinen, Samanlainen, Similaari (engl. Similar)
Kahden tai useamman kuvion sanotaan olevan yhdenmuotoiset, jos ne ovat saman muotoiset, mutta eivät välttämättä saman kokoiset.
Yhdenmuotoisten kuvioiden vastinsivujen suhde on vakio ja vastinkulmat ovat yhtä suuret.
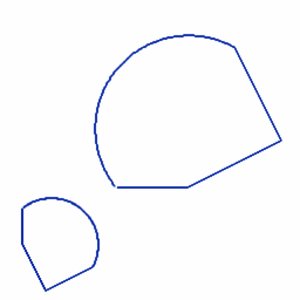
Katso myös Yhdenmuotoiset kolmiot, Yhtenevät kuviot, Kriteerejä kolmioiden yhdenmuotoisuudelle.
Yhdenmuotoiset kolmiot (engl. Similar triangles)
Kahden tai useamman kolmion sanotaan olevan yhdenmuotoisia, jos niiden kulmat ovat pareittain yhtä suuria. Tällöin kolmioiden kunkin vastinsivuparin sivujen pituuksien suhde on sama.
Katso myös Samanlainen, Yhdenmuotoinen, Similaari.
Yhdensuuntainen (engl. Parallel)
Täsmälleen samaan suuntaan osoittava. Aina samalla etäisyydellä oleva.
Katso myös Tangenttivektori, Suunnikas, Särmiön akseli, Kohtisuora, Vastakkaissuuntaiset.
Yhdiste (engl. Union)
Kahden tai useamman joukon yhdiste on joukko, joka saadaan ottamalla mukaan kaikki alkiot, jotka kuuluvat johonkin alkuperäisistä joukoista eikä mitään muita alkioita.
Joukkojen A ja B yhdiste on joukko, johon kuuluvat ne alkiot, jotka kuuluvat joko joukkoon A tai joukkoon B tai molempiin. Tätä joukkoa merkitään $ \mathrm{A} \cup \mathrm{B}. $
Katso myös Yhdisteen todennäköisyys, Funktio, Kuvaus, Joukkojen leikkaus, Leikkaus, Erillinen, Joukko, Numeroituva yhdiste, Pistevieras.
Yhdisteen todennäköisyys (engl. Probability of union)
Tapahtuman $ \mathrm{E}_1 \cup \mathrm{E}_2 $ todennäköisyys on \[ \mathrm{p(E}_1 \cup \mathrm{E}_2 ) = \mathrm{p(E}_1 ) + \mathrm{p(E}_2 ) - \mathrm{p(E}_1 \cap \mathrm{E}_2 ). \]
Katso myös Yhdiste, Erillisten tapahtumien todennäköisyys, Todennäköisyys.
Yhdistellä, Yhdistää (engl. Combine)
Liittää yhteen kaksi tai useampi suure. Sanaa voidaan myös käyttää tarkoittamaan kahden tai useamman joukon yhdisteen muodostamista. Kombinatoriikassa ja todennäköisyyslaskennassa sanaa voidaan käyttää tarkoittamaan kombinaatioiden muodostamista eli otoksen ottamista perusjoukosta.
Katso myös Laskutoimitus, Summa.
Yhdistelmä, Laskutoimitus, Yhdistetty funktio (engl. Composition)
Laskutoimitus on sääntö, joka liittää lukupariin luvun. Yhdistetty funktio eli kahden funktion yhdistelmä on funktio, joka muodostetaan soveltamalla funktioita peräkkäin eli ottamalla toisen funktion arvo ensimmäisen funktion argumentiksi.
Yhteenlasku ja kertolasku ovat peruslaskutoimituksia. Potenssiin korottaminen on laskutoimitus, joka liittää lukuihin $x$ ja $y$ luvun $x^y$.
Merkintä $e^{\sin x}$ tarkoittaa sinifunktion ja eksponenttifunktion yhdistettyä funktiota.
Funktioiden $f : A \to B$ ja $g : B \to C$ yhdistetty funktio on funktio $g \circ f : A \to C, (g \circ f)(a) = g(f(a)).$
Yhdistetty (engl. Composite)
Oliota, joka voidaan hajottaa pienemmiksi jaottomiksi olioiksi tai joka saadaan yhdistämällä kaksi tai useampia pienempiä olioita, kutsutaan yhdistetyksi. Esimerkiksi yhdistetty luku voidaan hajottaa alkulukujen tuloksi ja yhdistetty vektori saadaan laskemalla yhteen kaksi tai useampia vektoreita. Yhdistetty funktio saadaan soveltamalla peräkkäin kahta tai useampaa funktiota.
Yhdistetty funktio (engl. Composite function)
Funktioiden $f$ ja $g$ avulla muodostettua uutta funktiota $h(x) = f(g(x))$ kutsutaan yhdistetyksi funktioksi. Se on funktio, joka saadaan soveltamalla kahta tai useampaa funktiota peräkkäin.
Yhdistetty funktio, Yhdistelmä, Laskutoimitus (engl. Composition)
Laskutoimitus on sääntö, joka liittää lukupariin luvun. Yhdistetty funktio eli kahden funktion yhdistelmä on funktio, joka muodostetaan soveltamalla funktioita peräkkäin eli ottamalla toisen funktion arvo ensimmäisen funktion argumentiksi.
Yhteenlasku ja kertolasku ovat peruslaskutoimituksia. Potenssiin korottaminen on laskutoimitus, joka liittää lukuihin $x$ ja $y$ luvun $x^y$.
Merkintä $e^{\sin x}$ tarkoittaa sinifunktion ja eksponenttifunktion yhdistettyä funktiota.
Funktioiden $f : A \to B$ ja $g : B \to C$ yhdistetty funktio on funktio $g \circ f : A \to C, (g \circ f)(a) = g(f(a)).$
Yhdistetty luku (engl. Composite number)
Kokonaisluku, jolla on muitakin positiivisia tekijöitä kuin 1 ja luku itse. Yhdistetty luku on siis sellainen luku, joka ei ole alkuluku.
Katso myös Korkeasti yhdistetty luku, Alkuluku, Parillinen luku, Jaollisuus, Pseudoalkuluku, Fermat'n pseudoalkuluku.
Yhdistää, Yhdistellä (engl. Combine)
Liittää yhteen kaksi tai useampi suure. Sanaa voidaan myös käyttää tarkoittamaan kahden tai useamman joukon yhdisteen muodostamista. Kombinatoriikassa ja todennäköisyyslaskennassa sanaa voidaan käyttää tarkoittamaan kombinaatioiden muodostamista eli otoksen ottamista perusjoukosta.
Katso myös Laskutoimitus, Summa.
Yhteenlasku (engl. Addition, Add)
Tässä operaatiossa, jota merkitään symbolilla +, ensimmäisen suureen arvo kasvaa toisen suureen arvon verran. Yhteenlaskussa kaksi tai useampi yhteenlaskettava liitetään yhteen summaksi. Tämä on yhtäpitävää prosessin kanssa, jossa alkioiden kokonaismäärä kasvaa, kun joukkoja yhdistetään.
Katso myös Murtolukujen yhteenlasku, Vasta-alkio, Plus, Laskutoimitus, Vähennyslasku, Vähentäminen, Summa, Joukko, Binäärinen kuvaus, Kaksipaikkainen kuvaus, Ääretön summa.
Yhteenlasku (engl. Summation)
Summauksella tarkoitetaan prosessia äärettömän summan eli sarjan arvon löytämiseksi.
Yhteenlaskukaava (engl. Addition formula)
Trigonometrinen identiteetti, joka ilmaisee sellaisen trigonometrisen funktion, jonka argumentti on $x+y$ arvon sellaisten trigonometristen funktioiden avulla, joiden argumentteina ovat $x$ ja $y$. Esimerkiksi $\sin(x+y)=\sin x\cos y+\cos x\sin y$ on sinifunktion yhteenlaskukaava.
Katso myös Trigonometrinen identiteetti, $\cos(x+y)$, $\cot(x+y)$.
Yhteenlaskumenetelmä (engl. Addition method)
Menetelmä, jolla etsitään kahden tai useamman luvun tai suureen summa.
Katso myös Summa.
Yhteenlaskun neutraalialkio, Nolla-alkio (engl. Additive identity, Zero element)
Luku, joka ei muuta mitään lukua, jos se lasketaan yhteen tämän kanssa. Tavallisessa lukujärjestelmässä tämä luku on 0; siksi yhteenlaskun neutraalialkiota kutsutaan joskus nolla-alkioksi.
Alkio $e$, joka toteuttaa ehdon $a+e = e+a = a$ jokaiselle joukon alkiolle $a$. Joukoissa $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ yhteenlaskun neutraalialkio on 0. Ryhmän neutraalialkiota yhteenlaskun suhteen saatetaan kutsua myös nolla-alkioksi.
Katso myös Vasta-alkio, Neutraalialkio.
Yhteensopiva, Konsistentti (engl. Consistent)
Kahden tai useamman lauseen joukkoa sanotaan konsistentiksi, jos lauseet eivät ole keskenään ristiriidassa. On mahdollista, että kaikki lauseet ovat tosia samanaikaisesti.
Katso myös Looginen ominaisuus, Ristiriitainen.
Yhteinen (engl. Common)
Jokin on yhteinen, jos sillä on sama suhde joihinkin muihin asioihin. Esimerkiksi yhteinen juuri on useamman kuin yhden yhtälön juuri.
Yhteinen juuri (engl. Common root)
Luku, joka on useamman kuin yhden yhtälön juuri. Esimerkiksi $x=3$ on yhtälöiden $2x=6$ ja $(x-3)(x-5)=0$ yhteinen juuri.
Katso myös Yhtälön juuri.
Yhteinen jänne (engl. Common chord)
Jos kaksi ympyrää leikkaa toisensa pisteissä $A$ ja $B$, niin $AB$ on silloin ympyröiden yhteinen jänne.
Yhteinen monikerta (engl. Common multiple)
Luku $n$ on joidenkin lukujen yhteinen monikerta, jos n on jaollinen kaikilla näillä luvuilla.
Esimerkiksi 12 on 4:n ja 6:n yhteinen monikerta.
Katso myös Monikerta, Pienin yhteinen monikerta.
Yhteinen nimittäjä (engl. Common denominator)
Murtolukujen yhteinen nimittäjä on luku, jota voidaan käyttää näistä jokaisen nimittäjänä. Esimerkiksi 120 on murtolukujen 3/4, 4/5 ja 5/6 yhteinen nimittäjä, koska 3/4 = 90/120, 4/5 = 96/120 ja 5/6 = 100/120. Yhteinen nimittäjä mahdollistaa murtolukujen vertailun, yhteenlaskun ja vähennyslaskun.
Katso myös Murtolukujen yhteenlasku, Pienin yhteinen nimittäjä, Murtoluku, Nimittäjä.
Yhteinen tekijä (engl. Common divisor)
Luku $n$ on annettujen lukujen yhteinen tekijä, jos kaikki nämä luvut ovat $n$:llä jaollisia.
Esimerkiksi 6 on lukujen 12, 36 ja 60 yhteinen tekijä.
Yhteinen tekijä (engl. Common factor)
Tekijä, joka on yhteinen kahdelle tai useammalle eri luvulle eli luku, joka jakaa tasan jokaisen näistä eri luvuista.
Esimerkiksi 11 on lukujen 22, 110 ja 132 yhteinen tekijä.
Luku, joka on annetun lukujoukon jokaisen luvun tekijä.
Katso myös Suurin yhteinen tekijä, Tekijä.
Yhteisen nimittäjän etsiminen (engl. Find a common denominator)
Murtolukujen $\frac{a}{b}$, $\frac{c}{d}$, $\frac{e}{f}$, $\dots$ yhteinen nimittäjä voidaan löytää kertomalla keskenään kaikki nimittäjät $b$, $d$, $f$, $\dots$
Esimerkiksi murtolukujen $\frac{3}{4}$, $\frac{4}{5}$ ja $\frac{5}{6}$ yhteinen nimittäjä on $4 \cdot 5 \cdot 6 = 120$. Tämä ei ole pienin yhteinen nimittäjä, sillä myös $60$ on lukujen $4$, $5$ ja $6$ monikerta.
Katso myös Yhteinen nimittäjä.
Yhtenevä, Kongruentti (engl. Congruent)
Kaksi oliota ovat kongruentteja (tai yhteneviä), jos jokin yksinkertainen operaatio muuntaa ne toisikseen.
Yhtenevät kuviot voidaan muuntaa toisikseen kierrolla, peilauksella tai siirrolla.
Kongruentit luvut voidaan muuntaa toisikseen lisäämällä tai vähentämällä kustakin tietyn luvun monikerta.
Katso myös Yhtenevät kulmat.
Yhtenevä (ja samoin suuntautunut), Identtinen, Sama (engl. Identically distributed)
Kaksi asiaa ovat identtiset, jos ne ovat itse asiassa yksi ja sama asia.
Kaksi geometrista oliota ovat yhtenevät, jos niiden pisteet voi asettaa pareittain vastaamaan toisiaan siten, että vastinpisteiden etäisyydet kummassakin ovat samat. Yhtenevät kuviot saa toisistaan kierrolla, siirrolla, peilauksella tai näiden yhdistelmällä. Jos peilausta ei tarvita, sanotaan englantilaistyylisissä teksteissä toisinaan, että kuviot ovat identtiset. Tällöin ne ovat yhtenevät ja samoin suuntautuneet.
Siten kolmiulotteisilla olioilla identtisyys tarkoittaa samaa kuin yhtenevyys. Sen sijaan kaksi kaksiulotteista kuviota voivat olla yhteneviä, mutta eivät identtisiä, jos ne ovat toistensa peilikuvia, jolloin niitä ei saada toisistaan kiertämällä.
Katso myös Satunnaismuuttuja.
Yhtenevät kolmiot (engl. Congruent triangles)
Kaksi kolmiota ovat yhtenevät, jos niiden vastinsivut ja vastinkulmat ovat pareittain samat.
Katso myös Kolmio, Yhtenevät kuviot.
Yhtenevät kulmat (engl. Congruent angles)
Kulmat ovat yhtenevät, jos ne ovat samankokoiset.
Katso myös Kulma, Kongruentti, Yhtenevä.
Yhtenevät kuviot (engl. Congruent figures)
Kaksi kuviota tai kappaletta ovat yhtenevät, jos ne ovat identtiset kaikilla tavoilla sijaintia tai suunnistusta lukuun ottamatta eli ne voidaan saada toisistaan kierrolla, peilauksella tai siirrolla.
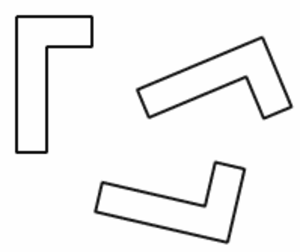
Katso myös Samanlainen, Yhdenmuotoinen, Similaari, Yhtenevät kolmiot.
Yhtenäinen (engl. Connected)
Topologinen avaruus $X$ on yhtenäinen, jos ei ole olemassa avoimia, epätyhjiä osajoukkoja $U,V \subset X$, joilla pätee $U \cap V=\emptyset$ ja $U \cup V = X$. Yhtenäisyys voidaan määritellä yhtäpitävästi myös seuraavilla tavoilla. Avaruus $X$ on yhtenäinen, jos ja vain jos ei ole olemassa jatkuvaa surjektiota $X \rightarrow \{0,1\}$, missä joukon $\{ 0, 1 \}$ topologia on diskreetti. Tai avaruus $X$ on yhtenäinen, mikäli sen ainoat sekä avoimet että suljetut osajoukot ovat $\emptyset$ sekä $X$.
Reaaliakselin yhtenäisiä osajoukkoja ovat välit (sekä rajoitetut että rajoittamattomat).
Vertaa käsitteisiin "polkuyhtenäinen" ja "murtoviivayhtenäinen".
Katso myös Kontinuumi, Hausdorff-avaruus, Hausdorffin avaruus, Lien ryhmä, Jatkumo.
Yhtenäinen verkko (engl. Connected graph)
Verkko, jossa mistä tahansa pisteestä päästään mihin tahansa toiseen pisteeseen verkon viivoja pitkin.
Katso myös Verkon solmu, Puu, Verkon viiva, Verkko.
Yhtyvä (engl. Coincident)
Kaksi asiaa ovat samanpaikkaisia, jos ne ovat samassa paikassa, ja samanarvoisia, jos niillä on sama arvo. Esimerkiksi kaksi suoraa yhtyvät, jos ne ovat samassa paikassa eli päällekkäin.
Yhtä kaukana (engl. Equidistant)
Samalla etäisyydellä, saman välimatkan päässä.

Yhtä todennäköinen (engl. Equally likely)
Kaksi tapahtumaa ovat yhtä todennäköisiä, jos pitkän ajanjakson kuluessa ne tapahtuvat yhtä usein.
Katso myös Todennäköisyys.
Yhtälö (engl. Equation)
Yhtälö on väite, jonka mukaan jokin luku tai lauseke on sama kuin jokin toinen luku tai lauseke. Esimerkiksi $3+x = 8$ ja $2x = x - 5$ ovat yhtälöitä.
Katso myös Diskriminantti, Algebra, Tason vektorimuotoinen yhtälö, Trigonometrinen yhtälö, Tuntematon, Yhtälöryhmä, Ratkaisu, Korvaaminen, Sijoittaminen, sijoitus, Yhtälöryhmä, Lineaarinen yhtälö, eqn, Kaava, Logaritmiyhtälö, Ympyrän yhtälö, Pallon yhtälö, Paraabelin yhtälö, Ellipsin yhtälö, Hyperbelin yhtälö, Kartioleikkauksen yhtälö, Differentiaaliyhtälö, Algebrallinen käyrä, Karakteristinen yhtälö, Besselin yhtälö, Karakteristinen yhtälö, Differenssiyhtälö, Diofantoksen yhtälö, Kartion yhtälö, Tason yhtälö, Palautuskaava.
Yhtälön juuri (engl. Root of an equation)
Sellainen yhtälössä esiintyvän tuntemattoman muuttujan arvo, jolla yhtälö on tosi.
Katso myös Diskriminantti, Yhteinen juuri, Algebran peruslause.
Yhtälöryhmä (engl. Simultaneous equations)
Jos on ratkaistava useampi kuin yksi yhtälö samanaikaisesti, näitä yhtälöitä kutsutaan yhtälöryhmäksi. Kahden tai kolmen yhtälön yhtälöryhmät voidaan usein ratkaista niin, että jokin tuntemattomista ratkaistaan muiden tuntemattomien avulla ja sijoitetaan tämä lauseke yhtälöihin. Tarvittaessa tätä toistetaan, kunnes jäljellä on yksi yhden tuntemattoman yhtälö. Useamman kuin kolmen yhtälön yhtälöryhmät on usein helpompi ratkaista matriisien avulla.
Katso myös Kahden tason leikkaus, Suorien leikkauspiste, Matriisi, Yhtälö, Suoran ja tason leikkauspiste.
Yhtälöryhmä (engl. System of equations)
Joukko yhtälöitä, jotka kaikki on toteutuvat yhtä aikaa. Usein fysikaalisia järjestelmiä tai prosesseja ei hallita yhdellä ainoalla yhtälöllä, vaan usean yhtä aikaa voimassa olevan yhtälön muodostamalla yhtälöryhmällä.
Katso myös Yhtälö.
Yhtäpitävä, Ekvivalentti (engl. Equivalent)
Kaksi väitettä $A$ ja $B$ ovat ekvivalentit, jos $A$:sta voidaan todistaa $B$ ja $B$:stä voidaan todistaa $A$.
Kaksi yhtälöä ovat ekvivalentit, jos niillä on täsmälleen sama ratkaisujoukko.
Kaksi normia ovat ekvivalentit, jos ne määrittelevät saman topologian. Toisin sanoen, $\| \cdot \|_1$ ja $\| \cdot \|_2$ ovat ekvivalentit, jos on olemassa sellaiset vakiot $c$ ja $d$, että $\| x \|_1 \le c\| x \|_2$ ja $\| x \|_2 \le d\| x \|_1$ kaikilla $x$. Äärellisulotteisen vektoriavaruuden kaikki normit ovat keskenään ekvivalentteja. Ääretönulotteisessa vektoriavaruudessa voi sen sijaan olla useita eri normeja.
Polkujen ekvivalenssi: Katso käsite "Polku".
Katso myös Samanarvoiset murtoluvut, Topologia.
Yhtäsuuri, Sama (engl. Equal)
Kaksi tai useampi luku ovat yhtä suuret, jos ne ovat samat tai niillä on sama arvo. Esimerkiksi \[ 18 = \frac{36}{2} = 9 + 9 = 20 - 2 = (4 \cdot 3) + 6. \]
Kaksi joukkoa ovat samat, jos niissä on samat alkiot.
Katso myös Likimäärin, Identiteetti, Suurempi tai yhtäsuuri kuin, Pienempi tai yhtäsuuri kuin, Tasasivuinen, Vertailtavissa olevat, Yhtäsuuruus.
Yhtäsuuruus (engl. Equality)
Väittämä kahdesta luvusta tai lukumäärästä, joita verrataan toisiinsa. Väittämä kertoo, että luvut tai lukumäärät ovat yhtä suuret tai niillä on sama arvo. Tällöin käytetään merkkiä $=$. Esimerkiksi $1+3 = 4$.
Katso myös Yhtäsuuri, Erisuuruus, Sama, Epäyhtälö.
Ykkösalkio, Kertolaskun neutraalialkio (engl. Multiplicative identity)
Luku, joka ei muuta mitään lukua, jos sillä kerrotaan tämä luku. Tavallisessa lukujärjestelmässä tämä luku on 1.
Alkio $e$, joka toteuttaa ehdon $ae = ea = a$ jokaisella joukon alkiolla $a$. Joukoissa $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ kertolaskun neutraalialkio on 1.
Katso myös Käänteisalkio, Kertolasku, Neutraalialkio, Kertolaskun käänteisalkio, Käänteisluku.
Yksi, 1 (engl. 1, One, Unity)
Eri tulkintojen mukaan yksi on pienin tai toiseksi pienin luonnollinen luku.
Yksi on kertolaskun neutraalialkio: yhdellä kertominen ei muuta lukua.
Yksi on peräkkäisten luonnollisten lukujen erotus.
Yksi on pienin neliöluku, kuutioluku jne.
Yksi ei ole alkuluku.
Yksi yhteen kuvaus, Yksi yhteen vastaavuus (engl. One to one mapping, One to one correspondence)
Kahden joukon välillä vallitsee yksi yhteen vastaavuus, jos ne voidaan kuvata toisilleen yksi yhteen kuvauksella.
Kuvaus joukkojen A ja B välillä on yksi yhteen kuvaus eli bijektio, jos siinä jokaista joukon A alkiota vastaa täsmälleen yksi joukon B alkio ja jokaista joukon B alkiota vastaa täsmälleen yksi joukon A alkio.
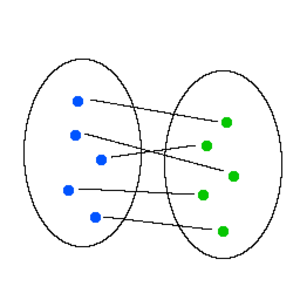
Katso myös Kuvaus, Funktio, Kuvaus, Joukko, Bijektio, Funktio.
Yksihuippuinen (engl. Unimodal)
Jakauma, jossa on vain yksi moodi. Luokiteltu aineisto on yksihuippuinen, mikäli siinä on vain yksi maksimiluokka (luokka, jossa on enemmän havaintoja kuin ympäröivissä luokissa). Vertaa: Kaksihuippuinen
Yksikkö (engl. Unit)
Esimerkiksi metri on pituuden yksikkö ja kilogramma massan yksikkö.
Kokonaislukujen renkaassa yksiköitä ovat luvut 1 ja -1.Luonnontieteissä yksiköllä tarkoitetaan standardia, johon vertaamista käytetään jonkin suureen mittaamiseen.
Algebrassa yksikkö-sanalla tarkoitetaan renkaan R kääntyvää alkiota eli sellaista alkiota $ x \in R $ , että on olemassa $ y \in R $ , jolla $ x \cdot y=1 $ .
Katso myös Yksikköpallo, Yksikkökuutio, Pinta-alayksikkö, SI-yksiköt, MKSA-järjestelmä.
Yksikkökuutio (engl. Unit cube)
Kuutio, jonka sivun pituus on 1. Yleensä sen kärjet sijaitsevat pisteissä $(0,\,0,\,0)$, $(0,\,0,\,1)$, $(0,\,1,\,0)$, $(0,\,1,\,1)$, $(1,\,0,\,0)$, $(1,\,0,\,1)$, $(1,\,1,\,0)$ ja $(1,\,1,\,1)$.
Katso myös Yksikkö, Kuutio, Säännöllinen heksaedri.
Yksikkömatriisi, Identiteettimatriisi (engl. Unit matrix, Identity matrix)
Lävistäjämatriisi, jonka kaikki päälävistäjän alkiot ovat ykkösiä (ja kaikki muut alkiot siis nollia). Yksikkömatriisia merkitään symbolilla $I$.
Koska yksikkömatriisi kerrottuna millä tahansa matriisilla $A$ antaa tulokseksi matriisin $A$, yksikkömatriisin voidaan ajatella olevan identiteettioperaattori tai neutraalialkio.
Katso myös Unitaarinen matriisi, Neutraalialkio, Identtinen laskutoimitus, Lävistäjämatriisi.
Yksikkömurtoluku (engl. Unit fraction)
Murtoluku, jonka osoittaja on 1.
Katso myös Murtoluku.
Yksikkönormaalivektori (engl. Unit normal, Unit normal vector)
Normaalivektori, jonka pituus on 1.
Katso myös Yksikkövektori, Normaalivektori.
Yksikköpallo (engl. Unit ball)
Pallo, jonka säde on 1. Yleensä 1-säteinen pallo, jonka keskipiste on origossa eli joukko $B = \{x \in \mathbf{R}^{3} : |x| \lt 1\}$.
Yksikkötangenttivektori (engl. Unit tangent, Unit tangent vector)
Tangenttivektori, jonka pituus on 1.
Katso myös Yksikkövektori, Tangenttivektori.
Yksikkövektori (engl. Unit vector)
Vektori, jonka pituus on 1. Vektorin $\overline{r}$ kanssa samansuuntainen yksikkövektori on vektori $\frac{1}{|\overline{r}|}\overline{r}$.
Katso myös Nollavektori, Vektori, Yksikkönormaalivektori, Yksikkötangenttivektori, $i$, $j$, Vektorin normi.
Yksikköympyrä (engl. Unit circle)
Yksikköympyrän yhtälö (engl. Equation of unit circle)
Origokeskisen yksikköympyrän (eli $1$-säteisen ympyrän) yhtälö on \[ x^{2}+y^{2}=1. \]
Katso myös Ympyrän yhtälö.
Yksikäsitteinen (engl. Unique)
Jokin on yksikäsitteinen, jos niitä on tai voi koskaan olla olemassa vain yksi.
Yksikäsitteinen tekijöihin jako (engl. Unique factorisation)
Luvun yksikäsitteinen tekijöihin jako tarkoittaa tapaa kirjoittaa tuo luku alkulukujen ja alkulukujen potenssien tulona kasvavassa järjestyksessä. Esimerkiksi luvun 360 yksikäsitteinen tekijöihin jako on $2^{3} \cdot 3^{2} \cdot 5$.
Sitä sanotaan yksikäsitteiseksi, koska jokaisella luvulla on vain yksi tällainen tekijöihin jako.Katso myös Ominaisuus, Määrite.
Yksikäsitteisen tekijöihinjaon alue, UFD (engl. Unique factorisation domain)
Kokonaisalue $R$ on yksikäsitteisen tekijöihinjaon alue, jos kaikilla $a \in R$, $a \neq 0$ on tekijöihinjako $a = u p_1 \dots p_k$, joka on yksikäsitteinen lukuunottamatta yksikköalkiota $u$ ja alkualkioiden $p_1, \dots, p_k$ järjestystä. (Yksikäsitteisen tekijöihinjaon alueessa alkualkion ja jaottoman alkion käsitteet ovat samat.)
Jokainen pääideaalialue on UFD, mutta ei toisin päin: Esimerkiksi $Z[X]$ on UFD mutta ei pääideaalialue, sillä $\langle 2, X, \rangle$ ei ole pääideaali.
Katso myös Pääideaalialue, Kokonaisalue, Gaussin kokonaisluvut, Gaussin luvut.
Yksinkertainen ryhmä (engl. Simple)
Ryhmä $G$ on yksinkertainen, mikäli $\{e\}$ ja $G$ ovat sen ainoat normaalit aliryhmät.
Katso myös Normaali aliryhmä.
Yksipaikkainen (engl. Unary)
Yksipaikkainen operaatio on operaatio, joka kohdistuu yhteen alkioon. Tällaisia ovat esimerkiksi vastaluvun tai itseisarvon muodostaminen.
Katso myös Kantaluku.
Yksitoista, 11 (engl. 11, Eleven)
11 on viides alkuluku.
$ \phi(11) = 10, \quad d(11)=2, \quad \sigma(11) = 12. $

Katso myös Alkuluku.
Yksivaippainen hyperboloidi (engl. Hyperboloid of one sheet)
Pyörähdyspinta, joka syntyy hyperbelin pyörähtäessä sen polttopisteet yhdistävän janan puolittajasuoran ympäri. Yksivaippaisen hyperboloidin yhtälö on \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1, \] missä $a, b, c$ ovat nollasta eroavia vakioita.
Katso myös Pyörähdyspinta.
Yleistetty tulo (engl. Extended product)
Merkinnällä $\prod_{i=1}^{n} x_i$ tarkoitetaan tuloa $x_{1} \cdot x_{2} \cdot \ldots \cdot x_{n}$.
Katso myös Tulo, Summamerkki, Merkintätapa, Notaatio.
Ylinumeroituva (engl. Uncountable, Non-denumerable)
Esimerkiksi reaalilukujen joukko on ylinumeroituva, kuten Georg Cantor on todistanut.
Joukko $J$ on ylinumeroituva, jos se on niin suuri, että sen alkioita ei voida numeroida. Tämä merkitsee täsmällisesti sitä, että ei ole olemassa surjektiivista kuvausta luonnollisten lukujen joukolta joukolle $J$.
Katso myös Cantor, Lukematon, Cantorin joukko, Numeroituva.
Ylittää (engl. Exceed)
Olla suurempi kuin jokin.
Yläindeksi (engl. Superscript)
Pieni kirjain tai numero, joka kirjoitetaan ylemmäksi kuin tavalliset merkit. $^{Kuten tämä.}$
Katso myös Merkintätapa, Notaatio.
Yläkolmiomatriisi (engl. Upper triangular matrix)
Matriisi, jossa kaikki päälävistäjän alapuolella olevat alkiot ovat nollia.
Katso myös Päälävistäjä, Kolmiomatriisi, LU-hajotelma, LDU-hajotelma.
Yläraja (engl. Upper bound)
Reaaliluku $n$ on annetun reaalilukujoukon $S$ yläraja, jos $n$ on suurempi tai yhtä suuri kuin jokainen joukon $S$ alkio.
Katso myös Supremum, Pienin yläraja, Reaaliluku.
Ympyrä (engl. Circle)
Ympyrä on niiden pisteiden muodostama joukko, jotka ovat samalla etäisyydellä tietystä kiinteästä pisteestä, jota kutsutaan ympyrän keskipisteeksi.
Ympyrä, jonka säde on $r$ ja keskipiste $C$, on niiden pisteiden joukko, joiden etäisyys pisteestä $C$ on täsmälleen $r$.
Jos ympyrän säde on $r$, niin ympyrän pinta-ala saadaan kaavasta $\pi \mathrm{r}^2$ ja ympyrän kehän pituus saadaan kaavasta $2\pi r$.

Katso myös Kaari, Arc, Ympyrän pinta-ala, Tasainen monitahokas, Kohtisuorasti leikkaavat ympyrät, Lemoinen ympyrä, Sisään piirretty ympyrä, Pisteen potenssi ympyrän suhteen, Sini, Ura, Isoympyrä, Piirakkadiagramma, Ellipsi, Lieriö, Yksikköympyrä, Tangentti, Pallo, Puoliympyrä, Segmentti, Sektori, Säde, Kiekko, Halkaisija, Kosini, Ympyrän keskipisteen määrittäminen, Monikulmion ympäri piirretty ympyrä, Jänne, Johnsonin lause, Euklidinen geometria, Ympyrän kehä, Kolmioon liittyvät ympyrät, Ympyrän keskipiste, Harppi, Oskuloiva ympyrä, Pii, $\pi$, Sekantti, Ympyräruuvikierre, Koaksiaaliset ympyrät, Konsyklinen, Kartioleikkaus, Kierto, Ekliptika, Episykli, Trokoidi, Feuerbachin ympyrä, Yhdeksän pisteen ympyrä, Kuvio.
Ympyräkartio (engl. Circular cone)
Kartio, jonka pohja on ympyrä.
Katso myös Kartio.
Ympyrän kehä (engl. Circumference)
Ympyrän reuna (piiri) tai ympyrän reunan pituus.
Katso myös Piiri, Ympyrä, Jänne, Ympyrän kehän pituus, Sekantti, Konsyklinen.
Ympyrän kehän pituus (engl. Find the length of the circumference of a circle)
Ympyrän kehän pituus $C$ lasketaan kaavalla $C = 2\pi r$ eli ympyrän säde $r$ kerrotaan luvulla $\pi$ ja näiden tulo kerrotaan luvulla 2.
Katso myös Mitata, Mitta, Ympyrän kehä, Pii, $\pi$.
Ympyrän keskipiste (engl. Centre of a circle)
Se ympyrän tason piste, joka on yhtä etäällä jokaisesta ympyrän kehän pisteestä.
Katso myös Keskipiste, Ympyrä.
Ympyrän keskipisteen määrittäminen (engl. Construct the centre of a circle)
Annetun ympyrän keskipiste määritetään seuraavasti. Valitaan ympyrän kehältä kolme pistettä, $A$, $B$ ja $C$. Piirretään janojen $AB$ ja $AC$ keskinormaalit. Keskinormaalit leikkaavat toisensa pisteessä $D$, joka on annetun ympyrän keskipiste. Vertaa tätä menettelyä annetun kolmion ympäri piirretyn ympyrän konstruoimiseen.
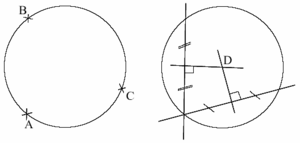
Katso myös Ympyrä, Konstruktio, Konstruointi.
Ympyrän parametrisoitu yhtälö (engl. Parametric equation of a circle)
Jos $(a,b)$ on ympyrän keskipiste ja $r$ säde, ympyrällä on parametrisoitu yhtälö $ x=a+ r \cos \theta , y = b+ r \sin \theta . $
Katso myös Ympyrän yhtälö.
Ympyrän piirtäminen (engl. Construct a circle)
Ympyrä piirretään harpin avulla. Valitaan piste ja asetetaan harpin kärki siihen. Siirretään kynää täysi kierros valitun pisteen ympäri liikuttamatta harpin kärkeä valitusta pisteestä.
Katso myös Ympyrän piirtäminen kolmen pisteen kautta, Konstruktio, Kolmion ympäri piirretyn ympyrän muodostaminen, Konstruointi.
Ympyrän piirtäminen kolmen pisteen kautta (engl. Construct a circle through three given points)
Jos on annettu kolme pistettä $A$, $B$ ja $C$ ja on piirrettävä ympyrä, joka kulkee kaikkien kolmen pisteen kautta, toimitaan seuraavasti. Piirretään janojen $AB$ ja $BC$ keskinormaalit. Etsitään piste $O$, jossa keskinormaalit leikkaavat toisensa. Piirretään harpin avulla ympyrä, jonka keskipiste on $O$ ja joka kulkee pisteen $A$ kautta. Tämä ympyrä kulkee myös pisteiden $B$ ja $C$ kautta.
Katso myös Ympyrän piirtäminen, Keskinormaalin piirtäminen, Suorien leikkauspiste.
Ympyrän pinta-ala (engl. Circle area, Area of circle, Area of a circle)
Jos ympyrän säde on $r$, sen pinta-ala saadaan kaavasta $A = \pi r^{2}$ eli ympyrän säde korotetaan toiseen potenssiin ja kerrotaan tulos luvulla $\pi$.
Katso myös Ympyrä, Säde, Ellipsin pinta-ala, Pii, $\pi$.
Ympyrän segmentin pinta-ala (engl. Area of segment)
$r$-säteisen ympyrän segmentin pinta-ala lasketaan kaavalla $$\frac{1}{2} r^2 (\alpha-\sin(\alpha)),$$ missä $\alpha$ on keskuskulma radiaaneissa.
Ympyrän sektorin massakeskipiste (engl. Centre of mass of a sector)
$r$-säteisen ympyrän sektorin, jonka keskuskulman suuruus (radiaaneissa) on $2\theta$, massakeskipiste sijaitsee sektorin symmetria-akselilla ja sen etäisyys ympyrän keskipisteestä on \[\frac{2r sin \theta}{3\theta}.\]
Katso myös Puoliympyrän massakeskipiste, Massakeskipiste, Painopiste, Tasoalueen massakeskipiste.
Ympyrän sektorin pinta-ala (engl. Area of a circular sector)
Jos ympyrän säde on $r$ ja sektorin keskuskulma on $\theta$ astetta, niin sektorin pinta-ala on $\pi r^2 \frac{\theta}{360}$. Jos $\theta$ on ilmaistu radiaaneina, niin silloin sektorin pinta-ala on $\frac{r^{2} \theta}{2}$.
Katso myös Sektori.
Ympyrän yhtälö (engl. Equation of circle, Circle equation)
Jos ympyrän keskipiste on $(a,b)$ ja säde on $r$, niin sen yhtälö on \[ (x-a)^2+(y-b)^2 = r^2. \] Jos ympyrän yhtälö on $x^2+y^2+2gx+2fy+c = 0$, sen keskipiste on $(-g,-f)$ ja säde on $\sqrt{g^2+f^2-c}$.
Katso myös Ympyrän parametrisoitu yhtälö, Konsyklisten pisteiden koordinaatit toteuttavat ympyrän yhtälön, Yhtälö, Yksikköympyrän yhtälö.
Ympyränkaaren massakeskipiste (engl. Centre of mass of an arc)
Ympyränkaaren, jota vastaavan keskuskulman suuruus (radiaaneissa) on $2\theta$, massakeskipiste sijaitsee kaaren symmetria-akselilla ja sen etäisyys ympyrän keskipisteestä on $\frac{r sin \theta}{\theta}$, missä $r$ on ympyrän säde.
Katso myös Puoliympyrän kaaren massakeskipiste, Massakeskipiste, Painopiste.
Ympyrärenkaan ala (engl. Area of annulus, Area of a ring)
Renkaan, jota rajoittavat sisäkkäiset toisiaan leikkaamattomat $x$- ja $y$-säteiset ympyrät, $x>y$, pinta-ala on $\pi (x^{2}-y^{2})$.
Ympyräruuvikierre (engl. Circular helix)
Ympyräruuvikierre syntyy, kun janaa kierretään lieriön ympäri ja samalla kuljetaan alas- tai ylöspäin suhteessa kartion korkeusjanaan. Säde pysyy tällöin koko ajan samana. Kartioruuvikierre taas syntyy, kun janaa kierretään kartion ympäri. Tällöin säde muuttuu koko ajan.
Katso myös Ympyrä, Säde, Ruuvikierre, Ruuviviiva.
Ympyröiden pakkaaminen (engl. Circle packing)
Tihein tapa pakata keskenään yhtäsuuria ympyröitä tasoon on tehdä kuvio, jossa ympyröiden keskipisteet ovat kuusikulmioruudukon (heksaruudukon) ruutujen keskipisteissä, ja jokainen ympyrä koskettaa kuutta muuta. Tällöin ympyröiden peittämä osuus tasosta on \[ \frac{\pi}{2 \sqrt{3}}. \]
Katso myös Pallojen pakkaaminen.
Ympäri piirretyn ympyrän säde (engl. Circumradius)
Kolmion tai minkä tahansa muun kuvion ympäri piirretyn ympyrän säde.
Katso myös Säde.
Ympäripiirretty pallo (engl. Circumsphere)
Pallo, joka koskettaa monitahokkaan kaikkia kärkiä. Jokaisen säännöllisen monitahokkaan, kuten esimerkiksi tetraedrin, ympäri voidaan piirtää tällainen pallo.
Katso myös Tetraedri, Pallo, Säännöllinen monitahokas.
Ypsilon (engl. Upsilon)
Kreikkalainen kirjain $ \upsilon $ (pieni kirjain) tai $ \Upsilon $ (iso kirjain), äännetään samoin kuin suomen y.

Katso myös Kreikkalaiset kirjaimet.
Yritys ja erehdys (engl. Trial and error, Trial and improvement)
Eräs tapa käsitellä vaikeita numeerisia ongelmia on arvata ratkaisu, katsoa mikä siinä on väärin, käyttää tätä tietoa uuden arvauksen tekemiseksi, ja niin edelleen.
Katso myös Perustelu.