Matematiikan verkkosanakirja

L'Hospitalin sääntö \[ \lim_{ \mathrm{x} \to \mathrm{a}} \frac {\mathrm{f(x)}}{\mathrm{g(x)}} = \frac{\displaystyle{\lim_{\mathrm{x} \to \mathrm{a}}}\frac{\mathrm{df}}{\mathrm{dx}}} {\displaystyle{\lim_{\mathrm{x} \to \mathrm{a}}}\frac{\mathrm{dg}}{\mathrm{dx}}} \] on hyödyllinen osamäärän raja-arvon löytämiseksi, jos sekä osoittaja että nimittäjä lähestyvät rajalla nollaa.

Esimerkiksi \[ \lim_{\mathrm{x} \to 1} \frac {\mathrm{x}^2 - 1}{\mathrm{x}^2 - 3 \mathrm{x} + 2} = \frac{\displaystyle{\lim_{\mathrm{x} \to 1}}2 \mathrm{x}} {\displaystyle{\lim_{\mathrm{x} \to 1}}2 \mathrm{x} - 3} = \frac{2}{-1} = -2 \]

Jos $f(a)=g(a)=0$ ja $g^{\prime}(a) \neq 0$, niin \[ \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{f^{\prime}(a)}{g^{\prime}(a)}. \]

Katso myös Lause, Sääntö, Bernoulli Johann.

Tehdä jokin suuremmaksi tai pitemmäksi. Usein sillä tarkoitetaan janan jatkamista suoraksi, jonka osa kyseinen jana on. Myös funktion määrittelyalueen suurentamista sanotaan funktion laajentamiseksi tai jatkamiseksi.

Katso myös Konstruktio, Konstruointi.

Tapa esittää havaintojoukon (datan) jakauma. Järjestetään havainnot nousevaan järjestykseen ja piirretään niiden alle laatikko, jonka vasen reuna on ensimmäisen kvartaalin kohdalla ja oikea reuna kolmannen kvartaalin kohdalla. Laatikon sisälle piirretään pystyviiva mediaanin kohdalle. Lopuksi laatikon sivuilta piirretään janat ("viikset") pienimpään ja suurimpaan havaintoon.

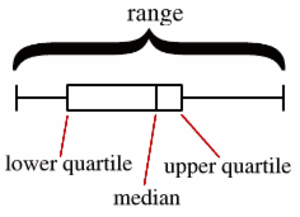
Katso myös Kaavio, Mediaani, Kvartiili, Neljännespiste, Kuvajoukko, Funktion kuvajoukko.

Mikä tahansa tapa peittää taso tai tason osa kokonaan käyttämällä laattoja, jotka voivat olla identtisiä tai epäidenttisiä. Usein tehdään palapelejä laatoittamalla tietty alue tietynmuotoisilla laatoilla.

Katso myös Laatta, Laatoitus, Tessellaatio.

Tason peittäminen kuvioilla, jotka eivät mene päällekkäin. On olemassa kolme mahdollista tason laatoitusta, joissa käytetään identtisiä säännöllisiä monikulmioita. Nämä ovat säännöllisistä kuusikulmioista, neliöistä ja tasasivuisista kolmioista koostuvat laatoitukset. Käyttämällä erilaisia säännöllisiä monikulmioita tai epäsäännöllisiä kuvioita saadaan paljon useampia laatoituksia. Joillakin laatoituksilla on kiertosymmetriaa, mutta ei kaikilla.

Katso myös Arkhimedeen laatoitus, Laatoitus.

Yksi kuvioista, joita käytetään tason peittämiseksi kokonaan.

Katso myös Laatoitus, Kuvio.

Funktion $f$ Taylorin sarjan jäännöstermin $R_{n}$ lauseke voidaan esittää muodossa \[ R_n = \frac{1}{n!} x^n f^{(n)}(a + \theta x), \] missä $\theta$ on välillä $(0,1)$.

Katso myös Taylorin sarja, Virhetermi, Jäännöstermi.

Äärellisen ryhmän $G$ aliryhmän $H$ kertaluku jakaa ryhmän $G$ kertaluvun.

Katso myös Jakaa, Lause, Ryhmä, Aliryhmä, Ryhmän kertaluku.

Lagrangen polynomi on $ P_n (x) = \sum L_r (x) f(x) , $ missä $ L_r (x) = \prod _{i=1, i \neq r} ^{n} \frac{x - x_i}{x_r - x_i } . $

Katso myös Polynomi.

Algoritmi, joka lajittelee annetun joukon alkioita jonkin kriteerin mukaiseen järjestykseen, esimerkiksi suuruuden mukaiseen järjestykseen.

Katso myös Algoritmi.

Operaattoria $\Delta \phi = \nabla \cdot (\nabla \phi) = \nabla^2 \phi$ kutsutaan Laplacen operaattoriksi. Kolmessa ulottuvuudessa se on \[ \nabla^2 \phi = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} + \frac{\partial^2 \phi}{\partial z^2}. \]

Katso myös Differentiaalioperaattori, Divergenssi, Laplacen yhtälö, Poissonin yhtälö.

Laplacen yhtälö on \[ \Delta f = \nabla^2 f = 0. \] Se on Poissonin yhtälön erikoistapaus. Kahdessa ulottuvuudessa Laplacen yhtälö voidaan kirjoittaa \[ \frac{\partial^2 f}{\partial x^2 } + \frac{\partial^2 f}{\partial y^2} = 0 . \]

Katso myös Laplacen operaattori, Poissonin yhtälö.

Lausekkeen arvon laskeminen tarkoittaa sen numeerisen arvon määrittämistä. Tämä arvo voidaan ilmaista funktioiden, kuten $\sin$ tai $\log$, avulla.

Selvittää äärellisen joukon alkioiden lukumäärä.

Laskemisen voi tehdä siten, että luettelee luonnollisia lukuja luvusta yksi alkaen samalla kun käy läpi joukon alkiot. Näin tulee samalla numeroineeksi joukon alkiot eli asettaneeksi ne yksi-yhteen -vastaavuuteen jonkin luonnollisten lukujen joukon alkusegmentin kanssa. Joissakin tapauksissa voi myös äärettömän joukon alkiot numeroida periaatteessa samalla tavoin, jolloin saadaan yksi-yhteen -vastaavuus niiden ja kaikkien luonnollisten lukujen välillä.

Neliö on kuvio, jossa on neljä yhtä pitkää sivua ja neljä suoraa kulmaa.

Laskemme neliön jostakin kertomalla sen itsellään eli korottamalla sen toiseen potenssiin.

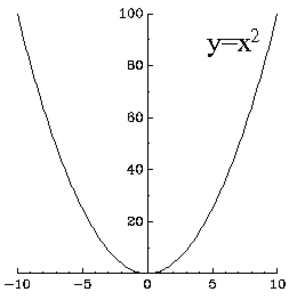
Katso myös Potenssiin korottaminen, Neliöluku, Neliöjuuri.

Lukujen avulla selvitetty ongelman ratkaisu.

Otos on samankokoinen kuin populaatio (perusjoukko). Toisin sanoen, jokainen populaation jäsen on mukana otoksessa.

Matematiikan osa-alue, joka käsittelee lukuja ja niillä tehtäviä laskutoimituksia.

Katso myös Laskin, Murtoluku, Alkeismatematiikka, Luonnollinen luku, Aritmetiikan peruslause.

Yleensä elektroniikkaa hyödyntävä laite laskutoimitusten suorittamiseksi nopeasti. Graafinen laskin pystyy myös tuottamaan funktioiden kuvaajia.

Katso myös Aritmetiikka, Laskento, Muistinäppäin, Graafinen laskin, Etumerkinvaihtonäppäin, Geometria.

Lukujen avulla selvitetty ongelman ratkaisu.

Päässälaskuun sekä paperilla laskemiseen pystyvä; kuten luku- tai kirjoitustaitoinen, mutta numeroilla sanojen sijasta toimiva.

Toimitus, jossa yhdestä tai useammasta joukon alkiosta muodostetaan jonkin säännön mukaan uusi saman tai eri joukon alkio. Kertominen, jakaminen, yhteenlaskeminen ja vähentäminen ovat erityisiä laskutoimituksia, joita käytetään lukujoukkojen alkioille. Kaksi lukua voidaan yhdistää soveltamalla jotakin näistä laskutoimituksista kolmannen luvun tuottamiseksi. Numerot 8 ja 2 kertomalla saadaan tulokseksi 16, jakamalla saadaan tulokseksi 4 (tai 1/4) yhteenlaskemalla saadaan tulokseksi 10 ja vähentämällä saadaan tulokseksi 6 (tai -6, miinus kuusi). Numeroiden järjestys laskutoimituksia tehtäessä on hyvin tärkeä.

Katso myös Yhteenlasku, Kertolasku, Potenssiin korottaminen, Identtinen laskutoimitus, Jakolasku, Kommutoida, Vähennyslasku, Vähentäminen, Funktio, Kuvaus, Yhdistää, Yhdistellä, Logaritmi, Eksponenttifunktio, Juuri, Antikommutatiivinen, Binäärinen kuvaus, Sivuluokka, Jakaminen, Kaksipaikkainen kuvaus.

Laskutoimitus on sääntö, joka liittää lukupariin luvun. Yhdistetty funktio eli kahden funktion yhdistelmä on funktio, joka muodostetaan soveltamalla funktioita peräkkäin eli ottamalla toisen funktion arvo ensimmäisen funktion argumentiksi.

Yhteenlasku ja kertolasku ovat peruslaskutoimituksia. Potenssiin korottaminen on laskutoimitus, joka liittää lukuihin $x$ ja $y$ luvun $x^y$.

Merkintä $e^{\sin x}$ tarkoittaa sinifunktion ja eksponenttifunktion yhdistettyä funktiota.

Funktioiden $f : A \to B$ ja $g : B \to C$ yhdistetty funktio on funktio $g \circ f : A \to C, (g \circ f)(a) = g(f(a)).$

Lattia- eli kokonaisosafunktion arvo luvulla x on suurin kokonaisluku, joka ei ole suurempi kuin x. Lattiafunktiolle käytetään merkintää $ \lfloor x \rfloor $ .

Katso myös Funktio, Kuvaus, Kattofunktio, Ominaisuus, jonka arvot ovat jatkuvia.

Matemaattinen väittämä, joka on todistettu oikeaksi.

Katso myös Puoliympyrän sisältämä kulma, Arkhimedeen lause, Jännenelikulmion kulmat, Jännenelikulmion vastakkaiset kulmat ovat supplementtikulmia, Pisteen potenssi ympyrän suhteen, Lisääminen puolittain epäyhtälöön, Eksponenttifunktion yhteenlaskukaava, Eulerin yhtälö, Peräkkäisten lukujen tulo, Epäyhtälön kertominen puolittain, Inkluusion ja ekskluusion periaate, Geometrinen todistus, Otaksuma, Tshebyshevin epäyhtälö, Peräkkäisten lukujen summa, Pythagoraan lause, Napoleonin lause, Samaa kaarta vastaavat kehäkulmat, Kahden neliön erotus, Sääntö, Jordanin käyrälause, Johnsonin lause, Etäisyyskaava, Analyyttisen jatkeen yksikäsitteisyys, Sylowin lause, Dirichlet'n lause, Riemannin poistuvan erikoispisteen lause, Ryhmäteorian isomorfialauseet, Väliarvolause, Rollen lause, Analyysin peruslause, Hölderin epäyhtälö, L'Hospitalin sääntö, Kyyhkyslakkaperiaate, Binomikaava, Alkulukulause, Aritmeettisen ja geometrisen keskiarvon välinen epäyhtälö, Kulmanpuolittajalause, Aubelin lause, Bangin lause, Bayesin kaava, Bayesin lause, Binomikerrointen laskusääntöjä, Cauchyn kriteerio, Cauchyn ryhmälause, Cauchy-Schwarzin epäyhtälö, Cauchyn integraalilause, Cavalierin lause, Cayley'n lause, Cayley-Hamiltonin lause, Keskeinen raja-arvolause, Cevan lause, Kiinalainen jäännöslause, Konjektuuri, Konsyklisten pisteiden koordinaatit toteuttavat ympyrän yhtälön, Lokeroperiaate, Divergenssilause, Gaussin lause, Greenin lause, Hermiittisen matriisin ominaisarvot, Ortogonaalisen matriisin ominaisarvot, Reaalisen symmetrisen matriisin ominaisarvot, Unitaarisen matriisin ominaisarvot, Vinosymmetrisen matriisin ominaisarvot, Eulerin kaava, Eulerin lause, Fermat'n suuri lause, Fermat'n pieni lause, Fermat'n viimeinen lause, Fermat-Eulerin lause, Neljän värin lause, Algebran peruslause, Aritmetiikan peruslause, Hoehnin lause, Bolzanon lause, Piin irrationaalisuus, Luvun 2 neliöjuuri on irrationaalinen, Lagrangen lause, Liouvillen lause, Menelausin lause.

Mikä tahansa numeroiden tai symbolien yhdistelmä, johon voidaan liittää merkitys. Esimerkiksi $x^2$ ja $x^2+y^2$ ovat lausekkeita, mutta $x^2+$ ei ole.

Jos muuttuja ilmaistaan toisten muuttujien avulla, niin tätä kutsutaan kyseisen muuttujan lausekkeeksi. Esimerkiksi $x = 2yz +12y^2$ on muuttujan $x$ lauseke.

Katso myös Likiarvo, Diskriminantti, Algebra, Differentiaali, Juurilauseke, Juurrettava, Polynomi, Identiteetti, Derivoida, Kerroin, Vakiotermi, Termi, Binomi, Integraali, Derivaatta, Monomi, Bilineaarinen lauseke, Kanoninen muoto, Rationaalilauseke, Rationaalifunktio.

Lausua jokin asia tietyllä tavalla tarkoittaa löytää tapa kirjoittaa tai sanoa kyseinen asia käyttämällä numeroita tai merkkejä.

Jos neliömatriisi $A$ voidaan esittää tulona $A = LDU$, missä $L$ on alakolmiomatriisi, $D$ on lävistäjämatriisi ja $U$ on yläkolmiomatriisi, kutsutaan tätä tuloa matriisin $A$ LDU-hajotelmaksi.

Katso myös Alakolmiomatriisi, Lävistäjämatriisi, Yläkolmiomatriisi, Neliömatriisi, Hajoittaa matriisi.

Henri Léon Lebesgue (1875-1941) oli ranskalainen matemaatikko. Hänet muistetaan Lebesguen mitan ja integraalin käsitteistä. Hän kirjoitti myös trigonometrisistä sarjoista, potentiaaliteoriasta ja topologiasta.

Legendren differentiaaliyhtälö on tavallinen toisen kertaluvun differentiaaliyhtälö \[ (1 - x^2) \frac{d^2 y}{dx^2} - 2x \frac{dy}{dx} + n(n+1)y = 0, \] missä $n$ on reaaliluku. Yhtälön ratkaisuja kutsutaan Legendren funktioiksi.

Katso myös Toisen kertaluvun differentiaaliyhtälö.

Legendren polynomit ovat Legendren differentiaaliyhtälön \[ (1 - x ^2) \frac{d^2 y}{dx^2} - 2x \frac{dy}{dx} + n(n+1)y = 0 \] ratkaisut silloin, kun $n$ on luonnollinen luku.

Katso myös Polynomi.

Symboli $ \left ( \frac{a}{p} \right ) $ tai $(a/p)$, missä a on kokonaisluku ja p alkuluku. Jos $a$ on jaollinen $p$:llä, $(a/p)=0$, jos $a$ on neliöjäänös modulo $p$ eli jos on olemassa kokonaisluku $x$ siten, että $x^2-a$ on jaollinen p:llä, niin $(a/p)=1$. Muussa tapauksessa $(a/p)=-1$. Ns. Eulerin kriteerin mukaan $(a/p)$ ja $a^{p-1\over 2}$ ovat kongruentteja modulo $p$.

\[ \frac{\pi}{4} = \sum _{i=0}^{\infty} \frac{(-1)^{i}}{2i+1} \]

Katso myös Piin arvon laskeminen, Ramanujanin arviot luvulle pii.

Leibnizin sääntö on derivoimissääntö \[(fg)^{(n)} = \sum_{i=1}^n {n \choose r} f^{(r)} g^{(n-r)} \]

Katso myös Sääntö, Tulon derivointisääntö.

Kaksi suoraa leikkaavat toisensa, jos ne kohtaavat jossakin pisteessä. Tasogeometriassa kaksi suoraa joko leikkaavat toisensa, ovat yhdensuuntaisia tai ovat sama suora. Myös muunlaiset kuviot voivat leikata toisiaan.

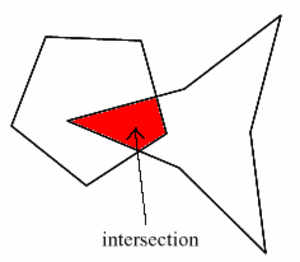
Katso myös Sisään piirretty kuvio.

Jos tapahtumat A ja B ovat riippumattomia, niin \[ \mathrm{p(A} \cap \mathrm{B)} = \mathrm{p(B|A)p(A) = p(B)p(A)} . \]

Katso myös Riippumattomat tapahtumat, Todennäköisyys, Joukkojen leikkaus.

Kahden asian leikkaus on se osa, joka on niille yhteinen, jossa ne kohtaavat tai menevät päällekkäin eli paikka, jossa ne leikkaavat.

Kaksi suoraa leikkaavat pisteessä, kaksi tasoa voivat leikata toisensa pitkin suoraa, kahden joukon leikkaus on myös joukko jne.

Katso myös Kahden tason leikkaus, Yhdiste, Funktio, Kuvaus, Joukkojen leikkaus, Johnsonin lause, Suorien leikkauspiste, Suoran ja tason leikkauspiste.

Kolmiulotteisen kappaleen ja tason leikkauskuvio. Esimerkiksi pallon ja tason leikkauskuvio on ympyrä.

Leikkauspiste on paikka, jossa kaksi tai useampi suora kohtaavat toisensa.

Kulma on piste, jossa kaksi monikulmion sivua kohtaavat.

Kärki on piste, jossa vähintään kolme monitahokkaan tahkoa kohtaavat.

Katso myös Piste.

Joukon ominaisuus on leikkausten suhteen suljettu, jos kyseisen ominaisuuden omaavien joukkojen leikkauksella on myös tämä ominaisuus. Esimerkiksi konveksisuus on tason osajoukkojen leikkausten suhteen suljettu ominaisuus ja transitiivisuus on relaatioiden leikkausten suhteen suljettu ominaisuus.

Katso myös Looginen ominaisuus, Hornin lauseke.

Aputulos, jota käytetään jonkin tärkeämmän teoreeman eli lauseen todistuksessa. Lauseen todistuksen yhteydessä saatetaan todistaa useitakin lemmoja.

Katso myös Zornin lemma.

Valitaan annetulta tasasivuiselta hyperbeliltä piste $P$. Piirretään hyperbelille tangentti pisteeseen $P$. Piirretään tangentin normaali, joka kulkee origon kautta. Merkitään pistettä, jossa normaali leikkaa tangentin kirjaimella $Q$. Pisteen $Q$ uraa kutsutaan lemniskaataksi.

Tämän käyrän yhtälö on muotoa $(x^{2}+y^{2})^{2} = a^{2}(x^{2}-y^{2})$. Napakoordinaattimuodossa yhtälö on $r^{2} = a^{2} cos 2\theta$.

Lemniskaatta on niiden ympyröiden verhokäyrä, joiden keskipisteet sijaitsevat annetulla tasakylkisellä hyperbelillä, ja jotka kulkevat hyperbelin keskipisteen kautta. Se on hyperbelin inversiokuvio hyperbelin keskipisteen suhteen. Se on Cassinin soikioiden erikoistapaus.

Katso myös Käyrä, Cassinin soikio.

Kolmion kolme symmediaania eli mediaanien kanssa kulman puolittajien suhteen symmetristä suoraa leikkaavat toisensa samassa pisteessä. Se on kolmion Lemoinen piste.

Katso myös Lemoinen ympyrä, Gergonnen kolmio.

Kolmion Lemoinen pisteen kautta piirretyt kolmion sivujen suuntaiset suorat leikkaavat kolmion sivut kuudessa pisteessä, jotka ovat kaikki samalla ympyrällä. Se on kolmion Lemoinen ympyrä.

Katso myös Ympyrä, Lemoinen piste, Kolmioon liittyvät ympyrät.

Kuvion kahden vastakkaisen sivun välinen etäisyys.

Topologinen ryhmä, jonka avaruusosa on sileä monisto, ja jossa laskutoimitus ja käänteisalkion ottaminen ovat paitsi jatkuvia myös sileitä.

Katso myös Ryhmä, Topologinen ryhmä, Yhtenäinen, Analyyttinen ryhmä.

Kappale, jota rajaa kaksi yhtenevää yhdensuuntaista tasokuviota (lieriön pohjat) ja vaippa, joka koostuu pohjakuvioiden reunojen vastinpisteitä yhdistävistä keskenään yhdensuuntaisista janoista (lieriön sivuviivat). Jos sivuviivat ovat kohtisuorassa pohjia vastaan, lieriö on suora. Jos pohjat ovat ympyröitä, lieriö on ympyrälieriö.

Katso myös Arkhimedeen lause, Ympyrä, Lieriön akseli, Kappale, Avaruusgeometria, Suora lieriö, Lieriön pinta-ala, Suoran ympyrälieriön pinta-ala, Lieriön tilavuus, Lieriön korkeusjana, Lieriön pohja.

Kolmiulotteinen koordinaatisto, jossa yksi akseleista on suora ja nimeltään $z$-akseli. Toiset kaksi koordinaattia ovat kulma, joka mitataan kiinnitetystä suunnatusta $z$-akselia vastaan kohtisuorasta suorasta vastapäivään, sekä kohtisuora etäisyys $z$-akselista. Lieriökoordinaatisto on siis kaksiulotteinen napakoordinaatisto $z$-akselilla lisättynä.

Katso myös Analyyttinen avaruusgeometria, Koordinaatisto.

Suora, joka kulkee lieriön kantojen keskipisteiden kautta, on lieriön akseli.

Katso myös Suora lieriö, Lieriö, Akseli.

Kohtisuoraan lieriön pohjasta sen kanteen (toiseen pohjaan) kulkevan jana.

Katso myös Lieriö.

Suoran ympyrälieriön, jonka korkeus on $h$ ja pohjan säde $r$, kaarevan pinnan pinta-ala on $2 \pi rh$. Siten koko lieriön pinta-ala on $2 \pi r(r+h)$.

Katso myös Lieriö.

Lieriöllä on kaksi pohjaa; ne ovat ne yleensä ympyrän muotoiset tasoalueet lieriön molemmissa päissä, joilla lieriö voi "seisoa".

Katso myös Suora lieriö, Lieriö.

Ympyrälieriön, jonka korkeus on $h$ ja pohjan säde $r$, tilavuus on $\pi r^{2} h$. Minkä tahansa lieriön, jonka pohjan pinta-ala on $A$ ja korkeus kohtisuorasti pohjaa vastaan mitattuna $l$, tilavuus on $Al$.

Katso myös Lieriö.

Olkoot $a, b \gt 0$. Hyperbelin \[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \] liittoakseli on pisteiden $(0,-b)$ ja $(0,b)$ välinen jana. Pisteiden $(-a,0)$ ja $(a,0)$ välistä janaa kutsutaan poikittaisakseliksi.

Katso myös Akseli.

Kompleksianalyysissä funktio $\phi : \mathbb{C} \mapsto \mathbb{C}$, $\phi(x,y) = u(x,y) + iv(x,y)$, on analyyttinen eli differentioituva jos ja vain jos sen reaali- ja imaginaariosat $u$ ja $v$ ovat differentioituvia ja toteuttavat Cauchy-Riemannin yhtälöt: \begin{eqnarray*} \frac{\partial u}{\partial x} &=\frac{\partial v}{\partial y}, \\ \frac{\partial v}{\partial x} &=-\frac{\partial u}{\partial y}. \end{eqnarray*} Funktioita $u$ ja $v$, joille nämä yhtälöt ovat voimassa, kutsutaan toistensa liittofunktioiksi.

Katso myös Funktio, Kuvaus, Analyyttinen funktio.

Kaksi hyperbeliä ovat toistensa liittohyperbelejä, jos niillä on samat asymptootit ja toisen liittoakseli on toisen poikittaisakseli ja päinvastoin. Liittohyperbelien yhtälöt voidaan siten esittää muodossa \[ \frac{x^2}{a^2}- \frac{y^2}{b^2} = 1, \frac{x^2}{a^2}- \frac{y^2}{b^2} = -1. \]

Katso myös Hyperbeli.

Kompleksiluvun $z = x+iy$ liittoluku eli kompleksikonjugaatti on $\bar{z} = x-iy$.

Katso myös Unitaarinen matriisi, Kompleksiluku, Normaali matriisi, Hermiittinen matriisi.

Laskutoimitus on liitännäinen, silloin, kun ei ole väliä, mihin sulkeet sijoitetaan, kun toimitus esiintyy kahdesti peräkkäin jossakin lausekkeessa.

Laskutoimitus $\circ$, jolla \[ a \circ (b \circ c)=(a \circ b) \circ c \] on voimassa kaikilla mahdollisilla $a, b, c$.

Likiarvo on ilmaus, joka kertoo suureen likimääräisen arvon. Esimerkiksi 22/7 on $\pi$:n likiarvo.

Katso myös Lauseke, Derivaatan numeerinen approksimointi, Toisen derivaatan numeerinen approksimointi, Trigonometristen funktioiden approksimointi.

Kun ilmaistaan jonkin luvun likiarvo, on kerrottava myös tarkkuus, jolla likiarvo on oikea.

Katso myös Likimääräinen, Lyhenne.

Merkkiä $\approx$ käytetään osoittamaan, että kaksi suuretta ovat lähes samat, mutta luultavasti eivät täsmälleen samat. Esimerkiksi voidaan sanoa, että $\pi \approx 3,1$.

Katso myös Yhtäsuuri, Sama.

Jokin on likimäärin oikea -- likiarvo -- jos se on lähellä todellista arvoa, mutta ei voida olla varmoja siitä, että se on täsmälleen oikea. Usein voidaan antaa arvio sille, kuinka paljon likiarvo poikkeaa todellisesta arvosta.

Katso myös Virhe, Noin, Likimain.

Lyhenne latinankielisestä sanasta "limes" (raja). Esimerkiksi merkintä $\lim_{x \to 0}$ tarkoittaa merkintää seuraavan lausekkeen raja-arvoa, kun $x$ lähestyy lukua 0.

Katso myös Lyhenne, Raja-arvo.

Sellaisten yhden tai useamman muuttujan yhtälöiden ja yhtälöryhmien tutkimusala, jossa yhtälöt sisältävät ainoastaan muuttujiensa monikertoja ja vakioita. Muuttujia ei siis ole korotettu potensseihin, eikä kerrottu keskenään.

Katso myös Vektori, Lineaarimuunnos, Vektoriavaruus, Matriisi, Lineaarinen optimointi, Lineaarinen ohjelmointi, Lineaarikuvaus.

Olkoon $X$ joukko. Relaatio $\le \subset X \times X$ on totaalinen järjestys, mikäli seuraavat ehdot pätevät

• $x \le x$ kaikilla $x \in X$.
• Jos $x \le y$ ja $y \le z$, niin tällöin $x \le z$ kaikilla $x,y,z \in X$.
• Kaikilla $x,y \in X$ pätee $x \le y$ tai $y \le x$.

Katso myös Osittaisjärjestys, Osittainen järjestys.

Jós $M$ ja $N$ ovat $R$-moduleita, kuvaus $f \colon M \rightarrow N$ on lineaarikuvaus, mikäli se toteuttaa ehdon

• $f(r a+s b)=r f(a)+s f(b)$ kaikilla $r,s \in R$ ja $a,b \in M$.

Katso myös Kuvaus, Isomorfismi, Nilpotentti, Endomorfismi, Riviavaruus, Karakteristinen polynomi, Isomorfia, Funktio.

Muunnos, jossa jokaisen kahden vektorin summan kuva on yhteenlaskettavien kuvavektoreiden summa ja skalaarilla kerrotun vektorin kuva on alkuperäisen vektorin kuva samalla skalaarilla kerrottuna. Lineaarinen muunnos voidaan esittää matriisin avulla; kuvavektori on alkuperäinen vektori tällä matriisilla kerrottuna.

Katso myös Ydin, Projektio, Lineaarialgebra.

Muunnos, jossa jokaisen kahden vektorin summan kuva on yhteenlaskettavien kuvavektoreiden summa ja skalaarilla kerrotun vektorin kuva on alkuperäisen vektorin kuva samalla skalaarilla kerrottuna. Lineaarinen muunnos voidaan esittää matriisin avulla; kuvavektori on alkuperäinen vektori tällä matriisilla kerrottuna.

Katso myös Ydin, Projektio, Lineaarialgebra.

Jós $M$ ja $N$ ovat $R$-moduleita, kuvaus $f \colon M \rightarrow N$ on lineaarikuvaus, mikäli se toteuttaa ehdon

• $f(r a+s b)=r f(a)+s f(b)$ kaikilla $r,s \in R$ ja $a,b \in M$.

Katso myös Kuvaus, Isomorfismi, Nilpotentti, Endomorfismi, Riviavaruus, Karakteristinen polynomi, Isomorfia, Funktio.

Yhtälö tai lauseke, jossa muuttujia ei ole kerrottu keskenään tai korotettu potenssiin; niitä on vain kerrottu vakioilla ja laskettu yhteen. Sama kuin ensimmäisen asteen yhtälö tai lauseke. Lauseke, yhtälö tms., joka sisältää vain itse muuttujia, ei niiden neliöitä, kuutioita, neliöjuuria tms.

Differentiaaliyhtälö, jossa tuntemattoman funktion derivaatat esiintyvät ainoastaan kerrottuina vakioilla tai annetuilla funktioilla, mutta ei toisillaan. Esimerkiksi \[ \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} + 2x^2 = \sqrt{x+1} \frac{\mathrm{d}y}{\mathrm{d}x} \] on toisen kertaluvun lineaarinen differentiaaliyhtälö.

Katso myös Differentiaaliyhtälö, Differentiaaliyhtälön aste.

Jos lukujen $x_1, \dots, x_n$ keskiarvo on $\bar x$, on lukujen $a x_1 + b, \dots, a x_n + b$ keskiarvo $a \bar x + b$.

Katso myös Keskiarvo, Aritmeettinen keskiarvo.

Haku, jossa etsittyä arvoa verrataan järjestetyn tietojoukon jokaiseen alkioon alusta loppuun, kunnes etsitty arvo löytyy tai kaikki alkiot on käyty läpi.

Katso myös Binäärihaku, Algoritmi.

Menetelmäkokoelma lineaaristen funktioiden optimoimiseksi (minimoimiseksi tai maksimoimiseksi) annettujen lineaaristen rajoitteiden vallitessa. Kahden tuntemattoman muuttujan tapauksessa graafiset menetelmät ovat usein hyödyllisiä. Monimutkaisemmissa ongelmissa joudutaan tavallisesti turvautumaan tietokoneiden apuun.

Katso myös Käypä alue, Lineaarialgebra.

Menetelmäkokoelma lineaaristen funktioiden optimoimiseksi (minimoimiseksi tai maksimoimiseksi) annettujen lineaaristen rajoitteiden vallitessa. Kahden tuntemattoman muuttujan tapauksessa graafiset menetelmät ovat usein hyödyllisiä. Monimutkaisemmissa ongelmissa joudutaan tavallisesti turvautumaan tietokoneiden apuun.

Katso myös Käypä alue, Lineaarialgebra.

Yhtälö muotoa \[Pu=f, \] missä $u$ ja $f$ ovat sopivat ehdot täyttäviä funktioita $\mathbb{R}^n$:ssä ja $P$ on differentiaalioperaattori muotoa \[P= \sum_{| \alpha | \leq k} a_ \alpha (x) \partial_ \alpha. \] Symboli $\alpha \in \mathbb{N}^n$ on nimeltään multi-indeksi. $ | \alpha |= \sum_{j=1}^n \alpha _j $ ja \[ \partial_ \alpha = \frac{ \partial^{| \alpha |}}{ \partial x_1^{ \alpha _1} \ldots \partial x_n^{ \alpha _n}}. \]

Katso myös Differentiaalioperaattori.

Joukko vektoreita on lineaarisesti riippumaton, jos yhtäkään joukon vektoreista ei voida esittää muiden joukon vektoreiden monikertojen summana.

Katso myös Vektoriavaruus, Virittää, Matriisin dimensio.

Kahden muuttujan $x ja y$ välillä on lineaarinen riippuvuus, jos niiden välinen yhteys voidaan esittää muotoa $x = ay+b$ olevan yhtälön avulla. Tämän yhtälön kuvaaja on suora.

Joukko vektoreita on lineaarisesti riippuva, jos yksi sen vektoreista voidaan esittää muiden vektorien monikertojen summana.

Yhtälö, jossa muuttujia on vain kerrottu vakioilla ja laskettu yhteen kertomatta niitä toisillaan ja korottamatta niitä mihinkään potenssiin, eli yhtälö, jossa yhtäsuuruusmerkin toisella puolella on muuttujien lineaarinen lauseke ja toisella puolella pelkkä luku.

Katso myös Lineaarinen yhtälöryhmä, Suoran yhtälö, Yhtälö.

Joukko yhtälöitä, joissa muuttujia ei ole kerrottu keskenään tai korotettu potenssiin; niitä on vain kerrottu vakioilla ja laskettu yhteen. Sama kuin ensimmäisen asteen yhtälöryhmä.

Katso myös Lineaarinen yhtälö, Matriisi, Cramerin sääntö, Fermat'n spiraali, Parabolinen spiraali.

Jos satunnaismuuttujan $X$ odotusarvo on $E(X)$, niin $E(a+b X)=a+b E(X)$.

Katso myös Odotusarvo, Teoreettinen keskiarvo, Lineaarisen funktion varianssi.

Jos satunnaismuuttujan $X$ varianssi on $Var(X)$, niin $Var(a+bX)=b^2Var(X)$.

Katso myös Varianssi, Lineaarisen funktion odotusarvo.

Kompleksitason $\mathbb{C}$ rajoitettu kokonainen funktio on vakio.

Tämän tuloksen avulla voidaan todistaa algebran peruslause.

Katso myös Kokonainen funktio, Lause.

Liouville luku on \[ \sum_{n=1}^{\infty} 10^{-n!}. \] Se on transsendenttinen.

Katso myös Transsendenttinen luku.

Liouville luku on \[ \sum_{n=1}^{\infty} 10^{-n!}. \] Se on transsendenttinen.

Katso myös Transsendenttinen luku.

Metristen avaruuksien välinen funktio $f \colon (X,d) \rightarrow (Y,d')$ toteuttaa Lipschitz-ehdon, mikäli on olemassa $c>0$ siten, että kaikilla $x,y \in X$ pätee $d'(f(x),f(y)) \le c d(x,y)$.

Jokainen Lipschitz-ehdon toteuttava funktio on jatkuva.

Katso myös Ehto, Jatkuva, Normiavaruus, Jatkuvuus.

Jos $x \gt y$, niin $x+a \gt y+a$ kaikilla $a$. Samoin, jos $x \lt y$, niin $x+a \lt y+a$ kaikilla $a$.

Katso myös Epäyhtälön kertominen puolittain, Erisuuruus, Suurempi kuin, Lause, Pienempi kuin, Epäyhtälö.

Kuvaus, jossa tason kaikki pisteet liukuvat kiinteän suoran suuntaisesti ja suorat kuvautuvat suoriksi.

Katso myös Perspektiivinen affiinikuvaus, Geometrinen muunnos.

Luonnollisen logaritmin lyhenne. $\ln x$ tarkoittaa luvun $x$ luonnollista logaritmia eli sellaista lukua, jolla $e^{\ln x}=x$.

Katso myös $\exp$, Luonnollinen logaritmi, Lyhenne, Eksponenttifunktio, Logaritmifunktion derivaatta, Yhtenevät kolmiot, $\arccot$-funktion integraalifunktio, $\arcosech$-identiteetti, $\arcoth$-identiteetti, $\arcoth$-funktion integraalifunktio, $\arctan$-funktion integraalifunktio, $\artanh$-funktion integraalifunktio, Kosekantin integraalifunktio, $\coth$-funktion integraalifunktio, Kotangentin integraalifunktio, Eksponenttifunktion integraalifunktio, Luonnollisen logaritmin integraali.

Logaritmin lyhenne on $\log$. Ellei käytetyn logaritmijärjestelmän kantalukua ilmoiteta alaindeksinä ($\log_k$), $\log$ tarkoittaa luonnollista logaritmia eli logaritmia järjestelmässä, jonka kantaluku on $e$.

Katso myös Lyhenne, Logaritmi.

Luvun $x$ $b$-kantainen logaritmi on se luku, eksponentti, jonka osoittamaan potenssiin luku $b$ on korotettava, jotta saataisiin $x$.

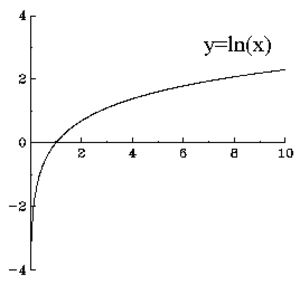
Katso myös 10-kantainen logaritmi, Briggsin logaritmi, Logaritmijärjestelmän kantaluku, Laskutoimitus, Luonnollinen logaritmi, $\log$, Logaritmikaava, Logaritminen, Logaritmiyhtälö, Kymmenkantainen logaritmi, Logaritmien laskusäännöt, Mantissa.

\[ \log _a ( xy) = \log _a x + \log _a y \] \[ \log _a (x^n) = n \log _a x \] \[ \log _a \left ( \frac{1}{x} \right ) = - \log _a x \] \[ \log _a a = 1\] \[ \log _a \left ( \frac{x}{y} \right ) = \log _a x - \log _a y \] \[ \log _a \left ( \sqrt[n]{x} \right ) = \frac{1}{n} \log _a x \] \[ \log _a 1 = 0 \] \[ e^{\mathrm{ln} x } = x \] \[ \mathrm{ln} (e^x) = x \] \[ \log _a x = \frac{\log _b x } {\log _b a } \] \[ e^{x \mathrm{ln} a } = a^x \]

Katso myös Logaritmi.

\[ \frac{d}{dx} \ln x = \frac{1}{x},\] kaikilla $x \gt 0$.

Katso myös $\ln$.

Luku, joka on korotettava annetun logaritmin osoittamaan potenssiin, jotta saataisiin se luku, jonka logaritmista on kysymys. Esimerkiksi luvun 1000 10-kantainen logaritmi on 3, koska $10^{3} = 1000$.

Katso myös Logaritmi.

Logaritmifunktioita koskeva identiteetti.

Katso myös Identiteetti, Logaritmi.

Logaritmeihin liittyvä. Muuttujien välinen logaritminen yhteys tarkoittaa, että ensimmäisen muuttujan sekä toisen muuttujan logaritmin tai molempien muuttujien logaritmien välillä on jokin yhteys. Tämä merkitsee usein, että kahden muuttujan eri potenssien välillä on jokin yhteys.

Katso myös Logaritmi.

Spiraali, joka leikkaa jokaisen origosta lähtevän säteen samassa kulmassa.

Katso myös Spiraali.

Yhtälö, jossa esiintyy muuttujan logaritmi. Tällaisille yhtälöille on usein vaikeaa löytää tarkkoja ratkaisuja. Joskus ne ovat yhtäpitäviä hyperbolisia funktioita sisältävien yhtälöiden kanssa.

Katso myös Logaritmi, Yhtälö.

Matematiikan haara, joka käsittelee sitä, miten yhdestä lauseesta saadaan seurauksena toisia lauseita tai miten lausejoukkoja voidaan yhdistää implikaatioketjuilla. Tällaiset suhteet voidaan kirjoittaa käyttämällä erityisiä merkkejä ja voidaan tutkia, miten erilaisista sääntöjoukoista saadaan erilaisia struktuureja.

Katso myös Babbage, Tautologinen.

Sellainen, jolla on vaikutusta vain pienellä etäisyydellä toisistaan oleviin asioihin. Esimerkiksi saatetaan sanoa, että funktio on lokaalisti lineaarinen, jos se on lineaarinen pienessä osassa määrittelyjoukkoaan.

Funktion lokaali minimi on arvo, joka on pienempi tai yhtä suuri kuin muut arvot sen ympäristössä, mutta ei välttämättä ole pienin arvo funktion koko arvojoukossa.

Periaate, jonka mukaan korkeintaan $n$ esinettä voidaan laittaa $n$ lokeroon siten, että kuhunkin lokeroon tulee korkeintaan yksi esine. Jos esineitä on enemmän kuin $n$, niin silloin ainakin yhteen lokeroon tulee useampi kuin yksi esine.

Katso myös Lause.

Kaikki meridiaanit pallon pinnalla vakiokulmassa leikkaava käyrä. Mercatorin projektiossa piirretyillä kartoilla loksodromit ovat suoria.

Katso myös Käyrä, Meridiaani, Pituuspiiri.

Ominaisuus, joka liittyy lauseiden tai lausejoukkojen totuuteen tai epätotuuteen sekä niiden seurauksiin.

Katso myös Leikkausten suhteen suljettu, Intransitiivinen, Epätosi, Alkeellinen, Konsistentti, monitulkintainen, Anomaalinen, Rikkoa, Todistamaton, Triviaali, Ilmeinen, Itsestään selvä, Riittävä, Välttämätön ehto, Kategorinen, Yhteensopiva, Väärä.

Operaattori, joka ottaa argumenteikseen loogisia väittämiä ja antaa tulokseksi väittämän, joka on tosi tai epätosi sen mukaan, mikä on niiden väittämien totuusarvo, joihin operaatio kohdistui.

Katso myös Operaattori, Ja, Ei, NAND, Tai, Poissulkeva tai.

Jos neliömatriisi $A$ voidaan esittää alakolmiomatriisin $L$ ja yläkolmiomatriisin $U$ tulona $A = LU$, tätä esitystä kutsutaan matriisin $A$ LU -hajotelmaksi. Esimerkiksi \[ \left ( \begin{array}{cc} 2 & 3 \\ -10 & -18 \end{array} \right ) = \left ( \begin{array}{cc} 1 & 0 \\ -5 & 1 \end{array} \right ) \left ( \begin{array}{cc} 2 & 3 \\ 0 & -3 \end{array} \right ). \]

Katso myös Alakolmiomatriisi, Yläkolmiomatriisi, Neliömatriisi, Hajoittaa matriisi.

Luku $\pi$ tunnettiin Saksassa pitkään nimellä Ludolphin luku, Ludolph von Ceulenin (28.1.1540-31.12.1610) mukaan, joka kulutti suuren osan elämästään laskemalla piin desimaalikehitelmän 35 ensimmäistä desimaalia geometristen kuvioiden avulla: 3,14159265358979323846264338327950288.

Katso myös Pii, $\pi$.

Selvittää äärellisen joukon alkioiden lukumäärä.

Laskemisen voi tehdä siten, että luettelee luonnollisia lukuja luvusta yksi alkaen samalla kun käy läpi joukon alkiot. Näin tulee samalla numeroineeksi joukon alkiot eli asettaneeksi ne yksi-yhteen -vastaavuuteen jonkin luonnollisten lukujen joukon alkusegmentin kanssa. Joissakin tapauksissa voi myös äärettömän joukon alkiot numeroida periaatteessa samalla tavoin, jolloin saadaan yksi-yhteen -vastaavuus niiden ja kaikkien luonnollisten lukujen välillä.

Lukumäärän mielessä ääretön.

Katso myös Ääretön, Ylinumeroituva.

Kuinka paljon tai kuinka monta jotakin on, kuinka suuri asia tai suure on. On olemassa erityyppisiä lukuja, kuten positiiviset luvut, negatiiviset luvut, kokonaisluvut, luonnolliset luvut, rationaaliluvut ja reaaliluvut.

Katso myös Vasta-alkio, Osittelulaki, Juurrettava, n:o, Neljäs potenssi, Reaaliluku, Luokkaluku, Kompleksiluku.

Tavallisesti käytämme lukujen esittämiseen kymmenjärjestelmää, jossa luku kirjoitetaan merkitsemällä numeroilla 0--9 oikealta lukien ykkösten, kymmenten, satojen, tuhansien jne. määrät. Esimerkiksi luvussa 123 on kolme ykköstä, kaksi kymmentä ja yksi sata: $123=3\cdot 1+2\cdot 10+1\cdot 100$. Kymmenen asemesta voidaan käyttää muitakin kantalukuja. Esim. seitsenjärjestelmässä luku 123 kirjoitetaan $234_7$, sillä $123=4\cdot 1+3\cdot 7+2\cdot 7^2$. Seitsenjärjestelmässä käytetään numeromerkkejä 0--6. Yleisestikin erilaisia numeromerkkejä tarvitaan kantaluvun ilmaisema määrä.

Katso myös 60-järjestelmä, Desimaali, Kolmijärjestelmä, Merkintätapa, Notaatio, Binäärilukujärjestelmä, Heksadesimaalilukujärjestelmä.

Suora jota käytetään reaalilukujen joukon havainnollistamiseen. Reaalilukua esittää piste, jonka etäisyys kiinteästä pisteestä, origosta, on kyseisen luvun itseisarvon suuruinen. Positiivisia lukuja esittävät pisteet ovat origon toisella ja negatiivisia lukuja esittävät toisella puolella.

Katso myös Kompleksitaso, Reaaliluku, Suora.

Lukuteoria tutkii kokonaislukuja, niiden ominaisuuksia ja niiden välisiä suhteita.

Katso myös Irrationaaliluku, Modulaariaritmetiikka, Monikerta, Diskreetti matematiikka, Tekijä, Alkeismatematiikka, Tekijä, Jono, Jakaja, Diofantoksen yhtälö, Palautuskaava.

Järjestää lukuja, kuvioita ja olioita niiden ominaisuuksien mukaan.

Tilastollinen aineisto, joka on kerätty havainnoimalla luokiteltua (kategorista) muuttujaa. Tällaista aineistoa ei voida järjestää millään luonnollisella tavalla, vaan ainoastaan jakaa se järjestämättömiin luokkiin.

Esimerkiksi luokkakavereiden silmien väri muodostaa luokitellun aineiston. Sen sijaan luokkakavereiden kokeesta saamat arvosanat eivät muodosta luokiteltua aineistoa, koska arvosanat voidaan järjestää luonnollisella tavalla, esimerkiksi suuruusjärjestykseen.

Katso myös Data, Aineisto.

Satunnaismuuttujaa tai sitä havainnoimalla saatua aineistoa kutsutaan luokka-arvoiseksi tai luokitelluksi tai kategoriseksi, jos sitä ei voi laittaa järjestykseen, vaan ainoastaan jakaa järjestämättömiin luokkiin.

Katso myös Satunnaismuuttuja.

Järjestämätön diskreetti tilastollinen muuttuja.

Katso myös Satunnaismuuttuja.

Luokkaluku on ratojen lukumäärä $h$ ryhmän $G$ itsellään määritellyssä konjugointitoiminnassa. Jos $O_1, \ldots, O_h$ ovat nämä radat ja $n_i = |O_i| = |G:G_{x_i}|$, missä $x_i \in O_i$ ja $i =1, \ldots, h$, niin saadaan luokkayhtälö \[ |G| = n_1 + \ldots + n_h. \]

Katso myös Luku.

Logaritmi, jonka kantaluku on $e$.

Katso myös Logaritmi, $\ln$.

Luku, joka ilmaisee lukumäärää: $1, 2, 3, \cdots$. Joskus halutaan puhua myös sellaisten olioiden lukumäärästä, joita ei ole yhtään. Silloin tarvitaan myös lukua $0$. Siksi matematiikassa sanotaan joskus, että luonnolliset luvut ovat $0, 1, 2, 3, \cdots$. Luonnollisten lukujen joukkoa merkitään symbolilla $\mathbb{N}$.

Katso myös Aritmetiikka, Laskento, Perusluku, Järjestysluku, Kokonaisluku, Reaaliluku, Joukko, Kokonaisluku, Bertrandin otaksuma.

\[ \int ln(x) \mathrm{d}x = x ln(x) - x + C. \]

Katso myös $\ln$.

Luottamusväli on tilastotieteilijän tapa tehdä tarkkuusarvioita. Arvioitaessa (estimoitaessa) tilastoaineiston perusteella perusjoukon tuntemattomia parametrejä liittyy arvioihin yleensä aina satunnaisvirhettä. Tämän virheen arvioimiseksi tilastotieteilijä muodostaa parametrin jakauman avulla luottamusvälin perusjoukon tuntemattomalle parametrille siten, että väli peittää (sisältää) tarkastelun kohteena olevan tuntemattoman parametrin etukäteen annetulla todennäköisyydellä (varmuudella, luotettavuudella). Varsin usein luottamusväli on muodostettu niin, että se peittää tarkastelun kohteena olevan tuntemattoman parametrin todennäköisyydellä (varmuudella, luottamustasolla) 0.95 eli 95:ssä tapauksessa 100:sta. Tietenkin muitakin todennäköisyyksiä voidaan käyttää.

Katso myös Tunnusluku, Tilastollinen tunnusluku.

Osoitetaan, että $\sqrt{2}$ on irrationaalinen.

Tehdään vastaoletus: $\sqrt{2}$ on rationaaliluku eli $\sqrt{2} = \frac{p}{q}$ joillakin kokonaisluvuilla $p, q$. Voimme olettaa, että luvuilla $p, q$ ei ole yhteisiä tekijöitä. Korottamalla yhtälön molemmat puolet toiseen potenssiin saamme nyt $2 = \frac{p^2}{q^2}$ ja tästä edelleen $2q^{2} = p^{2}$. Koska $2$ on vasemman puolen tekijä, on se myös oikean puolen tekijä, joten $p$ on parillinen eli jaollinen luvulla $2$. Siis $p = 2r$ jollakin kokonaisluvulla $r$. On siis $2q^{2} = 4r^{2}$ eli $q^{2} = 2r^{2}$. Tästä seuraa samoin kuin edellä, että $2$ on luvun $q$ tekijä. Siis luvuilla $p$ ja $q$ on yhteinen tekijä $2$. Mutta oletuksen mukaan luvuilla $p$ ja $q$ ei ole yhteisiä tekijöitä. Tämä ristiriita osoittaa, että lukua $\sqrt{2}$ ei voi esittää kahden kokonaisluvun osamääränä, joten vastaoletus on väärä ja $\sqrt{2}$ on irrationaalinen.

Katso myös Irrationaaliluku, Lause, Neliöjuuri.

Lyhyt tapa sanoa tai kirjoittaa jotain.

Katso myös $\arccos$, $\arccosec$, $\arccot$, $\arcosech$, $\arcosh$, $\arcoth$, $\arcsec$, $\arg$, int, v, $\tan$, rad, N, mg, Mikro-, ml, mm, Deka-, cm, Bin, Bitti, $\exp$, $\sin$, n:o, $\mod$, Joss, $\inf$, Noin, Likimain, eqn, Merkintätapa, Notaatio, $\ln$, $\Im(z)$, Nano, $\sec$, $\log$, Kymmenkantainen logaritmi, $\lim$, $\dim$, $\cos$, $\cot$, $\Re(z)$, $\cosh$, $\sinh$, $\arsinh$, $\artanh$, $\arcsin$, $\arctan$, Kosini, $\csc$, $\coth$, $\csch$, $\erf$, $\tr$, $\sech$, FFT.

Pienen etäisyyden päässä.

Luvun 2 potensseja kutsutaan joskus lähes täydellisiksi, koska luvun $2^n$ jakajien (lukuunottamatta lukua $2^n$ itseään) summa on $2^n-1$.

Ei tiedetä, onko olemassa sellaista paritonta lukua $n$, jonka jakajien summa (poislukien luku $n$) olisi $n-1$.

Katso myös Täydellinen luku.

Lukujono lähestyy tiettyä lukua raja-arvonaan, jos sen jäsenet tulevat jatkuvasti lähemmäksi tuota lukua niin, että luvun ja jonon jäsenten arvojen erotukset tulevat mitä hyvänsä lukua pienemmiksi itseisarvoltaan. Esimerkiksi jono, jonka ensimmäinen jäsen on 15 ja muut jäsenet saadaan lisäämällä edelliseen jäseneen 1 sekä jakamalla summa kahdella, eli jono 15, 8, 4,5, 2,75, 1,875, 1,4375, \dots , lähestyy lukua 1.

Annetun olion lähin olio on se olio, jonka etäisyys annetusta oliosta on kaikkein pienin. Tämä voi tarkoittaa pienintä etäisyyttä avaruudessa, lukusuoralla, jne.

Funktion $f \colon A \rightarrow B$ määrittelyjoukko on $A$. Toisin sanoen, funktion $f$ määrittelyjoukko on niiden pisteiden joukko, joissa $f$ on määritelty. Määrittelyjoukkoa kutsutaan myös lähtöjoukoksi.

Englannin kielen sana "domain" voi tarkoittaa myös aluetta eli euklidisen avaruuden avointa ja yhtenäistä osajoukkoa.

Katso myös Injektio, Funktio, Kuvaus, Komplementtijoukko, Joukko, Bijektio, Surjektio, Maalijoukko, Arvojoukko, Funktion maalijoukko, Kokonaisalue, Homotopia, Cauchyn integraalilause.

Jana, joka yhdistää mitkä tahansa kaksi monikulmion kärkeä, jotka eivät ole vierekkäisiä. Tai jana, joka yhdistää mitkä tahansa kaksi monitahokkaan kärkeä, jotka eivät ole saman vierekkäisiä tahkon kärkiä. Jos kärjet eivät ole saman sivutahkon kärkiä, puhutaan avaruuslävistäjästä.

Katso myös Monikulmio, Suora, Monitahokas.

Neliömatriisi, jonka kaikki muut, paitsi päälävistäjällä olevat alkiot, ovat nollia. Esimerkiksi \[ \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 4 \end{array} \right). \]

Katso myös Päälävistäjä, Yksikkömatriisi, Neliömatriisi, Normaali matriisi, Identiteettimatriisi, LDU-hajotelma.