Matematiikan verkkosanakirja

Kokonaisalue $R$ on yksikäsitteisen tekijöihinjaon alue, jos kaikilla $a \in R$, $a \neq 0$ on tekijöihinjako $a = u p_1 \dots p_k$, joka on yksikäsitteinen lukuunottamatta yksikköalkiota $u$ ja alkualkioiden $p_1, \dots, p_k$ järjestystä. (Yksikäsitteisen tekijöihinjaon alueessa alkualkion ja jaottoman alkion käsitteet ovat samat.)

Jokainen pääideaalialue on UFD, mutta ei toisin päin: Esimerkiksi $Z[X]$ on UFD mutta ei pääideaalialue, sillä $\langle 2, X, \rangle$ ei ole pääideaali.

Katso myös Pääideaalialue, Kokonaisalue, Gaussin kokonaisluvut, Gaussin luvut.

Monikulmion ulkokulma on kulma, joka muodostuu jatkettaessa monikulmion sivua: sivun ja sen viereisen sivun jatkeen välinen kulma eli monikulmion kulman vieruskulma.

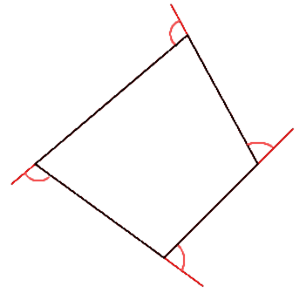
Katso myös Monikulmion kulmat, Sisäkulma.

Monikulmion, esimerkiksi kolmion, kulman vieruskulman puolittaja.

Katso myös Kulman puolittaja.

Ulottuvuuksia eli dimensioita ovat ne toisistaan riippumattomat suunnat, joihin mittaukset voidaan tehdä. Esimerkiksi tasolla on kaksi ulottuvuutta: Kun kaksi eri suuntaa $x$ ja $y$ on tasolta valittu, voidaan mikä tahansa muu tason suunta esittää siten, että ensin mennään tietty matka suuntaan $x$ ja sitten tietty matka suuntaan $y$.

Fysiikassa suureen dimensiolla tarkoitetaan suureen riippuvuutta yksikköjärjestelmän perusyksiköistä. Esimerkiksi suureen "pituus" perusyksikkö on metri ja suureen "aika" perusyksikkö on sekunti, joten suureen "nopeus" dimensio on metri/sekunti.

Vektoriavaruutta sanotaan äärellisulotteiseksi, jos sen kannassa on äärellinen määrä vektoreita. Kannan vektoreiden lukumäärä on hyvin määritelty ja yksikäsitteinen ja sitä kutsutaan kyseisen avaruuden dimensioksi. Jos vektoriavaruus ei ole äärellisulotteinen, sitä kutsutaan ääretönulotteiseksi.

Katso myös Frekvenssi, $\dim$, Vektoriavaruus, Vektoriavaruuden dimensio, Matriisin dimensio.

Neliömatriisi, joka toteuttaa ehdon $\overline{A}^{T} A = I$. Tässä $\overline{A}$ on matriisi, jonka alkiot ovat matriisin $A$ alkioiden kompleksikonjugaatteja. Jos matriisin $A$ alkiot ovat reaalilukuja, niin $A$ on ortogonaalinen matriisi.

Katso myös Matriisin transpoosi, Yksikkömatriisi, Ortogonaalinen matriisi, Liittoluku, Normaali matriisi, Kompleksikonjugaatti, Unitaarisen matriisin ominaisarvot, Identiteettimatriisi.

Unitaarisen matriisin ominaisarvojen itseisarvo on 1.

Katso myös Unitaarinen matriisi, Lause, Ominaisarvo.

Väite $\forall x (x^2 \ge 0)$ on tosi, koska jokaisen luvun neliö on suurempi tai yhtä suuri kuin nolla.

Universaalikvanttori on symboli $\forall$, joka luetaan "kaikilla" tai "jokaisella". Jos $P$ on ominaisuus, niin $\forall x P(x)$ tarkoittaa, että kaikilla olioilla on ominaisuus $P$.

Vertaa käsitteeseen "Olemassaolokvanttori".

Katso myös Eksistenssikvanttori, Olemassaolokvanttori.

Anglosaksinen massan yksikkö.

16 unssia on yksi naula, toinen angölosaksinen massan yksikkö, eli 16 oz = 1 lb.

Yksi unssi on noin 28,34952 g.

Polku, jonka piirtää jonkin säännön mukaan liikkuva piste. Esimerkiksi ympyrä on polku, jonka piirtää piste, joka liikkuu siten, että se pysyy aina samalla etäisyydellä kiinteästä pisteestä.

Niiden pisteiden joukko, jotka toteuttavat tietyn ehdon. Ehto liittyy tavallisesti pisteiden etäisyyteen tietyistä kiinteistä pisteistä tai kulmiin, joita ne muodostavat muiden pisteiden ja suorien kanssa.

Esimerkiksi niiden pisteiden ura, jotka ovat etäisyydellä $r$ kiinteästä pisteestä $C$, on ympyrä.

Katso myös Ympyrä, Konstruktio, Karteesinen soikio, Cassinin soikio, Rajoite, Rajoitusehto, Konstruointi, Vierintäkäyrä, Hyperpallo, Hyposykloidi.

Tilastotieteessä parametrin estimoinnin yhteydessä uskottavuus kertoo, kuinka todennäköinen jo tehty havainto olisi parametrin eri arvoilla. Uskottavuus on siten tuntemattoman parametrin funktio.

Katso myös Todennäköisyys, Ominaisuus, Määrite.

Kulman yksikkö. Yksi uusaste eli graadi on suoran kulman sadasosa. Tätä yksikköä käytetään paljon vähemmän kuin asteita tai radiaaneja.

Katso myös Kulma, Radiaani, Aste.

Yhdysvalloista peräisin oleva nimitys, jolla tarkoitetaan uudempaa koulumatematiikan oppisisältöä 1960-luvulla. Tätä edeltävän ajan koulumatematiikkaa kutsuttiin perinteiseksi.

Katso myös Matematiikka.