$j$
Kirjainta $\overrightarrow{j}$ käytetään merkitsemään $y$-akselin suuntaista yksikkövektoria. $\overrightarrow{j}=(0,\,1)$ kaksiulotteisessa avaruudessa ja $\overrightarrow{j}=(0,\,1,\,0)$ kolmiulotteisessa avaruudessa.
Katso myös Yksikkövektori, $i$, $k$.
Ja (engl. And)
Looginen operaattori, joka antaa tulokseksi 'tosi', jos sen molemmat argumentit ovat tosia, muussa tapauksessa tulos on 'epätosi'. Operaattorille JA käytetään merkintää $\wedge$.
Katso myös Looginen operaattori, Tai.
Jacobin determinantti (engl. Jacobian)
Funktion $f(x_1, x_2, \ldots, x_n) = (f_1(x_1, x_2, \ldots, x_n), \ldots, f_n(x_1, x_2, \ldots, x_n))$ Jacobin determinantti on \[ \left | \begin{array}{cccc} \frac{ \partial f_1}{ \partial x_1} & \frac{ \partial f_1}{ \partial x_2} & ... & \frac{ \partial f_1}{ \partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & ... & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & ... & \frac{\partial f_n}{\partial x_n} \end{array} \right|. \] Jacobin determinanttia tarvitaan muun muassa laskettaessa usean muuttujan funktion integraali muuttujanvaihdon avulla.
Katso myös Derivaatta, Determinantti, Hessen matriisi, Jacobin matriisi.
Jacobin matriisi (engl. Jacobian matrix)
Funktion $f(x_1, x_2, \ldots, x_n) = (f_1(x_1, x_2, \ldots, x_n), \ldots, f_n(x_1, x_2, \ldots, x_n))$ Jacobin matriisi on \[ \left( \begin{array}{cccc} \frac{ \partial f_1}{ \partial x_1} & \frac{ \partial f_1}{ \partial x_2} & ... & \frac{ \partial f_1}{ \partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & ... & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & ... & \frac{\partial f_n}{\partial x_n} \end{array} \right). \]
Katso myös Matriisi, Hessen matriisi, Jacobin determinantti, Osittaisderivaatta.
Jaettava (engl. Dividend)
Jakolaskussa lukua, joka jaetaan, kutsutaan jaettavaksi.
Katso myös Osamäärä, Jakolasku, Kokonaisluku, Jakaminen.
Jakaa (engl. Divides)
Jos jakojäännös on nolla jaettaessa luku $y$ luvulla $x$, sanotaan luvun $x$ jakavan luvun $y$ ja lukua $x$ kutsutaan luvun $y$ tekijäksi. Tällöin kirjoitetaan $x | y$.
Alkion $a$ sanotaan jakavan alkion $b$ renkaassa $R$, jos on olemassa sellainen $c \in R$, että $ac = b$.
Katso myös Jaollinen, |, Lagrangen lause.
Jakaa (uudelleen) osiin (engl. Subdivide)
Leikata jokin (aikaisempaakin) pienempiin palasiin.
Jakaa komponetteihin (engl. Resolve)
Kirjoittaa vektori tietynsuuntaisten komponenttien summaksi.
Katso myös Komponentti.
Jakaa luku tekijöihinsä, Hajoittaa luku tekijöihinsä (engl. Decompose a number)
Kirjoittaa luku alkulukujen tulona. Esimerkiksi $35 = 5 \cdot 7$ ja $36 = 2 \cdot 2 \cdot 3 \cdot 3 = 2^2 \cdot 3^2$.
Katso myös Jakaa tekijöihin, Jakaa murtoluku osamurtolukuihin, Hajoittaa matriisi.
Jakaa murtoluku osamurtolukuihin (engl. Decompose a fraction)
Murtoluvun jakamisella osamurtolukuihin tarkoitetaan sen esittämistä osamurtolukujen summana. Selvitetään asiaa esimerkin avulla. Olkoon $1/6$ tutkittava murtoluku. Jaetaan ensin nimittäjä $6$ tekijöihinsä: $6 = 2 \cdot 3$. Siis \[ \frac{1}{6} = \frac{1}{2} \cdot \frac{1}{3}. \] Tämä tarkoittaa, että voimme kirjoittaa \[ \frac{1}{6} = A \frac{1}{2} + B \frac{1}{3}. \] Etsitään seuraavaksi luvut $A$ ja $B$. Yhtälö \[ \frac{1}{6} = A\frac{1}{2} + B\frac{1}{3} = \frac{3A + 2B}{6} \] toteutuu, kun pätee \[ 1 = 3A + 2B. \] Eräs ratkaisu on $A = 1$, $B = -1$. Siis \[ \frac{1}{6} = \frac{1}{2} - \frac{1}{3}. \] Tämä menetelmä voi toimia myös siinä tapauksessa, jossa tutkittavan murtoluvun osoittaja ja nimittäjä ovat polynomeja.
Katso myös Jakaa luku tekijöihinsä, Hajoittaa luku tekijöihinsä.
Jakaa tekijöihin (engl. Factorise)
Alkutekijöihin jakaminen tarkoittaa luonnollisen luvun kirjoittamista jaottomien lukujen eli alkulukujen tulona. Esimerkiksi $20 = 2 \cdot 2 \cdot 5$.
Kirjoittaa kokonaisluku pienempien lukujen, yleensä alkulukujen, tulona.
Katso myös Polynomin tekijöihinjako, Kahden neliön erotus, Jakaa luku tekijöihinsä, Hajoittaa luku tekijöihinsä, Polynomien suurin yhteinen tekijä.
Jakaja, Tekijä (engl. Divisor)
Luvun $n$ jakaja eli tekijä on luku, jolla $n$ on jaollinen.
Yleensä sekä luku $1$ ja luku $n$ itse lasketaan luvun $n$ tekijöiksi. Alkuluku on sellainen positiivinen kokonaisluku, jonka ainoat tekijät ovat $1$ ja luku itse. Lukua $1$ ei yleensä kuitenkaan pidetä alkulukuna. Alkulukuina pidetään siis sellaisia lukuja, joilla on tasan kaksi eri tekijää.
Katso myös Yhteinen tekijä, Lukuteoria, Alkuluku, Kokonaisluku, Aito jakaja.
Jakaminen, Jakolasku (engl. Division, Divide)
Jakaminen tarkoittaa, että annettu lukumäärä olioita erotellaan tai lajitellaan yhtä suuriin ryhmiin. Jos esimerkiksi $6$ keksiä jaetaan tasan $3$ ihmisen kesken, kukin saa $2$ keksiä. Tämä voidaan kirjoittaa $6 \div 3 = 2$ tai $6 / 3 = 2$.
Jakolasku on kertolaskulle käänteinen laskutoimitus. Esimerkiksi $(6 / 3) \cdot 3 = 2 \cdot 3 = 6$ ja $(6 \cdot 3) / 3 = 18 / 3 = 6$.
Alkion $a$ jakaminen alkiolla $b$ tarkoittaa, että kerrotaan alkio $a$ alkion $b$ käänteisalkiolla. Jos siis merkki $/$ tarkoittaa jakamista, niin $a/b = a \cdot b^{-1}$.
Katso myös Käänteisalkio, Jakojäännös, Kertolasku, Osamäärä, Laskutoimitus, Jakokulmassa jako, Jaettava, Puolittaa, Kertolaskun käänteisalkio, Käänteisluku, Binäärinen kuvaus, Kaksipaikkainen kuvaus.
Jakauma (engl. Distribution)
Empiirinen jakauma (havaittu jakauma) kuvaa, miten tilastoaineistoon liittyvät muuttujanarvot ovat jakautuneet muuttujanarvojen suhteen. Empiiristä jakaumaa kuvataan usein pylväsdiagramman (luokittelu- tai järjestysasteikolla mitattu muuttuja) tai histogramman (intervalli- tai suhdeasteikolla mitattu muuttuja) avulla.
Teoreettinen jakauma: Mikäli muuttuja on diskreetti (mitattu luokittelu- tai järjestysasteikolla), tilastollinen jakauma on luettelo muuttujanarvoista ja niihin liittyvistä todennäköisyyksistä. Esimerkiksi nopanheitto $$ \begin{array}{lllllllllll} \textrm{Silmäluku} & x & 1 & 2 & 3 & 4 & 5 & 6\\ P(x=i) & & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \end{array} $$ Mikäli muuttuja on jatkuva (mitattu intervalli- tai suhdeasteikolla), tilastollinen jakauma on ei-negatiivinen funktio, joka määrittelee tapahtumien todennäköisyydet pinta-alojen avulla.
Katso myös Normaalijakauma, Tasainen jakauma, Binomijakauma, Tilastotiede, T-jakauma, Studentin t-jakauma, Varianssi, Diracin deltafunktio, Geometrinen jakauma, Priorijakauma, Posteriorijakauma, Asymptoottinen jakauma, Betajakauma, F-jakauma, Gammajakauma, Gaussin jakauma, Poisson-jakauma.
Jako teräväkulmaisiksi kolmioiksi (engl. Acute-angled triangle dissection)
Jokin tapa jakaa kuvio $S$ osiksi, joista jokainen on teräväkulmainen kolmio.
Jakojäännös (engl. Remainder)
Se mitä jää yli, kun jaetaan kokonaisluku tiettyyn määrään yhtä suuria osia.
Tutkitaan jakolaskua $\frac{a}{b}$, missä $a$ ja $b$ ovat positiivisia kokonaislukuja. Tällöin $a$ voidaan esittää muodossa $a=kb+r$, missä $k$ ja $r$ ovat luonnollisia lukuja ja $r \lt b$. Tällöin jakolaskun $\frac{a}{b}$ jakojäännös on $r$.
Katso myös Modulo, Osamäärä, Jakolasku, Kokonaisluku, Kongruenssi, Jakaminen.
Jakokulmassa jako (engl. Long division)
Jakolasku, Jakaminen (engl. Division, Divide)
Jakaminen tarkoittaa, että annettu lukumäärä olioita erotellaan tai lajitellaan yhtä suuriin ryhmiin. Jos esimerkiksi $6$ keksiä jaetaan tasan $3$ ihmisen kesken, kukin saa $2$ keksiä. Tämä voidaan kirjoittaa $6 \div 3 = 2$ tai $6 / 3 = 2$.
Jakolasku on kertolaskulle käänteinen laskutoimitus. Esimerkiksi $(6 / 3) \cdot 3 = 2 \cdot 3 = 6$ ja $(6 \cdot 3) / 3 = 18 / 3 = 6$.
Alkion $a$ jakaminen alkiolla $b$ tarkoittaa, että kerrotaan alkio $a$ alkion $b$ käänteisalkiolla. Jos siis merkki $/$ tarkoittaa jakamista, niin $a/b = a \cdot b^{-1}$.
Katso myös Käänteisalkio, Jakojäännös, Kertolasku, Osamäärä, Laskutoimitus, Jakokulmassa jako, Jaettava, Puolittaa, Kertolaskun käänteisalkio, Käänteisluku, Binäärinen kuvaus, Kaksipaikkainen kuvaus.
Jakso (engl. Period)
Jos funktiolla $f$ on sellainen ominaisuus, että $f(x+a)=f(x)$ kaikilla $x$, niin $a$ on funktion jakso.
Fysikaalinen järjestelmä saattaa olla sellainen, että se palaa säännöllisin väliajoin samaan tilaan. Tällainen väliaika on järjestelmän jakso.
Jaksollinen desimaaliluku (engl. Recurring decimal)
Desimaaliluku, jonka desimaaleissa sama numerojono toistuu jatkuvasti. Esimerkiksi 1/9 = 0,111111... tai 1/7 = 0,142857142857... Joskus jaksolliset desimaaliluvut kirjoitetaan merkitsemällä toistuva numerojono näkyviin vain kerran ja lisäämällä sen ensimmäisen ja viimeisen numeron päälle piste. Esimerkiksi $1/9 = 0,\dot{1}$ tai $1/7 = 0,\dot{1}4285\dot{7}$. Tämä ei ole kuitenkaan kovin yleinen merkintätapa.
Katso myös Kymmenmurtoluku.
Jakson kahdentuminen, Bifurkaatio (engl. Bifurcation)
Jakson kahdentumispiste (bifurkaatiopiste) on sellainen systeemin parametrien joukko, jossa systeemin käyttäytyminen muuttuu kvantitatiivisesti. Jokin systeemi voi esimerkiksi olla stabiili arvoilla $k \lt 1$ ja epästabiili arvoilla $k \gt 1$, missä $k$ on systeemin parametri. Tällöin $k = 1$ on jakson kahdentumispiste.
Katso myös Piste.
Jalka (engl. Feet, Foot)
Brittiläinen pituusyksikkö. Yksi jalka on 12 tuumaa eli 30,48 cm.
Katso myös Maili, Ortokolmio.
Jana (engl. Line segment)
Kahden pisteen, janan päätepisteiden, välinen suoran osa.
Katso myös Jänne, Suora, Puolisuora, Säde, Puolisäde, Suuntajana, Janan jatkaminen suoraksi, Murtoviiva, Sekantti, Suunnattu jana.
Janan jatkaminen suoraksi (engl. Continuation of a line)
Janan (jolla on määrätty pituus ja kaksi päätepistettä) jatke on ääretön suora, jonka osa kyseinen jana on.
Janan keskipisteen määrittäminen (engl. Construct a midpoint)
Annetun janan keskipiste voidaan määrittää seuraavasti. Piirretään janan keskinormaali. Janan keskipiste on se piste, jossa keskinormaali leikkaa janan.
Katso myös Konstruktio, Konstruointi.
Janan vektorimuotoinen yhtälö (engl. Vector equation of AB)
Jos on annettu pisteet $A$ ja $B$, joiden paikkavektorit ovat $\overline{a}$ ja $\overline{b}$, niin janan $AB$ yhtälö vektorimuodossa on $\overline{r} = (1-t)\overline{a} + t\overline{b}$, missä $t \in [0,\,1]$ on reaalinen parametri. Jos $t$ saa arvoja tämän välin ulkopuolelta, yhtälö määrittelee suoran pisteiden $A$ tai $B$ toisella puolella.
Katso myös Suoran yhtälö.
Jaollinen (engl. Divisible)
Luvun $x$ sanotaan olevan jaollinen luvulla $y$, jos jaettaessa luku $x$ luvulla $y$ on jakojäännös nolla.
Katso myös Jakaa.
Jaollisuus (engl. Divisibility)
Luku $a$ on jaollinen luvulla $b$, jos jakojäännös jaettaessa luku $a$ luvulla $b$ on nolla.
Katso myös Pariton, Jaottomuus, Parillinen, Yhdistetty luku, Kokonaisluku.
Jaoton (engl. Indivisible)
Ei jaollinen.
Katso myös Jaollinen.
Jaoton polynomi (engl. Irreducible polynomial)
Polynomi, jota ei voida jakaa alempiasteisiin tekijöihin.
Katso myös Polynomin tekijöihinjako, Polynomi.
Jaottomuus (engl. Primality)
Ominaisuus olla alkuluku. Joskus puhutaan jaottomuustesteistä, joiden avulla voidaan selvittää, onko annettu luku alkuluku vai ei.
Katso myös Alkuluku, Jaollisuus, Kokonaisluku, Suhteellinen alkuluku.
Jatkaa, Laajentaa (engl. Extend)
Tehdä jokin suuremmaksi tai pitemmäksi. Usein sillä tarkoitetaan janan jatkamista suoraksi, jonka osa kyseinen jana on. Myös funktion määrittelyalueen suurentamista sanotaan funktion laajentamiseksi tai jatkamiseksi.
Katso myös Konstruktio, Konstruointi.
Jatkumo, Kontinuumi (engl. Continuum)
Kontinuumilla voidaan matematiikassa tarkoittaa kahta eri asiaa: reaalilukujen joukkoa (reaaliakselia) tai kompaktia ja yhtenäistä metristä avaruutta.
Katso myös Joukko, Kompakti, Yhtenäinen.
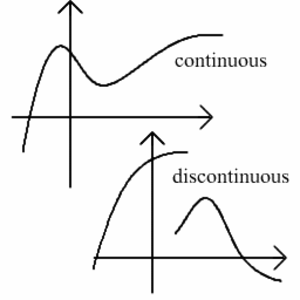
Jatkuva, Jatkuvuus (engl. Continuous, Continuity)
Jatkuva suure on sellainen, joka voi tietyin rajoituksin saada arvokseen minkä tahansa lukuarvon. Jatkuva suure on suure, joka ei ole diskreetti. Esimerkkejä jatkuvista suureista ovat pituus ja aika. Esimerkkejä diskreeteistä suureista ovat kengän koko ja kananmunien lukumäärä.
Muuttujan $x$ funktio on jatkuva, jos pieni muutos muuttujassa $x$ saa aikaan ainoastaan pienen muutoksen, ei äkillistä hyppäystä, funktion arvossa.
Funktio on jatkuva, jos sen arvo muuttuu vain vähän, kun funktion parametria muutetaan vain vähän.
Täsmällisemmin tämä voidaan ilmaista seuraavasti. Olkoon $f \colon \mathbb{R} \rightarrow \mathbb{R}$, ja olkoon $x_0 \in \mathbb{R}$. Sanomme, että $f$ on jatkuva pisteessä $x_0$, jos kaikilla $\epsilon \gt 0$ on olemassa sellainen $\delta >0$, että $|f(x)-f(x_0)| \lt \epsilon$ aina, kun $|x-x_0| \lt \delta$.
Sanomme, että $f$ on jatkuva joukossa $\mathbb{R}$, jos se on jatkuva kaikissa pisteissä $x_0 \in \mathbb{R}$.
Olkoot $(X, \tau)$ ja $(Y, \eta)$ topologisia avaruuksia. Kuvaus $f: X \to Y$ on jatkuva, jos jokaisen avoimen joukon $V \subset Y$ alkukuva $f^{-1}(U) \subset X$ on avoin. Jatkuvat kuvaukset säilyttävät yhtenäisyyden ja kompaktisuuden.
Olkoot $(X,d)$ ja $(Y, \rho )$ metrisiä avaruuksia. Kuvaus $f : X \to Y$ on jatkuva pisteessä $x \in X$, jos kaikilla $\varepsilon \gt 0$ on olemassa sellainen $\delta \gt 0$, että kaikilla $y \in X$, joilla $d(x,y) \lt \delta$, pätee $\rho(f(x),f(y)) \lt \varepsilon$. Kuvaus $f$ on jatkuva avaruudessa $X$, jos se on jatkuva jokaisessa pisteessä $x \in X$.
Katso myös Epäjatkuva, Derivoituva, Differentioituva, Diskreetti, Lipschitz-ehto, Tasaisesti jatkuva, Analyyttinen ryhmä, Bolzanon lause.
Jatkuva satunnaismuuttuja (engl. Continuous random variable)
Satunnaismuuttuja, joka voi saada minkä tahansa arvon tietyltä väliltä (kuten esimerkiksi paino).
Tämän vastakohta on diskreetti satunnaismuuttuja, joka saa arvoja vain äärellisestä tai numeroituvasti äärettömästä joukosta (kuten esimerkiksi perheen lasten lukumäärä).
Katso myös Normaalijakauma, Kertymäfunktio, Gaussin jakauma, Satunnaismuuttuja, Jatkuvan satunnaismuuttujan odotusarvo.
Jatkuva tasainen jakauma (engl. Continuous uniform distribution)
Jatkuvan tasaisen jakauman tiheysfunktio on \[ f(x) = \frac{1}{b-a}, \, x \in [a,b]. \] Jakauman odotusarvo on $\frac{a+b}{2}$, varianssi on $\frac{(b-a)^{2}}{12}$ ja momenttiemäfunktio on $M(t) = \frac{e^{bt} - e^{at}}{(b-a)t}$.
Katso myös Tasainen jakauma, Diskreetti tasainen jakauma.
Jatkuvan satunnaismuuttujan odotusarvo (engl. Mean of a continuous random variable)
Jos satunnaismuuttujan $X$ jakauman tiheysfunktio on $f(x)$, on satunnaismuuttujan $X$ odotusarvo \[ \mathrm{E}(X) = \int_{-\infty}^{\infty} xf(x) dx. \]
Katso myös Jatkuva satunnaismuuttuja.
Jatkuvasti derivoituva (engl. Continuously differentiable)
Funktio on jatkuvasti derivoituva, mikäli se on derivoituva ja sen derivaattafunktio on jatkuva. Funktion sanotaan olevan $C^n$-funktio, mikäli se on $n$ kertaa jatkuvasti derivoituva eli sillä on $n$:nnen kertaluvun jatkuva derivaattafunktio.
Jatkuvuus, Jatkuva (engl. Continuous, Continuity)
Jatkuva suure on sellainen, joka voi tietyin rajoituksin saada arvokseen minkä tahansa lukuarvon. Jatkuva suure on suure, joka ei ole diskreetti. Esimerkkejä jatkuvista suureista ovat pituus ja aika. Esimerkkejä diskreeteistä suureista ovat kengän koko ja kananmunien lukumäärä.
Muuttujan $x$ funktio on jatkuva, jos pieni muutos muuttujassa $x$ saa aikaan ainoastaan pienen muutoksen, ei äkillistä hyppäystä, funktion arvossa.
Funktio on jatkuva, jos sen arvo muuttuu vain vähän, kun funktion parametria muutetaan vain vähän.
Täsmällisemmin tämä voidaan ilmaista seuraavasti. Olkoon $f \colon \mathbb{R} \rightarrow \mathbb{R}$, ja olkoon $x_0 \in \mathbb{R}$. Sanomme, että $f$ on jatkuva pisteessä $x_0$, jos kaikilla $\epsilon \gt 0$ on olemassa sellainen $\delta >0$, että $|f(x)-f(x_0)| \lt \epsilon$ aina, kun $|x-x_0| \lt \delta$.
Sanomme, että $f$ on jatkuva joukossa $\mathbb{R}$, jos se on jatkuva kaikissa pisteissä $x_0 \in \mathbb{R}$.
Olkoot $(X, \tau)$ ja $(Y, \eta)$ topologisia avaruuksia. Kuvaus $f: X \to Y$ on jatkuva, jos jokaisen avoimen joukon $V \subset Y$ alkukuva $f^{-1}(U) \subset X$ on avoin. Jatkuvat kuvaukset säilyttävät yhtenäisyyden ja kompaktisuuden.
Olkoot $(X,d)$ ja $(Y, \rho )$ metrisiä avaruuksia. Kuvaus $f : X \to Y$ on jatkuva pisteessä $x \in X$, jos kaikilla $\varepsilon \gt 0$ on olemassa sellainen $\delta \gt 0$, että kaikilla $y \in X$, joilla $d(x,y) \lt \delta$, pätee $\rho(f(x),f(y)) \lt \varepsilon$. Kuvaus $f$ on jatkuva avaruudessa $X$, jos se on jatkuva jokaisessa pisteessä $x \in X$.

Katso myös Epäjatkuva, Derivoituva, Differentioituva, Diskreetti, Lipschitz-ehto, Tasaisesti jatkuva, Analyyttinen ryhmä, Bolzanon lause.
Jeni (engl. Yen)
Japanin rahayksikkö.
Jensenin epäyhtälö (engl. Jensen's inequality)
Olkoon $f \colon (a.b) \rightarrow \mathbb{R}$ konveksi funktio. Tällöin kaikilla luvuille $p_i$, joille $ \sum_{i=1}^n p_i=1 $ ja $ x_i \in (a,b) $, pätee \[f \left( \sum_{i=1}^n p_ix_i \right) \leq \sum_{i=1}^n p_i f(x_i). \] Jos $f$ on aidosti konveksi, on myös epäyhtälö tiukka.
Tärkeä seuraus tälle on se, että jos $X$ on satunnaismuuttuja, jolle $ \mathbb{P}(X=x_i)=p_i $, niin tällöin $ f( \mathbb{E} X) \leq \mathbb{E} f(X)$.
Katso myös Markovin epäyhtälö, Chebyshevin epäyhtälö.Jos $f$ on konveksi funktio, niin jokaiselle jonolle $x_1, x_2, \dots, x_n$ pätee \[ \mathrm{f} \left ( \frac {\mathrm{x}_{1} + \mathrm{x}_{2}+ ... + \mathrm{x}_{\mathrm{n}} }{\mathrm{n}} \right ) \leq \frac{ \mathrm{f}( \mathrm{x}_{1}) + \mathrm{f}( \mathrm{x}_{2}) +... + \mathrm{f}( \mathrm{x}_{ \mathrm{n} } ) }{ \mathrm{n}} .\] Jos $f$ on konkaavi, on epäyhtälö toisin päin.
Katso myös Erisuuruus, Markovin epäyhtälö, Konveksi, Konkaavi, Epäyhtälö.
Johnsonin lause (engl. Johnson's theorem)
Jos kolmella samasäteisellä ympyrällä $A$, $B$ ja $C$ on yhteinen piste, niin kolme muuta niiden leikkauspistettä sijaitsevat ympyrällä, jonka säde on sama kuin ympyröiden $A$, $B$ ja $C$ säde.
Johtaa (engl. Derive)
Etsiä kaava tai yhtälö jollekin. Päätelmäketjua, jossa tunnetuista tosiasioista lähtien päädytään uuteen kaavaan tai lauseeseen, sanotaan kaavan tai lauseen johtamiseksi.
Katso myös Perustelu.
Johtopäätös, Siksi, implikaationuoli (engl. Therefore)
Merkki $\Rightarrow$ on nimeltään implikaationuoli ja se tarkoittaa, että merkin oikeanpuoleinen väittämä on seuraus vasemmanpuoleisista väittämistä. Väittämä, joka on merkin $\Rightarrow$ perässä seuraa loogisesti siitä, mitä ennen merkkiä on.
Katso myös Seurata, Aiheuttaa jotakin, Olla jonkin riittävä ehto.
Jokaisella, Kaikilla (engl. For each, For all, For every)
Merkki $\forall$ tarkoittaa, että jokin on totta kaikilla tietyn muuttujan arvoilla.
Esimerkiksi $\forall x (x^{2} \ge 0)$ tarkoittaa, että kaikilla muuttujan $x$ arvoilla lausekkeen $x^{2}$ arvo on suurempi tai yhtä suuri kuin nolla.
Katso myös Muuttuja, On olemassa, Jollakin.
Jollakin, On olemassa (engl. There exists, Exists)
Symboli $\exists$ tarkoittaa, että jollakin tietyllä muuttujalla on sellainen arvo, jolla jokin on totta.
Esimerkiksi $ \exists x (x^3 \gt 0)$ tarkoittaa, että muuttujalla $x$ on (ainakin yksi) sellainen arvo, jolla $x^{3}$ on suurempi kuin nolla.
Katso myös Kaikilla, Jokaisella.
Jono (engl. Sequence)
Kun vaikkapa luokan oppilaat asettuvat peräkkäin, heistä muodostuu jono. Myös esineitä voi asetella jonoon.
Lukujono voi olla äärellinen tai ääretön. Jono $1,2,3$ on äärellinen lukujono. Luonnolliset luvut tavallisessa järjestyksessään muodostavat äärettömän lukujonon: $0,1,2,3,\ldots$. (Huomaa, että on sopimuskysymys, sisältyykö nolla luonnollisiin lukuihin vai ei.) Lukujonossa alkioiden järjestys on merkitsevä ja sama alkio voi esiintyä useammin kuin kerran. (Jonot $1,2$ ja $2,1$ ovat eri jonoja, mutta $\{1,2\}=\{2,1\}$.)
Ääreton reaalilukujono on funktio, jonka määrittelyjoukko on luonnollisten lukujen joukko ja arvot ovat reaalilukuja. Lyhyemmin merkittynä jono on funktio $s\colon \mathbb{N}\to\mathbb{R}.$ Sen arvoja $s(0),s(1),\ldots$ merkitään tavallisesti $s_0,s_1,\ldots$.
Katso myös Algebra, Lukuteoria, Erotusjono, Aritmeettinen jono, Termi, Geometrinen jono, Joukko, Fibonaccin jono, Kasautumispiste, Bernoullin luvut, Sarja, Monotoninen jono, Cauchy-jono, Harmoninen jono.
Jonokompakti (engl. Sequentially compact)
Topologinen avaruus $X$ on jonokompakti, mikäli sen jokaisella jonolla on suppeneva osajono.
Vertaa kompakti.
Katso myös Kompakti.
Jordanin käyrälause (engl. Jordan curve theorem)
Jokainen Jordanin käyrä eli jatkuva, yksinkertainen, umpinainen tasokäyrä jakaa tason kahteen erilliseen alueeseen, joita voidaan kutsua käyrän sisä- ja ulkopuoleksi.
Katso myös Taso, Lause, Käyrä, Erillinen, Suljettu käyrä, Pistevieras.
Jos (engl. If)
Sanonnat "jos X, niin Y" ja "X:stä seuraa Y" tarkoittavat, että aina silloin, kun X on tosi, myös Y on tosi.
Katso myös Seurata, Perustelu, Aiheuttaa jotakin, Olla jonkin riittävä ehto.
Jos ja vain jos (engl. If and only if)
Merkki $\Leftrightarrow$ tarkoittaa "jos ja vain jos" eli $A \Leftrightarrow B$ tarkoittaa "$A$ on tosi jos ja vain jos $B$ on tosi". Sama asia voidaan ilmaista sanomalla, että $A$ ja $B$ ovat loogisesti ekvivalentteja.
Katso myös Joss.
Josefuksen ongelma (engl. Josephus problem)
Oletetaan, että ringissä seisoo $m$ henkilöä ja että rinkiä kiertää henkilö, joka poistaa ringistä joka $n$:nnen henkilön. Josefuksen ongelma on: Kun luvut $m$ ja $n$ on annettu, kuinka minun pitäisi valita paikkani ringissä, jotta minut poistettaisiin viimeisenä?
Katso myös Modulaariaritmetiikka.
Joss (engl. iff)
Lyhenne ilmaisulle "jos ja vain jos". Tälle käytetään myös merkkiä $\Leftrightarrow$.
Katso myös Jos ja vain jos, Lyhenne.
Joukko (engl. Set)
Kokoelma matemaattisia olioita, joita kutsutaan joukon alkioiksi. Joukkoa, johon kuuluvat alkiot $a_1, \dots, a_n$, merkitään $\{a_1, \dots a_n\}$.
Luvut $1,2,3,4$ ja $5$ muodostavat joukon $\{1,2,3,4,5\}$.
Luonnollisten lukujen joukko $\mathbb{N}$ sisältää kaikki luonnolliset luvut. $$\mathbb{N}=\{1,2,3,\dots\}.$$
Teoreettisessa matematiikassa joudutaan tekemään ero joukon ja aidon luokan väliltä, jotta vältyttäisiin Russellin paradoksin osoittamalta ristiriidalta.
Ideana on, että luokaksi lasketaan mikä tahansa kokoelma, mutta joukoksi vain sellaiset, jotka saadaan rakennettua lähtien tyhjästä joukosta soveltaen toistuvasti joukko-opin aksioomia (ZFC).
Kaikkien joukkojen luokka (nk. Russelin luokka) $R$ ei voi olla joukko. Tämä nähdään seuraavasti:
Oletetaan, että $R$ on joukko. Tällöin voidaan muodostaa joukon $R$ osajoukko $A=\{x \in R : \neg x \in x \}$. Nyt pätee joko $A \in A$ tai $\neg A \in A$. Todistamme, että kumpikin vaihtoehto johtaa ristiriitaan.
Oletetaan $A \in A$. Tällöin $A$:n määritelmän nojalla $\neg A \in A$, koska kaikki $A$:n alkiot täyttävät tämän ehdon. Siis $A \in A$ ja $\neg A \in A$, mikä on ristiriita.
Oletetaan $\neg A \in A$. Tällöin $A$:n määritelmän nojalla $A$ kuuluu joukkoon $A$, eli $A \in A$, mikä on ristiriita.
Katso myös Yhteenlasku, Vasta-alkio, Käänteisalkio, Kolmikko, Reuna, Nollakohtien joukko, Pari, Kuva, Cantorin joukko, Mahtavuus, Sisältää, Raja, Yhdiste, Aidosti positiivinen, Yksi yhteen kuvaus, Yksi yhteen vastaavuus, Jäsen, Kuulua joukkoon, Tyhjä joukko, Komplementtijoukko, Ei-negatiivinen, Joukkojen leikkaus, Järjestetty, Kuvajoukko, Väli, Sisäosa, Erillinen, Osajoukko, Topologia, Lähtöjoukko, Maalijoukko, Funktion kuvajoukko, Arvojoukko, Funktion maalijoukko, Kertolaskun käänteisalkio, Käänteisluku, Luonnollinen luku, Rengas, Kokonaisluku, Jono, Virittäjistö, Avoin joukko, Sigma-algebra, Avoin peite, Kantaja, Karteesinen tulo, Normalisaattori, Kontinuumi, Suljettu joukko, Osittaisjärjestetty joukko, Mitallinen joukko, Sentralisaattori, Ekvivalenssiluokka, Russellin paradoksi, Attraktori, Pallo, Binäärinen relaatio, 2-paikkainen relaatio, Kategoria, Konjugaattiluokka, Jatkumo, Sivuluokka, Data, Aineisto, Pistevieras, Määrittelyjoukko, Alkio, Sisus, Alkio, Metrinen avaruus.
Joukkojen leikkaus (engl. Intersection of sets)
Joukkojen $A$ ja $B$ leikkaus on joukko, jonka alkioita ovat ne alkiot, jotka kuuluvat sekä joukkoon $A$ että joukkoon $B$. Sitä merkitään $A \cap B$.
Katso myös Yhdiste, Leikkauksen todennäköisyys, Leikkaus, Joukko.
Joukon halkaisija (engl. Diameter of a set)
Joukon halkaisijaksi kutsutaan joukon minkä tahansa kahden alkion välistä suurinta etäisyyttä.
Katso myös Halkaisija.
Jungin lause (engl. Jung's theorem)
Joukko, jonka läpimitta on pienempi tai yhtä suuri kuin 1, voidaan peittää ympyrällä, jonka halkaisija on $\frac{2}{\sqrt{3}}$.
Juuri (engl. Root)
Luvun $x$ neliöjuuri on se luku, joka on korotettava neliöön eli toiseen potenssiin, jotta saataisiin $x$. Luvun $x$ neliöjuurta merkitään $\sqrt{x}$. Luvun $x$ kuutiojuuri eli kolmas juuri on se luku, joka on korotettava kolmanteen potenssiin, jotta saataisiin $x$. Luvun $x$ kuutiojuurta merkitään $\sqrt[3]{x}$.
Yleisesti luvun $x$ $n$:s juuri on se luku, joka on korotettava positiivisen kokonaisluvun $n$ osoittamaan potenssiin, jotta saataisiin $x$. Luvun $x$ $n$:ttä juurta merkitään $\sqrt[n]{x}$.
Katso myös Kuutiojuuri, Juurilauseke, Juurrettava, Potenssiin korottaminen, Laskutoimitus, $n$:s juuri, Neliöjuuri.
Juurilauseke (engl. Radical)
Lauseke, joka sisältää juuren, erityisesti jos se ei ole kokonaisluku.
Katso myös Lauseke, Juurrettava, Juuri.
Juurimerkki (engl. Radical sign)
Merkkiä $\sqrt{\,}$, joka tarkoittaa sen alla olevan suureen neliöjuurta, sanotaan juurimerkiksi.
Katso myös Neliöjuuri.
Juurrettava (engl. Radicand)
Lausekkeessa kuten $\sqrt{5}$ juurimerkin alla olevaa lukua (tässä tapauksessa 5) kutsutaan juurrettavaksi.
Katso myös Luku, Lauseke, Juurilauseke, Juuri.
Jälki (engl. Trace, Spur)
Neliömatriisin jälki on sen päälävistäjällä olevien alkioiden summa.
Katso myös Päälävistäjä, Neliömatriisi, $\tr$.
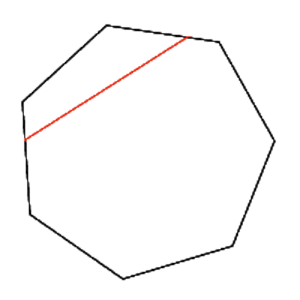
Jänne, Sekantti (engl. Chord or secant line, Secant, Secant line, Chord)
Jana, joka yhdistää kaksi kuvion reunan pistettä. Useimmiten reuna on ympyrän kehä. Ympyrän halkaisija on eräs ympyrän jänne.
Katso myös Kaari, Arc, Ympyrä, Tangentti, Segmentti, Säde, Halkaisija, Jana, $\sec$, Suorien leikkauspiste, Ympyrän kehä, Yhteinen jänne, Konsyklinen.
Jännenelikulmion kulmat (engl. Angles in a cyclic quadrilateral)
Jännenelikulmio on nelikulmio, joka on piirretty ympyrän sisään niin, että sen kärjet ovat ympyrän kehällä.
Jännenelikulmion vastakkaisten kulmien summa on $180^\circ$.
Katso myös Lause.
Jännenelikulmion vastakkaiset kulmat (engl. Opposite angles in a cyclic quadrilateral)
Jännenelikulmion vastakkaiset kulmat ovat toistensa supplementtikulmia eli niiden summa on $180^{\circ}$.
Jännenelikulmion vastakkaiset kulmat ovat supplementtikulmia (engl. Opposite angles of a cyclic quadrilateral are supplementary)
Jännenelikulmion vastakkaiset kulmat ovat supplementtikulmia
Katso myös Jännenelikulmion kulmat, Lause, Suplementtikulma.
Järjestetty (engl. Ordered)
Joukko on järjestetty, jos joukossa voidaan määritellä sellainen transitiivinen relaatio $<$, että jos $x$ ja $y$ ovat joukon eri alkioita, niin pätee joko $x \lt y$ tai $y \lt x$.
Tämä antaa mahdollisuuden asettaa minkä tahansa alkioparin ja siten myös koko joukon yksiselitteiseen järjestykseen. Siten reaalilukujen joukko on järjestetty, mutta kompleksilukujen joukko ei ole.
Katso myös Transitiivinen, Järjestys, Järjestämätön, Joukko.
Järjestetty pari (engl. Ordered pair)
Lukupari tai minkä tahansa alkioiden pari, jossa parin jäsenten järjestys on tärkeä. Järjestetty pari kirjoitetaan merkitsemällä sulkeet lukujen ympärille, esimerkiksi $(4,\,3)$.
Järjestettyjä pareja käytetään usein tietyn pisteen paikantamiseen kartalta tai ruudukolla. Esimerkiksi $(5,\,8)$ tarkoittaa pistettä, joka sijainti on 5 yksikköä oikealle sekä kahdeksan yksikköä ylös, ja se on eri piste kuin $(8,\,5)$.
Katso myös Pari.
Järjestys (engl. Order)
Joukon alkioiden kesken vallitseva relaatio, jota voidaan pitää relaatioiden "suurempi kuin" tai "suurempi tai yhtä suuri kuin" yleistyksenä. Järjestysrelaation $R$ tunnusomainen piirre on transitiivisuus: jos $a\, R\, b$ ja $b\, R\, c$, niin $a\, R\, c$.
Katso myös Kiertosymmetrian kertaluku, Transitiivinen, Funktio, Kuvaus, Järjestetty, Solmun aste, Osittaisjärjestys, Äärellisen joukon kertaluku, Asymptoottinen kasvunopeus, Ryhmän alkion kertaluku, Polynomin aste, Osittainen järjestys, Ryhmän kertaluku.
Järjestysluku (engl. Ordinal, Ordinal number)
Luku, joka osoittaa paikan tai järjestyksen, jossa jokin esiintyy. Esimerkiksi tämän päivän ruokajonossa Jenni oli ensimmäisenä, Mari toisena, Riina kolmantena, Kalle viidentenä, Timo kuudentena, Mikko yhdeksäntenä ja Toni kahdentenatoista. Ensimmäinen, toinen, kolmas, neljäs, viides, kuudes, seitsemäs, ... ovat järjestyslukuja ja ne kirjoitetaan 1., 2., 3., 4., 5., ... , 15., ... , 31., $\dots$, 52., $\dots$
Katso myös Perusluku, Luonnollinen luku.
Järjestämätön (engl. Unordered)
Olioiden joukko tai kokoelma on järjestämätön, jos sen olioiden järjestyksestä ei ole sovittu tai järjestyksellä ei ole väliä.
Katso myös Järjestetty.
Järjettömyys (engl. Absurdity)
Järjettömyys on asia, joka selvästi on mahdoton. Joskus voidaan todistaa väite todeksi osoittamalla, että väitteen epätotuudella olisi järjettömiä seurauksia.
Katso myös Ristiriitatodistus.
Jäsen, Alkio (engl. Member)
Jäännösluokkarengas (engl. Quotient ring)
Olkoon $R$ on rengas ja $I$ on sen (sekä vasemman- että oikeanpuoleinen) ideaali.
Merkitään $a + I=\{ a + i \mid i \in I \}$.
Jäännösluokkarengas $(R/I, +, *)$ määritellään niin, että $R/I=\{ a I \mid a \in R \}$. Laskutoimitukset määritellään niin, että $(a + I) + (b + I) = (a+b) + I$ ja $(a + I)*(b + I)=(ab) + I$. Yhtälöissä oikealla puolella on renkaan $R$ laskutoimitukset.
Voi käydä niin, että $a + I = b + I$, vaikka $a \neq b \in G$. Kuten jäännösluokkaryhmänkin kohdalla, voidaan osoittaa, että laskutoimitukset ovat riippumattomia edustajien valinnasta.
Jäännösluokkaryhmä (engl. Quotient group)
Olkoon $G$ ryhmä ja $H$ sen normaali aliryhmä. Jäännösluokkaryhmä $(G/H, *)$ määritellään seuraavasti.
$G/H$ on joukko $\{aH \mid a \in G\}$.
$(aH) * (bH)=(ab)H$, missä oikeanpuoleinen laskutoimitus on ryhmän $G$ laskutoimitus.
Voi käydä niin, että $aH=cH$, vaikka $a \neq c$. Jos $H$ on normaali aliryhmä, voidaan osoittaa, että jäännösluokkaryhmän laskutoimitus on riippumaton edustajien valinnasta, eli $(ab)H=(cd)H$ aina, kun $aH=cH$ ja $bH=dH$.
Jos $H$ on aliryhmä, joka ei ole normaali aliryhmä, voi käydä niin, että ylläesitetty riippumattomuus edustajasta ei päde. Tämän johdosta jäännösluokkaryhmä $G/H$ määritellään vain silloin, kun $H$ on normaali aliryhmä.
Olkoon $G=(\mathbb{Z},+)$ ja $H=\{ 2n \mid n \in \mathbb{Z}\}$. Jäännösluokkaryhmä $G/H$ on kahden alkion ryhmä, alkioita merkitään symboleilla $0$ ja $1$. Laskusäännöt ovat seuraavat
- $0 + 1 = 1$.
- $1 + 0 = 1$.
- $1 + 1 = 0$.
- $0 + 0 = 0$.
Katso myös Ryhmä, Normaali aliryhmä, Sivuluokka.
Jäännöstermi, Virhetermi (engl. Error term, Remainder term)
Taylorin sarjaan tai mihin tahansa sarjaan lliittyvä termi $R_{n}$. Yleensä tällaisen termin arvo saadaan mielivaltaisen pieneksi valitsemalla indeksi $n$ riittävän suureksi. Tämä voidaan osoittaa ilmaisemalla jäännöstermi sopivassa muodossa.
Katso myös Termi, Taylorin sarja, Maclaurinin sarja, Ominaisuus, jonka arvot ovat jatkuvia, Jäännöstermin Cauchyn lauseke, Jäännöstermin integraalilauseke, Lagrangen jäännöstermi.
Jäännöstermin Cauchyn lauseke (engl. Cauchy form)
Funktion $f$ Taylorin kehitelmän jäännöstermin $R_{n}$ Cauchyn lauseke on \[ R_{n} = \frac{(x-\xi)^{n}}{n!}(x-x_0) f^{(n+1)}(\xi), \] missä $\xi$ on lukujen $x_0$ ja $x$ välissä.
Jäännöstermin Cauchyn lauseke saadaan Schlömilchin lausekkeesta erikoistapauksena asettamalla $p = 1$.
Katso myös Taylorin sarja, Cauchy, Virhetermi, Jäännöstermi.
Jäännöstermin integraalilauseke (engl. Integral form)
Funktion $f$ Taylorin sarjan jäännöstermi $R_{n}$ voidaan kirjoittaa muodossa \[ R_n = \frac{1}{(n - 1)!} \int_a^x (x-t)^{(n-1)}f^{(n)}(t)dt. \]
Katso myös Taylorin sarja, Virhetermi, Jäännöstermi.