Matematiikan verkkosanakirja

Radiaanin, kulman yksikön, lyhenne.

Katso myös Lyhenne, Radiaani.

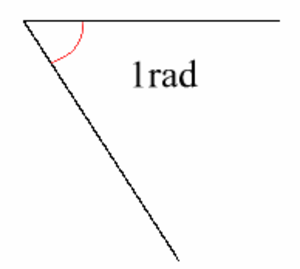
Kulman yksikkö. Radiaani on kulma, jonka muodostaa ympyrän säteen pituinen ympyrän kaari. Siten koko ympyrän muodostama kulma on $2 \pi$ radiaania. Radiaanien käyttö yksinkertaistaa joitakin kaavoja, kuten ympyräsektorin pinta-alan kaavaa.

Yksi radiaani on noin 57,29578 astetta. Radiaanin lyhenne on rad.

Katso myös Kulma, rad, Uusaste, Graadi, Ympyrän segmentin pinta-ala.

Kulmanopeuden yksikkö SI-järjestelmässä.

Katso myös SI-yksiköt.

Kulmakiihtyvyyden yksikkö SI-järjestelmässä.

Katso myös SI-yksiköt.

Sanalla arvo tarkoitetaan matematiikassa yleensä lukua tai muuta oliota, joka on jonkin muuttujan paikalla. Lausekkeelle tai funktiolle saadaan arvo sijoittamalla jotkin arvot sen muuttujien paikalle.

Sanotaan, että lukujoukko on ylhäältä rajoitettu, jos voidaan löytää luku, joka on suurempi tai yhtä suuri kuin jokainen lukujoukon luku. Tällaista lukua kutsutaan joukon ylärajaksi. Samalla tavoin lukujoukko on alhaalta rajoitettu, jos on olemassa luku, joka on pienempi tai yhtä suuri kuin jokainen lukujoukon luku. Tällaista lukua sanotaan joukon alarajaksi. Jos lukujoukko on sekä ylhäältä että alhaalta rajoitettu, sanotaan, että se on rajoitettu.

Funktio on rajoitettu, jos sen arvojoukko on rajoitettu.

Katso myös Joukko.

Lukujonon $(a_n)$ raja-arvo on luku, jota lukujonon luvut lähestyvät rajatta, kun $n$ kasvaa rajatta. Jonon ei kuitenkaan tarvitse ikinä saavuttaa raja-arvoaan. Kaikilla lukujonoilla ei ole raja-arvoa.

Täsmällisesti lukujonon raja-arvo voidaan määritellä seuraavasti. Luku $y$ on jonon $(a_n)$ raja-arvo, jos kaikilla $\epsilon>0$ on olemassa sellainen $n_0$, että $|y-a_n| \lt \epsilon$ aina, kun $n \gt n_0$.

Lukujonon $(a_n)$ raja-arvoa $y$ merkitään $y=\lim_{n\rightarrow \infty} a_n$.

Määritellään lukujono $(a_n)$ asettamalla $a_n = 1/n$ kaikilla positiivisilla kokonaisluvuilla $n$. Tällöin $\lim_{n \rightarrow \infty} a_n = 0$. Tämä voidaan perustella seuraavasti. Kun $\epsilon \gt 0$ on annettu, voidaan luvuksi $n_0$ valita mikä tahansa luku $n_0 \ge 1/\epsilon$. Jos nyt $n \gt n_0$, niin $$|a_n - 0| = \frac{1}{n} \lt \frac{1}{n_0} \le \epsilon.$$

Luku $y_0$ on funktion $f$ raja-arvo pisteessä $x_0$, jos $f(x)$ saadaan kuinka lähelle tahansa arvoa $y_0$, kunhan $x$ viedään riittävän lähelle arvoa $x_0$.

Täsmällisesti tämä voidaan määritellä seuraavasti. Luku $y_0$ on funktion $f \colon \mathbb{R} \rightarrow \mathbb{R}$ raja-arvo pisteessä $x_0$, jos seuraava pätee. Jokaisella $\epsilon>0$ on olemassa sellainen $\delta \gt 0$, että $|f(x)-y_0| \lt \epsilon$ aina, kun $|x-x_0| \lt \delta$ ja $x \neq x_0$.

Funktion $f$ raja-arvoa $y_0$ pisteessä $x_0$ merkitään $y_0=\lim_{x \rightarrow x_0} f(x)$.

Katso myös Analyysi, Differentiaali- ja integraalilaskenta, Integraali, Infinitesimaalinen, $\lim$, Derivaatta, Kasautumispiste, Epsilon-delta -analyysi.

Tavallisesti kaavan, yhtälön tai epäyhtälön muodossa esitetty sääntö, joka vaikuttaa systeemin käyttäytymiseen ja estää tiettyjä asioita tapahtumasta. Esimerkki: Ratkaistava yhtälö $x^2+x-2 = 0$, kun rajoitteena on, että ratkaisu toteuttaa ehdon $x \gt 0$. Yhtälön ratkaisut ovat $x = -2$ ja $x = 1$. Ratkaisu $x = -2$ ei kuitenkaan kelpaa, koska se ei toteuta rajoitetta $x \gt 0$.

Katso myös Erisuuruus, Ehto, Ura, Vapausaste, Reunaehto, Epäyhtälö.

Joukko on rajoitettu, jos se mahtuu jonkin ympyrän sisäpuolelle. Täsmällisemmin sanoen, metrisen avaruuden osajoukko $A$ on rajoitettu, jos on olemassa sellaiset avaruuden piste $p$ ja positiivinen luku $K$, että $A$ on joukon $\{x \mid d(x,p) \lt K \}$ osajoukko. Tässä $d(x,p)$ on pisteiden $x$ ja $p$ välinen etäisyys.

Katso myös Totalisti rajoitettu, Prekompakti, Riemannin poistuvan erikoispisteen lause, Metrinen avaruus.

Funktion $f(x)$ sanotaan olevan rajoitetusti heilahteleva suljetulla välillä $[a,b]$, jos on olemassa sellainen luku $M$, että \[ |f(x_1)-f(a)| + |f(x_2) - f(x_1)| + \cdots + |f(b) - f(x_{n-1})| \le M \] pätee kaikilla $a \lt x_1 \lt x_2 \lt \ldots \lt x_{n-1} \lt b$.

Tavallisesti kaavan, yhtälön tai epäyhtälön muodossa esitetty sääntö, joka vaikuttaa systeemin käyttäytymiseen ja estää tiettyjä asioita tapahtumasta. Esimerkki: Ratkaistava yhtälö $x^2+x-2 = 0$, kun rajoitteena on, että ratkaisu toteuttaa ehdon $x \gt 0$. Yhtälön ratkaisut ovat $x = -2$ ja $x = 1$. Ratkaisu $x = -2$ ei kuitenkaan kelpaa, koska se ei toteuta rajoitetta $x \gt 0$.

Katso myös Erisuuruus, Ehto, Ura, Vapausaste, Reunaehto, Epäyhtälö.

Ramanujan esitti useita arvioita piin arvolle, muun muassa \[ \pi \approx \left( 9^2 + \frac{19^2}{22} \right)^{1/4}, \] \[ \pi \approx \frac{63}{25} \frac{ 17 + 15 \sqrt{5} }{7 + 15 \sqrt{5} }, \] \[ 2 \pi \sqrt{2} \approx \frac{99^2}{1103}. \]

Katso myös Piin arvon laskeminen, Leibnizin kaava piin laskemiseksi.

Funktio muotoa $\frac{P}{Q}$, missä $P$ ja $Q$ ovat polynomifunktioita ja $Q$ ei ole nollapolynomi.

Katso myös Funktio, Kuvaus, Polynomirengas.

Murtolauseke, jossa sekä osoittajalauseke että nimittäjälauseke ovat polynomeja. Tällainen lauseke on määritelty niissä pisteissä, joissa nimittäjälauseke eroaa nollasta. Esimerkiksi \[ \frac {x^2 + 3x + 5 } { 2x^3 + x + 4 } \] on rationaalilauseke.

Rationaalifunktio on rationaalilausekkeen määräämä funktio.

Katso myös Lauseke, Polynomi, Elliptinen integraali.

Murtolauseke, jossa sekä osoittajalauseke että nimittäjälauseke ovat polynomeja. Tällainen lauseke on määritelty niissä pisteissä, joissa nimittäjälauseke eroaa nollasta. Esimerkiksi \[ \frac {x^2 + 3x + 5 } { 2x^3 + x + 4 } \] on rationaalilauseke.

Rationaalifunktio on rationaalilausekkeen määräämä funktio.

Katso myös Lauseke, Polynomi, Elliptinen integraali.

Luku on rationaalinen eli rationaaliluku, jos se voidaan kirjoittaa kahden kokonaisluvun osamääränä.

Katso myös Irrationaaliluku, Päättyvä desimaaliluku, Murtoluku, Kokonaisluku, Reaaliluku, Kokonaisluku, Q, Rationaalinen nollakohta.

Funktion $f \colon \mathbb{R} \rightarrow \mathbb{R}$ rationaalinen nollakohta on rationaaliluku $q$, jolle $f(q)=0$.

Katso myös Funktion nollakohta, Rationaaliluku.

Etsiä yhtälön tai ongelman ratkaisu.

Katso myös Ratkaisu.

Ratkaisu on vastaus ongelmaan. Toisinaan ratkaisuna ilmoitetaan lukuja kuten muuttujan arvo tai muuttujien arvot, jotka toteuttavat tietyn yhtälön tai yhtälöryhmän. Differentiaaliyhtälön ratkaisu on funktio tai joukko funktioita.

Ratkaisulla voidaan myös tarkoittaa laajempaa selostusta.

Katso myös Polynomin nollakohta, Ratkaista, Toisen asteen yhtälön ratkaisu, Ensimmäisen kertaluvun rekursioyhtälön ratkaisu, Yhtälö.

Jos $z=x+y i$ on kompleksiluku, niin $\Re(z)$ tarkoittaa luvun $z$ reaaliosaa eli $\Re(z) = x$.

Katso myös Lyhenne, $\Im(z)$.

Reaaliluku on luku, joka voidaan esittää desimaalilukuna. Desimaaliesitys voi sisältää äärettömän monta desimaalia.

Kokonaisluvut, murtoluvut, irrationaaliluvut ja transkendenttiset luvut ovat kaikki reaalilukuja, mutta imaginaariluvut eivät ole. Luvun on sijaittava tavallisella yksiulotteisella lukusuoralla, jotta se olisi reaalinen.

Katso myös Kompleksiluvun argumentti, Irrationaaliluku, Luku, Yläraja, Trigonometristen funktioiden tarkat arvot, Lukusuora, Rationaaliluku, Virhe, Kokonaisluku, Prosentti, Etumerkillä varustettu luku, Käänteisluku, Suurin lukua pienempi kokonaisluku, Alaraja, Luonnollinen luku, Suppenemissäde, Vektorin normi, Matriisin normi, Algebrallinen luku, Cauchy-Schwarzin epäyhtälö, Vertailtavissa olevat, Kompleksiluku.

Reaalisen symmetrisen matriisin ominaisarvot ovat reaalisia.

Katso myös Lause, Symmetrinen matriisi, Ominaisarvo.

Kauppojen alennusmyynneissä tavaroiden hinnat ovat alennettuja. Alkuperäisestä hinnasta on otettu rahaa pois, tavarat maksavat vähemmän. Myydäkseen tavaroita kauppiaat usein lupaavat kiinteän summan, joka otetaan pois kaikista hinnoista, esimerkiksi 5 euroa. Tällöin kaikki tavarat maksavat 5 euroa vähemmän.

Toisinaan kauppiaat alentavat hintoja kiinteällä prosentilla, esimerkiksi 10%:lla. Tällöin hinnasta otetaan pois 10 senttiä jokaista euroa kohti.

Alentaa jotakin, yleensä rahamäärää, tarkoittaa tehdä se pienemmäksi.

Katso myös Vähetä, Vähentyä.

Mikäli muuttujien välinen riippuvuus on lineaarista, eikä käyräviivaista, niin riippuvuutta (miten $Y$:n odotusarvo riippuu $X$:n saamasta arvosta) voidaan kuvata pienimmän neliösumman suoralla (eli PNS-suoralla). Mikäli käytössä on n havainnon otosaineisto $(x_i,y_i)$, on aineistoon sovitetun PNS - suoran yhtälö Y:lle $$ Y - \bar{Y} = b(X- \bar{X} ) , $$ missä $$ b = \frac{\sum (x_i - \bar{X} ) (y_i - \bar{Y} ) } { \sum ( x_i - \bar{X} ) ^2 } = \frac{\sum \frac{x_i y_i}{n} - \bar{X} \bar{Y} } {\sum \frac{x_i ^2 }{n} - \bar{X} ^2 } $$ Tulkinta: Mikäli selittävän muuttujan $X$ arvoa muutetaan yhdellä yksiköllä muuttuu muuttuja $Y$ keskimäärin $b$ yksikköä.

Ei harhainen. Noppaa sanotaan harhattomaksi tai reiluksi, jos noppaa heitettäessä on jokainen silmäluku yhtä todennäköinen tulos.

Jos noppaa toistuvasti heittäessäsi saat jatkuvasti tulokseksi silmälukuja kolme ja viisi, alat pian epäillä nopan olevan harhainen ja epäreilu.

Katso myös Epäreilu, Harhainen, Puolueellinen, Harhainen.

Prosessi, joka tavallaan 'puree omaa häntäänsä'.

Esimerkkinä luvun kertoman laskeminen. Oletetaan, että haluamme laskea kertoman 6!

Tiedämme, että 6! = 6 * 5!

Tiedämme myös, että 5! = 5 * 4!

ja että 4! = 4 * 3!

ja että 3! = 3 * 2!

ja että 2! = 2 * 1!

ja että 1! = 1 * 0!

ja vihdoin että 0! = 1.

Siis 1! = 1 * 1 = 1,

joten 2! = 2 * 1 = 2.

joten 3! = 3 * 2 = 6.

joten 4! = 4 * 6 = 24.

joten 5! = 5 * 24 = 120,

joten 6! = 6 * 120 = 720.

Prosessia kutsutaan rekursiiviseksi, koska siinä lasketaan yksi kertoma laskemalla aluksi tietty toinen kertoma, joka taas lasketaan laskemalla tietty kolmas kertoma jne, kunnes lopulta saavutetaan tapaus 0!, joka jo tunnetaan (0! = 1).

Olkoon $(x, \tau)$ topologinen avaruus, ja $A \subset X$. Joukosta $A$ voidaan tehdä topologinen avaruus määrittelemällä siellä relatiivitopologia $\tau'=\{ V \cap A \mid V \in \tau\}$.

Katso myös Topologia.

Kolmikko $(R, +, *)$ on rengas, mikäli $(R, +)$ on Abelin ryhmä, ja lisäksi seuraavat ehdot ovat voimassa:

• $a * (b + c) = a * b + a * c$ ja $(a + b) * c = a * c+ b * c$ kaikilla $a,b,c \in R$.
• $a * (b * c) = (a * b) * c$ kaikilla $a,b,c \in R$.
• On olemassa sellainen $e \in R \setminus \{0\}$, että kaikilla $a \in R \setminus \{0\}$ pätee $a * e = e * a = a$.

$(\mathbb{Z},+,\cdot)$ on rengas.

$(\mathbb{R},+,\cdot)$ on rengas.

$(\mathbb{N},+,\cdot)$ ei ole rengas, koska se ei sisällä alkioidensa käänteisalkioita yhteenlaskun suhteen.

Kokonaiskertoimiset polynomit muodostavat renkaan polynomien yhteen- ja kertolaskun suhteen.

Laskutoimitusta $+$ ajatellaan renkaan yhteenlaskuna, ja laskutoimitusta $*$ ajatellaan renkaan kertolaskuna.

Kertolaskumerkki $*$ jätetään yleensä pois, eli merkitään $ab =a * b$. Kertolaskun neutraalialkiota merkitään yleensä merkillä $1$.

Toisinaan renkaan määritelmässä ei vaadita, että kertolaskulla on neutraalialkio. Tällöin yllä määritetyä rengasta, jossa on kertolaskun neutraalialkio mukana, kutsutaan ykköselliseksi renkaaksi.

Jos kertolasku toteuttaa lisäksi ehdon

• $a * b = b * a$ kaikilla $a,b \in R$,

Katso myös Yksikkö, Ympyrärenkaan ala, Joukko, Lähtöjoukko, Ryhmä, Kunta, Moduli, Jäännösluokkarengas, Alirengas, Kokonaisalue, Polynomirengas, Vinokunta, Eukleideen rengas, Binäärinen kuvaus, Määrittelyjoukko, Euklidinen rengas, Gaussin kokonaisluvut, Gaussin luvut, Kaksipaikkainen kuvaus.

Vektori, joka saadaan laskemalla yhteen annettu joukko vektoreita.

Katso myös Vektori, Vektorien yhteenlasku.

Joukon tai kuvion reunan muodostavat ne pisteet, joiden ympäristössä on sekä kuvioon kuulumattomia että kuuluvia pisteitä.

Topologisen avaruuden osajoukon $A$ reuna $\partial A$ on joukon $A$ sulkeuman ja sisäpisteiden joukon välinen erotusjoukko.

Katso myös Joukko, Reunaehto.

Funktion arvo sen muuttujien määrittelyalueen reunalla. Reunaehdot yleensä tunnetaan, kun tehtävänä on etsiä tuntematon funktio. Reunaehdot auttavat tällöin esimerkiksi eliminoimaan integroinnin tuottamat tuntemattomat vakiot, jne.

Katso myös Reuna, Rajoite, Rajoitusehto.

Riemannin geometria on geometria, jossa kahden pisteen välisen etäisyyden antaa Riemannin etäisyysfunktio tavallisen Pythagoraan etäisyysfunktion sijaan. Riemannin geometriaa voi ajatella pallon pintana, jossa "suorat" ovat ympyröitä pallon pinnalla. Tällainen geometria on tärkeässä osassa yleisessä suhteellisuusteoriassa.

Riemannin geometriaa kutsutaan myös elliptiseksi geometriaksi.

Katso myös Metriikka.

Hypoteesi, jonka mukaan Riemannin zeta-funktio $\zeta(\mathrm{s}) = \sum^{\infty}_{\mathrm{n}=1} \mathrm{n}^{-\mathrm{s}}$ saa arvon $0$ vain silloin, kun kompleksiluku $s$ on $-2k$ jollakin luonnollisella luvulla $k$, tai kun kompleksiluvun $s$ reaaliosa on $1/2$.

Riemannin hypoteesia ei ole vielä onnistuttu todistamaan. On kuitenkin osoitettu, että sellaisia lukuja $s$, joiden reaaliosa on $1/2$ ja joilla Riemannin zeta-funktio saa arvon $0$, on äärettömän monta.

Katso myös Funktion nollakohta, Hypoteesi, Riemannin zeta-funktio, Kompleksiluku.

Olkoon $D$ alue ja $z_0 \in D$. Jos $f \colon D \setminus z_0 \to \mathbb{C}$ on holomorfinen ja $f$ on rajoitettu lähellä pistettä $z_0$, niin on olemassa $a \in \mathbb{C}$, siten, että $f(z) \to a$, kun $z \to z_0$. Jos määritellään $g \colon D \to \mathbb{C}$ seuraavasti \[ g(z)= \left \{ \begin{array}{cc} f(z) & z \neq z_0 \\ a & z=z_0, \end{array} \right . \] niin $g$ on holomorfinen.

Katso myös Lause, Rajoitettu, Holomorfinen, Analyyttinen.

Funktion $f(x)$ alle päätepisteiden $x=a$ ja $x=b$ väliin jäävä pinta-ala löydetään seuraavasti.

Väli $[a, b]$ jaetaan $n$:ään osaan jakopisteillä $x_{0}, x_{1},... x_{n}$, missä $x_{0}=a$ ja $x_{n}=b$. Osavälien pituudet ovat $x_{1} - x_{0}, ... ,x_{n} - x_{n-1}$. Kultakin osaväliltä $[x_{i}, x_{i+1}]$ valitaan piste $t_i$.

Edellä annettua jakoa vastaava funktion $f(x)$ Riemannin summa $R$ on luku \[ R = \sum_{i=0}^{n-1} (x_{i+1}-x_{i})f(t_{i}). \] Riemannin integraali $\int_{a}^{b} f(x)dx$ määritellään nyt luvun $R$ raja-arvona, kun pisimmän osavälin pituus lähestyy nollaa.

Funktio \[ \zeta(s) = \sum^{\infty}_{n=1} n^{-s}. \] Voidaan osoittaa, että tämä on sama funktio kuin $\prod_{p} (1-p^{-s})^{-1}$, missä tulo lasketaan kaikkien alkulukujen $p$ yli.

Katso myös Alkuluku, Summa, Funktio, Kuvaus, Riemannin hypoteesi.

Kaksi muuttujaa ovat riippumattomia, jos toisen muuttujan arvon muutos ei vaikuta toisen muuttujan arvoon.

Todennäköisyyslaskennassa kaksi tapahtumaa ovat riippumattomia, jos toisen tapahtuman tapahtumisen todennäköisyys ei riipu siitä, onko toinen tapahtuma tapahtunut vai ei. Esimerkiksi nopan heitossa on toisen heiton tulos riippumaton ensimmäisen heiton tuloksesta.

Todennäköisyyslaskennassa kaksi tapahtumaa $A$ ja $B$ ovat riippumattomia, jos pätee \[ \mathbb{P}(A \cap B) = \mathbb{P}(A)\mathbb{P}(B). \]

Kokoelma tapahtumia $\{ A_i : i \in I \}$ on riippumaton, jos \[ \mathbb{P} \left( \bigcap_{i \in J} A_i \right) = \prod_{i \in J} \mathbb{P}(A_i) \] pätee kaikilla äärellisillä $J \subset I$.

Diskreetit satunnaismuuttujat $X_1, \ldots, X_n$ ovat riippumattomia, jos kaikilla $x_1, \ldots, x_n$ pätee \[ \mathbb{P}(X_1 = x_1, \ldots, X_n = x_n) = \prod_{i=1}^n \mathbb{P}(X_i = x_i). \]

Katso myös Riippuva, Keskeinen raja-arvolause.

Tapahtumat $A$ ja $B$ ovat riippumattomia, mikäli tieto siitä, että $A$ on tapahtunut, ei lisää tietoa siitä, onko $B$ tapahtunut vai ei. Tapahtumat $A$ ja $B$ ovat riippumattomia, mikäli $$P(A|B) = P(A).$$ Tämä on yhtäpitävää sen kanssa, että $$P(AB) = P(A)P(B.)$$

Katso myös Leikkauksen todennäköisyys, Tapahtuma, Ehdollinen todennäköisyys.

Riippuva muuttuja on muuttuja, jonka arvo riippuu systeemin muiden muuttujien arvosta. Riippuvan muuttujan arvo ei ole suoraan tutkijan tai matemaatikon muutettavissa tai säädettävissä.

Riippuva tapahtuma on tapahtuma, jonka sattumisen todennäköisyys riippuu jonkin tai joidenkin muiden tapahtumien sattumisesta.

Katso myös Riippumaton.

Väittämä A on riittävä väittämälle B, jos se, että A on tosi, riittää tekemään myös väittämän B todeksi. Usein puhutaan väittämälle riittävistä ehdoista eli joukosta muita väittämiä, joista seuraa, että väittämä on tosi.

Jos väittämä A on sekä välttämätön että riittävä ehto väittämälle B, niin A ja B ovat loogisesti yhtäpitäviä.

Katso myös Looginen ominaisuus, Välttämätön ehto.

Olla noudattamatta sääntöä.

Katso myös Looginen ominaisuus.

Jonkin ikävän tapahtuman tapahtumisen todennäköisyys.

Katso myös Sattuma, Mahdollisuus.

Kolmiulotteisen avaruuden kaksi suoraa ovat ristikkäiset, jos ne eivät leikkaa toisiaan eivätkä ole yhdensuuntaisia.

Katso myös Suora.

Kun kaksi suoraa leikkaavat toisensa, muodostuu neljä kulmaa. Kulmat, jotka sijaitsevat toisiaan vastapäätä, ovat toistensa ristikulmia. Ristikulmat ovat yhtä suuret.

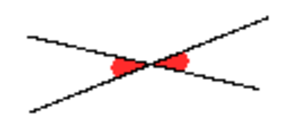
Katso myös Kulma.

Kahden (tai useamman) lauseen joukkoa sanotaan ristiriitaiseksi, jos lauseet tai niiden seuraukset ovat keskenään ristiriidassa.

Katso myös Konsistentti, Yhteensopiva.

Todistustyyppi, jossa aluksi oletetaan, että todistettava väite on epätosi. Tällaista oletusta kutsutaan vastaoletukseksi. Vastaoletusta käyttämällä yritetään sitten johtaa ristitiitainen tai epätodeksi tiedetty väite. Jos tässä onnistutaan, niin oletuksen, että todistettava väite on epätosi, on itse oltava epätosi, koska se johtaa ristiriitaan. Näin on osoitettu, että todistettava väite itse asiassa onkin tosi.

Esimerkki: On todistettava, että ei ole olemassa suurinta kokonaislukua.

Oletetaan, että on olemassa suurin kokonaisluku. Merkitään sitä kirjaimella $N$.

Lisätään lukuun $N$ luku $1$. Nyt $N+1$ on kokonaisluku ja $N+1 \gt N$. Tämä on ristiriidassa oletuksen, että on olemassa suurin kokonaisluku, kanssa. Siis oletus, että on olemassa suurin kokonaisluku, on epätosi. Näin on todistettu, että ei ole olemassa suurinta kokonaislukua.

Katso myös Järjettömyys, Oletus.

Vektorien $\vec{x}=(a, b, c)$ ja $\vec{y}=(d, e, f)$ vektori- eli ristitulo $\vec{x} \times \vec{y}$ on vektori, jonka määrittelee kaava \[\vec{x} \times \vec{y}=(bf-ce, cd-af, ae-bd).\]

Katso myös Tulo, Vektoreiden ristitulon ominaisuudet, Pistetulo, Antikommutatiivinen, Skalaaritulo, Sisätulo.

Vaakasuora suora taulukossa.

Katso myös Merkintätapa, Notaatio, Sarake.

Matriisin rivien virittämä vektoriavaruus.

Katso myös Vektoriavaruus, Lineaarikuvaus, Virittää, Matriisin aste, Matriisi, Kanta, Matriisin dimensio, Lineaarimuunnos.

Jos $f(x)$ on jatkuva kaikilla $a \leq x \leq b$ ja derivoituva kaikilla $a \lt x \lt b$ and $f(a)=f(b)$, niin on olemassa sellainen piste $a \lt c \lt b$, että $ \frac{\mathrm{df}}{\mathrm{dx}}(c) = 0$, tosin sanoen, on olemassa piste $c$, jossa funktion $f(x)$ tangentti on vaakasuora.

Katso myös Lause.

Kreikkalainen kirjain $\rho$ (pieni kirjain) tai P (iso kirjain) lausutaan roo. Sen äänneasu on sama kuin kirjaimen r.

Pieni kirjain $\rho$ on tiheyden tunnus. Sillä merkitään myös kaarevuussädettä sekä populaatiokorrelaatiokerrointa.

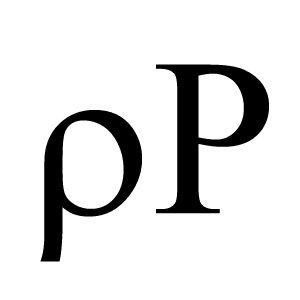
Katso myös Kreikkalaiset kirjaimet, Korrelaatiokerroin, Kaarevuussäde, Tiheys.

Numerot, joita roomalaiset käyttivät lukujärjestelmässään. I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII, XIII, XIV, XV, XVI, XVII, XVIII, XIX, XX, XXI, XXII, XXIII, $\dots$, XXXIX, XL (40), $\dots$, L (50), LI, LII, $\dots$, LXI (61), $\dots$, C (100), $\dots$, D (500), $\dots$, M (1000), $\dots$

Roomalaiset numerot kirjoitetaan siten, että numeron muodostavat numeromerkit asetetaan järjestykseen suurimmasta alkaen. Jos pienempiarvoinen numeromerkki on numerossa ennen suurempiarvoista, se tarkoittaa, että pienempiarvoinen on vähennettävä suuremmasta. Esimerkiksi XL (40) on viisikymmentä miinus kymmenen. CXL (140) on sata plus viisikymmentä miinus kymmenen.CM (900) on tuhat miinus sata.

Televisio-ohjelmien lopussa nähdään usein vuosiluku, jolloin televisioyhtiö on hankkinut ohjelman tekijänoikeudet. Esimerkiksi copyright BBC TV MCMXCV.

Katso myös Numero.

Vektorikentän $F = (F_{x}, F_{y}, F_{z})$ roottori $\nabla \times F$ määritellään seuraavasti: \[ \nabla \times F = \left( \begin{array}{c} \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \\ \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \\ \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \end{array} \right ). \]

Katso myös Vektorianalyysi, Derivaatta, Differentiaalioperaattori.

Matriisi, jota vastaava lineaarikuvaus kiertää tasoa kulman $\theta$ verran origon ympäri, on \[ \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right ) . \]

Katso myös Peilausmatriisi, Matriisi.

Olkoon $S$ niiden joukkojen $x$ muodostama joukko, jotka eivät ole itsensä alkioita. Onko $S$ joukon $S$ alkio vai ei? Jos $S$ on joukon $S$ alkio, niin joukon $S$ määritelmän mukaan $S$ ei ole joukon $S$ alkio. Jos $S$ ei ole joukon $S$ alkio, niin joukon $S$ määritelmän mukaan $S$ on joukon $S$ alkio. Molemmat vaihtoehdot johtavat siis ristiriitaan.

Russellin paradoksi johti 1900-luvun alussa joukkojen teorian täsmentymiseen siten, että yllä esiteltyä joukkoa $S$ ei uudessa joukkojen teoriassa voida määritellä.

Katso myös Paradoksi, Joukko.

Kolmiulotteinen käyrä, jonka piirtää ympyrän kehällä oleva piste ympyrän pyöriessä keskipisteensä ympäri ja samalla liikkuessa pyörimisakseliaan pitkin.

Ruuvikierteen parametrimuotoinen yhtälö on \[ x = r \cos(t), y = r \sin(t), z = c t. \]

Katso myös Käyrä, Ympyräruuvikierre, Kartioruuvikierre, Spiraali.

Kolmiulotteinen käyrä, jonka piirtää ympyrän kehällä oleva piste ympyrän pyöriessä keskipisteensä ympäri ja samalla liikkuessa pyörimisakseliaan pitkin.

Ruuvikierteen parametrimuotoinen yhtälö on \[ x = r \cos(t), y = r \sin(t), z = c t. \]

Katso myös Käyrä, Ympyräruuvikierre, Kartioruuvikierre, Spiraali.

Pari $(G, *)$ on ryhmä, jos $G$ on joukko, ja $*$ on laskutoimitus $G \times G \rightarrow G$, joka toteuttaa seuraavat ehdot:

• Kaikilla $a,b,c \in G$ pätee $a * (b * c) = (a * b) *c$.
• On olemassa sellainen $e \in G$, jolla $a * e = e * a = a$ kaikilla $a \in G$.
• Jokaisella $a \in G$ on olemassa sellainen $b \in G$, jolle $a * b = b * a = e$, missä $e$ on kuten edellisessä pykälässä.

Voidaan osoittaa, että määritelmän $e$ on yksikäsitteinen, ja sitä kutsutaan ryhmän neutraalialkioksi.

Voidaan myös osoittaa, että jokaisella $a \in G$ on yksikäsitteinen $b \in G$, joka toteuttaa määritelmän pykälän 3. Tätä alkiota $b$ kutsutaan alkion $a$ käänteisalkioksi, ja sitä merkitään $b=a^{-1}$.

Monoidi $(G,*)$ on ryhmä, jos se toteuttaa lisäksi seuraavan ehdon:

• Jokaisella $a \in G$ on olemassa sellainen $b \in G$, jolle $a * b = b * a = e$, missä $e$ on ryhmän neutraalialkio.

Pari $(\mathbb{Z},+)$ on ryhmä.

Pari $(\mathbb{R}\setminus\{0\}, \cdot)$ on ryhmä.

Kääntyvät $n \times n$-matriisit muodostavat ryhmän matriisien kertolaskun suhteen.

Jos kontekstista on selvää, mikä laskutoimitus on ryhmällä $(G,*)$, voidaan merkitä lyhyesti $G=(G,*)$.

Katso myös Transformaatioryhmä, Isomorfinen, Monoidi, Abelin ryhmä, Rengas, Kunta, Aliryhmä, Normaali aliryhmä, Jäännösluokkaryhmä, Abstrakti algebra, Syklinen ryhmä, Virittäjistö, Topologinen ryhmä, Normalisaattori, Lien ryhmä, Permutaatioryhmä, Diedriryhmä, Sentralisaattori, Galois'n ryhmä, Ryhmän alkion kertaluku, Algebrallinen topologia, Analyyttinen ryhmä, Cauchyn ryhmälause, Cayley'n lause, Ryhmän keskus, Kommutaattori, Konjugaattiluokka, Ryhmän konjugoidut alkiot, Permutaatio, Lagrangen lause, Ryhmän kertaluku.

Olkoot $G$ ryhmä ja $g$ $G$:n alkio. Alkion $g$ kertaluku on pienin positiivinen kokonaisluku $n$, jolla pätee $g^n = 1$.

Katso myös Järjestys, Ryhmä, Ominaisuus, jonka arvot ovat diskreettejä, Alkio, Ryhmän kertaluku.

Äärellisen ryhmän kertaluku on ryhmän alkioiden lukumäärä. Jos ryhmä on ääretön, on myös kertaluku ääretön. Ryhmän $G$ kertalukua merkitään $|G|$.

Katso myös Järjestys, Ryhmä, Ryhmän alkion kertaluku, Ominaisuus, jonka arvot ovat diskreettejä, Cauchyn ryhmälause, Lagrangen lause.

Ryhmän $G$ osajoukkoa \[ Z(G)= \{ g \in G : gx = xg \text{ kaikilla } x \in G \} \] kutsutaan ryhmän $G$ keskukseksi. Se on itsekin ryhmä.

Katso myös Keskipiste, Kommutoida, Ryhmä, Sentralisaattori.

Ryhmän $G$ alkioita $g$ ja $h$ sanotaan konjugoiduiksi, jos $g = x h x^{-1}$ jollakin $G$:n alkiolla $x$.

Konjugointi on ekvivalenssirelaatio, joten se osittaa ryhmän ekvivalenssiluokkiin. Näitä ekvivalenssiluokkia kutsutaan ryhmän konjugaattiluokiksi.

Katso myös Ryhmä, Ekvivalenssirelaatio, Konjugaattiluokka, Alkio.

1. Olkoon $\theta \colon G \rightarrow H$ ryhmähomomorfismi. Tällöin $\ker \theta \triangleleft G$, ja on olamassa ryhmäisomorfismi $ \bar{\theta} : G/ \ker \theta \to Im (\theta) $ siten, että $\theta$ faktorisoituu \[ G \to G/ ker \theta \overset{\bar{\theta}}{\longrightarrow} Im(\theta) \hookrightarrow H. \] Huomaa erityisesti, että $ G/ \ker \theta \cong Im(\theta) $ .
2. Oletetaan, että $H \leq G$ ja $K \triangleleft G$. Tällöin $HK \leq G$ ja $K \triangleleft HK$. Tällöin pätee lisäksi \[ H/ (H \cap K) \cong HK/K. \]
3. Oletetaan, että $N \triangleleft G$. Tällöin $H \mapsto H/N$ on bijektio sellaisten $G$:n aliryhmien $H$, että $N \leq H$, ja ryhmän $G/N$ aliryhmien välillä. Tällöin $H \triangleleft G$ (oletuksella $N \triangleleft H$) jos ja vain jos $H/N \triangleleft G/N$, ja siis \[ \frac{G/N}{H/N} \cong G/H.\]

Katso myös Lause.