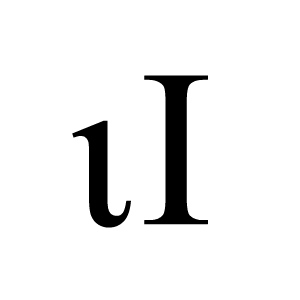Matematiikan verkkosanakirja

Imaginaariyksikkö. Yhtälön $i^{2} = -1$ toteuttava kompleksiluku. Koska $i$ ei ole reaaliluku, se ei ole suurempi eikä pienempi kuin $1$.

Kirjainta $i$ käytetään myös $x$-akselin suuntaisen yksikkövektorin merkintänä: $\vec{i} = (1,0)$ kaksiulotteisessa avaruudessa ja $\vec{i} = (1,0,0)$ kolmiulotteisessa avaruudessa.

Isoa kirjainta $I$ käytetään merkitsemään identtistä kuvausta sekä yksikkömatriisia.

Katso myös Yksikkövektori, Imaginaariluku, $k$, $j$.

Olkoon $R$ rengas. Joukko $I \subset R$ on renkaan $R$ vasen ideaali, jos seuraavat ehdot pätevät:

• $a - b \in I$ kaikilla $a,b \in I$.
• $ma \in I$ kaikilla $a \in I$ ja $m \in R$.

Renkaan oikeanpuoleinen ideaali määritellään samoin, paitsi että jälkimmäinen ehto korvataan ehdolla

• $am \in I$ kaikilla $a \in I$ ja $m \in R$.

$I$ on renkaan $R$ ideaali, jos se on sekä vasemman- että oikeanpuoleinen ideaali.

Olkoon $R=(\mathbb{Z}, + , \cdot)$ ja $n \in \mathbb{Z} \setminus \{0\}$. Kaikkien luvulla $n$ jaollisten kokonaislukujen joukko on renkaan $R$ ideaali.

Katso myös Maksimaalinen, Jäännösluokkarengas, Homomorfismin ydin, Pääideaalialue.

Alkio $a$ on idempotentti laskutoimituksen $\cdot$ suhteen, mikäli $a \cdot a =a$. Esimerkiksi $1$ on idempotentti kertolaskun suhteen. Kaksipaikkainen laskutoimitus on idempotentti, jos jokainen alkio on idempotentti ko. operaation suhteen. Esimerkiksi yhdiste ja leikkaus ovat idempotentteja operaatioita.

Väittämä, joka sanoo, että kaksi lauseketta ovat yhtä suuret kaikilla niissä esiintyvien muuttujien arvoilla.

Katso myös Trigonometrinen identiteetti, Lauseke, Yhtäsuuri, Hyperbolinen identiteetti, Muuttuja, Logaritmikaava, Binomikertoimien summa, Skalaarikolmitulon laskusääntöjä, Vektorikolmitulon laskusääntöjä, $\arcosh$-identiteetti, Sama.

Lävistäjämatriisi, jonka kaikki päälävistäjän alkiot ovat ykkösiä (ja kaikki muut alkiot siis nollia). Yksikkömatriisia merkitään symbolilla $I$.

Koska yksikkömatriisi kerrottuna millä tahansa matriisilla $A$ antaa tulokseksi matriisin $A$, yksikkömatriisin voidaan ajatella olevan identiteettioperaattori tai neutraalialkio.

Katso myös Unitaarinen matriisi, Neutraalialkio, Identtinen laskutoimitus, Lävistäjämatriisi.

Kaksi asiaa ovat identtiset, jos ne ovat itse asiassa yksi ja sama asia.

Kaksi geometrista oliota ovat yhtenevät, jos niiden pisteet voi asettaa pareittain vastaamaan toisiaan siten, että vastinpisteiden etäisyydet kummassakin ovat samat. Yhtenevät kuviot saa toisistaan kierrolla, siirrolla, peilauksella tai näiden yhdistelmällä. Jos peilausta ei tarvita, sanotaan englantilaistyylisissä teksteissä toisinaan, että kuviot ovat identtiset. Tällöin ne ovat yhtenevät ja samoin suuntautuneet.

Siten kolmiulotteisilla olioilla identtisyys tarkoittaa samaa kuin yhtenevyys. Sen sijaan kaksi kaksiulotteista kuviota voivat olla yhteneviä, mutta eivät identtisiä, jos ne ovat toistensa peilikuvia, jolloin niitä ei saada toisistaan kiertämällä.

Katso myös Satunnaismuuttuja.

Funktio joukolta sille itselleen, jossa jokaisen alkion kuva on alkio itse: $f:A\to A$, $f(x)=x$ kaikilla $x\in A$.

Katso myös Funktio, Kuvaus.

Kuvaus, joka kuvaa jokaisen alkion itselleen, eli kuvaus, joka ei muuta mitään alkiota. Sitä merkitään joskus kirjaimella $I$, joten $I(x)=x$ kaikilla kuvauksen määrittelyjoukon alkioilla $x$.

Katso myös Kuvaus, Funktio.

Funktio joukolta sille itselleen, jossa jokaisen alkion kuva on alkio itse: $f:A\to A$, $f(x)=x$ kaikilla $x\in A$.

Katso myös Funktio, Kuvaus.

Laskutoimitus, joka pitää kaikki alkiot samoina. Esimerkiksi luvulla 1 kertominen ja luvun 0 lisääminen ovat identtisiä laskutoimituksia.

Katso myös Laskutoimitus, Yksikkömatriisi, Kategoria, $\cos(x+y)$, Identiteettimatriisi.

Olkoon $R$ rengas. Joukko $I \subset R$ on renkaan $R$ vasen ideaali, jos seuraavat ehdot pätevät:

• $a - b \in I$ kaikilla $a,b \in I$.
• $ma \in I$ kaikilla $a \in I$ ja $m \in R$.

Renkaan oikeanpuoleinen ideaali määritellään samoin, paitsi että jälkimmäinen ehto korvataan ehdolla

• $am \in I$ kaikilla $a \in I$ ja $m \in R$.

$I$ on renkaan $R$ ideaali, jos se on sekä vasemman- että oikeanpuoleinen ideaali.

Olkoon $R=(\mathbb{Z}, + , \cdot)$ ja $n \in \mathbb{Z} \setminus \{0\}$. Kaikkien luvulla $n$ jaollisten kokonaislukujen joukko on renkaan $R$ ideaali.

Katso myös Maksimaalinen, Jäännösluokkarengas, Homomorfismin ydin, Pääideaalialue.

Lyhenne, joka tarkoittaa "riippumattomia, samalla tavalla jakautuneita satunnaismuuttujia". Esimerkiksi noppaa toistuvasti heitettäessä ovat saadut silmäluvut "riippumattomia, samalla tavalla jakautuneita satunnaismuuttujia".

Monitahokas, jossa on 12 kärkeä, 30 särmää ja 20 tahkoa. Säännöllisen ikosaedrin kaikki tahkot ovat samanlaisia tasasivuisia kolmioita. Säännöllinen ikosaedri on yksi viidestä Platonin kappaleesta.

Katso myös 30, Kolmekymmentä, Monitahokas.

Sanoa tai olettaa, että kaksi asiaa ovat yhtä suuret. Esimerkiksi joskus asetetaan samoiksi kertoimet, mikä tarkoittaa, että oletetaan $x$:ien kokonaismäärän olevan sama yhtälön molemmilla puolilla, $x$:n neliöiden kokonaismäärän olevan sama yhtälön molemmilla puolilla, jne.

Jokin on triviaali, jos on hyvin ilmeistä, onko se totta vai epätotta. Usein suuri joukko väittämiä sisältää joitakin triviaaleja väittämiä.

Joskus tätä sanaa käytetään liian paljon. Pitäisi sanoa jonkin olevan itsestäänselvä vain, jos se todella on sitä, ei silloin jos se vain näyttää siltä tai emme jaksa vaivautua todistamaan sitä.

Katso myös Looginen ominaisuus.

$\mathrm{Im}(z)$ on kompleksiluvun $z$ imaginaariosa. Jos $z = x+iy$, niin $\mathrm{Im}(z) = y$.

Katso myös Lyhenne, $\Re(z)$.

Kompleksiluku, jonka toinen potenssi on negatiivinen reaaliluku; negatiivisen luvun neliöjuuri. Imaginaariluvut voidaan esittää imaginaariyksikön $i$ avulla muodossa $ai$, missä $a$ on reaaliluku. Imaginaarilukuja on tapana havainnollistaa reaalilukusuoraa vastaan kohtisuoralla lukusuoralla, imaginaariakselilla. Reaali- ja imaginaariakseli määrittävät yhdessä kompleksilukutason.

Katso myös $i$, Kompleksiluku.

Lauseen implikaatio on jokin, joka seuraa kyseisestä lauseesta.

Merkki $\Rightarrow$ on nimeltään implikaationuoli ja se tarkoittaa, että merkin oikeanpuoleinen väittämä on seuraus vasemmanpuoleisista väittämistä. Väittämä, joka on merkin $\Rightarrow$ perässä seuraa loogisesti siitä, mitä ennen merkkiä on.

Katso myös Seurata, Aiheuttaa jotakin, Olla jonkin riittävä ehto.

Yhtälö, kaava tai funktio on implisiittinen, jos se ei ilmaise yhtä muuttujaa muiden muuttujien avulla. Esimerkiksi yhtälö $ab = a+b$ on implisiittinen sekä muuttujan $a$ että muuttujan $b$ suhteen. Yhtäpitävä muuttujan $a$ suhteen eksplisiittinen yhtälö on $a = \frac{b}{b-1}$ olettaen, että $b \ne 1$.

Katso myös Implisiittinen derivointi, Eksplisiittinen.

Jos implisiittinen yhtälö derivoidaan suoraan muuntamatta sitä ensin eksplisiittiseksi, niin tätä kutsutaan implisiittiseksi derivoinniksi. Tällöin joudutaan useinkin käyttämään tulon derivointisääntöä.

Tarkastellaan esimerkiksi yhtälöä $\mathrm{xy} = 2$. Derivoidaan yhtälö $x$:n suhteen käyttämällä tulon derivointisääntöä: $\frac{\mathrm{d}}{\mathrm{dx}}(xy) = 0$ jos ja vain jos \[ \frac{\mathrm{dx}}{\mathrm{dx}}y + x \frac{\mathrm{dy}}{\mathrm{dx}} = 0 \] jos ja vain jos \[ y + x \frac{\mathrm{dy}}{\mathrm{dx}} = 0. \]

Katso myös Derivointisääntö, Implisiittinen.

Funktio $1_A : A \to \{ 0,1 \}$, joka määritellään asettamalla \[ 1_A(x) = \left\{ \begin{array}{cc} 1 & \text{ jos } x \in A \\ 0 & \text{ jos } x \not\in A. \end{array} \right. \] Indikaattoreihin liittyy hyödyllisiä identiteettejä, kuten \[ 1_{A \cap B}(x)= \min(1_A(x),1_B(x)) = 1_A(x) \cdot 1_B(x), \] \[ 1_{A \cup B}(x)= \max(1_A(x),1_B(x)) = 1_A(x) + 1_B(x) - 1_A(x) \cdot 1_B(x), \] \[ 1_{A^{c}}(x) = 1 - 1_A(x). \]

Katso myös Funktio, Kuvaus.

Eräs todistustyyppi.

Olkoon $H$ väite, jossa esiintyy kokonaislukumuuttuja $n$. Todistetaan induktiolla, että $H$ on tosi kaikilla luvuilla $n$:

1) Todistetaan ensin, että $H$ on tosi arvolla $n=1$.

2) Todistetaan sitten, että oletuksesta, että $H$ on tosi arvolla $n=k$ seuraa, että $H$ on tosi arvolla $n=k+1$.

Todistus on nyt valmis, koska kohdan 1) perusteella $H$ on tosi arvolla $n=1$; kohdan 2) perusteella $H$ on tosi arvolla $n=2$; kohdan 2) perusteella $H$ on tosi arvolla $n=3$; kohdan 2) perusteella $H$ on tosi arvolla $n=4$; jne.

Kohdan 2) oletusta, että $H$ on tosi arvolla $n=k$, kutsutaan induktio-oletukseksi.

Suurimman alarajan eli infimumin lyhenne.

Katso myös Infimum, Suurin alaraja.

Infimumin eli reaalilukujoukon suurimman alarajan lyhenne.

Katso myös Lyhenne, Infimum, Suurin alaraja.

Epätyhjällä alhaalta rajoitetulla reaalilukujen joukon osajoukolla on suurin alaraja eli infimum.

Reaaliluku $a$ on joukon $A$ alaraja, jos kaikki joukon $A$ alkiot ovat suurempia tai yhtäsuuria kuin $a$. Joukon $A$ infimum on suurin tällaisista luvuista $a$.

Reaalilukujoukon $\{ x \in \mathbb{R} : x \gt 1 \}$ suurin alaraja on $1$.

Reaalilukujoukon$\{ x \in \mathbb{R} : 3 \ge x \ge 2 \}$ suurin alaraja on $2$.

Reaalilukujoukon $\{ x \in \mathbb{Z} : x \textrm{ on positiivinen ja pariton } \}$ suurin alaraja on $1$.

Katso myös $\inf$, Alaraja, Inf.

Sana "infinitesimaalinen" on muodostettu latinan sanasta "infinitesimus", joka merkitsee sananmukaisesti "äärettömän mones osa". Differentiaali- ja integraalilaskenta perustui alkuvaiheessaan intuitiiviseen ajatukseen infinitesimaalisista luvuista (eli lyhyemmin infinitesimaaleista), jotka ovat äärettömän lähellä nollaa mutta joilla voi kuitenkin jakaa. Tämän ajatuksen täsmällinen muotoilu osoittautui ongelmalliseksi, ja 1800-luvun alkupuolella infinitesimaalisten lukujen käyttö korvattiin täsmällisillä, raja-arvon käsitteeseen perustuvilla määritelmillä. Tästä huolimatta infinitesimaalit elävät edelleen merkinnöissä ja matemaatikkojen kielikuvana.

Abraham Robinson onnistui kehittämään täsmällisen infinitesimaalien kalkyylin 1960-luvulla. Sitä tutkivaa matematiikan osaa kutsutaan epästandardiksi analyysiksi.

Katso myös Muuttuja, Raja-arvo, Delta.

Injektiivinen kuvaus on kuvaus, joka ei kuvaa mitään kahta määrittelyjoukon eri alkiota samaksi arvojoukon alkioksi.

Kuvaus $f : A \to B$ on injektiivinen, jos se toteuttaa ehdon $f(p) = f(q) \Rightarrow p = q$ kaikilla $p, q \in A$. Vertaa käsitteisiin surjektiivinen ja bijektiivinen.

Katso myös Surjektiivinen, Injektio, Bijektiivinen, Monomorfismi.

Kuvaus eli funktio on injektiivinen, jos se kuvaa eri pisteet eri pisteiksi, toisin sanoen, jos se ei kuvaa mitään kahta eri määrittelyjoukon alkiota samaksi arvojoukon alkioksi.

Katso myös Kuvaus, Kuvajoukko, Injektiivinen, Surjektio, Lähtöjoukko, Funktion kuvajoukko, Määrittelyjoukko, Funktio.

Kuvaus $\theta : A \to B$, $\theta(a) = a$, missä $A \subset B$. Tätä kuvausta merkitään $A \hookrightarrow B$.

Katso myös Kuvaus, Funktio.

Jos $|E|$ on esimerkiksi äärellisen joukon alkioiden lukumäärä tai kuvion $E$ pinta-ala, niin pätee \[|A \cup B| = |A| + |B| - |A \cap B|,\] \[|A\cup B\cup C| = |A| + |B| + |C| - |A\cap B|- |B\cap C| -|C\cap A| + |A\cap B \cap C|\] ja yleisesti \[|\bigcup_{i=1}^n A_i| = \sum_{i=1}^n |A_i|-\sum_{i

Katso myös Lause, Äärellisen joukon kertaluku.

Usein tietokoneohjelmissa käytetty lyhenne englannin sanasta "integer" (kokonaisluku) tai luvun kokonaisosa. $\textrm{int}(x)$ tarkoittaa luvun $x$ kokonaisosaa eli lukua, joka saadaan jättämällä luvusta pois sen murto-osa tai desimaaliosa.

Katso myös Lyhenne, Suurin lukua pienempi kokonaisluku, Kokonaisluku.

Integraali voi tarkoittaa kahta eri asiaa. Funktion $f$ integraalifunktio eli määräämätön integraali $F$ on mikä tahansa funktio, jonka derivaatta on $f$.

Funktion määrätty integraali yli välin $[a,b]$, \[\int_a^b f(x) dx,\] on sellaisen summan raja-arvo, jonka termit ovat muotoa $f(x_i)(x_{i+1}-x_i)$, missä $a=x_0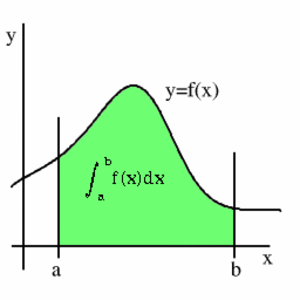

Määrätty integraali voidaan toisinaan laskea integraalifunktion avulla. Kaikille funktioille ei ole tarkkaa integraalifunktion kaavaa. Tällöin joudutaan käyttämään numeerista integrointia eli arvioimaan pinta-alaa numeeristen menetelmien avulla.

Katso myös Pyörähdyskappaleen tilavuus, Lauseke, Differentiaali- ja integraalilaskenta, Epäoleellinen integraali, Integraalifunktio, Määräämätön integraali, Raja-arvo, Määrätty integraali, Antiderivaatta, Konvoluutio, Gammafunktio, Differentiaaliyhtälö, Variaatiolaskenta, Polkuintegraali, Käyräintegraali, Elliptinen integraali, $\erf$, Virhefunktio, Fourier'n kertoimet, Fourier'n muunnos.

Funktion $f$ integraalifunktio eli määräämätön integraali, jota merkitään \[\int f(x)\,dx,\] on mikä tahansa funktio $F$, jonka derivaatta $F'$ on funktio $f$.

Katso myös Integraali, Määrätty integraali.

Määrittää monesta hyvin pienestä muotoa $f(x)\Delta x$ olevasta yhteenlaskettavasta koostuvan summan raja-arvo, kun yhteenlaskettavat pienenevat ja niiden määrä samalla kasvaa rajatta. Tällainen tilanne esiintyy esimerkiksi silloin, kun määritetään positiivisen funktion $f$ ja $x$-akselin välissä olevan alueen pinta-ala: tämä ala voidaan suurin piirtein jakaa suorakaiteen muotoisiin osiin, joiden korkeus on $f(x)$ ja kanta $\Delta x$.

Integrointi voidaan usein toteuttaa derivoinnin käänteisoperaationa. Tämän vuoksi jotkut funktiot voidaan integroida helposti, mutta usein funktio täytyy jakaa osiin, käyttää sijoitusta tai kirjoittaa se jollakin muulla erilaisella tavalla, jotta nähdään, miten se voidaan integroida. Joidenkin funktioiden integraalilla ei ole lainkaan tarkkaa kaavaa. Tällöin joudutaan käyttämään numeerisia menetelmiä pinta-alan laskemiseksi.

Katso myös Integrointisääntö.

Määrätyn integraalin laskeminen tai funktion integraalifunktion määritys. Differentiaaliyhtälön ratkaisemista kutsutaan usein yhtälön integroimiseksi.

Katso myös Integrointivakio, Greenin lause.

Jos integroitava funktio on rationaalifunktio, on sen integroiminen usein helpointa jakamalla se osamurtolukuihin. Esimerkiksi:

\[ \int \frac {1}{\mathrm{x}^2 + 3 \mathrm{x} + 2} \mathrm{dx} = \int \frac {1}{ \mathrm{(x + 1)(x + 2)}}\mathrm{dx} = \int \left ( \frac {1}{\mathrm{x}+1} - \frac {1}{\mathrm{x} + 2} \right ) \mathrm{dx} = \ln ( \mathrm{x} + 1) - \ln ( \mathrm{x} + 2) + \mathrm{C} = \ln \left ( \frac{\mathrm{x} + 1}{\mathrm{x}+2} \right ) + \mathrm{C}. \]

Katso myös Integrointisääntö.

Kutsutaan myös integroinniksi muuttujan vaihdon avulla.

Integrointi sijoituksen avulla perustuu yhtälöön \[ \int f^{\prime}(g(x)) g ^{\prime}(x) dx = f(g(x)) + C. \]

Joskus hankalat integraalit on helpompaa laskea sopivan sijoituksen avulla. Olkoon esimerkiksi \[ \mathrm{I} = \int_0^1 \frac{1}{\sqrt{1-x^2}} dx. \] Sijoitetaan $x = \sin(u)$, jolloin \[ \frac{\mathrm{dx}}{\mathrm{du}} = \cos(u) \] ja \[ 1-x^2 = 1 - \sin^2(u) = \cos^2(u). \] Kun $x = 0$, niin $u = 0$, ja kun $x = 1$, niin $u = \pi / 2$. Saadaan \[ \mathrm{I} = \int_{0}^{\pi / 2} \frac{1}{\sqrt{\cos^2(u)}}\cos(u) \mathrm{du} = \int_{0}^{\pi / 2} \mathrm{du} = \pi / 2. \]

Katso myös Integrointisääntö.

On monia sääntöjä, joita voidaan käyttää monimutkaisten funktioiden integroimiseen. Esimerkkejä tällaisista säännöistä ovat osamurtohajotelma, jonka avulla voidaan integroida murtolausekkeilla määriteltyjä funktioita, sekä osittaisintegrointi, jonka avulla voidaan integroida tulolausekkeista muodosiettuja funktioita.

Kaikkia funktioita ei kuitenkaan voida integroida symbolisesti. On myös olemassa menetelmiä, joilla integraalien likiarvoja voidaan laskea numeerisesti.

Katso myös Summan integrointi, Sääntö, Integroida, Määrärätyn integraalin laskusääntöjä, Osittaisintegrointi, Integrointi osamurtolukujen avulla, Integrointi sijoituksen avulla.

Kun funktio integroidaan, niin tehdään jotakin, joka on vastakkaista derivoinnille, eli etsitään sellainen funktio, jonka derivaatta annettu funktio on. Mutta derivaattafunktio ei kerro integraalifunktionsa etäisyyttä $x$-akselista, vaan ainoastaan, kuinka nopeasti integraalifunktio kasvaa tai vähenee kussakin $x$-akselin pisteessä. Integraalifunktion etäisyys $x$-akselista on siis tuntematon, joten meidän täytyy lisätä integraalifunktioon vakio, jonka arvoa emme tunne. Tätä vakiota kutsutaan integrointivakioksi.

Esimerkki: Funktio $3x^2 + 3$ saadaan derivoimalla funktiot $x^3 + 3x$ ja $x^3 + 3x - 1984$ ja $x^3 + 3x + 100$ jne. Kirjoitamme siis funktion $3x^2 + 3$ integraalifunktion muodossa $x^3 + 3x + C$, missä $C$ on integrointivakio.

Katso myös Vakio, Integrointi.

Interpolointi tarkoittaa funktion arvon estimointia pisteessä, jonka molemmin puolin funkion arvo tunnetaan yhdessä tai useammassa pisteessä. Estimoitua arvoa kutsutaan interpolaatioksi tai interpoloiduksi arvoksi.

Katso myös Estimaatti, Funktio, Kuvaus, Ekstrapoloida.

Relaatio $\sim$ on intransitiivinen, jos se ei ole transitiivinen eli jos ehdoista $a\sim b$ ja $b\sim c$ ei välttämättä seuraa $a\sim c$.

Tämä voi helposti tapahtua esimerkiksi palloilusarjassa, jossa A voittaa B:n ja B voittaa C:n, mutta A ei kuitenkaan välttämättä voita C:tä. Siten voittaminen on intransitiivinen relaatio.

Katso myös Transitiivinen, Looginen ominaisuus.

Jokin, joka ei muutu tietyssä kuvauksessa; arvo, joka pysyy samana, kun siihen sovelletaan tiettyä funktiota.

Pisteen $A$ kuvapiste inversiokuvauksessa ympyrän $C$ suhteen, jonka säde on $r$ ja keskipiste $O$, on se puolisuoralla $OA$ sijaitseva piste $B$, jolle $OA\cdot OB= r^{2}$.

Annettua ympyrää sanotaan inversioympyräksi. Kolmessa ulottuvuudessa käytetään inversioympyrän sijasta inversiopalloa.

Tämä kuvaus pitää paikallaan inversioympyrän, kaikki inversioympyrän kanssa ortogonaaliset ympyrät sekä pisteen $O$ kautta kulkevat suorat. Se ei myöskään muuta kulmien kokoja. Ympyrät ja suorat, jotka eivät kulje $O$:n kautta kuvautuvat kuvauksessa ympyröiksi.

Katso myös Käänteis-.

Kuvaus $f \colon A \rightarrow A$ on involuutio, jos $f^{-1}=f$, tai yhtäpitävästi, $f^2=id_A$.

Katso myös Kuvaus, Funktio.

Kreikan kirjain $\iota$, lausutaan 'joota'.

Katso myös Kreikkalaiset kirjaimet.

Irrationaaliluku on reaaliluku, jota ei voida kirjoittaa kahden kokonaisluvun suhteena. Esimerkkejä irrationaaliluvuista ovat mm. $\sqrt{2}$, $e$ ja $\pi$.

Katso myös Lukuteoria, Rationaaliluku, Transsendenttinen luku, Reaaliluku, Piin irrationaalisuus, Luvun 2 neliöjuuri on irrationaalinen.

Relaatio $R \subset A \times A$ on irrefleksiivinen, mikäli millään $a \in A$ ei päde $a R a$.

Vertaa refleksiivinen.

Isometria eli isometrinen kuvaus säilyttää kaikki vastinpisteiden etäisyydet.

Tason isometrisia kuvauksia ovat siirto, kierto ja peilaus sekä näistä yhdistämällä saadut kuvaukset. Isometrinen kuvaus muuntaa kuvion alkuperäisen kuvion kanssa yhteneväksi kuvioksi.

Katso myös Perspektiivinen affiinikuvaus, Kuva, Isometrinen, Geometrinen muunnos.

Kaksi kuviota $A$ ja $B$ ovat keskenään isometrisiä, mikäli ne voidaan muuntaa toisikseen yhdistelemällä kierto-, siirto- ja peilauskuvauksia.

Metriset avaruudet $(A,d)$ ja $(B,d')$ ovat keskenään isometrisiä, mikäli on olemassa bijektio $f \colon A \rightarrow B$, joka toteuttaa ehdon $d(x,y)=d(f(x),f(y))$ kaikilla $x,y \in A$.

Katso myös Isometria.

Homomorfismi, joka on myös bijektio. Isomorfismi on siis bijektiivinen kuvaus, joka säilyttää määrittelyjoukkonsa algebrallisen struktuurin.

Katso myös Kuvaus, Isomorfinen, Bijektio, Homomorfismi, Lineaarikuvaus, Automorfismi, Morfismi, Homeomorfismi, Lineaarimuunnos, Funktio.

Kahden matemaattisen struktuurin sanotaan olevan isomorfisia, jos niiden välillä on isomorfismi eli bijektiivinen kuvaus, joka säilyttää struktuurien laskutoimitukset tai jotkin struktuurien relaatiot. Toisin sanoen struktuurit $G$ ja $H$ ovat isomorfiset, jos on olemassa bijektiivinen kuvaus $f : G \to H$ ja jos struktuurien laskutoimitukset $\ast$ vastaavat toisiaan niin, että $f(p\ast q) = f(p)\ast f(q)$ kaikilla $p, q \in G$.

Isomorfisia struktuureja voidaan monissa yhteyksissä pitää samoina.

Vektoriavaruudet $V$ ja $W$ ovat isomorfiset, jos on olemassa lineaarikuvaus (isomorfismi) $\varphi : V \to W$, jolla on lineaarinen käänteiskuvaus tai yhtäpitävästi, jos $\varphi$ on lineaarinen bijektio. Vertaa epimorfismi, monomorfismi.

Kahden ryhmän tai monoidin isomorfismi: katso homomorfismi.

Katso myös Isomorfismi, Ryhmä, Cayley'n lause, Isomorfia.

Homomorfismi, joka on myös bijektio. Isomorfismi on siis bijektiivinen kuvaus, joka säilyttää määrittelyjoukkonsa algebrallisen struktuurin.

Katso myös Kuvaus, Isomorfinen, Bijektio, Homomorfismi, Lineaarikuvaus, Automorfismi, Morfismi, Homeomorfismi, Lineaarimuunnos, Funktio.

Kaksi kuviota ovat isoperimetriset, jos niiden ympärysmitat ovat samat.

Etsittävä kaikkien sellaisten kuvioiden, joilla on sama ympärysmitta, joukosta se, jonka pinta-ala on suurin. Ongelman ratkaisu on ympyrä.

Pallon pinnalle piirretty ympyrä, jonka säde on sama kuin pallon säde. Isoympyrä on suurin ympyrä, joka voidaan piirtää annetun pallon pinnalle. Maapallon päiväntasaaja on isoympyrä.

Katso myös Pallokaksikulmio, Ympyrä, Pallogeometria, Meridiaani, Pituuspiiri.

Iteratiivinen menetelmä on jokin, joka liittyy jonkin tekemiseen yhä uudestaan. Esimerkiksi joitakin yhtälöitä voidaan ratkaista numeerisesti iteratiivisella kaavalla, jota sovellettaessa yhä uudestaan saadaan lukujono, joka suppenee kohti yhtälön tarkkaa ratkaisua.

Katso myös Iterointi.

Toistaa samankaltaista laskusuoritusta yhä uudelleen, yleensä niin, että kussakin toistossa käytetään hyväksi edellisessä toistossa saatuja tuloksia.

Iteroiminen tarkoittaa saman menettelyn toistamista yhä uudestaan.

Joskus voidaan löytää yhtälölle likimääräinen ratkaisu iteroimalla. Ratkaistaan esimerkiksi yhtälö $x^{2}+x = 5$. Kirjoitetaan yhtälö muotoon $x = \sqrt{5-x}$ ja määritellään jono $(x_{n})$ kaavalla $x_{n} = \sqrt{5-x_{n-1}}$. Valitsemalla ensimmäiseksi arvaukseksi $x_{0} = 1$ saadaan $x_{1} = 2$, $x_{2} = 1,7320508$, $x_{3} = 1,807747$, $x_{4} = 1,7866877$, $\dots$ Tarkan ratkaisun 7-desimaalinen likiarvo on $1,7912878$.

Katso myös Iteratiivinen, Aritmeettinen prosessi.

Sarja on itseisesti suppeneva, jos sen termeistä itseisarvo ottamalla saatu sarja suppenee.

Katso myös Itseisarvo, Suppeneminen, Konvergenssi, Sarja, Supeta.

Positiivisen (plusmerkkisen) luvun itseisarvo on luku itse, ja negatiivisen (miinusmerkkisen) luvun itseisarvo saadaan tiputtamalla luvun edestä pois miinus.

Luvun itseisarvo on sama kuin luku itse, jos luku on positiivinen, ja sama kuin luvun vastaluku, jos luku on negatiivinen. Itseisarvoa voi pitää luvun etäisyytenä nollasta.

Luvun $x$ itseisarvoa merkitään $|x|$. Esimerkiksi $|3| = 3$ ja $|-5| = 5$.

Katso myös Funktio, Kuvaus, Itseinen suppeneminen.

Jokin on triviaali, jos on hyvin ilmeistä, onko se totta vai epätotta. Usein suuri joukko väittämiä sisältää joitakin triviaaleja väittämiä.

Joskus tätä sanaa käytetään liian paljon. Pitäisi sanoa jonkin olevan itsestäänselvä vain, jos se todella on sitä, ei silloin jos se vain näyttää siltä tai emme jaksa vaivautua todistamaan sitä.

Katso myös Looginen ominaisuus.