s (engl. s)
Sekunnin, SI-järjestelmän ajan yksikön, lyhenne.
s.y.t. (engl. gcd, gcf)
Suurimman yhteisen tekijän lyhenne.
Katso myös Suurin yhteinen tekijä.
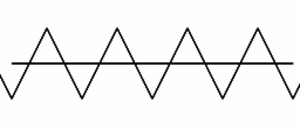
Saha-aalto (engl. Saw tooth, Sawtooth)
Jaksollinen funktio, joka koostuu affiineista paloista, jotka vuorotellen kasvavat ja vähenevät. Kaikilla paloilla on sama pituus ja sama kulmakertoimen itseisarvo.
Salausmenetelmä (engl. Cipher)
Tapa salata kirjainjono muuntamalla se jonkin säännön avulla toiseksi jonoksi kirjaimia tai numeroita.
Katso myös Funktio, Kuvaus, Kryptografia, Kryptologia.
Sama, Identtinen, Yhtenevä (ja samoin suuntautunut) (engl. Identically distributed)
Kaksi asiaa ovat identtiset, jos ne ovat itse asiassa yksi ja sama asia.
Kaksi geometrista oliota ovat yhtenevät, jos niiden pisteet voi asettaa pareittain vastaamaan toisiaan siten, että vastinpisteiden etäisyydet kummassakin ovat samat. Yhtenevät kuviot saa toisistaan kierrolla, siirrolla, peilauksella tai näiden yhdistelmällä. Jos peilausta ei tarvita, sanotaan englantilaistyylisissä teksteissä toisinaan, että kuviot ovat identtiset. Tällöin ne ovat yhtenevät ja samoin suuntautuneet.
Siten kolmiulotteisilla olioilla identtisyys tarkoittaa samaa kuin yhtenevyys. Sen sijaan kaksi kaksiulotteista kuviota voivat olla yhteneviä, mutta eivät identtisiä, jos ne ovat toistensa peilikuvia, jolloin niitä ei saada toisistaan kiertämällä.
Katso myös Satunnaismuuttuja.
Sama, Yhtäsuuri (engl. Equal)
Kaksi tai useampi luku ovat yhtä suuret, jos ne ovat samat tai niillä on sama arvo. Esimerkiksi \[ 18 = \frac{36}{2} = 9 + 9 = 20 - 2 = (4 \cdot 3) + 6. \]
Kaksi joukkoa ovat samat, jos niissä on samat alkiot.
Katso myös Likimäärin, Identiteetti, Suurempi tai yhtäsuuri kuin, Pienempi tai yhtäsuuri kuin, Tasasivuinen, Vertailtavissa olevat, Yhtäsuuruus.
Samaa kaarta vastaavat kehäkulmat (engl. Angles in the same segment)
Mitkä tahansa kaksi saman ympyrän samaan kaarta vastaavaa kehäkulmaa ovat yhtä suuret.
Katso myös Kulma, Lause, Keskuskulmalause, Segmentti, Keskuskulma.
Samanarvoiset murtoluvut (engl. Equivalent fractions)
Murtoluvut, joilla on sama arvo.
Esimerkiksi murtoluvuilla 2/3, 4/6, 6/9, 8/12, 10/15, $\dots$, 20/30, $\dots$, 100/150, $\dots$ on sama arvo.
Katso myös Supistaminen, Murtoluku, Ekvivalentti, Yhtäpitävä.
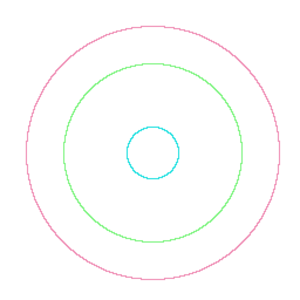
Samankeskinen (engl. Concentric)
Jos kahdella tai useammalla kuviolla on sama keskipiste, ne ovat samankeskisiä.
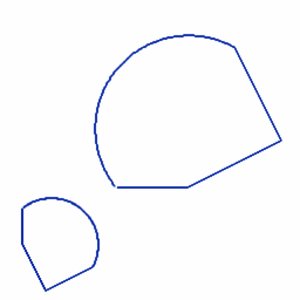
Samanlainen, Yhdenmuotoinen, Similaari (engl. Similar)
Kahden tai useamman kuvion sanotaan olevan yhdenmuotoiset, jos ne ovat saman muotoiset, mutta eivät välttämättä saman kokoiset.
Yhdenmuotoisten kuvioiden vastinsivujen suhde on vakio ja vastinkulmat ovat yhtä suuret.
Katso myös Yhdenmuotoiset kolmiot, Yhtenevät kuviot, Kriteerejä kolmioiden yhdenmuotoisuudelle.
Samassa tasossa oleva (engl. Coplanar)
Pistejoukko on samassa tasossa, jos on olemassa yhteinen taso, jossa kaikki nämä pisteet sijaitsevat. Jokaiselle kolmen pisteen joukolle voidaan löytää tällainen taso, mutta vain joillekin neljän tai useamman pisteen joukoille.
Katso myös Taso, Kollineaarinen.
Sana (engl. Word)
Tietotekniikassa sana on se määrä tietoa, jonka kulloinkin käytössä oleva järjestelmä pystyy käsittelemään yhdellä alkeisoperaatiolla. Yleensä sana on 4 tai 8 tavua, eli 32 tai 64 bittiä.
Sarake (engl. Column)
Taulukon pystyrivi. Taulukon alkion paikan antavan lukuparin jälkimmäinen luku.
Katso myös Rivi, Merkintätapa, Notaatio.
Sarakeavaruus (engl. Column space)
Matriisin sarakkeiden virittämä vektoriavaruus.
Katso myös Vektoriavaruus, Virittää, Matriisi, Matriisin dimensio.
Sarja (engl. Series)
Jono, jonka $n$:s termi on toisen jonon $n$:n ensimmäisen termin summa. Esimerkiksi luonnollisten lukujen jono \[ 1, 2, 3, 4, 5, 6, 7, ... \] johtaa sarjaan \[ 1, 3, 6, 10, 15, 21, 28, .... \]
Katso myös Vuorotteleva sarja, Analyysi, Suppenemiskriteeri, Differentiaali- ja integraalilaskenta, Aritmeettinen sarja, Neliölukujen summa, Geometrinen sarja, Jono, Peräkkäisten kokonaislukujen summa, Peräkkäisten kuutioiden summa, Itseinen suppeneminen, Ääretön sarja, Asymptoottinen sarja, Ääretön tulo.
Sata, 100 (engl. 100, Hundred)
Sattuma, Mahdollisuus (engl. Chance)
Jokin tapahtuu sattumalta, jos sen tapahtumista ei voi ennustaa varmasti, vaan voidaan puhua ainoastaan sen tapahtumisen todennäköisyydestä.
Jonkin tapahtumisen mahdollisuus on sen tapahtumisen todennäköisyys. Sanaa käytetään myös kuvaamaan tilaisuutta tehdä jotakin.
Katso myös Riski, Tapahtuma, Todennäköisyys, Otosavaruus, Ominaisuus, Määrite.
Satunnainen (engl. Random)
Todennäköisyyslaskennassa käytetty termi tapahtumista, joita ei voi ennustaa. Satunnaisuus ei merkitse sitä, että kaikki tulosvaihtoehdot olisivat yhtä todennäköisiä vaan sitä että järjestystä, missä ne tapahtuvat ei voi ennustaa.
Katso myös Benfordin laki, Ominaisuus, Määrite, Satunnaismuuttuja.
Satunnaiskävely (engl. Random walk)
Prosessi, jossa hiukkasen paikka muuttuu askelittain ja jossa jokaisen askeleen suunta valitaan satunnaisesti. Yksiulotteisessa satunnaiskävelyssä on vain kaksi mahdollista suuntaa valittavina. Useampiulotteisessa satunnaiskävelyssä kunkin askeleen suunta voidaan valita suuresta joukosta mahdollisuuksia.
Satunnaismuuttuja (engl. Random variable)
Muuttuja, jonka arvon määrää satunnaiskokeen tulos. Jos esimerkiksi heitämme noppaa ja merkitsemme $X = \text{" silmäluku nopanheitossa"}$, on $X$ satunnaismuuttuja. Tällöin $X$ saa jonkin arvoista $1, 2, 3, 4, 5, 6$ ja arvo riippuu nopanheiton tuloksesta.
Usein voidaan sanoa, mikä on annetun satunnaismuuttujan jakauma. Jakauma kertoo, millä todennäköisyydellä kyseinen satunnaismuuttuja saa kunkin arvonsa. Edellä nopanheitossa on kukin silmäluku yhtä todennäköinen.
Diskreetin satunnaismuuttujan saamat arvot kuuluvat annettuun äärelliseen tai numeroituvasti äärettömään joukkoon (usein kokonaislukujen joukkoon), kun taas jatkuva satunnaismuuttuja voi saada mielivaltaisia reaalilukuarvoja (yleensä joltakin väliltä). Edellä nopanheitossa satunnaismuuttuja $X$ on diskreetti.
Funktio $X : \Omega \to \mathbb{R}$, missä $\Omega$ on perusjoukko eli alkeistapahtumien joukko. Jos $\Omega$ on äärellinen tai numeroituvasti ääretön, satunnaismuuttujan $X$ sanotaan olevan diskreetti.
Katso myös Muuttuja, Identtinen, Sama, Yhtenevä (ja samoin suuntautunut), Jatkuva satunnaismuuttuja, Bernoullin koe, Satunnainen, Harhaton estimaattori, Varianssi, Luokiteltu, Luokka-arvoinen, Luokka-arvoinen muuttuja, Kategorinen, Keskeinen raja-arvolause, Diskreetti satunnaismuuttuja, Markovin ketju.
Satunnaistaminen (engl. Randomisation)
Suunnitelluissa kokeissa käytetty menetelmä. Koeyksilöt (esim. koehenkilöt) jaetaan satunnaisesti eri tavalla käsiteltäviin ryhmiin (esim. rokotettavat - ei rokotettavat). Satunnaistus takaa se, että käsittelyn vaikutusta tutkittaessa ei ryhmien muodostuksesta aiheudu ylimääräistä harhaa (systemaattista virhettä). Koeyksilöiden väliset erot ovat jakautuneet tasaisesti eri ryhmiin.
$\sec$
Sekantin lyhenne. $\sec x$ tarkoittaa luvun $x$ sekanttia eli lukua $1/cos x$.
Katso myös $\arcsec$, Tangentin ja kosinin välinen yhteys, Sekantin neliö, Lyhenne, Sekanttifunktio, Arkussekantti, Hyperbolinen sekantti, Eulerin luvut.
$\sech$
Hyperbolisen sekantin lyhenne. $\mathrm{sech}(x)$ tarkoittaa luvun $x$ hyperbolista sekanttia eli lukua $1/\mathrm{cosh}(x)$.
Katso myös Lyhenne, $\cosh$, Hyperbolinen sekantti, Eulerin luvut.
Segmentti (engl. Segment)
Ympyrän kaaren ja sen päätepisteet yhdistävän jänteen rajoittama ympyrän osa.

Katso myös Ympyrä, Samaa kaarta vastaavat kehäkulmat, Puoliympyrä, Jänne, Ympyrän segmentin pinta-ala, Sekantti.
Seitsemän, 7 (engl. 7, Seven)
Seitsemäs perusluku. Neljäs alkuluku ja toinen heksaedriluku. 7 on kolmas Mersennen luku ja toinen Mersennen alkuluku.
$7!+1$ on neliö. Vain luvuilla 4, 5 ja 7 on tämä ominaisuus.
Luvun 7 Fermat'n osamäärä on neliö. Ainoat luvut, joilla on tämä ominaisuus, ovat 3 ja 7.
7 on kolmas onnenluku.
7 väriä riittää värittämään minkä tahansa kartan toruksen pinnalla.
$\phi(7) = 6$, $d(7) = 2$, $\sigma(7) = 84$.
Katso myös Onnekkaat luvut, Mersennen luku, Seitsemänkulmio, Mersennen alkuluku, Fermat'n osamäärä.
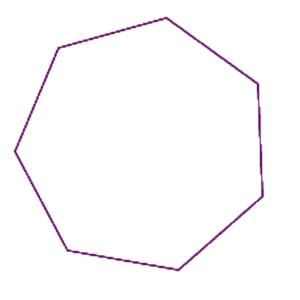
Seitsemänkulmio (engl. Septagon, Heptagon)
Monikulmio, jossa on seitsemän sivua ja seitsemän kulmaa.
Säännöllisessä seitsemänkulmiossa on seitsemän yhtä pitkää sivua ja seitsemän yhtä suurta kulmaa.
Katso myös Seitsemän, 7, Monikulmio.
Seitsemäntoista, 17 (engl. 17, Seventeen)
17 on seitsemäs alkuluku ja kolmas Fermat'n alkuluku.
Säännöllinen 17-kulmio on piirrettävissä vain harppia ja viivoitinta käyttäen.
17 on kahden neljännen potenssin summa: 17 = $1^{4} + 2^{4}.$
$\phi(17) = 16, d(17) = 2, \sigma(17) = 18$.
17 on seitsemäs alkuluku ja kolmas Fermat'n alkuluku.
Säännöllinen 17-kulmio voidaan konstruoida käyttämällä vain harppia ja viivoitinta.
17 on kahden neljännen potenssin summa: $17 = 1^{4}+2^{4}$.
$\phi(17) = 16$, $d(17) = 2$, $\sigma(17) = 18$.

Katso myös Fermat'n alkuluku.
Sekaluku (engl. Mixed number)
Luku, joka on kokonaisluvun ja aidon murtoluvun yhdistelmä, itse asiassa summa. Esimerkiksi 3 1/4, 5 1/2 ja 7 3/4 ovat sekalukuja.
Katso myös Aito murtoluku, Murtoluku.
Sekantin neliö (engl. $sec^2$)
Merkintä $\sec^{2}(x)$ tarkoittaa samaa kuin $[\sec(x)]^{2}$.
Katso myös Merkintätapa, Notaatio, $\sec$.
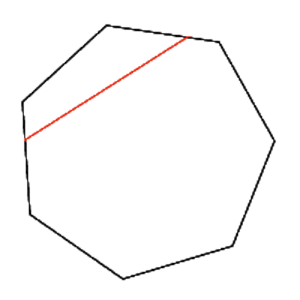
Sekantti, Jänne (engl. Chord or secant line, Secant, Secant line, Chord)
Jana, joka yhdistää kaksi kuvion reunan pistettä. Useimmiten reuna on ympyrän kehä. Ympyrän halkaisija on eräs ympyrän jänne.
Katso myös Kaari, Arc, Ympyrä, Tangentti, Segmentti, Säde, Halkaisija, Jana, $\sec$, Suorien leikkauspiste, Ympyrän kehä, Yhteinen jänne, Konsyklinen.
Sekanttifunktio (engl. Secant, Secant function)
Jos suorakulmaisessa kolmiossa yhden kulman suuruus on $x$, niin kulman $x$ sekantti on hypotenuusan pituuden suhde $x$:n viereisen kateetin pituuteen. $x$:n sekantti on yhtä suuri kuin $1/\cos x$.
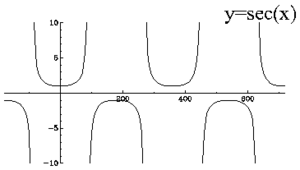
Katso myös $\sec$, Trigonometrinen funktio, $\cos$, Kosini, Kosekantti.
Sektori (engl. Sector)
Sektori on käyrän ja kahden säteen rajoittama alue. Usein käyrä on ympyrän kaari, mutta se voi olla myös osa jotain muuta käyrää.
Kaaren ja kahden säteen rajoittama ympyrän osa tai muun keskipisteellisen kuvion osa.

Katso myös Ympyrä, Puoliympyrä, Ympyrän sektorin pinta-ala, Kuvio.
Sekunti (engl. Second)
Ajan yksikkö SI-järjestelmässä. Sekunnin lyhenne on s. Yhdessä minuutissa on 60 sekuntia eli 60 s = 1 min.
Sekunti on myös kulman yksikkö, yksi sekunti on 1/60 minuuttia.
Katso myös SI-yksiköt.
Sentralisaattori (engl. Centralizer)
Olkoon $G$ ryhmä ja $x \in G$. Alkion $x$ sentralisaattori on joukko \[ C_G(x)= \{g \in G \mid gxg ^{-1}=x \}, \] eli $x$:n kiinnittäjä konjugoinnin suhteen.
Katso myös Joukko, Ryhmä, Stabilisaattori, Ryhmän keskus, Konjugaattiluokka.
Sentti (engl. Cent)
Rahayksikkö, joka on yhtä suuri kuin dollarin tai euron sadasosa.
Katso myös Euro.
Sentti (engl. Centi)
Etuliite, joka tarkoittaa sadasosaa. Tälle käytetään lyhennettä c. Esimerkiksi 1 cm eli yksi senttimetri tarkoittaa metrin sadasosaa.
Katso myös Milli-.
Senttilitra (engl. Centilitre, Centiliter)
Tilavuuden yksikkö, joka on yhtä suuri kuin litran sadasosa tai kymmenen millilitraa. Senttilitran lyhenne on cl.
Katso myös Tilavuus.
Senttimetri (engl. Centimetre, Centimeter)
Pituuden mitta, sama kuin 10 millimetriä tai metrin sadasosa. Senttimetrin lyhenne on cm.
Katso myös Viivoitin, cm, MKSA-järjestelmä, Metri, Millimetri, Kuutiosenttimetri.
Septiljoona (engl. Septillion)
$10^{42}$.
Katso myös Kymmenen potenssit.
Seurata, Aiheuttaa jotakin, Olla jonkin riittävä ehto (engl. Imply, Implies)
Merkki $\Rightarrow$ tarkoittaa "jos ... niin ...". $A\Rightarrow B$ voidaan lukea "jos $A$ niin $B$" tai "$A$:sta seuraa $B$".
$\Rightarrow$ voidaan ajatella loogisena operaattorina, joka antaa tulokseksi "epätosi", jos ensimmäinen argumentti on tosi ja toinen epätosi, muussa tapauksessa tulos on "tosi".
""A:sta seuraa B"" tarkoittaa, että jos A on tosi, myöskin B:n on oltava tosi. Saman voi ilmaista sanomalla, että A on B:lle riittävä ehto.
Esimerkiksi $x \gt 0 \Rightarrow x \gt -1$. Jos nimittäin $x \gt 0$, on tällöin myös välttämättä $x \gt -1$.
Matematiikassa väitteen $a \Rightarrow b$ totuus määräytyy pelkästään lauseiden $a$ ja $b$ totuusarvojen perusteella. Väite $a \Rightarrow b$ on epätosi pelkästään silloin, kun väite $a$ on tosi ja $b$ epätosi, ja tosi kaikissa muissa tapauksissa.
Tällainen tulkinta merkille $\Rightarrow$ vangitsee syy-seuraussuhteesta matemaattisen päättelyn kannalta olennaiset piirteet. Se ei kuitenkaan vastaa täysin arkiajattelun "jos...niin...", päättelyitä, sillä väitteen $a \Rightarrow b$ totuus ei vaadi minkäänlaista sisäistä syy-seuraussuhdetta lauseiden $a$ ja $b$ totuudelle. Erityisesti, jos $a$ on epätosi lause, on $a \Rightarrow b$ tosi, oli $b$ mikä lause tahansa. Siis esimerkiksi "Kuu on juustoa $\Rightarrow$ Lehmät lentävät" on tosi väite.
Katso myös Jos, Perustelu, Johtopäätös, Siksi, implikaationuoli, Seurata jostakin, Olla seuraus, Kontrapositio.
Seurata jostakin, Olla seuraus (engl. Is implied by)
$A$ seuraa $B$:stä tarkoittaa sitä, että jos $B$ tiedetään, voidaan tästä päätellä $A$.
Oletetaan, että $x \gt 0$. Nyt $x \neq 0$ seuraa siitä, että $x \gt 0$.
Katso myös Seurata, Aiheuttaa jotakin, Olla jonkin riittävä ehto.
Seuraus, Korollaari (engl. Corollary)
Jos väite $B$ seuraa välittömästi väitteestä $A$ ilman merkittäviä uusia todistusaskelia, niin silloin väitettä $B$ kutsutaan väitteen $A$ korollaariksi eli seuraukseksi.
Korollaari on yleensä jonkin päätuloksen vähäisempi välitön seuraus.
Seuraus, Implikaatio (engl. Implication)
Lauseen implikaatio on jokin, joka seuraa kyseisestä lauseesta.
Shillinki (engl. Shilling)
Rahayksikkö, jota käytettiin Isossa-Britanniassa ennen valuutan muuttamista kymmenjärjestelmään. Yksi shillinki oli 12 penceä ja yksi punta 20 shillinkiä.
SI-yksiköt (engl. MKSA units, SI units)
SI on lyhenne ranskan kielen sanoista "Système International d'Unités" (kansainvälinen mittayksikköjärjestelmä). Sen perusyksiköt ovat pituuden yksikkö metri, massan yksikkö kilogramma, ajan yksikkö sekunti, sähkövirran yksikkö ampeeri, lämpötilan yksikkö kelvin, ainemäärän yksikkö mooli ja valovoiman yksikkö kandela. Kaikki muut järjestelmän yksiköt perustuvat näihin seitsemään yksikköön.
Katso myös Sekunti, Radiaania sekunnissa, Radiaania sekunnissa toiseen, Newton, Yksikkö, Neliömetri, Metri, Kuutiometri.
Sieventää (engl. Simplify)
Lausekkeen sieventäminen tarkoittaa, että poistetaan siitä tarpeettomat luvut ja termit. Yleensä tämä tehdään supistamalla tai jakamalla tekijöihin.
Katso myös Supistaminen, Korvaaminen, Sijoittaminen, sijoitus, Jakaa tekijöihin.
Sigma (engl. Sigma)
Kreikan aakkoston kirjain $\sigma$ (pieni kirjain) tai $\Sigma$ (iso kirjain).
Pientä sigmaa käytetään usein otannan standardipoikkeaman merkkinä. Suurta sigmaa käytetään usein summan merkkinä.
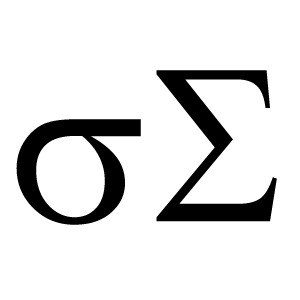
Katso myös Kreikkalaiset kirjaimet, Keskihajonta.
Sigma-algebra (engl. Sigma algebra)
Jos $X$ on joukko, kokoelma $\Gamma$ joukon $X$ osajoukkoja on sigma-algebra, mikäli se toteuttaa seuraavat ehdot:
- Jos $\mathcal{U}$ on numeroituva kokoelma joukon $\Gamma$ alkioita, myös joukon $\mathcal{U}$ alkioiden yhdiste on joukon $\Gamma$ jäsen.
- Jos $U \in \Gamma$, myös joukon $U$ komplementti kuuluu joukkoon $\Gamma$.
Katso myös Joukko, Mitta-avaruus, Mitallinen joukko.
Siirto (engl. Translation, Slide)
Geometrinen kuvaus, jossa jokaista pistettä siirretään sama matka samaan suuntaan.
Katso myös Siirtosymmetria, Geometrinen muunnos.
Siirtopeilaus (engl. Glide)
Siirtopeilaus on eräs geometristen muunnosten tyyppi. Se saadaan yhdistämällä yhdensuuntaissiirto ja peilaus siten, että siirto on peilaussuoran suuntainen.
Katso myös Geometrinen muunnos.
Siirtosymmetria (engl. Translational symmetry)
Kuviolla on siirtosymmetria, jos on olemassa siirto, joka vie jokaisen kuvion pisteen saman kuvion pisteeksi. Esimerkiksi tapetti, jossa on toistuva kuvio; jos sitä siirtää oikean määrän, se näyttää samalta kuin ennen siirtoa.
Sijoittaa (engl. Assign)
Kun muuttujalle annetaan jokin tietty arvo, sanotaan että kyseinen arvo sijoitetaan muuttujalle.
Sijoittaminen, sijoitus, Korvaaminen (engl. Substitution)
Yleensä yhtälön yksinkertaistamiseksi tehtävä yhtälössä esiintyvän termin vaihtaminen toiseen termiin tai lukuun.
Tarkastellaan esimerkiksi yhtälöitä (1): $x+y=6$ ja (2): $2x+3y=14$.
Yhtälöstä (1) seuraa, että $y=6-x$. Jos korvataan $y$ yhtälössä (2) lausekkeella $6-x$ saadaan $2x+3(6-x)=14$.
Siten $2x+18-3x=14$ eli $x=4$.
Siksi, Johtopäätös, implikaationuoli (engl. Therefore)
Merkki $\Rightarrow$ on nimeltään implikaationuoli ja se tarkoittaa, että merkin oikeanpuoleinen väittämä on seuraus vasemmanpuoleisista väittämistä. Väittämä, joka on merkin $\Rightarrow$ perässä seuraa loogisesti siitä, mitä ennen merkkiä on.
Katso myös Seurata, Aiheuttaa jotakin, Olla jonkin riittävä ehto.
Sileä kuvaus (engl. Smooth function)
Kuvaus $f \colon \mathbb{R}^n \rightarrow \mathbb{R}^m$ on sileä, mikäli sillä on kaikkien kertalukujen kaikki osittaisderivaatat.
Katso myös Derivoituva, Differentioituva, Funktio, Kuvaus, Analyyttinen ryhmä.
Similaari, Samanlainen, Yhdenmuotoinen (engl. Similar)
Kahden tai useamman kuvion sanotaan olevan yhdenmuotoiset, jos ne ovat saman muotoiset, mutta eivät välttämättä saman kokoiset.
Yhdenmuotoisten kuvioiden vastinsivujen suhde on vakio ja vastinkulmat ovat yhtä suuret.

Katso myös Yhdenmuotoiset kolmiot, Yhtenevät kuviot, Kriteerejä kolmioiden yhdenmuotoisuudelle.
Simpsonin sääntö (engl. Simpson's rule)
Eräs numeerisen integroinnin menetelmä. Menetelmä saadaan integroimalla astetta 2 oleva Lagrangen interpolaatiopolynomi, joka saa välin päätepisteissä ja keskipisteessä saman arvon kuin funktio $f(x)$: \[ \int_{a}^{b} f(x) dx \approx \frac{b-a}{6}[f(a) + 4f(\frac{a + b}{2}) + f(b)]. \]
Tästä saadaan yleisemmin: \[ \int _a ^b y dx \approx \frac{1}{3} h [ ( y_0 + y_n ) + 4 ( y_1 + y_3 + \ldots + y_{n-1} )+ 2 ( y_2 + y_4 + \ldots + y_{n-2} ) ], \] missä pisteet $a=x_{0}, x_{1}, \ldots, x_{n-1}, x_{n}=b$ jakavat välin $[a,b]$ tasaisesti $n$:ään yhtä pitkään $h=(b-a)/n$:n pituiseen osaan ja $y_{i}=y(x_{i})$.
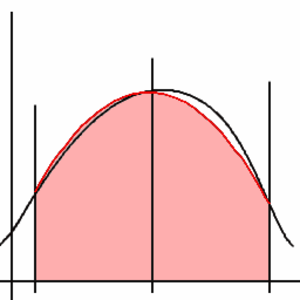
Katso myös Sääntö, Keskipistesääntö, Trapetsisääntö.
Simpukkakäyrä (engl. Cochleoid)
Simsonin suora (engl. Pedal line, Simson's line, Simson's line or pedal line, Simson line)
Piirretään annetun kolmion ympäri ympyrä ja valitaan siltä piste $P$. Piirretään pisteestä $P$ kolmion sivuja tai niiden jatkeita vastaan kohtisuorat janat. Näiden janojen ja kolmion sivujen tai niiden jatkeiden leikkauspisteet sijaitsevat samalla suoralla, jota kutsutaan Simsonin suoraksi.
Katso myös Deltoidi.
$\sin(-x)$
$\sin (-x) = -\sin x$, kaikilla $x \in \mathbf{R}$.
Katso myös Trigonometrinen identiteetti, Pariton funktio.
$\sin(2x)$
Kaikilla $x \in \mathbb{R}$ pätee \[ \sin (2x) = 2 \sin(x) \cos(x). \]
Katso myös $\sin$, Kaksinkertaisen kulman kaava.
$\sin(x/2)$
Kaikilla $x$ pätee \[ \sin \left( \frac{x}{2} \right) = \pm \frac{\sqrt{1 - \cos(x)}}{2}. \]
Katso myös $\sin$, Puolikkaan kulman kaava, Neliöjuuri.
$\sin(x+180^{\circ})$
$\sin (x+180^{\circ}) = \sin (x+\pi) = -\sin x$, kaikilla $x \in \mathbf{R}$.
Katso myös Trigonometrinen identiteetti.
$\sin(x+90^\circ)$
$\sin(x+90^{\circ})=sin(x + \frac{\pi}{2}) = \cos x$
90 astetta on radiaaneina $\pi/2$.
Katso myös Trigonometrinen identiteetti.
$\sin$
Sinin lyhenne.
$\sin x$ tarkoittaa luvun $x$ siniä eli sellaisen suorakulmaisen kolmion kulman, jonka suuruus on $x$, vastaisen sivun suhdetta hypotenuusaan.
Katso myös Tangenttifunktio, Trigonometrinen yhtälö, Sinin neliö, $\sin(2x)$, Sini, Trigonometrian Pythagoraan lause, Lyhenne, Kotangentti, Kosinin derivaatta, Kosekantti, Kosinin integraalifunktio, Kotangentin integraalifunktio, $e^{ix}$, $e^{x+iy}$, Fourier'n sarja, $\sin(x/2)$, $\tan(x/2)$.
Singulaarinen matriisi (engl. Singular matrix)
Neliömatriisi, jonka determinantti on nolla ja jolla ei sen vuoksi ole käänteismatriisia.
Katso myös Determinantti, Neliömatriisi.
$\sinh(2x)$
Kaikilla $x$ pätee \[ \sinh(2x) = 2\sinh(x)\cosh(x). \]
Katso myös $\sinh$, $\sinh(x+y)$.
$\sinh(x)\cosh(y)$
Kaikilla $x,y$ on voimassa \[ \sinh(x)\cosh(y) = \frac{\sinh(x+y)+\sinh(x-y)}{2}. \]
$\sinh(x)\sinh(y)$
Kaikilla $x,y$ pätee \[ \sinh(x)\sinh(y) = \frac{\cosh(x+y)-\cosh(x-y)}{2}. \]
$\sinh(x+y)$
Kaikilla $x,y$ pätee \[ \sinh(x+y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y). \]
Katso myös $\cosh$, $\sinh$, $\sinh(2x)$.
$\sinh$
Lyhennys hyperboliselle sinifunktiolle.
$\sinh(x)$ määritellään kaavalla $(e^{x}-e^{-x})/2$.
Katso myös Lyhenne, Hyperbolinen, $\cosh$, Hyperbolinen funktio, $\cosh(2x)$, $\cosh(x)-\cosh(y)$, $\cosh(x)\cosh(y)$, $\cosh$-funktion derivaatta, $\cosh$-funktion integraalifunktio, $\cosh(x)$:n neliö miinus $\sinh(x)$:n neliö, $\coth$-funktion integraalifunktio, $\cosh(x+y)$, $\sinh(2x)$, $\sinh(x+y)$, Hyperbolinen sini, $\sinh(x)\cosh(y)$, $\sinh(x)\sinh(y)$.
Sini (engl. Sine)
Jos suorakulmaisessa kolmiossa yhden kulman suuruus on $x$, niin kulman $x$ sini on $x$:n vastaisen kateetin pituuden suhde hypotenuusan pituuteen.
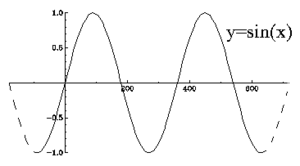
Katso myös Trigonometria, Suora kulma, $\sin$, Ympyrä, Kosini, Arkussini, Trigonometrinen funktio.
Sinilause (engl. Sine rule, Sin rule)
Jos kolmion sivujen pituudet ovat $a$, $b$ ja $c$ ja jos $A$ on sivun $a$ vastainen kulma, $B$ sivun $b$ vastainen kulma ja $C$ sivun $c$ vastainen kulma, niin \[\frac{a}{sin A} = \frac{b}{sin B} = \frac{c}{sin C} = 2R,\] missä $R$ on kolmion ympäri piirretyn ympyrän säde.
Katso myös Sääntö, Kosinilause.
Sinin neliö (engl. $sin^2$)
Merkintä $\sin^{2}(x)$ tarkoittaa samaa kuin $[sin(x)]^{2}$.
Katso myös $\sin$, Merkintätapa, Notaatio.
Sinin tarkkoja arvoja (engl. Particular values of sin)
$\sin 0^{\circ} = 0$,
$\sin 30^{\circ} = \sin \frac{\pi}{6} = \frac{1}{2}$,
$\sin 45^{\circ} = \sin \frac{\pi}{4} = \frac{1}{\sqrt{2}}$,
$\sin 60^{\circ} = \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2}$,
$\sin 90^{\circ} = \sin \frac{\pi}{2} = 1$,
$\sin 180^{\circ} = \sin \pi = 0$,
Katso myös Trigonometristen funktioiden tarkat arvot.
Sisus, Sisäosa (engl. Interior)
Joukon $A$ sisus, jota merkitään $\mathrm{int}(A)$ tai $A^{0}$, on kaikkien joukon $A$ avoimien osajoukkojen yhdiste. Piste $b \in \mathrm{int}(A)$, jos ja vain jos jokin pisteen $b$ ympäristö sisältyy kokonaan joukkoon $A$. Joukon sisäosa on avoin joukko. Vertaa käsitteeseen reuna.
Katso myös Joukko.
Sisä-, Sisäpuolinen (engl. Internal)
Sisäpuolella oleva.
Monikulmion sisäkulma on kahden vierekkäisen sivun monikulmion sisäpuolelle muodostama kulma.
Katso myös Sisäkulma.
Sisäkulma (engl. Internal angle, Interior angle)
Sellainen monikulmion kulma, jonka kyljet ovat monikulmion sivuja ja jonka aukeama (ainakin kulman kärjen lähellä) on monikulmion sisäpuolella.
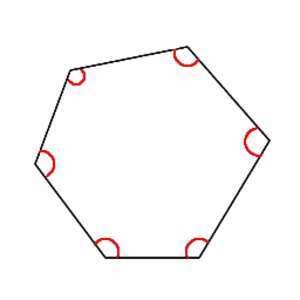
Katso myös Sisäkulmien summa, Sisä-, Sisäpuolinen, Monikulmion kulmat, Ulkokulma, Säännöllisen monikulmion kulmat.
Sisäkulmien summa (engl. Sum of interior angles)
Kolmion sisäkulmien summa on $180^{\circ}.$
Nelikulmion sisäkulmien summa on $360^{\circ}.$
Viisikulmion sisäkulmien summa on $540^{\circ}.$
Monikulmion, jossa on $n$ sivua, eli $n$-kulmion sisäkulmien summa on $(180n-360)^{\circ}.$
Sisältää (engl. Contains)
Merkki $\in$ tarkoittaa, että tietty joukko sisältää tietyn alkion. Esimerkiksi $a \in A$ tarkoittaa, että joukko $A$ sisältää alkion $a$ eli $a$ kuuluu joukkoon $A$.
Katso myös Kuulua joukkoon, Joukko, Alkio.
Sisäosa, Sisus (engl. Interior)
Joukon $A$ sisus, jota merkitään $\mathrm{int}(A)$ tai $A^{0}$, on kaikkien joukon $A$ avoimien osajoukkojen yhdiste. Piste $b \in \mathrm{int}(A)$, jos ja vain jos jokin pisteen $b$ ympäristö sisältyy kokonaan joukkoon $A$. Joukon sisäosa on avoin joukko. Vertaa käsitteeseen reuna.
Katso myös Joukko.
Sisäpuolinen, Sisä- (engl. Internal)
Sisäpuolella oleva.
Monikulmion sisäkulma on kahden vierekkäisen sivun monikulmion sisäpuolelle muodostama kulma.
Katso myös Sisäkulma.
Sisätulo, Pistetulo, Skalaaritulo (engl. Dot product, Scalar, inner or dot product, Inner product, Scalar product)
Kahden vektorin $\mathbf{a}$ ja $\mathbf{b}$ pistetulo eli skalaaritulo, jota merkitään $\mathbf{a} \cdot \mathbf{b}$ tai $<\mathbf{a},\mathbf{b}>$, on reaaliluku. Kolmialkioisten vektorien pistetulo määritellään kaavalla \[ \left ( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right ) \cdot \left ( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right ) = a_1 b_1 + a_2 b_2 + a_3 b_3. \] $n$-alkioisten vektorien pistetulo määritellään vastaavasti. Pistetulo voidaan myös määritellä kaavalla $\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos \theta $, missä $\theta$ on vektorien $\mathbf{a}$ ja $\mathbf{b}$ välinen kulma ja $|\mathbf{a}|$, $|\mathbf{b}|$ ovat vektorien $\mathbf{a}$ ja $\mathbf{b}$ pituudet.
Huomaa, että kaikilla vektoreilla $\mathbf{a}$, $\mathbf{b}$ ja $\mathbf{c}$ sekä kaikilla reaaliluvuilla $k$ pätee: \begin{eqnarray*} \mathbf{a} \cdot \mathbf{b} &=& \mathbf{b} \cdot \mathbf{a}\\ \mathbf{a} \cdot (\mathbf{b}+\mathbf{c}) &=& \mathbf{a} \cdot \mathbf{b}+\mathbf{a} \cdot \mathbf{c}\\ (k\mathbf{a}) \cdot \mathbf{b}& = & k(\mathbf{a} \cdot \mathbf{b})\\ &=&\mathbf{a} \cdot (k\mathbf{b}). \end{eqnarray*}
Reaalilukukertoimisen vektoriavaruuden $V$ kuvaus $\langle,\rangle : V \times V \rightarrow \mathbb{R}$ on sisätulo, jos se toteuttaa kaikilla $v, w \in V$ ja kaikilla $\mu, \lambda \in \mathbb{R}$ seuraavat ehdot:
1) $\langle v,v\rangle \geq 0$ ja $\langle v,v\rangle = 0$ jos ja vain jos $v = 0$,
2) $\langle v,w\rangle = \langle w,v\rangle $,
3) $\langle \mu u + \lambda v, w\rangle = \mu \langle u,w\rangle + \lambda \langle v,w\rangle$.
Katso myös Tulo, Vektoritulo, Ristitulo, Euklidinen normi, Bilineaarinen muoto, Cauchy-Schwarzin epäyhtälö.
Sisätuloavaruus (engl. Inner product space)
Vektoriavaruus $E$, jonka kerroinkunta on $\mathbf{F}$ (joko $\mathbb{C}$ tai $\mathbb{R}$) ja joka on varustettu sisätulolla. Kuvaus $E \times E \to \mathbf{F}$, $(x,y) \mapsto s(x,y)$, on sisätulo, jos se toteuttaa seuraavat ehdot:
- [1)] $s(x,x) \geq 0$ ja $s(x,x) = 0$ jos ja vain jos $x=0$,
- [2)] $s(x,y) = \overline{s(y,x)}$,
- [3)] $s(\lambda x + \mu y,z) = \lambda s(x,z) + \mu s(y,z)$.
Katso myös Vektoriavaruus, Euklidinen avaruus.
Sisään piirretty kuvio (engl. Inscribe)
Geometrisen kuvion sisään piirretty toinen kuvio siten, että näillä kuvioilla on yhteisiä pisteitä, mutta ne eivät leikkaa toisiaan. Yleensä jompikumpi kuvioista on ympyrä.
Katso myös Leikata, Konstruktio, Konstruointi.
Sisään piirretty ympyrä (engl. Incircle or inscribed circle, Inscribed circle, Incircle)
Ympyrä, joka on piirretty annetun monikulmion sisään siten, että jokainen monikulmion sivu on ympyrän tangentti. Kolmion sisään piirretyn ympyrän keskipiste on kolmion kulmien puolittajien leikkauspiste.

Katso myös Ympyrä, Sisään piirretyn ympyrän keskipiste, Kolmioon liittyvät ympyrät, Kolmion sisään piirretyn ympyrän muodostaminen, Gergonnen kolmio, Gergonnen piste.
Sisään piirretyn ympyrän keskipiste (engl. Incentre, Incenter)
Monikulmion jokaista sivua sivuavan ympyrän keskipiste. Jos monikulmio on kolmio, tämä piste on kolmion kulmien puolittajien leikkauspiste.
Katso myös Kulman puolittaja, Ortosentri, Sisään piirretty ympyrä, Keskipiste, Kolmion ympäri piirretyn ympyrän keskipiste, Kolmion sisään piirretyn ympyrän keskipisteen määrittäminen.
Sivu (engl. Side)
Kuvion sivu on kahta sen kärkeä yhdistävä jana.
Sivuluokka (engl. Coset)
Olkoon $H$ ryhmän $G$ aliryhmä. Ryhmän $G$ alkioon $g$ liittyvä vasen sivuluokka on joukko \[ gH = \{ gh : h \in H \}. \] Vastaavasti alkioon $g$ liittyvä oikea sivuluokka on joukko \[ Hg = \{ hg : h \in H \}. \]
Katso myös Laskutoimitus, Joukko, Jäännösluokkaryhmä, Alkio.
Sivunormaalisuora (engl. Binormal line, Binormal)
Kolmiulotteisen avaruuden käyrän sivunormaali annetussa käyrän pisteessä on sellainen suora, joka on kohtisuorassa kyseiseen pisteeseen piirrettyjä tangenttisuoraa ja normaalisuoraa vastaan.
Katso myös Vektori, Sivunormaalivektori.
Sivunormaalivektori (engl. Binormal vector)
Käyrän annettuun pisteeseen piirretty sivunormaalivektori on vektori, joka on kyseiseen pisteeseen piirretyn sivunormaalisuoran suuntainen.
Tangentti-, normaali- ja sivunormaalivektorit muodostavan oikeakätisen joukon.
Katso myös Vektori, Tangenttivektori, Piste, Käyrä, Normaalivektori, Sivunormaalisuora.
Sivutahkoverkko (engl. Net)
Tasokuvio, joka saadaan, kun monitahokas leikataan auki pitkin eräitä särmiään ja taivutetaan tasoon. Samalla monitahokkaalla on yleensä monia eri sivutahkoverkkoja, jotka riippuvat siitä, miten leikkaukset tehdään.
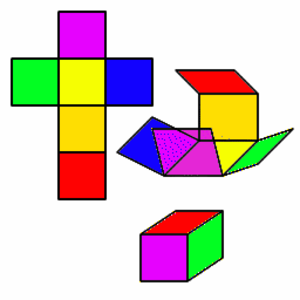
Katso myös Avaruusgeometria, Oktaedrin sivutahkoverkko, Kuvio.
Skalaari (engl. Scalar)
Tavallinen luku, jolla on vain suuruus, ei suuntaa. Sanaa käytetään yleensä sellaisissa yhteyksissä, joissa esiintyy myös vektoreita. Tällöin skalaarin vastakohtana voi pitää vektoria. Vektorillahan on sekä suuruus että suunta.
Katso myös Vektori, Vektorialgebra.
Skalaarikolmitulon laskusääntöjä (engl. Scalar triple product identity)
$\mathbf{a}\cdot(\mathbf{b} \times \mathbf{c}) = \mathbf{b}\cdot(\mathbf{c} \times \mathbf{a})=\mathbf{c}\cdot(\mathbf{a} \times \mathbf{b})$
Katso myös Identiteetti.
Skalaarilla kertominen (engl. Scalar multiplication)
Vektori tai matriisi kerrotaan skalaarilla kertomalla sen jokainen alkio kyseisellä skalaarilla. Esimerkiksi \[ 5 \left ( \begin{array}{c} 1 \\ 3 \\ 5 \end{array} \right ) = \left ( \begin{array}{c} 5 \times 1 \\ 5 \times 3 \\ 5 \times 5 \end{array} \right ) = \left ( \begin{array}{c} 5 \\ 15 \\ 25 \end{array} \right ) \] \[ 2 \left ( \begin{array}{cc} 4 & 3 \\ 1 & 2 \end{array} \right ) = \left ( \begin{array}{cc} 2 \times 4 & 2 \times 3 \\ 2 \times 1 & 2 \times 2 \end{array} \right ) = \left ( \begin{array}{cc} 8 & 6 \\ 2 & 4 \end{array} \right ) \]
Katso myös Vektorialgebra.
Skalaaritulo, Pistetulo, Sisätulo (engl. Dot product, Scalar, inner or dot product, Inner product, Scalar product)
Kahden vektorin $\mathbf{a}$ ja $\mathbf{b}$ pistetulo eli skalaaritulo, jota merkitään $\mathbf{a} \cdot \mathbf{b}$ tai $<\mathbf{a},\mathbf{b}>$, on reaaliluku. Kolmialkioisten vektorien pistetulo määritellään kaavalla \[ \left ( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right ) \cdot \left ( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right ) = a_1 b_1 + a_2 b_2 + a_3 b_3. \] $n$-alkioisten vektorien pistetulo määritellään vastaavasti. Pistetulo voidaan myös määritellä kaavalla $\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos \theta $, missä $\theta$ on vektorien $\mathbf{a}$ ja $\mathbf{b}$ välinen kulma ja $|\mathbf{a}|$, $|\mathbf{b}|$ ovat vektorien $\mathbf{a}$ ja $\mathbf{b}$ pituudet.
Huomaa, että kaikilla vektoreilla $\mathbf{a}$, $\mathbf{b}$ ja $\mathbf{c}$ sekä kaikilla reaaliluvuilla $k$ pätee: \begin{eqnarray*} \mathbf{a} \cdot \mathbf{b} &=& \mathbf{b} \cdot \mathbf{a}\\ \mathbf{a} \cdot (\mathbf{b}+\mathbf{c}) &=& \mathbf{a} \cdot \mathbf{b}+\mathbf{a} \cdot \mathbf{c}\\ (k\mathbf{a}) \cdot \mathbf{b}& = & k(\mathbf{a} \cdot \mathbf{b})\\ &=&\mathbf{a} \cdot (k\mathbf{b}). \end{eqnarray*}
Reaalilukukertoimisen vektoriavaruuden $V$ kuvaus $\langle,\rangle : V \times V \rightarrow \mathbb{R}$ on sisätulo, jos se toteuttaa kaikilla $v, w \in V$ ja kaikilla $\mu, \lambda \in \mathbb{R}$ seuraavat ehdot:
1) $\langle v,v\rangle \geq 0$ ja $\langle v,v\rangle = 0$ jos ja vain jos $v = 0$,
2) $\langle v,w\rangle = \langle w,v\rangle $,
3) $\langle \mu u + \lambda v, w\rangle = \mu \langle u,w\rangle + \lambda \langle v,w\rangle$.
Katso myös Tulo, Vektoritulo, Ristitulo, Euklidinen normi, Bilineaarinen muoto, Cauchy-Schwarzin epäyhtälö.
Soikio, Ovaali (engl. Oval)
Yleinen nimitys ellipsille tai ellipsin muotoiselle kuviolle; litistetty ympyrä.
Katso myös Ellipsi, Karteesinen soikio, Kuvio.
Solmu (engl. Knot)
Kolmiulotteisen avaruuden suljettu käyrä, joka ei leikkaa itseään ja jota ei voi purkaa yksinkertaiseksi silmukaksi leikkaamatta käyrää.
Solmun aste (engl. Order of a vertex)
Verkon solmun aste on siitä lähtevien verkon särmien lukumäärä.
Katso myös Järjestys.
Sophie Germainin alkuluku (engl. Sophie Germain prime, Germain prime)
Alkulukua $p$ kutsutaan Sophie Germainin alkuluvuksi, jos $2p+1$ on myös alkuluku.
Katso myös Alkuluku.
Sovellus (engl. Application)
Tietyn matematiikan osan sovellus on jokin asia, jossa kyseistä matematiikan osaa voidaan käyttää hyväksi. Esimerkiksi planeettojen auringon ympäri tapahtuvan kiertoliikkeen tutkiminen on dynamiikan sovellus.
Katso myös Matematiikka ja tietojenkäsittely, Dynaaminen systeemi.
Soveltava matematiikka (engl. Applied mathematics)
Soveltava matematiikka tutkii reaalimaailman tilanteisiin liittyviä matemaattisia malleja sekä sitä, miten näitä malleja voidaan parantaa ja muuttaa parempien tuloksien saamiseksi. Lisäksi soveltava matematiikka tutkii erilaisia matemaattisen mallintamisen tekniikoita ja niiden käyttöä eri tilanteissa.
Katso myös Matematiikka.
Sovittaa (engl. Fit)
Käyrän sanotaan sopivan annettuun pistejoukkoon, jos kaikki joukon pisteet ovat kohtuullisen lähellä käyrää. Käyrän etäisyyttä pistejoukosta voidaan mitata monella eri tavalla. Tällaisen käyrän etsimistä kutsutaan käyrän sovittamiseksi pistejoukkoon.
Spiraali (engl. Spiral)
Kiinteän pisteen ympäri kiertävän ja siitä samalla loitontuvan pisteen kulkema polku.
Kolmiulotteisen avaruuden spiraalia kutsutaan ruuvikierteeksi tai ruuviviivaksi.

Katso myös Käyrä, Logaritminen spiraali, Arkhimedeen spiraali, Ruuvikierre, Ruuviviiva, Fermat'n spiraali, Parabolinen spiraali, Hyperbolinen spiraali.
Splini (engl. Spline)
Oletetaan, että meillä on jono datapisteitä $(x_i,y_i)$. Haluamme sovittaa käyrän datapisteiden kautta.
Eräs tapa on sovittaa kaikkien kahden peräkkäisen pisteen välille polynomikäyrät. Tässä vaaditaan vielä se, että pisteissä, joissa eri polynomikäyrät kohtaavat, molemmilla kohtaavilla käyrillä on sama gradientti.
Käyrää, jonka nämä kaikki polynomikäyrät yhdessä muodostavat, kutsutaan spliniksi.
Katso myös Käyrä.
Stabilisaattori (engl. Stabilizer)
Olkoon $G$ ryhmä, joka toimii joukossa $X$ (Katso toiminta). Pisteen $x \in X$ stablisaattori on joukko $\{g \in G \mid gx=x\}$. Voidaan todistaa, että stabilisaattori on ryhmän $G$ aliryhmä.
Katso myös Aliryhmä, Normalisaattori, Toiminta, Sentralisaattori.
Standardi normaalijakauma (engl. Standard Normal distribution)
Jatkuva jakauma, eräs erikoistapaus normaalijakaumasta. Sitä merkitään $N(0,1)$, ja se on määritelty kaavalla \[ f(x) = \frac{1}{\sqrt{2 \pi}} \exp \left ( - \frac{1}{2} x ^2 \right ) . \]
Sen keskiarvo on 0 ja varianssi 1. Sen MGF on \[ M( \theta ) = \exp ( \frac{1}{2} \theta ^2 ) .\]
Katso myös Normaalijakauma, Gaussin jakauma.
Stokastinen (engl. Stochastic)
Satunnainen, ennustamaton.
Struktuuri (engl. Structure)
Topologiseen avaruuteen, järjestettyyn joukkoon, ryhmään jne. kuuluu joukko, ja joukossa määritelty struktuuri. Esimerkikisi topologisen avaruuden struktuuri on topologia, järjestetyn joukon struktuuri on järjestysrelaatio, ja ryhmän struktuuri on ryhmän laskutoimitus.
Studentin t-jakauma, T-jakauma (engl. Student's t-distribution, t-distribution)
Keskiarvotesteissä käytetty jakauma. Jakauman nimi johtuu siitä, että sen esitti 1900-luvun alussa Guinness-panimon laaduntarkkailusta vastaava pääkemisti William S. Gosset salanimellä "Student". Mikäli käytössä on otos $X_i, i=1,n$ normaalisti jakautuneesta perusjoukosta jonka odotusarvo on $ \mu $, noudattaa suure $$ \mathrm{t} = \frac{\bar{\mathrm{x}} - \mu } {\mathrm{s} / \sqrt{\mathrm{n}}} , $$ missä $$ \mathrm{s}^2 = \sum _{\mathrm{i}=1} ^{\mathrm{n}} \frac{ ( \mathrm{x}_{\mathrm{i}} - \bar{\mathrm{x}} ) ^{2} } {\mathrm{n}-1} , $$ t-jakaumaa vapausasteilla $n-1$. t-jakauma on symmetrinen ja muistuttaa muodoltaan normaalijakaumaa. t-jakauma kuvaa normaalisti jakautuneesta perusjoukosta poimitun otoksen otoskeskiarvon vaihtelua, kun vaihtelun mittana käytetään poimitun otoksen perusteella arvioitua keskiarvon hajontaa. Vapausasteiden lukumäärä ottaa huomioon käytettävissä olevan tiedon tarkkuuden. Kun havaintoja (vapausasteita) on vähän, otoksesta arvioitu keskihajonta on epätarkka, ja t-jakauman hännät ovat voimakkaammat kuin normaalijakauman hännät. Kun havaintojen lukumäärä (vapausasteiden lukumäärä) kasvaa, keskihajonnalle tehdyn arvion tarkkuus kasvaa ja t-jakauma lähestyy normaalijakaumaa.
Katso myös Normaalijakauma, t-taulukko, Vapausaste, Jakauma, T-testi, F-jakauma, Gaussin jakauma.
Suhde (engl. Ratio)
Suureiden $a$ ja $b$ suhde on $\frac{a}{b}$, ja se kertoo, kuinka monta kertaa $a$ on $b$:n suuruinen. Merkki, jota usein käytetään osoittamaan kahden suureen suhdetta on $a:b$.
Katso myös Verrannollisuus, Verranto, Mitta-asteikko, Kosini, Kultaisen leikkauksen suhde, Kaksoissuhde, Kultainen leikkaus, Menelausin lause.
Suhteellinen alkuluku (engl. Relatively prime)
Luvut $a$ ja $b$ ovat suhteellisia alkulukuja (tai $a$ on alkuluku $b$:n suhteen), jos $a$:lla ja $b$:llä ei ole muita yhteisiä tekijöitä kuin 1.
Katso myös Keskenään jaottomat luvut, Jaottomuus.
Suljettu (engl. Closed)
Olkoot $f \colon X^n \rightarrow X$ kuvaus ja $A \subset X$. Joukko $A$ on suljettu kuvauksen $f$ suhteen, jos $f(a_1, \dots, a_n) \in A$ kaikilla $(a_1, \dots, a_n) \in A^n$.
Topologisen avaruuden osajoukko on suljettu, jos ja vain jos sen komplementti on avoin.
Suljettu alue (engl. Closed region)
Suljetun alueen muodostavat tason suljettu käyrä ja kaikki sen sisälle jäävät pisteet.
Katso myös Suljettu käyrä.
Suljettu joukko (engl. Closed set)
Olkoon $X$ topologinen avaruus. Joukko $C \subset X$ on suljettu, mikäli $X \setminus C$ on avoin.
Olkoon $X$ metrinen avaruus. Joukko $C \subset X$ on suljettu, mikäli $C$ sisältää kaikkien suppenevien osajonojensa rajapisteet.
Joukko $[0,1] \subset \mathbb{R}$ on suljettu. Joukko $]0,1[ \subset \mathbb{R}$ ei ole suljettu, koska on olemassa suppeneva jono $(1/n)_n$, jonka jäsenet kuuluvat joukkoon $]0,1[$, mutta jonka rajapiste $0$ ei kuulu joukkoon $]0,1[$.
Katso myös Joukko, Avoin joukko.
Suljettu käyrä (engl. Closed curve)
Jatkuva käyrä, jonka alku- ja päätepiste ovat sama piste. Suljettu käyrä sulkee sisäänsä alueen, joten sillä on sekä sisä- että ulkopuoli.
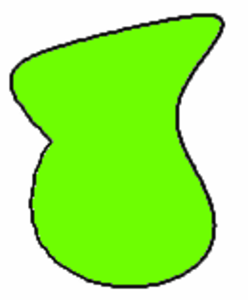
Katso myös Piiri, Käyrä, Jordanin käyrälause, Suljettu alue.
Suljettu väli (engl. Closed interval)
Väli, joka sisältää päätepisteensä. Esimerkiksi niiden lukujen $x$ joukko, joille $ 0 \leq x \leq 1 $, on suljettu väli. Suljettua väliä, jonka päätepisteet ovat $a$ ja $b$, merkitään $[a,b]$. Välit muotoa $(-\infty, b]$, $[a, \infty)$ ja $(-\infty, \infty)$ ovat myös suljettuja, mutta ne eivät ole rajoitettuja, kuten väli muotoa $[a,b]$.
Katso myös Avoin väli, Väli.
Sulkeuma (engl. Closure)
Olkoon $X$ topologinen avaruus ja $A \subset X$. Joukon $A$ sulkeuma $\bar{A}$ on pienin suljettu avaruuden $X$ osajoukko, joka sisältää joukon $A$. Joukon $A$ sulkeuma on leikkaus kaikista suljetuista avaruuden $X$ osajoukoista, jotka sisältävät joukon $A$.
Joukko $X_0 \subset X$ on tiheä, jos $\bar{X_0}=X$. Tällöin jokaista joukon $X$ pistettä voidaan approksimoida mielivaltaisen tarkasti joukon $X_0$ pisteillä. Esimerkiksi rationaalilukujen joukko on tiheä reaalilukujen joukossa.
Sulut, () (engl. (), brackets, parentheses)
Suluilla ( ) osoitetaan laskujärjestys. Suluissa oleva osakaava lasketaan ennen muuta kaavaa.
2 + 3 x 5 = 17
(2 + 3) x 5 = 25
Summa (engl. Sum)
Kokonaislukujen 3, 5, 7, 2, 8 ja 12 summa on 37.
Yhteenlaskun tulos.
Katso myös Yhteenlasku, Yhteenlaskumenetelmä, Sisäkulmien summa, Yhdistää, Yhdistellä, Riemannin zeta-funktio, Ääretön summa, Geometrisen jonon osasumma.
Summakaava (engl. Factorisation formula, Sum formula)
Trigonometrinen identiteetti, joka ilmaisee kahden trigonometrisen funktion summan toisten trigonometristen funktioiden avulla. Myös monilla muilla funktioilla on summakaavoja.
Katso myös Trigonometrinen identiteetti, $cos(x)-cos(y)$, $\cos(x)+\cos(y)$, Kaksinkertaisen kulman kaava.
Summamerkki (engl. Summation sign)
Esimerkiksi $ \sum _{i=0} ^{n} i^2 $ tarkoittaa kaikkien lukujen $ i^2 $ summaa, missä $i$ saa arvot 0:sta n:ään. eli $ \sum _{i=0} ^{n} i^2 = 0^{2}+1^{2}+...+n^{2}.$
Jos muuttujan arvoaluetta ei anneta, niin summaus suoritetaan yli kaikkien mahdollisten muuttujan arvojen. $ \sum _{i} \frac{1}{i^2} $ tarkoittaa kaikkien lukujen $ \frac{1}{i^2} $ summaa, missä $i$ saa kaikki kokonaislukuarvot.
Merkkiä $ \Sigma $ käytetään merkitsemään sitä seuraavien termin tai termien summaa. Summaus suoritetaan yli arvoalueen, jonka päätepisteet merkitään summamerkin ala- ja yläpuolelle.
Summan derivointi (engl. Term by term differentiation)
Jos $y(x) = f(x)+g(x)$, niin \[ \frac{dy}{dx} = \frac{df}{dx} + \frac{dg}{dx}.\] Toisin sanoen summan derivaatta on yhteenlaskettavien derivaattojen summa.
Katso myös Derivointisääntö, Summan integrointi.
Summan integrointi (engl. Term by term integration)
Jos $y(x) = f(x)+g(x)$, niin \[ \int y(x)\,dx = \int f(x)\,dx + \int g(x)\, dx.\] Toisin sanoen summan integraalifunktio on yhteenlaskettavien integraalifunktioiden summa.
Katso myös Summan derivointi, Integrointisääntö.
Summan momenttiemäfunktio (engl. MGF of a sum)
Jos $X$ ja $Y$ ovat riippumattomia jakaumia, joiden MGF:t ovat $M_X$ ja $M_Y$, niin $ M_{X+Y}( \theta )=M_X ( \theta ) M_Y ( \theta ) . $
Katso myös MGF, Momenttiemäfunktio.
Suora (engl. Line)
Geometrian perusolio; euklidisessa geometriassa aksioomin määritelty: kahteen pisteeseen liittyy aina yksi ja vain yksi suora; suoran pisteillä on olemassa relaatio "piste on kahden muun pisteen välissä"; suoraa voidaan jatkaa, ts. jos $A$ ja $B$ ovat suoran pisteitä, niin on olemassa suoran piste $C$, niin että $B$ on $A$:n ja $C$:n välissä.
Katso myös Kulman puolittaja, Asymptootti, Tangenttivektori, Ristikkäiset suorat, Kohtisuorat suorat, Lukusuora, Oikokulma, Puolittaja, Kiertosymmetrian akseli, Pyörähdysakseli, Filonin suora, Kohtisuora, Tangentti, Jana, Normaali, Pisteen kautta kulkeva suora, Kahden pisteen välinen jana, Vaakasuora, Puolisuora, Säde, Puolisäde, Geometria, Kantapiste, Euklidinen geometria, Suoran yhtälö, Suunnattu suora, Lävistäjä, Janan jatkaminen suoraksi, Koordinaattiakseli, Akseli, Normaalivektori, Kateetti, Analyyttinen avaruusgeometria, Kaksoissuhde, Diagonaali, Hyperbelin johtosuora, Ellipsin johtosuora, Särmä, Verkon viiva, Symmetria-akseli.
Suora kartio (engl. Right cone)
Kartio, jonka akseli on kohtisuorassa pohjaa vastaan. Kartion pohjakuvion on oltava keskipisteellinen, kuten ympyrä tai ellipsi.
Katso myös Kartion akseli, Kartio, Kartion pohja.
Suora kulma (engl. Right angle, Right angle)
Neljäsosakierros; kulma, jonka asteluku on 90.
Suorakulmainen kolmio on kolmio, jonka kulmista yksi on suora kulma. Neliössä ja suorakulmiossa on neljä suoraa kulmaa. Suoran kulman merkki on $\perp$.
Katso myös Terävä kulma, Kulma, Puoliympyrän sisältämä kulma, Tangenttifunktio, Sini, Oikokulma, Hypotenuusa, Kosini, Tylppä kulma.
Suora lieriö (engl. Right cylinder)
Lieriö, jonka akseli on kohtisuorassa kantoja vastaan.
Katso myös Lieriön akseli, Lieriö, Lieriön pohja.
Suora pyramidi (engl. Right pyramid)
Pyramidi, jonka akseli on kohtisuorassa pohjaa vastaan. Pyramidin pohjan on oltava monikulmio, jolla on keskipiste, esimerkiksi säännöllinen monikulmio tai suorakaide.
Katso myös Pyramidin akseli, Pyramidi, Kohtisuora, Pyramidin pohja.
Suora särmiö (engl. Right prism)
Särmiö, jonka akseli on kohtisuorassa kantoja vastaan.
Katso myös Särmiön akseli, Särmiö, Prisma, Kohtisuora, Särmiön pohja.
Suoraa vastaan kohtisuoran suoran piirtäminen (engl. Construct a perpendicular through a given point)
Annettua suoraa $L$ vastaan kohtisuora ja pisteen $P$ kautta kulkeva suora piirretään seuraavasti. Piirretään harpin avulla ympyrä, jonka keskipiste on $P$ ja joka on niin suuri, että se leikkaa suoran $L$ kahdessa pisteessä $A$ ja $B$. Piirretään harpin avulla kaksi ympyrää, joilla on sama säde sekä keskipisteet $A$ ja $B$. Ympyrät leikkaavat toisensa pisteessä $C$. Pisteiden $P$ ja $C$ kautta kulkeva suora on haluttu suora.
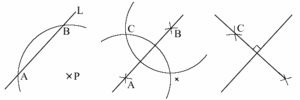
Katso myös Konstruktio, Konstruointi.
Suoraan verrannollinen, Verrannollinen (engl. Directly proportional, Proportional)
Kahta suuretta sanotaan suoraan verrannollisiksi, tai pelkästään verrannollisiksi, jos niiden suhde on vakio. Tällöin yhden suureen kaksinkertaistuessa toinenkin kaksinkertaistuu.
Katso myös Suoraan verrannollisuus.
Suoraan verrannollisuus (engl. Direct proportion)
Kaksi suuretta ovat suoraan verrannolliset, jos toisen suureen kuvaaja toisen suhteen on origon kautta kulkeva suora. Jos siis toinen suureista kaksinkertaistuu, niin toinenkin kaksinkertaistuu, jne.
Katso myös Suoraan verrannollinen, Kaava, Verrannollinen.
Suorakaide (engl. Oblong)
Suorakulmion toinen nimi. Joskus sanotaan, että suorakaide on suorakulmio, jonka sivut ovat eripituiset. Siten neliö on suorakulmion erikoistapaus, mutta se ei ole suorakaide.
Katso myös Suorakaide, Suorakulmio.
Suorakaide, Suorakulmio (engl. Rectangle)
Erityinen nelikulmio; suunnikas, jonka sisäkulmien asteluku on 90. Suorakulmion vastakkaiset sivut ovat yhtä pitkät ja yhdensuuntaiset. Suorakulmiolla on kaksi symmetria-akselia ja kiertosymmetria, jonka kertaluku on 2.

Katso myös Suunnikas, Neljäkäs, Suorakaide, Nelikulmio, Suorakaiteen pinta-ala, Kultainen suorakulmio.
Suorakaiteen pinta-ala (engl. Area of a rectangle)
Jos suorakaiteen sivujen pituudet ovat $a$ ja $b$, niin sen pinta-ala on $ab$.
Katso myös Suorakaide, Suorakulmio.
Suorakulmainen kolmio (engl. Right-angled triangle, Right angled triangle, Right triangle)
Suorakulmainen kolmio on kolmio, jonka yksi kulmista on suora kulma. Trigonometriset funktiot määritellään tällaisen kolmion sivujen suhteina. Suoran kulman vastainen sivu on aina kolmion pisin sivu. Sitä kutsutaan kolmion hypotenuusaksi. Muut kaksi suorakulmaisen kolmion sivua ovat sen kateetit. Pythagoraan lause kertoo suorakulmaisen kolmion sivujen pituuksien välisen yhteyden.
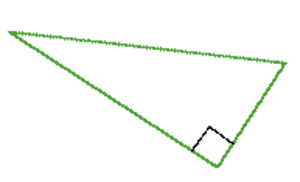
Katso myös Pythagoraan lause, Kolmio, Tasasivuinen kolmio.
Suorakulmaisen hyperbelin polttopisteet (engl. Focus of a rectangular hyperbola)
Jos suorakulmaisen hyperbelin asymptootit ovat $x$- ja $y$-akselit ja hyperbeli kulkee pisteen $(c,c)$ kautta, sen polttopisteet ovat $(c \sqrt{2}, c \sqrt{2})$ ja $(-c \sqrt{2}, -c \sqrt{2})$.
Katso myös Hyperbelin polttopisteet.
Suorakulmaisen särmiön pinta-ala (engl. Area of a cuboid)
Jos $a, b , c$ ovat suorakulmaisen särmiön sivujen pituudet, niin sen pinta-ala on $2(ab+ac+bc)$.
Suorakulmaisen särmiön tilavuus (engl. Volume of a cuboid)
Suorakulmaisen särmiön, jonka sivujen pituudet ovat $x$, $y$ ja $z$, tilavuus on $x \cdot y \cdot z = xyz$.
Suorakulmio, Suorakaide (engl. Rectangle)
Erityinen nelikulmio; suunnikas, jonka sisäkulmien asteluku on 90. Suorakulmion vastakkaiset sivut ovat yhtä pitkät ja yhdensuuntaiset. Suorakulmiolla on kaksi symmetria-akselia ja kiertosymmetria, jonka kertaluku on 2.

Katso myös Suunnikas, Neljäkäs, Suorakaide, Nelikulmio, Suorakaiteen pinta-ala, Kultainen suorakulmio.
Suoran ja akselin leikkauspiste (engl. Intercept)
Piste, jossa suora leikkaa x-akselin tai y-akselin.
Katso myös Suorien leikkauspiste, Akseli.
Suoran ja tason leikkauspiste (engl. Intersection of a line and a plane)
Jos suora ei sijaitse tasossa, suora ja taso leikkaavat yhdessä pisteessä. Jos suoran määrittävät yhtälöt ovat $x = pz + d$, $y = qz + e$ ja tason yhtälö on $z=m x+n y+c$, on suoran ja tason leikkauspiste \begin{eqnarray*} x&=&\frac{d-n q d+n e p+c p}{1-m p-n q}\\ y&=&\frac{e-m p e+m d q+c q}{1-m p-n q}\\ z&=&\frac{m d+n e+c}{1-m p-n q}. \end{eqnarray*}
Katso myös Yhtälöryhmä, Leikkaus, Suoran yhtälö, Tason yhtälö.
Suoran pyramidin sivusärmän pituus (engl. Pyramid slant height)
Jos pyramidin pohja on säännöllinen $n$-kulmio, jonka sivun pituus on $x$, niin pyramidin sivisärmän pituus $s$ löydetään seuraavasti. Säännöllisen $n$-kulmion, jonka sivun pituus on $x$, ympäri piirretyn ympyrän säde $R = \frac{x}{2 cos \theta}$, missä $\theta = 90-\frac{180}{n}$. Tällöin $s^{2} = h^{2}+R^{2}$, missä $h$ on pyramidin korkeus. Siten pyramidin särmän korkeus $s = \sqrt{ h^{2} + \frac{x^{2}}{4 cos^{2} \theta} }$.
Katso myös Suoran pyramidin sivutahkon korkeus.
Suoran pyramidin sivutahkon korkeus (engl. Pyramid face height)
Jos suoran pyramidin pohja on säännöllinen $n$-kulmio, jonka sivun pituus on $x$, niin pyramidin sivutahkon korkeuden $f$ löytämiseksi todetaan, että säännöllisen $n$-kulmion apoteema eli sen keskipisteen etäisyys minkä tahansa sivun keskipisteestä on $r = \frac{x tan \theta}{2}$, missä $\theta = 90-\frac{180}{n}$. Tällöin $f^{2} = h^{2}+r^{2}$, missä $h$ on pyramidin korkeus. Siten pyramidin tahkon korkeus on $f = \sqrt{ h^{2} + \frac{x^{2} tan^{2} \theta}{4} }$.
Katso myös Suoran pyramidin sivusärmän pituus.
Suoran vektorimuotoinen yhtälö (engl. Vector equation of a line)
Suoran, joka kulkee pisteen $\overline{a}$ kautta, ja jonka suuntavektori on $\overline{r}$, yhtälö on \[\overline{x} = \overline{a}+t\overline{r},\] missä parametri $t$ käy läpi kaikki reaaliluvut. Tämä yhtälö pätee kaikissa ulottuvuuksissa.
Katso myös Vektori, Tason vektorimuotoinen yhtälö, Suoran yhtälö.
Suoran yhtälö (engl. Equation of a line, Equation of a straight line)
Tasossa:
Jos suora leikkaa $y$-akselin pisteessä $c$ ja sen kulmakerroin on $m$, on suoran yhtälö $y = mx+c$. Pisteiden $(a,b)$ ja $(c,d)$ kautta kulkevan suoran yhtälö on \[ \frac{x-a}{c-a} = \frac{y-b}{d-b}. \]
Kolmiulotteisessa avaruudessa:
Pisteiden $(a,b,c)$ ja $(d,e,f)$ kautta kulkevan suoran yhtälö on \[ \frac{x-a}{d-a} = \frac{y-b}{e-b} =\frac{z-c}{f-c}. \] Suoran yhtälö voidaan kirjoittaa myös yhtälöparina $y = mx+c$, $z = nx+d$. Tämä suora leikkaa $yz$-tason pisteessä $y = c$, $z = d$.
Katso myös Janan vektorimuotoinen yhtälö, Suoran vektorimuotoinen yhtälö, Kahden tason leikkaus, Lineaarinen yhtälö, Suora, Suorien leikkauspiste, Suoran yhtälö, Pinnan normaalisuoran yhtälö, Suoran ja tason leikkauspiste.
Suoran yhtälö (engl. Cartesian equation of a line)
Jos on annettu piste $P = (a, b, c)$ ja suuntavektori $\overrightarrow{d} = (u, v, w)$, niin pisteen $P$ kautta kulkevan ja vektorin $\overrightarrow{d}$ kanssa yhdensuuntaisen suoran yhtälö on \[\frac{x-a}{u} = \frac{y-b}{v} = \frac{z-c}{w}.\] Huomaa, että lukujen $u$, $v$ ja $w$ on oltava eri suuria kuin 0.
Katso myös Suoran yhtälö.
Suoran ympyrälieriön pinta-ala, Lieriön pinta-ala (engl. Area of a right circular cylinder, Area of a cylinder)
Suoran ympyrälieriön, jonka korkeus on $h$ ja pohjan säde $r$, kaarevan pinnan pinta-ala on $2 \pi rh$. Siten koko lieriön pinta-ala on $2 \pi r(r+h)$.
Katso myös Lieriö.
Suorien leikkauspiste (engl. Intersection of lines)
Kaksi suoraa, jotka eivät ole yhdensuuntaisia, leikkaavat toisensa yhdessä pisteessä.
Jos suorien yhtälöt ovat $y = mx+c$ ja $y = nx+d$, niin niiden leikkauspiste on $( (d-c)/(m-n),\, (md-nc)/(m-n) )$.
Katso myös Piste, Pisteen potenssi ympyrän suhteen, Yhtälöryhmä, Suoran ja akselin leikkauspiste, Jänne, Leikkaus, Kantapiste, Suoran yhtälö, Ympyrän piirtäminen kolmen pisteen kautta, Kolmion ympäri piirretyn ympyrän muodostaminen, Sekantti, Menelausin lause.
$\sup$
Pienimmän ylärajan eli supremumin lyhenne.
Katso myös Supremum, Pienin yläraja.
Supeta (engl. Converge)
Jono suppenee kohti jotakin lukua, jos jonon alkiot tulevat lähemmäksi ja lähemmäksi kyseistä lukua, kun jonossa mennään eteenpäin.
Katso myös Hajaantua, Itseinen suppeneminen, Cauchyn kriteerio.
Supistaminen (engl. Cancel)
Jos murtoluvun osoittajalla ja nimittäjällä on yhteinen tekijä, kumpikin voidaan jakaa tällä tekijällä ja korvata jaon tuloksella. Näin syntyneellä murtoluvulla on sama arvo kuin alkuperäisellä.
Jos yhtälön molemmilla puolilla on sama nollasta poikkeava tekijä, se voidaan jakaa pois yhtälön molemmilta puolilta, ja yhtälö jää edelleen voimaan.
Esimerkiksi murtoluvusta $\frac{12}{8}$ voidaan supistaa pois $4$, jolloin tulokseksi saadaan $\frac{3}{2}$.
Katso myös Murtoluvun supistaminen, Samanarvoiset murtoluvut, Muuntaa, Sieventää.
Supistumaton murtoluku (engl. Irreducible fraction)
Murtoluku, jota ei voi enää supistaa eli murtoluku, jonka osoittajan ja nimittäjän suurin yhteinen tekijä on 1.
Suplementtikulma (engl. Supplementary angle)
Kaksi kulmaa, joiden astelukujen summa on 180 astetta, ovat toistensa suplementtikulmat.
Esimerkiksi nelikulmion vastakkaiset kulmat ovat parittain toistensa suplementtikulmia, jos nelikulmion kärjet sijaitsevat ympyrällä.
Annetun kulman suplementtikulmaksi sanotaan erityisesti kumpaakin niistä kahdesta kulmasta, jotka täydentävät annetun kulman oikokulmaksi.
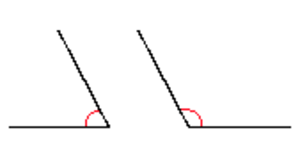
Katso myös Kulma, Jännenelikulmion kulmat, Komplementtikulma.
Suppeneminen, Konvergenssi (engl. Convergence)
Olkoon $X$ topologinen avaruus. Jono $(x_i)$ avaruuden $X$ pisteitä suppenee kohti pistettä $x \in X$, mikäli seuraava ehto pätee: Jos $U$ on pisteen $x$ ympäristö, niin $U$ sisältää kaikki jonon $(x_i)$ pisteet äärellistä määrää lukuunottamatta.
Olkoon $(x_i)$ jono avaruuden $\mathbb{R}^n$ pisteitä. Jono $(x_i)$ suppenee kohti pistettä $x \in \mathbb{R}^n$, mikäli pisteiden $x_i$ ja $x$ etäisyys saadaan kuinka pieneksi tahansa valitsemalla riittävän suuri $i$.
Täsmällisemmin sama voidaan ilmaista seuraavasti: Jono $(x_i)$ suppenee kohti pistettä $x \in \mathbb{R}^n$, mikäli jokaisella $\epsilon>0$ on olemassa sellainen $i_0 \in \mathbb{N}$, että kaikilla $i \gt i_0$ pätee $|x_i - x| \lt \epsilon$.
Katso myös Tasainen suppeneminen, Itseinen suppeneminen.
Suppenemiskriteeri (engl. Test for convergence)
Testi, jonka avulla saadaan selville, suppeneeko tietty sarja vai ei.
Esimerkki suppenemiskriteeristä on seuraava sääntö: Jos \[\lim_{n \to \infty} \frac{a_{n+1}}{a_{n}} = A\] ja $-1 Katso myös Sarja.
Suppenemissäde (engl. Radius of convergence)
Kompleksisen potenssisarjan $\sum a_n(z-z_0)^n$ suppenemissäde on suurin luku $r$, jolla pätee seuraava:
- Aina kun $|z-z_0| \lt r$, niin $\sum a_n(z-z_0)^n$ suppenee.
Katso myös Reaaliluku.
Supremum, Pienin yläraja (engl. Supremum, Least upper bound)
Supremum on pienin yläraja.
Olkoon $A$ joukko reaalilukuja. Sanomme, että reaaliluku $x$ on joukon $A$ yläraja, jos $x$ on vähintään yhtä suuri kuin jokainen joukon $A$ alkio. Joukon $A$ supremum on pienin niistä reaaliluvuista $x$, jotka ovat joukon $A$ ylärajoja.
Joukon $\{ x \in \mathbb{R} : x \lt 10\}$ supremum on 10.
Joukon $\{ x \in \mathbb{R} : x \le 11 \}$ supremum on 11.
Joukon $\{ x \in \mathbb{R} : 10 \le x \le 12 \}$ supremum on 12.
Joukolla $\{ x \in \mathbb{R} : x \ge 5 \}$ ei ole supremumia reaalilukujen joukossa.
Surjektiivinen (engl. Surjective, Onto)
Kuvaus joukosta $A$ joukkoon $B$ on surjektiivinen, jos jokainen joukon $B$ alkio on vähintään yhden $A$:n alkion kuva.
Kuvaus $f : A \to B$ on surjektiivinen, jos se toteuttaa ehdon \[ (\forall b \in B)(\exists a \in A)(f(a) = b). \]
Vertaa käsitteisiin injektiivinen ja bijektiivinen.
Katso myös Yksi yhteen kuvaus, Yksi yhteen vastaavuus, Bijektiivinen, Injektiivinen, Surjektio.
Surjektio (engl. Mapping onto, Surjection)
Sanomme, että kuvaus on surjektio, jos sen kuvajoukko on sama kuin sen maalijoukko.
Täsmällisemmin, kuvaus $f \colon A \rightarrow B$ on surjektio, jos jokaisella $b \in B$ joukko $f^{-1}b$ on epätyhjä, tai toisin sanoen jokaiselle $b \in B$ on olemassa $a \in A$, jolle $b=f(a)$.
Katso myös Surjektiivinen, Kuvaus, Injektio, Kuvajoukko, Lähtöjoukko, Funktion kuvajoukko, Määrittelyjoukko, Funktio.
Surkastunut (engl. Degenerate)
Surkastuneen kolmion kaikki kärjet sijaitsevat samalla suoralla, joten se on kutistunut täysin litteäksi, eikä oikeastaan ole kolmio ollenkaan. Samalla tavalla voidaan puhua muunlaisista surkastuneista olioista, kuten surkastunut paraabeli, joka on pelkkä suora, tai surkastunut ellipsi, joka on pelkkä piste. Yleisesti surkastunut olio on olio, josta ei voi tietää, mikä se on; se näyttää joltakin yksinkertaisemmalta.
Katso myös Bilineaarinen muoto.
Suunnattu derivaatta (engl. Directional derivative)
Kahden muuttujan reaaliarvoisen funktion $f(x,y)$ derivaatta suuntaan $(u, v)$ pisteessä $(p, q)$ on funktion $f$ muutosnopeus pisteessä $(p,q)$ mentäessä suuntaan $(u, v)$. Tässä oletetaan, että vektorin $(u,v)$ pituus on $1$. Suunnatulle derivaatalla käytetään merkintää $D_{(u,v)} f(p,q)$. Siis \[ D_{(u,v)} f(p,q) = \lim_{h \to 0} \frac {f(p+hu,q+hv) - f(p,q)}{h}. \] Kolmen tai sitä useamman muuttujan funktion suunnattu derivaatta määritellään vastaavasti.
Katso myös Derivaatta, Osittaisderivaatta.
Suunnattu jana, Suuntajana (engl. Directed line segment)
Jana, jonka toinen päätepiste on sovittu alkupisteeksi ja toinen päätepiste loppupisteeksi. Joskus vektoria voidaan ajatella suunnattuna janana.
Katso myös Jana.
Suunnattu suora (engl. Directed line)
Kullakin suoralla on kaksi mahdollista suuntaa. Suunnattu suora saadaan, kun valitaan näistä suunnista toinen (kumpi tahansa) suoran suunnaksi.
Katso myös Suora.
Suunnattu verkko (engl. Digraph)
Suunnattu verkko on verkko, jossa jokaiseen verkon viivaan on liitetty suunta (eli toinen solmu on viivan alkupiste ja toinen sen loppupiste).
Katso myös Verkko.
Suunnikas (engl. Parallelogram)
Erityinen nelikulmio, jossa vastakkaiset sivut ovat yhdensuuntaiset. Suunnikkaan lävistäjät puolittavat toisensa.

Katso myös Neljäkäs, Yhdensuuntainen, Puolisuunnikas, Suorakaide, Suorakulmio, Nelikulmio, Suunnikkaan pinta-ala.
Suunnikkaan pinta-ala (engl. Area of a parallelogram)
Jos suunnikkaan kahden yhdensuuntaisen sivun pituus on $a$ ja näiden sivujen välinen etäisyys on $l$, niin suunnikkaan ala on $al$.
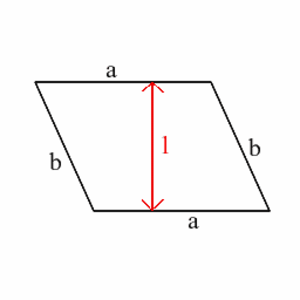
Katso myös Suunnikas.
Suuntajana, Suunnattu jana (engl. Directed line segment)
Jana, jonka toinen päätepiste on sovittu alkupisteeksi ja toinen päätepiste loppupisteeksi. Joskus vektoria voidaan ajatella suunnattuna janana.
Katso myös Jana.
Suuntakosinikaava (engl. Direction cosine formula)
Jos kahden origon kautta kulkevan suoran suuntakosinit ovat $a$, $b$, $c$ ja $d$, $e$, $f$, niin suorien väliselle kulmalle $x$ pätee yhtälö \[ \cos(x) = ad + be +cf. \]
Katso myös Kaava, Suuntakosinit.
Suuntakosinit (engl. Direction cosines)
Origon kautta kulkevan suoran suuntakosinit ovat sen suuntakulmien kosinit eli kosinit suoran ja $x$-, $y$- sekä $z$-akselien väliin jäävistä kulmista.
Jos suoran suuntakosinit ovat $a$, $b$, $c$, niin pätee $a^{2} + b^{2} + c^{2} = 1$.
Katso myös Kosini, Suuntakulmat, Suuntakosinikaava.
Suuntakulmat (engl. Direction angles)
Olkoot $p$ kolmiulotteisen avaruuden $\mathbb{R}^3$ piste ja $l$ pisteen $p$ ja origon kautta kulkeva suora. Suoran $l$ ja positiivisten $x$-, $y$- ja $z$-akselien väliin jäävät kolme kulmaa ovat suoran $l$ suuntakulmat.
Katso myös Analyyttinen avaruusgeometria, Suuntakosinit.
Suure (engl. Quantity)
Suure on jotain, joka voidaan mitata. Esimerkiksi pituus on suure, jolla mitataan vaikkapa koulun etäisyys kodista. Jotta mittaaminen olisi mahdollista, tarvitaan pituudelle yksikkö ja lisäksi tämän yksikön mukainen mitta. Pituuden yksiköksi on sovittu "metri". Mitattaessa koulun etäisyys kodista lasketaan esimerkiksi mittanauhan avulla, kuinka monta pituuden yksikköä eli metriä tämä etäisyys on. Tulos voisi olla esimerkisi 437 metriä.
Muita suureita ovat esimerkiksi aika, massa, lämpötila ja nopeus. Ajan yksikkö on "sekunti", massan yksikkö on "gramma" ja lämpötilan yksikkö on "celsiusaste". Nopeus on suureista pituus ja aika johdettu suure. Nopeuden yksikkö on "metri sekunnissa".
Katso myös Vakio, Ominaisuus, jonka arvot ovat numeerisia, Ominaisuus, Määrite.
Suurempi kuin (engl. Greater than)
Merkki $>$ tarkoittaa, että merkin vasemmalla puolella oleva suure on suurempi kuin merkin oikealla puolella oleva suure.
Seitsemän on suurempi kuin viisi: $7 \gt 5$.
Yksitoista on suurempi kuin neljä: $11 \gt 4$.
Miinus kaksi on suurempi kuin miinus neljä: $-2 \gt -4$.
Merkki \gt on erityisen hyödyllinen verrattaessa lukuja toisiinsa.
Katso myös Lisääminen puolittain epäyhtälöön, Epäyhtälön kertominen puolittain, Suurempi tai yhtäsuuri kuin, Aidosti positiivinen, Vertailtavissa olevat.
Suurempi tai yhtäsuuri kuin (engl. Greater than or equal to)
Merkki $\geq$ tarkoittaa, että merkin vasemmalla puolella oleva suure on joko suurempi tai yhtäsuuri kuin merkin oikealla puolella oleva suure. Esimerkiksi $a \geq b$ tarkoittaa, että pätee joko $a>b$ tai $a=b$.
Katso myös Yhtäsuuri, Suurempi kuin, Ei-negatiivinen, Sama.
Suurennoksen keskus (engl. Centre of enlargement)
Piste, joka pysyy paikallaan suurennoksessa.
Katso myös Keskipiste, Suurennuskuvaus.
Suurennuskuvaus (engl. Enlargement, Homothety)
Geometrinen kuvaus (yhdenmuotoisuuskuvaus), joka suurentaa kaiken samassa suhteessa. Tällainen kuvaus siis säilyttää kuvion kulmat ja pituuksien suhteet samoina.
Katso myös Pienennyskuvaus, Suurennoksen keskus, Mitta-asteikko.
Suurin alaraja, Infimum (engl. Greatest lower bound, Infimum)
Epätyhjällä alhaalta rajoitetulla reaalilukujen joukon osajoukolla on suurin alaraja eli infimum.
Reaaliluku $a$ on joukon $A$ alaraja, jos kaikki joukon $A$ alkiot ovat suurempia tai yhtäsuuria kuin $a$. Joukon $A$ infimum on suurin tällaisista luvuista $a$.
Reaalilukujoukon $\{ x \in \mathbb{R} : x \gt 1 \}$ suurin alaraja on $1$.
Reaalilukujoukon$\{ x \in \mathbb{R} : 3 \ge x \ge 2 \}$ suurin alaraja on $2$.
Reaalilukujoukon $\{ x \in \mathbb{Z} : x \textrm{ on positiivinen ja pariton } \}$ suurin alaraja on $1$.
Suurin lukua pienempi kokonaisluku (engl. Greatest integer function, floor, $\lfloor x \rfloor$)
Suurinta kokonaislukua, joka on pienempi tai yhtäsuuri kuin reaaliluku $x$, merkitään $[x]$ tai $\lfloor x \rfloor$. Funktio $x\mapsto \lfloor x\rfloor$ on esimerkki porrasfunktiosta.
Katso myös int, Pienempi kuin, Reaaliluku, Kokonaisluku, Kattofunktio, Askelfunktio.
Suurin yhteinen tekijä (engl. Greatest common factor, Greatest common divisor)
Suurin kokonaisluku, joka on tekijänä kahdessa tai useammassa kokonaisluvussa.
Lukujen $6=2 \times 3$ ja $4=2 \times 2$ suurin yhteinen tekijä on $2$. Lukujen $7$, $14=2\times 7$ ja $28=2\times 2 \times 7$ suurin yhteinen tekijä on $7$.
Katso myös s.y.t., Pienin yhteinen monikerta, Eukleideen algoritmi, Yhteinen tekijä, Dirichlet'n lause, Polynomien suurin yhteinen tekijä.
Suurten lukujen laki (engl. Law of large numbers)
Keskeinen tilastollinen tulos. Riippumattomien, samoin jakautuneiden satunnaismuuttujien keskiarvo lähenee satunnaismuuttujien yhteistä odotusarvoa, kun satunnaismuuttujien lukumäärä kasvaa rajatta. Tästä seuraa, että jonkin tapahtuman sattumisen suhteellinen frekvenssi riippumattomassa toistokeessa lähestyy tapahtuman todennäköisyyttä yksittäisessä kokeessa toistojen lukumäärän kasvaessa rajatta.
Syklinen ryhmä (engl. Cyclic group)
Ryhmä on syklinen, jos se on yhden alkion virittämä.
Ryhmä $(\mathbb{Z},+)$ on syklinen, koska se on yksiön $\{1\}$ virittämä.
Ryhmä $(\mathbb{Q},+)$ ei ole syklinen; itse asiassa mikään äärellinen osajoukko ei viritä sitä.
Ryhmä $(\{0,1,2\},+)$, $0+0=0, 1+0=0+1=1, 2+0=0+2=2, 1+1=2, 2+1=1+2=0, 2+2=1$ on syklinen, koska se on yksiön $\{1\}$ virittämä.
Jos $G$ on syklinen ryhmä, on olemassa sellainen $n \in \mathbb{Z}$, että seuraava pätee: Jos merkitään $H=\{k n \mid k \in \mathbb{Z}\}$, niin $G$ on isomorfinen ryhmän $(\mathbb{Z},+)/H$ kanssa.
Katso myös Ryhmä, Normaali aliryhmä, Virittäjistö, Diedriryhmä.
Sykloidi (engl. The Helen of geometers, Cycloid)
Polku, jonka ympyrän kiinnitetty piste kulkee ympyrän pyöriessä pitkin suoraa tai jotakin käyrää. Tavallisesti tämä piste sijaitsee ympyrän kehällä.
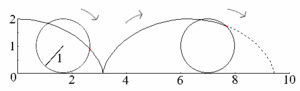
Katso myös Käyrä, Brakistokroni, Vierintäkäyrä, Hyposykloidi.
Sylinterikoordinaatit, Lieriökoordinaatit (engl. Cylindrical coordinates)
Kolmiulotteinen koordinaatisto, jossa yksi akseleista on suora ja nimeltään $z$-akseli. Toiset kaksi koordinaattia ovat kulma, joka mitataan kiinnitetystä suunnatusta $z$-akselia vastaan kohtisuorasta suorasta vastapäivään, sekä kohtisuora etäisyys $z$-akselista. Lieriökoordinaatisto on siis kaksiulotteinen napakoordinaatisto $z$-akselilla lisättynä.
Katso myös Analyyttinen avaruusgeometria, Koordinaatisto.
Sylowin lause (engl. Sylow's theorem)
Olkoon $p$ alkuluku ja $G$ ryhmä, jonka kertaluku on $p^ms$, missä $(p,s)=1$. Tällöin $G$:n aliryhmä $H$ on $G$:n Sylowin $p$-aliryhmä, jos $|H|=p^m$. Sylowin lause sanoo seuraavaa:
- Kaikilla ylläolevat ehdot toteuttavilla $G$ on Sylowin $p$-aliryhmiä.
- Mitkä tahansa kaksi Sylowin $p$-aliryhmää ovat toistensa konjugaatteja.
- Sylowin $p$-aliryhmien lukumäärä $n_p$ toteuttaa ehdon $ n_p \equiv 1 ( \mathrm{mod}\ p)$.
Katso myös Lause.
Symmetria (engl. Symmetry)
Kuviolla on symmetriaa, jos se ei muutu heijastuksessa tai kierrossa, joka on pienempi kuin täysi kierros.
Jollakin on symmetriaa, jos se ei muutu jossakin tietyssä operaatiossa tai kuvauksessa. Esimerkiksi sillä on peilaussymmetriaa, jos se ei muutu peilauksessa, ja kiertosymmetriaa, jos se ei muutu kierrossa.
Katso myös Siirtosymmetria, Epäsymmetria, Kiertosymmetria, Pyörähdyssymmetria, Peilaussymmetria.
Symmetria-akseli (engl. Mirror line, Line of symmetry, Axis of reflectional symmetry)
Suora, joka jakaa annetun kuvion kahteen osaan, jotka ovat toistensa peilikuvia.
Katso myös Peilaussymmetria, Suora, Akseli.
Symmetriakeskus (engl. Point of symmetry, Centre of rotation, Centre of symmetry)
Piste $P$ on kuvion symmetriakeskus, jos jokaista kuvion pistettä $A$ vastaa toinen kuvion piste $B$ siten, että $P$ on janan $AB$ keskipiste.
Katso myös Piste, Keskipiste, Kiertosymmetria, Pyörähdyssymmetria, Myötäpäivään.
Symmetrinen (engl. Symmetric)
Esimerkiksi neliö on symmetrinen neljän eri peilauksen lisäksi myös sellaisen kierron suhteen, jossa sitä kierretään 90 astetta keskipisteensä ympäri.
Matriisi on symmetrinen, jos se pysyy samana, kun sen kaikki alkiot peilataan lävistäjän suhteen.
Äärellisen monta eri arvoa saava satunnismuuttuja on jakaumaltaan symmetrinen, jos se saa kaikki arvonsa samalla todennäköisyydellä. Tällaista jakaumaa sanotaan myös diskreetiksi tasaiseksi jakaumaksi.Perusesimerkki symmetriasta on tasokuvion peilisymmetrsia suoran suhteen: kuvio on peilisymmetrinen, jos se on sama kuin peilikuvansa, toisin sanoen jos peilauskuvaus jonkin suoran suhteen ei muuta kuviota lainkaan. Yleisemmin sanomme, että joukko on symmetrinen jonkin kuvauksen suhteen, jos tuo kuvaus ei muuta joukkoa lainkaan, vaan kuvajoukko yhtyy alkuperäiseen joukkoon. Esimerkiksi neliö on symmetrinen neljän eri peilauksen lisäksi myös sellaisen kierron suhteen, jossa sitä kierretään 90 astetta keskipisteensä ympäri.
Relaatio $ \sim $ on symmetrinen, jos $ x \sim y \implies y \sim x $ kaikilla relaation $ \sim $ määrittelyjoukon alkioilla $ x, y $.
Bilineaarinen muoto $ \varphi : V^2 \to \mathbf{F} $ on symmetrinen, jos $ \varphi (v,w) = \varphi (w,v) \forall v,w \in V $ .
Katso myös Antisymmetrinen.
Symmetrinen matriisi (engl. Symmetric matrix)
Neliömatriisia $A$, jonka alkiot ovat $A_{ij}$, kutsutaan symmetriseksi, jos $A_{ij}=A_{ji}$ pätee kaikilla $i$ ja $j$. Toisin sanoen, jos $A$ on sama matriisi kuin sen transpoosi $A^T$. Esimerkiksi \[ \left ( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \end{array} \right ) \] on symmetrinen matriisi.
Katso myös Matriisin transpoosi, Reaalisen symmetrisen matriisin ominaisarvot, Hermiittinen matriisi.
Symmetrinen ryhmä (engl. Symmetric group)
Kertaluvun $n$ symmetrinen ryhmä $S_n$ on joukon $\{1, \dots, n\}$ kaikkien permutaatioiden muodostama ryhmä. Laskutoimituksena on kuvausten yhdistäminen ja neutraalialkiona identtinen permutaatio.
Katso myös Permutaatioryhmä.
Systemaattinen virhe, Harha (engl. Bias)
Tilastollinen menetelmä on harhainen, mikäli tapahtumiin liittyvät todennäköisyydet eivät ole oikeat. Esimerkiksi yksinkertaisessa satunnaisotannassa kaikki poimintatodennäköisyydet eivät ole yhtä suuria (perusjoukossa on ryhmä alkioita, joiden poimintatodennäköisyys on suurempi kuin muiden alkioiden.) Tilastollinen parametrin estimaatti (arvio) on harhainen, mikäli estimaatin odotusarvo poikkeaa parametrin todellisesta arvosta. Harha on estimaatin odotusarvon ja parametrin todellisen arvon välinen erotus.
Katso myös Harhaton estimaattori, Harhainen.
Säde (engl. Radius, Radii)
Ympyrän säde on ympyrän keskipisteen etäisyys ympyrän kehästä tai jana, joka yhdistää keskipisteen mihin tahansa kehän pisteeseen. Säännöllisen monikulmion säde on monikulmion keskipisteen etäisyys mistä tahansa monikulmion kärjestä.
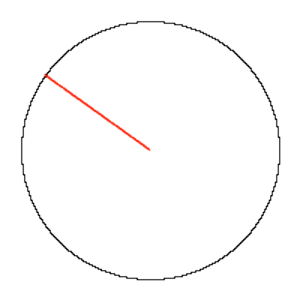
Katso myös Ympyrän pinta-ala, Ympyrä, Jänne, Ympäri piirretyn ympyrän säde, Kaarevuussäde, Säännöllisen monitahokkaan säde, Sekantti, Ympyräruuvikierre.
Säde, Puolisuora, Puolisäde (engl. Half line, Ray)
Janalla on kaksi päätepistettä, kun taas suora jatkuu kahteen suuntaan äärettömiin.
Puolisuora on suoran ja janan tapainen geometrinen olio, jolla on yksi päätepiste ja joka jatkuu toiseen suuntaan äärettömiin.
Särmiö, Prisma (engl. Prism)
Särmiö on erityinen monitahokas, jonka kaksi pohjaa muodostuvat kahdesta täsmälleen samanlaisesta ja samankokoisesta kuviosta. Nämä pohjakuviot ovat yhdensuuntaiset ja ne on erotettu toisistaan suunnikkailla, jotka ovat usein suorakaiteita.
Jos särmiö leikataan osiin pohjien suuntaisesti, niin uudet pohjat ovat täsmälleen samanlaiset kuin vanhat pohjat.
Kappale, joka muodostuu kahdesta yhtenevästä pohjakuviosta, joiden vastaavat sivut ovat yhdensuuntaiset, sekä suunnikkaan muotoisista tahkoista, jotka yhdistävät pohjat toisiinsa. Jos muut tahkot ovat kohtisuorassa pohjia vastaan, särmiö on suora särmiö. Jos suoran särmiön pohjat ovat säännöllisiä monikulmioita, särmiö on säännöllinen särmiö. Kolmioprisman pohjat ovat kolmioita, neliöprisman pohjat ovat neliöitä jne.
Katso myös Särmiön akseli, Kappale, Avaruusgeometria, Suora särmiö, Kolmioprisma, Särmiön pohja, Prisman korkeusjana, Monitahokas.
Särmiön akseli (engl. Axis of a prism)
Suora, joka kulkee särmiön kummankin kantatahkon keskipisteiden kautta on yhdensuuntainen kaikkien muiden tahkojen kanssa ja nimeltään särmiön akseli.
Katso myös Suora särmiö, Särmiö, Prisma, Yhdensuuntainen, Särmiön pohja, Akseli.
Särmiön pohja (engl. Base of a prism)
Kahta identtistä, yhdensuuntaista särmiön eli prisman tahkoa kutsutaan sen pohjiksi. Usein prisma nimetään sen pohjan kuvion mukaan. Esimerkiksi kolmioprisma on särmiö, jonka pohjat ovat kolmioita.
Katso myös Särmiön akseli, Suora särmiö, Särmiö, Prisma.
Särmä (engl. Edge of a figure or solid, Edge)
Tason monikulmion muodostavia janoja kutsutaan monikulmion särmiksi. Särmiä ovat myös ne janat, joita pitkin kaksi avaruuden monitahokkaan tahkoa leikkaavat.
Katso myös Monikulmio, Suora.
Säännöllinen (engl. Regular)
Monikulmion sanotaan olevan säännöllinen, jos sen kaikki sivut ovat yhtä pitkiä ja kaikki kulmat yhtä suuria.
Kappaleen sanotaan olevan säännöllinen, jos sen kaikki tahkot ovat identtisiä säännöllisiä monikulmioita ja kaikki sopet ovat yhteneviä. Platonin monitahokkaat ovat ainoat säännölliset monitahokkaat, kaikki muut monitahokkaat ovat joko puolisäännöllisiä tai epäsäännöllisiä kappaleita.Katso myös Epäsäännöllinen, Platonin kappaleet.
Säännöllinen heksaedri, Kuutio (engl. Regular hexahedron, Cube)
Kuutio on säännöllinen kolmiulotteinen kappale, jonka tahkot ovat keskenään samanlaisia neliöitä. Kuutiolla on 6 tahkoa, 12 särmää ja 8 kärkeä. Kuutio on yksi Platonin kappaleista. Kuutiota kutsutaan myös (säännölliseksi) heksaedriksi.
Katso myös Kuution tilavuus, Tasainen monitahokas, Yksikkökuutio, Avaruusgeometria, Kuution pinta-ala, Platonin kappaleet.
Säännöllinen matriisi, Kääntyvä matriisi (engl. Invertible matrix)
Neliömatriisi, jolla on käänteismatriisi. Käänteismatriisi on olemassa jos ja vain jos matriisin determinantti ei ole nolla. Säännöllistä matriisia kutsutaan myös kääntyväksi matriisiksi.
Katso myös Determinantti, Neliömatriisi.
Säännöllinen monitahokas (engl. Regular polyhedron, Regular solid)
Monitahokas, jonka kaikki tahkot ovat keskenään samanlaisia monikulmioita. Ainoat säännölliset monitahokkaat, jotka ovat olemassa, ovat säännölliset 4-, 6-, 8-, 12- ja 20-tahokkaat.
Katso myös Ympäripiirretty pallo, Monitahokas, Platonin kappaleet.
Säännöllisen monikulmion kulmat (engl. Interior angle of a regular polygon)
$n$-kulmion sisäkulmien summa on $180^{\circ}\cdot n-360^{\circ}$. Siten säännöllisen $n$-kulmion jokaisen sisäkulman asteluku on $180-\frac{360}{n}$.
Katso myös Sisäkulma.
Säännöllisen monitahokkaan sisäsäde (engl. Short radius of a regular polygon)
Olkoon $P$ säännöllinen $n$-tahokas, jonka sivun pituus on $x$. Merkitään sisempää sädettä symbolilla $r$. Se voidaan määrittää seuraavasti. Olkoon $O$ monitahokkaan keskipiste, $A$ eräs kärki ja $X$ kärjen $A$ viereisen sivun keskipiste. Tiedetään, että kahden sivun välinen kulma on $180-\frac{360}{n}$, joten kulma $OAX$ on puolet tästä, eli $$\theta = 90 -\frac{180}{n}.$$ Nyt pätee $\tan \theta = \frac{r}{x/2}$, joten $$ r = \frac{x \tan \theta }{2}.$$
Katso myös Säännöllisen monitahokkaan säde.
Säännöllisen monitahokkaan säde (engl. Radius of a regular polygon)
Olkoon $P$ säännöllinen $n$-tahokas, jonka sivun pituus on $x$. Merkitään sen (ulko)sädettä symbolilla $R$. Se voidaan määrittää seuraavasti: Olkoon $O$ monitahokkaan keskipiste, $A$ eräs kärki ja $X$ pisteen $A$ viereisen sivun keskipiste. Kahden vierekkäisen sivun välinen kulma on $180 - \frac{360}{n}$, joten kulma OAX on $$\theta = 90-\frac{180}{n}.$$ Nyt $\cos \theta = \frac{x/2}{R}$, joten $$R=\frac{x}{2 \cos \theta}.$$
Katso myös Säde, Säännöllisen monitahokkaan sisäsäde.
Säännöllisen viisikulmion piirtäminen (engl. Construct a regular pentagon)
Säännöllinen viisikulmio voidaan piirtää seuraavalla tavalla. Piirretään ympyrä ja jokin sen halkaisija $AB$. Piirretään halkaisijaa $AB$ vastaan kohtisuora halkaisija $CD$. Olkoon $O$ ympyrän keskipiste ja $X$ janan $OC$ keskipiste. Etsitään janalta $OD$ sellainen piste $Y$, että $XY = XA$. Sitten piirretään kaari, jonka säde on $AY$ ja keskipiste $A$. Tämä kaari leikkaa ympyrän pisteissä $E$ ja $F$. Pisteet $E$, $F$ ja $A$ ovat säännöllisen viisikulmion kolme kärkipistettä. Loput kaksi kärkipistettä löydetään seuraavasti. Piirretään kaari, jonka keskipiste on $E$ ja säde $EA$. Tämä kaari leikkaa ympyrän kärkipisteessä $G$. Lopuksi piirretään kaari, jonka keskipiste on $F$ ja säde $FA$. Tämä kaari leikkaa ympyrän kärkipisteessä $H$.
Katso myös Konstruktio, Konstruointi.
Sääntö (engl. Rule)
Väittämä, joka usein tai aina on tosi. Jos jokin on tosi aina, saatetaan käyttää vahvempaa nimitystä laki.
Sääntöön saattaa liittyä ehtoja, tällöin sääntö on tosi vain, jos ehdot ovat voimassa.
Katso myös Sinilause, Derivointisääntö, Ketjusääntö, Lause, Kosinilause, Leibnizin sääntö, Integrointisääntö, Tulon derivointisääntö, Osamäärän derivointisääntö, Potenssin derivointisääntö, Keskipistesääntö, Simpsonin sääntö, Trapetsisääntö, L'Hospitalin sääntö, Cramerin sääntö.