v (engl. yr)
Vaakasuora (engl. Horizontal)
Maanpinnan suuntainen; $xy$-tasossa $x$-akselin suuntainen.
Katso myös Vino, Kursiivi (kirjoitus), Pystysuora, Suora.
Vaakavektori (engl. Row vector)
Vektori, jonka alkiot on kirjoitettu sulkujen sisään riviksi, esimerkiksi $(1 5 7)$. Vektoria $\left ( \begin{array}{c} 1 \\ 5 \\ 7 \end{array} \right )$ kutsutaan pystyvektoriksi.
Katso myös Vektori, Pystyvektori.
Vaatia (engl. Require)
Lauseen sanotaan vaativan tiettyjä ehtoja, jos kyseiset ehdot ovat välttämättömiä sille, että lause on tosi. Sama ilmaistaan usein sanomalla, että kyseiset ehdot seuraavat lauseesta.
Katso myös Perustelu, Välttämätön ehto.
Vaativuus (engl. Complexity)
Algoritmin vaativuudella tarkoitetaan sen suorittamisen vaatimien yksinkertaisten laskenta-askelten tai muistipaikkojen lukumäärää. Tämä riippuu yleensä algoritmille annetun syötteen koosta. Hyvä algoritmi on sellainen, jonka vaativuus ei kasva liian nopeasti syötteen koon kasvaessa.
Katso myös Ominaisuus, Määrite.
Vaihdannainen, Kommutatiivinen (engl. Commutative)
Yhteenlaskua kutsutaan vaihdannaiseksi, koska yhteenlaskun lopputulos on sama riippumatta siitä kummassa järjestyksessä yhteenlasku suoritetaan. Yhteenlaskettavien laskujärjestys voidaan siis vaihtaa ilman, että se vaikuttaa laskun lopputulokseen.
Esimerkiksi $3+5$ antaa saman tuloksen kuin $5+3$.
Kertolasku on myös vaihdannainen. Vähennyslasku ja jakolasku sen sijaan eivät ole vaihdannaisia. Esimerkiksi $2-1$ on eri luku kuin $1-2$ ja samoin $4/2$ on eri luku kuin $2/4$.
Laskutoimitus $\circ$ on vaihdannainen, jos se toteuttaa ehdon $a \circ b = b \circ a$ kaikilla laskutoimituksen määrittelyjoukkoon kuuluvilla alkioilla $a$ ja $b$.
Katso myös Kommutoida, Abelin ryhmä, Antikommutatiivinen, Binäärinen kuvaus, Vektorien tensoritulo, Kaksipaikkainen kuvaus.
Vaihdos, Transpositio, Vaihto (engl. Transposition)
Permutaatio, jossa kahden alkion paikat vaihtuvat keskenään.
Katso myös Parillinen permutaatio, Pariton permutaatio, Permutaatio.
Vaihtaa suuntaa, Peruuttaa (engl. Reverse)
Vektorin suunnan vaihtaminen tarkoittaa, että se asetetaan osoittamaan vastakkaiseen suuntaan. Yhteenlaskun peruuttaminen tarkoittaa vastaavaa vähennyslaskua.
Kääntää jokin takaperin.
Vaihtelevuus (engl. Variability)
Kuinka paljon jokin vaihtelee. Epätäsmällinen synonyymi käsitteille varianssi, vaihteluväli ja keskihajonta.
Katso myös Keskihajonta, Tunnusluku, Tilastollinen tunnusluku, Varianssi, Vaihteluväli.
Vaihteluväli (engl. Range of data, Range)
Vaihteluväli on tietojoukon suurimman ja pienimmän yksikön välinen erotus. Vaihteluväli on karkea mitta sille, miten laajalle joukko on levinnyt.
Katso myös Vaihtelevuus, Tunnusluku, Tilastollinen tunnusluku, Hajonta.
Vaihto, Transpositio, Vaihdos (engl. Transposition)
Permutaatio, jossa kahden alkion paikat vaihtuvat keskenään.
Katso myös Parillinen permutaatio, Pariton permutaatio, Permutaatio.
Vaihtoehtoinen hypoteesi, Vastahypoteesi (engl. Alternate hypothesis)
Nollahypoteesin vastakohta. Mikäli nollahypoteesi ei ole tosi, on vaihtoehtoinen hypoteesi tosi ja kääntäen. Vaihtoehtoisesta hypoteesista käytetään merkintää $H_1$.
Katso myös Nollahypoteesi, Alternoida.
Vaihtolajittelu (engl. Exchange sort)
Vaihtolajittelu on eräs lajittelualgoritmi. Algoritmin syöte on jono lukuja sekalaisessa järjestyksessä ja algoritmin tuloste on nämä luvut suuruusjärjestykseen järjestettyinä.
Vaihtolajittelu toimii siten, että ensin etsitään jonon pienin alkio ja vaihdetaan se jonon ensimmäisen alkion kanssa. Sitten etsitään toiseksi pienin alkio ja vaihdetaan se jonossa toisena olevan alkion kanssa. (Huomaa, että toiseksi pienintä alkiota etsittäessä ei jonon ensimmäistä alkiota tarvitse enää tutkia, koska sen jo tiedetään olevan jonon pienin alkio.) Samaan tapaan jatketaan, kunnes lopulta jono on järjestetty kokonaan.
Vaihtolajittelu voi ensi silmäyksellä vaikuttaa varsin käyttökelpoiselta lajittelualgoritmilta. Tämä ei kuitenkaan pitkien jonojen kohdalla pidä paikkaansa. Syynä on se, että lajittelematta olevan jonon osan pienimmän alkion etsimiseen kuluu aika, joka on suoraan verrannollinen lajittelematta olevan jonon osan pituuteen. Näin koko jonon lajitteluun kuluva aika on suoraan verrannollinen koko jonon pituuden neliöön.
On olemassa lajittelualgoritmeja, esimerkikisi pikalajittelu (engl. quick sort) ja kekolajittelu (engl. heap sort), joissa lajitteluun kuluva aika on suoraan verrannollinen lukuun $n \log n$, missä $n$ on jonon pituus.
Katso myös Algoritmi, Kuplalajittelu.
Vaihtoraha (engl. Change)
Esimerkiksi jos ostan jotain, joka maksaa 2.80 euroa, saattaisin maksaa 3 euroa ja saisin 20 senttiä takaisin. Tällöin kyseistä 20 senttiä kutsutaan vaihtorahaksi.
Vaihtoraha on raha, jonka saat takaisin, kun olet maksanut jotain, koska yleensä annat ensiksi hieman liikaa rahaa.
Vakio (engl. Constant)
Suure, joka ei muutu eli jolla on sama arvo koko ajan. Vakion vastakohta on muuttuja eli jokin, joka voi muuttua.
Suure, josta oletetaan, että se ei koskaan muutu.
Esimerkkejä: Vakionopeudella ajava auto ei kiihdytä eikä hiljennä vauhtia. Funktion $y = ax^{2}$ kuvaaja, missä a on vakio; kun liikutaan kuvaajalla, niin $x$ ja $y$ muuttuvat, mutta $a$ pysyy samana.
Katso myös Kaprekarin vakio, Neperin luku, $e$, Muuttuja, Pii, $\pi$, Brunin vakio, Integrointivakio, Suure, Eulerin vakio, Euler-Mascheronin vakio.
Vakiofunktio (engl. Constant function)
Vakiotermi (engl. Constant term)
Lausekkeen tai yhtälön vakiotermi on termi, joka ei sisällä tekijänään mitään muuttujan lauseketta. Esimerkiksi lausekkeen $x^2+2x+4$ vakiotermi on 4.
Katso myös Lauseke.
Valinta-aksiooma (engl. Axiom of choice)
Jokaista joukkoa $S$ kohti on olemassa sellainen funktio $f$, että jos $X$ on joukon $S$ epätyhjä osajoukko, niin $f(X)$ on joukon $X$ alkio. Funktio $f$ poimii siis alkion jokaisesta joukon $S$ epätyhjästä osajoukosta $X$. Tällaista funktiota $f$ kutsutaan valintafunktioksi.
Valinta-aksiooma on riippumaton muista joukko-opin aksioomista. Jotkut pitävät sitä epäintuitiivisena, koska sillä on paradoksaalisia seurauksia (kts. Banach-Tarskin paradoksi).
Katso myös Aksiooma, Banachin-Tarskin paradoksi, Zornin lemma.
Valita (engl. Choose)
Merkintä $$^{p}C_{r} \quad \mbox{tai} \quad {p \choose r}$$ tarkoittaa lukua, joka kertoo, kuinka monella eri tavalla $p$:stä oliosta voidaan valita $r$ oliota. Katso hakusana "Kombinaatio".
Katso myös Kertoma, Kombinaatio, Kombinatoriikka, Merkintätapa, Notaatio, Tapahtuma, Todennäköisyys, Otosavaruus, Tetraedriluku, Binomikerroin, Binomikaava, Permutaatio.
van der Waerdenin käyrä, Takagin käyrä (engl. Blancmange curve)
Takagin käyrä määritellään kaavalla \[ y(x) = \sum_{k=0}^{\infty} \frac{f(2^kx)}{2^k}, \] missä $f$ on ns. sahanteräfunktio. Käyrä tunnetaan myös van der Waerdenin käyränä. Takagin käyrä on esimerkki käyrästä, joka ei ole derivoituva missään pisteessä.
Vandermonden determinantti (engl. Vandermonde determinant)
Lukujen $x_{1},...,x_{n}$ Vandermonden determinantti on \[ \left | \begin{array}{cccc} 1 & 1 & ... & 1 \\ x_1 & x_2 & ... & x_n \\ x_1^2 & x_2^2 & ... & x_n^2 \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n-1} & x_2 ^{n-1} & ... & x_n^{n-1} \end{array} \right |. \] Se on yhtä suuri kuin lukujen $x_{1},...,x_{n}$ erotusten tulo: $ \prod _{1 \leq i \lt j \leq n}(x_j - x_i)$.
Katso myös Tulo, Erotus, Determinantti.
Vapausaste (engl. Degree of freedom)
Vapaiden havaintojen lukumäärä. Esimerkiksi otosvarianssin lausekkeessa $$ s^2= {\frac{1}{n-1}} \sum_1^n (x_i-\overline x)^2 $$ jakajana on luku $n-1$. Tämä johtuu siitä, että kun otoskeskiarvo $\overline x$ on laskettu, jäljellä on vain $n-1$ vapaata havaintoa. Mikäli lasketaan poikkeamat $d_i= (x_i-\overline x)$, on niiden summa aina $= 0$. Jos nyt tunnetaan $n-1$ poikkeamaa, on viimeinen $$ d_n = 0 - \sum_1^{n-1} d_i. $$ Se ei enää ole vapaa.
Katso myös T-jakauma, Studentin t-jakauma, Ominaisuus, jonka arvot ovat diskreettejä, Rajoite, Rajoitusehto, F-jakauma.
Variaatiokerroin (engl. Coefficient of variation)
Havaintoarvojen variaatiokerroin lasketaan kaavalla \[ 100 \times \frac{s}{\bar{x}}, \] missä $s$ on keskihajonta ja $\bar{x}$ on keskiarvo.
Variaatiokerroin on havaintoarvojen suhteellisen hajonnan mitta prosentteina ilmaistuna.
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Keskihajonta.
Variaatiolaskenta (engl. Calculus of variation, Calculus of variations)
Analyysin haara, jossa tutkitaan keinoja löytää määrätyn integraalin avulla esitetyn funktion minimi- tai maksimikohta.
Esimerkkinä olkoon niin sanottu brakistokroniongelma: Olkoot $A = (0,1)$ ja $L = (1,0)$ kaksi tason pistettä. On etsittävä sellainen pisteet $A$ ja $L$ yhdistävä tason käyrä, jota pitkin kitkatta liukuva kappale kulkee pisteestä $A$ pisteeseen $L$ lyhimmässä mahdollisessa ajassa. Jos $u : [0,1] \to \mathbb{R}$ on pisteiden $A$ ja $L$ kautta kulkeva käyrä, niin silloin kappaleen matkaan käyttämä aika pitkin käyrää $u$ on \[ T(u) = \frac{1}{\sqrt{2g}} \int_0^1 \sqrt{ \frac{1+u'(x)^2}{1-u(x)}}dx. \] Ongelma saadaan siis ratkaistua, kun löydetään sellainen pisteiden $A$ ja $L$ kautta kulkeva käyrä $u$, jolla $T(u)$ saa pienimmän arvonsa.
Katso myös Differentiaali- ja integraalilaskenta, Integraali, Differentiaaliyhtälö, Bernoulli Johann, Ääriarvo.
Varianssi (engl. Variance)
Varianssi on odotusarvosta laskettujen neliöllisten poikkeamien odotusarvo: $$ \mathrm{Var}(X) = \sigma^2 =\mathrm{E}(X -(\mathrm{E}(X))^2. $$ Voidaan osoittaa, että $\mathrm{Var}(X) = \mathrm{E}(X^2) - (\mathrm{E}(X))^2$. Normaalijakauman toinen parametri $\sigma ^2$ on normaalijakauman varianssi. Otosvarianssi $s²$ on vastaavasti: $$ s² = \frac{1}{n-1} \sum_{i=1}^n ( X_i - \bar{X})^2,$$ missä $n$ on otoksen koko ja $\bar{X}$ on otoskeskiarvo: $$ \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i. $$ Luokitellusta aineistosta otosvarianssi lasketaan kaavalla: $$ S^2 = \frac{1}{n-1} \sum_{i=1}^{k} f_i (X_i - \bar{X})^2, $$ missä $f_i$ on luokan $X_i$ frekvenssi, $i = 1, \ldots, k$, ja $\bar{X}$ on keskiarvo: $$ \bar{X} = \frac{1}{n} \sum_{i=1}^{k} f_i X_i. $$ Varianssin neliöjuuri on hajontamittana paljon käytetty keskihajonta.
Katso myös Normaalijakauma, Vaihtelevuus, Korrelaatiokerroin, Jakauma, Keskihajonta, Tunnusluku, Tilastollinen tunnusluku, Lineaarisen funktion varianssi, Kovarianssi, Hajonta, Gaussin jakauma, Satunnaismuuttuja.
Varianssianalyysi (engl. Analysis of variance)
Erityisesti suunniteltuihin kokeisiin liittyvä testimenettely. Testissä tutkitaan (analysoidaan), voiko k eri tavalla käsitellyssä ryhmässä olla sama teoreettinen odotusarvo (käsittelyllä ei ole vaikutusta). Yleisesti testin avulla voidaan tutkia, voiko k otosta tulla perusjoukoista, joilla on sama odotusarvo. Lähtö-oletuksena on: Vertailtavat ryhmät ovat jakautuneet normaalisti, ja kaikissa ryhmissä vaihtelu on yhtä suurta (varianssit ovat samoja - yleensä tuntemattomia.) Keskiarvojen yhtäsuuruutta tutkitaan vertaamalla ryhmäkeskiarvojen vaihtelun suuruutta ryhmien sisäiseen vaihteluun F-testin avulla. \[F = \frac{\left ( \frac{\sum _i n_i ( \bar{x_i} - \bar{x} ) ^2}{k-1} \right ) } {\left ( \frac{\sum _i \sum _j ( x_{ij} - \bar{x_i} ) ^2}{n-k} \right ) } , \] Missä $ x_{ij} $ j:s havainto ryhmässä (otoksessa) $i$, $ \bar{x_i} $ ryhmän (otoksen) $i$ keskiarvo, $ n_i $ on otoskoko ryhmässä (otoksessa) $i$ ja $ \bar{x} $ on koko aineiston keskiarvo. Mikäli nollahypoteesi keskiarvojen yhtäsuuruudesta pitää paikkansa, Testisuure noudattaa $F$-jakaumaa vapausasteilla $k-1$, $n-k$, missä $n$ on havaintojen kokonaismäärä.. Mikäli odotusarvo yhdessäkin ryhmässä poikkeaa muista, testisuure saa suuria arvoja. Testi on siis yksisuuntainen.
Katso myös Tilastollinen testi.
Varjo (engl. Shadow)
Olion takana oleva alue, johon valo ei osu, koska olio on sen tiellä.
Varman tapauksen todennäköisyys (engl. Probability of whole sample space, Probability of sure event)
Jos S on koko otosavaruus, niin p(S)=1.
Katso myös Todennäköisyys.
Vasta-alkio (engl. Additive inverse)
Jos yhteenlaskun neutraalialkio on 0, niin alkion $a$ vasta-alkio $a'$ on se alkio, jolla $a+a' = a'+a = 0$. Joukoissa $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ alkion $a$ vasta-alkio on $-a$, mutta joukossa $\mathbb{N}$ alkioilla ei ole vasta-alkioita.
Katso myös Yhteenlasku, Nolla-alkio, Yhteenlaskun neutraalialkio, Luku, Käänteis-, Vähennyslasku, Vähentäminen, Joukko.
Vastaesimerkki (engl. Counter example, Counter-example, Counterexample)
Esimerkki, joka osoittaa esitetyn yleisen väittämän vääräksi.
Katso myös Todistaa vääräksi.
Vastahypoteesi, Vaihtoehtoinen hypoteesi (engl. Alternate hypothesis)
Nollahypoteesin vastakohta. Mikäli nollahypoteesi ei ole tosi, on vaihtoehtoinen hypoteesi tosi ja kääntäen. Vaihtoehtoisesta hypoteesista käytetään merkintää $H_1$.
Katso myös Nollahypoteesi, Alternoida.
Vastainen kulma (engl. Vertical angle)
Vastakkaissuuntaiset (engl. Antiparallel)
Kaksi yhdensuuntaista suuntajanaa tai vektoria, jotka osoittavat päinvastaisiin suuntiin, ovat vastakkaissuuntaiset.

Katso myös Yhdensuuntainen.
Vastakohtaiset kulmat (engl. Alternate angles)
Kun suora leikkaa kahta yhdensuuntaista suoraa, niin vastakohtaisia kulmapareja ovat syntyneistä leikkauskulmista sellaiset, jotka ovat eri puolilla leikkaavaa suoraa, mutta joille molemmille leikkaava suora on vasen kylki tai molemmille oikea kylki.
Katso myös Kulma, Alternoida.
Vastapäivään (engl. Anticlockwise, Counterclockwise)
Kiertää vastakkaiseen suuntaan kuin kellon viisarit eli ylhäältä vasemmalle, vasemmalta alas, alhaalta oikealle ja oikealta ylös. Kierto vastapäivään on myötäpäivään kierron vastakohta. Suunta, johon maa kiertäisi, jos sitä katsoisi Pohjoisnavan yläpuolelta.
Matematiikassa kiertosuuntaa vastapäivään sanotaan positiiviseksi kiertosuunnaksi.
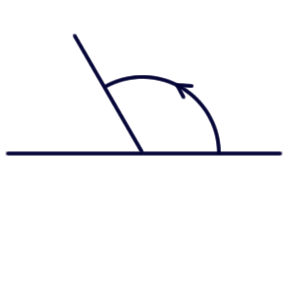
Katso myös Kierto, Myötäpäivään, Kierron muuttaminen vastakkaissuuntaiseksi, Kiertosuunta.
Vastaus (engl. Answer)
Asia, joka halutaan saada selville matemaattista ongelmaa ratkaistaessa. Esimerkiksi luku, joka saadaan laskun lopputuloksena.
Katso myös Matemaattinen päättely.
Vastinkulmat (engl. Corresponding angles)
Vastinkulmat ovat ne yhtä suuret kulmat, jotka muodostuvat suoran leikatessa kahta yhdensuuntaista suoraa. Sanaa käytetään muissakin yhteyksissä. Esimerkiksi yhdenmuotoisissa kuvioissa toisiaan vastaavat ja siis yhtäsuuret kulmat ovat vastinkulmia.
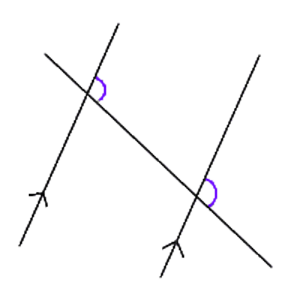
Katso myös Kulma.
Vedonlyöntisuhde, Klassinen todennäköisyys (engl. Odds)
Todennäköisyyslaskennassa voittamisen todennnäköisyyden suhde häviämisen todennnäköisyyteen.
Tapahtuman tapahtumisen todennäköisyys jaettuna todennäköisyydellä, että se ei tapahdu. Matematiikassa on yleensä hyödyllistä puhua vain pelkistä todennäköisyyksistä.
Katso myös Todennäköisyys.
Vektoreiden ristitulon ominaisuudet (engl. Vector product laws)
$a \times b = -b \times a.$ $a \times (b+c) = (a \times b)+(a \times c).$
Katso myös Vektoritulo, Ristitulo.
Vektori (engl. Vector)
Alkeismatematiikassa vektori on suure, jolla on koko ja suunta. Esimerkiksi tuulta saatettaisiin mitata vektorilla, koska sillä on sekä nopeus että suunta. Joskus on hyödyllistä ajatella vektoria suunnattuna janana.
Korkeammassa matematiikassa vektori määritellään vektorialgebran säännöt toteuttavan oliojoukon jäsenenä eli vektoriavaruuden alkiona.
Katso myös Nollavektori, Suoran vektorimuotoinen yhtälö, Tason vektorimuotoinen yhtälö, Yksikkövektori, Tangenttivektori, Resultantti, Paikkavektori, Pystyvektori, Komponentti, Skalaari, Geometria, Analyyttinen tasogeometria, Vektoriavaruus, Normaalivektori, Vektorin normi, Vektorialgebra, Vaakavektori, Sivunormaalisuora, Sivunormaalivektori, Analyyttinen avaruusgeometria, Ominaisvektori, Lineaarialgebra.
Vektorialgebra (engl. Vector algebra)
\newcommand{\v}[1]{\mathbf{#1}} Vektorialgebran laskusäännöt ovat:
- [Yhteenlasku:] Jos $\v{x}=(x_{1}, x_{2}, ... , x_{n})$ ja $\v{y}=(y_{1}, y_{2}, ... , y_{n}),$ niin $\v{x}+\v{y}=(x_{1}+y_{1}, x_{2}+y_{2},\dots , x_{n}+y_{n})$.
- [Skalaarilla kertominen:] Jos $\v{x}=(x_{1}, x_{2}, ... , x_{n})$ on vektori ja $t$ on skalaari, niin $t\v{x}=(tx_{1}, tx_{2},$ ..., $tx_{n})$.
Katso myös Algebra, Vektori, Vektorien yhteenlasku, Skalaari, Vektoriavaruus, Skalaarilla kertominen.
Vektorianalyysi (engl. Vector calculus)
Vektorianalyysi tutkii vektoriarvoisia funktioita sekä sitä, miten näitä funktioita voidaan derivoida ja integroida.
Katso myös Roottori, Divergenssi.
Vektoriavaruuden dimensio (engl. Dimension of a vector space)
Vektoriavaruuden dimensio on sama kuin sen kannan alkioiden lukumäärä. Voidaan osoittaa, että kaikissa vektoriavaruuden kannoissa on sama määrä alkioita. Kannan alkioiden lukumäärä voi toki olla myös ääretön.
Katso myös Dimensio, Ulottuvuus, Kanta.
Vektoriavaruus (engl. Vector space)
$F$-modulia kutsutaan $F$-vektoriavaruudeksi, jos $F$ on kunta.
Olkoon $V=\{ x\bar i + y \bar j + z \bar k \mid x,y,z \in \mathbb{R}\}$ tavallisten $3$-ulotteisten vektoreiden joukko. Tällöin $V$ on $\mathbb{R}$-vektoriavaruus vektoreiden tavanomaisten laskutoimitusten suhteen.
Katso myös Vektori, Ydin, Lineaarinen riippumattomuus, Dimensio, Ulottuvuus, Virittää, Aliavaruus, Normiavaruus, $\ell^p$-avaruus, Euklidinen avaruus, Banachin avaruus, Vektorialgebra, Sarakeavaruus, Riviavaruus, Kanta, Bilineaarinen muoto, Kategoria, Matriisin dimensio, Hilbertin avaruus, Sisätuloavaruus, Lineaarialgebra.
Vektorien tensoritulo (engl. Tensor product of vectors, Dyadic product)
Vektorien $a$ ja $b$ tensoritulo määritellään kaavalla \[ a \otimes b = (b \cdot c) a, \] missä $c$ voi olla mikä tahansa vektori. Tensoritulo ei ole kommutatiivinen.
Katso myös Tulo, Vaihdannainen, Kommutatiivinen.
Vektorien yhteenlasku (engl. Vector addition)
Kaksi vektoria lasketaan yhteen asettamalla toinen vektori niin, että sen alkupiste on ensimmäisen vektorin loppupiste. Tällöin vektorien summa on vektori, jonka alkupiste on ensimmäisen vektorin alkupiste ja loppupiste toisen vektorin loppupiste.
Esimerkiksi vektorit $(1, 2)$ ja $(4, 3)$ lasketaan yhteen komponenteittain: $(1, 2)+(4, 3)=(1+4, 2+3)=(5, 5)$.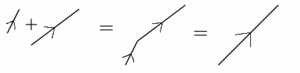
Katso myös Resultantti, Komponentti, Vektorialgebra.
Vektorikolmitulo (engl. Vector triple product)
Vektoreiden $\overline{A}$, $\overline{B}$ ja $\overline{C}$ vektorikolmitulo on vektori $\overline{A} \times (\overline{B} \times \overline{C})$. Se on sama kuin vektori $(\overline{A} \cdot \overline{C}) \overline{B} - (\overline{A} \cdot \overline{B}) \overline{C}$.
Katso myös Kolmitulo, Vektorikolmitulon laskusääntöjä.
Vektorikolmitulon laskusääntöjä (engl. Vector triple product identity)
$\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c} $
Katso myös Vektorikolmitulo, Identiteetti.
Vektorin normi (engl. Modulus of a vector)
Vektorin $\mathrm{v}$ normi, $\| \mathrm{v} \|$, on sen suuruus.
Katso myös Nollavektori, Vektori, Yksikkövektori, $\mod$, Reaaliluku, Matriisin normi.
Vektorin pituus (engl. Length of a vector)
Vektorin $\vec{r} = (a, b, c)$ pituus on $|\vec{r}| = \sqrt{a^2+b^2+c^2}$.
Vektoritulo, Ristitulo (engl. Cross product, Vector product)
Vektorien $\vec{x}=(a, b, c)$ ja $\vec{y}=(d, e, f)$ vektori- eli ristitulo $\vec{x} \times \vec{y}$ on vektori, jonka määrittelee kaava \[\vec{x} \times \vec{y}=(bf-ce, cd-af, ae-bd).\]
Katso myös Tulo, Vektoreiden ristitulon ominaisuudet, Pistetulo, Antikommutatiivinen, Skalaaritulo, Sisätulo.
Venyttää, Venytys (engl. Stretch)
Venytys on kuvaus, jossa kuviota vedetään tai venytetään yhteen suuntaan. Yksi suora pysyy aina venytyksessä paikallaan ja kaikki muut kuvion pisteet liikkuvat kohtisuorassa paikallaan pysyvää suoraa vastaan. Paikallaan pysyvää suoraa kutsutaan invariantiksi suoraksi.
Venyttää tarkoittaa tehdä jokin pidemmäksi.
Katso myös Perspektiivinen affiinikuvaus, Geometrinen muunnos.
Venytys, Venyttää (engl. Stretch)
Venytys on kuvaus, jossa kuviota vedetään tai venytetään yhteen suuntaan. Yksi suora pysyy aina venytyksessä paikallaan ja kaikki muut kuvion pisteet liikkuvat kohtisuorassa paikallaan pysyvää suoraa vastaan. Paikallaan pysyvää suoraa kutsutaan invariantiksi suoraksi.
Venyttää tarkoittaa tehdä jokin pidemmäksi.
Katso myös Perspektiivinen affiinikuvaus, Geometrinen muunnos.
Verho, Verhokäyrä (engl. Envelope, Tangent curve)
Käyrä tai pinta, joka sivuaa jokaista suora-, käyrä-, taso- tai pintaperheen jäsentä.
Kahdessa ulottuvuudessa käyräperheen $f(x,y,t) = 0$, missä $t$ on parametri, verhokäyrän yhtälö voidaan löytää ratkaisemalla yhtälöryhmä \[ \left \{ \begin{array}{l} f(x, y, t)=0, \\ \frac{\partial}{\partial t } f(x, y, t) = 0. \end{array} \right. \]Verkko (engl. Graph in graph theory, Graph)
Äärellinen joukko tason pisteitä ja näitä yhdistäviä janoja. Pisteitä kutsutaan usein verkon solmuiksi ja janoja verkon viivoiksi tai kaariksi.
Verkkoja ja niiden ominaisuuksia tutkiva matematiikan ala on nimeltään verkkoteoria.
Katso myös Verkon solmu, kauppamatkustajan ongelmat, Puukaavio, Puu, Königsbergin sillat, Suunnattu verkko, Eulerin kulku, Hamiltonin kulku, Tasoverkko, Yhtenäinen verkko, Päätöspuu, Verkon viiva, Neljän värin ongelma.
Verkkoteoria (engl. Graph theory)
Pisteiden ja niitä yhdistävien viivojen muodostamia verkkoja koskeva tutkimusala. Tunnettuja verkkoteorian ongelmia ovat kauppamatkustajan ongelma (mikä on lyhin reitti, joka kulkee kaikkien kaupunkien kautta annetussa kaupunkien ja niitä yhdistävien teiden verkossa) ja Königsbergin (nyk. Kaliningrad) siltojen ongelma (onko mahdollista kävellä Königsbergin kaupungin kaikkien seitsemän sillan yli siten, että kunkin sillan yli kuljetaan täsmälleen kerran ja että lopulta päädytään samaan pisteeseen, josta kävely alkoi).
Katso myös kauppamatkustajan ongelmat, Diskreetti matematiikka, Puukaavio, Königsbergin sillat, Eulerin kulku, Hamiltonin kulku, Tasoverkko, Neljän värin ongelma.
Verkon solmu (engl. Node, Vertex of a graph, Vertex)
Verkko muodostuu pisteistä eli solmuista ja niiden välisistä yhteyksistä eli verkon sivuista tai särmistä.
Katso myös Piste, Yhtenäinen verkko, Verkon viiva, Verkko.
Verkon viiva (engl. Arc, Edge of a graph, Edge, Arc of a graph)
Verkkoteoriassa verkon pisteitä eli solmuja yhdistäviä janoja kutsutaan verkon viivoiksi.
Katso myös Verkon solmu, Suora, Yhtenäinen verkko, Verkko.
Verkon väritys (engl. Colouring)
Verkko jakaa tason erillisiin alueisiin, joista kukin voidaan värittää jollakin värillä. Jos vaaditaan, että kahta vierekkäistä aluetta ei väritetä samalla värillä, niin voidaan kysyä, kuinka monta eri väriä annetun verkon värittämiseen silloin tarvitaan. Voidaan myös kysyä, kuinka monta väriä tarvitaan tietynlaisella pinnalla olevan verkon värittämiseen. Esimerkiksi pallon pinnalla olevan verkon värittämiseen saatetaan tarvita useampi väri kuin tasossa olevan verkon värittämiseen.
Verrannollinen, Suoraan verrannollinen (engl. Directly proportional, Proportional)
Kahta suuretta sanotaan suoraan verrannollisiksi, tai pelkästään verrannollisiksi, jos niiden suhde on vakio. Tällöin yhden suureen kaksinkertaistuessa toinenkin kaksinkertaistuu.
Katso myös Suoraan verrannollisuus.
Verrannollisuus (engl. Common ratio)
Jos suureille a, b, c ja d pätee a : b = c : d, niin suureita sanotaan verrannollisiksi. Näin on asian laita esimerkiksi silloin, kun a ja b ovat johonkin kuvioon kuuluvien janojen pituudet ja c ja d ovat vastaavien janojen pituudet yhdenmuotoisessa kuviossa.
Katso myös Aritmeettisen jonon erotus, Suhde, Geometrinen jono.
Verranto (engl. Proportion)
Neljän suureen sanotaan olevan verrannollisia, jos ensimmäisen ja toisen suureen suhde on yhtä suuri kuin kolmannen ja neljännen suhde. Esimerkiksi 3:4 = 6:8 tai 3/4 = 6/8. Hyvän esimerkin verrannosta antaa kartan mittakaava. Esimerkiksi etäisyys kartalla : todellinen etäisyys = 1 : 50000.
Katso myös Kymmenmurtoluku, Histogrammi, Merkintätapa, Notaatio, Suhde.
Verrata (engl. Compare)
Tutkia kahden asian tai olion välisiä yhteneväisyyksiä ja eroja.
Katso myös Erotus, Kvartiilivälin pituus, Keskiarvo, Aritmeettinen keskiarvo, Mediaani, Moodi, Tyyppiarvo, Keskihajonta, Tilastotiede, Kuvajoukko, Funktion kuvajoukko.
Versiera (engl. Versiera, Witch of Agnesi)
Olkoon $PQ$ ympyrän halkaisija. Piirretään ympyrälle tangentti pisteeseen $Q$. Valitaan piste $R$ ympyrän kehältä ja jatketaan suoraa $PR$ niin, että se leikkaa tangentin pisteessä $S$. Piirretään pisteen $S$ kautta suora, joka on yhdensuuntainen $PQ$:n kanssa. Piirretään toinen suora, joka kulkee pisteen $R$ kautta ja on yhdensuuntainen tangentin kanssa. Merkitään näiden kahden suoran leikkauspistettä $P'$:lla. Pisteen $P'$ uraa pisteen $R$ kiertäessä koko ympyrän kehän kutsutaan versieraksi tai Agnesin noidaksi.
Tämän käyrän yhtälö on muotoa $xy^{2} = 4a^{2}(2a-x)$, missä $a$ on ympyrän säde.
Vertailtavissa olevat (engl. Comparable)
Mitkä tahansa kaksi reaalilukua $p$ ja $q$ ovat vertailtavissa, koska täsmälleen yksi seuraavista pätee: $p \lt q$, $p = q$ tai $p \gt q$.
Katso myös Yhtäsuuri, Suurempi kuin, Pienempi kuin, Reaaliluku, Sama.
Viereinen (engl. Adjacent)
Kolmion tai muun monikulmion kulman viereiset sivut ovat ne kaksi kolmion tai monikulmion sivua, jotka ovat kyseisen kulman kylkinä. Kolmion sivun viereiset kulmat ovat ne kolmion kulmat, joiden kärjet ovat sivun päätepisteet.
Katso myös Vieruskulma.
Vierintäkäyrä (engl. Roulette)
Käyrä, jonka jotakin käyrää pitkin vierivän kappaleen kiinnitetty piste tai jana piirtää.
Katso myös Ura, Sykloidi, Pistevierintäkäyrä, Trokoidi.
Vieruskulma (engl. Adjacent angles)
Kulmat $\angle AOB$ ja $\angle BOC$ ovat vieruskulmia, jos $A$, $O$ ja $C$ ovat samalla suoralla. Kulman ja sen vieruskulman summa on $180^{\circ}$.
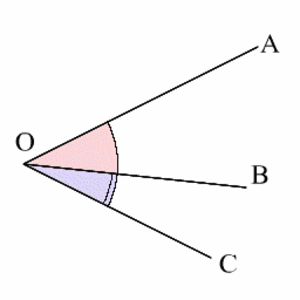
Vieten kaava (engl. Viete's formula)
\[ \pi = \frac{2}{\sqrt{\frac{1}{2}} \sqrt{\frac{1}{2}+ \frac{1}{2} \sqrt{\frac{1}{2}}} \sqrt{\frac{1}{2}+ \frac{1}{2} \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{\frac{1}{2}}}} \ldots } \]
Katso myös Piin arvon laskeminen.
Viisi, 5 (engl. 5, Five)
Viisi on kolmas alkuluku. Se on ainoa alkuluku, joka kuuluu kahteen eri alkulukukaksospariin: $(3, 5)$ ja $(5, 7)$.
Viisi on Fermat'n alkuluku: $5 = 2^{2^{1}} + 1$.
Ns. parittoman Goldbachin otaksuman mukaan $5$ on suurin pariton luku, jota ei voida kirjoittaa kolmen alkuluvun summana. Otaksumaa ei ole todistettu.
Viisi on viides Fibonaccin luku.
Säännöllisiä monitahokkaita eli Platonin kappaleita on viisi.
Viisi on toinen (neliö)pyramidiluku: $5 = 1^{2} + 2^{2}$.
$\phi(5) = 4$, $d(5) = 2$, $\sigma(5) = 6$.

Katso myös Viisikulmio, Fermat'n alkuluku, Fibonaccin luku, Platonin kappaleet.
Viisikulmio (engl. Pentangle, Pentagon)
Monikulmio, jossa on viisi sivua ja viisi kulmaa.
Säännöllisessä viisikulmiossa on viisi yhtä pitkää sivua ja viisi yhtä suurta kulmaa.
Katso myös Viisi, 5, Pentagrammi, Nelikulmio, Monikulmio.
Viisikymmentä, 50 (engl. Fifty, 50)
50 on pienin luku, joka voidaan kirjoittaa kahdella eri tavalla kahden neliön summaksi: $50 = 5^{2} + 5^{2} = 7^{2} + 1^{2}.$

Katso myös Kymmenen monikerta.
Viisitoista, 15 (engl. 15, Fifteen)
15 on viides kolmioluku ja kolmas kuusikulmioluku.
$\phi(15) = 8$, $d(15) = 4$, $\sigma(15) = 24$,

Katso myös Eulerin $\varphi$-funktio.
Viivoitin (engl. Ruler)
Laite, jolla voidaan piirtää suoria viivoja ja mitata etäisyyksiä.
Katso myös Senttimetri.
Vino, Kursiivi (kirjoitus) (engl. Oblique)
Vino suora on kalteva suora, joka voi kallistua vasemmalle, oikealle, ylös tai alas. Se on suora, joka ei ole pystysuora eikä vaakasuora. Kursiivi on vinoa kirjoitusta.
Lävistäjän suuntainen tai kalteva.
Katso myös Pystysuora, Vaakasuora.
Vinokunta (engl. Skew field, Division ring or skew field, Division ring)
Ykkösellinen rengas, jossa jokaisella nollasta poikkeavalla alkiolla on käänteisalkio.
Vinokunta on struktuuri, jolla on kaikki muut kunnan ominaisuudet lukuunottamatta sitä, että vinokunnassa kertolaskun ei tarvitse olla vaihdannainen.
Katso myös Rengas.
Vinosymmetrinen matriisi (engl. Skew symmetric matrix)
Neliömatriisia $A$ kutsutaan vinosymmetriseksi, jos $-A = A^T$. Huomaa, että tällöin päälävistäjän jokaisen alkion on oltava nolla,
Katso myös Päälävistäjä, Matriisin transpoosi, Vinosymmetrisen matriisin ominaisarvot.
Vinosymmetrisen matriisin ominaisarvot (engl. Eigenvalues of a skew-symmetric matrix)
Vinosymmetrisen matriisin ominaisarvot ovat imaginaarisia tai 0.
Katso myös Lause, Ominaisarvo, Vinosymmetrinen matriisi.
Virhe (engl. Error)
Todellisen arvon ja likiarvon välinen erotus. Tätä voidaan mitata sen suuruudella (absoluuttinen virhe) tai suhteena todelliseen arvoon (suhteellinen virhe).
Katso myös Likimääräinen, Reaaliluku, Keskivirheen arvio.
Virhefunktio (engl. Error function)
Funktio \[ \mathrm{erf}(z) = \frac{2}{\sqrt{\pi}} \int_{0}^{z}e^{-s^2} ds.\] Todennäköisyyslaskennassa virhefunktio liittyy normaalijakauman tiheysfunktion integraaliin. Se esiintyy myös joidenkin osittaisdifferentiaaliyhtälöiden ratkaisuissa.
Katso myös Normaalijakauma, Funktio, Kuvaus, Integraali, $\erf$, Gaussin jakauma.
Virhetermi, Jäännöstermi (engl. Error term, Remainder term)
Taylorin sarjaan tai mihin tahansa sarjaan lliittyvä termi $R_{n}$. Yleensä tällaisen termin arvo saadaan mielivaltaisen pieneksi valitsemalla indeksi $n$ riittävän suureksi. Tämä voidaan osoittaa ilmaisemalla jäännöstermi sopivassa muodossa.
Katso myös Termi, Taylorin sarja, Maclaurinin sarja, Ominaisuus, jonka arvot ovat jatkuvia, Jäännöstermin Cauchyn lauseke, Jäännöstermin integraalilauseke, Lagrangen jäännöstermi.
Virittäjistö (engl. Generator)
Olkoon $G$ ryhmä. Joukko $A \subset G$ on ryhmän $G$ virittäjistö, jos joukon $A$ virittämä ryhmän $G$ aliryhmä on koko $G$.
Katso myös Joukko, Ryhmä, Syklinen ryhmä.
Virittävä puu (engl. Spanning tree)
Verkon virittävä puu on puu, joka sisältää verkon jokaisen pisteen.
Katso myös Puu.
Virittää (engl. Span)
Olkoon $G$ ryhmä, ja $A \subset G$. Joukon $A$ virittämä ryhmän $G$ aliryhmä on pienin ryhmän $G$ aliryhmä, joka sisältää joukon $A$.
Aivan vastaavasti määritellään myös renkaassa $Q$ joukon $A \subset Q$ virittämä alirengas, $R$-modulissa $M$ joukon $A \subset M$ virittämä $R$-alimoduli ja niin edelleen.
Yllä sana pienin on ymmärrettävä inkluusion mielessä: Joukko $A$ on pienin joukko, jolla on ominaisuus $P$, jos ja vain jos $A$:lla on ominaisuus $P$, ja $A \subset B$ kaikilla sellaisilla $B$, joilla on ominaisuus $P$.
Kaikki $2$-ulotteiset vektorit mudostavat tavallisten vektorien laskutoimitusten suhteen $\mathbb{R}$-vektoriavaruuden $\mathbb{R}^2$.
Yksiö $\{2\bar i + 3 \bar j\}$ virittää vektoriavaruudessa $\mathbb{R}^2$ vektorialiavaruuden $\{ r 2\bar i + r 3 \bar j \mid r \in \mathbb{R} \}$.
Katso myös Lineaarinen riippumattomuus, Vektoriavaruus, Sarakeavaruus, Riviavaruus, Kanta.
Virtuaalinen, Näennäinen (engl. Virtual)
Esimerkiksi virtuaalinen työ on työ, joka olisi tehty voimalla, jota ei todellisuudessa ollut olemassa.
Virtuaalinen kuva on olemassa tietokoneen muistissa, mutta ei nähtävänä.
Ei todellinen.
Vuorotteleva sarja (engl. Alternating series)
Sarja, jossa toisiaan seuraavat termit ovat vuorotellen positiivisia ja negatiivisia.
Katso myös Sarja.
Vuosi (engl. Year)
Sen ajan pituus, jonka kuluessa maa kiertää kerran auringon ympäri. Yksi kalenterivuosi on 365 päivää, karkausvuosina 366 päivää. Karkausvuosia ovat vuodet, joiden vuosiluku on neljällä jaollinen, paitsi ne sadalla jaolliset, jotka eivät ole jaollisia luvulla 400. Keskimäärin yksi vuosi on 365,2425 päivää, kun karkausvuodet otetaan huomioon. Tämä on lähellä todellista arvoa, joka on hieman yli 365,2424 päivää. Uuden vuoden aattona vuoteen lisätään joskus ylimääräisiä sekunteja, jotta kalenteri pysyisi tarkalleen vuodenaikojen tahdissa.
Vuosisata (engl. Century)
Sata vuotta.
Vuotuinen (engl. Annual)
Kerran joka vuosi tapahtuva.
Katso myös Vuosi, Frekvenssi.
Vähenevä jono (engl. Decreasing sequence, Monotonic decreasing sequence)
Jonoa $(u_{n})$ kutsutaan väheneväksi, jos $u_{n+1} \le u_{n}$ on voimassa kaikilla $n$.
Katso myös Monotoninen jono.
Vähennyslasku, Vähentäminen (engl. Subtraction, Subtract)
Jos vähennät yhdestätoista kuusi, saat viisi: 11-6 = 5.
Kahdentoista ja neljän välinen erotus on kahdeksan: 12-4 = 8.
Ottaa pois, etsiä kahden suureen välinen erotus. Vähennyslasku on yhteenlaskun käänteislaskutoimitus.
Vähennyslaskun merkki on -.
b:n vähentäminen a:sta tarkoittaa, että lisätään a:han b:n vasta-alkio. Siis a-b on yhtä suuri kuin a+(-b), missä - on vähennyslaskun merkki.
Katso myös Yhteenlasku, Vasta-alkio, Laskutoimitus, Vähentää, Erotus, Binäärinen kuvaus, Kaksipaikkainen kuvaus.
Vähentyä, Vähetä (engl. Decrease)
Pienentyä, tulla pienemmäksi.
Jonoa kutsutaan väheneväksi, jos sen jokainen alkio on pienempi tai yhtä suuri kuin edeltäjänsä. Jonoa kutsutaan aidosti väheneväksi, jos sen jokainen alkio on pienempi, mutta ei yhtä suuri, kuin edeltäjänsä.
Katso myös Alentaa, Redusoida, Palauttaa, Pelkistää, Kasvaa, Kasvattaa.
Vähentäminen, Vähennyslasku (engl. Subtraction, Subtract)
Jos vähennät yhdestätoista kuusi, saat viisi: 11-6 = 5.
Kahdentoista ja neljän välinen erotus on kahdeksan: 12-4 = 8.
Ottaa pois, etsiä kahden suureen välinen erotus. Vähennyslasku on yhteenlaskun käänteislaskutoimitus.
Vähennyslaskun merkki on -.
b:n vähentäminen a:sta tarkoittaa, että lisätään a:han b:n vasta-alkio. Siis a-b on yhtä suuri kuin a+(-b), missä - on vähennyslaskun merkki.
Katso myös Yhteenlasku, Vasta-alkio, Laskutoimitus, Vähentää, Erotus, Binäärinen kuvaus, Kaksipaikkainen kuvaus.
Vähentää (engl. Deduct)
Kun vähennät jotakin, niin otat jotakin pois. Jos $21$:stä vähennät $9$, niin otat pois $9$ ja jäljelle jää $12$. Siis $21 - 9 = 12$.
Katso myös Vähennyslasku, Vähentäminen.
Vähetä, Vähentyä (engl. Decrease)
Pienentyä, tulla pienemmäksi.
Jonoa kutsutaan väheneväksi, jos sen jokainen alkio on pienempi tai yhtä suuri kuin edeltäjänsä. Jonoa kutsutaan aidosti väheneväksi, jos sen jokainen alkio on pienempi, mutta ei yhtä suuri, kuin edeltäjänsä.
Katso myös Alentaa, Redusoida, Palauttaa, Pelkistää, Kasvaa, Kasvattaa.
Väite (engl. Claim)
Usein esitettäessä matematiikkaa tehdään väite eli väitös, jonka sanotaan olevan tosi, vaikka sitä ei vielä ole todistettu, ja sitten todistetaan se.
Väli (engl. Interval)
Kaikki luvut, jotka ovat kahden tietyn luvun välissä, muodostavat välin. Samoin kaikki pisteet, jotka sijaitsevat kahden tietyn pisteen välissä suoralla.
Väli on mikä tahansa osajoukko $I \subset \mathbf{R}$, joka toteuttaa seuraavan ehdon: jos $x \lt y \lt z$ ja $x, z \in I$, niin $y \in I$.
On olemassa yhdeksän erityyppistä väliä luokiteltuina sen mukaan, onko väli rajoitettu molemmista tai jommasta kummasta päästä ja kuuluvatko välin päätepisteet väliin vai eivät.
Katso myös hakusana "Yhtenäinen".
Katso myös Suljettu väli, Avoin väli, Joukko.
Väliarvolause (engl. Mean value theorem)
Jos $f(x)$ on jatkuva kaikilla $a \leq x \leq b$ ja derivoituva kaikilla $a \lt x \lt b$, niin on olemassa luku $a \lt c \lt b$, jolle pätee \[ \frac{\mathrm{d}f}{\mathrm{dx}}(c) = \frac{f(b)-f(a)}{b-a}. \] Toisin sanoen, on olemassa sellainen luku $c$, että pisteen $(c,f(c))$ kautta kulkeva funktion $f(x)$ tangentti on yhdensuuntainen pisteiden $(a,f(a))$ ja $(b,f(b))$ kautta kulkevan suoran kanssa.
Katso myös Lause.
Välissä (engl. Between)
Jos $x$ on $a$:n ja $b$:n välissä ja $a$ on pienempi kuin $b$, niin todennäköisesti tarkoitetaan \[ a \lt x \lt b, \] mutta saatetaan myös tarkoittaa \[ a \leq x \lt b \text{ tai } a \lt x \leq b \text{ tai } a \leq x \leq b. \] Tämä on esimerkki tapauksesta, jossa matemaattisen merkintätavan tarkkuus on hyvin hyödyllinen väärinymmärryksen välttämiseksi.
Välttämätön ehto (engl. Necessary)
$A$ on välttämätön ehto $B$:lle tarkoittaa, että $B$ ei voi olla tosi, ellei $A$ ole tosi.
Käsitteitä välttämätön ja riittävä ei pidä sekoittaa toisiinsa.
Katso myös Looginen ominaisuus, Vaatia, Riittävä.
Värähdellä (engl. Vibrate)
Liikkua jatkuvasti edestakaisin.
Kuten heilahtelu, mutta värähtely on yleensä säännöllistä tai fysikaalista, kun taas heilahtelu voisi olla epäsäännöllistä ja viitata johonkin abstraktiin suureeseen, joka vaihtelee edestaksisin.
Katso myös Heilahtelu.
Väärä, Epätosi (engl. False)
Toden vastakohta.
Katso myös Looginen ominaisuus, Epätosi propositiolause, Falsum.