Hajaantua (engl. Diverge)
Jonon sanotaan hajaantuvan, mikäli se ei suppene. Hajaantuva jono voi lähestyä ääretöntä tai pysyä rajoitettuna heilahdellen kahden tai useamman luvun välillä. Esimerkiksi jonot \[ 1, 2, 4, 8, 16, 32, \ldots \] ja \[ 1, 0, 1, 0, 1, 0, \ldots \] hajaantuvat.
Katso myös Supeta.
Hajoita ja hallitse (engl. Divide and conquer)
Ratkaisumenetelmä, jossa ongelma jaetaan useiksi pienemmiksi osaongelmiksi, joista kukin ratkaistaan erikseen. Tämä on usein helpompaa kuin yrittää ratkaista koko ongelma kerralla.
Katso myös Algoritmi.
Hajoittaa luku tekijöihinsä, Jakaa luku tekijöihinsä (engl. Decompose a number)
Kirjoittaa luku alkulukujen tulona. Esimerkiksi $35 = 5 \cdot 7$ ja $36 = 2 \cdot 2 \cdot 3 \cdot 3 = 2^2 \cdot 3^2$.
Katso myös Jakaa tekijöihin, Jakaa murtoluku osamurtolukuihin, Hajoittaa matriisi.
Hajoittaa matriisi (engl. Decompose a matrix)
Matriisin hajoittaminen tarkoittaa sen esittämistä tietyt ominaisuudet omaavien matriisien tulona. Esimerkiksi matriisin $LU$-hajotelmassa matriisi esitetään alakolmio- ja yläkolmiomatriisien tulona.
Katso myös LU-hajotelma, Choleskyn hajotelma, Jakaa luku tekijöihinsä, Hajoittaa luku tekijöihinsä, LDU-hajotelma.
Hajonta (engl. Dispersion)
Otoksen havaintoarvojen vaihtelua kutsutaan hajonnaksi.
Hajontaa kuvaavat useat tunnusluvut: varianssi, keskihajonta, vaihteluväli, kvartiilipoikkeama. Näistä keskihajonta on yleisin. Hajonnan tunnusluvut mittaavat havaintoarvojen keskittymistä odotusarvon ympärille.
Katso myös Kvartiilivälin pituus, Keskihajonta, Varianssi, Vaihteluväli.
Hajontakuvio, Korrelaatiodiagramma (engl. Scatter diagram, Scatter graph, Scatter plot)
Hajontakuvio eli korrelaatiodiagramma on graafinen esitystapa, jonka avulla voidaan pareittain (X ja Y) tarkastella muuttujien välisiä riippuvuuksia tilastoaineistossa. Hajontakuviossa havainnot $i, i=1,...n$ merkitään koordinaatistoon pisteillä paikoissa $(X_i,Y_i), i=1,...n$. Mikäli muuttujien välillä arvellaan olevan syy - seuraus-riippuvuussude, piirretään kuva niin, että syy (selittävä) muuttuja on X-akselilla ja seuraus (selitettävä) muuttuja Y-asteikolla. Hajontakuvio on käyttökelpoinen esitystapa tutkittaessa:
- Ovatko muuttujat riippumattomia, vai esiintyykö muuttujien välillä riippuvuuksia.
- Riippuvuuden muotoa - onko riippuvuus lineaarista vai käyräviivaista.
- Miten osa-aineistot suhtautuvat toisiinsa.
- onko aineistosta poikkeavia (virheellisesti talletettuja) havaintoja.
Halkaisija (engl. Diameter)
Jana, joka yhdistää kaksi ympyrän kehän pistettä ja kulkee ympyrän keskipisteen kautta jakaen ympyrän kahteen yhtä suureen osaan.
Suurin etäisyys kuvion tai kappaleen reunasta toiseen reunaan.
Yleensä puhutaan ympyrän halkaisijasta, joka on mikä tahansa ympyrän keskipisteen kautta kulkeva suora.

Katso myös Ympyrä, Puoliympyrä, Jänne, Sekantti, Konsyklinen, Joukon halkaisija.
Hamiltonin kierros (engl. Hamiltonian circuit, Hamiltonian cycle)
Hamiltonin kulku, joka päättyy samaan pisteeseen, josta alkio.
Katso myös Hamiltonin kulku.
Hamiltonin kulku (engl. Hamiltonian path)
Hamiltonin kulku annetussa verkossa on sellainen kulku, jolla jokainen verkon piste esiintyy täsmälleen kerran.
Katso myös Hamiltonin kierros, Verkkoteoria, Verkko.
Hankelin funktio, Besselin funktio (kolmas laji) (engl. Hankel function, Bessel function of the third kind)
Kolmannen lajin Besselin funktioita on kahdenlaisia: \[ H_n^{(1)}(z)=J_n(z)+iY_n(z) \] ja \[ H_n^{(2)}(z)=J_n(z)-iY_n(z), \] missä $J_n$ ja $Y_n$ ovat ensimmäisen ja ja toisen lajin Besselin funktioita. Kolmannen lajin Besselin funktiot ovat Besselin yhtälön ratkaisuja.
Katso myös Funktio, Kuvaus, Bessel Friedrich Wilhelm, Besselin yhtälö, Besselin funktio (ensimmäinen laji), Besselin funktio (toinen laji), Neumannin funktio.
Hanoin tornit (engl. Tower of Hanoi)
Ikivanha ongelma, jossa on annettu joukko kiekkoja, jotka kaikki ovat erikokoisia, sekä kolme alustaa, joihin kiekkoja saa asettaa. Alussa kaikki kiekot ovat yhdellä alustalla päällekkäin koon mukaisessa järjestyksessä suurin alimpana. Kaikki kiekot on siirrettävä jommallekummalle kahdesta muusta alustasta siten, että suurempaa kiekkoa ei koskaan saa asettaa pienemmän päälle. Vain yhtä kiekkoa kerrallaan saa siirtää. Ongelma voidaan ratkaista millä tahansa kiekkojen lukumäärällä, mutta jos kiekkoja on paljon, ratkaisuun tarvittavien siirtojen määrä on hyvin suuri. On olemassa tarina munkeista, jotka toteuttavat ratkaisua 64 kiekon tapauksessa siirtämällä yhtä kiekkoa joka sekunti. Kun munkit saavat työnsä valmiiksi, tulee maailmanloppu. Mutta aika, joka ratkaisuun kuluu, on paljon pitempi kuin maailmankaikkeuden tähänastinen ikä $\dots$
Katso myös Peli.
Harha, Systemaattinen virhe (engl. Bias)
Tilastollinen menetelmä on harhainen, mikäli tapahtumiin liittyvät todennäköisyydet eivät ole oikeat. Esimerkiksi yksinkertaisessa satunnaisotannassa kaikki poimintatodennäköisyydet eivät ole yhtä suuria (perusjoukossa on ryhmä alkioita, joiden poimintatodennäköisyys on suurempi kuin muiden alkioiden.) Tilastollinen parametrin estimaatti (arvio) on harhainen, mikäli estimaatin odotusarvo poikkeaa parametrin todellisesta arvosta. Harha on estimaatin odotusarvon ja parametrin todellisen arvon välinen erotus.
Katso myös Harhaton estimaattori, Harhainen.
Harhainen, Epäreilu, Puolueellinen (engl. Unfair)
Nopan sanotaan olevan epäreilu, jos jokaisen silmäluvun saaminen ei ole yhtä todennäköistä.
Jos monen nopanheiton jälkeen on paljon kolmosia ja viitosia, mutta vähän muita silmälukuja, on syytä epäillä, että noppa ei ole symmetrinen vaan epäreilu ja harhainen.
Ei reilu; harhainen. Mahdolliset alkeistapaukset eivät ole yhtä todennäköisiä.
Harhainen (engl. Biased)
Puolueellinen, epäreilu. Kaikki mahdolliset tulokset eivät ole yhtä todennäköisiä. Noppaa sanotaan harhaiseksi, jos kaikki silmäluvut 1, 2, 3, 4, 5 ja 6 eivät ole yhtä todennäköisiä.
Tutkimuksessa harhainen otos on otos, joka ei heijasta oikein koko tutkittavaa populaatiota. Jos esimerkiksi tutkitaan ihmisten työmatkaan käyttämiä kulkuvälineitä haastattelemalla ihmisiä linja-autoasemalla, niin saadaan harhainen otos.
Katso myös Epäreilu, Harhainen, Puolueellinen, Harha, Systemaattinen virhe, Reilu, Harhaton.
Harhaton, Reilu (engl. Fair)
Ei harhainen. Noppaa sanotaan harhattomaksi tai reiluksi, jos noppaa heitettäessä on jokainen silmäluku yhtä todennäköinen tulos.
Jos noppaa toistuvasti heittäessäsi saat jatkuvasti tulokseksi silmälukuja kolme ja viisi, alat pian epäillä nopan olevan harhainen ja epäreilu.
Katso myös Epäreilu, Harhainen, Puolueellinen, Harhainen.
Harhaton estimaattori (engl. Unbiased estimator)
Estimaattori $ \mathrm{T(X)} $ on parametrin $\theta$ harhaton estimaattori mikäli $ \mathrm{E(T(X))}=\theta $
Katso myös Harha, Systemaattinen virhe, Tunnusluku, Tilastollinen tunnusluku, Harhaton keskiarvo, Satunnaismuuttuja.
Harhaton keskiarvo (engl. Unbiased mean)
Harhaton estimaattori populaation keskiarvolle. Jos $(x_i)$ on otos kokoa $n$, frekvensseillä $f_i$, on harhaton keskiarvo \[ \bar{X} = \frac{1}{n} \sum x_i f_i . \]
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Harhaton estimaattori.
Harmoninen jono (engl. Harmonic sequence, Harmonic progression)
Jono \[ 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots. \]
Katso myös Jono, Harmoninen sarja.
Harmoninen keskiarvo (engl. Harmonic mean)
Nollasta eroavien lukujen $a_1, a_2, \ldots, a_n$ harmoninen keskiarvo on \[ H = \frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+...+\frac{1}{a_n}}. \]
Katso myös Paikantamistunnusluku, Keskiluku.
Harmoninen kolmio (engl. Harmonic triangle)
Leibnizin harmoninen kolmio on murtolukukolmio, jossa kukin murtoluku on kahden alapuolella olevan murtoluvun summa: \[ \begin{array}{ccccccccccc} & & & & & 1/1 & & & & & \\ & & & & 1/2 & & 1/2 & & & & \\ & & & 1/3 & & 1/6 & & 1/3 & & & \\ & & 1/4 & & 1/12 & & 1/12 & & 1/4 & & \\ & 1/5 & & 1/20 & & 1/30 & & 1/20 & & 1/5 & \\ 1/6 & & 1/30 & & 1/60 & & 1/60 & & 1/30 & & 1/6 \end{array} \]
Harmoninen konjugaatti, Harmoninen liittopiste (engl. Harmonic conjugate)
Janan $AB$ pisteen $X$ harmoninen liittopiste janan $AB$ suhteen on janan $AB$ määräämän suoran piste $Y\ne X$, jolle pätee \[\frac{AX}{XB}=\frac{AY}{YB}.\]
Katso myös Piste.
Harmoninen liittopiste, Harmoninen konjugaatti (engl. Harmonic conjugate)
Janan $AB$ pisteen $X$ harmoninen liittopiste janan $AB$ suhteen on janan $AB$ määräämän suoran piste $Y\ne X$, jolle pätee \[\frac{AX}{XB}=\frac{AY}{YB}.\]
Katso myös Piste.
Harmoninen sarja (engl. Harmonic series)
Harmoniseksi sarjaksi kutsutaan jonoa, jonka $n$:s jäsen on harmonisen jonon $n$ ensimmäisen jäsenen summa: \[ 1, 1 + \frac{1}{2}, 1 + \frac{1}{2} + \frac{1}{3}, 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}, 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}, \ldots. \] Harmoninen sarja ei suppene, vaan kasvaa rajatta kohti ääretöntä.
Katso myös Harmoninen jono.
Harppi (engl. Compasses)
Väline, jolla voidaan piirtää ympyränkaaria ja ympyröitä. Klassisen tasogeometrian piirustustehtävät on ratkaistava vain harppia ja viivoitinta käyttäen. Esimerkiksi janan puolittaminen tai kulman puolittaminen onnistuu siten, että piirretään harpilla kaksi samansäteistä ympyrää.
Katso myös Ympyrä, Konstruktio, Konstruoituva, Konstruointi.
Harshadin luku, Nivenin luku (engl. Harshad number)
Luku, joka on jaollinen numeroidensa summalla. Esimerkiksi $1729$ on Harshadin luku, koska $1729 = 19 \cdot 91$ ja $19 = 1 + 7 + 2 + 9$. Harshadin lukuja kutsutaan myös Nivenin luvuiksi.
Harva matriisi (engl. Sparse matrix)
Matriisi, jonka alkioista suurin osa on nollia. Nollasta eroavat alkiot voivat olla matriisissa aivan hajallaan tai jollakin tavalla kasautuneet. Esimerkiksi seuraavia matriiseja kutsutaan yleensä harvoiksi: \[ \left ( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right ), \qquad \left ( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 5 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right ) , \qquad \left ( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 3 & 0 \\ 2 & 0 & 0 \end{array} \right ) \]
Hausdorff-avaruus, Hausdorffin avaruus (engl. Hausdorff space)
Topologinen avaruus $X$ on Hausdorff-avaruus, mikäli kaikilla $x,y \in X$, $x \neq y$, on olemassa sellaiset avoimet joukot $U,V \subset X$, joilla $x \in U, y \in V$ ja $U \cap V = \emptyset$.
Katso myös Kompakti, Yhtenäinen, Topologinen monisto.
Hausdorffin avaruus, Hausdorff-avaruus (engl. Hausdorff space)
Topologinen avaruus $X$ on Hausdorff-avaruus, mikäli kaikilla $x,y \in X$, $x \neq y$, on olemassa sellaiset avoimet joukot $U,V \subset X$, joilla $x \in U, y \in V$ ja $U \cap V = \emptyset$.
Katso myös Kompakti, Yhtenäinen, Topologinen monisto.
Heavisiden askelfunktio (engl. Heaviside step function, Heaviside function)
Heavisiden askelfunktio $\mathrm{H}(t)$ määritellään asettamalla \[ \mathrm{H}(t)= \left\{ \begin{array}{c} 0, t \lt 0 \\ 1, t \geq 0 \end{array} \right. \] Tällöin $\mathrm{H}^{\prime}(x)= \delta(x)$, missä $\delta$ on Diracin deltafunktio. Derivaatta $\mathrm{H}^{\prime}(x)$ ei ole määritelty pisteessä $x=0$.
Katso myös Diracin deltafunktio, Askelfunktio.
Hehtaari (engl. Hectare)
Pinta-alan yksikkö. Yksi hehtaari on 10000 neliömetriä. Neliön, jonka sivun pituus on 100 m, pinta-ala on yksi hehtaari.
Katso myös Pinta-ala, Pinta-alayksikkö, Neliömetri, Aari.
Hehto (engl. hecto)
Etuliite, joka tarkoittaa sataa. Sille käytetään merkkiä h. Esimerkiksi 1 hl eli 1 hehtolitra on sata litraa.
Heilahtelu (engl. Oscillation)
Heilahtelu tarkoittaa liikkumista toistuvasti eteen- ja taaksepäin tai ylös- ja alaspäin.
Katso myös Värähdellä.
Heksadesimaalilukujärjestelmä (engl. Hexadecimal)
Heksadesimaalijärjestelmä on lukujärjestelmä, jonka kantaluku on 16. Heksadesimaalijärjestelmässä käytetään numeromerkkeinä numeroita 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ja kirjaimia A, B, C, D, E ja F. Sitä käytetään lähinnä tietojenkäsittelyssä.
Katso myös Lukujärjestelmä, Kantaluku.
Heksaedri, Kuusitahokas (engl. Hexahedron)
Kappale, jossa on kuusi tahkoa. Säännöllinen kuusitahokas on kuutio.
Katso myös Monitahokas.
Helmitaulu, Abakus (engl. Abacus)
Muinainen laskuväline.
Antiikin kreikkalaiset ja roomalaiset käyttivät laskutoimitusten apuna kiviä, joita sijoitettiin vaakasuoralle alustalle kaiverretuille viivoille. Viivat edustivat ykkösiä, kymmeniä, satoja jne. Nykyisin monissa maissa käytetään yhä samalla periaatteella toimivia helmitauluja, joissa viivat ja kivet on korvattu vaakasuorilla tangoilla, joihin on kiinnitetty renkaita.
Heptagrammi (engl. Heptagram)
Seitsensakarainen tähti.

Hermiittinen matriisi (engl. Hermitian matrix)
Neliömatriisia $A$ kutsutaan hermiittiseksi, jos se on kompleksikonjugaattinsa transpoosi eli $A = \bar{A}^T$. (Jos $A$ on reaalinen, tarkoittaa hermiittinen samaa kuin symmetrinen.)
Katso myös Matriisin transpoosi, Symmetrinen matriisi, Liittoluku, Hermiittisen matriisin ominaisarvot, Normaali matriisi, Kompleksikonjugaatti.
Hermiittisen matriisin ominaisarvot (engl. Eigenvalues of a Hermitian matrix)
Hermiittisen matriisin ominaisarvot ovat reaalisia.
Katso myös Lause, Ominaisarvo, Hermiittinen matriisi.
Hermitoitu matriisi (engl. Hermitian conjugate, Associate matrix)
Kompleksisen matriisin $A$ hermitoitu matriisi on matriisin $A$ konjugaattimatriisin transpoosi. Sille käytetään usein merkintää $A^H$ tai $A^{*}$.
Katso myös Matriisi, Frobeniuksen normi.
Heronin kaava (engl. Heron's formula, Hero's formula)
Jos $a$, $b$ ja $c$ ovat kolmion sivujen pituudet sekä $s = (a+b+c)/2$, niin kolmion pinta-ala on \[ A = \sqrt{s(s-a)(s-b)(s-c)}. \]
Katso myös Kolmio.
Heronin ongelma (engl. Heron's problem)
Etsittävä lyhin kahta annettua pistettä yhdistävä käyrä, jolla on täsmälleen yksi yhteinen piste annetun suoran kanssa.
Hessen matriisi (engl. Hessian matrix)
Reaaliarvoisen funktion $y(x_{1}, x_{2}, ... x_{n})$ Hessen matriisi on funktion $y$ toisen kertaluvun osittaisderivaattojen muodostama matriisi: \[ \left( \begin{array}{cccc} \frac{\partial^2 y}{\partial x_1 \partial x_1} & \frac{\partial^2 y}{\partial x_1 \partial x_2} & ... & \frac{\partial^2 y}{\partial x_1 \partial x_n} \\ \frac{\partial^2 y}{\partial x_2 \partial x_1} & \frac{\partial^2 y}{\partial x_2 \partial x_2} & ... & \frac{\partial^2 y}{\partial x_2 \partial x_n} \\ \vdots & \vdots & ... & \vdots \\ \frac{\partial^2 y}{\partial x_n \partial x_1} & \frac{\partial^2 y}{\partial x_n \partial x_2} & ... & \frac{\partial^2 y}{\partial x_n \partial x_n} \end{array} \right). \]
Katso myös Matriisi, Jacobin determinantti, Jacobin matriisi, Osittaisderivaatta.
Hetkellinen muutosnopeus (engl. Instantaneous rate of change)
Jos suure muuttuu ajan kuluessa, voidaan selvittää, kuinka nopeasti se muuttuu mittaamalla tietyn ajanjakson kuluessa tapahtuneen muutoksen määrä ja jakamalla se ajanjakson pituudella. Jos annetaan ajanjakson pituuden pienentyä rajatta, saadaan selville, kuinka nopeasti suure muuttuu yhdellä ainoalla ajanhetkellä. Tätä kutsutaan hetkelliseksi muutosnopeudeksi.
Katso myös Muutosnopeus.
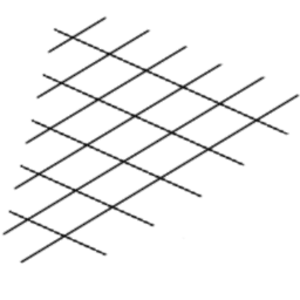
Hila (engl. Lattice)
Hila on joukko, joka muodostuu kahden tasavälisesti sijaitsevista, yhdensuuntaisista suorista koostuvan joukon leikkauspisteistä. Niiden pisteiden joukko, joiden paikka voidaan kirjoittaa kahden (tai kolmessa ulottuvuudessa kolmen) eri vektorin kokonaislukumonikertojen summana. Esimerkiksi pistejoukko $\{(0,0),(0,1),(1,0),(0,2),(1,1),(2,0), \dots\}$. Sanaa hila käytetään joskus myös suorajoukoista, jotka muodostavat tällaisen pistejoukon.
Hilbert (engl. Hilbert)
David Hilbert (1862-1943) oli saksalainen matemaatikko.
Hän tutki invarianttien teoriaa, algebrallista lukuteoriaa ja antoi merkittävän panoksen geometrian moderniin tutkimukseen. Hän perusti vaikutusvaltaisen aksiomaattisen lähestymistavan matematiikkaan.
Vuonna 1900 hän esitti kuuluisan 23 ratkaisemattoman matemaattisen ongelman listansa. Monet näistä ongelmista onnistuttiin ratkaisemaan 1900-luvulla.
Myöhemmässä elämässään hän teki töitä integraaliyhtälöiden, variaatiolaskennan, logiikan ja matematiikan filosofian parissa. Hilbertin avaruus on nimetty hänen mukaansa.
Katso myös Hilbertin hotelli, Hilbertin avaruus.
Hilbertin avaruus (engl. Hilbert space)
Olkoon $H$ sisätulolla $\langle x,y \rangle$ varustettu reaalinen tai kompleksinen vektoriavaruus ja $|x| = \sqrt{\langle x,x \rangle}$ sisätulon indusoima normi. Jos $H$ on tämän normin suhteen täydellinen eli jokainen Cauchy-jono suppenee $H$:ssa, kutsutaan $H$:ta Hilbertin avaruudeksi. Hilbertin avaruus on siis sellainen Banachin avaruus, missä normi on sisätulon indusoima.
Katso myös Vektoriavaruus, Banachin avaruus, Hilbert.
Hilbertin hotelli (engl. Hilbert hotel)
Kuvitteellinen hotelli, jossa on äärettömän monta huonetta, jotka on numeroitu 1, 2, 3, 4, $\dots$
Vaikka hotelli on täynnä, niin yksi vieras saadaan majoitettua hotelliin pyytämällä kaikkia vieraita siirtymään seuraavaan huoneeseen, mikä vapauttaa huoneen numero 1.
Itse asiassa, jos pyydetään jokaista vierasta siirtymään $n$ huonetta eteenpäin, voidaan vapauttaa ensimmäiset $n$ huonetta ja majoittaa mikä tahansa äärellinen määrä vieraita.
Jos hotelliin saapuu (numeroituva) ääretön määrä uusia vieraita, heidät voidaan majoittaa pyytämällä huoneessa numero 1 asuvaa henkilöä siirtymään huoneeseen numero 2, huoneessa 2 asuvaa siirtymään huoneeseen 4, huoneessa 3 asuvaa siirtymään huoneeseen 6, jne. Tämä vapauttaa kaikki huoneet, joiden numero on pariton.
Hilbertin hotelli havainnollistaa joitakin äärettömien joukkojen yllättäviä ominaisuuksia.
Katso myös Hilbert.
Histogrammi (engl. Histogram)
Histogrammi on tietynlainen pylväskaavio eli pylväsdiagrammi, jota käytetään luokitellun aineiston esittämiseen. Histogrammissa kuhunkin luokkaan kuuluvien arvojen lukumäärää esittää suorakulmaisen pylvään pinta-ala.
Pylväiden leveys voi toisinaan vaihdella, mutta ne piirretään aina vierekkäin kiinni toisiinsa sen merkiksi, että mikä tahansa arvo on aineistossa mahdollinen.
Katso myös Verranto, Frekvenssi.
Hoehnin lause (engl. Hoehn's theorem)
Jos pentagrammin sivut varustetaan perättäin numeroin $1, 2, 3, \ldots, 10$, niin parillisin numeroin varustettujen sivujen pituuksien tulo on yhtä suuri kuin parittomin numeroin varustettujen sivujen pituuksien tulo.
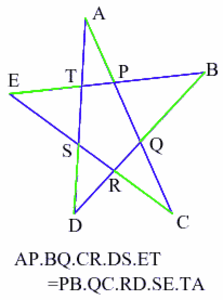
Katso myös Pentagrammi, Lause.
Holomorfinen, Analyyttinen (engl. Holomorphic)
Olkoon $D \subset \mathbb{C}$ alue eli avoin yhtenäinen joukko. Kuvaus $f \colon D \rightarrow \mathbb{C}$ on holomorfinen, jos sillä on kompleksinen derivaatta kaikissa pisteissä.
Katso myös Derivoituva, Differentioituva, Kokonainen funktio, Analyyttisen jatkeen yksikäsitteisyys, Riemannin poistuvan erikoispisteen lause, Cauchyn integraalilause.
Homeomorfinen (engl. Homeomorphic)
Kaksi topologista avaruutta $(X,\tau)$ ja $(Y,\tau')$ ovat homeomorfiset, jos on olemassa homeomorfismi $f \colon X \rightarrow Y$. Homeomorfismi on jatkuva kuvaus, jolla on jatkuva käänteiskuvaus.
Topologisten avaruuksien osajoukot $A \subset X$ ja $B \subset Y$ ovat homeomorfiset, jos on olemassa homeomorfismi $f \colon A \rightarrow B$, kun joukoille $A$ ja $B$ oletetaan relatiivitopologiat.
Katso myös Topologinen monisto, Homomorfinen.
Homeomorfismi (engl. Homeomorphism)
Olkoot $X$ ja $Y$ topologisia avaruuksia. Funktio $f : X \to Y $ on homeomorfismi avaruuksien $X$ ja $Y$ välillä, jos $f$ on jatkuva bijektio, jonka käänteiskuvaus on myös jatkuva. Jos avaruuksien $X$ ja $Y$ välillä on homeomorfismi, niiden sanotaan olevan homeomorfiset.
Katso myös Isomorfismi, Homomorfismi, Diffeomorfismi, Morfismi, Isomorfia.
Homogeeninen (engl. Homogeneous, Homogeneal, Homogenous)
Jokin asia on homogeeninen, jos se on samanlaista kaikkialla. Esimerkiksi kulhollinen puhdasta vettä on homogeeninen, mutta kulhollinen, jossa on vettä ja perunoita, ei ole.
Homogeeninen differentiaaliyhtälö (engl. Homogeneous differential equation)
Ensimmäisen kertaluvun differentiaaliyhtälöä kutsutaan homogeeniseksi, jos se on muotoa \[ y'(x) + p_1(x)y(x) = 0. \]
Toisen kertaluvun differentiaaliyhtälöä kutsutaan homogeeniseksi, jos se on muotoa \[ y''(x) + p_2(x)y'(x) + p_1(x)y(x) = 0. \]
Yleisesti, kertalukua $n$ oleva homogeeninen differentiaaliyhtälö on muotoa \[ y^{(n)}(x) + p_{n-1}(x)y^{(n-1)}(x) + \cdots + p_2(x)y'(x) + p_1(x)y(x) = 0. \]
Katso myös Differentiaaliyhtälö.
Homogeeniset koordinaatit (engl. Homogeneous coordinates)
Kahdessa ulottuvuudessa pisteen $(x,y)$ homogeeniset koordinaatit ovat sellaiset luvut $a,b,c$, joilla pätee $x = a/c$ ja $y = b/c$. Homogeeniset koordinaatit määritellään $n$ ulottuvuudessa samalla tavalla; silloin homogeenisiä koordinaatteja on $n+1$ kappaletta.
Homogeenisessä koordinaatistossa piste äärettömyydessä voidaan esittää asettamalla $c = 0$.
Katso myös Koordinaatti.
Homomorfinen (engl. Homomorphic)
Kuvaus on homomorfinen, mikäli se on homomorfismi.
Katso myös Homomorfismi, Homeomorfinen.
Homomorfismi (engl. Homomorphism)
Homomorfismi tarkoittaa struktuurin säilyttävää kuvausta kahden algebrallisen struktuurin välillä.
Jos $(G, \cdot)$ ja $(H, *)$ ovat monoideja tai ryhmiä, kuvaus $f \colon G \rightarrow H$ on homomorfismi, mikäli pätee
- $f(a \cdot b) = f(a) * f(b)$ kaikilla $a,b \in G$ ja
- $f(e_G)=e_H$.
Jos $(G, +, \cdot)$ ja $(H, +, \cdot)$ ovat renkaita tai kuntia, kuvaus $f \colon G \rightarrow H$ on homomorfismi, mikäli se on homomorfismi ryhmien $(G, +)$ ja $(H, +)$ välillä ja toteuttaa ehdot
- $f(a \cdot b) = f(a) \cdot f(b)$ kaikilla $a,b \in G$ ja
- $f(1_G)=1_H$.
Jos $G$ ja $H$ ovat ryhmiä, ehto $f(e_G)=e_H$ seuraa ehdosta $f(a \cdot b)=f(a) * f(b)$. Voidaan myös todistaa, että ryhmien homomorfismi toteuttaa ehdon $f(a^{-1})=f(a)^{-1}$ kaikilla $a \in G$.
Kuvaus $f: x \mapsto 2x$ on ryhmähomomorfismi $(\mathbb{Z},+) \rightarrow (\mathbb{Z}, +)$.
Olkoon $a$ positiivinen reaaliluku. Kuvaus $f: x \mapsto a^x$ on ryhmähomomorfismi $(\mathbb{R}, +) \rightarrow (\mathbb{R} \setminus \{0\}, \cdot)$.
Katso myös Kuvaus, Isomorfismi, Homomorfismin ydin, Automorfismi, Epimorfismi, Monomorfismi, Endomorfismi, Morfismi, Homomorfinen, Homeomorfismi, Algebrallinen topologia, Isomorfia, Funktio.
Homomorfismin ydin (engl. Kernel of a homomorphism)
Olkoon $f \colon G \rightarrow H$ kahden algebrallisen objektin välinen homomorfismi. Homomorfismin $f$ ydin on niiden $x \in G$ joukko, joille $f(x)=e$, missä $e$ on struktuurin $H$ neutraalialkio.
Jos $G$ ja $H$ ovat renkaita tai kuntia, joissa on kaksi eri laskutoimitusta, yllä neutraalialkio tarkoittaa nimenomaan yhteenlaskun neutraalialkiota.
Katso myös Ydin, Homomorfismi, Ideaali, Ihanne, Aliryhmä.
Homotopia (engl. Homotopy)
Olkoot $f \colon X \rightarrow Y$ ja $g \colon X \rightarrow Y$ topologisten avaruuksien välisiä jatkuvia kuvauksia.
Jatkuva kuvaus $H \colon X \times I \rightarrow Y$ on homotopia kuvausten $f$ ja $g$ välillä, mikäli $H(x,0)=f(x)$ ja $H(x,1)=g(x)$ kaikilla $x \in X$. Edellä $I$ on suljettu yksikköväli.
Homotopia on siis tapa muuttaa jatkuvasti kuvaus $f$ kuvaukseksi $g$.
Jatkuva kuvaus $f$ on kutistuva, mikäli on olemassa homotopia kuvaukselta $f$ jollekin vakiokuvaukselle.
Avaruus $X$ on yhdesti yhtenäinen, mikäli jokainen jatkuva kuvaus $f \colon S^1 \rightarrow X$ on kutistuva, missä $S^1$ on yksikköympyrän kehä.
Hornin lauseke (engl. Horn clause)
Hornin lauseke on logiikassa kaava muotoa $$ (p_1 \wedge \dots \wedge p_n) \Rightarrow q.$$
Katso myös Leikkausten suhteen suljettu, Kaava.
Huippu (engl. Apex)
Kartion kärkeä, pyramidin sitä kärkeä, jossa pyramidin kolmionmuotoiset sivutahkot yhtyvät, ja tasakylkisen kolmion sitä kärkeä, joka on yhteinen sen yhtä pitkille sivuille, kutsutaan joskus huipuksi.
Hylkäämisvirhe, 1. lajin erhe (engl. Type I error)
Tilastollinen päättely on päätöksentekoa epävarmuuden vallitessa, ja päättelyssä tehdään joskus virheitä. Hylkäämisvirhe tapahtuu, kun nollahypoteesi (väite, oletus), joka pitää paikkansa hylätään. Hylkäämisvirhettä pidetään erittäin pahana virheenä ja tilastotieteilijä pyrkii kontrolloimaan hylkäämisvirheen esiintymiseen liittyvän riskitodennäköisyyden avulla (varovaisuusperiaate).
Hyperbeli (engl. Hyperbola)
Funktion $y = 1/x$ kuvaajan muotoinen kuvio.
Sellaisen kappaleen radan muoto, joka putoaa aurinkokuntaan, mutta paiskautuu siitä pois riittävän suuren nopeutensa takia, eikä koskaan palaa takaisin.
Yksi kartioleikkauksista. Muut ovat ellipsi ja paraabeli.
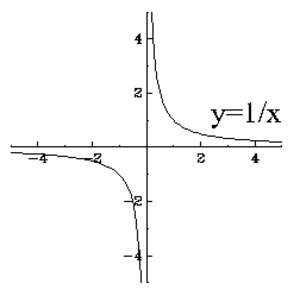
Katso myös Hyperbolinen, Hyperbelin yhtälö, Kartioleikkaus, Liittohyperbelit, Hyperbelin johtosuora.
Hyperbelin eksentrisyys (engl. Eccentricity of a hyperbola)
Hyperbelin, jonka asymptootit ovat suorat $\frac{x}{a} = \pm \frac{y}{b}$ ja joka leikkaa $x$-akselin, eksentrisyys $e$ on $> 1$ ja toteuttaa yhtälön $b^{2} = a^{2}(e^{2}-1)$.
Katso myös Eksentrisyys, Tasasivuisen hyperbelin eksentrisyys.
Hyperbelin johtosuora (engl. Directrix of a hyperbola)
Jos hyperbelin asymptootit ovat $\frac{x}{a} = \pm \frac{y}{b}$, sen eksentrisyys on $e$ ja hyperbeli leikkaa $x$-akselin, niin sen johtosuorat ovat $x = \pm \frac{a}{e}$.
Katso myös Suora, Hyperbeli, Tasasivuisen hyperbelin johtosuora.
Hyperbelin polttopisteet (engl. Focus of a hyperbola)
Hyperbelin, jonka asymptootit ovat suorat $\frac{x}{a} = \frac{y}{b}$ ja $\frac{x}{a} = -\frac{y}{b}$ ja joka leikkaa $x$-akselin pisteissä $a$ ja $-a$, polttopisteet ovat $(ae,0)$ ja $(-ae,0)$, missä $e$ on hyperbelin eksentrisyys.
Katso myös Piste, Suorakulmaisen hyperbelin polttopisteet.
Hyperbelin yhtälö (engl. Equation of a hyperbola)
Hyperbelin, jonka asymptootit ovat suorat $\frac{x}{a} = \frac{y}{b}$ ja $\frac{x}{a} = -\frac{y}{b}$ ja joka leikkaa $x$-akselin pisteissä $a$ ja $-a$, yhtälö on \[\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1.\]
Katso myös Asymptootti, Hyperbeli, Kartioleikkauksen yhtälö, Kartioleikkaus, Yhtälö, Tasasivuisen hyperbolin yhtälö.
Hyperbolinen (engl. Hyperbolic)
Hyperbelin muotoinen. Trigonometrisia funktioita muistuttavista funktioista kuten cosh tai sinh käytetty nimitys.
Hyperbolinen funktio (engl. Hyperbolic function)
Trigonometrisiin funktioihin läheisesti liittyvä funktiojoukko.
Hyperbolinen sini määritellään kaavalla \[ \sinh(x) = \frac{e^{x} - e^{-x}}{2}. \]
Hyperbolinen kosini määritellään kaavalla \[ \cosh(x) = \frac{e^{x} + e^{-x}}{2}. \]
Hyperbolinen tangentti määritellään kaavalla \[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)}. \] Hyperbolinen kotangentti määritellään kaavalla \[ \coth(x) = \frac{1}{\tanh(x)}. \]
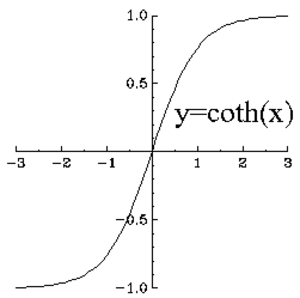
Katso myös Hyperbolinen identiteetti, Funktio, Kuvaus, Trigonometrinen funktio, Hyperbolinen kosekantti, Hyperbolinen sekantti, Hyperbolinen kosini, Hyperbolinen tangentti, Hyperbolinen sini, Hyperbolinen kotangentti, Käänteinen hyperbolinen funktio, Areafunktio.
Hyperbolinen geometria (engl. Lobachevskian geometry, Hyperbolic geometry)
Geometrian ala, jossa paralleeliaksiooma on korvattu aksioomalla, jonka mukaan annetun pisteen kautta kulkee useita yhdensuuntaisia suoria. Kaksiulotteista hyperbolista geometriaa voi havainnollistaa satulapinnalla. Hyperbolisessa geometriassa kolmion kulmien summa on alle $180^{\circ}$.
Hyperbolisen geometrian keksivät toisistaan riippumatta Lobatsevski ja Bolyai.
Katso myös Geometria.
Hyperbolinen identiteetti (engl. Hyperbolic identity)
Hyperbolisia funktioita koskeva kaava, joka on tosi kaikilla kaavan muuttujien arvoilla.
Katso myös Identiteetti, Hyperbolinen funktio.
Hyperbolinen kosekantti (engl. Hyperbolic cosecant)
Hyperbolinen kosekantti $\mathrm{csch}(x)$ määritellään kaavalla \[ \mathrm{csch}(x) = \frac{1}{\mathrm{sinh}(x)} = \frac{2}{e^x - e^{-x}}. \]
Katso myös Hyperbolinen funktio, $\csch$.
Hyperbolinen kosini (engl. Hyperbolic cosine)
Funktio, jota merkitään $\cosh(x)$ ja joka määritellään kaavalla \[ \cosh(x) = \frac{e^x + e^{-x}}{2}. \]
Katso myös Neperin luku, $e$, Eksponenttifunktio, $\cosh$, Hyperbolinen funktio, Hyperbolinen tangentti.
Hyperbolinen kotangentti (engl. Hyperbolic cotangent)
Funktio, jota merkitään $\coth(x)$ ja joka määritellään asettamalla \[ \coth(x) = \frac{\cosh(x)}{\sinh(x)} = \frac{e^x + e^{-x}}{e^x - e^{-x}}. \]
Katso myös Hyperbolinen funktio, $\coth$.
Hyperbolinen sekantti (engl. Hyperbolic secant)
Funktio, jota merkitään $\mathrm{sech}(x)$ ja joka määritellään kaavalla \begin{eqnarray*} \mathrm{sech}(x) &=& \frac{1}{\mathrm{cosh}(x)} \\ &=& \frac{2}{e^x + e^{-x}}. \end{eqnarray*}.
Katso myös $\sec$, $\cosh$, Hyperbolinen funktio, $\sech$.
Hyperbolinen sini (engl. Hyperbolic sine)
Funktio, jota merkitään $\sinh(x)$ ja joka määritellään kaavalla \[ \sinh(x) = \frac{e^x - e^{-x}}{2}. \]
Katso myös Neperin luku, $e$, Eksponenttifunktio, $\sinh$, Hyperbolinen funktio, Hyperbolinen tangentti.
Hyperbolinen spiraali (engl. Hyperbolic spiral)
Spiraali, jonka yhtälö napakoordinaateissa on \[ r = \frac{a}{\theta}. \]
Katso myös Spiraali.
Hyperbolinen tangentti (engl. Hyperbolic tangent)
Funktio, jota merkitään $\tanh(x)$ ja joka määritellään asettamalla \[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}. \]
Katso myös Hyperbolinen funktio, Hyperbolinen kosini, Hyperbolinen sini.
Hyperbolisen kosinin käänteisfunktio (engl. Inverse hyperbolic cosine)
Hyperbolisen kosinin cosh(x) käänteisfunktiolle käytetään merkintää arcosh(x).
Katso myös $\arcosh$, $\cosh$, $\arcosh$-identiteetti, Käänteinen hyperbolinen funktio, Areafunktio.
Hyperbolisen sinin käänteisfunktio (engl. Inverse hyperbolic sine)
Hyperbolisen sinin sinh(x) käänteisfunktiota merkitään arsinh(x).
Katso myös $\arsinh$, $\arcoth$-identiteetti, $\arsinh$-identiteetti, Käänteinen hyperbolinen funktio, Areafunktio.
Hyperpallo (engl. Hypersphere)
Kaksiulotteisen ympyrän ja kolmiulotteisen pallon yleistys $n$-ulotteiseen avaruuteen, $n \ge 4$: hyperpallo on niiden pisteiden $(x_1, x_2, \ldots, x_n)$ joukko, joille pätee \[ x_1^2 + x_2^2 + \cdots + x_n^2 = r^2, \] missä $r \ge 0$ on hyperpallon säde.
Hypertaso (engl. Hyperplane)
$n$-ulotteisen avaruuden $(n-1)$-ulotteinen osajoukko, joka jakaa tason kahteen erilliseen osaan samalla tavalla kuin kaksiulotteinen taso jakaa kolmiulotteisen avaruuden kahteen erilliseen osaan.
Hyposykloidi (engl. Hypocycloid)
Paikallaan pysyvän isomman ympyrän sisäpintaa pitkin vierivän pienemmän ympyrän kehän kiinnitetyn pisteen piirtämä käyrä.
Olkoot $R$ isomman ympyrän säde ja $r$ pienemmän ympyrän säde. Jos $R/r = m/n$ on rationaaliluku, on hyposykloidi suljettu käyrä ja se koskettaa isomman ympyrän kehää $m$ kertaa. Jos $R/r$ on irrationaaliluku, ei hyposykloidi ole umpinainen käyrä.
Katso myös Ura, Sykloidi, Pistevierintäkäyrä, Trokoidi, Deltoidi, Hypotrokoidi.
Hypoteesi (engl. Hypothesis)
Luonnontieteissä hypoteesi on olettamus, jonka uskotaan olevan oikea ja jonka perusteella voidaan tehdä ennusteita, joiden todenmukaisuutta voidaan testata. Jos ennusteet osoittautuvat oikeiksi pitkällä aikavälillä, hypoteesiä saatetaan ruveta kutsumaan teoriaksi.
Katso myös Otaksuma, Riemannin hypoteesi, Konjektuuri.
Hypotenuusa (engl. Hypotenuse)
Suorakulmaisen kolmion pisin sivu. Se on aina suoran kulman vastainen sivu.
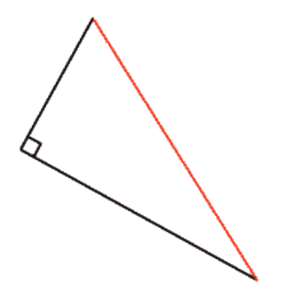
Katso myös Suora kulma, Kolmio, Kosini.
Hypotrokoidi (engl. Hypotrochoid)
Paikallaan pysyvän isomman ympyrän sisäpintaa pitkin vierivän pienemmän ympyrän kiinnitetyn pisteen piirtämä käyrä. Tämä piste voi sijaita ympyrän kehällä tai sisällä.
Katso myös Trokoidi, Hyposykloidi.
Hyvinmääritelty (engl. Well-defined)
Oletetaan, että haluamme määritellä kuvauksen $f \colon X \rightarrow Y$. Eräs tapa määritellä $f$ on jakaa $X$ osiin $X=U_1 \cup \dots \cup U_n$, ja määritellä kaikki rajoittumat $f|U_i \colon U_i \rightarrow Y$. Tarkoitus on siis määritellä $f$ niin, että jos $x \in U_i$, $f(x)=f|U_i(x)$. Jotta voisimme toimia näin, meidän pitää todistaa, että jos $x \in U_i \cap U_j$, $f(x)$:n määritelmät $U_i$:n ja $U_j$:n avulla johtavat samaan lopputulokseen. Tämän todistamista kutsutaan sen todistamiseksi, että $f$ on hyvinmääritelty.
Usein funktioita määritellään sellaisilla tavoilla, että ei ole ilmeistä, että määritelmä todella karakterisoi funktion. Tällaisessa tapauksessa pitää todistaa erikseen, että määritelmä todella määrittelee funktion ja tällaista todistusta kutsutaan sen todistamiseksi, että funktio on hyvinmääritelty.
Hyvitysmenetelmä (engl. Compensation)
Toisinaan laskettaessa kahden luvun tuloa tulee lasku helpommaksi, jos toinen luvuista pyöristetään ensin ylös- tai alaspäin ja näin tehty "virhe" hyvitetään lopuksi yhteen- tai vähennyslaskulla.
On esimerkiksi laskettava tulo $99 \cdot 5$. Pyöristämme ensin luvun $99$ ylöspäin luvuksi $100$ ja laskemme $100 \cdot 5 = 500$. Sen jälkeen vähennämme luvusta $500$ luvun $5$ eli luvun $(100-99) \cdot 5$ ja saamme vastauksen $495$.
Hyväksymisalue (engl. Acceptance region)
Hypoteesintestauksessa ne testisuureen arvot, joiden perusteella nollahypoteesi jää voimaan (nollahypoteesia ei voi hylätä), muodostavat hyväksymisalueen.
Katso myös Kriittinen alue.
Hyväksymisvirhe, 2. lajin erhe (engl. Type II error)
Tilastollinen päättely on päätöksentekoa epävarmuuden vallitessa, ja päättelyssä tehdään joskus virheitä. Hyväksymisvirhe tapahtuu, kun nollahypoteesi (väite, Oletus), joka ei pidä paikkaansa hyväksytään. Koska tilastotieteilijä pyrkii kontrolloimaan hylkäämisvirheet todennäköisyyttä, hän on hyväksymisvirheen tapahtuminen pakko hyväksyä. Ts. Pienet poikkeamat todellisuudesta jäävät huomaamatta. Hyväksymisvirheen esiintymistä voidaan kontrolloida tiedon määrää (otoskokoa) lisäämällä.
Hävitä (engl. Vanish)
Funktio häviää jossakin pisteessä, jos sen arvo siinä on nolla. Funktio häviää kokonaan, jos sen arvo on nolla kaikissa pisteissä.
Hölderin epäyhtälö (engl. H\"older's inequality, Holder's inequality)
Jos $p>1$ ja $1/p+1/q=1$, niin \[ \sum_{i=1}^n \left | a_ib_i \right | \leq \left ( \sum_{i=1}^n|a_i|^p \right )^{{1}/{p}} \left ( \sum_{i=1}^n|b_i|^q \right )^{{1}/{q}}. \]
Jos $p=q=2$, niin epäyhtälö tunnetaan Cauchy-Schwarzin epäyhtälönä.
Katso myös Erisuuruus, Lause, $\ell^p$-avaruus, Cauchy-Schwarzin epäyhtälö, Epäyhtälö.