Matematiikan verkkosanakirja

Merkintä $g(x)=O(f(x))$ tarkoittaa, että $g(x)$ on pienempi tai yhtä suuri kuin funktio $f(x)$ jollain vakiolla kerrottuna kaikilla riittävän suurilla muuttujan $x$ arvoilla.

Esimerkiksi $g(x) = O(x^{2})$ tarkoittaa, että on olemassa vakiot $k$ ja $n$, joilla $g(x) \leq kx^{2}$ kaikilla $x \gt n$.

Katso myös Merkintätapa, Notaatio, Asymptoottinen kasvunopeus.

Odotusarvolla on alunperin tarkoitettu odotettavissa olevaa voittoa pelissä $$ E(x) = \sum_1^k x_i \cdot P(x_i), $$ missä $x_i$ on voitto ja $ P(x_i) $ ko. voiton todennäköisyys.

Odotusarvo on myös satunnaismuuttujan teoreettinen keskiarvo. Mikäli samasta joukosta poimitaan äärettömän monta otosta ja jokaisesta otoksesta lasketaan jokin tilastollinen suure, on suureen keskiarvo näissä otoksissa suureen odotusarvo.

Mikäli muuttuja on diskreetti, sen odotusarvo on $$ E(x) = \sum_1^k x_i \cdot P(x_i). $$ Jatkuvan satunnaismuuttujan odotusarvo on vastaavasti $$ E(x) = \int x \cdot f(x) dx. $$

Katso myös Keskiarvo, Aritmeettinen keskiarvo, Todennäköisyys, Lineaarisen funktion odotusarvo.

Kulma, jonka asteluku on $180^{\circ}$ on oikokulma. Kaksi suoraa kulmaa muodostaa yhteensä oikokulman.

Katso myös Kulma, Suora kulma, Suora.

Kappale, jossa on kahdeksan kolmionmuotoista tahkoa.

Säännöllinen oktaedri on oktaedri, jonka kahdeksan tahkoa ovat kaikki keskenään yhteneväisiä tasasivuisia kolmioita.

Säännöllinen oktaedri on yksi Platonin monitahokkaista.

Katso myös Kahdeksan, 8, Kolmio, Oktaedrin sivutahkoverkko, Monitahokas, Platonin kappaleet.

On olemassa useita tapoja piirtää oktaedrin vaippa. Jokainen niistä koostuu kahdeksan tasasivuisen kolmion muodostamasta kuviosta. Yksi niistä on kuuden yhteen liitetyn kolmion rivi, jonka molemmilla puolilla on keskellä riviä yksi ylimääräinen kolmio. Kun tämä kuvio taitetaan kokoon, siitä muodostuu oktaedri.

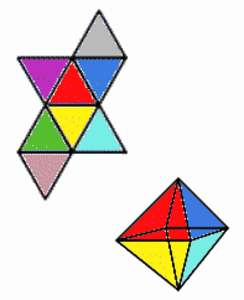
Katso myös Oktaedri, Kolmio, Sivutahkoverkko.

Olemassaololause (tai -todistus) osoittaa, että jokin tietyt ominaisuudet omaava luku tai olio on varmasti olemassa. Se ei kuitenkaan välttämättä kerro, mikä tällainen luku tai olio on.

Katso myös Perustelu.

Eksistenssikvanttori on symboli $\exists$, joka luetaan "on olemassa" tai "jollakin". Jos $P$ on ominaisuus, niin $\exists x P(x)$ tarkoittaa, että on olemassa sellainen olio, jolla on ominaisuus $P$.

Vertaa käsitteeseen "Universaalikvanttori".

Väite $\exists x (5 = 3+x)$ on tosi, koska voidaan valita $x=2$.

Väite $\exists x ( x \cdot 0 = 5)$ on epätosi, sillä ei ole olemassa lukua, joka kerrottuna nollalla antaisi tulokseksi luvun viisi.

Katso myös Universaalikvanttori.

Todistuksen alussa päätetään usein tietyt asiat, jotka ovat kiistattomasti tosia niin kauan kuin todistusta käsitellään. Näitä asioita kutsutaan oletuksiksi.

Tämä tarkoittaa, että tiedetään, millaisissa tilanteissa todistus pätee. Esimerkiksi kaksi suoraa leikkaavat toisensa täsmälleen yhdessä pisteessä olettaen, että ne eivät ole yhdensuuntaisia.

Epäsuoran todistuksen tekemiseksi oletetaan jotakin, jonka arvellaan olevan epätosi ja yritetään osoittaa, että seuraukset ovat selvästi virheellisiä. Tällaista epäsuoraan todistukseen liittyvää oletusta kutsutaan vastaoletukseksi.

Katso myös Aksiooma, Ristiriitatodistus.

Merkki $\Rightarrow$ tarkoittaa "jos ... niin ...". $A\Rightarrow B$ voidaan lukea "jos $A$ niin $B$" tai "$A$:sta seuraa $B$".

$\Rightarrow$ voidaan ajatella loogisena operaattorina, joka antaa tulokseksi "epätosi", jos ensimmäinen argumentti on tosi ja toinen epätosi, muussa tapauksessa tulos on "tosi".

""A:sta seuraa B"" tarkoittaa, että jos A on tosi, myöskin B:n on oltava tosi. Saman voi ilmaista sanomalla, että A on B:lle riittävä ehto.

Esimerkiksi $x \gt 0 \Rightarrow x \gt -1$. Jos nimittäin $x \gt 0$, on tällöin myös välttämättä $x \gt -1$.

Matematiikassa väitteen $a \Rightarrow b$ totuus määräytyy pelkästään lauseiden $a$ ja $b$ totuusarvojen perusteella. Väite $a \Rightarrow b$ on epätosi pelkästään silloin, kun väite $a$ on tosi ja $b$ epätosi, ja tosi kaikissa muissa tapauksissa.

Tällainen tulkinta merkille $\Rightarrow$ vangitsee syy-seuraussuhteesta matemaattisen päättelyn kannalta olennaiset piirteet. Se ei kuitenkaan vastaa täysin arkiajattelun "jos...niin...", päättelyitä, sillä väitteen $a \Rightarrow b$ totuus ei vaadi minkäänlaista sisäistä syy-seuraussuhdetta lauseiden $a$ ja $b$ totuudelle. Erityisesti, jos $a$ on epätosi lause, on $a \Rightarrow b$ tosi, oli $b$ mikä lause tahansa. Siis esimerkiksi "Kuu on juustoa $\Rightarrow$ Lehmät lentävät" on tosi väite.

Katso myös Jos, Perustelu, Johtopäätös, Siksi, implikaationuoli, Seurata jostakin, Olla seuraus, Kontrapositio.

$A$ seuraa $B$:stä tarkoittaa sitä, että jos $B$ tiedetään, voidaan tästä päätellä $A$.

Oletetaan, että $x \gt 0$. Nyt $x \neq 0$ seuraa siitä, että $x \gt 0$.

Katso myös Seurata, Aiheuttaa jotakin, Olla jonkin riittävä ehto.

Kreikkalainen kirjain $\omega$ (pieni kirjain) tai $\Omega$ (iso kirjain). Lausutaan oomega. Äänneasu sama kuin suomen pitkä o-äänne.

Katso myös Kreikkalaiset kirjaimet.

Kreikkalainen kirjain o (pieni kirjain) tai O (iso kirjain). Kirjaimen nimi on omikron ja se äännetään samoin kuin suomen lyhyt o.

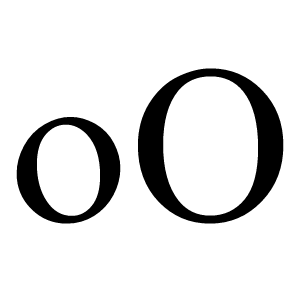
Katso myös Kreikkalaiset kirjaimet.

Lukua $\lambda$ kutsutaan matriisin $A$ ominaisarvoksi, jos on olemassa sellainen nollasta eroava vektori $\mathbf{v}$, että $A\mathbf{v}=\lambda\mathbf{v}$. Vektoria $\mathbf{v}$ kutsutaan tällöin ominaisvektoriksi.

Katso myös Karakteristinen yhtälö, Hermiittisen matriisin ominaisarvot, Ortogonaalisen matriisin ominaisarvot, Reaalisen symmetrisen matriisin ominaisarvot, Unitaarisen matriisin ominaisarvot, Vinosymmetrisen matriisin ominaisarvot, Ominaisvektori.

Sellainen tiedonpalanen tai ilmaisu, joka kertoo oliosta muutakin kuin vain sen, mikä olio on kyseessä. Esimerkiksi koko tai väri voi olla olion ominaisuus.

Katso myös Affiini, Algebrallinen, Yksikäsitteinen tekijöihin jako, Kanoninen, Sattuma, Mahdollisuus, Satunnainen, Karteesinen, Alternoida, Vaativuus, Suure, Uskottavuus.

Ominaisuus, jonka arvot voivat olla ainoastaan kokonaislukuja. Esimerkiksi kappaleen ulottuvuuksien lukumäärä tai yhtälön ratkaisujen lukumäärä. Yleensä nämä ovat positiivisia kokonaislukuja.

Katso myös Kiertosymmetrian kertaluku, Mahtavuus, Vapausaste, Matriisin aste, Ryhmän alkion kertaluku, Polynomin aste, Ominaisuus, jonka arvot ovat numeerisia, Differentiaaliyhtälön aste, Ryhmän kertaluku.

Ominaisuus, jonka arvot voivat olla mitä tahansa lukuja. Jotkin tällaiset ominaisuudet, esimerkiksi lämpötila, voivat saada myös negatiivisia arvoja, mutta useimmat tällaiset ominaisuudet, esimerkiksi massa, voivat saada ainoastaan positiivisia arvoja.

Katso myös Tarkkuus, Kompleksiluvun argumentti, Tilavuus, Muutosnopeus, Nopeus, Lattia, Kokonaisosa, Todennäköisyys, Eksentrisyys, Determinantti, Ominaisuus, jonka arvot ovat numeerisia, Kaarevuus, Virhetermi, Jäännöstermi.

Ominaisuus, joka ilmaistaan luvulla, kuten paino tai aika. Tällaiset ominaisuudet ovat erilaisia kuin esimerkiksi ominaisuus "olla pyöreä", joka kappaleella joko on tai ei ole ja jota ei ilmaista luvulla.

Katso myös Ominaisuus, jonka arvot ovat jatkuvia, Ominaisuus, jonka arvot ovat diskreettejä, Suure.

Neliömatriisin $A$ ominaisvektori $v$ on sellainen nollasta eroava vektori, jonka suunta ei muutu, kun siihen sovelletaan matriisia $A$. Toisin sanoen, $Av = \lambda v$ jollakin $\lambda$. Lukua $\lambda$ kutsutaan matriisin $A$ ominaisarvoksi.

Katso myös Vektori, Ominaisarvo, Matriisi.

Symboli $\exists$ tarkoittaa, että jollakin tietyllä muuttujalla on sellainen arvo, jolla jokin on totta.

Esimerkiksi $ \exists x (x^3 \gt 0)$ tarkoittaa, että muuttujalla $x$ on (ainakin yksi) sellainen arvo, jolla $x^{3}$ on suurempi kuin nolla.

Katso myös Kaikilla, Jokaisella.

Luku $28$ on onnekas luku, koska

$28 \to 2^{2}+8^{2} = 4+64 = 68$,

$68 \to 6^{2}+8^{2} = 36+64 = 100$,

$100 \to 1^{2}+0^{2}+0^{2} = 1+0+0 = 1$.

Luku $28$ voidaan siis muuntaa luvuksi $1$ menetelmällä, jossa luvun numeroita toistuvasti korotetaan neliöön ja lisätään yhteen. Luku $32$ on myös onnellinen luku, koska

$32 \to 3^{2}+2^{2} = 9+4 = 13$,

$13 \to 1^{2}+3^{2} = 1+9 = 10$,

$10 \to 1^{2}+0^{2} = 1+0 = 1$.

Mutta $24$ on onneton luku. Voitko nähdä miksi?

Katso myös Onneton luku.

Kirjoitetaan parittomat luonnolliset luvut jonoon $1,3,5,7,9,11,\ldots$ Koska ensimmäinen ykköstä suurempi pariton luku on $3$, poistetaan jonosta joka kolmas ja saadaan $1,3,7,9,13,15,19,\ldots$ Ensimmäinen $3$:a suurempi pariton luku näistä on $7$, siis poistetaan joka seitsemäs näistä ja saadaan $1,3,7,9,13,15,21,25,31,\ldots$. Jatketaan. Jäljelle jäävät ovat onnekkaita lukuja.

Katso myös 13, Kolmetoista, 3, Kolme, Seitsemän, 7, Yhdeksän, 9.

Luku, joka ei ole onnekas. Luku, joka ei muunnu luvuksi $1$ menetelmällä, jossa luvun numeroita toistuvasti korotetaan neliöön ja lisätään yhteen. Esimerkiksi luku $24$ on onneton, koska

$24 \rightarrow 2^2 + 4^2 = 4 + 16 = 20$,

$20 \rightarrow 2^2 + 0^2 = 4 + 0 = 4$,

$4 \rightarrow 4^2 = 16$,

$16 \rightarrow 1^2 + 6^2 = 1 + 36 = 37$,

$37 \rightarrow 3^2 + 7^2 = 9 + 49 = 58$,

$58 \rightarrow 5^2 + 8^2 = 25 + 64 = 89$,

$89 \rightarrow 8^2 + 9^2 = 64 + 81 = 145$,

$145 \rightarrow 1^2 + 4^2 + 5^2 = 1 + 16 + 25 = 42$,

$42 \rightarrow 4^2 + 2^2 = 16 + 4 = 20$. Päädyttiin siis samaan lukuun $20$ kuin ensimmäisellä rivillä.

Katso myös Onnekas luku.

Kuvaus, joka liittää funktioon jonkin toisen funktion. Esimerkiksi derivaattaoperaattori $D$ liittää funktioon $f$ sen derivaatan $Df = f"$.

Katso myös Looginen operaattori, Funktio, Kuvaus, Antikommutaattori, Differentiaalioperaattori.

Paras jollakin tavalla; usein ongelman nopein tai tehokkain ratkaisu.

Katso myös Optimointi.

Paras, nopein tai tehokkain esimerkki jostakin.

Jossain mielessä ja joidenkin rajoitusten vallitessa parhaan muuttujan arvon etsiminen.

Katso myös Optimaalinen.

Pisteen $y$-koordinaatti suorakulmaisessa koordinaatistossa.

Katso myös $y$-akseli, $x$-akseli, Abskissa, Koordinaattiakseli, Koordinaatti.

Koordinaattijärjestelmän peruspiste, jonka kaikki koordinaatit ovat yhtä suuria kuin nolla, eli $(0,\,0)$ tai $(0,\,0,\,0)$ jne.

Katso myös Piste, Paikkavektori.

Suorassa kulmassa oleva, suorakulmainen.

Katso myös Kohtisuorasti leikkaavat ympyrät, Kohtisuora.

Reaalista neliömatriisia $A$ kutsutaan ortogonaaliseksi, jos se on sama matriisi kuin sen transpoosin käänteismatriisi eli $A = (A^T)^{-1}$.

Jos ortogonaalinen matriisi on reaalinen, niin se on myös normaali.

Katso myös Unitaarinen matriisi, Matriisin transpoosi, Neliömatriisi, Käänteismatriisi, Ortogonaalisen matriisin ominaisarvot, Normaali matriisi.

Ortogonaalisen matriisin ominaisarvojen itseisarvo on 1.

Katso myös Lause, Ortogonaalinen matriisi, Ominaisarvo.

Kolmio, jonka kärjet ovat annetun kolmion korkeusjanojen kantapisteet.

Katso myös Kolmion korkeusjana, Kolmio, Kantapiste.

Piste, jossa kolmion kolme korkeusjanaa leikkaavat toisensa.

Katso myös Kolmion korkeusjana, Keskipiste, Sisään piirretyn ympyrän keskipiste, Kolmion ortokeskuksen määrittäminen, Eulerin pisteet, Eulerin suora.

Joukko alkioita, jotka ovat jäsenenä jossakin suuremmassa joukossa. Osajoukko voi olla koko suurempi joukko, sen aito osa tai tyhjä joukko. Olkoon esimerkiksi \[ \lbrace Anna, Kaisa, Tapio, Emma, Joni, Katri, Tommi \rbrace \] joukko ystäviä. Tämän joukon osajoukkoja ovat muiden muassa koko joukko \[ \lbrace Anna, Kaisa, Tapio, Emma, Joni, Katri, Tommi \rbrace, \] sen aito osa \[ \lbrace Kaisa, Emma, Joni, Tommi \rbrace \] sekä tyhjä joukko $\lbrace \rbrace$.

Joukko $A$ on joukon $B$ osajoukko, jos jokainen joukon $A$ alkio on myös joukon $B$ alkio. Tällöin merkitään $A \subset B$. Huomaa, että $\emptyset \subset B$ ja $B \subset B$ ovat aina voimassa oli $B$ mikä joukko tahansa.

Katso myös Tyhjä joukko, Joukko, Aito osajoukko, Ketju, Alkio.

Luku, jonka osoittama määrä kertoja jokin luku voidaan jakaa tasan toisella luvulla, jakolaskun tulos.

Jos kymmenen jaetaan viidellä, osamäärä on kaksi (10/5 = 2). Jos kolmetoista jaetaan kolmella, osamäärä on neljä ja jakojäännös yksi (13/3 = 4+1/3).

Katso myös Jakojäännös, Jaettava, Jakolasku, Kokonaisluku, Jakaminen.

Funktioiden $f(x)$ ja $g(x)$ osamäärän $f(x)/g(x)$ derivointisääntö on \[ \frac{\mathrm{d}}{\mathrm{dx}} \left( \frac{f(x)}{g(x)} \right) = \frac{1}{g^2} \left( g \frac {\mathrm{d}f}{\mathrm{dx}}-f \frac {\mathrm{d}g}{\mathrm{dx}} \right). \]

Katso myös Derivointisääntö, Sääntö, Tulon derivointisääntö.

Relaatio $\le \subset A \times A$ on joukon $A$ osittaisjärjestys, jos

• $a \le a$ kaikilla $a \in A$.
• Jos $a \le b$ ja $b \le a$ niin $a=b$ kaikilla $a,b \in A$.
• Jos $a \le b$ ja $b \le c$ niin $a \le c$ kaikilla $a,b,c \in A$.

Katso myös Järjestys, Totaalinen järjestys, Lineaarijärjestys, Esijärjestys, Osittaisjärjestetty joukko, Tiukka osittaisjärjestys.

Olkoon $f(x, y)$ kahden muuttujan $x, y$ reaaliarvoinen funktio. Tällöin funktion $f$ osittaisderivaattaa muuttujan $x$ suhteen merkitään $\frac{\partial f}{\partial \mathrm{x}}$ ja se määritellään raja-arvona \[ \frac{\partial f}{\partial x} = \lim_{h \to 0} \frac{f(x + h, y) - f(x, y)}{h}. \]

Tämä on funktion $f$ erotusosamäärän raja-arvo muuttujan $x$ suhteen pisteessä $(x,y)$. Muuttujaa $y$ käsitellään tässä ikään kuin se olisi vakio. Osittaisderivaatta muuttujan $y$ suhteen määritellään samoin.

Esimerkiksi, jos $f(x, y) = x^2 + xy + 2y^2$, on $\frac{\partial f}{\partial x} = 2x + y$ ja $ \frac{\partial f}{\partial y} = x + 2y$.

Useamman kuin kahden muuttujan reaaliarvoisen funktion osittaisderivaatat määritellään vastaavalla tavalla.

Katso myös Normaali, Derivaatta, Differentiaalioperaattori, Suunnattu derivaatta, Eksakti differentiaali, Ääriarvo, Hessen matriisi, Jacobin matriisi.

Osittaisintegroinnin kaava on \[ \int \mathrm{u} \frac{\mathrm{dv}}{\mathrm{dx}} \mathrm{dx} = \mathrm{uv} - \int \mathrm{v} \frac{\mathrm{du}}{\mathrm{dx}} \mathrm{dx} + C. \]

Katso myös Integrointisääntö, Tulon derivointisääntö.

Joukko $A$ on osittaisjärjestetty, jos siinä on määritelty osittainen järjestys $\le \subset A \times A$.

Katso myös Joukko, Osittaisjärjestys, Ketju, Osittainen järjestys.

Relaatio $\le \subset A \times A$ on joukon $A$ osittaisjärjestys, jos

• $a \le a$ kaikilla $a \in A$.
• Jos $a \le b$ ja $b \le a$ niin $a=b$ kaikilla $a,b \in A$.
• Jos $a \le b$ ja $b \le c$ niin $a \le c$ kaikilla $a,b,c \in A$.

Katso myös Järjestys, Totaalinen järjestys, Lineaarijärjestys, Esijärjestys, Osittaisjärjestetty joukko, Tiukka osittaisjärjestys.

Lauseke $5 \cdot (6+3)$ voidaan laskea kahdella tavalla. Yksi tapa laskea tämä on laskea ensin sulkeissa oleva summa. Näin saadaan $5 \cdot 9 = 45$. Toinen tapa on kertoa ensin kumpikin sulkeiden sisällä oleva luku $5$:llä ja laskea tulot yhteen. Näin saadaan $5 \cdot 6 + 5\cdot 3 = 30 + 15 = 45$. Tulokset ovat samat, koska kertolasku noudattaa osittelulakia yhteenlaskun suhteen.

Operaatio $\otimes$ noudattaa osittelulakia operaation $\oplus$ suhteen, jos $A \otimes (B \oplus C) = (A \otimes B) \oplus (A \otimes C)$ kaikilla $A$, $B$ ja $C$. Esimerkiksi kertolasku noudattaa osittelulakia yhteenlaskun suhteen, koska $A(B + C) = AB + AC$. Toisaalta yhteenlasku ei noudata osittelulakia kertolaskun suhteen, koska $A + (BC)$ ei ole välttämättä sama kuin $(A + B)(A + C)$.

Katso myös Luku.

Logiikan kaksi osittelulakia ovat \[a \wedge (b \vee c) = (a \wedge b) \vee (a \wedge c)\] ja \[a \vee (b \wedge c) = (a \vee b) \wedge (a \vee c).\]

Katso myös De Morganin lait.

Kokonaisluvun ositus on sellainen kokoelma kokonaislukuja, joiden summa kyseinen kokonaisluku on.

Esimerkiksi luvun $4$ ositukset ovat $1+1+1+1$, $1+1+2$, $1+3$, $2+2$ ja $4$.

Joukon ositus on sen jako pareittain erillisiksi epätyhjiksi osajoukoiksi, joiden yhdiste on koko alkuperäinen joukko.

Joukossa määritellyn ekvivalenssirelaation määräämät ekvivalenssiluokat muodostavat joukon osituksen.

Katso myös Tasajako, Ekvivalenssiluokka, Ekvivalenssirelaatio, Konjugaattiluokka.

Olkoon $C$ käyrä ja $P$ piste käyrällä $C$. Käyrän $C$ oskuloiva ympyrä pisteessä $P$ on raja-arvoympyrä ympyröistä, jotka kulkevat käyrän $C$ pisteiden $U$, $V$ ja $W$ kautta, kun pisteiden $U$, $V$ ja $W$ annetaan konvergoida kohti pistettä $P$. Oskuloiva ympyrä on siis ympyrä, joka parhaiten approksimoi käyrää pisteessä $P$.

Katso myös Ympyrä, Kaarevuussäde.

Taulukossa tietyssä paikassa olevan tiedon asemaa osoittavat rivin ja sarakkeen numerot.

Katso myös Merkintätapa, Notaatio.

Verbit "osoittaa" ja "näyttää" tarkoittavat matematiikassa samaa kuin verbi "todistaa".

Katso myös Perustelu.

Murtoluvussa murtoviivan yläpuolelle kirjoitettu luku. Se kertoo kuinka monta nimittäjän osoittamaa murto-osaa murtoluku käsittää.

Esimerkiksi $\frac{3}{4}$ tarkoittaa lukua, joka koostuu kolmesta yhtäsuuresta murto-osasta, ja jokainen näistä on neljäsosa. $\frac{4}{9}$ tarkoittaa, että luvussa on neljä osaa ja jokainen niistä on yhdeksäsosa.

Katso myös Aito murtoluku, Epämurtoluku, Murtoluku, Nimittäjä, Supistumaton murtoluku, Kokonaisluku.

Otaksuma on jokin asia, jonka arvellaan mahdollisesti pitävän paikkansa, mutta jota ei vielä ole todistettu todeksi. Esimerkki otaksumasta on Goldbachin otaksuma, jonka mukaan jokainen parillinen luku (paitsi 2) voidaan kirjoittaa kahden alkuluvun summana. Se on osoittautunut todeksi kaikilla parillisilla luvuilla, joita on kokeiltu, mutta vielä ei ole todistettu, että se pätee yleisesti.

Katso myös Alkulukukaksosten otaksuma, Hypoteesi, Lause, Goldbachin otaksuma, Bertrandin otaksuma.

Tilastollinen tapa kerätä tietoa. Perusjoukosta poimitaan havaintoja satunnaisesti. Havainnot mitataan (haastatellaan) ja tiedot yleistetään koko perusjoukkoa koskeviksi. Esimerkiksi vaaligallupit: Satunnaisesti valituilta äänioikeutetuilta henkilöiltä kysytään: "Mitä puoluetta äänestäisitte, jos nyt olisi vaalit?" Vastausten perusteella arvioidaan puolueiden kannatusluvut (tulokset yleistetään kaikkia äänioikeutettuja koskeviksi). Mikäli kyseessä ei ole otos (satunnainen valinta), ei tuloksia voi yleistää.

Perusjoukosta tutkimusta varten kerätty osajoukko (näyte) on otos (satunnaisnäyte), mikäli siihen tulevat alkiot on valittu satunnaisesti (arvottu). Otoksen perusteella lasketut tulokset voidaan yleistää koko perusjoukkoa koskeviksi. Mikäli havainnot kerätään muuten, (esimerkiksi etsitään vapaaehtoisia kokeeseen halukkaita henkilöitä, kyseessä on näyte - ei otos) ei tuloksia voi välttämättä yleistää koko perusjoukkoa koskeviksi.

Katso myös Otospiste.

Satunnaiskokeen kaikki mahdolliset tulokset. Esimerkiksi rahanheitossa otosavaruus on joukko $\Omega = \mathrm{ \{kruuna, klaava \} }$. Tutkimuksen kohteena oleva perusjoukko.

Katso myös Avaruus, Sattuma, Mahdollisuus, Valita, Tapahtuma, Todennäköisyys, Otospiste.

Yksi satunnaiskokeen mahdollinen tulos. Yksi otosavaruuden alkio (alkeistapahtuma).

Katso myös Otos, Otosavaruus.

Otoksesta laskettu tunnusluku, kuten keskiarvo tai varianssi. Otostunnusluvut ovat yleensä estimaatteja (arvioita) vastaaville perusjoukon teoreettisille tunnusluvuille. Otostunnuslukuja merkitään yleensä latinalaisilla kirjaimilla.

Katso myös Kriittinen arvo, Tunnusluku, Tilastollinen tunnusluku.

Yleinen nimitys ellipsille tai ellipsin muotoiselle kuviolle; litistetty ympyrä.

Katso myös Ellipsi, Karteesinen soikio, Kuvio.