Paikallinen, Lokaali (engl. Local)
Sellainen, jolla on vaikutusta vain pienellä etäisyydellä toisistaan oleviin asioihin. Esimerkiksi saatetaan sanoa, että funktio on lokaalisti lineaarinen, jos se on lineaarinen pienessä osassa määrittelyjoukkoaan.
Funktion lokaali minimi on arvo, joka on pienempi tai yhtä suuri kuin muut arvot sen ympäristössä, mutta ei välttämättä ole pienin arvo funktion koko arvojoukossa.
Paikantamistunnusluku, Keskiluku (engl. Measure of central tendency)
Keskilukuja ovat tilastoaineiston (jakauman) paikkaa (keskipistettä) kuvaavat luvut. Tunnetuimmat keskiluvut ovat:
- Keskiarvo - jakauman tasapainopiste.
- Mediaani - arvo, joka jakaa jakauman keskeltä kahteen yhtäsuureen osaan.
- Moodi - jakauman korkein kohta (yleisin muuttujanarvo).
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Mediaani, Moodi, Tyyppiarvo, Harmoninen keskiarvo.
Paikkajärjestelmä (engl. Place value)
Kymmenjärjestelmässä numeron paikka luvussa on tärkeä. Esimerkiksi luvun 45556 kolmella viitosella on jokaisella eri arvo, joka riippuu niiden paikasta luvussa. Tässä tapauksessa niiden arvot ovat 5000, 500 ja 50.
Kymmenjärjestelmä perustuu luvun ryhmittelyyn kymmenen potensseiksi, ja kymmenjärjestelmän luvut kirjoitetaan merkitsemällä näkyviin tämä ryhmittely. Luvussa 2365 numero 2 esittää kahta tuhatta, numero 3 kolmea sataa, numero 6 kuutta kymmentä ja numero 5 viittä ykköstä.
Katso myös Merkitsevin tai vähiten merkitsevä numero, Desimaaliluku, Merkintätapa, Notaatio, Kymmenjärjestelmän luku.
Paikkavektori (engl. Position vector)
Pisteen paikkavektori on vektori, joka yhdistää origon tähän pisteeseen. Pisteen $P=(x,\,y,\,z)$ paikkavektori on $\overrightarrow{OP}=x\overrightarrow{i}+ y\overrightarrow{j}+z\overrightarrow{k}=(x,\,y,\,z).$
Painopiste (engl. Centroid)
Kuvion painopiste on piste, jonka koordinaatit ovat kuvion kärkien koordinaattien keskiarvo. Erityisesti kolmion painopiste on sen keskijanojen leikkauspiste.
Katso myös Keskipiste, Kolmion ympäri piirretyn ympyrän keskipiste, Keskijana, Mediaani, Kolmion painopisteen määrittäminen, Kolmion massakeskipiste, Eulerin suora.
Painopiste, Massakeskipiste (engl. Barycentre, Center of mass, Centre of mass)
Kohdissa $(x_{i}, y_{i}, z_{i})$ sijaitsevista pistemassoista $m_{i}$ koostuvan kappaleen massakeskipiste eli painopiste on $(\bar{x}, \bar{y}, \bar{z})$, missä $\bar{x} = \frac{\sum_i x_im_i}{\sum_i m_i}$, jne.
Jos kappaleen $V$ massatiheys pisteessä $(x, y, z)$ on $p(x, y, z)$ ja kappaleen kokonaismassa on $M$, niin sen massakeskipiste eli painopiste on $(\bar{x}, \bar{y}, \bar{z})$, missä $\bar{x} = \frac{\int_V x p dV}{M}$, jne.
Karkeasti sanoen on kaksiulotteisen kappaleen massakeskipiste se piste, josta tuettuna kappale pysyy vaakatasossa, kun taas kolmiulotteisen kappaleen massakeskipiste on se piste, joka jää aina kohtisuoraan kappaleen kiinnityspisteen alapuolelle kiinnitettiinpä kappale roikkumaan mistä pisteestä tahansa.
Katso myös Keskipiste, Pyramidin massakeskipiste, Ympyränkaaren massakeskipiste, Puolipallonkuoren massakeskipiste, Puolipallon massakeskipiste, Kolmion massakeskipiste, Pyörähdyskappaleen massakeskipiste, Ympyrän sektorin massakeskipiste, Kartion vaipan massakeskipiste, Kartion massakeskipiste, Tasoalueen massakeskipiste.
Palauttaa, Alentaa, Redusoida, Pelkistää (engl. Reduce)
Kauppojen alennusmyynneissä tavaroiden hinnat ovat alennettuja. Alkuperäisestä hinnasta on otettu rahaa pois, tavarat maksavat vähemmän. Myydäkseen tavaroita kauppiaat usein lupaavat kiinteän summan, joka otetaan pois kaikista hinnoista, esimerkiksi 5 euroa. Tällöin kaikki tavarat maksavat 5 euroa vähemmän.
Toisinaan kauppiaat alentavat hintoja kiinteällä prosentilla, esimerkiksi 10%:lla. Tällöin hinnasta otetaan pois 10 senttiä jokaista euroa kohti.
Alentaa jotakin, yleensä rahamäärää, tarkoittaa tehdä se pienemmäksi.
Redusointi eli pelkistäminen on jonkin aineen tai asian palauttamista tai purkamista niiksi yksinkertaisemmiksi osiksi, joista se on muodostunut.Palautuskaava (engl. Recurrence relation)
Kaava, joka määrittelee lukujonon kertomalla, kuinka lukujonon seuraava luku saadaan edellisistä luvuista eli palautetaan näihin. Esimerkiksi Fibonaccin luvut määrittelee palautuskaava $F_n = F_{n-1} + F_{n-2}$. Tämä kertoo, että lukujonon seuraava luku on kahden edellisen summa. Kaksi ensimmästä Fibonaccin lukua ovat $F_0 = 0$ ja $F_1 = 1$. Loput saadaan edellä esitetyn palautuskaavan avulla.
Joskus palautuskaava voidaan muuntaa tavalliseksi kaavaksi, joka antaa lukujonon jäsenen $f_n$ suoraan luvun $n$ funktiona, mutta aina tällaisen muunnoksen löytäminen ei ole helppoa.
Katso myös Lukuteoria, Fibonaccin luku, Ensimmäisen kertaluvun rekursioyhtälön ratkaisu, Differenssiyhtälö, Yhtälö, Korkeamman kertaluvun palautuskaava, Ensimmäisen kertaluvun palautuskaava.
Palindromi (engl. Palindrome)
Luku tai sana, joka on sama alusta loppuun ja lopusta alkuun luettuna.
Luvut 2332, 121, 646 ja 22 ovat palindromilukuja.
On olemassa palindromisanoja ja lauseita kuten ANNA, SAIPPUAKAUPPIAS tai TIKAT NAKERTAVAT REKAN TAKIT.
Pallo (engl. Sphere)
Kappale, jonka muodostavat kaikki ne kolmiulotteisen avaruuden pisteet, joiden etäisyys kiinteästä pisteestä eli pallon keskipisteestä on $r$. Luku $r$ on pallon säde.

Katso myös Pallon tilavuus, Tasainen monitahokas, Pallokaksikulmio, Puolipallo, Ympyrä, Kappale, Avaruusgeometria, Pallon yhtälö, Pallon pinta-ala, Pallo, Ympäripiirretty pallo, Hyperpallo.
Pallo (engl. Ball)
Normilla $| \cdot |$ varustetun vektoriavaruuden $V$ osajoukko, joka on muotoa \[ B_r(z) = \{ x \in V \mid |x - z| \lt r \} \] tai muotoa \[ \bar{B}_r(z) = \{ x \in V \mid |x - z| \leq r \}, \] missä $r \in \mathbb{R}$ ja $z \in V$. Edellistä kutsutaan avoimeksi palloksi ja jälkimmäistä suljetuksi palloksi.
Katso myös Yksikköpallo, Pallo, Joukko.
Pallogeometria (engl. Spherical geometry)
Pallon pinnalla pätevä geometria. Tässä geometriassa kolmion kulmien summa on yli 180 astetta, ja kaksi eri suoraa leikkaavat toisensa aina kahdessa pisteessä.
Katso myös Isoympyrä.
Pallojen pakkaaminen (engl. Sphere packing)
Kysymys, mikä on tihein tapa pakata keskenään samanlaisia palloja avaruuteen, on avoin, eli sen ratkaisua ei tunneta. Ilmeinen ratkaisu on sijoittaa kuusikulmiomaisesti pakattuja kerroksia päällekkäin (katso ympyröiden pakkaaminen) niin, että jokainen pallo koskettaa 12 muuta. Kuitenkaan ei ole onnistuttu todistamaan, etteikö parempaa tapaa voisi löytyä.
Katso myös Ympyröiden pakkaaminen.
Pallokaksikulmio (engl. Lune)
Pallon pinta-ala (engl. Surface area of a sphere, Area of a sphere)
Jos pallon säde on $r$, niin sen pinta-ala on $4\pi r^2$.
Katso myös Pallo.
Pallon tilavuus (engl. Volume of sphere, Volume of a sphere, Sphere volume)
$r$-säteisen pallon tilavuus on \[\frac{4}{3} \pi r^{3}.\]
Katso myös Kartion tilavuus, Pallo, Cavalierin lause.
Pallon yhtälö (engl. Equation of a sphere)
Origokeskisen, $r$-säteisen pallon yhtälö on \[ x^{2}+y^{2}+z^{2} = r^{2}. \] Jos pallon keskipiste on $(a,b,c)$ ja säde on $r$, on pallon yhtälö \[ (x-a)^{2}+(y-b)^{2}+(z-c)^{2} = r^{2}. \]
Pallovyöhykkeen ala (engl. Area of a zone)
Pallovyöhykkeen, joka on kahden etäisyydellä $h$ toisistaan olevan tason $r$-säteisestä pallonpinnasta erottama osa, pinta-ala on $2\pi rh$. Arkhimedeen lause antaa tämän kaavan.
Katso myös Arkhimedeen lause, Monitahokkaan pinta-ala.
Paloittain jatkuva (engl. Piecewise continuous)
Olkoon $A \subset \mathbb{R}$ väli. Funktio $A \rightarrow \mathbb{R}$ on paloittain jatkuva, mikäli sen epäjatkuvuuskohtien joukko on lokaalisti äärellinen, ja sillä on toispuoleiset raja-arvot kaikissa epäjatkuvuuskohdissa.
Katso myös Epäjatkuva.
Paraabeli (engl. Parabola)
Käyrä, jonka muodostavat ne pisteet, joiden etäisyys kiinteästä pisteestä, polttopisteestä, ja kiinteästä suorasta, johtosuorasta, on sama.
Paraabelin yhtälö on muotoa $y = ax^{2}+bx+c$, jossa $a$, $b$ ja $c$ ovat vakioita ja $a$ on eri suuri kuin 0.
Vinosti ilmaan heitetyn kappaleen lentorata on paraabeli, jos ilman vastusta ei ole ja jos painovoima on kaikkialla samansuuntainen (kuten likimain on maan pinnalla).
Paraabelin inversiokuvio kuvauksessa, jossa inversiokeskus on paraabelin polttopiste, on kardioidi. Paraabelin inversiokuvio jossa inversiokeskus on paraabelin huippu, on Diokleen kissoidi.
Katso myös Kartioleikkaus.
Paraabelin yhtälö (engl. Equation of a parabola)
Jos paraabelin polttopiste on $(a,0)$ ja johtosuora on $x=-a$, on paraabelin yhtälö $y^{2} = 4ax$.
Katso myös Kartioleikkauksen yhtälö, Kartioleikkaus, Yhtälö, Kartioleikkauksen polttopiste.
Parabelin eksentrisyys (engl. Eccentricity of a parabola)
Parabelin eksentrisyys $e$ on $1$.
Katso myös Eksentrisyys.
Parabolinen spiraali, Fermat'n spiraali (engl. Parabolic spiral, Fermat's spiral)
Paradoksi (engl. Paradox)
Perustelu, joka näyttää järkevältä, mutta antaa selvästi virheellisen johtopäätöksen.
Katso myös Zenonin paradoksi, Banachin-Tarskin paradoksi, Russellin paradoksi.
Paralleeliaksiooma (engl. Parallel postulate)
Viides Eukleideen viidestä aksioomasta. Se muotoillaan yleensä seuraavasti. Jos on annettu suora $L$ ja piste $P$, joka ei sijaitse suoralla $L$, niin on olemassa täsmälleen yksi suora, joka kulkee pisteen $P$ kautta ja on yhdensuuntainen suoran $L$ kanssa.
Jos tätä aksioomaa ei oleteta, saadaan epäeuklidisia geometrioita.
Katso myös Postulaatti.
Parametri (engl. Parameter)
Useita samankaltaisia funktiota luokitteleva muuttuja.
Muuttuja, jonka avulla määritellään muiden muuttujien riippuvuus toisistaan.
Pari (engl. Pair)
Kaksi kappaletta jotakin ryhmiteltynä yhteen.
Katso myös Järjestetty pari, Joukko.
Parillinen (engl. Even)
Jaollinen luvulla $2$. Esimerkiksi $6$ on parillinen, koska $6 = 2 \cdot 3$.
Kahdella jaollinen. Kaikki tunnetut täydelliset luvut ovat parillisia. Ainoa parillinen alkuluku on 2.
Katso myös Pariton, Jaollisuus.
Parillinen funktio (engl. Even function)
Funktio $f \colon \mathbb{R} \rightarrow \mathbb{R}$ on parillinen, jos $f(x)=f(-x)$ pätee kaikilla $x \in \mathbb{R}$. Esimerkiksi $\cos(x)$ on parillinen funktio.
Katso myös $\cos(-x)$, Funktio, Kuvaus, Pariton funktio.
Parillinen luku (engl. Even number)
Kokonaisluku, joka on jaollinen luvulla 2, eli luku, joka jaettuna kahdella antaa tulokseksi kokonaisluvun.
Parillisen luvun viimeinen numero on 0, 2, 4, 6 tai 8.
Laskettaessa yhteen kaksi paritonta lukua on tulos aina parillinen luku.
Katso myös Yhdistetty luku.
Parillinen permutaatio (engl. Even permutation)
Permutaatio, joka saadaan yhdistettynä permutaationa parillisesta määrästä transpositioita. Huomaa, että sama permutaatio voidaan saada transpositioiden yhdistettynä kuvauksena usealla eri tavalla. Parillisuus on kuitenkin ominaisuus, joka ei riipu siitä, kuinka transpositiot valitaan.
Katso myös Transpositio, Pariton permutaatio, Vaihto, Permutaatio, Vaihdos.
Pariton (engl. Odd)
Parittomat luvut ovat lukuja, jotka eivät ole parillisia. Esimerkiksi $7$ on pariton, koska $7 = 2\cdot 3 + 1$.
Kokonaisluku on pariton, jos se ei ole jaollinen kahdella.
Katso myös Parillinen, Jaollisuus.
Pariton funktio (engl. Odd function)
Funktio $f$ on pariton, jos se toteuttaa ehdon $f(-x) = -f(x)$ kaikilla muuttujan $x$ arvoilla. Esimerkki parittomasta funktiosta on $\sin x$.
On mahdollista, että funktio ei ole pariton eikä parillinen. Tällainen funktio on esimerkiksi $f(x)=1+2x$. Ainoastaan funktio $f(x)=0$ on sekä pariton että parillinen.
Katso myös $\tan(-x)$, $\sin(-x)$, Funktio, Kuvaus, Parillinen funktio.
Pariton luku (engl. Odd number)
Kokonaisluku, joka kahdella jaettuna antaa jakojäännöksen 1. Esimerkiksi $15/2 = 7$, jakojäännös 1, joten 15 on pariton luku. Lueteltaessa kokonaislukuja järjestyksessä parittomat luvut vuorottelevat parittomien lukujen kanssa - pariton, parillinen, pariton, parillinen, ...
Pariton permutaatio (engl. Odd permutation)
Permutaatio, joka saadaan yhdistettynä kuvauksena parittomasta määrästä transpositioita.
Permutaatio voidaan saada yhdistettynä kuvauksena transpositioista usealla eri tavalla. Kuitenkin parittomuus on ominaisuus, joka on riippumaton siitä, kuinka transpositiot valitaan.
Katso myös Transpositio, Parillinen permutaatio, Vaihto, Permutaatio, Vaihdos.
Parittaisten otosten t-testi (engl. t-test for paired sample)
Parittaisten otosten t-testi on erityisesti koesuunnitteluun liittyvä testausmenettely, mutta käytännössä esiintyy myös eräitä muita ennen - jälkeen tilanteita, joissa sitä voidaan käyttää. Ongelmana parittaisten otosten t-testissä on: "Onko tutkittavalla käsittelyllä vaikutusta kohteeseen?" Ongelman ratkaisemiseksi poimitaan otos, jonka alkiot mitataan, alistetaan käsittelylle ja mitataan uudelleen. Käytössä on näin kahdet mittaustulokset samoista havainnoista (parittaiset otokset) - ei kaksi riippumatonta otosta. Ongelman ratkaisemiseksi lasketaan mittaustulosten erotukset $$ d_i = X_{jälkeen}-X_{ennen} $$ Erotuksiin liittyen voidaan tutkia nollahypoteesia: $$ H_o: \mathrm{E}(d)=d_o $$ Ts. käsittelyn vaikutus on $d_o$. Usein $d_o=0$ jolloin testattava hypoteesi on "Käsittelyllä ei ole vaikutusta". Mikäli erotusten $d_i$ keskiarvo on jakautunut normaalisti, voidaan annettua hypoteesia testata t-testillä $$ t= {{(\overline {d} - d_o)}\over {s_d\cdot \sqrt{1\over n}}} $$ Mikäli testattava hypoteesi pitää paikkansa, t-testisuure saa lähellä nollaa olevia arvoja ja noudattaa t-jakaumaa vapausasteilla $(n-1)$. Muussa tapauksessa t-testisuure saa suuria positiivisia tai suuria negatiivisia arvoja.
Katso myös Tilastollinen testi.
Pascal
Blaise Pascal (1623--1662). Ranskalainen matemaatikko ja filosofi, joka tutki kartioleikkauksia ja todennäköisyyslaskentaa.
Katso myös Pascalin kolmio.
Pascal (engl. Pascal)
Paineen yksikkö. Yksi Pascal on yhtä suuri kuin yksi Newton neliömetriä kohti eli 1 Pa = 1 N/m$^{2}$.
Pascalin kolmio (engl. Pascal's triangle)
Kolmion muotoon järjestetty joukko lukuja, jossa ylimmällä rivillä on kaksi ykköstä, jokainen rivi alkaa ja päättyy ykköseen ja muut luvut ovat yhtä suuria kuin välittömästi sen yläpuolella olevien kahden luvun summa. Pascalin kolmion luvut ovat binomikertoimia.
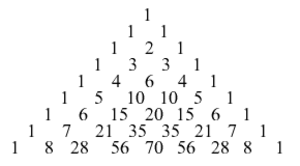
Katso myös Pascal, Kombinatoriikka, Tetraedriluku, Kokonaisluku.
Peilaus (engl. Reflection)
Geometrinen kuvaus, joka liittyy suoraan $L$, peilaussuoraan. Kuvauksessa jokainen piste $P$ kuvautuu suoran $L$ toiselle puolelle pisteeksi $Q$ niin, että $P$ ja $Q$ ovat yhtä etäällä $L$:stä ja suora $PQ$ on kohtisuorassa suoraa $L$ vastaan. Peilaus kuvaa jokaisen kuvion alkuperäisen kanssa yhteneväksi kuvioksi niin, että kuvioiden suunnistukset ovat vastakkaisia.
Katso myös Kierto, Peilaussymmetria, Geometrinen muunnos.
Peilausmatriisi (engl. Reflection matrix)
Matriisi, jota vastava kuvaus peilaa tason suoran $y=\tan x \psi$ suhteen, on muotoa $$\left ( \begin{array}{ll} \cos 2 \psi & \sin 2 \psi \\ \sin 2 \psi & \cos 2 \psi \end{array} \right )$$
Katso myös Rotaatiomatriisi, Kiertomatriisi, Matriisi.
Peilaussymmetria (engl. Reflectional symmetry, Reflective symmetry, Reflection symmetry)
Kuvio on peilaussymmetrinen, jos on olemassa jokin suora $L$, jossa peilaten kuvio pysyy itsenään, ts. jokaisen pisteen kuva kuuluu myös kuvattavaan kuvioon.
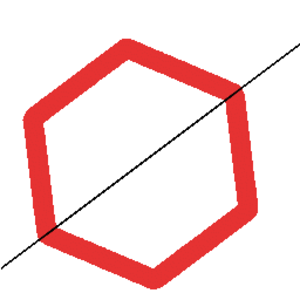
Katso myös Peilaus, Symmetria, Bilateraalinen symmetria, Symmetria-akseli.
Peli (engl. Game)
Peliteoriassa (pelien matemaattisessa tutkimuksessa) peli on kilpailutilanne, jossa seuraavat ehdot ovat voimassa:
- Pelissä on mukana äärellinen määrä pelaajia.
- Jokaisella pelaajalla on äärellinen määrä vaihtoehtoja jokaisessa pelin vaiheessa.
- Pelaaja ei tiedä etukäteen, mitä muut pelaajat aikovat tehdä.
- Pelin lopussa pelaajat joko voittavat tai häviävät jotakin riippuen pelin tuloksesta.
Katso myös Hanoin tornit, Nollasummapeli, Nim.
Pelkistää, Alentaa, Redusoida, Palauttaa (engl. Reduce)
Kauppojen alennusmyynneissä tavaroiden hinnat ovat alennettuja. Alkuperäisestä hinnasta on otettu rahaa pois, tavarat maksavat vähemmän. Myydäkseen tavaroita kauppiaat usein lupaavat kiinteän summan, joka otetaan pois kaikista hinnoista, esimerkiksi 5 euroa. Tällöin kaikki tavarat maksavat 5 euroa vähemmän.
Toisinaan kauppiaat alentavat hintoja kiinteällä prosentilla, esimerkiksi 10%:lla. Tällöin hinnasta otetaan pois 10 senttiä jokaista euroa kohti.
Alentaa jotakin, yleensä rahamäärää, tarkoittaa tehdä se pienemmäksi.
Redusointi eli pelkistäminen on jonkin aineen tai asian palauttamista tai purkamista niiksi yksinkertaisemmiksi osiksi, joista se on muodostunut.Pentagrammi (engl. Pentagram)
Viisisakarainen tähti, joka muodostuu jatkamalla viisikulmion sivuja siten, että ne kohtaavat toisensa pareittain.

Katso myös Viisikulmio, Hoehnin lause.
Perhosefekti, Perhosvaikutus (engl. Butterfly effect)
Kuuluisa ajatus kaaosteoriassa: pienellä häiriöllä voi monimutkaisessa systeemissä olla suuri vaikutus systeemin tilaan. Ilmakehä on esimerkki tällaisesta systeemistä: perhosen siipien heilahdus Kiinassa voi aiheuttaa hirmumyrskyn viikkoa myöhemmin Amerikassa.
Perhosvaikutus, Perhosefekti (engl. Butterfly effect)
Kuuluisa ajatus kaaosteoriassa: pienellä häiriöllä voi monimutkaisessa systeemissä olla suuri vaikutus systeemin tilaan. Ilmakehä on esimerkki tällaisesta systeemistä: perhosen siipien heilahdus Kiinassa voi aiheuttaa hirmumyrskyn viikkoa myöhemmin Amerikassa.
Permutaatio (engl. Permutation)
Jokainen (mikä tahansa) niistä erilaisista järjestyksistä, joihon annetun joukon alkiot voidaan laittaa.
Jos käytössä olisi vain kaksi sanaa "kissa" ja "istui", voitaisiin niistä muodostaan ainoastaan kaksi lausetta: "kissa istui" ja "istui kissa".
Jos käytössä olisi kolme sanaa "kissa", "istui" ja "matolla", voitaisiin niistä muodostaa seuraavat lauseet:
"kissa istui matolla",
"kissa matolla istui",
"istui matolla kissa",
"istui kissa matolla",
"matolla kissa istui",
"matolla istui kissa".
Kahdella eri sanalla on siten kaksi permutaatiota, kun taas kolmella eri sanalla on kuusi permutaatiota.
Annetun joukon osajoukon alkioiden asettaminen uuteen järjestykseen. Permutaatiota voidaan myös ajatella joukon bijektiona itselleen. Annetun $n$ alkion joukon $r$ alkion permutaatioiden lukumäärä on \[ {^n}P_r = \frac{n!}{(n-r)!}. \] Äärellisen joukon kaikkien alkioiden mikä tahansa uuteen järjestykseen asettaminen. Permutaatio on pariton tai parillinen riippuen siitä, onko sen vaihtojen lukumäärä pariton vai parillinen. Permutaatio on syklinen, jos se ainoastaan siirtää alkioita eteenpäin tietyn paikkaluvun verran eli on tietyn pituinen kierto. Transpositio eli vaihto on 2-kierto. Jokainen permutaatio voidaan esittää järjestystä vaille yksikäsitteisesti 2-kiertojen tulona. Huomaa, että kokoa $n$ olevan joukon kaikkien permutaatioiden joukko muodostaa ryhmän $S_n$, jossa laskutoimituksena on kuvausten yhdistäminen. Parilliset permutaatiot muodostavat tämän ryhmän aliryhmän $A_n$.
Katso myös Transpositio, Funktio, Kuvaus, Valita, Kombinaatio, Kombinatoriikka, Ryhmä, Parillinen permutaatio, Pariton permutaatio, Permutaatioryhmä, Erilliset permutaatiot, Vaihto, Vaihdos.
Permutaation etumerkki (engl. Signature)
Jos permutaatio saadaan identtisestä permutaatiosta parillisella määrällä transpositioita, on permutaatio positiivinen. Jos taas permutaatio saadaan identtisestä permutaatiosta parittomalla määrällä transpositioita, on permutaatio negatiivinen.
Permutaation etumerkki ei riipu sen transpositiojonon valinnasta, jolla permutaatio saadaan identtisestä permutaatiosta.
Permutaatioryhmä (engl. Permutation group)
Joukon $X$ permutaatioryhmä muodostuu kaikista joukon $X$ permutaatioista. Laskutoimituksena permutaatioryhmässä on kuvausten yhdistäminen, ja neutraalialkiona identtinen kuvaus. Permutaation käänteisalkio on sen käänteiskuvaus.
Voidaan osoittaa, että yllä kuvailtu struktuuri on ryhmä riippumatta joukosta $X$. Joukko $X$ voi olla yhtä hyvin äärellinen kuin ääretönkin.
Katso myös Ryhmä, Symmetrinen ryhmä, Permutaatio.
Perspektiivikeskus (engl. Centre of perspectivity, Centre of perspective)
Jos kaksi kuviota ovat perspektiivisessä asemassa toisiinsa nähden, niin kaikki suorat, jotka yhdistävät kuvioiden vastinpisteet, leikkaavat toisensa samassa pisteessä. Tätä pistettä kutsutaan perspektiivikeskukseksi.
Katso myös Keskipiste.
Perspektiivinen affiinikuvaus (engl. Perspective affinity)
Eräs tason geometrinen kuvaus. Perspektiivisen affiinikuvauksen määrittelevät suora $l$, suunta $d$ ja suhde $r$. Piirretään annetun pisteen $P$ kautta $d$:n suuntainen suora. Se leikkaa suoran $l$ pisteessä $X$. Etsitään sellainen piste suoran $PX$ piste $P'$, että janan $P'X$ pituuden suhde janan $PX$ pituuteen on $r$. Tällöin piste $P'$ on pisteen $P$ kuva perspektiivisessä affinikuvauksessa.
Isometriat, yhdenmuotoisuuskuvaukset, yhdensuuntaissiirrot ja venytykset ovat kaikki perspektiivisiä affiinikuvauksia.
Yhdestä tai useammasta perspektiivisestä affiinikuvauksesta yhdistetty kuvaus on yleinen affiinikuvaus.
Katso myös Transformaatio, Liukumuunnos, Isometria, Venytys, Venyttää.
Perspektiiviset kuviot (engl. Perspective)
Jos kaikki suorat, jotka yhdistävät kahden geometrisen kuvion vastinpisteet, leikkaavat toisensa yhdessä pisteessä, niin sanotaan, että nämä kaksi kuviota ovat perspektiivisessä asemassa toisiinsa nähden.
Perusluku (engl. Cardinal number)
Luku, joka ilmaisee lukumäärää, kuten 1, 2, 3 jne.
Katso myös Järjestysluku, Mahtavuus, Luonnollinen luku.
Perustelu (engl. Argument)
Matemaattinen todistus, mahdollisesti melko epämuodollinen.
Katso myös Jos, Seurata, Päätelmä, Olemassaolo, Johtaa, Määrittää, Vaatia, Yritys ja erehdys, Aiheuttaa jotakin, Olla jonkin riittävä ehto, Matemaattinen päättely, Kombinatorinen argumentti, Päätellä, Osoittaa, Näyttää, Todistaa vääräksi.
Peruuttaa, Vaihtaa suuntaa (engl. Reverse)
Vektorin suunnan vaihtaminen tarkoittaa, että se asetetaan osoittamaan vastakkaiseen suuntaan. Yhteenlaskun peruuttaminen tarkoittaa vastaavaa vähennyslaskua.
Kääntää jokin takaperin.
Peräkkäinen (engl. Consecutive)
Asiat, jotka seuraavat välittömästi toisiaan, ovat peräkkäisiä. Esimerkiksi maanantai, tiistai ja keskiviikko ovat kolme peräkkäistä viikonpäivää ja 58, 60 ja 62 ovat kolme peräkkäistä parillista lukua.
Peräkkäisten kokonaislukujen summa (engl. Sum of integers)
Lukujen $1, 2, \dots, n$ summa on $1 + 2 + \dots +n = \frac{n(n+1)}{2}$
Katso myös Sarja.
Peräkkäisten kuutioiden summa (engl. Sum of cubes)
Kuutioiden summa saadaan seuraavasti: $1^3 + 2^3 + 3^3 + \dots + n^3 =\frac{n^2(n+1)^2}{4}$.
Katso myös Neliölukujen summa, Sarja.
Peräkkäisten lukujen summa (engl. Sum of consecutive numbers)
Jos $n$ on pariton, niin $n$:n peräkkäisen luvun summa on luvun $n$ monikerta.
Katso myös Lause.
Peräkkäisten lukujen tulo (engl. Product of consecutive numbers)
$n$:n tai useamman peräkkäisen kokonaisluvun tulo on $n$:n monikerta.
Katso myös Lause.
Pienempi kuin (engl. Less than)
Merkki $<$ tarkoittaa, että merkin vasemmalla puolella oleva suure on pienempi kuin merkin oikealla puolella oleva suure.
Merkki $<$ on erityisen hyödyllinen verrattaessa lukuja toisiinsa. Seitsemän on pienempi kuin yhdeksän: $7 \lt 9$. Miinus yksitoista on pienempi kuin miinus viisi: $-11 \lt -5$.
Katso myös Lisääminen puolittain epäyhtälöön, Epäyhtälön kertominen puolittain, Pienempi tai yhtäsuuri kuin, Suurin lukua pienempi kokonaisluku, Vertailtavissa olevat.
Pienempi tai yhtäsuuri kuin (engl. Less than or equal to)
Merkki $\leq$ tarkoittaa, että merkin vasemmalla puolella oleva suure on joko pienempi tai yhtäsuuri kuin merkin oikealla puolella oleva suure. Esimerkiksi $a \leq b$ tarkoittaa, että joko $a \lt b$ tai $a=b$.
Katso myös Yhtäsuuri, Pienempi kuin, Sama.
Pienennyskuvaus (engl. Reduction)
Geometrinen kuvaus (yhdenmuotoisuuskuvaus), joka pienentää kaiken samassa suhteessa. Tällainen kuvaus siis säilyttää kuvion kulmat ja pituuksien suhteet samoina.
Katso myös Mitta-asteikko, Suurennuskuvaus.
Pienin, Alin (engl. Lowest)
Joukon pienin alkio on alkio, joka on pienempi tai yhtä suuri kuin joukon muut alkiot.
Pienin yhteinen monikerta (engl. Lowest common multiple, Least common multiple)
Pienin luku, jossa jokainen annetun lukujoukon luku on tekijänä. Esimerkiksi lukujen 2, 3 ja 4 eräs yhteinen monikerta on 24, mutta pienin yhteinen monikerta on 12.
Katso myös Yhteinen monikerta, Monikerta, Suurin yhteinen tekijä.
Pienin yhteinen nimittäjä (engl. Lowest common denominator)
Pienin luku, jonka tekijänä on jokainen kahden tai useamman murtoluvun nimittäjä.
Katso myös Yhteinen nimittäjä, pyj.
Pienin yläraja, Supremum (engl. Supremum, Least upper bound)
Supremum on pienin yläraja.
Olkoon $A$ joukko reaalilukuja. Sanomme, että reaaliluku $x$ on joukon $A$ yläraja, jos $x$ on vähintään yhtä suuri kuin jokainen joukon $A$ alkio. Joukon $A$ supremum on pienin niistä reaaliluvuista $x$, jotka ovat joukon $A$ ylärajoja.
Joukon $\{ x \in \mathbb{R} : x \lt 10\}$ supremum on 10.
Joukon $\{ x \in \mathbb{R} : x \le 11 \}$ supremum on 11.
Joukon $\{ x \in \mathbb{R} : 10 \le x \le 12 \}$ supremum on 12.
Joukolla $\{ x \in \mathbb{R} : x \ge 5 \}$ ei ole supremumia reaalilukujen joukossa.
Pii, $\pi$ (engl. Pi)
Kreikan kielen kirjain $\pi$ (pieni kirjain) tai $\Pi$ (suuri kirjain).
Kirjainta $\pi$ käytetään esittämään ympyrän kehän suhdetta sen halkaisijaan, toisin sanoen, $\pi = \frac{C}{d}$, missä $C=2\pi r$ on ympyrän kehän pituus ja $d=2r$ on ympyrän halkaisija.
$\pi$:n arvo on likimain 3.142 tai $\frac{22}{7}$. Tarkkaa arvoa ei voi esittää murtolukuna ja desimaalikehitelmäkin on äärettömän pitkä.
r-säteisen ympyrän pinta-ala on $A=\pi r^2$.
Seuraavassa joitakin kymmeniä $\pi$:n desimaalikehitelmän desimaaleja: 3,1415926535897932384626433832795028841971693993751058209749445923078164062862 08998628034825342117068
Kirjainta $\Pi$ käytetään tulon merkkinä samalla tavoin kuin kirjainta $\Sigma$ käytetään summan merkkinä.
$\Pi_{r=1}^k r = k! = 1 \times 2 \times \dots \times (k-1) \times k$.
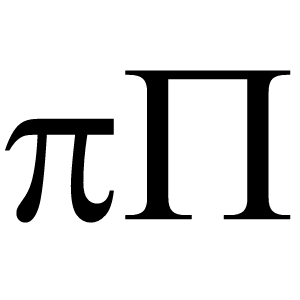
Katso myös Ympyrän pinta-ala, Vakio, Piin arvon laskeminen, Kreikkalaiset kirjaimet, Ympyrä, Transsendenttinen luku, Ympyrän kehän pituus, Ludolfin luku, Buffonin neula, Piin irrationaalisuus.
Piin arvon laskeminen (engl. Calculating pi, Formula for pi)
On olemassa monia tapoja laskea luvun $\pi$ arvo. Esimerkiksi \[\pi = 4 \cdot ( 1-(1/3)+(1/5)-(1/7)+\dots )\] (Leibnizin sarja) tai \[\pi = 2 \cdot \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots\] (Wallisin kaava).
Katso myös Vieten kaava, Kaava, Leibnizin kaava piin laskemiseksi, Wallisin kaava, Pii, $\pi$, Ramanujanin arviot luvulle pii.
Piin irrationaalisuus (engl. Irrationality of pi)
Luku $\pi$ on irrationaalinen eli sitä ei voida esittää kahden kokonaisluvun $m,n$ osamääränä $m/n$.
Katso myös Irrationaaliluku, Lause, Pii, $\pi$.
Piirakkadiagramma (engl. Pie chart, Pie graph)
Graafinen esitystapa, missä muuttujan arvot (taulukon elementit) esitetään erivärisinä ympyrän sektoreina, jolloin tulos muistuttaa paloiksi leikattua piirakkaa. Käyttökelpoinen esitystapa tutkittaessa, miten suuren osuuden kokonaisuudesta kukin sektori muodostaa.
Piiri (engl. Perimeter)
Kuvion reuna tai tämän reunan pituus.
Katso myös Pinta-ala, Piirin puolikas, Ympyrän kehä, Suljettu käyrä.
Piirin puolikas (engl. Semiperimeter)
Puolet kuvion piiristä. Esiintyy monissa kolmiota koskevissa kaavoissa, mm. Heronin kaavassa.
Katso myös Piiri.
Piirtokolmio (engl. Set square)
Yleensä muovista, toisinaan myös puusta, valmistettu kolmio, joka on hyödyllinen piirrettäessä kohtisuoria ja yhdensuuntaisia suoria. On olemassa kahdenlaisia kulmaviivaimia, joiden kulmat ovat joko $90^{\circ}$, $60^{\circ}$ ja $30^{\circ}$ tai $90^{\circ}$, $45^{\circ}$ ja $45^{\circ}$.
Katso myös Konstruktio, Konstruointi.
Piirtää ympyrä monikulmion ympäri (engl. Circumscribe)
Piirtää ympyrä monikulmion ulkopuolelle siten, että se sisältää kaikki monikulmion kärjet. Kolmion ympäri voidaan aina piirtää ympyrä. Jos monikulmiossa on enemmän kuin kolme kärkeä, sen ympäri ei välttämättä voi piirtää ympyrää. Tetraedrin ympäri voidaan piirtää pallo, joka sivuaa kaikkia sen kärkiä.

Katso myös Monikulmion ympäri piirretty ympyrä, Konstruktio, Konstruointi.
Pinnan normaalisuoran yhtälö (engl. Equation of a normal line)
Olkoot $P$ pinta $g(x,y,z)=k$ ja $A$ pinnan $P$ piste paikkavektorina $\mathbf{a}$. Tällöin pisteen $A$ kautta kulkevalla pinnan $P$ normaalisuoralla on yhtälö $\mathbf{r} = \mathbf{a} + \lambda \nabla g(a)$, missä $\lambda$ on reaalilukuparametri.
Katso myös Suoran yhtälö.
Pinnan tangenttitason yhtälö (engl. Equation of a tangent plane)
Olkoon $P$ pinta $g(x,y,z)=k$ ja $A$ piste pinnalla $P$ paikkavektorina $\mathbf{a}$. Tällöin pinnan $P$ pisteeseen $A$ piirretyllä tangenttitasolla on yhtälö $(\mathbf{r}-\mathbf{a}) \cdot \nabla g(a) = 0$.
Katso myös Tason yhtälö.
Pint (engl. Pint)
Anglosaksinen tilavuusyksikkö. Merkitys Britanniassa ja Yhdysvalloissa erilainen.
Tätä yksikköä käytetään vielä runsaasti joidenkin nesteiden, erityisesti maidon sekä oluen ja muiden alkoholijuomien, mittaamiseen. Yksi pint on 1/8 gallonaa. Yksi pint on noin 0,5682624 litraa Britanniassa ja noin 0,473 litraa Yhdysvalloissa.
Katso myös Tilavuus.
Pinta-ala (engl. Area)
Kuvion kaksiulotteinen koko. Kuten muukin mittaaminen, kuvion pinta-alan määritys perustuu siihen, kuinka monen mittayksikön ja mittayksikön tasaosan kokoinen mitattava kuvio on. Mittayksiköksi otetaan yleensä neliö, esimerkiksi neliö, jonka sivun pituus on yksi pituuden mittayksikkö.
Erimuotoisten kuvioiden muuntaminen neliöiksi on usein ongelmallista. Pinta-ala onkin kautta aikojen ollut haaste matematiikalle. Integraalilaskenta antaa usein keinon määritellä ja määrittää pinta-aloja. On kuitenkin olemassa kuvioita, joille ei edes ole mahdollista määritellä pinta-alaa mielekkäästi.
Kaksiulotteisen kohteen, pinnan, pinta-ala on sen koon mitta. Pinta-ala kertoo, miten monta pintayksikköä, yksikköneliöä, tarvitaan peittämään pinta. Pinta-alan yksikkö on pituusyksikön toinen potenssi, esimerkiksi m$^2$ eli neliömetri.
Koska ei useintaan ole mahdollista peittää kuviota täydellisesti neliöillä, pinta-alan määrittelemiseen ja laskemiseen on kehitetty monia matemaattisia tekniikoita. Integraalilaskenta on yksi näistä.
On olemassa kuvioita, joiden pinta-ala on hankala tai jopa mahdoton laskea tai edes määritellä. Monet fraktaalikuviot ovat tällaisia.
Katso myös Käyrien väliin jäävä pinta-ala, Tilavuus, Pinta-alayksikkö, Piiri, Hehtaari, Neliömetri, Monitahokkaan pinta-ala, Aari.
Pinta-alayksikkö (engl. Unit of area)
Standardikokoinen pinta-ala, jota käytetään muiden pinta-alojen mittaamiseen.
Katso myös Pinta-ala, Hehtaari, Yksikkö, Neliömetri, Aari.
Piste (engl. Point)
Geometrinen objekti, jolla on paikka, mutta ei kokoa.
Katso myös Vieruskulma, Verkon solmu, Tangenttivektori, Symmetriakeskus, Keskipiste, Keskipiste, Leikkauspiste, Kulma, Kärki, Origo, Suorien leikkauspiste, Harmoninen liittopiste, Harmoninen konjugaatti, Kantapiste, Ellipsin polttopiste, Hyperbelin polttopisteet, Päätepiste, Kiintopiste, Napa, Piste, joka jakaa janan annetussa suhteessa, Normaalivektori, Kasautumispiste, Jakson kahdentuminen, Bifurkaatio, Sivunormaalivektori, Kriittinen piste, Kaksoissuhde, Kartioleikkauksen polttopiste.
Piste, joka jakaa janan annetussa suhteessa (engl. Point dividing a line segment)
Olkoot $A$ ja $B$ pisteitä avaruudessa, joiden paikkavektorit ovat $\mathbf{a}$ ja $\mathbf{b}$, ja olkoon $\lambda ; \mu$ annettu suhde. Pistellä, joka jakaa janan $AB$ tässä suhteessa, on paikkavektori \[ \frac{ \mu \mathbf{a} + \lambda \mathbf{b} }{ \lambda + \mu } . \]
Katso myös Piste.
Pisteen etäisyys suorasta (engl. Distance of a point from a line)
Tasossa pisteen $(x_{1},y_{1})$ etäisyys suorasta $ax+by+c = 0$ on \[ \frac{ |ax_{1}+by_{1}+c| }{ \sqrt{a^{2}+b^{2}} }. \]
Katso myös Etäisyyskaava, Etäisyys.
Pisteen etäisyys tasosta (engl. Distance of a point from a plane)
Pisteen etäisyys tasosta on sen janan pituus, jonka toinen päätepiste on kyseessä oleva piste ja jonka toinen päätepiste sijaitsee tasolla ja joka on kohtisuorassa tasoa vastaan.
Jos $P$ on piste $(a,b,c)$ ja $L$ on yhtälön $u x + v y + w z +t =0$ määräämä taso, lasketaan pisteen $P$ etäisyys tasosta $L$ kaavalla $$\frac{ | u a + v b + w c + t| }{ (u^2 + v^2 + w^2 )^{1/2} }.$$
Katso myös Etäisyyskaava, Etäisyys.
Pisteen kautta kulkeva suora (engl. Line through a point)
Suoran, joka kulkee annetun pisteen $(x_{1},y_{1})$ kautta ja jonka kulmakerroin on $m$, yhtälö on $y=y_1+ m(x-x_{1})$.
Katso myös Suora.
Pisteen potenssi ympyrän suhteen (engl. Intersecting chords theorem)
Oletetaan, että ympyrän $C$ jänne $A$ leikkaa $C$:n pisteissä $P$ ja $Q$, jänne $B$ leikkaa $C$:n pisteissä $R$ ja $S$ ja että jänteet $A$ ja $B$ leikkaavat toisensa pisteessä $X$. Tällöin $PX \cdot XQ = RX \cdot XS$. Huomaa, että piste $X$ voi sijaita ympyrän $C$ sisäpuolella, ulkopuolella tai kehällä. Tulo $PX\cdot XQ$ on pisteen $X$ potenssi ympyrän $C$ suhteen.
Katso myös Tulo, Ympyrä, Lause, Jänne, Suorien leikkauspiste, Sekantti.
Pistetulo, Skalaaritulo, Sisätulo (engl. Dot product, Scalar, inner or dot product, Inner product, Scalar product)
Kahden vektorin $\mathbf{a}$ ja $\mathbf{b}$ pistetulo eli skalaaritulo, jota merkitään $\mathbf{a} \cdot \mathbf{b}$ tai $<\mathbf{a},\mathbf{b}>$, on reaaliluku. Kolmialkioisten vektorien pistetulo määritellään kaavalla \[ \left ( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right ) \cdot \left ( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right ) = a_1 b_1 + a_2 b_2 + a_3 b_3. \] $n$-alkioisten vektorien pistetulo määritellään vastaavasti. Pistetulo voidaan myös määritellä kaavalla $\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos \theta $, missä $\theta$ on vektorien $\mathbf{a}$ ja $\mathbf{b}$ välinen kulma ja $|\mathbf{a}|$, $|\mathbf{b}|$ ovat vektorien $\mathbf{a}$ ja $\mathbf{b}$ pituudet.
Huomaa, että kaikilla vektoreilla $\mathbf{a}$, $\mathbf{b}$ ja $\mathbf{c}$ sekä kaikilla reaaliluvuilla $k$ pätee: \begin{eqnarray*} \mathbf{a} \cdot \mathbf{b} &=& \mathbf{b} \cdot \mathbf{a}\\ \mathbf{a} \cdot (\mathbf{b}+\mathbf{c}) &=& \mathbf{a} \cdot \mathbf{b}+\mathbf{a} \cdot \mathbf{c}\\ (k\mathbf{a}) \cdot \mathbf{b}& = & k(\mathbf{a} \cdot \mathbf{b})\\ &=&\mathbf{a} \cdot (k\mathbf{b}). \end{eqnarray*}
Reaalilukukertoimisen vektoriavaruuden $V$ kuvaus $\langle,\rangle : V \times V \rightarrow \mathbb{R}$ on sisätulo, jos se toteuttaa kaikilla $v, w \in V$ ja kaikilla $\mu, \lambda \in \mathbb{R}$ seuraavat ehdot:
1) $\langle v,v\rangle \geq 0$ ja $\langle v,v\rangle = 0$ jos ja vain jos $v = 0$,
2) $\langle v,w\rangle = \langle w,v\rangle $,
3) $\langle \mu u + \lambda v, w\rangle = \mu \langle u,w\rangle + \lambda \langle v,w\rangle$.
Katso myös Tulo, Vektoritulo, Ristitulo, Euklidinen normi, Bilineaarinen muoto, Cauchy-Schwarzin epäyhtälö.
Pistevieras, Erillinen (engl. Disjoint)
Joukot $A$ ja $B$ ovat erilliset eli pistevieraat, jos niiden leikkaus on tyhjä eli ei ole olemassa alkiota, joka kuuluu molempiin joukkoihin. Tällöin merkitään $A \cap B = \emptyset$. Yleisemmin on joukkojen kokoelma $C$ erillinen, jos mitkä tahansa kaksi $C$:n eri joukkoa ovat pistevieraat.
Katso myös Yhdiste, Jordanin käyrälause, Joukko.
Pistevierintäkäyrä (engl. Point roulette)
Vierintäkäyrä, jonka jotakin käyrää pitkin vierivän kappaleen kiinnitetty piste piirtää.
Katso myös Episykloidi, Vierintäkäyrä, Hyposykloidi.
Pituuspiiri, Meridiaani (engl. Meridian)
Maapallon napojen kautta kulkeva isoympyrä.
Nollapituuspiiri on Greenwichin kautta kulkeva pituuspiiri.
Pituuspiirin sijaintia kuvaa sen pituusaste, joka on meridiaanin tason ja nollameridiaanin tason välinen kulma.
Katso myös Loksodromi, Isoympyrä.
Platonin kappaleet (engl. Platonic solid)
Platonin kappaleiksi kutsutaan säännöllisiä monitahokkaita eli monitahokkaita, joiden kaikki tahkot ovat täsmälleen samanlaisia säännöllisiä monikulmioita. Platonin kappaleita on viisi: tetraedri, kuutio, oktaedri, dodekaedri ja ikosaedri.
Katso myös Viisi, 5, Tasainen monitahokas, Säännöllinen, Avaruusgeometria, Tetraedri, Säännöllinen monitahokas, Monitahokas, Kuutio, Säännöllinen heksaedri.
Platonin luku (engl. Plato's number, 216)
216 on pienin kuutio, joka voidaan kirjoittaa kolmen kuution summana $216 = 6^3 = 3^3 + 4^3 + 5^3$.
Plus (engl. Plus)
Merkkiä + sanotaan plusmerkiksi. Sitä käytetään yhteenlaskussa, esimerkiksi $1+2$ tarkoittaa, että lukuun 1 lisätään luku 2. Sillä käytetään myös tarkoittamaan, että jokin on positiivinen eikä negatiivinen, esimerkiksi $+4$ erotukseksi luvusta $-4$.
Katso myös Yhteenlasku, Etumerkki, Positiivinen.
Plus-miinusmerkki (engl. Plus minus sign, Plus or minus sign)
Merkki $\pm$ tarkoittaa, että voidaan joko lisätä tai vähentää merkkiä seuraava lauseke. Esimerkiksi $\pm 1$ tarkoittaa joko plus yksi tai miinus yksi.
Tätä merkkiä käytetään useimmin neliöjuuren edessä ilmaisemassa, että voidaan valita joko positiivinen tai negatiivinen neliöjuuri.
Poikkeama (engl. Deviation)
Poikkeamalla tarkoitetaan yleisesti jonkin suureen arvon erotusta toisesta, "oikeasta", arvosta.
Jos meillä on otos lukuja, voimme laskea lukujen keskiarvon. Kunkin otoksen luvun poikkeama on tällöin luvun erotus keskiarvosta. Huomaa, että näiden poikkeamien summa on nolla. Tätä havaintoa voidaan käyttää hyväksi keskiarvon laskemisessa seuraavalla tavalla. Oletetaan, että otoksen koko on $10$ ja että oikea otoskeskiarvo on $6$, mutta tätä ei tiedetä. Arvataan, että otoskeskiarvo olisi esimerkiksi $5$, ja lasketaan yhteen otoksen lukujen poikkeamat luvusta $5$. Tulokseksi tulee $10$, joten poikkeamien keskiarvo on $10 / 10 = 1$. Oikea otoskeskiarvo on siten $5+1 = 6$.
Katso myös Keskiarvo, Aritmeettinen keskiarvo.
Poikkeava havainto, Äärihavainto (engl. Outlier)
Poikkeavalla havainnolla tarkoitetaan yleensä yksinäistä (joissakin tapauksissa myös muutaman havainnon muodostamaa ryhmää), joka poikkeaa selvästi muista havainnoista. Poikkeavuuden syy (esim. mittausvirhe) on aina syytä selvittää.
Poikkeus (engl. Exception)
Esimerkki, joka ei noudata tiettyä sääntöä.
Sanonta 'Poikkeus vahvistaa säännön' ei lainkaan pidä paikkaansa matematiikassa.
Poisson-jakauma (engl. Poisson distribution)
Harvinaisen tapahtuman esiintymiskertojen lukumäärän jakauma suuressa perusjoukossa. Jakaumaa merkitään Poisson($\lambda$), missä $\lambda \gt 0$ on jakauman parametri. Jakauman pistetodennäköisyysfunktio on \[ \mathrm{P}(X=r) = e^{-\lambda } \frac{\lambda^r }{r!}, r = 0, 1, 2, \ldots, \] odotusarvo ja varianssi ovat $\lambda$ ja todennäköisyysgeneroiva funktio on $G(t) = e^{\lambda(t-1)}$.
Katso myös Jakauma.
Poissonin yhtälö (engl. Poisson's equation)
Poissonin yhtälö on $\nabla^2 f = s$, missä funktio $s$ on annettu.
Katso myös Laplacen yhtälö, Laplacen operaattori.
Poissulkeva tai (engl. XOR)
Kaksipaikkainen looginen operaattori, joka antaa totuusarvon 'tosi', kun täsmälleen toinen sen argumenteista on 'tosi', ja muulloin totuusarvon 'epätosi'.
Katso myös Looginen operaattori.
Polaarikoordinaateissa määritellyn kaaren pituus (engl. Polar arc length)
Jos käyrä on määritelty polaarikoordinaateissa yhtälöllä $r = f(\theta)$, niin käyrän pituus kulmien $\theta=a, \theta=b$ välissä saadaan kaavalla \[ \int _a ^b \sqrt { \left ( r^2 + \left ( \frac{dr}{d \theta} \right ) ^2 \right ) } d \theta . \]
Katso myös Kaaren pituus, Polun pituus.
Polkuintegraali (engl. Contour integral)
Jos $f$ on kompleksitason alueessa $D$ määritelty funktio ja $C$ on polku alueessa $D$, niin funktion $f$ integraalia pitkin polkua $C$ kutsutaan polkuintegraaliksi ja merkitään $\int_C f(z) dz$.
Tällainen integraali voidaan määritellä seuraavasti: Polku $C$ jaetaan $n$ osaan, joiden päätepisteet ovat $x_{0}, \ldots, x_n$, ja kustakin osasta poimitaan piste $z_i$. Yllä mainittu integraali on summan $\sum_i f(z_i)(x_i - x_{i-1})$ raja-arvo, kun $n$ kasvaa rajatta ja pisimmänkin polun osan pituus lähestyy nollaa, mikäli tämä raja-arvo on olemassa.
Katso myös Kompleksitaso, Integraali, Tasa-arvokäyrä, Käyräintegraali.
Polun pituus (engl. Parametric arc length)
Oletetaan, että kaari eli injektiivinen polku $p \colon [a,b] \rightarrow \mathbb{R}^2$ on määritelty yhtälöillä $x=f(t)$, $y=g(t)$. Tällöin polun $p$ pituus saadaan kaavalla \[ \int _a ^b \left ( \left ( \frac{dx}{dt} \right ) ^2 + \left ( \frac{dy}{dt} \right ) ^2 \right )^{1/2} dt . \]
Katso myös Kaaren pituus, Polaarikoordinaateissa määritellyn kaaren pituus.
Polynomi (engl. Polynomial)
Polynomi on lauseke, joka sisältää muuttujan tai muuttujien kokonaislukupotensseja tai niiden tuloja, joita on laskettu yhteen sekä kerrottu lukukertoimilla. Muuttujien eksponenttien on oltava positiivisia kokonaislukuja tai nollia. Esimerkiksi $3x^{2}+2x+1$, $x^{11}+2x$, $a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+ ... +a_{n}x^{n}$ ja $x^2+2xy +y^2$ ovat polynomeja.
Katso myös Algebra, Polynomin tekijöihinjako, Lauseke, Polynomin nollakohta, Toisen asteen lauseke, Jaoton polynomi, Kerroin, Monomi, Lagrangen polynomi, Polynomin aste, Karakteristinen polynomi, Kuutiollinen polynomi, Kolmannen asteen polynomi, Neljännen asteen polynomi, Rationaalilauseke, Rationaalifunktio, Polynomien suurin yhteinen tekijä, Legendren polynomit.
Polynomien suurin yhteinen tekijä (engl. Greatest common divisor of polynomials)
Polynomien $p(x)$ ja $q(x)$ suurin yhteinen tekijä on polynomi, joka on jaollinen kaikilla polynomien $p(x)$ ja $q(x)$ yhteisillä tekijöillä. Suurin yhteinen tekijä on vakiotekijää vaille yksikäsitteinen.
Katso myös Polynomi, Suurin yhteinen tekijä, Jakaa tekijöihin.
Polynomifunktio (engl. Polynomial function)
Funktio, jonka arvo on reaalisella kertoimella kerrottujen muuttujan kokonaislukupotenssien summa. Esimerkiksi \[f(x) = x^{4}+3x+1,\] \[f(x) = 5x^{2}+x\] ja \[f(x) = 10x^{57}+3x^{16}+12x^{5}.\]
Katso myös Funktio, Kuvaus, Algebran peruslause.
Polynomin aste (engl. Order of a polynomial, Degree of a polynomial)
Polynomin tai polynomiyhtälön aste on siinä esiintyvän muuttujan korkeimman potenssin lukuarvo.
Polynomin aste on siinä esiintyvän muuttujan korkeimman potenssin lukuarvo. Siis polynomin $a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0$ aste on $n$, mikäli $a_n \neq 0$.
Neliöllisen polynomin aste on 2, kuutiollisen polynomin aste on 3, jne. Vakiopolynomin aste on 0.
Polynomin aste on sen korkein potenssi, joten polynomin $\sum_{n=0}^N a_n x^n$ aste on se suurin luku $n$, jolla $a_n \neq 0$.
Katso myös Polynomi, Järjestys, Ominaisuus, jonka arvot ovat diskreettejä.
Polynomin nollakohta (engl. Root of a polynomial)
Polynomin $p(x)$ nollakohta on se muuttujan arvo, jolla polynomin arvo on yhtä suuri kuin 0. Se on yhtälön $p(x)=0$ ratkaisu.
Polynomin $f \in K[X]$ nollakohta on se alkio $\alpha \in K$, jolla $f(\alpha)=0_{K}$.
Katso myös Algebrallinen, Nolla, Polynomin tekijöihinjako, Polynomi, Ratkaisu, Kolmannen asteen polynomiyhtälön juuret.
Polynomin tekijöihinjako (engl. Factorise a polynomial)
Polynomin jakaminen tekijöihin tarkoittaa, että se kirjoitetaan alkuperäistä polynomia alempiasteisten polynomien tulona.
Esimerkiksi polynomi $x^{2}-3x-10$ voidaan jakaa tekijöihin kirjoittamalla se muodossa $(x-5)(x+2)$. Polynomi $x^{3}-2x^{2}-15x$ voidaan jakaa tekijöihin kirjoittamalla se muodossa $(x^{2}+3x)(x-5)$ tai $(x^{2}-5x)(x+3)$ tai $x(x-5)(x+3)$.
Jos $c$ on polynomin nollakohta, niin $x-c$ on polynomin tekijä. Tästä voi olla hyötyä jaettaessa tekijöihin toisen, kolmannen ja neljännen asteen polynomeja. Ei ole kuitenkaan olemassa yleistä menetelmää polynomin jakamiseksi tekijöihin nopeasti.
Katso myös Polynomin nollakohta, Polynomi, Jaoton polynomi, Jakaa tekijöihin, Kuutiollinen polynomi, Kolmannen asteen polynomi, Neljännen asteen polynomi.
Polynomirengas (engl. Polynomial ring)
Olkoon $R$ rengas. Muuttujien $X_i$, $i=1 \dots n$ monomeja ovat lausekkeet $\Pi_{i=1 \dots n} X_i^{p_i}$, $p_i \in \mathbb{N}$. Polynomirenkaan alkiot ovat tyyppiä $\Sigma_M r_M M$, missä summausindeksi käy läpi kaikki muuttujien $X_i$ monomit, ja $r_M \in R$, $r_M$ eroaa nollasta vain äärellisen monella monomilla $M$.
Polynomien yhteen- ja kertolasku tapahtuu samoilla laskulaeilla kuin tavallisten reaalikertoimisten polynomienkin.
Katso myös Rengas, Rationaalifunktio.
Pons asinorum (engl. Pons asinorum)
Aasinsilta. Tällä nimellä kutsutaan geometrian teoreemaa, jonka mukaan tasakylkisen kolmion kantakulmat ovat yhtä suuret.
Positiivinen (engl. Positive)
Suurempi kuin 0. Luvut 13, 0,22, 7456,98, 23/5, $4\frac{3}{4}$ ja 1/5 ovat kaikki positiivisia.
Positiivisten reaalilukujen joukkoa merkitään $\mathbf{R}^{+}$, ja se sisältää kaikki reaaliluvut, jotka ovat suurempia kuin nolla.
Katso myös Plus, Negatiivinen.
Posteriorijakauma (engl. Posterior distribution)
Bayesilaisessa tilastotieteessä voidaan kokeen jälkeen soveltaa Bayesin kaavaa, ja muodostaa sen avulla uusi jakauma, jossa kokeen tulokset on otettu huomioon. Tätä uuttaa jakaumaa kutsutaan posteriorijakaumaksi.
Katso myös priorijakauma.
Katso myös Jakauma, Priorijakauma.
Postulaatti (engl. Postulate)
Väittämä, jonka oletamme todeksi voidaksemme rakentaa sen pohjalta matemaattista teoriaa, mutta jonka ei tarvitse olla totta. Toisenlainen väittämä johtaisi toisenlaiseen matemaattiseen teoriaan. Esimerkiksi Euklideen aksioomat sisältävät ns. paralleelipostulaatin, jonka olettaminen todeksi johtaa euklidisen geometrian kehittämiseen, kun taas sen olettaminen epätodeksi johtaa epäeuklidisen geometrian kehittämiseen.
Katso myös Paralleeliaksiooma, Aksiooma.
Potenssi, Eksponentti (engl. Power)
Lausekkeessa $a^b$ luku $a$ on korotettu potenssiin $b$. Lukua $b$ sanotaan tässä yhteydessä myös eksponentiksi ja lukua $a$ kantaluvuksi.
Potenssien laskusäännöt (engl. Index laws)
Potenssien laskusäännöt ovat sääntöjä, joiden mukaan potensseja voidaan yhdistää: \begin{eqnarray*} a^0 &=& 1 \\ a^{-m} &=& \frac{1}{a^m} \\ a^{1/n} &=& \sqrt[n]{a} \\ a^m \cdot a^n &=& a^{m+n} \\ \frac{a^m}{a^n} &=& a^{m-n} \\ (a^m)^n &=& a^{mn} \\ a^m\cdot b^m &=& (ab)^{m} \end{eqnarray*}
Katso myös Potenssiin korottaminen, Eksponentti.
Potenssifunktion $x^n$ derivaatta (engl. Derivative $x^n$)
Kaikilla kokonaisluvuilla $n \ge 0$ pätee $$\frac{\mathrm{d}}{\mathrm{d}x} x^n = n x^{n-1}.$$ Kaava on voimassa myös negatiivisilla kokonaisluvuilla.
Potenssiin korottaminen (engl. Raise to a power)
Jos $b$ on positiivinen kokonaisluku, luvun $a$ korottaminen potenssiin $b$ tarkoittaa sellaisen tulon muodostamista, jossa on $b$ tekijää, joista jokainen on $a$. Esimerkiksi $3^{4} = 3 \times 3 \times 3 \times 3 = 81$.
Katso myös Laskutoimitus, Korottaa toiseen, Laskea neliö jostakin, Eksponenttifunktio, Juuri, Potenssien laskusäännöt, Neliö.
Potenssin derivointisääntö (engl. Power rule)
Jos $f(x) = x^n$, missä $n$ on kokonaisluku, niin $\frac{\mathrm{d}f}{\mathrm{dx}} = n x^{n-1}$.
Katso myös Derivointisääntö, Sääntö.
Potenssisarja (engl. Power series)
Sarja muotoa \[ \mathrm{a}_0 + \mathrm{a}_1 \mathrm{x} + \mathrm{a}_2 \mathrm{x}^2 + \mathrm{a}_3 \mathrm{x}^3 + ... + \mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} + ... \] Potenssisarjojen avulla voidaan esittää monenlaisia funktioita.
Katso myös Ääretön sarja, Taylorin sarja, Maclaurinin sarja, Eulerin luvut.
Predikaatti (engl. Predicate)
Symboli, joka kuvaa jotain valittua ominaisuutta. Jos $P$ on predikaatti, ilmaus $P(x)$ tarkoittaa, että symbolin $x$ nimeämällä oliolla on predikaatin $P$ kuvaama ominaisuus.
Yllä $P$ on yksipaikkainen predikaatti. Vastaavasti voidaan määritellä useampipaikkaiset predikaatit. Jos esim. $Q$ on kaksipaikkainen predikaatti, $Q(x,y)$ tarkoittaa, että $x$ on $Q$:n tarkoittamassa relaatiossa $y$:hyn.
Logiikassa halutaan usein tehdä ero kielellisen tason ja itse asioiden tason välille. Relaatiot ovat matemaattisia olioita; asioiden ominaisuuksia ja niiden välisiä suhteita. Predikaatit puolestaan ovat relaatioiden nimiä logiikan formaalikielissä.
Prekompakti, Totalisti rajoitettu (engl. Totally bounded)
Metrinen avaruus on prekompakti, jos jokaista lukua $\epsilon \gt 0$ kohti voidaan löytää äärellinen määrä avoimia $\epsilon$-säteisiä palloja, jotka peittävät koko avaruuden. Täydellinen metrinen avaruus on prekompakti jos ja vain jos se on jonokompakti tai vain kompakti.
Katso myös Rajoitettu, Kompakti.
Priorijakauma (engl. Prior distribution)
Bayesilaisessa tilastotieteessä lähdetään liikkeelle ennakko-olettamuksiimme perustuvasta arviosta sille, mikä on tilanteessa oikea jakauma. Tätä kutsutaan priorijakaumaksi. Sen jälkeen tehdään kokeita, joiden perusteella priorijakaumaa muokataan posteriorijakaumaksi. Tässä muokkaamisessa käytetään Bayesin kaavaa.
Katso myös Jakauma, Posteriorijakauma.
Prisma, Särmiö (engl. Prism)
Särmiö on erityinen monitahokas, jonka kaksi pohjaa muodostuvat kahdesta täsmälleen samanlaisesta ja samankokoisesta kuviosta. Nämä pohjakuviot ovat yhdensuuntaiset ja ne on erotettu toisistaan suunnikkailla, jotka ovat usein suorakaiteita.
Jos särmiö leikataan osiin pohjien suuntaisesti, niin uudet pohjat ovat täsmälleen samanlaiset kuin vanhat pohjat.
Kappale, joka muodostuu kahdesta yhtenevästä pohjakuviosta, joiden vastaavat sivut ovat yhdensuuntaiset, sekä suunnikkaan muotoisista tahkoista, jotka yhdistävät pohjat toisiinsa. Jos muut tahkot ovat kohtisuorassa pohjia vastaan, särmiö on suora särmiö. Jos suoran särmiön pohjat ovat säännöllisiä monikulmioita, särmiö on säännöllinen särmiö. Kolmioprisman pohjat ovat kolmioita, neliöprisman pohjat ovat neliöitä jne.
Katso myös Särmiön akseli, Kappale, Avaruusgeometria, Suora särmiö, Kolmioprisma, Särmiön pohja, Prisman korkeusjana, Monitahokas.
Prisman korkeusjana (engl. Altitude of a prism)
Prisman pohjasta toiseen pohjaan kulkeva jana, joka on kohtisuorissa molempia pohjia vastaan.
Projektio (engl. Projection)
Kuvaus, joka kuvaa geometriset oliot tasolle. Usein kuvaus, joka "litistää" jokaisen avaruuden pisteen annetulle tasolle kohtisuorassa suunnassa tasoa vastaan.
Katso myös Lineaarimuunnos, Lineaarikuvaus.
Prosentti (engl. Percent)
Prosentti tarkoittaa samaa kuin sadasosa. Prosentin merkki on %. Esimerkiksi 24 % on 24 sadasosaa eli 24/100 ja 7 % = 7/100.
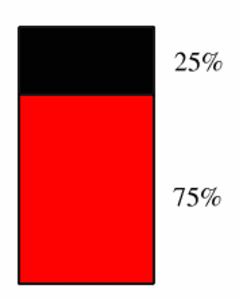
Katso myös Algebra, Reaaliluku.
Prosenttiosuus (engl. Percentage)
Suuretta kuten 25 prosenttia tai 33 % kutsutaan prosenttiosuudeksi. Se on tapa ilmaista murto-osa sadasosien lukumääränä, esimerkiksi 25 prosenttia merkitsee $\frac{25}{100}$.
Pseudoalkuluku, Fermat'n pseudoalkuluku (engl. Fermat pseudoprime, Pseudoprime)
$p$ on pseudoalkuluku kantaluvun $n$ suhteen, mikäli $p$ jakaa luvun $n^{p-1}-1$, mutta $p$ ei ole alkuluku. Esimerkiksi, $341$ jakaa luvun $2^{340}-1$, joten $341$ on pseudoalkuluku kantaluvun $2$ suhteen.
Katso myös Alkuluku, Yhdistetty luku, Carmichaelin luku, Fermat.
Punta (engl. Pound)
Ison-Britannian rahayksikkö. Vuonna 2003 yksi pint maitoa tai keksipaketti saattaisi maksaa yhden punnan. Yksi punta on sata penceä.
Puolikkaan kulman kaava (engl. Half angle formula)
Kaava, joka ilmaisee trigonometrisen funktion, jonka argumenttina on $x/2$, sellaisten trigonometristen funktioiden avulla, joiden argumenttina on $x$.
Katso myös Trigonometrinen identiteetti, $\cos(x/2)$, $\sin(x/2)$, $\tan(x/2)$.
Puolipallo (engl. Hemisphere)
Puolikas pallosta.
Puolipallolla on yksi kaareva tahko, yksi tasossa sijaitseva ympyränmuotoinen tahko ja yksi ympyränmuotoinen särmä.

Katso myös Puolipallon tilavuus, Puolipallon pinta-ala, Pallo, Päiväntasaaja, Ekvaattori.
Puolipallon massakeskipiste (engl. Centre of mass of a hemisphere)
Puolipallon, jonka säde on $r$, massakeskipiste on puolipallon symmetria-akselilla etäisyydellä $\frac{3}{8}r$ puolipallon keskipisteestä.
Katso myös Pyörähdyskappaleen massakeskipiste, Massakeskipiste, Painopiste.
Puolipallon pinta-ala (engl. Area of a hemisphere)
Puolipallon, jonka säde on $r$, pinta-ala on $3 \pi r^2$. Tästä kaarevan osan osuus on $2 \pi r^2$.
Katso myös Puolipallo.
Puolipallon tilavuus (engl. Volume of a hemisphere)
Puolipallon, jonka säde on $r$, tilavuus on $\frac{2}{3} \pi r^{3}$.
Katso myös Puolipallo.
Puolipallonkuoren massakeskipiste (engl. Centre of mass of a hemispherical shell)
$r$-säteisen puolipallonkuoren massakeskipiste sijaitsee puolipallon symmetria-akselilla etäisyydellä $r/2$ puolipallon keskipisteestä.
Katso myös Massakeskipiste, Painopiste.
Puolisuora, Säde, Puolisäde (engl. Half line, Ray)
Janalla on kaksi päätepistettä, kun taas suora jatkuu kahteen suuntaan äärettömiin.
Puolisuora on suoran ja janan tapainen geometrinen olio, jolla on yksi päätepiste ja joka jatkuu toiseen suuntaan äärettömiin.
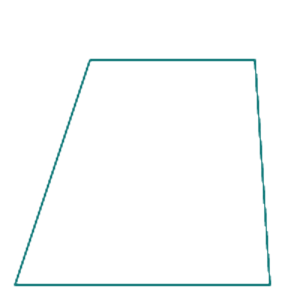
Puolisuunnikas (engl. Trapezium or trapezoid, Trapezium, Trapezoid)
Nelikulmio, jossa on kaksi keskenään yhdensuuntaista sivua. Jos kaksi muuta, erisuuntaista sivua ovat yhtä pitkät, kuvio on joko tasakylkinen puolisuunnikas tai suunnikas.
Katso myös Tasakylkinen puolisuunnikas, Suunnikas, Neljäkäs, Nelikulmio.
Puolisäde, Puolisuora, Säde (engl. Half line, Ray)
Janalla on kaksi päätepistettä, kun taas suora jatkuu kahteen suuntaan äärettömiin.
Puolisuora on suoran ja janan tapainen geometrinen olio, jolla on yksi päätepiste ja joka jatkuu toiseen suuntaan äärettömiin.
Puolittaa (engl. Bisect)
Jos puolitat jotakin, niin jaat sen kahteen yhtä suureen osaan. Puolittaja voi olla piste, suora tai taso, joka jakaa jonkin kahteen yhtä suureen osaan.
Katso myös Konstruktio, Konstruointi.
Puolittaa (engl. Halve)
Puolittaja (engl. Bisector)
Puolittaa jotakin tarkoittaa jakaa se kahteen yhtä suureen osaan. Kulman puolittaja on suora, joka puolittaa annetun kulman.
Katso myös Kulman puolittaja, Keskinormaali, Suora.
Puoliympyrä (engl. Semicircle)
Ympyrän puolikas. Se on ympyrän halkaisijan ja sen päätepisteet yhdistävän kaaren rajoittama ympyrän osa.

Katso myös Puoliympyrän sisältämä kulma, Kaari, Arc, Ympyrä, Segmentti, Sektori, Halkaisija, Kuvio.
Puoliympyrän kaaren massakeskipiste (engl. Centre of mass of a semicircular arc)
Puoliympyrän kaaren massakeskipiste sijaitsee kaaren symmetria-akselilla ja sen etäisyys ympyrän keskipisteestä on $\frac{2r}{\pi}$, jossa $r$ on ympyrän säde.
Katso myös Ympyränkaaren massakeskipiste.
Puoliympyrän massakeskipiste (engl. Centre of mass of a semicircular lamina)
Puoliympyrän massakeskipiste sijaitsee alueen symmetria-akselilla ja sen etäisyys ympyrän keskipisteestä on $\frac{4r}{3\pi}$, jossa $r$ on ympyrän säde.
Katso myös Ympyrän sektorin massakeskipiste, Tasoalueen massakeskipiste.
Puoliympyrän sisältämä kulma (engl. Angle in a semicircle, Thales theorem)
Kulma, jonka kärki on ympyrän kehällä ja jonka kyljet kulkevat ympyrän halkaisijan päätepisteiden kautta, on suora kulma.
Katso myös Suora kulma, Lause, Puoliympyrä.
Puolueellinen, Epäreilu, Harhainen (engl. Unfair)
Nopan sanotaan olevan epäreilu, jos jokaisen silmäluvun saaminen ei ole yhtä todennäköistä.
Jos monen nopanheiton jälkeen on paljon kolmosia ja viitosia, mutta vähän muita silmälukuja, on syytä epäillä, että noppa ei ole symmetrinen vaan epäreilu ja harhainen.
Ei reilu; harhainen. Mahdolliset alkeistapaukset eivät ole yhtä todennäköisiä.
Puu (engl. Tree)
Yhtenäinen verkko, jossa ei ole suljettuja silmukoita.
Katso myös Virittävä puu, Yhtenäinen verkko, Verkko.
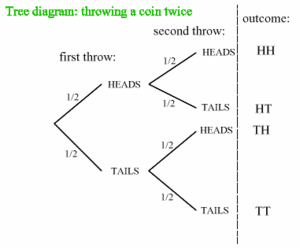
Puukaavio (engl. Tree diagram)
Diagrammityyppi, jota käytetään todennäköisyyslaskennassa. Sitä käytetään esittämään erilaisia lopputuloksia, joita voi sattua tapahtumajonon tuloksena. Se on puun muotoinen ja haarautuu joka kerran, kun on olemassa enemmän kuin yksi mahdollinen tapahtuma, joka voi sattua.
Katso myös Verkkoteoria, Verkko.
pyj (engl. lcd)
Lyhenne ilmaisulle "pienin yhteinen jaettava".
Katso myös Pienin yhteinen nimittäjä.
Pylväsdiagramma (engl. Bar chart, Bar graph)
Pylväsdiagramma on graafinen esitystapa, jota käytetään erityisesti kuvattaessa luokittelu- tai järjestysasteikolla mitatun muuttujan frekvenssijakaumaa. Pylväsdiagrammassa luokiteltu aineisto kuvataan toisistaan erillään olevilla pylväillä, joiden pituus (myös pinta-ala, sillä pylväät ovat yhtä leveitä) on verrannollinen luokan frekvenssiin (havaintojen lukumäärään). Pylväät voivat olla joko pysty- tai vaakasuorassa.
Pyramidi (engl. Pyramid)
Kappale, jonka pohja on monikulmio ja muut tahkot kolmioita, joilla on yhteinen kärki (jota kutsutaan huipuksi). Suora pyramidi on pyramidi, jonka pohja on säännöllinen monikulmio ja jonka huippu on kohtisuoraan pohjan keskipisteen yläpuolella.
Katso myös Suora pyramidi, Avaruusgeometria, Neliöpohjainen pyramidi, Pyramidin akseli, Tetraedri, Kartio, Pyramidin pohja, Pyramidin korkeusjana, Monitahokas.
Pyramidin akseli (engl. Axis of a pyramid)
Suora, joka kulkee pyramidin kärjen ja kannan keskipisteen kautta, on pyramidin akseli.
Katso myös Suora pyramidi, Pyramidi, Pyramidin pohja, Akseli.
Pyramidin korkeusjana (engl. Altitude of a pyramid)
Kohtisuoraan pyramidin pohjasta sen kärkeen kulkeva jana.
Katso myös Kartion kärki, Pyramidi.
Pyramidin massakeskipiste (engl. Centre of mass of a pyramid)
Pyramidin massakeskipiste sijaitsee pohjan keskipisteen sekä kärjen välisellä janalla ja jakaa sen suhteessa $1:3$.
Katso myös Kartion massakeskipiste, Massakeskipiste, Painopiste.
Pyramidin pinta-ala (engl. Area of a pyramid)
Pyramidin, jonka kanta on säännöllinen $n$-sivuinen monikulmio ja jonka kärki on suoraan kannan keskipisteen yläpuolella, kokonaispinta-ala on $nA+B$, missä $A$ on yhden kaltevan tahkon pinta-ala ja $B$ kannan pinta-ala.
Säännöllisen $n$-kulmion pinta-ala on $$ \frac{1}{4} x^2 n \tan (90 - \frac{180}{n} ) , $$ missä $x$ on yhden särmän pituus, joten tämä on kannan pinta-ala.
Pyramidin tahkon korkeus on $$ f = \sqrt{h^2 + \frac{1}{4} x^2 \tan ^2 (90 - \frac{180}{n} ) } , $$ missä $h$ on pyramidin korkeus.
Siten jokaisen tahkon pinta-ala on $xf/2$ (puoli kertaa kanta kertaa tahkon korkeus).
Yhdistämällä nämä tiedot saadaan pyramidin kokonaispinta-alaksi \[ \frac{n}{2}x \sqrt{h^2 + \frac{1}{4} x^2 \tan ^2 \theta } + \frac{1}{4} x^2 n \tan \theta , \] missä $ \theta = 90 - \frac{180}{n}. $
Pyramidin pohja (engl. Base of a pyramid)
Pyramidin pohja on pyramidin tahkoista se, joka ei ole kolmion muotoinen. (Jos pyramidin kaikki tahkot ovat kolmioita, mikä tahansa niistä voi olla pohja.) Usein pyramidi nimetään sen pohjan kuvion mukaan. Esimerkiksi neliöpohjainen pyramidi on pyramidi, jonka pohja on neliö.
Katso myös Suora pyramidi, Pyramidin akseli, Pyramidi.
Pystysuora (engl. Vertical)
Maanpintaa vastaan kohtisuora; $xy$-tasossa $y$-akselin suuntainen.
Katso myös Vino, Kursiivi (kirjoitus), Vaakasuora.
Pystyvektori (engl. Column vector)
Vektori, jonka koordinaatit on kirjoitettu sulkujen sisään allekkain sarakkeeksi, esimerkiksi \[ \left( \begin{array}{l} 5 \\ 1 \\ 7 \end{array} \right). \]
Katso myös Vektori, Vaakavektori.
Pythagoraan lause (engl. Pythagorean theorem, Pythagoras' theorem)
Lause, joka on nimetty vuosina 585-500 eKr. eläneen kreikkalaisen matemaatikon Pythagoraan mukaan. Pythagoraan oletettavasti keksimä lause koskee suorakulmaisen kolmion sivuja, ja sen mukaan "hypotenuusa sivuna piirretyn neliön pinta-ala on yhtä suuri kuin kateetit sivuina piirrettyjen neliöiden pinta-alojen summa". Lauseelle on esitetty aikojen kuluessa yli 350 erilaista todistusta.
Katso myös Lause, Kolmio, Suorakulmainen kolmio.
Pyöristys (engl. Round, Rounding off)
Pyöristys on menettely, jossa luku kirjoitetaan lähimmäksi kokonaisluvuksi tai lähimmäksi desimaaliluvuksi, jossa on annettu määrä desimaaleja tai lähimmäksi täydeksi kymmeen-, sata-, tuhat- jne luvuksi. Pyöristämisestä on hyötyä arvioitaessa laskujen vastauksia.
Se, pyöristetäänkö ylöspäin vai alaspäin, riippuu ensimmäisestä desimaalista, joka EI ole mukana pyöristetyssä luvussa. Jos tämä desimaali on 5 tai sitä suurempi, pyöristetään ylöspäin, jos se on 4 tai sitä pienempi, pyöristetään alaspäin. Esimerkiksi
1,845 1,9 2
18,45 18 20
184,5 185 200
1845 1800 2000.
Katso myös Estimaatti.
Pyörähdys, Kierros (engl. Revolution)
Täysi kierros, joka päättyy samaan suuntaan mistä alkoi. Yksi pyörähdys on 360 astetta.
Katso myös Pyörähdyskappale, Kierto, Pyörähdyskappaleen pinnan pinta-ala, Pyörähdyskappaleen pinta-ala.
Pyörähdysakseli, Kiertosymmetrian akseli (engl. Axis of rotational symmetry)
Suora, joka pysyy paikallaan kierrossa.
Katso myös Kiertosymmetria, Pyörähdyssymmetria, Suora, Akseli.
Pyörähdysellipsoidi (engl. Ellipsoid of revolution)
Kolmiulotteinen kappale, joka saadaan ellipsin pyörähtäessä jonkin akselinsa ympäri. Pyörähdysellipsoidi on se ellipsoidin erikoistapaus, jossa kaikki pyörähdysakselin kanssa kohtisuorat leikkaukset ovat ympyröitä.
Katso myös Pyörähdyskappale, Ellipsoidi.
Pyörähdyskappale (engl. Solid of revolution)
Kappale, joka saadaan kiertämällä kaksiulotteista käyrää 360 astetta akselin ympäri. Kiertyessään käyrä muodostaa pinnan, jonka sisäpuolelle jää pyörähdyskappale.
Katso myös Pyörähdyskappaleen tilavuus, Kappale, Pyörähdyspinta, Pyörähdys, Kierros, Pyörähdyskappaleen pinnan pinta-ala, Pyörähdyskappaleen pinta-ala, Pyörähdyskappaleen massakeskipiste, Pyörähdysellipsoidi.
Pyörähdyskappaleen massakeskipiste (engl. Centre of mass of a solid of revolution)
Pyörähdyskappaleen, joka saadaan $x$-akselin, suorien $x=a$ ja $x=b$ sekä funktion $y=f(x)$ kuvaajan rajoittaman alueen pyörähtäessä $x$-akselin ympäri $360^{\circ}$, massakeskipiste on $(\overline{x}, 0)$, missä \[\overline{x} = \frac{\int_{a}^{b} \pi xy^{2} dx}{\int_{a}^{b} \pi y^{2} dx}.\]
Pyörähdyskappaleen, joka saadaan $y$-akselin, suorien $y=p$ ja $y=q$ sekä funktion $x=g(y)$ kuvaajan rajoittaman alueen pyörähtäessä $y$-akselin ympäri $360^{\circ}$, massakeskipiste on $(0, \overline{y})$, missä \[\overline{y} = \frac{\int_{p}^{q} \pi x^{2}y dy}{\int_{p}^{q} \pi x^{2} dy}.\]Katso myös Pyörähdyskappale, Puolipallon massakeskipiste, Kartion massakeskipiste, Massakeskipiste, Painopiste.
Pyörähdyskappaleen pinnan pinta-ala, Pyörähdyskappaleen pinta-ala (engl. Area of revolution, Area of a surface of revolution)
Jos käyrä $y=f(x), x \in [a,b]$ pyörähtää $360^{\circ}$ $x$-akselin ympäri, niin muodostuvan pyörähdyskappaleen pinta-ala on \[ 2 \pi \int _a ^b y \sqrt { \left ( \left ( \frac{dx}{dt} \right ) ^2 + \left ( \frac{dy}{dt} \right ) ^2 \right ) } dt . \]
Jos käyrä $x=g(y), y \in [p,q]$ pyörähtää $360^{\circ}$ $y$-akselin ympäri, niin muodostuvan pyörähdyskappaleen pinta-ala on \[ 2 \pi \int _p ^q x \sqrt { \left ( \left ( \frac{dx}{dt} \right ) ^2 + \left ( \frac{dy}{dt} \right ) ^2 \right ) } dt . \]
Katso myös Pyörähdyskappale, Pyörähdys, Kierros.
Pyörähdyskappaleen pinta-ala, Pyörähdyskappaleen pinnan pinta-ala (engl. Area of revolution, Area of a surface of revolution)
Jos käyrä $y=f(x), x \in [a,b]$ pyörähtää $360^{\circ}$ $x$-akselin ympäri, niin muodostuvan pyörähdyskappaleen pinta-ala on \[ 2 \pi \int _a ^b y \sqrt { \left ( \left ( \frac{dx}{dt} \right ) ^2 + \left ( \frac{dy}{dt} \right ) ^2 \right ) } dt . \]
Jos käyrä $x=g(y), y \in [p,q]$ pyörähtää $360^{\circ}$ $y$-akselin ympäri, niin muodostuvan pyörähdyskappaleen pinta-ala on \[ 2 \pi \int _p ^q x \sqrt { \left ( \left ( \frac{dx}{dt} \right ) ^2 + \left ( \frac{dy}{dt} \right ) ^2 \right ) } dt . \]
Katso myös Pyörähdyskappale, Pyörähdys, Kierros.
Pyörähdyskappaleen tilavuus (engl. Volume of revolution)
Pyörähdyskappaleen, joka saadaan $x$-akselin, suorien $x=a$ ja $x=b$ sekä funktion $y=f(x)$ kuvaajan rajoittaman alueen pyörähtäessä $x$-akselin ympäri $360^{\circ}$, tilavuus on \[\int_{a}^{b} \pi y^{2} dx.\]
Pyörähdyskappaleen, joka saadaan $y$-akselin, suorien $y=p$ ja $y=q$ sekä funktion $x=g(y)$ kuvaajan rajoittaman alueen pyörähtäessä $y$-akselin ympäri $360^{\circ}$, tilavuus on \[\int_{p}^{q} \pi x^{2} dy.\]
Katso myös Tilavuus, Pyörähdyskappale, Integraali.
Pyörähdyspinta (engl. Surface of revolution)
Sellaista pintaa, joka saadaan kiertämällä jotakin käyrää akselin ympäri 360 astetta, kutsutaan pyörähdyspinnaksi.
Katso myös Pyörähdyskappale, Katenoidi, Yksivaippainen hyperboloidi.
Pyörähdyssymmetria, Kiertosymmetria (engl. Rotational symmetry, Rotation symmetry)
Kierrettäessä tasasivuista kolmiota sen keskipisteen ympäri se voidaan asettaa omille ääriviivoilleen kolme kertaa täyden kierroksen aikana, joten sen kiertosymmetrian asteen sanotaan olevan kolme.
Jos kuviota kierrettäessä se sopii omille ääriviivoilleen useammin kuin kerran täyden kierroksen aikana, niin kuviolla on kiertosymmetriaa.
Katso myös Symmetriakeskus, Kiertosymmetrian kertaluku, Symmetria, Kierto, Kiertosymmetrian akseli, Pyörähdysakseli.
Päiväntasaaja, Ekvaattori (engl. Equator)
Päiväntasaaja on Maapallon keskellä molemmista Navoista yhtä kaukana kulkeva ympyräviiva. Päiväntasaaja jakaa Maapallon pohjoiseen ja eteläiseen pallonpuoliskoon (eli puolipalloon).
Geometriassa ekvaattori on se pyörähdyspinnan akselia vastaan kohtisuora ympyrä, joka jakaa pinnan kahteen yhtenevään osaan.
Katso myös Puolipallo.
Pääideaalialue (engl. Principal ideal domain)
Olkoon $R$ vaihdannainen rengas. Ideaali $I \subset R$ on pääideaali, jos olemassa sellainen $a\in I$, että $I$ voidaan esittää muodossa $I=\{ma \mid m \in R\}$.
Alkio $0 \neq a \in R$ on nollanjakaja, jos $ab=0$ jollain $0 \neq b \in R$.
Vaihdannainen rengas $R$ on pääideaalialue, jos siinä ei ole nollanjakajia, ja sen jokainen ideaali on pääideaali.
Jokainen kunta on pääideaalialue. Kunnan ainoat ideaalit ovat $\{0\}$ ja koko kunta.
Kokonaislukujen rengas on pääideaalialue.
Katso myös Ideaali, Ihanne, Yksikäsitteisen tekijöihinjaon alue, UFD, Gaussin kokonaisluvut, Gaussin luvut.
Päälävistäjä (engl. Leading diagonal)
Matriisin se lävistäjä, joka alkaa matriisin vasemmassa ylänurkassa olevasta alkiosta. Yleensä matriisin päälävistäjästä puhuttaessa on kyseessä oleva matriisi neliömatriisi. Tällöin päälävistäjä päättyy matriisin oikeassa alanurkassa olevaan alkioon.
Katso myös Jälki, Kolmiomatriisi, Lävistäjämatriisi, Yläkolmiomatriisi, Nauhamatriisi, Vinosymmetrinen matriisi.
Pääpolynomi (engl. Monic)
Polynomi on pääpolynomi, jos sen korkeimman asteen kerroin on ykkönen.
$x^3 + 2x^2 + 3x + 4$ on pääpolynomi.
$2x^3 + 3x^2 + 4x + 5$ ei ole pääpolynomi.
Päässä laskeminen (engl. Mental arithmetic)
Laskujen tekeminen päässä laskimella tai paperilla laskemisen asemesta.
Päätellä (engl. Deduce)
Tehdä päättely eli päätyä oletuksista johtopäätökseen loogisin päättelyaskelin. Matematiikassa tällaisia päättelyjä kutsutaan todistuksiksi. Matematiikan ulkopuolella teemme usein johtopäätöksiä löysemmin perustein. Esimerkiksi siitä, että kaikki tähän mennessä havaitut korpit ovat mustia, saatamme päätellä, että kaikki korpit ovat mustia.
Katso myös Perustelu.
Päätelmä (engl. Inference)
Jonkin asian loogisten seurauksien toteaminen.
Katso myös Perustelu.
Päätepiste (engl. End point)
Piste, johon jana tai käyrä päättyy.
Katso myös Piste.
Päättyvä desimaaliluku (engl. Terminating decimal)
Desimaalimurtoluku, jolla on loppu; numeroiden jono desimaalipilkun jälkeen ei jatku äärettömiin. Esimerkiksi 0,1, 0,563472, 0,667.
Kaikki päättyvät desimaaliluvut ovat rationaalilukuja, mutta jokaisen rationaaliluvun desimaalilukuesitys ei ole päättyvä. Esimerkiksi 1/3 on rationaalinen, mutta sen desimaaliesityksessä on äärettömän monta desimaalia.Katso myös Rationaaliluku, Kymmenmurtoluku.
Päätösongelma (engl. Decision problem)
Ongelma, johon vastataan aina joko kyllä tai ei.
Päätöspuu (engl. Decision tree)
Tapa esittää jossakin tilanteessa ajallisesti toisiaan seuraavat mahdolliset asiat (esimerkiksi eri päätösvaihtoehdot) piirtämällä puu, jossa on oksa jokaista mahdollisuutta kohti.
Katso myös Kombinatoriikka, Verkko.