$k$
Kirjainta $\overrightarrow{k}$ käytetään merkitsemään $z$-akselin suuntaista yksikkövektoria, $\overrightarrow{k}=(0,\,0,\,1)$.
Se voi myös merkitä kappaleen jäykkyyttä.
Pieni kirjain k on myös kilon lyhenne ja tarkoittaa tuhatta, esimerkiksi 1 g tarkoittaa yhtä grammaa ja 1 kg yhtä kilogrammaa eli 1000 grammaa.
Kaaren pituus (engl. Arc length)
Etäisyys käyrää pitkin mitattuna. $xy$-tasossa olevan kaaren pituus voidaan määrittää esimerkiksi integroimalla $\sqrt{dx^{2}+dy^{2}}$ käyrää pitkin.
Katso myös Käyrä, Polun pituus, Polaarikoordinaateissa määritellyn kaaren pituus.
Kaarevuus (engl. Curvature)
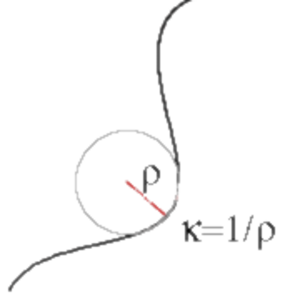
Mitta sille, kuinka kaareutunut käyrä on annetussa pisteessä. Kaarevuudelle käytetään symbolia $\kappa$.
Jos käyrän ajatellaan koostuvan lukuisista infinitesimaalisista eri säteisten ja keskipisteisten ympyröiden kaarista, niin silloin käyrän kaarevuus annetussa pisteessä on kyseisessä pisteessä olevan ympyränkaaren säteen käänteisluku. Jos ympyränkaaren säde kyseisessä pisteessä on $\rho$, on $\kappa = \frac{1}{\rho}$.
Karteesisessa koordinaatistossa $xy$-tason käyrän $y = f(x)$ kaarevuus missä tahansa pisteessä lasketaan kaavalla \[ \kappa = \frac{\frac{d^2 x}{dx^2}} {\left( 1 + \left( \frac{dy}{dx} \right)^2 \right)^{3/2}}. \]
Katso myös Kaarevuuskeskipiste, Ominaisuus, jonka arvot ovat jatkuvia.
Kaarevuuskeskipiste (engl. Center of curvature, Centre of curvature)
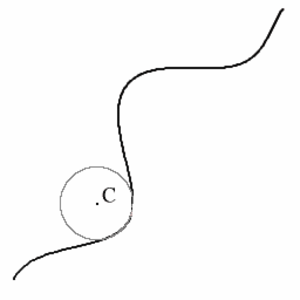
Käyrän kaarevuuspiste jossain pisteessä on kyseiseen pisteeseen piirretyn oskuloivan ympyrän keskipiste.
Käyrän kaarevuuskeskipiste pisteessä $r$ saadaan kaavalla $c= r + \rho \hat{n}$, missä $\rho$ on kaarevuussäde pisteessä $r$ ja $\hat{n}$ on yhden yksikön pituinen käyrän normaalivektori pisteessä $r$.
Katso myös Keskipiste, Käyrä, Kaarevuus.
Kaarevuussäde (engl. Radius of curvature)
Käyrän kaarevuussäde jossain pisteessä on kyseiseen pisteeseen piiretyn oskuloivan ympyrän säde. Sitä merkitään symbolilla $\rho$.
Katso myös Roo, Säde, Oskuloiva ympyrä.
Kaari, Arc (engl. Arc, Arc of a curve)
Mikä tahansa yhtenäinen osa käyrää viivaa; erityisesti ympyrän kehän yhtenäinen osa.

Katso myös Ympyrä, Puoliympyrä, Käyrä, Jänne, Sekantti, Konsyklinen.
Kaarisulkeet (engl. Brackets)
Merkkejä ( ja ) käytetään osoittamaan, että tietty osa lauseketta on määritettävä ennen kuin yhdistetään se muuhun lausekkeeseen. Esimerkiksi $a(b+c)$ tarkoittaa, että on laskettava ensin $b+c$ ja kerrottava summa sitten luvulla $a$.
Katso myös Aaltosulkeet, Merkintätapa, Notaatio, Kahden neliön erotus.
Kaava (engl. Formula, Formulae)
Joidenkin lausekkeiden yhtäsuuruutena ilmaistu sääntö. Esimerkiksi kolmion alan kaava on $A=\frac{1}{2}ah$, missä $A$ on ala, $a$ kolmion kanta ja $h$ kolmion korkeus. Suorakulmaisen särmiön tilavuuden kaava on $V=abc$, missä $V$ on tilavuus, $a$ särmiön pituus, $b$ sen leveys ja $c$ sen korkeus.
Katso myös Suoraan verrannollisuus, Piin arvon laskeminen, Hornin lauseke, Cauchyn integraalikaava, Suuntakosinikaava, Yhtälö, Kartion yhtälö.
Kaavio (engl. Chart)
'Kaavio' on yleinen sana erilaisille kuville ja diagrammeille, joita käytetään aineiston, yleensä frekvenssiaineiston, esittämiseen.
Katso myös Pylväsdiagramma, Piirakkadiagramma, Laatikko ja viikset -kuvio.
Kaavio, Diagramma (engl. Diagram)
Yleisnimitys tilastoaineiston graafiselle esitykselle. Diagrammoja ovat esimerkiksi laatikkodiagramma, pylväsdiagramma, histogramma ja korrelaatiodiagramma. Diagrammojen avulla tutkija oppii paremmin ymmärtämään aineistonsa ja diagrammojen avulla tutkija esittää aineistoon liittyvät päätelmänsä lukijoilleen.
Katso myös Pylväsdiagramma.
Kahdeksan, 8 (engl. 8, Eight)
Kahdeksan on pienin lukua yksi suurempi kuutioluku.
Kahdeksan on ainoa kuutioluku $n^{3}$, jolle $n^{3} + 1$ on neliöluku. Luvut $8$ ja $9$ ovat lukujen $2$ ja $3$ lisäksi ainoat alkulukujen potenssit, joiden erotus on $1$.
Kahdeksan on kuudes Fibonaccin luku ja ykkösen lisäksi ainoa Fibonaccin luku, joka on kuutio.
Kahdeksan on kuution kärkien ja oktaedrin sivutahkojen lukumäärä. Se on myös kuperien deltaedrien lukumäärä.
$\phi(8) = 4$, $d(8) = 4$, $\sigma(8) = 15$.

Katso myös Kahdeksankulmio, Oktaedri, Fibonaccin luku.
Kahdeksankulmio (engl. Octagon)
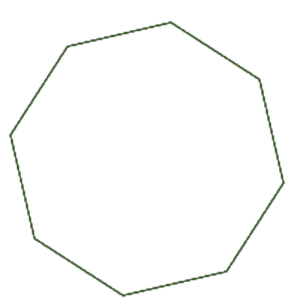
Monikulmio, jossa on kahdeksan sivua ja kahdeksan kulmaa. Säännöllisessä kahdeksankulmiossa on kahdeksan yhtä pitkää sivua ja kahdeksan yhtä suurta kulmaa.
Katso myös Kahdeksan, 8, Monikulmio.
Kahdeksantoista, 18 (engl. 18, Eighteen)
18 on kolmas seitsemänkulmioluku.
$\phi(18) = 6$, $d(18) = 6$, $\sigma(18) = 39$.

Kahden kokonaislukumuuttujan neliömuoto (engl. Binary quadratic form over Z)
Funktio $f : \mathbf{Z}^{2} \to \mathbf{Z}$, joka on muotoa $f(x,y) = ax^{2}+bxy+cy^2$ joillakin kokonaisluvuilla $a$, $b$ ja $c$. Neliömuodon $f$ diskriminantti määritellään lukuna $\Delta(f) = b^{2}-4ac$. Jos $f$ on positiivisesti definiitti eli $f(x,y) \gt 0$ kaikilla $(x,\,y) \in \mathbf{Z}^{2} \setminus {(0,0)}$, niin $\Delta(f) \lt 0$, ja jos $a,\, c \gt 0$ sekä $\Delta(f) \lt 0$, niin $f$ on positiivisesti definiitti. Samoin $f$ on negatiivisesti definiitti jos ja vain jos $a, c \lt 0$ sekä $\Delta(f) \lt 0$.
Kahden neliön erotus (engl. Difference of two squares)
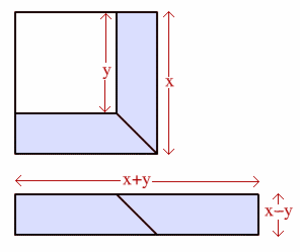
Kertomalla sulut auki lausekkeesta $(x+y)(x-y)$ saadaan $(x+y)(x-y) = x^{2}-xy+yx-y^{2}$. Toisaalta $x^{2}-xy+yx-y^{2} = x^{2}-y^{2}$. Siten $x^{2}-y^{2} = (x+y)(x-y)$. Tämä tulos on usein hyödyllinen, koska sen avulla voidaan yksinkertaistaa laskuja.
Lauseketta $x^{2}-y^{2}$ kutsutaan kahden neliön erotukseksi. Esimerkiksi $6^{2}-5^{2} = (6+5)(6-5) = 11 \cdot 1 = 11$ ja $17^{2}-15^{2} = (17+15)(17-15) = 32 \cdot 2 = 64$.
Katso myös Kaarisulkeet, Lause, Neliöluku, Jakaa tekijöihin.
Kahden pisteen välinen jana (engl. Line between two points)
Annetut pisteet $(x_{1},y_{1})$ ja $(x_{2},y_{2})$ yhdistävän janan kulmakerroin on \[m = \frac{ y_{2}-y_{1} }{ x_{2}-x_{1} },\] pituus on \[ \sqrt{(x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}}, \] yhtälö on \[ y-y_{1} = \frac{ y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_1) \] ja keskipiste on \[( \frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2} ). \]
Katso myös Suora.
Kahden tason leikkaus (engl. Intersection of two planes)
Kahden tason leikkaus on suora, jos tasot eivät ole yhdensuuntaisia.
Jos tasojen yhtälöt ovat $z=mx+ny+c$ ja $z=px+qy+d$, niin niiden leikkauksen muodostavan suoran yhtälöpari on $z=mx+ny+c$, $z=px+qy+d$. Suoralle kuuluvat siis ne pisteet, jotka toteuttavat molemmat yhtälöt. Erityisesti yhtälö $(n-q)y=(p-m)x+d-c$ ei kuvaa suoraa vaan tasoa, joka on yhdensuuntainen $z$-akselin kanssa ja sisältää tutkimamme leikkaussuoran.
Katso myös Yhtälöryhmä, Leikkaus, Suoran yhtälö, Tason yhtälö.
Kahden tason välinen kulma (engl. Dihedral angle)
Olkoot $P$ ja $Q$ tasoja, joiden leikkaus on suora $L$. Piirretään tasoon $P$ suoraa $L$ vastaan kohtisuorassa oleva suora $a$ ja piirretään tasoon $Q$ suoraa $L$ vastaan kohtisuorassa oleva suora $b$. Tasojen $P$ ja $Q$ välinen kulma on suorien $a$ ja $b$ välinen kulma.
Katso myös Kulma, Taso, Kohtisuora.
Kaikilla, Jokaisella (engl. For each, For all, For every)
Merkki $\forall$ tarkoittaa, että jokin on totta kaikilla tietyn muuttujan arvoilla.
Esimerkiksi $\forall x (x^{2} \ge 0)$ tarkoittaa, että kaikilla muuttujan $x$ arvoilla lausekkeen $x^{2}$ arvo on suurempi tai yhtä suuri kuin nolla.
Katso myös Muuttuja, On olemassa, Jollakin.
Kaksikymmenluku (engl. Twenties)
Vuodet 1920--29.
Kaksikymmentä, 20, Tiu (engl. 20, Twenty)
20 kappaletta on kansanomaisesti tiu.
20 on neljäs tetraedriluku.
Ikosaedrin sivutahkojen ja säännöllisen dodekaedrin kärkien lukumäärä.
20 on puolitäydellinen luku.
$\phi(20) = 8, \quad d(20) = 6, \quad \sigma(20) = 42$.

Katso myös Kymmenen monikerta, Tetraedriluku.
Kaksinkertaisen kulman kaava (engl. Double angle formula)
Trigonometrinen identiteetti, joka ilmaisee kulman $2A$ trigonometrisen funktion kulman $A$ trigonometristen funktioiden avulla. Esimerkiksi $\sin(2A) = 2\sin(A)\cos(A)$. Tällaiset identiteetit saadaan trigonometristen funktioiden summakaavojen erikoistapauksina.
Katso myös Trigonometrinen identiteetti, $\sin(2x)$, $\cos(2x)$, $\tan(2x)$, $\cot(2x)$, Summakaava.
Kaksinkertaistaa (engl. Double)
Kun jotakin kaksinkertaistetaan tai jokin kaksinkertaistuu, siitä tulee kaksi kertaa niin suuri kuin se oli alun perin. Kaksinkertaistaminen on sama kuin kahdella kertominen.
Katso myös Kertolasku.
Kaksipaikkainen kuvaus, Binäärinen kuvaus (engl. Binary operation)
Funktio, joka kuvaa annetun joukon alkioparin saman joukon alkioksi. Esimerkiksi yhteenlasku ja kertolasku ovat binäärisiä kuvauksia.
Luonnollisten lukujen vähennyslasku ei ole binäärinen kuvaus, koska kahden luonnollisen luvun erotus ei välttämättä ole luonnollinen luku. Esimerkiksi $1-2 = -1$ ei ole luonnollinen luku.
Katso myös Yhteenlasku, Modulo, Kertolasku, Laskutoimitus, Neutraalialkio, Jakolasku, Vaihdannainen, Kommutatiivinen, Vähennyslasku, Vähentäminen, Rengas, Antikommutaattori, Groupoidi, Jakaminen.
Kaksitoista, 12, Tusina (engl. 12, Twelve, a dozen)
Lukumäärän 12 ilmaisin on kansanomaisesti tusina. 12 on pienin kokonaisluku, joka voidaan kirjoittaa kahdella eri tavalla aitojen tekijöidensä tuloksi: 12 = 3 x 4 = 2 x 6.
12 on pienin runsas luku ja siten myös pienin ylirunsas luku.
12 on kuution ja säännöllisen oktaedrin särmien, dodekaedrin sivutahkojen ja säännöllisen ikosaedrin kärkien lukumäärä.
12 on kolmas viisikulmioluku.
?(12) = 4, d(12) = 6, ?(12)=28.

Kaksiulotteinen (engl. Two dimensional)
Tasolla tapahtuva.
Katso myös Taso.
Kaksiulotteinen (engl. Bivariate)
Kaksi toisistaan riippumatonta muuttujaa sisältävää oliota kutsutaan kaksiulotteiseksi.
Katso myös Muuttuja.
Kaksoisintegraali (engl. Double integral)
Kahden muuttujan funktio voidaan joissakin tapauksissa integroida molempien muuttujien suhteen. Esimerkiksi \[ \int\int (x + x y + y^2) dy dx = \int (x y + \frac{x y^2}{2} + \frac{y^3}{3})dx = \frac{x^2 y}{2} + \frac{x^2 y^2}{4} + \frac{x y^3}{3}. \] Integrointivakio on tässä tapauksessa muotoa $C(x) + D(y)$, missä $C(x)$ on muuttujan $x$ funktio ja $D(y)$ on muuttujan $y$ funktio.
Kaksoissuhde (engl. Cross ratio)
Jos pisteet $A$, $B$, $C$ ja $D$ ovat samalla suoralla, niin osamäärää \[ \frac{AB \cdot CD}{AD \cdot CB} \] kutsutaan kaksoissuhteeksi. Sille käytetään merkintää $\{ AB, CD \}$ tai $[ A, B, C, D ]$.
Kalenteri (engl. Calendar)
Järjestelmä vuoden päivien ryhmittelemiseksi viikkoihin ja kuukausiin. Nykyisin noudatettavan gregoriaanisen kalenterin määräsi käyttöön otettavaksi paavi Gregorius XII vuonna 1582, mutta se otettiin eri maissa käyttöön eri aikoina.
Gregoriaanista kalenteria edelsi juliaaninen kalenteri, jonka käytön määräsi Julius Caesar vuonna 46 eKr.
Kalenterien perustana on toisaalta aika, jona maa tekee kierroksen auringon ympäri, toisaalta aika, jona maa kiertää akselinsa ympäri.
Katso myös Merkintätapa, Notaatio.
Kalteva (engl. Inclined)
Kallistunut.
Kalteva taso on kallistunut taso. Sitä käytetään usein fysiikassa, koska kappaleet vierivät alas kaltevaa pintaa enemmän tai vähemmän samalla tavalla kuin ne putoavat ilmassa, kuitenkin paljon hitaammin.
Katso myös Kaltevuus.
Kaltevuus (engl. Slope)
Yleinen sana sille, kuinka jyrkkä suora tai käyrä on eli kuinka vaakasuorasti se kulkee. Tarkka mitta kaltevuudelle on suoran kulmakerroin.
Katso myös Maksimi, Kaltevuuskulma, Kalteva, Minimi, Gradientti.
Kaltevuuskulma (engl. Inclination)
Kuinka paljon jokin suunta poikkeaa vaakasuorasta.
Katso myös Kaltevuus, Gradientti.
Kanoninen (engl. Canonical)
Kanoninen muoto on tavallinen, usein yleisesti sovittu tapa kirjoittaa tai ilmaista jotakin. Esimerkiksi suoran yhtälön kanoninen muoto on $y=ax+b$.
Katso myös Merkintätapa, Notaatio, Ominaisuus, Määrite.
Kanoninen muoto (engl. Canonical form)
Kun matriisiluokka ja muunnostyyppi on annettu, niin usein voidaan määritellä muoto, johon kaikki kyseisen luokan matriisit voidaan näillä muunnoksilla muuntaa. Tällaista muotoa kutsutaan kanoniseksi muodoksi. Esimerkiksi jokainen symmetrinen matriisi voidaan muuntaa lävistäjämatriisiksi käyttämällä similariteettimuunnosta, joten "diagonaalinen" on symmetristen matriisien kanoninen muoto.
Kanta (engl. Basis)
Joukko tutkittavan vektoriavaruuden vektoreita, joiden avulla voidaan esittää kaikki kyseisen avaruuden vektorit.
Vektoriavaruuden kannan vektorit virittävät kyseisen avaruuden ja ovat lineaarisesti riippumattomia. Kannan vektoreiden lukumäärä on sama kuin kyseisen avaruuden dimensio.
Katso myös Lineaarinen riippumattomuus, Vektoriavaruus, Virittää, Vektoriavaruuden dimensio, Riviavaruus.
Kantaja (engl. Support)
Olkoon $X$ topologinen avaruus ja $f \colon X \rightarrow \mathbb{C}$. Kuvauksen $f$ kantaja joukon $\{ x \in X \mid f(x) \neq 0 \}$ sulkeuma.
Katso myös Joukko.
Kantaluku (engl. Base of a number system, Base or radix, Radix, Base)
Luku, jonka potenssien avulla esitetään muut luvut annetussa lukujärjestelmässä. Esim. kymmenjärjestelmän kantaluku on 10, 12-järjestelmän kantaluku on 12.
(1) Luku, jonka potenssien avulla esitetään muut luvut annetussa lukujärjestelmässä. Esim. kymmenjärjestelmän kantaluku on 10, 12-järjestelmän kantaluku on 12. (2) Logaritmin kantaluvuksi kutsutaan lukua, jonka potenssien perusteella logaritmi on määritelty.
Ns. Briggsin logaritmin kantaluku on 10. Tämä ilmaistaan myös sanomalla, että Briggsin logaritmi on 10-kantainen. Se merkitsee sitä, että esim. Briggsin logaritmi luvusta 100 on 2, sillä $100=10^2$. Yleisesti $a$-kantaista logaritmia merkitään~$\log_a$. Esim. $\log_{10}100=2$.
Katso myös 12-järjestelmä, Yksipaikkainen, Kolmijärjestelmä, Kymmenjärjestelmä, Merkintätapa, Notaatio, Binäärilukujärjestelmä, Heksadesimaalilukujärjestelmä.
Kantapiste (engl. Foot, Foot of a perpendicular)
Olkoot $L$ suora ja $P$ piste. Pisteen $P$ kautta kulkevan suoran $L$ normaalin ja suoran $L$ leikkauspistettä $Q$ sanotaan normaalin kantapisteeksi.
Samoin jos piirretään kolmion tai jonkin muun kuvion korkeusjana, niin pistettä, jossa korkeusjana leikkaa sivun, jota vastaan se on kohtisuorassa, sanotaan korkeusjanan kantapisteeksi.Katso myös Piste, Kohtisuora, Ortokolmio, Suora, Suorien leikkauspiste.
Kappale (engl. Solid)
Kolmiulotteinen kuvio, jolla on pituus, leveys ja korkeus (tai syvyys).
Katso myös Katkaistu kartio, Pyörähdyskappale, Tahko, Torus, Särmiö, Prisma, Lieriö, Kartio, Pallo, Kiekko, Ellipsoidi, Duaalinen monitahokas, Monitahokas.
Kaprekarin jono (engl. Kaprekar's process)
Järjestetään annetun luvun numerot nousevaan järjestykseen. Olkoon näin muodostunut luku $m$. Järjestetään sitten luvun numerot laskevaan järjestykseen. Olkoon tämä luku $n$. Lasketaan erotus $n-m$. Toistetaan sama menettely tällä uudella luvulla jne.
Kaikilla kolminumeroisilla luvuilla menettely johtaa lopulta lukuun 495, johon prosessi pysähtyy.
Kaikilla nelinumeroisilla luvuilla prosessissa päädytään lopulta lukuun 6174, johon prosessi pysähtyy. Luvut, joissa kaikki numerot ovat yhtä suuria, ovat poikkeuksia.
Kaikilla viisinumeroisilla luvuilla prosessissa päädytään lopulta yhteen kolmesta syklistä, ei mihinkään kiinteään lukuun.
Katso myös Kaprekarin vakio, Aritmeettinen prosessi.
Kaprekarin luku (engl. Kaprekar number)
Kaprekarin luvulla $k$ on ominaisuus $k = q+r$, $k^{2} = q \cdot 10^{n}+r$, missä $q \gt 0$ ja $r \lt 10^{n}$. Kaprekarin lukuja ovat esimerkiksi $9$, $4$5 ja $297$, koska $9^{2} = 81$, $8+1 = 9$; $45^{2} = 2025$, $20+25 = 45$ ja $297^{2} = 88209$, $88+209 = 297$.
Kaprekarin vakio (engl. Kaprekar's constant)
Luku 6174. Jos Kaprekarin prosessia sovelletaan neljänumeroiseen lukuun, tähän vakioon päädytään lopulta. Luvut, joissa kaikki numerot ovat yhtä suuria, ovat tässä poikkeuksia.
Katso myös Kaprekarin jono, Vakio.
Karakteristinen polynomi (engl. Characteristic polynomial)
Neliömatriisin $A$ karakteristinen polynomi on muuttujan $x$ polynomi $\left| A - Ix \right|$. Jos $A$ on $n \times n$-matriisi, niin sen karakteristinen polynomi on kertalukua $n$. Karakteristisen polynomin nollakohdat ovat matriisin ominaisarvot.
Katso myös Polynomi, Lineaarikuvaus, Matriisi, Cayley-Hamiltonin lause, Karakteristinen yhtälö, Lineaarimuunnos.
Karakteristinen yhtälö (engl. Auxiliary equation)
Toisen kertaluvun vakiokertoimisen differentiaaliyhtälön $\frac{d^2 y}{dx^2} + a \frac{dy}{dx}+ b y = f(x)$ karakteristinen yhtälö on $m^2 + a m + b =0$.
Katso myös Differentiaaliyhtälö, Yhtälö, Toisen kertaluvun differentiaaliyhtälö.
Karakteristinen yhtälö (engl. Characteristic equation)
Neliömatriisin $A$ karakteristinen yhtälö on $| A - Ix| = 0$, missä $I$ on yksikkömatriisi.
Esimerkiksi, jos $A = \left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right)$, niin $A$:n karakteristinen yhtälö on \[ \left| \left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) - \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) x \right | = 0 \] eli \[ \left| \left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) - \left( \begin{array}{cc} x & 0 \\ 0 & x \end{array} \right) \right| = \left| \begin{array}{cc} 1- x & 2 \\ 3 & 4-x \end{array} \right| = (1-x)(4-x) - 2 \cdot 3 = x^2 -5 x -2 = 0. \]
Karakteristisen yhtälön ratkaisut ovat matriisin ominaisarvot.
Katso myös Determinantti, Ominaisarvo, Matriisi, Cayley-Hamiltonin lause, Karakteristinen polynomi, Yhtälö.
Karteesinen (engl. Cartesian)
René Descartesin eli Cartesiuksen työhön, erityisesti suorakulmaisiin koordinaatistoihin, liittyvä.
Katso myös Koordinaattitaso, Karteesinen koordinaatisto, Analyyttinen geometria, Karteesinen soikio, Ominaisuus, Määrite, Descartesin lehti.
Karteesinen koordinaatisto (engl. Cartesian coordinate system)
Suorakulmainen koordinaattijärjestelmä. Karteesinen koordinaatisto kuvaa minkä tahansa pisteen paikan tasolla kahden luvun avulla ja minkä tahansa pisteen paikan avaruudessa kolmen luvun avulla käyttäen kahta tai kolmea akselia, jotka ovat toisiaan vastaan kohtisuorassa ja joita pitkin pisteen paikka mitataan. Karteesinen koordinaattijärjestelmä on nimetty Descartesin mukaan. Hänen töissään esiintyy kyseisen järjestelmän perusajatus, tosin ilman vaatimusta koordinaattiakselien välisestä kohtisuoruudesta.
Katso myös $z$-akseli, $y$-akseli, $x$-akseli, Abskissa, Karteesinen, Analyyttinen tasogeometria, Akseli, Koordinaatisto.
Karteesinen soikio (engl. Cartesian oval)
Olkoot $A$ ja $B$ kaksi tason pistettä sekä $a$ ja $m$ kaksi reaalilukuvakiota. Käyrää, johon kuuluvat täsmälleen ne tason pisteet $P$, joilla $AP + m BP = a$, kutsutaan karteesiseksi soikioksi. Tämä käyrä koostuu itse asiassa kahdesta soikiosta.
Karteesisen soikion yhtälö karteesisessa koordinaatistossa on \[ [(1-m^2)(x^2+y^2)+2m^2cx+a^2-m^2c^2]^2 =4a^2(x^2+y^2), \] missä $c$ on pisteiden $A$ ja $B$ välinen etäisyys.
Katso myös Ura, Soikio, Ovaali, Karteesinen.
Karteesinen tulo (engl. Cartesian product)
Joukkojen $A$ ja $B$ karteesinen tulo on joukko $A \times B = \{ (a,b) \mid a \in A ,b \in B \}$.
Katso myös Joukko.
Kartio (engl. Cone)
Kappale, jonka muodostavat puolisuorat, jotka yhdistävät kiinteän avaruuden pisteen (kartion kärjen) jonkin tasokäyrän kaikkiin pisteisiin. Tasokäyrän ympäröimä tasokuvio on kartion pohja.
Jos kartion pohja on ympyrä, kartio on ympyräkartio. Jos kartion kärjen ja ympyrän keskipisteen yhdistävä suora on kohtisuorassa pohjaa vastaan, kartio on suora ympyräkartio. Kyseinen suora on tällöin kartion akseli.
Katso myös Kartion kärki, Kartion tilavuus, Katkaistu kartio, Suora kartio, Kappale, Avaruusgeometria, Kartion akseli, Pyramidi, Ympyräkartio, Kartion korkeusjana, Kartion pinta-ala, Kartion pohja, Kartioleikkaus, Kartion yhtälö.
Kartioleikkauksen polttopiste (engl. Focus of a conic section)
Jos kartioleikkaus määritellään niiden pisteiden urana, joiden etäisyys annetusta suorasta (ns. johtosuorasta) on vakiosuhteessa $r$ etäisyyteen annetusta pisteestä, niin tätä annettua pistettä kutsutaan kartioleikkauksen polttopisteeksi. Jos $r = 1$, kyseessä on paraabeli; jos $r \lt 1$, kyseessä on ellipsi; jos $r \gt 1$, kyseessä on hyperbeli.
Katso myös Piste, Paraabelin yhtälö, Kartioleikkaus.
Kartioleikkauksen yhtälö (engl. Equation of a conic)
Kartioleikkauksen yleinen yhtälö on $ax^{2}+2hxy+by^{2}+2gx+2fy+c=0.$
Jos $h^2-ab$ on negatiivinen, on kartioleikkaus ellipsi.
Jos $h^2-ab$ on nolla, on kartioleikkaus paraabeli.
Jos $h^2-ab$ on positiivinen, on kartioleikkaus hyperbeli.
Katso myös Paraabelin yhtälö, Ellipsin yhtälö, Hyperbelin yhtälö, Kartioleikkaus, Yhtälö, Tasasivuisen hyperbolin yhtälö.
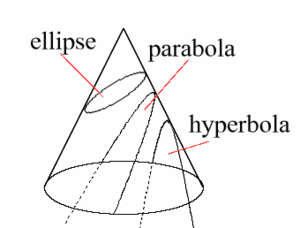
Kartioleikkaus (engl. Conic, Conic section)
Kaksiulotteinen käyrä (ellipsi, paraabeli tai hyperbeli), joka saadaan leikkaamalla suora ympyräkartio tasolla. Nämä käyrät ovat myös kahden muuttujan toisen asteen yhtälöiden ratkaisujoukkojen kuvaajia.
Tällaisten käyrien yleinen yhtälö on $ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0$. Käyrän tyyppi määräytyy lukujen $ \Delta = abc + 2fgh - af^2 - bg^2 - ch^2$ ja $h^2 - ab$ perusteella seuraavasti:
| $\Delta \neq 0 $ | $\Delta = 0$ | |
| $h^{2}-a b \lt 0$ | ellipsi | yksi piste |
| $h^{2}-a b = 0$ | paraabeli | kaksi yhdensuuntaista suoraa tai yksi suora tai ei ratkaisua reaalilukujen joukossa |
| $h^{2}-a b \gt 0$ | hyperbeli | kaksi toisensa leikkaavaa suoraa |
Katso myös Ympyrä, Ellipsi, Kartio, Paraabeli, Käyrä, Hyperbeli, Paraabelin yhtälö, Hyperbelin yhtälö, Eksentrisyys, Analyyttinen tasogeometria, Kartioleikkauksen yhtälö, Kartioleikkauksen polttopiste.
Kartion akseli (engl. Axis of a cone)
Suora, joka kulkee kartion kärjen ja kannan keskipisteen kautta, on kartion akseli.
Katso myös Kartion kärki, Suora kartio, Kartio, Akseli, Kartion pohja.
Kartion korkeusjana (engl. Altitude of a cone)
Kartion pohjasta kohtisuoraan kartion kärkeen kulkeva jana.
Katso myös Kartion kärki, Kartio.
Kartion kärki (engl. Vertex of a cone)
Piste, jonka kautta kaikki kartion sivusuorat kulkevat.
Katso myös Kartion akseli, Kartio, Kartion korkeusjana, Pyramidin korkeusjana.
Kartion massakeskipiste (engl. Centre of mass of a cone)
Ympyräpohjaisen kartion massakeskipiste sijaitsee pohjan keskipisteen sekä kärjen välisellä janalla ja jakaa sen suhteessa $1:3$.
Katso myös Pyramidin massakeskipiste, Pyörähdyskappaleen massakeskipiste, Massakeskipiste, Painopiste.
Kartion pinta-ala (engl. Area of a right circular cone, Area of a cone)
Jos suoran ympyräkartion pohjan säde on $r$ ja korkeus on $h$, niin sen vaipan pinta-ala on $\pi r \sqrt{r^2 + h^2}$. Kartion kokonaispinta-ala on siis \[\pi r^2 + \pi r \sqrt{r^2 + h^2} = \pi r (r + \sqrt{r^2 + h^2}). \]
Katso myös Kartio.
Kartion pohja (engl. Base of a cone)
Kartion pohja on se yleensä pyöreä tasoalue, jolla kartio "seisoo".
Katso myös Suora kartio, Kartion akseli, Kartio.
Kartion tilavuus (engl. Volume of cone, Volume of a cone)
Ympyräkartion, jonka korkeus on $h$ ja pohjan säde $r$, tilavuus on $\frac{1}{3} \pi r^{2} h$.
Minkä tahansa kartion, jonka pohjan pinta-ala on $A$ ja korkeus (kohtisuorasti pohjaa vastaan mitattuna) $l$, tilavuus on $Al/3$.
Katso myös Pallon tilavuus, Kartio.
Kartion vaipan massakeskipiste (engl. Centre of mass of a conical shell)
Ympyräpohjaisen kartion vaipan massakeskipiste sijaitsee pohjan keskipisteen sekä kärjen välisellä janalla ja jakaa sen suhteessa $1:2$.
Katso myös Massakeskipiste, Painopiste.
Kartion yhtälö (engl. Equation of a cone)
Oletetaan, että suoran ympyräkartion pohja on origokeskinen ja $r$-säteinen $xy$-tason ympyrä ja leikkaa $z$-akselin pisteessä $z = 0$. Oletetaan lisäksi, että kartion kärki sijaitsee $z$-akselin pisteessä $z = h$ eli kartion korkeus on $h$. Tällainen kartio voidaan kuvata kahden yhtälön avulla. Pohjaan kuuluvat ne pisteet $(x,y,z)$, joille pätee $x^2+y^2 \lt r^2$ ja $z = 0$. Vaippaan kuuluvat ne pisteet $(x,y,z)$, joille pätee $x^2 + y^2 = (r(h-z)/h))^2$ ja $0 \le z \le h$.
Kartioruuvikierre (engl. Conical helix)
Kartioruuvikierre syntyy, kun janaa kierretään kartion ympäri ja samalla liikutaan kartion korkeusjanaan nähden alas- tai ylöspäin.

Katso myös Ruuvikierre, Ruuviviiva.
Kasaantua, Kerääntyä (engl. Accumulate)
Kokoontua yhden paikan lähelle.
Kasautumispiste (engl. Accumulation point, Limit point)
Piste $x$ on joukon $S$ kasautumispiste, jos jokainen pisteen $x$ ympäristö $N_x$ toteuttaa ehdon $N_x \cap S \setminus \{x \} \neq \emptyset$.
Kasvaa, Kasvattaa (engl. Increase)
Kasvattaa jotain tarkoittaa tehdä se suuremmaksi.
Tulla suuremmaksi. Jonoa sanotaan kasvavaksi, jos jokainen jonon jäsen on suurempi tai yhtä suuri kuin edellinen jonon jäsen. Jono on aidosti kasvava, jos jokainen jonon jäsen on suurempi mutta ei yhtä suuri kuin edellinen jonon jäsen.
Kasvattaa, Kasvaa (engl. Increase)
Kasvattaa jotain tarkoittaa tehdä se suuremmaksi.
Tulla suuremmaksi. Jonoa sanotaan kasvavaksi, jos jokainen jonon jäsen on suurempi tai yhtä suuri kuin edellinen jonon jäsen. Jono on aidosti kasvava, jos jokainen jonon jäsen on suurempi mutta ei yhtä suuri kuin edellinen jonon jäsen.
Kasvava jono (engl. Increasing sequence, Monotonic increasing sequence)
Jonoa $(u_n)$ sanotaan kasvavaksi, jos $u_{n} \ge u_{n-1}$ pätee kaikilla $n$.
Katso myös Monotoninen jono.
Kateetti (engl. Cathetus)
Suora, joka on kohtisuorassa toista suoraa tai tasoa vastaan. Tavallisesti kateeteiksi kutsutaan suorakulmaisen kolmion suoran kulman kylkinä olevia sivuja. Suoran kulman vastaista sivua kutsutaan hypotenuusaksi.
Katso myös Suora.
Kategoria (engl. Category)
Kategoria on sellainen joukko $C$ funktioita, joka on suljettu funktioiden yhdistämisen suhteen ja joka sisältää kaikkien funktioidensa määrittely- ja arvojoukoilla määritellyt identiteettifunktiot. Toisin sanoen, jos $f : S \to U$ ja $g : U \to V$ ovat $C$:ssä, niin myös $g \circ f : S \to V$ on $C$:ssä, ja jos $f : U \to V$ on $C$:ssä, niin identiteettifunktiot $\mathrm{id}_U : U \to U$ ja $\mathrm{id}_V : V \to V$ ovat myös $C$:ssä.
Useimmat matemaatikot määrittelevät kategorian joukkona objekteja sekä joukkona morfismeja, jotka ovat funktioita objektilta toiselle. Morfismien yhdistämisen on tällöin oltava liitännäinen ja jokaista objektia kohti on oltava identiteettimorfismi. Reaalilukukertoimiset vektoriavaruudet muodostavat erään esimerkin kategoriasta: objekteja ovat vektoriavaruudet ja morfismeja ovat vektoriavaruuksien väliset lineaarikuvaukset.
Katso myös Identtinen laskutoimitus, Funktio, Kuvaus, Joukko, Vektoriavaruus, Morfismi, Groupoidi, Funktori.
Kategorinen (engl. Categorical)
Jotakin asiaa - kuten sääntöä, teoriaa tai systeemiä - kutsutaan kategoriseksi, jos se ei salli poikkeuksia.
Katso myös Looginen ominaisuus.
Kategorinen, Luokiteltu, Luokka-arvoinen (engl. Nominal, Categorical or nominal, Categorical)
Satunnaismuuttujaa tai sitä havainnoimalla saatua aineistoa kutsutaan luokka-arvoiseksi tai luokitelluksi tai kategoriseksi, jos sitä ei voi laittaa järjestykseen, vaan ainoastaan jakaa järjestämättömiin luokkiin.
Katso myös Satunnaismuuttuja.
Katenoidi (engl. Catenoid)
Pyörähdyspinta, joka syntyy ketjukäyrän pyörähtäessä x-akselin ympäri.
Katenoidi on ainoa minimipinta, joka on myös pyörähdyspinta.
Kun kaksi samansäteistä metallirengasta upotetaan saippualiuokseen, nostetaan pois ja erotetaan toisistaan varovasti siten, että molemmat metallirenkaat pysyvät samansuuntaisina ja kohtisuorassa niiden keskipisteiden kautta kulkevaa suoraa vastaan, niin tällöin syntyvän saippuakalvon muoto on katenoidi.Katso myös Pyörähdyspinta, Ketjukäyrä.
Katkaiseminen (engl. Truncate)
Kappaletta sanotaan katkaistuksi, jos siitä on poistettu osia. Yleensä kappale katkaistaan leikkaamalla siitä kärjet pois. Katkaistut kappaleet ovat hyviä säiliöitä, jogurttipurkki on usein katkaistu kartio.
Desimaaliluku katkaistaan, kun sen viimeiset desimaalit jätetään merkitsemättä.
Katso myös Katkaistu kartio, Konstruktio, Konstruointi.
Katkaistu kartio (engl. Truncated cone or frustum, Frustum, Truncated cone, Frustrum)
Kappale, jota rajoittavat kaksi yhdensuuntaista tasoa ja niiden väliin jäävä osa kartion vaippaa.
Katso myös Katkaiseminen, Kappale, Avaruusgeometria, Katkaistun kartion vaipan pinta-ala, Katkaistu pyramidi.
Katkaistu pyramidi (engl. Frustrum of a pyramid, Frustum of a pyramid)
Monikulmio, joka jää jäljelle, kun pyramidin huippu leikataan pois pitkin pyramidin pohjan suuntaista tasoa.
Katso myös Katkaistu kartio.
Katkaistun kartion vaipan pinta-ala (engl. Curved surface area of a frustrum)
Oletetaan, että suora ympyräkartio, jonka pohjan säde on $r$ ja jonka korkeus on $h$, katkaistaan korkeudelta $a$ ja yläosa heitetään pois. Näin saadun katkaistun suoran ympyräkartion vaipan pinta-ala lasketaan seuraavasti:
Alkuperäisen kartion vaipan pinta-ala on $\pi r\sqrt{r^2+h^2}$. Poisleikatun osan (kartio sekin) vaipan pinta-ala on $\pi q \sqrt{q^2+(h-a)^2}$, missä $q = r(h-a)/h$ on poisleikatun kartion pohjan säde eli katkaistun kartion pienemmän pohjan säde. Katkaistun kartion vaipan pinta-ala on nyt näiden pinta-alojen erotus: \[ A = \pi [r \sqrt{r^2+h^2} - q \sqrt{q^2+(h-a)^2}]. \] Jos tiedämme ainoastaan katkaistun kartion korkeuden $a$ ja sen pohjien säteet $r$ ja $q$, niin silloin $h$ lasketaan ensin kaavalla $h = ar/(r-q)$ ja sen jälkeen katkaistun kartion vaipan pinta-ala lasketaan yllä annetulla kaavalla.
Katso myös Katkaistu kartio.
Kattofunktio (engl. Ceil or ceiling function, Ceil, Ceiling function)
Kattofunktio $\lceil \cdot \rceil \colon \mathbb{R} \rightarrow \mathbb{Z}$ määritellään seuraavasti: $\lceil x \rceil$ on pienin kokonaisluku, joka on suurempi tai yhtä suuri kuin $x$.
Katso myös Lattia, Kokonaisosa, Funktio, Kuvaus.
Kauppamatkustajan ongelma (engl. Travelling salesman)
Vanha ongelma, joka voidaan aina ratkaista, mutta joka on vaikea ratkaista nopeasti.
Kauppamatkustajan on käytävä tietyissä paikoissa jossakin järjestyksessä. Paikat on yhdistetty toisiinsa tietyillä teillä, joiden pituudet tiedetään. Missä järjestyksessä kauppamatkustajan on kierrettävä paikat, jotta koko matkan pituus olisi mahdollisimman lyhyt?
kauppamatkustajan ongelmat (engl. Travelling salesman problems)
Kuuluisa ongelma, jossa on annettu tietty verkosto teitä sekä paikat, joissa on vierailtava jossakin järjestyksessä, ja on löydettävä lyhin tie kiertää kaikki paikat. Ongelma voidaan aina ratkaista tutkimalla jokainen mahdollinen reitti ja etsimällä niistä lyhin, mutta joidenkin verkkojen tapauksessa tämä voi viedä hyvin pitkän ajan. Nopeampia tapoja ratkaista ongelma on vaikeaa tai mahdotonta löytää.
Katso myös Verkkoteoria, Verkko.
Kellokäyrä (engl. Bell curve, Bell-shaped curve)
Normaalijakauman tiheysfunktion nimi. \[ f(x)= \frac{1}{\sqrt{2 \pi}} \exp(-x)^2. \] Kuvaaja on symmetrinen ja muistuttaa muodoltaan jossakin määrin kirkon kelloa.
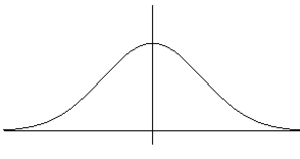
Katso myös Normaalijakauma, Käyrä, Gaussin jakauma.
Kerran, Yhden kerran (engl. Once)
Yksi kerta.
Katso myös Frekvenssi.
Kerroin (engl. Coefficient)
Vakio, jolla kerrotaan siihen liittyvä muuttuja. Esimerkiksi polynomissa $2x^{2}+3y+z+ax$ termin $x^{2}$ kerroin on 2, termin $y$ kerroin on 3, termin $z$ kerroin on 1 (jota ei yleensä merkitä näkyviin) ja termin $x$ kerroin on $a$.
Yleensä kerroin sijoitetaan siihen liittyvän muuttujan eteen, mutta tämä ei ole välttämätöntä: esimerkiksi $3x$ ja $x3$ tarkoittavat samaa asiaa, mutta $3x$ on paljon tavallisempi.
Mitä tahansa tekijää tai termiä voidaan kutsua termin muun osan kertoimeksi. Tavallisinta on pitää lukua tai vakiota muuttujien tulon kertoimena.
Katso myös Lauseke, Polynomi, Termi, Binomikerroin, Fourier'n kertoimet.
Kertolasku (engl. Multiplication, Multiply)
Menettely tai yleistys menettelystä, jossa jokin suure lasketaan yhteen itsensä kanssa tietty määrä kertoja. Se on jakolaskun käänteislaskutoimitus.
Kertolasku $5 \cdot 4$ voisi tarkoittaa joko viittä neljän ryhmää eli $4+4+4+4+4$ tai viittä laskettuna itsensä kanssa yhteen kolme kertaa eli $5+5+5+5$. Kertolasku on sekä vaihdannainen että liitännäinen laskutoimitus.
Liitännäinen, vaihdannainen sekä yhteenlaskun suhteen ositteleva laskutoimitus, joka liittää kahteen alkioon $a$ ja $b$ kolmannen alkion, alkioiden $a$ ja $b$ tulon $ab$, missä $a$ ja $b$ kuuluvat johonkin joukoista $\mathbf{N}$, $\mathbf{Z}$, $\mathbf{Q}$, $\mathbf{R}$ tai $\mathbf{C}$.
Katso myös Vasta-alkio, Ykkösalkio, Kertolaskun neutraalialkio, Käänteisalkio, Kertominen, Tulo, Laskutoimitus, Allekkain kertolasku, Suurempi tai yhtäsuuri kuin, Jakolasku, Kaksinkertaistaa, Kertolaskun käänteisalkio, Käänteisluku, Binäärinen kuvaus, Jakaminen, Kaksipaikkainen kuvaus, Ääretön tulo.
Kertolaskun käänteisalkio, Käänteisalkio, Käänteisluku (engl. Multiplicative inverse)
Luvun käänteisalkio on se luku, jolla alkuperäinen luku on kerrottava, jotta saataisiin tulokseksi kertolaskun neutraalialkio.
Jos kertolaskun neutraalialkio on 1, niin alkion $a$ käänteisalkio $a'$ on se alkio, jolla $aa' = a'a = 1$. Luvulla 0 ei ole käänteisalkiota. Joukossa $\mathbb{N}$ vain luvulla 1 on käänteisalkio. Joukossa $\mathbb{Z}$ vain luvuilla 1 ja $-1$ on käänteisalkio. Sen sijaan joukoissa $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ alkion $a \neq 0$ käänteisalkio on $1/a$.
Katso myös Ykkösalkio, Kertolaskun neutraalialkio, Kertolasku, Käänteis-, Jakolasku, Joukko, Kunta, Jakaminen.
Kertolaskun neutraalialkio, Ykkösalkio (engl. Multiplicative identity)
Luku, joka ei muuta mitään lukua, jos sillä kerrotaan tämä luku. Tavallisessa lukujärjestelmässä tämä luku on 1.
Alkio $e$, joka toteuttaa ehdon $ae = ea = a$ jokaisella joukon alkiolla $a$. Joukoissa $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ kertolaskun neutraalialkio on 1.
Katso myös Käänteisalkio, Kertolasku, Neutraalialkio, Kertolaskun käänteisalkio, Käänteisluku.
Kertoma (engl. Factorial)
Positiivisen kokonaisluvun $n$ kertoma $n!$ on tulo \[ n! = 1 \cdot 2 \cdot \ldots \cdot (n-1) \cdot n. \] Siten esimerkiksi luvun $4$ kertoma on $4! =1\cdot 2\cdot 3\cdot 4 = 24$. Sopimuksen mukaan on $0! = 1$.
Kertoma $n!$ kasvaa hyvin nopeasti luvun $n$ kasvaessa: \[ 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120, 6! =720, 7! = 5040, 8! = 40320, 9! = 362880. \]
Katso myös Valita, Kokonaisluku, Gammafunktio, Brocardin ongelma.
Kertominen (engl. Times)
Kolme kertaa seitsemän on kaksikymmentäyksi. Tätä voidaan merkitä symbolilla $\cdot$ eli $3 \cdot 7 = 21$.
Katso myös Kertolasku.
Kertymäfunktio (engl. Cumulative distribution function)
Satunnaismuuttujan $X$ kertymäfunktio $F(x)$ antaa todennäköisyyden, että $X$ on pienempi tai yhtä suuri kuin annettu arvo $x$. Siis $F(x) = \mathrm{P}( X\le x )$. Jos $X$:n arvojoukko sisältyy väliin $[a, b]$, niin $F(a) = 0$ ja $F(b) = 1$.
Katso myös Funktio, Kuvaus, Jatkuva satunnaismuuttuja.
Kerääntyä, Kasaantua (engl. Accumulate)
Kokoontua yhden paikan lähelle.
Keskeinen raja-arvolause (engl. Central limit theorem)
Olkoon jakauman odotusarvo $\mu$ ja varianssi $\sigma^2$. Jos $(X_i)$ on jono kyseisen jakauman riippumattomia satunnaismuuttujia ja $S_n = \frac{1}{n} \sum_{i=1}^{n} X_i$, niin satunnaismuuttujan $S_n$ jakauma lähestyy normaalijakaumaa $N(\mu, \frac{\sigma^2}{n})$, kun $n \to \infty$.
Katso myös Normaalijakauma, Lause, Keskiarvo, Aritmeettinen keskiarvo, Gaussin jakauma, Riippumaton, Satunnaismuuttuja.
Keskenään jaottomat luvut (engl. Coprime)
Kahden luvun sanotaan olevan keskenään jaottomia, jos niillä ei ole muita yhteisiä tekijöitä kuin luku 1. Kahta keskenään jaotonta lukua kutsutaan myös suhteellisiksi alkuluvuiksi.
Katso myös Multiplikatiivinen, Dirichlet'n lause, Suhteellinen alkuluku, Eulerin lause.
Keskiarvo, Aritmeettinen keskiarvo (engl. Mean, Arithmetic mean)
Lukujen $x_1, x_2, \ldots, x_n$ aritmeettinen keskiarvo on \[ \bar{x} = \frac{1}{n} \sum x_i . \] Tunnetuin intervalli- ja suhdeasteikolla käytetty paikantamistunnusluku. Muuttujanarvojen painopiste.
Katso myös Normaalijakauma, Korrelaatiokerroin, Odotusarvo, Teoreettinen keskiarvo, Paikantamistunnusluku, Keskiluku, Moodi, Tyyppiarvo, Verrata, Harhaton keskiarvo, Tasaisen jakauman odotusarvo, Lineaarinen funktio ja keskiarvo, Aritmeettisen ja geometrisen keskiarvon välinen epäyhtälö, Keskeinen raja-arvolause, Variaatiokerroin, Poikkeama, Gaussin jakauma, Geometrinen keskiarvo, Keskiverto.
Keskiarvojen erotuksen t-testi (engl. t-test for difference in means)
Ongelmana keskiarvojen erotuksen t-testissä on: "Onko keskiarvo perusjoukoissa $A$ ja $B$ sama? Tutkimusta varten molemmista perusjoukoista poimitaan satunnaisotos $ X_{A,1} , X_{A,2} , ... , X_{A,n_A} $ ja $ X_{B,1}, X_{B,2} , ... , X_{B,n_B} $. Mikäli otoskeskiarvot ovat jakautuneet normaalisti, ja molemmissa perusjoukoissa on sama varianssi, voidaan esitettyä ongelmaa tutkia t-testin avulla. Testattava nollahypoteesi on tällöin $$ H_o: \mu_A = \mu_B. $$ Keskiarvojen erotuksen t-testi mittaa keskiarvojen eron suuruutta käyttäen mittana keskiarvojen erotuksen keskihajontaa. $$ t= {{(\overline {X}_1 - \overline{X}_2)}\over {s\cdot \sqrt{\displaystyle {1\over n_1} + {1\over n_2}}}}, $$ missä $$ s = \sqrt{ {(n_1-1)\cdot s_1^2 + (n_2-1)\cdot s_2^2)} \over {n_1-1+n_2-1}}$$ on estimaatti perusjoukkojen yhteiselle tuntemattomalle varianssille. Mikäli oletukset (otoskeskiarvojen normaalisuus, sama varianssi) ovat voimassa, noudattaa testisuure nollahypoteesin voimassaollessa t-jakaumaa vapausasteilla $n_A+n_B-2$. Lähellä nollaa olevat testisuureen arvot tukevat nollahypoteesia, ja suuret poikkeamat nollasta osoittavat, että nollahypoteesi ei pidä paikkaansa.
Katso myös Tilastollinen testi.
Keskiarvon t-testi (engl. t-test for mean)
Ongelmana keskiarvon t-testissä on: "Onko perusjoukon keskiarvo annettu luku $ \mu_o $?" Tutkimusta varten perusjoukosta poimitaan satunnaisotos $ X_1 , X_2 , ... , X_n $. Mikäli otoskeskiarvo on jakautuneet normaalisti, voidaan esitettyä ongelmaa tutkia t-testin avulla. Testattava nollahypoteesi on nyt $$ H_o: \mu = \mu_o $$ ja testisuure $$ t= {{(\overline {X} - \mu_o)}\over {s\cdot \sqrt{1\over n}}} $$ $$ t= {{(\overline {X} - \mu_o)}\over {s / \sqrt{n}}} $$ noudattaa normaalisuusoletuksen nollahypoteesin voimassaollessa t-jakaumaa vapauasteilla $n-1$. Lähellä nollaa olevat testisuureen arvot tukevat nollahypoteesia, ja suuret poikkeamat nollasta osoittavat, että nollahypoteesi ei pidä paikkaansa.
Katso myös Tilastollinen testi.
Keskihajonta (engl. Standard deviation)
Varianssin neliöjuuri. Yleisesti käytetty hajontamitta, varsinkin kun tarkasteltava muuttuja noudattaa normaalijakaumaa. (Esimerkiksi otoskeskiarvo)
Katso myös Vaihtelevuus, Tunnusluku, Tilastollinen tunnusluku, Varianssi, Kuvajoukko, Funktion kuvajoukko, Verrata, Sigma, Variaatiokerroin, Hajonta, Keskivirheen arvio.
Keskijana, Mediaani (engl. Median, Median of a triangle)
Jana, joka yhdistää kolmion kärjen ja sen vastaisen sivun keskipisteen. Kolmion kolme mediaania leikkaavat toisensa samassa pisteessä ja tämä piste on kolmion painopiste.
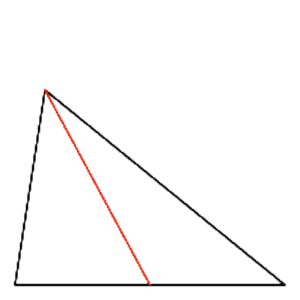
Katso myös Mediaalikolmio, Painopiste, Kolmion massakeskipiste.
Keskiluku, Paikantamistunnusluku (engl. Measure of central tendency)
Keskilukuja ovat tilastoaineiston (jakauman) paikkaa (keskipistettä) kuvaavat luvut. Tunnetuimmat keskiluvut ovat:
- Keskiarvo - jakauman tasapainopiste.
- Mediaani - arvo, joka jakaa jakauman keskeltä kahteen yhtäsuureen osaan.
- Moodi - jakauman korkein kohta (yleisin muuttujanarvo).
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Mediaani, Moodi, Tyyppiarvo, Harmoninen keskiarvo.
Keskinormaali (engl. Perpendicular bisector)
Annetun janan $L$ keskinormaali on suora, joka on kohtisuorassa janaa $L$ vastaan ja kulkee janan $L$ keskipisteen kautta.
Katso myös Keskipiste, Puolittaja.
Keskinormaalin piirtäminen (engl. Construct a perpendicular bisector)
Janan $AB$ keskinormaali piirretään seuraavasti. Piirretään harpin avulla kaksi ympyrää, joilla on sama säde ja keskipisteet $A$ ja $B$. Ympyrät leikkaavat toisensa pisteissä $C$ ja $D$. Piirretään suora $CD$. Se on janan $AB$ keskinormaali.
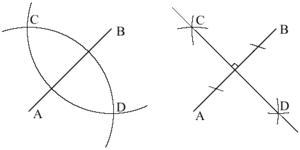
Katso myös Ympyrän piirtäminen kolmen pisteen kautta, Konstruktio, Kolmion ympäri piirretyn ympyrän muodostaminen, Konstruointi.
Keskipiste (engl. Middle)
Piste, joka on jonkin puolivälissä, samalla etäisyydellä jokaisesta päätepisteestä tai jokaisesta sivusta.
Katso myös Piste.
Keskipiste (engl. Centre)
Jonkin keskikohta.
Erityisesti janan keskipiste on sen puolivälissä oleva piste.
Ympyrän keskipiste on piste, joka on samalla etäisyydellä jokaisesta ympyrän kehän pisteestä.
Kolmiolla on useita, eri tavoin määriteltyjä "keskipisteitä", kuten kolmion korkeusjanojen leikkauspiste, kolmion sisään piirretyn ympyrän keskipiste, kolmion keskijanojen leikkauspiste eli painopiste ja kolmion ympäri piirretyn ympyrän keskipiste.
Puhuttaessa kuvion tai kappaleen keskipisteestä tarkoitetaan usein sen massakeskipistettä.
Katso myös Piste, Symmetriakeskus, Ortosentri, Suurennoksen keskus, Keskinormaali, Sisään piirretyn ympyrän keskipiste, Kolmion ympäri piirretyn ympyrän keskipiste, Painopiste, Perspektiivikeskus, Ympyrän keskipiste, Kaarevuuskeskipiste, Massakeskipiste, Painopiste, Ryhmän keskus, Keskipiste.
Keskipiste (engl. Midpoint)
Kahden pisteen puolivälissä oleva piste, samalla etäisyydellä molemmista pisteistä.
Tetraedrin särmien keskipisteitä yhdistävät janat muodostavat oktaedrin.
Katso myös Mediaalikolmio, Keskipiste, Feuerbachin ympyrä, Yhdeksän pisteen ympyrä.
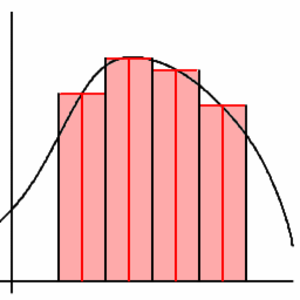
Keskipistesääntö (engl. Midpoint rule, Mid-ordinate rule)
Jos käyrän $y=f(x)$ alle jäävä pinta-ala jaetaan pystysuoriin kaistaleisiin, niin suorien $x=a$ ja $x=b$ väliin jäävän kaistaleen pinta-ala on likimain $(b-a)f\left( \frac{a+b}{2} \right)$, toisin sanoen, kaistaleen leveys kerrottuna kaistaleen pituudella kaistaleen keskipisteessä.
Tästä saadaan numeerisen integroinnin approksimointisääntö, jota kutsutaan keskipistesäännöksi: Jaetaan väli $[a,b]$ jakopisteillä $a=x_{0}, x_{1}, \ldots, x_{n-1}, x_{n}=b$ $n$:ään yhtä pitkään osaan. Kunkin jakovälin pituus on siis $h=(b-a)/n$. Olkoot $x_{i+1/2}$ jakovälin $[x_i,x_{i+1}]$ keskipiste ja $y_k=y(x_k)$. Tällöin \[ \int_a ^b y dx \approx h (y_{\frac{1}{2}} + y_{1 \frac{1}{2}} + \ldots + y_{n\frac{1}{2}} ). \]
Katso myös Sääntö, Simpsonin sääntö, Trapetsisääntö.
Keskiverto, Geometrinen keskiarvo (engl. Geometric mean)
Jos luvut $a_1, a_2, \ldots, a_n$ ovat ei-negatiivisia, on niiden geometrinen keskiarvo luku \[ M_g = \sqrt[n]{\prod_{i=1}^n a_i}. \] Geometrinen keskiarvo on hyödyllinen esimerkiksi keskimääräisten muutosten, kuten keskimääräisen inflaatiovauhdin, laskemisessa.
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Aritmeettisen ja geometrisen keskiarvon välinen epäyhtälö.
Keskivirheen arvio (engl. Estimated standard error)
Otoskeskiarvon keskivirheen arvio lasketaan kaavalla \[ \frac{s}{\sqrt{n}}, \] missä $n$ on otoskoko ja $s$ on otoksesta laskettu keskihajonta: \[ s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}. \]
Katso myös Virhe, Keskihajonta.
Keskuskulma (engl. Centre angle, Central angle)
Kulma, jonka kärki on ympyrän keskipiste ja jonka kyljet kulkevat tietyn ympyränkaaren päätepisteiden kautta, on tätä kaarta vastaava keskuskulma. Vastaavasti kulma, jonka kärki on ympyrän keskipiste ja jonka kyljet kulkevat tietyn ympyrän jänteen päätepisteiden kautta, on tätä jännettä vastaava keskuskulma.
Katso myös Kulma, Keskuskulmalause, Samaa kaarta vastaavat kehäkulmat.
Keskuskulmalause (engl. Central angle theorem)
Annetun ympyrän kaaren muodostaman minkä tahansa kehäkulman asteluku on puolet vastaavan keskuskulman asteluvusta.
Katso myös Samaa kaarta vastaavat kehäkulmat, Keskuskulma.
Ketju (engl. Chain)
Osittaisjärjestetyn joukon osajoukko on ketju, jos se on täydellisesti järjestetty indusoidun osittaisjärjestysrelaation suhteen.
Katso myös Osajoukko, Osittaisjärjestetty joukko.
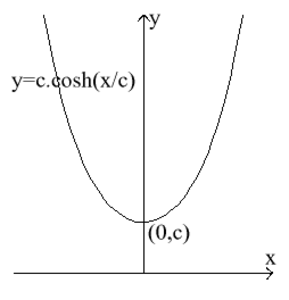
Ketjukäyrä (engl. Catenary)
Käyrä, jonka muodostaa päätepisteistään kiinnitetty vapaasti riippuva köysi. Sen yhtälö on \[ y = c \cdot cosh (x/c) \] eli \[ y = c\frac{e^{x/c}+e^{-x/c}}{2}. \]
Katso myös Käyrä, Bernoulli Johann, Katenoidi.
Ketjumurtoluku (engl. Continued fraction)
Ketjumurtoluku on lauseke muotoa \[ \alpha = a_0 + \frac{1}{a_1 + \frac{1}{a_2+ \ldots }}. \] Tämä voidaan esittää lyhyemmin muodossa \[ \alpha = [a_0, a_1, a_2, \ldots]. \]
Annetun luvun $\alpha$ ketjumurtoluku voidaan etsiä seuraavasti: Asetetaan $\alpha_0 = \alpha$ ja määritellään $a_i = \lfloor \alpha_i \rfloor$ ja \[ \alpha_{i+1} = \frac{1}{\alpha_i + a_i}, \] jolloin $\alpha_i = a_i+1 / \alpha_{i+1}$. Saadaan esimerkiksi \[ \sqrt{5}= 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + ...}}}. \]
Katso myös Murtoluku, Merkintätapa, Notaatio.
Ketjusääntö (engl. Chain rule)
Yhdistetyn funktion derivaatan muodostaminen perustuu ketjusääntöön: \[\frac{ d f(g(x)) }{dx} = \frac{ d f(g(x)) }{d g(x)} \cdot \frac{d g(x)}{dx} = f'(g(x)) g'(x).\]
Katso myös Derivointisääntö, Sääntö.
Khi (engl. Chi)
Kreikkalainen kirjain $\chi$ (pieni kirjain) tai X (iso kirjain), luetaan kii. Sen äänneasu on kova k.
Pienellä kirjaimella $\chi$ merkitään $\chi^{2}$-jakaumaa.
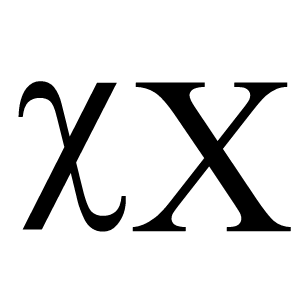
Katso myös Kreikkalaiset kirjaimet.
Khi-toiseen taulukko (engl. Chi-squared table)
Khi-toiseen jakauman arvot tapauksissa P=0.05, 0,01, 0,001. Vasemmanpuoleisin sarake kertoo vapausasteiden lukumäärän.
| Vapausasteiden lukumäärä | P = 0.05 | P = 0.01 | P = 0.001 |
| 1 | 3.84 | 6.64 | 10.83 |
| 2 | 5.99 | 9.21 | 13.82 |
| 3 | 7.82 | 11.35 | 16.27 |
| 4 | 9.49 | 13.28 | 18.47 |
| 5 | 11.07 | 15.09 | 20.52 |
| 6 | 12.59 | 16.81 | 22.46 |
| 7 | 14.07 | 18.48 | 24.32 |
| 8 | 15.51 | 20.09 | 26.13 |
| 9 | 16.92 | 21.67 | 27.88 |
| 10 | 18.31 | 23.21 | 29.59 |
| 11 | 19.68 | 24.73 | 31.26 |
| 12 | 21.03 | 26.22 | 32.91 |
| 13 | 22.36 | 27.69 | 34.53 |
| 14 | 23.69 | 29.14 | 36.12 |
| 15 | 25.00 | 30.58 | 37.70 |
| 16 | 26.30 | 32.00 | 39.25 |
| 17 | 27.59 | 33.41 | 40.79 |
| 18 | 28.87 | 34.81 | 42.31 |
| 19 | 30.14 | 36.19 | 43.82 |
| 20 | 31.41 | 37.57 | 45.32 |
| 21 | 32.67 | 38.93 | 46.80 |
| 22 | 33.92 | 40.29 | 48.27 |
| 23 | 35.17 | 41.64 | 49.73 |
| 24 | 36.42 | 42.98 | 51.18 |
| 25 | 37.65 | 44.31 | 52.62 |
| 26 | 38.89 | 45.64 | 54.05 |
| 27 | 40.11 | 46.96 | 55.48 |
| 28 | 41.34 | 48.28 | 56.89 |
| 29 | 42.56 | 49.59 | 58.30 |
| 30 | 43.77 | 50.89 | 59.70 |
| 31 | 44.99 | 52.19 | 61.10 |
| 32 | 46.19 | 53.49 | 62.49 |
| 33 | 47.40 | 54.78 | 63.87 |
| 34 | 48.60 | 56.06 | 65.25 |
| 35 | 49.80 | 57.34 | 66.62 |
| 36 | 51.00 | 58.62 | 67.99 |
| 37 | 52.19 | 59.89 | 69.35 |
| 38 | 53.38 | 61.16 | 70.71 |
| 39 | 54.57 | 62.43 | 72.06 |
| 40 | 55.76 | 63.69 | 73.41 |
| 41 | 56.94 | 64.95 | 74.75 |
| 42 | 58.12 | 66.21 | 76.09 |
| 43 | 59.30 | 67.46 | 77.42 |
| 44 | 60.48 | 68.71 | 78.75 |
| 45 | 61.66 | 69.96 | 80.08 |
| 46 | 62.83 | 71.20 | 81.40 |
| 47 | 64.00 | 72.44 | 82.72 |
| 48 | 65.17 | 73.68 | 84.03 |
| 49 | 66.34 | 74.92 | 85.35 |
| 50 | 67.51 | 76.15 | 86.66 |
| 51 | 68.67 | 77.39 | 87.97 |
| 52 | 69.83 | 78.62 | 89.27 |
| 53 | 70.99 | 79.84 | 90.57 |
| 54 | 72.15 | 81.07 | 91.88 |
| 55 | 73.31 | 82.29 | 93.17 |
| 56 | 74.47 | 83.52 | 94.47 |
| 57 | 75.62 | 84.73 | 95.75 |
| 58 | 76.78 | 85.95 | 97.03 |
| 59 | 77.93 | 87.17 | 98.34 |
| 60 | 79.08 | 88.38 | 99.62 |
| 61 | 80.23 | 89.59 | 100.88 |
| 62 | 81.38 | 90.80 | 102.15 |
| 63 | 82.53 | 92.01 | 103.46 |
| 64 | 83.68 | 93.22 | 104.72 |
| 65 | 84.82 | 94.42 | 105.97 |
| 66 | 85.97 | 95.63 | 107.26 |
| 67 | 87.11 | 96.83 | 108.54 |
| 68 | 88.25 | 98.03 | 109.79 |
| 69 | 89.39 | 99.23 | 111.06 |
| 70 | 90.53 | 100.42 | 112.31 |
| 71 | 91.67 | 101.62 | 113.56 |
| 72 | 92.81 | 102.82 | 114.84 |
| 73 | 93.95 | 104.01 | 116.08 |
| 74 | 95.08 | 105.20 | 117.35 |
| 75 | 96.22 | 106.39 | 118.60 |
| 76 | 97.35 | 107.58 | 119.85 |
| 77 | 98.49 | 108.77 | 121.11 |
| 78 | 99.62 | 109.96 | 122.36 |
| 79 | 100.75 | 111.15 | 123.60 |
| 80 | 101.88 | 112.33 | 124.84 |
| 81 | 103.01 | 113.51 | 126.09 |
| 82 | 104.14 | 114.70 | 127.33 |
| 83 | 105.27 | 115.88 | 128.57 |
| 84 | 106.40 | 117.06 | 129.80 |
| 85 | 107.52 | 118.24 | 131.04 |
| 86 | 108.65 | 119.41 | 132.28 |
| 87 | 109.77 | 120.59 | 133.51 |
| 88 | 110.90 | 121.77 | 134.74 |
| 89 | 112.02 | 122.94 | 135.96 |
| 90 | 113.15 | 124.12 | 137.19 |
| 91 | 114.27 | 125.29 | 138.45 |
| 92 | 115.39 | 126.46 | 139.66 |
| 93 | 116.51 | 127.63 | 140.90 |
| 94 | 117.63 | 128.80 | 142.12 |
| 95 | 118.75 | 129.97 | 143.32 |
| 96 | 119.87 | 131.14 | 144.55 |
| 97 | 120.99 | 132.31 | 145.78 |
| 98 | 122.11 | 133.47 | 146.99 |
| 99 | 123.23 | 134.64 | 148.21 |
| 100 | 124.34 | 135.81 | 149.48 |
Kiekko (engl. Disk, Disc)
Kierron muuttaminen vastakkaissuuntaiseksi (engl. Convert clockwise to anticlockwise)
1/4-kierto myötäpäivään on sama asia kuin 3/4-kierto vastapäivään. 1/2-kierto myötäpäivään on sama asia kuin 1/2-kierto vastapäivään. Yleisesti, kierto $f$:s osan täydesta kierroksesta myötäpäivään on sama asia kuin $(1-f)$:s osa täydestä kierroksesta vastapäivään.
Asteina tämä ilmaistaan vähentämällä kierron asteluku $360^{\circ}$:sta. Esimerkiksi $180^{\circ}$ myötäpäivään $= 180^{\circ}$ vastapäivään ja $181^{\circ}$ myötäpäivään $= 179^{\circ}$ vastapäivään.Katso myös Vastapäivään, Myötäpäivään.
Kierros, Pyörähdys (engl. Revolution)
Täysi kierros, joka päättyy samaan suuntaan mistä alkoi. Yksi pyörähdys on 360 astetta.
Katso myös Pyörähdyskappale, Kierto, Pyörähdyskappaleen pinnan pinta-ala, Pyörähdyskappaleen pinta-ala.
Kierros (engl. Circuit)
Kierros on polku tai kulku, joka päättyy samaan pisteeseen kuin se, josta polku alkoi.
Katso myös Konsyklinen, Kierto.
Kierto (engl. Rotation)
Käännös, suunnan muutos.
Kuvaus, jossa kuviota käännetään tietyn kulman verran kiinteän pisteen ympäri, jota kutsutaan kierron keskukseksi.
Kierron keskus voi sijaita kierrettävän kuvion sisä- tai ulkopuolella. Jos kuviota kierretään vastapäivään, kiertoa kutsutaan positiiviseksi kierroksi. Negatiivinen kierto kiertää kuviota myötäpäivään.
Katso myös Peilaus, Pyörähdys, Kierros, Kiertosymmetria, Pyörähdyssymmetria, Vastapäivään, Myötäpäivään, Kiertosuunta, Geometrinen muunnos.
Kierto (engl. Cycle)
Permutaatio, missä osa alkioista permutoidaan syklisesti ja loput alkiot pysyvät paikoillaan. Esimerkiksi \[ \langle 1,2,3,4,5 \rangle \mapsto \langle 1,4,3,2,5 \rangle \] on kierto.
Jos kierto $\gamma$ permutoi täsmälleen $l$ alkiota, niin $l$ on $\gamma$:n pituus ja $\gamma$:n kertaluku on $l$, toisin sanoen $\gamma^l = e$, missä $e$ on identtinen permutaatio. Jokainen permutaatio voidaan esittää järjestystä vaille yksikäsitteisesti erillisten kiertojen tulona.
Kiertomatriisi, Rotaatiomatriisi (engl. Rotation matrix)
Matriisi, jota vastaava lineaarikuvaus kiertää tasoa kulman $\theta$ verran origon ympäri, on \[ \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right ) . \]
Katso myös Peilausmatriisi, Matriisi.
Kiertosuunta (engl. Direction of rotation)
Piste tai jana voi kiertää pyörimisakselinsa ympäri kahteen eri suuntaan. Matematiikassa positiivinen kiertosuunta on vastapäivään ja negatiivinen kiertosuunta myötäpäivään.
Katso myös Kierto, Vastapäivään, Myötäpäivään.
Kiertosymmetria, Pyörähdyssymmetria (engl. Rotational symmetry, Rotation symmetry)
Kierrettäessä tasasivuista kolmiota sen keskipisteen ympäri se voidaan asettaa omille ääriviivoilleen kolme kertaa täyden kierroksen aikana, joten sen kiertosymmetrian asteen sanotaan olevan kolme.
Jos kuviota kierrettäessä se sopii omille ääriviivoilleen useammin kuin kerran täyden kierroksen aikana, niin kuviolla on kiertosymmetriaa.
Katso myös Symmetriakeskus, Kiertosymmetrian kertaluku, Symmetria, Kierto, Kiertosymmetrian akseli, Pyörähdysakseli.
Kiertosymmetrian akseli, Pyörähdysakseli (engl. Axis of rotational symmetry)
Suora, joka pysyy paikallaan kierrossa.
Katso myös Kiertosymmetria, Pyörähdyssymmetria, Suora, Akseli.
Kiertosymmetrian kertaluku (engl. Order of symmetry)
Kuvion kiertosymmetrian kertaluku on se määrä, kuinka monta kertaa kuvio voidaan sitä kierrettäessä asettaa omille ääriviivoilleen täyden kierroksen aikana.
Neliö voidaan asettaa neljä kertaa omille ääriviivoilleen täyden kierroksen aikana. Neliön kiertosymmetrian kertaluvun sanotaan olevan neljä. Suorakulmio, joka ei ole neliö, voidaan asettaa kaksi kertaa omille ääriviivoilleen täyden kierroksen aikana. Sen kiertosymmetrian kertaluku on kaksi.
Katso myös Järjestys, Kiertosymmetria, Pyörähdyssymmetria, Ominaisuus, jonka arvot ovat diskreettejä.
Kiihdyttää, Kiihtyä (engl. Accelerate)
Kun jokin kiihtyy, niin sen nopeus kasvaa. Kiihtyvyys mitataan jakamalla tietyn ajan kuluessa tapahtunut nopeuden muutos kyseisen ajanjakson pituudella, joten kiihtyvyyden yksikkö on metri sekunnissa toiseen.
Kiihtyä, Kiihdyttää (engl. Accelerate)
Kun jokin kiihtyy, niin sen nopeus kasvaa. Kiihtyvyys mitataan jakamalla tietyn ajan kuluessa tapahtunut nopeuden muutos kyseisen ajanjakson pituudella, joten kiihtyvyyden yksikkö on metri sekunnissa toiseen.
Kiinalainen jäännöslause (engl. Chinese remainder theorem)
Olkoot $n_1, n_2, \ldots, n_k$ kokonaislukuja ja $m_1, m_2, \ldots, m_k$ pareittain suhteellisia alkulukuja, missä $k \ge 2$. Tällöin kongruenssiryhmällä $x \equiv n_1 \mathrm{mod}\ m_1$, $x \equiv n_2 \mathrm{mod}\ m_2$, $\ldots$, $x \equiv n_k \mathrm{mod}\ m_k$ on ratkaisu ja tämä ratkaisu on yksikäsitteinen $\mathrm{mod}\ m_1 m_2 \cdots m_k$.
Katso myös Modulaariaritmetiikka, Lause.
Kiintopiste (engl. Fixed point)
Olkoot $X$ joukko ja $f \colon X \rightarrow X$. Piste $x \in X$ on kuvauksen $f$ kiintopiste, jos pätee $f(x)=x$.
Katso myös Transformaatio, Piste, Kiintopistelause.
Kiintopistelause (engl. Fixed point theorem)
Lause, joka sanoo, että kuvauksella on tiettyjen ehtojen vallitessa kiintopiste.
Esimerkki: Olkoot $[a,b] \subseteq \mathbb{R}$ ja $f : [a,b] \to [a,b]$. Jos on olemassa sellainen $0 \le L \lt 1$, että \[ |f(x)-f(y)| \le L|x-y| \] pätee kaikilla $x, y \in [a,b]$, niin kuvauksella $f$ on yksikäsitteinen kiintopiste. Toisin sanoen, on olemassa täsmälleen yksi sellainen piste $v \in [a,b]$, että $f(v) = v$. Tätä tulosta kutsutaan Banachin kiintopistelauseeksi.
Katso myös Kiintopiste, Brouwerin kiintopistelause.
Kilo (engl. Kilo)
Etuliite, joka tarkoittaa tuhatta. Kilolle käytetään merkkiä k, esimerkiksi km on tuhat metriä.
Tietojenkäsittelyssä laskettaessa tavujen lukumäärää kilo tarkoittaa lukua $2^{10}$ eli 1024.
Kilometri (engl. Kilometer, Kilometre)
Pituuden mitta. Yksi kilometri on sama kuin tuhat metriä.
Katso myös Metri, Senttimetri.
Kilotavu (engl. Kilobyte)
1024 eli $2^{10}$ tavua.
Katso myös Tavu.
Klassinen todennäköisyys, Vedonlyöntisuhde (engl. Odds)
Todennäköisyyslaskennassa voittamisen todennnäköisyyden suhde häviämisen todennnäköisyyteen.
Tapahtuman tapahtumisen todennäköisyys jaettuna todennäköisyydellä, että se ei tapahdu. Matematiikassa on yleensä hyödyllistä puhua vain pelkistä todennäköisyyksistä.
Katso myös Todennäköisyys.
Koaksiaalinen (engl. Coaxial)
Sama-akselinen, saman akselin ympärillä oleva.
Koaksiaaliset ympyrät (engl. Coaxial circles)
Kaksi tai useampi ympyrä, jotka kulkevat annetun pisteparin kautta. Tällaisia ympyröitä on jokaista pisteparia kohti ääretön määrä.
Katso myös Ympyrä.
Koe (engl. Experiment)
Yksittäinen järjestetty satunnaistapahtuma. Esimerkiksi nopan tai rahan heitto. Kokeita käytetään erityisesti syy-seuraussuhteen selvittämiseen. Esimerkiksi tutkittaessa lannoituksen vaikutusta satoisuuteen jaetaan tasalaatuinen alue ruutuihin. Ruudut jaetaan satunnaisesti koeryhmiin, joita lannoitetaan määrätyn kaavion mukaisesti. Yksittäinen ruutu, jonka lannoitemäärä tunnetaan, on koe, jossa mitataan ruudun sato.
Katso myös Buffonin neula.
Kofaktori (engl. Cofactor)
Neliömatriisin $A$ alkioon $a_{ij}$ liittyvä kofaktori on sellaisen $A$:n alimatriisin determinantti, joka saadaan poistamalla $A$:sta rivi $i$ ja sarake $j$.
Esimerkiksi neliömatriisin $\left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right)$ alkioon $2$ liittyvä kofaktori on $\left| \begin{array}{cc} 4 & 6 \\ 7 & 9 \end{array} \right| = 4 \times 9 - 6 \times 7 = -6$.
Katso myös Determinantti, Matriisi.
Kohtisuora (engl. Perpendicular)
Kaksi suoraa ovat kohtisuorassa toisiaan vastaan, jos niiden välinen kulma on suora kulma. Vaakasuora suora on kohtisuorassa pystysuoraa vastaan ja päin vastoin.
Katso myös Suora pyramidi, Ortogonaalinen, Suora särmiö, Yhdensuuntainen, Suora, Kantapiste, Normaalivektori, Kahden tason välinen kulma.
Kohtisuorasti leikkaavat ympyrät (engl. Orthogonal circles)
Kaksi ympyrää, jotka leikkaavat toisensa suorassa kulmassa, ovat ortogonaaliset. Huomaa, että jos ympyrät leikkaavat toisensa yhdessä pisteessä kohtisuorasti, ne leikkaavat myös toisessa leikkauspisteessä kohtisuorasti.
Katso myös Ortogonaalinen, Ympyrä.
Kohtisuorat suorat (engl. Perpendicular lines)
Tason kohtisuorille suorille, joiden kulmakertoimet ovat $m_{1}$ ja $m_{2}$, pätee $m_{1} \cdot m_{2} = -1$.
Katso myös Suora.
Kokonainen funktio (engl. Entire)
Kompleksilukujen joukossa $\mathbf{C}$ määritelty funktio, joka on analyyttinen koko $\mathbf{C}$:ssä.
Katso myös Holomorfinen, Analyyttinen, Liouvillen lause.
Kokonaisalue (engl. Integral domain)
Olkoon $R$ vaihdannainen rengas. Alkio $0 \neq a \in R$ on nollanjakaja, jos $ab = 0$ jollain $0 \neq b \in R$. Vaihdannainen rengas $R$ on kokonaisalue, jos siinä ei ole nollanjakajia.
Kokonaislukujen rengas on kokonaisalue.
Määritellään rengas $R=(\{0,1,2,3\},+_R,*_R)$, ja siellä laskutoimitukset seuraavasti: $a +_R b = c$, jos luvuilla $a+b$ (kokonaislukujen yhteenlasku) ja $c$ on sama jakojäännös jaettaessa $4$:llä. (Kokonaislukujen jakolasku.) Samoin $a *_R b = c$, jos luvuilla $ab$ (kokonaislukujen kertolasku) ja $c$ on sama jakojäännös jaettaessa $4$:llä. (Kokonaislukujen jakolasku.)
Nyt $R$ on vaihdannainen rengas, mutta se ei ole kokonaisalue, koska $2 *_R 2 = 0$.
Katso myös Rengas, Yksikäsitteisen tekijöihinjaon alue, UFD.
Kokonaislaskenta, Laskenta (engl. Census)
Otos on samankokoinen kuin populaatio (perusjoukko). Toisin sanoen, jokainen populaation jäsen on mukana otoksessa.
Kokonaisluku (engl. Whole number)
Kokonaisluku voi olla positiivinen tai negatiivinen. Positiiviset kokonaisluvut ovat $1,2,3,4,\ldots$. Negatiiviset kokonaisluvut ovat $-1,-2,-3,-4,\ldots$. Nolla on kokonaisluku, joka ei ole positiivinen eikä negatiivinen. Positiivisia kokonaislukuja sanotaan luonnollisiksi luvuiksi. On sopimuskysymys, luetaanko myös nolla luonnolliseksi luvuksi.
Katso myös Rationaaliluku, Reaaliluku, Luonnollinen luku, Kokonaisluku.
Kokonaisluku (engl. Integer)
Kokonaisluku voi olla positiivinen tai negatiivinen. Positiiviset kokonaisluvut ovat $1,2,3,4,\ldots$. Negatiiviset kokonaisluvut ovat $-1,-2,-3,-4,\ldots$. Nolla on kokonaisluku, joka ei ole positiivinen eikä negatiivinen. Positiivisia kokonaislukuja sanotaan luonnollisiksi luvuiksi. On sopimuskysymys, luetaanko myös nolla luonnolliseksi luvuksi.
Kokonaislukujen joukolle $\{\dots, -3, -2, -1, 0, 1, 2, 3,\dots\}$ käytetään merkintää $\mathbb{Z}$.
Katso myös int, Mersennen luku, Monikerta, Jakojäännös, Osoittaja, Rationaaliluku, Osamäärä, Jaottomuus, Kertoma, Nimittäjä, Jaettava, Jaollisuus, Tekijä, Kuutioluku, Kokonaisluku, Tekijä, Tetraedriluku, Pascalin kolmio, Suurin lukua pienempi kokonaisluku, Joukko, Fermat'n osamäärä, Luonnollinen luku, Automorfinen luku, Jakaja, Eulerin $\varphi$-funktio, Monikulmioluku.
Kokonaisosa, Lattia (engl. Floor)
Lattia- eli kokonaisosafunktion arvo luvulla x on suurin kokonaisluku, joka ei ole suurempi kuin x. Lattiafunktiolle käytetään merkintää $ \lfloor x \rfloor $ .
Katso myös Funktio, Kuvaus, Kattofunktio, Ominaisuus, jonka arvot ovat jatkuvia.
Kollineaarinen (engl. Collinear)
Pistejoukko on kollineaarinen, jos kaikki pisteet sijaitsevat samalla suoralla eli jos on olemassa suora, joka kulkee kaikkien joukon pisteiden kautta. Jokainen kahden pisteen muodostama joukko on kollineaarinen, mutta jokainen kolmen pisteen muodostama joukko ei ole.
Kolmen tai useamman tason muodostama joukko on kollineaarinen, jos kaikki tasot leikkaavat pitkin yhtä suoraa.
Katso myös Samassa tasossa oleva.
Kolmannen asteen polynomi, Kuutiollinen polynomi (engl. Cubic)
Polynomi, joka sisältää muuttujansa kuution eli kolmannen potenssin, mutta ei tätä korkeampia potensseja. Esimerkiksi polynomi $2x^3 + x +14$ on kuutiollinen.
Katso myös Polynomin tekijöihinjako, Polynomi, Cardanon menetelmä, Elliptinen integraali.
Kolmannen asteen polynomiyhtälön juuret (engl. Roots of a cubic)
Jos yhtälön $ ax^3 + bx^2 +cx +d = 0 \quad ( a \neq 0 ) $ juuret ovat $ \alpha, \beta, \gamma , $ tällöin \[ \alpha + \beta + \gamma = - \frac{b}{a} , \] \[ \beta \gamma + \gamma \alpha + \alpha \beta = \frac{c}{a} , \] \[ \alpha \beta \gamma = - \frac{d}{a} . \]
Katso myös Polynomin nollakohta.
Kolmannen asteen yhtälö (engl. Cubic equation)
Yhtälö muotoa $a x^3 + b x^2 + c x + d = 0$, missä kerroin $a \neq 0$, eli muuttujan $x$ kolmannen asteen polynomiyhtälö. Tällaisella yhtälöllä on $1$, $2$ tai $3$ reaalista ratkaisua eli juurta.
Kolmannen lajin elliptinen integraali (engl. Elliptic integral of the third kind)
Elliptinen integraali muotoa \[ \int_{0}^{x} \frac{dt}{(1+nt^2)\sqrt{((1-t^2)(1-k^2t^2))}}, \] missä $k$ on elliptinen moduuli ja $n$ on parametri, ns. elliptinen karakteristika.
Katso myös Elliptinen integraali.
Kolmannen poissuljetun laki (engl. Excluded third, Excluded middle)
Kolmannen poissuljetun laki kuuluu seuraavasi: Jos $\phi$ on mikä tahansa väite, niin $\phi \vee \neg \phi$ on tosi.
Kolmannen poissuljetun laki sanoo siis, että mikä tahansa väite joko on tosi tai ei ole tosi; kolmatta vaihtoehtoa ei ole.
Kolme, 3 (engl. 3, Three)
3 = 2 + 1. Kolme on toinen alkuluku ja toinen kolmioluku.
Kolme on Fermat'n alkuluku: 3 = $2^{2^{0}}$ + 1.
Elämme kolmiulotteisessa maailmassa.
Luku on kolmella jaollinen, jos ja vain jos sen numeroiden summa on kolmella jaollinen.
3 on toinen onnenluku.
3 on ensimmäinen Mersennen alkuluku: 3 = $2^{2}$ - 1.
?(3) = 2, d(3) = 2, ?(3) = 4.
Kolme on yhtä suuri kuin kaksi plus yksi. Se on toinen alkuluku ja toinen kolmioluku.
Se on Fermat'n alkuluku, sillä se on yhtä suuri kuin $2^{2^{0}}+1$. 3 on tavallisen arkimaailmamme ulottuvuuksien lukumäärä. Luku on jaollinen kolmella jos ja vain jos sen numeroiden summa on jaollinen kolmella. 3 on toinen onnenluku. 3 on pienin Mersennen alkuluku: $3 = 2^{2}-1$. $\phi(3) = 2$, $d(3) = 2$, $\sigma(3) = 4$.
Katso myös Onnekkaat luvut, Kolmio, Mersennen alkuluku, Fermat'n alkuluku.
Kolmekymmentä, 30 (engl. 30, Thirty)
30 on suurin sellainen luku $n$, että kaikilla $n$:ää pienemmillä yhdistetyillä luvuilla on jokin yhteinen tekijä $n$:n kanssa.
Säännöllisen dodekaedrin ja säännöllisen ikosaedrin särmien lukumäärä on 30.

Katso myös Kymmenen monikerta, Dodekaedri, Ikosaedri.
Kolmen ympyrän lause (engl. Pivot theorem)
Valitaan annetun kolmion $ABC$ sivulta $BC$ piste $D$, sivulta $CA$ piste $E$ ja sivulta $AB$ piste $F$. Tällöin kolmioiden $AEF$, $BFD$ ja $CDE$ ympäri piirretyillä ympyröillä on yhteinen piste.
Kolmetoista, 13 (engl. 13, Thirteen, baker's dozen)
13 on kuudes alkuluku ja kahden neliön summa: $4+9 = 13$. Se on viides Luckyn luku ja seitsemäs Fibonaccin luku. Se on Arkhimedeen monitahokkaiden lukumäärä.
$\phi(13) = 12$, $d(13) = 2$, $\sigma(13) = 14$.

Katso myös Arkhimedeen monitahokas, Onnekkaat luvut, Alkuluku, Fibonaccin luku.
Kolmijako (engl. Trisect)
Kolmeen yhtä suureen osaan jakaminen. Tätä sanaa käytetään usein tarkoittamaan kulman jakamista kolmeen yhtä suureen osaan. Kulman kolmiajakoa on mahdotonta suorittaa pelkästään harpin ja viivoittimen avulla.
Katso myös Konstruktio, Konstruointi.
Kolmijalka (engl. Tripod)
Laite, esimerkiksi, jossa on kolme jalkaa, esimerkiksi kameran jalusta.
Kolmijärjestelmä (engl. Ternary)
Lukujärjestelmä, jonka kantaluku on kolme.
Katso myös Lukujärjestelmä, Kantaluku, Binäärilukujärjestelmä.
Kolmikko (engl. Triple)
Kolmen alkion järjestetty joukko eli kolmijäseninen jono.
Katso myös Joukko.
Kolmikulmainen (engl. Triangular)
Kolmion muotoinen.
Katso myös Kolmio.
Kolmikymmenluku (engl. Thirties)
Vuodet 1930--39.
Kolmio (engl. Triangle)
Monikulmio, jossa on kolme sivua.
Kolmion kulmien summa on aina $180^{\circ}$.
Kolmioita voidaan luokitella; joko kulmien mukaan, kuten teräväkulmainen, tylppäkulmainen, suorakulmainen tai tasakulmainen kolmio; tai sivujen mukaan, kuten erisivuinen, tasakylkinen tai tasasivuinen kolmio.
Katso myös 3, Kolme, Kolmion korkeusjana, Vastainen kulma, Kolmion tangenttikolmio, Kolmioepäyhtälö, Erisivuinen kolmio, Mediaalikolmio, Kolmikulmainen, Neliöpohjainen pyramidi, Oktaedri, Tetraedri, Pythagoraan lause, Ortokolmio, Suorakulmainen kolmio, Monikulmio, Oktaedrin sivutahkoverkko, Tasakylkinen kolmio, Hypotenuusa, Tasasivuinen kolmio, Teräväkulmainen kolmio, Heronin kaava, Tylppäkulmainen kolmio, Yhtenevät kolmiot, Kosinilause, Kolmion ala, Cevan lause, Gergonnen kolmio, Menelausin lause.
Kolmioepäyhtälö (engl. Triangle inequality)
Jos $a$, $b$ ja $c$ ovat kolmion sivujen pituudet, niin $a+b \geq c$.
Katso myös Erisuuruus, Kolmio, Metriikka, Epäyhtälö, Metrinen avaruus.
Kolmioluku (engl. Triangular number)
Luku, jonka osoittamasta määrästä pisteitä voidaan muodostaa kolmion muotoinen kuvio. Esimerkiksi $1$, $3$, $6$ ja $10$ ovat kaikki kolmiolukuja.
$n$:s kolmioluku on $\frac{n(n+1)}{2}$.Jokainen luonnollinen luku on enintään kolmen kolmioluvun summa.
Jos $t$ on kolmioluku, niin $8t+1$ on neliöluku. $n$:nnen kolmioluvun neliö on yhtä suuri kuin $n$:n ensimmäisen kuutioluvun summa. Jotkin kolmioluvut ovat myös neliölukuja, mutta mikään kolmioluku ei voi olla kolmas, neljäs tai viides potenssi.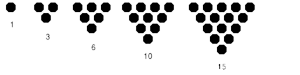
Katso myös Erotusjono, Neliöluku, Tetraedriluku, Monikulmioluku.
Kolmiomatriisi (engl. Triangular matrix)
Matriisi, jonka kaikki päälävistäjän yläpuolella olevat alkiot tai kaikki päälävistäjän alapuolella olevat alkiot ovat nollia.
Katso myös Päälävistäjä, Alakolmiomatriisi, Yläkolmiomatriisi, Matriisi.
Kolmiomittaus (engl. Triangulate)
Kolmiomittaus on tapa selvittää maapallon pinnalla olevien paikkojen välisiä etäisyyksiä mittaamalla kiintopisteiden muodostamien suurten kolmioiden kulmia.
Kolmion ala (engl. Area of triangle, Area of a triangle)
Kolmion alan $A$ voi laskea eri tavoin sen mukaan, mitä osia kolmiosta tunnetaan.
Jos tunnetaan sivu $a$ ja sitä vastaava korkeus $h$, niin $A=\frac{1}{2}ah$. Jos kolmio on suorakulmainen ja sen lyhemmät sivt ovat $a$ ja $b$, niin $A=\frac{1}{2}ab$. Jos kolmiosta tunnetaan sivut $a$ ja $b$ ja niiden välinen kulma $C$, niin $A=\frac{1}{2}ab\sin C$. Jos kolmiosta tunnetaan kaikki sivut, $a$, $b$ ja $c$, ja jos $p=\frac{1}{2}(a+b+c)$, niin \[A=\sqrt{p(p-a)(p-b)(p-c)}.\]Katso myös Kolmio.
Kolmion korkeusjana (engl. Altitude of triangle)
Kolmion korkeusjana on kolmion kärjestä vastakkaiselle sivulle piirretty sivua vastaan kohtisuora jana.
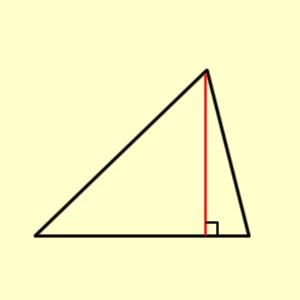
Katso myös Korkeus, Ortosentri, Ortokolmio, Feuerbachin ympyrä, Yhdeksän pisteen ympyrä.
Kolmion massakeskipiste (engl. Centre of mass of a triangular lamina)
Kolmion massakeskipiste sijaitsee millä tahansa kolmion keskijanalla ja jakaa jokaisen keskijanan kärjestä lukien suhteessa $2:1$.
Katso myös Painopiste, Keskijana, Mediaani, Massakeskipiste, Painopiste, Tasoalueen massakeskipiste.
Kolmion ortokeskuksen määrittäminen (engl. Construct the orthocentre)
Kolmion $ABC$ ortokeskus eli korkeusjanojen leikkauspiste määritetään seuraavasti. Piirretään kärjen $A$ kautta kulkeva suora, joka on kohtisuorassa sivua $BC$ vastaan. Piirretään kärjen $B$ kautta kulkeva suora, joka on kohtisuorassa sivua $CA$ vastaan. Näiden kahden suoran leikkauspiste on kolmion $ABC$ korkeusjanojen leikkauspiste.
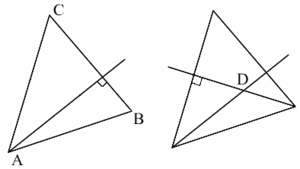
Katso myös Ortosentri, Konstruktio, Konstruointi.
Kolmion painopisteen määrittäminen (engl. Construct the centroid)
Kolmion $ABC$ painopiste määritetään seuraavasti. Etsitään sivujen $AB$ ja $AC$ keskipisteet $D$ ja $E$. Piirretään janat $CD$ ja $BE$. Niiden leikkauspiste $F$ on kolmion painopiste.
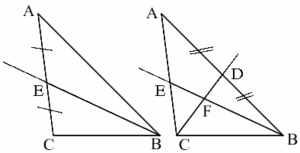
Katso myös Painopiste, Konstruktio, Konstruointi.
Kolmion sisään piirretyn ympyrän keskipisteen määrittäminen (engl. Construct the incentre)
Annetun kolmion sisään piirretyn ympyrän keskipiste määritetään seuraavasti. Piirretään kolmion minkä tahansa kahden kulman puolittajat. Näiden kulmanpuolittajien leikkauspiste on kolmion sisään piirretyn ympyrän keskipiste.
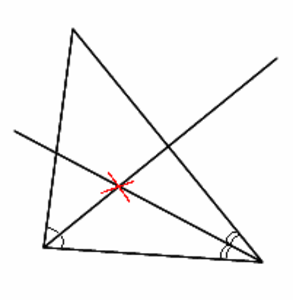
Katso myös Sisään piirretyn ympyrän keskipiste, Konstruktio, Konstruointi.
Kolmion sisään piirretyn ympyrän muodostaminen (engl. Construct the inscribed circle of a triangle)
Kolmion sisään piirretty ympyrä muodostetaan seuraavasti. Piirrä kahden kolmion kulman kulmanpuolittajat. Olkoon $A$ näiden leikkauspiste. Piirrä pisteestä $A$ jotakin kolmion sivua vastaan kohtisuora jana. Olkoon $B$ janan ja kyseisen kolmion sivun leikkauspiste. Piirrä lopuksi ympyrä, jonka keskipiste on $A$ ja säde on $AB$.
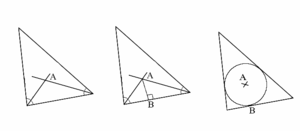
Katso myös Kulman puolittaja, Sisään piirretty ympyrä, Konstruktio, Konstruointi.
Kolmion tangenttikolmio (engl. Tangential triangle)
Annetun kolmion $ABC$ ympäri piirretyn ympyrän pisteisiin $A$, $B$ ja $C$ piirretyt ympyrän tangentit muodostavat uuden kolmion, jota sanotaan kolmion $ABC$ tangenttikolmioksi.
Katso myös Kolmio, Tangentti, Monikulmion ympäri piirretty ympyrä.
Kolmion ympäri piirretyn ympyrän keskipiste (engl. Circumcentre, Circumcenter)
Kolmion ympäri piirretyn ympyrän keskipiste on kolmion sivujen keskinormaalien leikkauspiste.
Katso myös Keskipiste, Sisään piirretyn ympyrän keskipiste, Painopiste, Eulerin suora.
Kolmion ympäri piirretyn ympyrän muodostaminen (engl. Construct the outscribed circle)
Kolmion $ABC$ ympäri piirretty ympyrä muodostetaan seuraavasti. Piirretään sivujen $AB$ ja $BC$ keskinormaalit. Ne leikkaavat toisensa pisteessä $D$. Piirretään ympyrä, jonka keskipiste on $D$ ja joka kulkee pisteen $A$ kautta. Tämä ympyrä on kolmion $ABC$ ympäri piirretty ympyrä.
Katso myös Ympyrän piirtäminen, Keskinormaalin piirtäminen, Suorien leikkauspiste, Konstruktio, Konstruointi.
Kolmioon liittyvät ympyrät (engl. Circles of a triangle)
Annettuun kolmioon liittyen voidaan piirtää useita ympyröitä, kuten esimerkiksi kolmion sisään piirretty ympyrä, kolmion ympäri piirretty ympyrä ja yhdeksän pisteen ympyrä.
Katso myös Lemoinen ympyrä, Sisään piirretty ympyrä, Ympyrä, Monikulmion ympäri piirretty ympyrä, Feuerbachin ympyrä, Yhdeksän pisteen ympyrä.
Kolmioprisma (engl. Triangular prism)
Särmiö, jonka pohjat ovat kolmioita.
Tunnetun suklaamerkin suklaa on pakattu pitkään kolmion muotoiseen särmiöön.

Kolmitulo (engl. Triple product)
Kolmen vektorin tulo.
Katso myös Vektorikolmitulo.
Kombinaatio (engl. Combination)
Kombinaatio on annetusta joukosta valittu tietynkokoinen osajoukko, missä alkioiden valintajärjestyksellä ei ole merkitystä. Esimerkiksi lottonumeroiden $7$-alkioinen kombinaatio on joukon $\{ 1,2, \ldots, 39 \}$ mikä tahansa $7$-alkioinen osajoukko. Tällaisten kombinaatioiden lukumäärän antaa binomikerroin $${n \choose k} = \frac{n!}{k!(n-k)!},$$ missä $n!$ on luvun $n$ kertoma eli luku $1 \cdot 2 \cdots (n-1) \cdot n$.
Esimerkiksi kirjaimista $A, B, C, D$ voidaan valita kaksi eri kirjainta $$ {4 \choose 2} = \frac{4!}{2!(4-2)!} = \frac{4 \times 3 \times 2 \times 1}{(2 \times 1) \times (2 \times 1)} = 6$$ eri tavalla, kun valintajärjestykseen ei kiinnitetä huomiota. Nämä $6$ eri tapaa ovat $AB, AC, AD, BC, BD, CD$.
Katso myös Valita, Kombinatoriikka, Binomikerroin, Permutaatio.
Kombinatoriikka (engl. Combinatorics)
Matematiikan alue, joka tutkii eri tapoja valita ja järjestää annetun joukon alkioita. Kombinatoriikassa tutkitaan myös sitä, kuinka monella eri tavalla jokin asia voidaan tehdä.
Katso myös Diskreetti matematiikka, Alkeismatematiikka, Valita, Kombinaatio, Pascalin kolmio, Kombinatorinen argumentti, Päätöspuu, Permutaatio.
Kombinatorinen argumentti (engl. Combinatorial argument)
Argumentti, joka perustuu joukon alkioiden järjestysten tai kombinaatioiden lukumäärien laskemiseen tai siihen, kuinka monella eri tavalla jokin asia voidaan tehdä.
Katso myös Perustelu, Kombinatoriikka.
Kommutaattori (engl. Commutator)
Ryhmän $G$ kahden alkion $a$ ja $b$ kommutaattori $[a,b]$ määritellään asettamalla \[ [a,b] = a \cdot b \cdot a^{-1} \cdot b^{-1}. \]
Kvanttimekaniikassa operaattorien $A$ ja $B$ kommutaattori $[A,B]$ on $AB-BA$.
Katso myös Ryhmä, Antikommutaattori, Kommutaattorialiryhmä, Alkio.
Kommutaattorialiryhmä (engl. Commutator subgroup)
Ryhmän $G$ kommutaattorialiryhmä $G'$ on $G$:n kommutaattorien generoima aliryhmä eli alkioiden $[a,b]$, missä $a,b \in G$, generoima $G$:n aliryhmä.
Katso myös Aliryhmä, Kommutaattori.
Kommutatiivinen, Vaihdannainen (engl. Commutative)
Yhteenlaskua kutsutaan vaihdannaiseksi, koska yhteenlaskun lopputulos on sama riippumatta siitä kummassa järjestyksessä yhteenlasku suoritetaan. Yhteenlaskettavien laskujärjestys voidaan siis vaihtaa ilman, että se vaikuttaa laskun lopputulokseen.
Esimerkiksi $3+5$ antaa saman tuloksen kuin $5+3$.
Kertolasku on myös vaihdannainen. Vähennyslasku ja jakolasku sen sijaan eivät ole vaihdannaisia. Esimerkiksi $2-1$ on eri luku kuin $1-2$ ja samoin $4/2$ on eri luku kuin $2/4$.
Laskutoimitus $\circ$ on vaihdannainen, jos se toteuttaa ehdon $a \circ b = b \circ a$ kaikilla laskutoimituksen määrittelyjoukkoon kuuluvilla alkioilla $a$ ja $b$.
Katso myös Kommutoida, Abelin ryhmä, Antikommutatiivinen, Binäärinen kuvaus, Vektorien tensoritulo, Kaksipaikkainen kuvaus.
Kommutoida (engl. Commute)
Jonkin joukon (tai kunnan tai ryhmän tms.) kaksi alkiota kommutoivat tietyn operaation suhteen, jos järjestys, jossa alkioita sovelletaan operaatiossa, ei vaikuta lopputulokseen.
Esimerkiksi alkioiden $a$ ja $b$ sanotaan kommutoivan operaation $*$ suhteen, jos $a * b = b * a$.
Katso myös Laskutoimitus, Vaihdannainen, Kommutatiivinen, Kunta, Ryhmän keskus, Alkio.
Kompakti (engl. Compact)
Topologinen avaruus on kompakti, mikäli sen jokaisella avoimella peitteellä on äärellinen osapeite.
Heine-Borelin lauseen mukaan suljettu ja rajoitettu reaaliväli $[a,b]$ on kompakti.
Avaruuden $\mathbb{R}^n$ kompakteja osajoukkoja ovat täsmälleen kaikki suljetut ja rajoitetut joukot.
Metrisen avaruuden osajoukko on kompakti jos ja vain jos se on jonokompakti.
Kompaktin avaruuden kuva jatkuvassa kuvauksessa on kompakti. Kompaktin avaruuden suljetut osajoukot ovat kompakteja. Kompakteissa Hausdorff-avaruuksissa pätee vahvempikin ehto: Osajoukko on kompakti jos ja vain jos se on suljettu.
Katso myös Totalisti rajoitettu, Prekompakti, Avoin peite, Kontinuumi, Jonokompakti, Hausdorff-avaruus, Hausdorffin avaruus, Jatkumo.
Kompleksikonjugaatti, Liittoluku (engl. Complex conjugate)
Kompleksiluvun $z = x+iy$ liittoluku eli kompleksikonjugaatti on $\bar{z} = x-iy$.
Katso myös Unitaarinen matriisi, Kompleksiluku, Normaali matriisi, Hermiittinen matriisi.
Kompleksiluku (engl. Complex number)
Kompleksiluvut koostuvat reaaliluvuista ja imaginaariluvuista. Jos imaginaariluvuilla ajatellaan olevan oma lukusuoransa, joka on kohtisuorassa reaalilukusuoraa vastaan, niin silloin kompleksiluvut ovat näiden lukusuorien muodostaman kompleksitason pisteitä. Kompleksiluvun reaali- ja imaginaariosa ovat silloin aivan kuten reaalitason pisteen $x$- ja $y$-koordinaatti.
Kompleksiluku on luku muotoa $x+yi$, missä $x, y$ ovat reaalilukuja ja $i$ toteuttaa yhtälön $i^2 = -1$.
Kompleksilukujen joukkoa merkitään symbolilla $\mathbb{C}$. Siis $\mathbb{C} = \{ x+i y : x,y \in \mathbb{R} \}$.
Katso myös Luku, Argand, Imaginaariluku, Reaaliluku, Kompleksiluvun käänteisluku, Riemannin hypoteesi, Analyyttinen funktio, Liittoluku, Kompleksikonjugaatti, Eulerin kaava, Algebran peruslause, Gaussin luku, Gaussin kokonaisluku.
Kompleksiluvun argumentti (engl. Argument of a complex number)
Jos $z$ on nollasta eroava kompleksiluku ja $Z$ lukua $z$ edustava kompleksitason piste, niin luvun $z$ argumentti, $\arg z$, on $z$:n paikkavektorin ja positiivisen reaaliakselin välinen kulma. Jos $z=x+iy$, niin $\arg z=\theta$, missä $\theta$ on ehdot \[ \cos\theta=\frac{x}{|z|},\quad \sin\theta=\frac{y}{|z|} \] toteuttava luku. $\theta$ voidaan rajata välille $-\pi \lt \theta \le \pi$.
Katso myös Kulma, $\arg$, Reaaliluku, Kompleksiluvun moduli, Ominaisuus, jonka arvot ovat jatkuvia.
Kompleksiluvun käänteisluku (engl. Reciprocal of a complex number)
Jos $z=x+yi $, \[ \frac{1}{z} = \frac{x-iy}{x^2 + y^2 } = \frac{\overline{z}}{|z|^2} . \] Jos $z=re^{\phi i}$, niin $\frac{1}{z}= \frac{1}{r} e^{-\phi i}$.
Katso myös Käänteisluku, Kompleksiluku.
Kompleksiluvun moduli (engl. Modulus of a complex number)
Kompleksiluvun $z$ moduli $|z|$ tarkoittaa lukua $z$ vastaavan kompleksitason pisteen etäisyyttä origosta. Jos $z$ on annettu muodossa $z=x+yi$, saadaan moduli kaavalla $|z|=(x^2 + y^2)^{1/2}$. Jos $z$ on annettu muodossa $z=re^{\phi i}$, on $|z|=r$. Kompleksikonjugaattia käyttäen saadaan $|z|=(z \overline{z})^{1/2}$.
Katso myös Kompleksiluvun argumentti, Argand.
Kompleksinen (engl. Complex)
Matematiikassa jotakin kutsutaan kompleksiseksi, jos siinä on kyse kompleksiluvuista eli luvuista, joilla on reaalinen osa ja imaginaarinen osa.
Joskus kompleksisella tarkoitetaan samaa kuin monimutkaisella.
Kompleksitaso (engl. Argand diagram, Argand plane, Complex plane)
Koordinaattitaso, jonka määrittelevät kaksi akselia: reaaliakseli ja imaginaariakseli. Nämä akselit ovat kohtisuorassa toisiaan vastaan.
Katso myös Taso, Lukusuora, Argand, Polkuintegraali.
Komplementin todennäköisyys (engl. Probability of complement)
Koska E ja sen komplementti E' ovat erillisiä, tiedetään, että $ \mathrm{p(E} \cup \mathrm{E} ^{\prime} ) = \mathrm{p(E)+p(E} ^{\prime} {)}. $ Mutta $ \mathrm{E} \cup \mathrm{E} ^{\prime} = \mathrm{S} $ ja $p(S)=1$, joten $p(E)+p(E")=1$ eli $p(E")=1-p(E)$ .
Katso myös Erillisten tapahtumien todennäköisyys, Komplementtijoukko.
Komplementti (engl. Complement)
Jonkin asian komplementti on se, mikä tarvitaan kyseisen asian täydentämiseksi. Kulman komplementti on kulma, joka tarvitaan, jotta kulmat yhdessä muodostaisivat suoran kulman.
Katso myös Funktio, Kuvaus, Komplementtijoukko, Komplementtikulma.
Komplementtijoukko (engl. Complement of a set)
Joukon $A$ komplementtijoukko eli komplementti perusjoukon $S$ suhteen koostuu niistä joukon $S$ alkioista, jotka eivät kuulu joukkoon $A$. Joukon $A$ komplementtia merkitään usein $\overline{A}$, $\mathrm{C}A$, $A^{\mathrm{c}}$ tai $S \setminus A$. Huomaa, että $A \cap \overline{A} = \emptyset$ ja $A \cup \overline{A} = S$.
Katso myös Komplementti, Komplementin todennäköisyys, Joukko, Lähtöjoukko, Määrittelyjoukko.
Komplementtikulma (engl. Complementary angle)
Kaksi kulmaa, joiden summa on suora kulma, ovat toistensa komplementtikulmia.
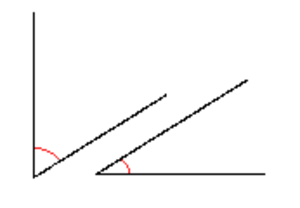
Katso myös Kulma, Komplementti, Suplementtikulma.
Komponentti (engl. Component)
Jos kahden tai useamman vektorin $\bf a$, $\bf b$, $\bf c$, $\dots$\ summa on yhtä suuri kuin annettu vektori $\bf x$, niin vektoreita $\bf a$, $\bf b$, $\bf c$, $\dots$\ kutsutaan vektorin $\bf x$ komponenteiksi. Samoin jos $x=(p,q)$, niin $x = (p,0)+(0,q)$, joten $(p,0)$ ja $(0,q)$ ovat $x$:n komponentit.
Katso myös Vektori, Vektorien yhteenlasku, Jakaa komponetteihin.
Kongruenssi (engl. Congruence)
Olkoot $x$ ja $y$ kokonaislukuja ja $m$ positiivinen kokonaisluku. Jos erotus $x-y$ on jaollinen luvulla $m$ (eli jaettaessa luvut $x$ ja $y$ luvulla $m$ on jakojäännös sama), niin sanotaan, että $x$ ja $y$ ovat kongruentteja modulo $m$, ja merkitään $x \equiv y (\mathrm{mod}\ m)$. Lauseketta $x \equiv y (\mathrm{mod}\ m)$ kutsutaan kongruenssiksi.
Esimerkiksi $9 \equiv 5 (\mathrm{mod}\ 4)$ pitää paikkansa, koska $9 - 5 = 4$.
Katso myös Modulaariaritmetiikka, Jakojäännös.
Kongruentit luvut (engl. Congruent numbers)
Kaksi lukua $a$ ja $b$ ovat kongruentteja modulo $m$, jos jakolaskuissa \[ \frac{a}{m} \quad\text{ja}\quad \frac{b}{m}\] jakojäännökset ovat samat. Tällöin $a-b$ on luvun $m$ monikerta. Esimerkiksi luvut 7 ja 52 ovat kongruentteja modulo 5, koska niiden erotus 45 on 5:n monikerta.
Katso myös Modulaariaritmetiikka, $\mod$.
Kongruentti, Yhtenevä (engl. Congruent)
Kaksi oliota ovat kongruentteja (tai yhteneviä), jos jokin yksinkertainen operaatio muuntaa ne toisikseen.
Yhtenevät kuviot voidaan muuntaa toisikseen kierrolla, peilauksella tai siirrolla.
Kongruentit luvut voidaan muuntaa toisikseen lisäämällä tai vähentämällä kustakin tietyn luvun monikerta.
Katso myös Yhtenevät kulmat.
Konjektuuri, Otaksuma (engl. Conjecture)
Otaksuma on jokin asia, jonka arvellaan mahdollisesti pitävän paikkansa, mutta jota ei vielä ole todistettu todeksi. Esimerkki otaksumasta on Goldbachin otaksuma, jonka mukaan jokainen parillinen luku (paitsi 2) voidaan kirjoittaa kahden alkuluvun summana. Se on osoittautunut todeksi kaikilla parillisilla luvuilla, joita on kokeiltu, mutta vielä ei ole todistettu, että se pätee yleisesti.
Katso myös Alkulukukaksosten otaksuma, Hypoteesi, Lause, Goldbachin otaksuma, Bertrandin otaksuma.
Konjugaattiluokka (engl. Conjugacy class)
Ryhmän $G$ alkion $x$ konjugaattiluokka on joukko \[ \{ g x g^{-1} : g \in G \}. \] Konjugaattiluokat muodostavat ryhmän $G$ osituksen.
Aliryhmän $H \le G$ konjugaattiluokka on joukko \[ \{ g H g^{-1} : g \in G \}. \] Tämä on sama kuin $\{ H \}$ täsmälleen silloin, kun $H$ on $G$:n normaali aliryhmä.
Katso myös Ositus, Joukko, Ryhmä, Normaali aliryhmä, Sentralisaattori, Ryhmän konjugoidut alkiot, Alkio.
Konkaavi (engl. Concave)
Jos kuviossa on painauma tai onkalo, niin kuvio on konkaavi.
Kuvion konkaavisuutta voidaan testata seuraavasti. Valitaan kuvion sisältä kaksi pistettä ja yhdistetään ne janalla. Jos nämä kaksi pistettä voidaan valita siten, että kyseinen jana käy kuvion ulkopuolella, niin silloin kuvio on konkaavi.
Monikulmio on konkaavi, jos sillä on sisäkulma, joka on yli 180 astetta.
Funktiota $f$ kutsutaan konkaaviksi, jos $f(t \cdot x+(1-t) \cdot y) \ge t \cdot f(x)+(1-t) \cdot f(y)$ pätee kaikilla funktion $f$ määrittelyjoukkoon kuuluvilla alkioilla $x, y$ ja kaikilla reaaliluvuilla $t \in [0,1]$. Toisin sanoen, jos kahden käyrän pisteen kautta kulkevan suoran leikkaama käyrän osa jää kokonaan kyseisen suoran yläpuolelle.
Funktio $f$ on konkaavi, jos funktio $-f$ on konveksi.

Katso myös Jensenin epäyhtälö, Konveksi.
Konkaavi funktio (engl. Concave function)
Olkoon $I \subseteq \mathbb{R}$ väli. Funktiota $f \colon I \rightarrow \mathbb{R}$ kutsutaan konkaaviksi, jos \[ f(t \cdot x+(1-t) \cdot y) \ge t \cdot f(x)+(1-t) \cdot f(y) \] pätee kaikilla $x,y \in I$ ja $0 \le t \le 1$. Toisin sanoen, jos funktion kuvaajan kahden eri pisteen välille piirretään jana, kulkee funktio näiden pisteiden välillä janan yläpuolella.
Katso myös Funktio, Kuvaus, Konveksi funktio.
Konkaavi monikulmio (engl. Concave polygon, Re-entrant polygon)
Konkaavissa monikulmiossa on ainakin yksi kupera kulma eli kulma, joka on suurempi kuin $180^{\circ}$.
Katso myös Kupera kulma, Monikulmio, Konveksi monikulmio.
Konservatiivinen, Eksakti (engl. Conservative)
Vektorikenttää $f$ sanotaan konservatiiviseksi (tai eksaktiksi), jos jokaisella umpinaisella polulla $C$ pätee \[ \int _C f \cdot d\bar{s} = 0, \] toisin sanoen, vektorikentän $f$ integraali umpinaisen polun ympäri on nolla. Tämä pätee jos ja vain jos on olemassa sellainen skalaarikenttä $\phi$, että $f = - \nabla \phi$. Skalaarikenttää $\phi$ kutsutaan vektorikentän $f$ potentiaaliksi.
Katso myös Kunta, Käyräintegraali.
Konservatiivinen voima (engl. Conservative force)
Voima, joka voidaan kirjoittaa potentiaalin gradienttina eli muodossa $f(x) = - \nabla \phi(x)$ jollakin $\phi(x)$. Miinusmerkkiä käytetään edellä yleisesti, koska silloin $\phi(x)$ voidaan tulkita voimakentän $f(x)$ potentiaalienergiaksi pisteessä $x$.
Katso myös Gradientti.
Konsistentti, Yhteensopiva (engl. Consistent)
Kahden tai useamman lauseen joukkoa sanotaan konsistentiksi, jos lauseet eivät ole keskenään ristiriidassa. On mahdollista, että kaikki lauseet ovat tosia samanaikaisesti.
Katso myös Looginen ominaisuus, Ristiriitainen.
Konstruktio, Konstruointi (engl. Construction)
Geometriassa konstruointi tarkoittaa tietyn geometrisen olion muodostamista piirtämällä se käyttämällä apuna vain kynää, harppia ja viivoitinta. Joskus muilla matematiikan aloilla puhutaan todistuksesta konstruktion avulla, kun osoitetaan, että jokin on mahdollista muodostamalla tai laskemalla esimerkki siitä.
Katso myös Kolmijako, Katkaiseminen, Piirtokolmio, Sisään piirretty kuvio, Puolittaa, Laajentaa, Jatkaa, Ura, Ympyrän piirtäminen, Kolmion sisään piirretyn ympyrän keskipisteen määrittäminen, Kolmion painopisteen määrittäminen, Ympyrän keskipisteen määrittäminen, Suoraa vastaan kohtisuoran suoran piirtäminen, Keskinormaalin piirtäminen, Piirtää ympyrä monikulmion ympäri, Kulmanpuolittajan piirtäminen, Harppi, Janan keskipisteen määrittäminen, Kolmion ympäri piirretyn ympyrän muodostaminen, Kolmion ortokeskuksen määrittäminen, Säännöllisen viisikulmion piirtäminen, Kolmion ympäri piirretyn ympyrän keskipisteen määrittäminen, Kolmion sisään piirretyn ympyrän muodostaminen.
Konstruointi, Konstruktio (engl. Construction)
Geometriassa konstruointi tarkoittaa tietyn geometrisen olion muodostamista piirtämällä se käyttämällä apuna vain kynää, harppia ja viivoitinta. Joskus muilla matematiikan aloilla puhutaan todistuksesta konstruktion avulla, kun osoitetaan, että jokin on mahdollista muodostamalla tai laskemalla esimerkki siitä.
Katso myös Kolmijako, Katkaiseminen, Piirtokolmio, Sisään piirretty kuvio, Puolittaa, Laajentaa, Jatkaa, Ura, Ympyrän piirtäminen, Kolmion sisään piirretyn ympyrän keskipisteen määrittäminen, Kolmion painopisteen määrittäminen, Ympyrän keskipisteen määrittäminen, Suoraa vastaan kohtisuoran suoran piirtäminen, Keskinormaalin piirtäminen, Piirtää ympyrä monikulmion ympäri, Kulmanpuolittajan piirtäminen, Harppi, Janan keskipisteen määrittäminen, Kolmion ympäri piirretyn ympyrän muodostaminen, Kolmion ortokeskuksen määrittäminen, Säännöllisen viisikulmion piirtäminen, Kolmion ympäri piirretyn ympyrän keskipisteen määrittäminen, Kolmion sisään piirretyn ympyrän muodostaminen.
Konstruoituva (engl. Constructible)
Perinteisessä geometriassa jotakin kutsutaan konstruoituvaksi, jos se voidaan konstruoida pekästään harpin ja viivoittimen avulla. Esimerkiksi neliöt, tasasivuiset kolmiot ja kulman puolittajat ovat konstruoituvia. Sen sijaan esimerkiksi kulman kolmeen yhtä suureen osaan jakavat janat eivät ole konstruoituvia.
Katso myös Harppi.
Konsyklinen (engl. Concyclic)
Pisteitä, jotka ovat samalla ympyränkehällä, kutsutaan konsyklisiksi. Jokainen kolmen pisteen joukko, joka ei ole kollineaarinen, on siten konsyklinen.
Monikulmiota kutsutaan konsykliseksi, jos sen kaikki kärkipisteet ovat jonkin ympyrän kehällä.
Katso myös Kulma, Kaari, Arc, Ympyrä, Nelikulmio, Halkaisija, Jänne, Ympyrän kehä, Sekantti, Kierros, Konsyklisten pisteiden koordinaatit toteuttavat ympyrän yhtälön.
Konsyklisten pisteiden koordinaatit toteuttavat ympyrän yhtälön (engl. Coordinates of concyclic points satisfy the circle equation)
Jos on annettu joukko konsyklisiä pisteitä, niin on olemassa sellaiset vakiot $p$, $q$ and $r$, että pisteiden koordinaatit toteuttavat ympyrän yhtälön $(x-p)^2 + (y-q)^2 = r^2$.
Katso myös Lause, Ympyrän yhtälö, Konsyklinen.
Kontinuumi, Jatkumo (engl. Continuum)
Kontinuumilla voidaan matematiikassa tarkoittaa kahta eri asiaa: reaalilukujen joukkoa (reaaliakselia) tai kompaktia ja yhtenäistä metristä avaruutta.
Katso myös Joukko, Kompakti, Yhtenäinen.
Kontrapositio (engl. Contrapositive)
Väitteen $P \Rightarrow Q$ kontrapositio on väite $\neg Q \Rightarrow \neg P$, missä $\neg Q$ on lauseen $Q$ negaatio. Väite on aina loogisesti ekvivalentti kontrapositionsa kanssa.
Katso myös Seurata, Käänteisväittämä, Käänteinen, Aiheuttaa jotakin, Olla jonkin riittävä ehto, Tautologinen.
Konveksi (engl. Convex)
Jokin on konveksi, jos se on ulospäin kaareutunut ja siinä ei ole ulkonevia piikkejä. Konveksi on konkaavin vastakohta.
Kuvion konveksisuutta voi tutkia seuraavasti. Valitaan kuviosta kaksi pistettä ja yhdistetään ne janalla. Jos tämä jana sijaitsee aina kuvion sisäpuolella valittiinpa kyseiset kaksi pistettä kuinka tahansa, niin kuvio on silloin konveksi.
Funktiota $f$ sanotaan konveksiksi, jos \[ f(t \cdot x + (1-t) \cdot y) \le t \cdot f(x) + (1-t) \cdot f(y) \] pätee kaikilla funktion $f$ määrittelyjoukkoon kuuluvilla alkioilla $x, y$ sekä kaikilla reaaliluvuilla $t \in [0,1]$. Toisin sanoen, jos kahden käyrän pisteen kautta piirretyn suoran leikkaama käyrän osa jää kokonaan kyseisen suoran yläpuolelle.
Jos edellä pätee aito epäyhtälö eli pätee \[ f(t \cdot x+(1-t) \cdot y) \lt t \cdot f(x)+(1-t) \cdot f(y) \] kaikilla $x, y$ ja kaikilla $t \in (0,1)$, niin funktion $f$ sanotaan olevan aidosti konveksi. Vertaa käsitteeseen "konkaavi".
Katso myös Jensenin epäyhtälö, Konkaavi, Konveksi monikulmio.
Konveksi funktio (engl. Convex function)
Funktio $f \colon A \rightarrow \mathbb{R}$, missä $A$ on väli, on konveksi, jos \[ f(tx+(1-t)y) \le t f(x)+(1-t)f(y) \] pätee kaikilla $x,y \in A$ ja $0 \le 1 \le t$. Tämä tarkoittaa sitä, että jos funktion kuvaajan kahden pisteen välille piirretään jana, kulkee funktio näiden pisteiden välillä janan alapuolella.
Katso myös Funktio, Kuvaus, Konkaavi funktio.
Konveksi monikulmio (engl. Convex polygon)
Monikulmio, jonka kaikki kulmat ovat pienempiä kuin $180^{\circ}$.

Katso myös Kulma, Monikulmio, Konveksi, Konkaavi monikulmio.
Konveksi monitahokas (engl. Convex polyhedron)
Monitahokas, jonka jokainen tahko sijaitsee tasossa, joka ei leikkaa monitahokkaan muiden osien kanssa.
Katso myös Monitahokas.
Konvergenssi, Suppeneminen (engl. Convergence)
Olkoon $X$ topologinen avaruus. Jono $(x_i)$ avaruuden $X$ pisteitä suppenee kohti pistettä $x \in X$, mikäli seuraava ehto pätee: Jos $U$ on pisteen $x$ ympäristö, niin $U$ sisältää kaikki jonon $(x_i)$ pisteet äärellistä määrää lukuunottamatta.
Olkoon $(x_i)$ jono avaruuden $\mathbb{R}^n$ pisteitä. Jono $(x_i)$ suppenee kohti pistettä $x \in \mathbb{R}^n$, mikäli pisteiden $x_i$ ja $x$ etäisyys saadaan kuinka pieneksi tahansa valitsemalla riittävän suuri $i$.
Täsmällisemmin sama voidaan ilmaista seuraavasti: Jono $(x_i)$ suppenee kohti pistettä $x \in \mathbb{R}^n$, mikäli jokaisella $\epsilon>0$ on olemassa sellainen $i_0 \in \mathbb{N}$, että kaikilla $i \gt i_0$ pätee $|x_i - x| \lt \epsilon$.
Katso myös Tasainen suppeneminen, Itseinen suppeneminen.
Konvoluutio (engl. Convolution)
Funktioiden $f(x)$ ja $g(x)$ konvoluutio $c(x)$ määritellään kaavalla \[ c(x) = \int_0 ^{x} f(t)g(x-t)dt. \]
Katso myös Funktio, Kuvaus, Integraali.
Koordinaatisto (engl. Coordinate system)
Systemaattinen tapa kuvata pisteen paikka avaruudessa kolmen luvun avulla (tai tasossa kahden luvun avulla). Yleensä koordinaatistoon kuuluu ainakin yksi akseliksi kutsuttu suora, jolta mitataan yhden koordinaatin etäisyys kiinnitetystä pisteestä. Toiset koordinaatit voidaan määritellä samalla tavalla etäisyyksinä koordinaattisuorilla, jotka ovat kohtisuorassa ensin mainitun akselin kanssa. Toiset koordinaatit voidaan määritellä myös esimerkiksi kulmien avulla.
Katso myös Karteesinen koordinaatisto, Napakoordinaatit, Lieriökoordinaatit, Sylinterikoordinaatit.
Koordinaatiston vaihto (engl. Change of coordinates)
Tason tai avaruuden pisteitä sekä vektoreita voidaan esittää eri koordinaatistoissa. Yhteys samaa pistettä tai vektoria kahdessa eri koordinaatistossa, vanhassa ja uudessa, esittävien koordinaattien välillä riippuu käytetyistä koordinaatistoista. Jos molemmat käytetyt koordinaatistot ovat suoraviivaisia, esimerkiksi tavallisia suorakulmaisia koordinaatistoja, niin vektorin uudet koordinaatit saadaan kertomalla sen vanhat koordinaatit matriisilla $M$, jonka sarakkeina ovat vanhan koordinaatiston kantavektorien koordinaatit uudessa koordinaatistossa.
Katso myös Koordinaatti.
Koordinaatti (engl. Coordinate, Co-ordinate)
Yksi tai kaksi (tai kolme) lukua, joita käytetään kuvaamaan pisteen paikkaa tasossa (tai avaruudessa). \end{newdefinition} \begin{newdefinition} {11}
Katso myös Algebra, Ordinaatta, Koordinaatiston vaihto, Geometria, Analyyttinen tasogeometria, Koordinaattiakseli, Analyyttinen avaruusgeometria, Homogeeniset koordinaatit.
Koordinaattiakseli (engl. Co-ordinate axis)
Origon sisältävä suora, jota käytetään pisteiden paikan mittaamiseen. Esimerkiksi $x$-akselia käytetään pisteen $x$-koordinaatin löytämiseen seuraavasti. Piirretään pisteestä $x$-akselille kohtisuorassa akselia vastaan oleva suora. Sitten mitataan, kuinka kaukana origosta suora leikkaa $x$-akselin. Tämä etäisyys, $+$- tai $-$-merkillä varustettuna, on pisteen $x$-koordinaatti.
Katso myös $z$-akseli, $y$-akseli, $x$-akseli, Ordinaatta, Suora, Analyyttinen tasogeometria, Koordinaatti, Akseli.
Koordinaattitaso (engl. Cartesian plane, Coordinate plane)
Jos valitaan tasolta yksi piste origoksi ja kaksi origon kautta kulkevaa suoraa $x$- ja $y$-akseleiksi, niin on saatu koordinaattitaso; taso, jolla olevan pisteen paikkaa voidaan merkitä koordinaattiparilla, jonka koordinaatit on annettu akselien suhteen.
Katso myös Taso, Karteesinen, Analyyttinen tasogeometria.
Korkeamman kertaluvun derivaatta (engl. Higher order derivative)
Kun funktiota derivoidaan useita kertoja, saadaan funktion korkeamman kertaluvun derivaattoja. Jos funktiota derivoidaan kaksi, kertaa saadaan toinen eli toisen kertaluvun derivaatta; jos funktiota derivoidaan kolme kertaa, saadaan kolmas eli kolmannen kertaluvun derivaatta; jos funktiota derivoidaan neljä kertaa, saadaan neljäs derivaatta; jne. Funktion $y$ kertaluvua $n$ olevaa derivaattaa merkitään $\frac{\mathrm{d}^{\mathrm{n}}\mathrm{y}}{\mathrm{dx}^{\mathrm{n}}}$.
Esimerkiksi, jos $\mathrm{y} = \frac{1}{\mathrm{x}}$, niin \begin{eqnarray*} \frac{\mathrm{d}y}{\mathrm{d}x} &=& \frac{-1}{x^2} \\ \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} &=& \frac{2}{x^3} \\ \frac{\mathrm{d}^3 y}{\mathrm{d}x^3} &=& \frac{-6}{x^4} \\ \vdots \\ \frac{\mathrm{d}^n y}{\mathrm{d}x^n} &=& \frac{(-1)^n n!}{x^{n+1}} \end{eqnarray*}
Katso myös Derivaatta, Toinen derivaatta.
Korkeamman kertaluvun palautuskaava (engl. Higher order recurrence relation)
Palautuskaava, jossa lukujonon $(u_n)$ luku $u_n$ määritellään lukujen $u_{n-1}$ ja $u_{n-2}$ tai jonkin aikaisemman luvun $u_{n-i}$ avulla. Esimerkiksi $u_{n} = u_{n-1}-u_{n-3}$ on tällainen palautuskaava.
Katso myös Fibonaccin yhtälö, Palautuskaava.
Korkeasti yhdistetty luku (engl. Highly composite number)
Luku, jolla on enemmän tekijöitä kuin millään sitä pienemmällä luvulla. Pienimmät korkeasti yhdistetyt luvut ovat 2, 4, 6, 12, 24, 36, 48 ja 60.
Katso myös Kuusikymmentä, 60, Yhdistetty luku.
Korkeus (engl. Altitude)
Kuvion tai kappaleen kärjen etäisyys vastakkaisesta sivusta tai sivutahkosta. Joskus myös kärjestä kyseiselle sivulle tai sivutahkolle piirretty kohtisuora jana.
Matematiikassa korkeus on tavallisesti jonkin kuvion tai kappaleen kärjen kohtisuora etäisyys kuvion kannasta tai kappaleen pohjasta. Korkeus voi olla myös kahden kuvioon liittyvän yhdensuuntaisen janan kohtisuora etäisyys. Korkeudella voidaan tarkoittaa myös janaa, joka yhdistää kärjen kohtisuorasti kantaan jne. Tähden korkeus on sen etäisyys horisontissa kulmamitalla ilmoitettuna.
Katso myös Kolmion korkeusjana, Kulma.
Korkeuskulma (engl. Angle of elevation)
Horisontin yläpuolelle muodostunut kulma.
Katso myös Kulma, Negatiivinen korkeuskulma.
Korollaari, Seuraus (engl. Corollary)
Jos väite $B$ seuraa välittömästi väitteestä $A$ ilman merkittäviä uusia todistusaskelia, niin silloin väitettä $B$ kutsutaan väitteen $A$ korollaariksi eli seuraukseksi.
Korollaari on yleensä jonkin päätuloksen vähäisempi välitön seuraus.
Korottaa toiseen, Laskea neliö jostakin, Neliö (engl. Squaring, To square)
Neliö on kuvio, jossa on neljä yhtä pitkää sivua ja neljä suoraa kulmaa.
Laskemme neliön jostakin kertomalla sen itsellään eli korottamalla sen toiseen potenssiin.
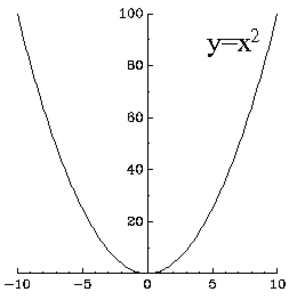
Katso myös Potenssiin korottaminen, Neliöluku, Neliöjuuri.
Korrelaatio, Korrelaatiokerroin (engl. Correlation)
Satunnaismuuttujien $X$ ja $Y$ välisen riippuvuuden mitta.
Korrelaatiokertoimista on eri versioita, joista tunnetuimmat ovat Pearsonin korrelaatiokerroin, joka mittaa muuttujien välisen lineaarisen riippuvuuden voimakkuutta, sekä Spearmanin järjestyskorrelaatiokerroin, joka mittaa muuttujien välisen riippuvuuden monotonisuutta.
Korrelaatiokerroin ei kerro mitään muuttujien välisistä kausaaliyhteyksistä eli siitä, onko toinen muuttujista toisen syy tai seuraus vai ei. Kaksi satunnaismuuttujaa voivat korreloida voimakkaasti, mutta olla silti kausaalisesti riippumattomia, ja kahden satunnaismuuttujan välillä voi olla syy-seuraus -suhde, vaikka ne olisivatkin korreloimattomia.
Riippumattomat satunnaismuuttujat ovat aina korreloimattomia, mutta korreloimattomat satunnaismuuttujat eivät välttämättä ole riippumattomia.
Katso myös Korrelaatiokerroin, Tunnusluku, Tilastollinen tunnusluku, Korreloida, Kovarianssi.
Korrelaatiodiagramma, Hajontakuvio (engl. Scatter diagram, Scatter graph, Scatter plot)
Hajontakuvio eli korrelaatiodiagramma on graafinen esitystapa, jonka avulla voidaan pareittain (X ja Y) tarkastella muuttujien välisiä riippuvuuksia tilastoaineistossa. Hajontakuviossa havainnot $i, i=1,...n$ merkitään koordinaatistoon pisteillä paikoissa $(X_i,Y_i), i=1,...n$. Mikäli muuttujien välillä arvellaan olevan syy - seuraus-riippuvuussude, piirretään kuva niin, että syy (selittävä) muuttuja on X-akselilla ja seuraus (selitettävä) muuttuja Y-asteikolla. Hajontakuvio on käyttökelpoinen esitystapa tutkittaessa:
- Ovatko muuttujat riippumattomia, vai esiintyykö muuttujien välillä riippuvuuksia.
- Riippuvuuden muotoa - onko riippuvuus lineaarista vai käyräviivaista.
- Miten osa-aineistot suhtautuvat toisiinsa.
- onko aineistosta poikkeavia (virheellisesti talletettuja) havaintoja.
Korrelaatiokerroin, Korrelaatio (engl. Correlation)
Satunnaismuuttujien $X$ ja $Y$ välisen riippuvuuden mitta.
Korrelaatiokertoimista on eri versioita, joista tunnetuimmat ovat Pearsonin korrelaatiokerroin, joka mittaa muuttujien välisen lineaarisen riippuvuuden voimakkuutta, sekä Spearmanin järjestyskorrelaatiokerroin, joka mittaa muuttujien välisen riippuvuuden monotonisuutta.
Korrelaatiokerroin ei kerro mitään muuttujien välisistä kausaaliyhteyksistä eli siitä, onko toinen muuttujista toisen syy tai seuraus vai ei. Kaksi satunnaismuuttujaa voivat korreloida voimakkaasti, mutta olla silti kausaalisesti riippumattomia, ja kahden satunnaismuuttujan välillä voi olla syy-seuraus -suhde, vaikka ne olisivatkin korreloimattomia.
Riippumattomat satunnaismuuttujat ovat aina korreloimattomia, mutta korreloimattomat satunnaismuuttujat eivät välttämättä ole riippumattomia.
Katso myös Korrelaatiokerroin, Tunnusluku, Tilastollinen tunnusluku, Korreloida, Kovarianssi.
Korrelaatiokerroin (engl. Correlation coefficient)
Korrelaatiokerroin mittaa, miten läheisessä suhteessa kahden muuttujan tai joukon arvot ovat keskenään. Muuttujien X ja Y korrelaatiokerroin määritellään kaavalla \[ \rho = \frac{\mathrm{Cov(X, Y)}}{\sqrt{\mathrm{Var(X)Var(Y)}}} . \]
Jos korrelaatiokerroin on 1 tai -1, niin muuttujien välillä vallitsee lineaarinen riippuvuus. Jos korrelaatiokerroin on 0, niin muuttujat ovat korreloimattomia mutta eivät välttämättä riippumattomia.
Kahden yhtä suuren otoksen $x_{i}$ ja $y_{i}$ välinen korrelaatiokerroin on $ \mathrm{r} = \frac{ \sum _{\mathrm{i}} ( \mathrm{x}_{\mathrm{i}} - \bar{\mathrm{x}} )( \mathrm{y}_{\mathrm{i}} - \bar{\mathrm{y}} ) } { \sqrt{ \left ( \sum _{\mathrm{i}} ( \mathrm{x}_{\mathrm{i}} - \bar{\mathrm{x}} ) ^2 \right ) \left ( \sum _{\mathrm{i}} ( \mathrm{y}_{\mathrm{i}} - \bar{\mathrm{y}} ) ^2 \right ) }} . $
Katso myös Korrelaatiokerroin, Tunnusluku, Tilastollinen tunnusluku, Varianssi, Roo, Korrelaatio, Kovarianssi.
Korreloida (engl. Correlate)
Kahden suureen sanotaan korreloivan, jos niiden välillä on yhteys. Yleensä suureet ovat silloin verrannolliset.
Tilastotieteessä käytetään useita eri tyyppisiä korrelaatiokertoimia kertomaan kahden suureen välisen korrelaation määrästä jossakin tietyssä aineistossa.
Katso myös Korrelaatiokerroin, Korrelaatio.
Korvaaminen, Sijoittaminen, sijoitus (engl. Substitution)
Yleensä yhtälön yksinkertaistamiseksi tehtävä yhtälössä esiintyvän termin vaihtaminen toiseen termiin tai lukuun.
Tarkastellaan esimerkiksi yhtälöitä (1): $x+y=6$ ja (2): $2x+3y=14$.
Yhtälöstä (1) seuraa, että $y=6-x$. Jos korvataan $y$ yhtälössä (2) lausekkeella $6-x$ saadaan $2x+3(6-x)=14$.
Siten $2x+18-3x=14$ eli $x=4$.
Korvata (engl. Substitute)
Sijoittaa jokin asia toisen asian paikalle. Usein tällä tarkoitetaan sitä, että vaihdetaan yhtälössä muuttujan tilalle lauseke, jolla on sama arvo kuin muuttujalla.
Kosekantin derivaatta (engl. Cosecant derivative, csc derivative, cosec derivative)
\[ \frac{\mathrm{d}}{\mathrm{d}x}\mathrm{csc}(x) = -\cot(x)\mathrm{csc}(x). \]
Kosekantin integraalifunktio (engl. cosec integral)
\[ \int \mathrm{csc}(x) \mathrm{d}x = -\ln | \mathrm{csc}(x) + \cot(x)| + C. \]
Kosekantti (engl. Cosecant)
Kulman $\theta$ kosekantti $\mathrm{csc}(\theta)$ määritellään kaavalla \[ \mathrm{csc}(\theta) = \frac{1}{\sin(\theta)}. \]
Jos suorakulmaisen kolmion yksi kulma on $\theta$, niin kulman $\theta$ kosekantti on hypotenuusan pituus jaettuna kulman $\theta$ vastaisen sivun pituudella. Toisin sanoen, \[ \mathrm{csc}(\theta) = \frac{\mbox{hypotenuusan pituus}}{\mbox{vastaisen sivun pituus}}. \]
Katso myös $\sin$, Sekanttifunktio, Trigonometrinen funktio, $\csc$.
Kosini (engl. Cosine)
Jos suorakulmaisessa kolmiossa yhden kulman asteluku on $\theta$, niin kulman $\theta$ kosini $\cos(\theta)$ on $\theta$:n viereisen kateetin pituuden suhde hypotenuusan pituuteen.
Kulman kosini voidaan luonnehtia myös seuraavasti. Jos vektoria $P = (1,0)$ kierretään origon ympäri vastapäivään $\theta$ astetta, niin $\cos(\theta)$ on silloin vektorin $P$ $x$-koordinaatti.
Katso myös Trigonometria, Suora kulma, Sini, Ympyrä, Hypotenuusa, Suhde, Trigonometrinen funktio, Kosinilause, $\cos$, Kosini, Suuntakosinit.
Kosini, $\cos$ (engl. cos)
Kosinin lyhenne. $\cos(x)$ tarkoittaa kulman $x$ kosinia eli suorakulmaisen kolmion kulman, jonka asteluku on $x$, viereisen kateetin pituuden suhdetta hypotenuusan pituuteen.
Katso myös Tangenttifunktio, Trigonometrinen yhtälö, Trigonometrian Pythagoraan lause, Lyhenne, Kotangentti, Kosini, Sekanttifunktio, $\cos(2x)$, $\cos(x+y)$, $cos(x)-cos(y)$, Kosinin derivaatta, $\cos(x)+\cos(y)$, $\cos(x)\cos(y)$, Kosinin potenssisarjakehitelmä, Kosinin integraalifunktio, $e^{ix}$, $e^{x+iy}$, Fourier'n sarja, $\cos(x/2)$, $\tan(x/2)$.
Kosinilause (engl. Cosine law, Law of cosines, Cosine rule)
Jos kolmion sivujen pituudet ovat $a$, $b$, $c$ ja jos $A$ on sivun $a$ vastainen kulma, niin \[ a^2 = b^2 + c^2 - 2bc \cdot \cos(A). \]
Katso myös Kulma, Trigonometrinen identiteetti, Sinilause, Kolmio, Kosini, Sääntö.
Kosinin derivaatta (engl. cos derivative)
Kosinin integraalifunktio (engl. cos integral)
Kosinin potenssisarjakehitelmä (engl. cos power series)
Kaikilla reaaliluvuilla $x$ pätee \[ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - ... + \frac{(-1)^n x^{2n} }{(2n)!} + ... . \]
Kosinin tarkkoja arvoja (engl. Particular values of cos)
$\cos 0^{\circ} = 1$,
$\cos 30^{\circ} = \cos \frac{\pi}{6} = \frac{\sqrt{3}}{2}$,
$\cos 45^{\circ} = \cos \frac{\pi}{4} = \frac{1}{\sqrt{2}}$,
$\cos 60^{\circ} = \cos \frac{\pi}{3} = \frac{1}{2}$,
$\cos 90^{\circ} = cos \frac{\pi}{2} = 0$,
$\cos 180^{\circ} = cos \pi = -1$.
Katso myös Trigonometristen funktioiden tarkat arvot.
Kotangentin derivaatta (engl. cot derivative)
Kotangentin integraalifunktio (engl. cot integral)
Kotangentti (engl. Cotangent)
Jos suorakulmaisessa kolmiossa yhden kulman suuruus on $x$, niin kulman $x$ kotangentti on $x$:n viereisen sivun pituuden suhde $x$:n vastaisen sivun pituuteen. Yleisemmin sanottuna on $\cot(\theta) = \frac{x}{y}$, missä $(x,y)$ on piste, joka saadaan, kun vektoria $(1,0)$ kierretään origon ympäri vastapäivään kulman $\theta$ verran. Siis \[ \cot(\theta) = \frac{1}{\tan(\theta)} = \frac{\cos(\theta)}{\sin(\theta)}. \]
Katso myös $\arctan$, $\tan$, $\sin$, Trigonometrinen funktio, $\cos$, $\cot$, Kosini.
Kovarianssi (engl. Covariance)
Satunnaismuuttujien $X$ ja $Y$ kovarianssi on \[ \mathrm{cov}(X,Y) = \mathbb{E} \left( (X-\mathbb{E}(X))(Y-\mathbb{E}(Y)) \right) = \mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y). \] Satunnaismuuttujien $X$ ja $Y$ korrelaatiokerroin on \[ \mathrm{corr}(X,Y) = \frac{\mathrm{cov}(X,Y)}{\sqrt{\mathrm{Var}(X)\mathrm{Var}(Y)}}. \] Sen arvot ovat välillä $[-1,1]$ ja osoittavat muuttujien $X$ ja $Y$ lineaarisen korrelaation asteen, kun $\mathrm{corr}(X,Y) \approx \pm 1$.
Katso myös Korrelaatiokerroin, Korrelaatiokerroin, Tunnusluku, Tilastollinen tunnusluku, Varianssi, Korrelaatio.
Kreikkalaiset kirjaimet (engl. Greek letters)
Kreikkalaisten antiikin aikana sekä nykyisin käyttämät kirjaimet. Monet näistä ovat yleisesti käytössä matematiikassa latinalaisten kirjainten lisänä. Ensimmäiset kreikkalaiset kirjaimet ovat $\alpha, \beta, \gamma, \delta, \epsilon, \zeta, \eta, \theta$; viimeinen kirjain on $\omega$.
Katso myös Omega, Ypsilon, Merkintätapa, Notaatio, Theta, Tau, Roo, Omikron, Gamma, Eta, Khi, Beta, Alfa, Pii, $\pi$, Sigma, Epsilon, Delta, Ioota.
Kriittinen alue (engl. Critical region)
Hypoteesin testauksessa ne testisuureen arvot, joiden perusteella nollahypoteesi hylätään, muodostavat kriittisen alueen.
Katso myös Hyväksymisalue.
Kriittinen arvo (engl. Critical value)
Hypoteesin testauksessa kriittinen arvo on hyväksymisalueen ja hylkäämisalueen välinen rajapiste.
Katso myös Nollahypoteesi, Otostunnusluku.
Kriittinen piste (engl. Critical point)
Funktion $f(x)$ kriittisiä pisteitä ovat ne pisteet $x_0$, joissa $f'(x_0) = 0$ tai joissa $f(x)$ ei ole derivoituva.
Katso myös Piste.
Kriteerejä kolmioiden yhdenmuotoisuudelle (engl. Criteria for triangles to be similar)
1. Kaksi kolmiota ovat yhdenmuotoiset, jos niiden kaksi vastinkulmaa ovat yhtä suuret.
2. Kaksi kolmiota ovat yhdenmuotoiset, jos niiden kaksi vastinsivua ovat verrannolliset ja näiden sivujen väliset vastinkulmat ovat yhtä suuret.
3. Kaksi kolmiota ovat yhdenmuotoiset, jos niiden kaikki vastinsivut ovat verrannolliset.
Katso myös Samanlainen, Yhdenmuotoinen, Similaari, Kriteerejä kolmioiden yhtenevyydelle.
Kriteerejä kolmioiden yhtenevyydelle (engl. Criteria for triangles to be congruent)
1. Kaksi kolmiota ovat yhtenevät, jos jokainen kolmion kolmesta sivusta on yhtä suuri kuin toisen kolmion vastaava sivu. (SSS)
2. Kaksi kolmiota ovat yhtenevät, jos kolmion kaksi sivua ja niiden välinen kulma ovat yhtä suuret kuin toisen kolmion vastaavat kaksi sivua ja niiden välinen kulma. (SKS)
3. Kaksi kolmiota ovat yhtenevät, jos kolmion kaksi kulmaa ja niiden välinen sivu ovat yhtä suuret kuin toisen kolmion vastaavat kaksi kulmaa ja niiden välinen sivu. (KSK)
Yllä kriteerien lyhenteissä S = sivu ja K = kulma.
Katso myös Yhtäsuuri, Kriteerejä kolmioiden yhdenmuotoisuudelle, Sama.
Kriteeri (engl. Criterion)
Testi, joka olion on läpäistävä, jotta sillä olisi jokin tietty ominaisuus tai jotta se olisi jonkin tietyn joukon alkio.
Kroneckerin delta (engl. Kronecker Delta)
Symbolia $\delta_{i,j}$ kutsutaan Kroneckerin deltaksi. Se on määritelmän mukaan $1$, kun $i = j$, ja $0$ muulloin.
Katso myös Merkintätapa, Notaatio, Delta.
Krossi (engl. Gross, 144)
Tusina tusinaa eli 144.

Kryptografia, Kryptologia (engl. Cryptology, Cryptography)
Tieteenala, joka tutkii salakirjoitusmenetelmiä eli tapoja salata annettu viesti sekä selvittää eli purkaa salattu viesti.
Katso myös Alkuluku, Matematiikka ja tietojenkäsittely, Salausmenetelmä.
Kryptologia, Kryptografia (engl. Cryptology, Cryptography)
Tieteenala, joka tutkii salakirjoitusmenetelmiä eli tapoja salata annettu viesti sekä selvittää eli purkaa salattu viesti.
Katso myös Alkuluku, Matematiikka ja tietojenkäsittely, Salausmenetelmä.
Kulma (engl. Angle)
Kun kaksi suoraa leikkaavat toisensa, muodostuu kulmia. Kulman suuruus on se määrä, jonka verran toista suoraa on käännettävä, jotta suorat sijaitsisivat päällekkäin. Kulman suuruutta mitataan asteina tai radiaaneina, joskus myös gooneina (uusasteina).
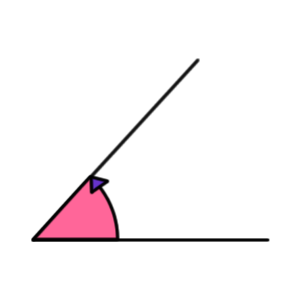
Katso myös Terävä kulma, Vieruskulma, Vastakohtaiset kulmat, Korkeus, Korkeuskulma, Kompleksiluvun argumentti, Nollakulma, Vastainen kulma, Suora kulma, Negatiivinen korkeuskulma, Vastinkulmat, Oikokulma, Suplementtikulma, Monikulmion kulmat, Samaa kaarta vastaavat kehäkulmat, Ristikulmat, Radiaani, Aste, Eksplementtikulmat, Komplementtikulma, Myötäpäivään, Tylppä kulma, Uusaste, Graadi, Geometria, Euklidinen geometria, Keskuskulma, Yhtenevät kulmat, Kosinilause, Konveksi monikulmio, Konsyklinen, Analyyttinen avaruusgeometria, Kahden tason välinen kulma, Eksplementtikulma.
Kulma, Leikkauspiste, Kärki (engl. Corner)
Leikkauspiste on paikka, jossa kaksi tai useampi suora kohtaavat toisensa.
Kulma on piste, jossa kaksi monikulmion sivua kohtaavat.
Kärki on piste, jossa vähintään kolme monitahokkaan tahkoa kohtaavat.
Katso myös Piste.
Kulmakiihtyvyys (engl. Angular acceleration)
Vektorisuure, joka on yhtä suuri kuin kulmanopeuden muutosnopeus. Kulmakiihtyvyys on siis kulman muutosnopeuden muutosnopeus.
Kulman puolittaja (engl. Angle bisector)
Kulman puolittaja on puolisuora, joka jakaa annetun kulman kahteen yhtä suureen osaan.
Katso myös Puolittaja, Sisään piirretyn ympyrän keskipiste, Suora, Ulkokulman puolittaja, Kulmanpuolittajan piirtäminen, Kolmion sisään piirretyn ympyrän muodostaminen.
Kulmanopeus (engl. Angular velocity)
Vektorisuure, joka ilmaisee kulman muutosnopeuden. Kulmanopeus on siis vektori, jonka pituus ilmaisee pyörivän kappaleen yhdessä sekunnissa peittämän kulman koon radiaaneina ja jonka suunta on kohtisuorassa kappaleen pyörimissuuntaa vastaan "oikean käden säännön" mukaisesti (kun sormet osoittavat kappaleen pyörimissuuntaan, niin peukalo osoittaa kulmanopeusvektorin suuntaan).
Kulmanpuolittajalause (engl. Angle bisector theorem)
Olkoon ABC kolmio. Piirretään kulmaan B kulman puolittaja ja merkitään P:llä sen ja sivun AC leikkauspistettä. Tällöin on voimassa AP/AB = CP/CB.
Tämä on helppo todistaa sinilauseen avulla.
Katso myös Lause.
Kulmanpuolittajan piirtäminen (engl. Construct an angle bisector)
Annetun kahden suoran, joiden leikkauspiste on $A$, välisen kulman puolittaja piirretään seuraavasti.
Piirretään harpin avulla ympyrä, jonka keskipiste on $A$ (ympyrän säde voi olla mikä tahansa). Tämä ympyrä leikkaa annetut kaksi suoraa pisteissä $B$ ja $C$. Piirretään harpin avulla kaksi ympyrää, joilla on sama säde sekä keskipisteet $B$ ja $C$. Ympyrät leikkaavat toisensa pisteessä $D$. Suora $AD$ on haluttu kulman puolittaja.
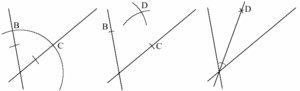
Katso myös Kulman puolittaja, Konstruktio, Konstruointi.
Kulmio (engl. gon)
Tietyn sivujen määrän omaavaa monikulmiota tarkoittava loppuliite, esimerkiksi nelikulmio tai kuusikulmio. Jos sivuja on $n$ kappaletta, puhutaan $n$-kulmiosta.
Katso myös $n$-kulmio, Takaliite, Monikulmio.
Kultainen leikkaus, Kultaisen leikkauksen suhde (engl. Golden ratio, Golden section)
Kultaisen leikkauksen suhde on suhde $p:q$, missä luvut $p$ ja $q$ toteuttavat ehdon $p:q = q:(p-q)$.
Jos jana jaetaan kahteen osaan siten, että pitemmän osan pituuden suhde lyhyemmän osan pituuteen on yhtä suuri kuin koko janan pituuden suhde pitemmän osan pituuteen, niin osien pituuksien suhde on kultaisen leikkauksen suhde.
Kultaisen leikkauksen suhteen arvo on $(1+\sqrt{5})/2$ eli noin $1,618$. Fibonaccin lukujonossa kahden peräkkäisen jäsenen suhde lähestyy kultaisen leikkauksen suhdetta. Suorakulmiota, jonka sivujen suhde on kultaisen leikkauksen suhde, sanotaan kultaiseksi suorakulmioksi. Tätä kuviota on käytetty paljon maalaustaiteessa ja kuvanveistossa. Ketjumurtolukuna kultaisen leikkauksen suhde kirjoitetaan \[1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \dots}}}.\]
Katso myös Suhde, Kultainen suorakulmio.
Kultainen suorakulmio (engl. Golden rectangle)
Suorakulmio, jonka sivujen pituuksien suhde on kultaisen leikkauksen suhde.

Katso myös Suorakaide, Suorakulmio, Kultaisen leikkauksen suhde, Kultainen leikkaus.
Kultaisen leikkauksen suhde, Kultainen leikkaus (engl. Golden ratio, Golden section)
Kultaisen leikkauksen suhde on suhde $p:q$, missä luvut $p$ ja $q$ toteuttavat ehdon $p:q = q:(p-q)$.
Jos jana jaetaan kahteen osaan siten, että pitemmän osan pituuden suhde lyhyemmän osan pituuteen on yhtä suuri kuin koko janan pituuden suhde pitemmän osan pituuteen, niin osien pituuksien suhde on kultaisen leikkauksen suhde.
Kultaisen leikkauksen suhteen arvo on $(1+\sqrt{5})/2$ eli noin $1,618$. Fibonaccin lukujonossa kahden peräkkäisen jäsenen suhde lähestyy kultaisen leikkauksen suhdetta. Suorakulmiota, jonka sivujen suhde on kultaisen leikkauksen suhde, sanotaan kultaiseksi suorakulmioksi. Tätä kuviota on käytetty paljon maalaustaiteessa ja kuvanveistossa. Ketjumurtolukuna kultaisen leikkauksen suhde kirjoitetaan \[1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \dots}}}.\]
Katso myös Suhde, Kultainen suorakulmio.
Kunta (engl. Field)
Ykkösellinen rengas $(F, +, *)$ on kunta, mikäli $(F \setminus \{0\}, *)$ on Abelin ryhmä.
Joukko $F$, joka on varustettu vaihdannaisilla ja liitännäisillä laskutoimituksilla $+, \cdot : F \times F \to F$ ja joka toteuttaa ehdot:
1) Joukossa $F$ on nolla-alkio $0$ laskutoimituksen $+$ suhteen ja ykkösalkio $1$ laskutoimituksen $\cdot$ suhteen ja nämä ovat eri alkioita. Kaikilla $z \in F$ pätee siis $0 + z = z$ ja $1 \cdot z = z$.
2) Jokaisella joukon $F$ alkiolla on vasta-alkio laskutoimituksen $+$ suhteen. Kaikilla $z \in F$ on siis olemassa sellainen $w \in F$, että $z+w = 0$. 3) Jokaisella joukon $F$ alkiolla nolla-alkiota $0$ lukuunottamatta on käänteisalkio laskutoimituksen $\cdot$ suhteen. Kaikilla $z \in F$, $z \neq 0$, on siis olemassa sellainen $w \in F$, että $z \cdot w = 1$.
4) Osittelulaki $z \cdot (v + w) = (z \cdot v) + (z \cdot w)$ on voimassa kaikilla $z, v, w \in F$.
Lukujoukot $\mathbb{Q}, \mathbb{R}$ ja $\mathbb{C}$ yhteen- ja kertolaskulla varustettuina ovat kuntia.
Kunnan määritelmä voidaan esittää myös seuraavasti: $F$ on kunta, jos $F$ on vaihdannainen ryhmä laskutoimituksen $+$ suhteen, $F \setminus {0}$ on vaihdannainen ryhmä laskutoimituksen $\cdot$ suhteen ja osittelulaki 4) on voimassa.
Katso myös Käänteisalkio, Kommutoida, Kertolaskun käänteisalkio, Käänteisluku, Ryhmä, Kuntalaajennus, Alikunta, Bilineaarinen muoto, Galois'n kunta, Äärellinen kunta.
Kuntalaajennus (engl. Field extension)
Olkoon $F$ kunta. Kunta $L$ on kunnan $F$ laajennus, jos $F$ on kunnan $L$ alikunta. Jos $L$ on kunnan $F$ laajennus, merkitään $L / F$. Jos $L$ on lisäksi äärellisulotteinen $F$-vektoriavaruus, sanotaan, että $L$ on kunnan $F$ äärellinen laajennus.
Katso myös Kunta, Galois'n ryhmä, Algebrallinen laajennus.
Kupera kulma (engl. Reflex angle)
Kulmaa sanotaan kuperaksi, jos se on suurempi kuin oikokulma eli $180^{\circ}$.
Katso myös Terävä kulma, Eksplementtikulmat, Tylppä kulma, Konkaavi monikulmio.
Kuplalajittelu (engl. Bubble sort)
Kuplalajittelu on järjestysalgoritmi. Syötteenä on jono lukuja (jonon pituus $n$) sekalaisessa järjestyksessä, ja tarkoituksena on järjestää luvut suuruusjärjestykseen.
Kuplalajittelu käy lukujonon läpi $n$ kertaa. Ensimmäisellä läpikäynnillä ensin vertaillaan ensin 1. ja 2. paikan lukuja, ja vaihdetaan ne keskenään, mikäli 1. paikan luku on suurempi. Sitten vertaillaan lukuja 2. ja 3. paikan lukuja, ja vaihdetaan ne keskenään, jos 2. paikan luku on suurempi. Jatketaan samaan tapaan taulukon loppuun. Tämän jälkeen taulukossa on välttämättä suurin luku viimeisenä.
Seuraavat läpikäynnit ovat muutoin samanlaisia, mutta 2. läpikäynnillä pysähdytään taulukon lopun sijaan paikassa $n-1$, 3. läpikäynnillä paikassa $n-2$ ja niin edelleen.
Lopputulos on se, että taulukon luvut ovat suuruusjärjestyksessä.
Katso myös Algoritmi, Vaihtolajittelu.
Kursiivi (kirjoitus), Vino (engl. Oblique)
Vino suora on kalteva suora, joka voi kallistua vasemmalle, oikealle, ylös tai alas. Se on suora, joka ei ole pystysuora eikä vaakasuora. Kursiivi on vinoa kirjoitusta.
Lävistäjän suuntainen tai kalteva.
Katso myös Pystysuora, Vaakasuora.
Kuulua joukkoon (engl. Member of, In)
Esimerkiksi $a \in A$ tarkoittaa, että alkio $a$ on joukossa $A$.
Merkki $\in$ tarkoittaa, että annettu alkio on tietyn joukon jäsen eli että alkio on kyseisessä joukossa.
Huomaa, että sana "sisältyä" tarkoittaa eri asiaa, jota myös merkitään eri symbolilla.
Kuusi, 6 (engl. 6, Six)
$6 = 3!$; kuusi on (ykkösen jälkeen) pienin täydellinen luku ja pienin luku, joka ei ole alkuluvun potenssi ja kolmas kolmioluku. Se on ainoa parillinen täydellinen luku, joka ei ole peräkkäisten kuutioiden summa.
Se on toinen primoriaaliluku.
Se on lukujen 1, 2 ja 3 summa ja tulo; ainoa luku, jolla on tällainen ominaisuus.
Kuusi on toinen automorfiluku. Se on kolmioluku, jonka neliökin on kolmioluku.
Se on kuution sivutahkojen, tetraedin särmien ja säännöllisen oktaedrin kärkien lukumäärä.
$\phi(6) = 2$, $d(6) = 4$ ja $\sigma(6) = 12$.

Katso myös Kuusikulmio, Automorfinen luku.
Kuusikulmio (engl. Hexagon, Hexagonal)
Monikulmio, jossa on kuusi sivua ja kuusi kulmaa.
Säännöllisessä kuusikulmiossa on kuusi yhtä pitkää sivua ja kuusi yhtä suurta kulmaa.
Suoria, jotka yhdistävät vastakkaiset kärjet toisiinsa, kutsutaan päälävistäjiksi. Suoria, jotka yhdistävät kärjet vastakkaisen kärjen viereiseen kärkeen, kutsutaan lävistäjiksi.
Katso myös 6, Kuusi, Monikulmio.
Kuusikymmentä, 60 (engl. Sixty, 60)
Kuusi kymmentä. Se on erittäin yhdistetty luku: sillä on enemmän tekijöitä kuin millään pienemmällä luvulla.

Katso myös Korkeasti yhdistetty luku, Kymmenen monikerta.
Kuusitahokas, Heksaedri (engl. Hexahedron)
Kappale, jossa on kuusi tahkoa. Säännöllinen kuusitahokas on kuutio.
Katso myös Monitahokas.
Kuusitoista, 16 (engl. 16, Sixteen)
16 on neljäs neliöluku ja luvun kaksi neljäs potenssi, $2^4$. Tämä merkitsee, että $16 = 2^{(2^2)} = (2^2)^2$.
Jos neliön sivu on neljä pituusyksikköä, niin neliön piiri on 16 pituusyksikköä ja ala 16 pinta-alayksikköä. 16 on ainoa luku, jolla on tällainen ominaisuus.
$\phi(16) = 8$, $d(16) = 5$, $\sigma(16) = 31$.

Kuutio, Säännöllinen heksaedri (engl. Regular hexahedron, Cube)
Kuutio on säännöllinen kolmiulotteinen kappale, jonka tahkot ovat keskenään samanlaisia neliöitä. Kuutiolla on 6 tahkoa, 12 särmää ja 8 kärkeä. Kuutio on yksi Platonin kappaleista. Kuutiota kutsutaan myös (säännölliseksi) heksaedriksi.
Katso myös Kuution tilavuus, Tasainen monitahokas, Yksikkökuutio, Avaruusgeometria, Kuution pinta-ala, Platonin kappaleet.
Kuutiojuuri (engl. Cube root)
Luvun kuutiojuuri on luku, jonka kuutio eli kolmas potenssi on kyseinen luku. Luvun $x$ kuutiojuurta merkitään $\sqrt[3]{x}$. Esimerkiksi luvun 27 kuutiojuuri $\sqrt[3]{27}$ on 3, koska $3^3 = 3 \cdot 3 \cdot 3 = 27$.
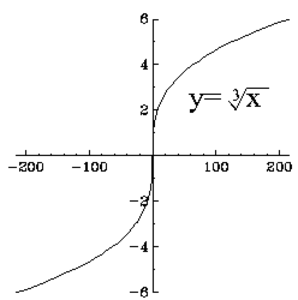
Katso myös $n$:s juuri, Kuutioluku, Juuri.
Kuutiollinen käyrä (engl. Cubic curve)
Algebrallinen käyrä, joka toteuttaa kahden muuttujan kolmannen asteen polynomiyhtälön.
Katso myös Käyrä.
Kuutiollinen polynomi, Kolmannen asteen polynomi (engl. Cubic)
Polynomi, joka sisältää muuttujansa kuution eli kolmannen potenssin, mutta ei tätä korkeampia potensseja. Esimerkiksi polynomi $2x^3 + x +14$ on kuutiollinen.
Katso myös Polynomin tekijöihinjako, Polynomi, Cardanon menetelmä, Elliptinen integraali.
Kuutioluku (engl. Cube number)
Kuutioluku on luku, joka on jonkin luvun kolmas potenssi, eli luku, joka saadaan kertomalla alkuperäinen luku itsellään ja tulos vielä alkuperäisellä luvulla. Esimerkiksi $8 = 2^3 = 2 \cdot 2 \cdot 2$ ja $27 = 3^3 = 3 \cdot 3 \cdot 3$ ovat kuutiolukuja.
Katso myös Kuutiojuuri, Neliöluku, Kokonaisluku.
Kuutiometri (engl. Cubic metre)
Tilavuuden mittayksikkö. Yksi kuutiometri on sellaisen kuution tilavuus, jonka kaikki sivut ovat metrin pituisia. Yksi kuutiometri on 1000 litraa. Kuutiometri on SI-järjestelmän mittayksikkö tilavuudelle.
Katso myös SI-yksiköt.
Kuutiomillimetri (engl. Cubic millimetre)
Yksi kuutiomillimetri on sellaisen kuution tilavuus, jonka kaikkien sivujen pituus on yksi millimetri. Kuutiomillimetrin lyhenne on $mm^{3}$.
Kuution kaksinkertaistaminen (engl. Duplication of the cube)
Antiikista peräisin oleva ongelma, jossa kysytään, onko mahdollista konstruoida annetusta kuutiosta toinen tilavuudeltaan kaksinkertainen kuutio pelkästään harppia ja viivoitinta käyttäen. Tämä osoittautuu mahdottomaksi. Ongelman ratkaisu näet vaatisi konstruoimaan janan, jonka pituus on $\sqrt[3]{2}$. Voidaan kuitenkin osoittaa, että harpilla ja viivoittimella voidaan konstruoida neliöjuuria, mutta ei kuutiojuuria.
Kuution pinta-ala (engl. Area of a cube)
Jos kuution sivun pituus on $a$, niin kuution pinta-ala on $6 a^2$.
Katso myös Kuutio, Säännöllinen heksaedri.
Kuution tilavuus (engl. Volume of a cube)
Kuution, jonka sivun pituus on 2, tilavuus on $2 \cdot 2 \cdot 2 = 2^{3} = 8$.
Kuution, jonka sivun pituus on 3, tilavuus on $3^{3} = 27$.
Kuution, jonka sivun pituus on $a$, tilavuus on $a \cdot a \cdot a = a^{3}$.
Katso myös Kuutio, Säännöllinen heksaedri.
Kuutiosenttimetri (engl. Cubic centimetre)
Yksi kuutiosenttimetri on sellaisen kuution tilavuus, jonka leveys, syvyys ja korkeus ovat yksi senttimetri. Kuutiosenttimetrin lyhenne on $cm^{3}$.
Katso myös Millilitra, Senttimetri.
Kuva (engl. Image)
Kuvauksen tulos. Esimerkiksi neliön kuva kuvauksessa voisi olla toinen neliö, suunnikas tai suorakulmio, riippuen kuvauksesta.
Joukon $A$ kuva kuvauksessa $f : A \to B$ on joukko $f(A) = \{f(a): a \in A\} \subset B$.
Kuvajoukko, Funktion kuvajoukko (engl. Range of a function, Range)
Funktion $f \colon A \rightarrow B$ kuvajoukko on joukko $fA$, eli niiden maalijoukon pisteiden joukko, jotka funktio saa arvonaan. Funktion $f$ maalijoukko $B$ ja kuvajoukko $fA$ ovat sama joukko täsmälleen silloin, kun $f$ on surjektio.
Katso myös Injektio, Funktio, Kuvaus, Keskihajonta, Joukko, Bijektio, Surjektio, Maalijoukko, Arvojoukko, Funktion maalijoukko, Verrata, Arvo, Tuloste, Laatikko ja viikset -kuvio.
Kuvata, Muuntaa, Muuttaa joksikin, Muunnos (engl. Transform)
Muuttaa joukko kuvioita tai lukuja tai olioita toisiksi kuvioiksi, luvuiksi tai olioiksi jonkin säännön mukaisesti.
Katso myös Fourier'n muunnos.
Kuvaus, Funktio (engl. Map, Mapping)
Joukkojen $A$ ja $B$ välinen kuvaus $m$ on sääntö, joka liittää jokaiseen joukon $A$ alkioon yhden $B$:n alkion. Tätä merkitään $m : A \to B$ ja sanotaan, että $m$ on kuvaus joukosta $A$ joukkoon $B$.
Jokaiseen $B$:n alkioon ei kuvauksessa välttämättä liity $A$:n alkiota; jotkut $B$:n alkiot taas saattavat liittyä useampaan kuin yhteen $A$:n alkioon.
Katso myös Identtinen kuvaus, Inkluusiokuvaus, Isomorfismi, Yksi yhteen kuvaus, Yksi yhteen vastaavuus, Injektio, Funktio, Kuvaus, Bijektio, Surjektio, Maalijoukko, Arvojoukko, Funktion maalijoukko, Homomorfismi, Lineaarikuvaus, Involuutio, Automorfismi, Funktionaali, Toiminta, Morfismi, Ekvivalenssirelaation projektio, Bilineaarinen muoto, Isomorfia, Lineaarimuunnos.
Kuvaus, Funktio (engl. Function)
Sääntö lukujen muuttamiseksi toisiksi luvuiksi. Sääntö voisi esimerkiksi olla: kerro kahdella ja lisää yksi. Tämä sääntö muuttaa luvun $3$ luvuksi $2 \cdot 3 + 1 = 7$ ja luvun $4$ luvuksi $2 \cdot 4 + 1 = 9$.
Funktio eli kuvaus on erityinen relaatio kahden joukon välillä, jossa jokaiseen ensimmäisen joukon alkioon liittyy täsmälleen yksi toisen joukon alkio (ensimmäisen joukon alkion kuva). Ensimmäistä joukkoa kutsutaan funktion määrittelyjoukoksi ja toista joukkoa maali- tai arvojoukoksi.
Monia funktioita voidaan parhaiten havainnollistaa niiden kuvaajien avulla.
Olkoot $A$ ja $B$ joukkoja. Funktio $f : A \to B$ on niiden järjestettyjen parien $(a,b)$, missä $a \in A$ ja $b \in B$, muodostama joukko $f$, joka toteuttaa ehdot:
1) Jokaisella $a \in A$ on olemassa sellainen $b \in B$, jolla $(a,b) \in f$.
2) Jos $(a,b) \in f$ ja $(a,c) \in f$, niin $b = c$.
Sitä yksikäsitteistä alkiota $y$, jolla $(x,y) \in f$, merkitään $f(x)$.
Katso myös Algebra, Modulo, Transformaatio, Parametri, Operaattori, Järjestys, Kuvaus, Identtinen funktio, Komplementti, Yhdistetty funktio, Vakiofunktio, Itseisarvo, Funktion argumentti, Yhdiste, Yksi yhteen kuvaus, Yksi yhteen vastaavuus, Lattia, Kokonaisosa, Minimi, Leikkaus, Pariton funktio, Kuvajoukko, Polynomifunktio, Metriikka, Käänteisfunktio, Interpoloida, Trigonometrinen funktio, Lähtöjoukko, Maalijoukko, Funktion kuvajoukko, Arvojoukko, Funktion maalijoukko, Diffeomorfismi, Homotopia, Rationaalifunktio, Testifunktio, Parillinen funktio, Ackermannin funktio, Kattofunktio, Konveksi funktio, Konkaavi funktio, Morfismi, Sulkeuma, Sileä kuvaus, Mitallinen funktio, Transsendenttifunktio, Permutaation etumerkki, Todennäköisyyden aksioomat, Alkeisdeformaatio, Momenttiemäfunktio, Askelfunktio, Riemannin zeta-funktio, Konvoluutio, Analyyttinen funktio, Gammafunktio, Hyperbolinen funktio, Algebrallinen funktio, Automorfinen funktio, Besselin funktio (ensimmäinen laji), Besselin funktio (toinen laji), Neumannin funktio, Besselin funktio (kolmas laji), Hankelin funktio, Betafunktio, Kategoria, Salausmenetelmä, Liittofunktiot, Kertymäfunktio, Määrittelyjoukko, Virhefunktio, Eulerin $\varphi$-funktio, Permutaatio, Ääriarvo, Fourier'n muunnos, Funktori, Identtinen kuvaus, Indikaattori, Bolzanon lause, Funktio.
Kuvio (engl. Shape)
Jonkin fyysinen muoto; avaruuden osan muoto, jonka se vie.
Kuvio (engl. Figure)
Kuvio on mikä tahansa kaksiulotteinen muoto tai joukko muotoja, kuten kolmio tai neliö.
Katso myös Laatta, Ympyrä, Tahko, Puoliympyrä, Sektori, Tason neljännes, Monikulmio, Soikio, Ovaali, Sivutahkoverkko, Geometria, Euklidinen geometria, Täydellinen nelikulmio.
Kuvion pohja (engl. Base, Base of a shape)
Tasoalue tai jana, joka on kuvion tai kappaleen pohja; se, jolla kuvio tai kappale "lepää".
Kvantifioida (engl. Quantify)
Ilmaista jotakin käyttämällä lukuja. Esimerkiksi älykkyys voidaan kvantifioida älykkyysosamäärän avulla.
Kvartiili, Neljännespiste (engl. Quartile)
Ala- ($Q_1$), keski- ($Q_2$) ja ylä- ($Q_3$) kvartiili ovat tunnuslukuja, jotka jakavat tilastoaineiston 4 yhtä suureen osaan. Ala-kvartiilin ($Q_1$) alapuolella on neljännes, keski-kvartiilin ($Q_2$) alapuolella puolet ja ylä-kvartiilin ($Q_3$) alapuolella kolme neljäsosaa aineistosta. Keski-kvartiilia kutsutaan yleensä mediaaniksi ja merkitään $Md$:llä.
Katso myös Kvartiilivälin pituus, Mediaani, Tunnusluku, Tilastollinen tunnusluku, Laatikko ja viikset -kuvio.
Kvartiilivälin pituus (engl. Interquartile range)
Alakvartiilin ja yläkvartiilin välinen etäisyys. \[ IQR = \mathrm{Q}_3-\mathrm{Q}_1 \]
Katso myös Kvartiili, Neljännespiste, Tunnusluku, Tilastollinen tunnusluku, Verrata, Hajonta.
Kymmenen monikerta (engl. Multiple of 10, Multiple of ten)
Luvut, joiden tekijänä on 10, ovat kymmenen monikertoja. Niiden viimeinen numero on 0, jos ne kirjoitetaan kymmenjärjestelmässä.
Katso myös Sata, 100, Tuhat, 1000, Kaksikymmentä, 20, Tiu, 30, Kolmekymmentä, 50, Viisikymmentä, Kuusikymmentä, 60, Kymmenen potenssit, 70, 40, 80, 90.
Kymmenen potenssit (engl. Power of 10, Power of ten)
Luvut, joka muodostetaan kertomalla lukua 10 itsellään tietty määrä kertoja. Kun kymmenen potenssit kirjoitetaan kymmenjärjestelmässä, niiden lopussa on kyseinen määrä nollia.
Eräitä ensimmäisiä kymmenen potensseja ovat
$10 = 10^{1} =$ kymmenen $100 = 10^{2} =$ sata $1000 = 10^{3} =$ tuhat $1000000 = 10^{6} =$ miljoona $1000000000 = 10^{9} =$ miljardi $1000000000000 = 10^{12} =$ biljoona $10^{18} =$ triljoona $10^{24} =$ kvadriljoona $10^{30} =$ kvintiljoona $10^{36} =$ sekstiljoona $10^{42} =$ septiljoona $10^{48} =$ oktiljoona $10^{54} =$ noniljoona $10^{60} =$ desiljoona.Katso myös Miljoona, 1000000, Biljoona, 1 000 000 000 000, Sata, 100, Tuhat, 1000, Septiljoona, Myriadi, Miljardi, Kymmenen monikerta.
Kymmenjärjestelmä (engl. Decimal system)
Kymmenjärjestelmä on lukujärjestelmä, jonka kantaluku on 10. Kymmenjärjestelmässä luvut esitetään käyttäen numeroita 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9.
Katso myös Desimaalikehitelmä, Kantaluku.
Kymmenjärjestelmän luku, Desimaaliluku (engl. Decimal number)
Luku, joka on kirjoitettu kymmenjärjestelmässä.
Katso myös Paikkajärjestelmä, Kymmenmurtoluku, Numero.
Kymmenkantainen logaritmi (engl. log10)
10-kantaisen logaritmin eli Briggsin logaritmin lyhenne on $\log_{10}$ tai $\lg$.
Kymmenmurtoluku (engl. Decimal fraction)
Murtoluku, jonka nimittäjä on jokin kymmenen potenssi, kuten 10, 100 tai 1000. Esimerkiksi 3/10, 34/100 ja 5/100 ovat desimaalimurtolukuja. Ne kirjoitetaan desimaalilukuina 0,3, 0,34 ja 0,05, kun taas 0,5 tarkoittaa lukua 5/10.
Katso myös Jaksollinen desimaaliluku, Päättyvä desimaaliluku, Verranto, Murtoluku, Desimaaliluku, Kymmenjärjestelmän luku.
Kürschakin lause (engl. Kurschak's theorem, Kürsháks Theorem)
Yksikköympyrän sisään piirretyn säännöllisen kaksitoistakulmion pinta-ala on 3.
Kyyhkyslakkaperiaate, Lokeroperiaate (engl. Pigeon hole principle, Dirichlet principle)
Periaate, jonka mukaan korkeintaan $n$ esinettä voidaan laittaa $n$ lokeroon siten, että kuhunkin lokeroon tulee korkeintaan yksi esine. Jos esineitä on enemmän kuin $n$, niin silloin ainakin yhteen lokeroon tulee useampi kuin yksi esine.
Katso myös Lause.
Kärki, Leikkauspiste, Kulma (engl. Corner)
Leikkauspiste on paikka, jossa kaksi tai useampi suora kohtaavat toisensa.
Kulma on piste, jossa kaksi monikulmion sivua kohtaavat.
Kärki on piste, jossa vähintään kolme monitahokkaan tahkoa kohtaavat.
Katso myös Piste.
Käypä alue (engl. Feasible region)
Lineaarisessa ohjelmoinnissa käyväksi alueeksi kutsutaan niiden pisteiden joukkoa, jotka toteuttavat jokaisen rajoitusehdon (rajoitteen). Käypä alue on aina konveksi.
Katso myös Lineaarinen optimointi, Lineaarinen ohjelmointi.
Käyrien väliin jäävä pinta-ala (engl. Area between curves)
Kahden käyrän rajoittaman alueen pinta-ala voidaan määrittää samoin kuin käyrän ja $x$-akselin välisen alueen pinta-ala.
Olkoot $f(x)$ ja $g(x)$ kaksi välillä $[a,b]$ määriteltyä funktiota ja olkoon $f(x)\le g(x)$, kun $a\le x\le b$. Silloin käyrien $y=g(x)$, $y=f(x)$ ja suorien $x=a$ ja $x=b$ väliin jäävä pinta-ala on \[ \int_a^b(g(x)-f(x))dx. \] Jos käyrät leikkaavat toisensa, eli jos $f(x)\le g(x)$ ei ole voimassa koko välillä $[a,b]$, pinta-ala on laskettava osissa.
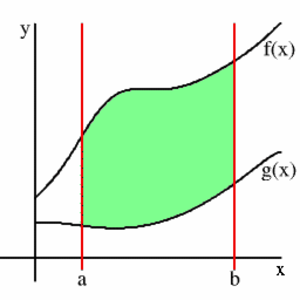
Katso myös Pinta-ala.
Käyrä (engl. Curve)
Viiva, joka ei välttämättä ole suora. Käyrä on usein funktion kuvaaja, liikkuvan kappaleen kulkureitti tai suoran kuva jossakin kuvauksessa.

Katso myös Kaari, Arc, Asymptootti, Kaaren pituus, Tangenttivektori, Tautokroni, Loksodromi, Kellokäyrä, Lemniskaatta, Ketjukäyrä, Jordanin käyrälause, Verho, Verhokäyrä, Geronon lemniskaatta, Splini, Kaarevuuskeskipiste, Normaalivektori, Algebrallinen käyrä, Astroidi, Sivunormaalivektori, Takagin käyrä, van der Waerdenin käyrä, Murtoviiva, Suljettu käyrä, Simpukkakäyrä, Kartioleikkaus, Ruuvikierre, Ruuviviiva, Tasa-arvokäyrä, Kuutiollinen käyrä, Sykloidi, Spiraali.
Käyräintegraali (engl. Curvilinear integral, Path integral, Line integral)
Olkoon $f(x,y)$ kaksiulotteisen avaruuden reaaliarvoinen funktio. Oletetaan, että haluamme integroida funktion $f$ jotakin kaksiulotteisen avaruuden käyrää $C$ pitkin. Tällaista integraalia merkitään $\int_C f ds$ ja sitä kutsutaan käyräintegraaliksi.
Jos käyrällä $C$ on parametriesitys $C = (x(s),y(s))$, missä $s \in [s_0, s_1]$, niin käyräintegraali $\int_C f ds$ voidaan määritellä seuraavasti: \[ \int_C f ds = \int_{s_0}^{s_1} f(x(s),y(s)) ds = \lim_{N \to \infty} \sum_{i=0}^N f (x(s_i), y(s_i)) |(x(s_{i+1}), y(s_{i+1})) - (x(s_i), y(s_i))|, \] missä raja-arvo lasketaan sellaisten välin $[s_0,s_1]$ jakojen yli, joissa pisimmänkin jakovälin pituus lähestyy nollaa $N$:n kasvaessa rajatta.
Käyräintegraali määritellään kolmiulotteisessa avaruudessa vastaavalla tavalla.
Katso myös Integraali, Konservatiivinen, Eksakti, Polkuintegraali.
Käyrän sovitus (engl. Curve fitting)
Käyrän sovituksella tarkoitetaan sellaisen, yleensä yksinkertaisen, käyrän etsimistä, jonka etäisyys annetun joukon pisteistä on pienin.
Käännepiste (engl. Point of inflexion, Point of inflection, Inflection point)
Funktion käännepiste on sellainen funktion kuvaajan piste, jossa kaarevuus vaihtaa merkkiään. Kahdesti derivoituvan funktion käännepiste on piste, jossa toinen derivaatta on nolla ja vaihtaa merkkinsä positiivisesta negatiiviseksi tai toisinpäin.
Esimerkiksi piste $x = -\frac{1}{3}$ on polynomin $y = x^{3} + x^{2} + x + 1$ käännepiste, koska toinen derivaatta $\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} = 6 x + 2$ on nolla pisteessä $x = - \frac{1}{3}$ ja vaihtaa siinä merkkinsä negatiivisesta positiiviseksi.
Katso myös Toinen derivaatta.
Käänteinen (engl. Converse)
Väittämän 'jos A, niin B' käänteinen väittämä on 'jos B, niin A'. On tärkeää muistaa, että väittämä ja sen käänteisväittämä eivät ole yhtäpitäviä; ne on todistettava erikseen, ja jos toinen niistä on tosi, niin toisen ei tarvitse olla.
Katso myös Käänteisväittämä, Kontrapositio.
Käänteinen hyperbolinen funktio, Areafunktio (engl. Inverse hyperbolic function)
Käänteisiä hyperbolisia funktioita ovat arsinh(x), arcosh(x), artanh(x) ja arcoth(x). Nämä ovat toisinaan hyödyllisiä laskettaessa integraaleja sijoitusmenetelmän avulla.
Katso myös Hyperbolinen funktio, Hyperbolisen kosinin käänteisfunktio, Hyperbolisen sinin käänteisfunktio.
Käänteis- (engl. Inverse)
Luvun käänteisluku on 1 jaettuna luvulla. Funktion tai kuvauksen käänteisfunktio tai -kuvaus on funktio tai kuvaus, joka "palauttaa" alkuperäisen funktion. Joukon alkion käänteisalkio tai -luku tietyn operaation suhteen on se alkio, joka on yhdistettävä alkuperäisen alkion kanssa, jotta saataisiin tulokseksi operaation käänteisalkio.
Esimerkiksi luvun 5 käänteisluku on 1/5.
Yhteenlaskun käänteislaskutoimitus on vähennyslasku.
Myötäpäivään kierron käänteisoperaatio on vastapäivään kierto.
Luvun 5 käänteisluku yhteenlaskun suhteen on $-5$, koska $5+(-5)$ on sama kuin yhteenlaskun neutraalialkio $0$.
Käänteisalkion käänteisalkio on aina alkuperäinen alkio.
Katso myös Vasta-alkio, Käänteisalkio, Inversiokuvaus, Käänteisväittämä, Kääntää, Kääntyvä, Kertolaskun käänteisalkio, Käänteisluku, Käänteismatriisi.
Käänteisalkio, Kertolaskun käänteisalkio, Käänteisluku (engl. Multiplicative inverse)
Luvun käänteisalkio on se luku, jolla alkuperäinen luku on kerrottava, jotta saataisiin tulokseksi kertolaskun neutraalialkio.
Jos kertolaskun neutraalialkio on 1, niin alkion $a$ käänteisalkio $a'$ on se alkio, jolla $aa' = a'a = 1$. Luvulla 0 ei ole käänteisalkiota. Joukossa $\mathbb{N}$ vain luvulla 1 on käänteisalkio. Joukossa $\mathbb{Z}$ vain luvuilla 1 ja $-1$ on käänteisalkio. Sen sijaan joukoissa $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ alkion $a \neq 0$ käänteisalkio on $1/a$.
Katso myös Ykkösalkio, Kertolaskun neutraalialkio, Kertolasku, Käänteis-, Jakolasku, Joukko, Kunta, Jakaminen.
Käänteisfunktio (engl. Inverse function)
Funktion $f : X \to Y$ käänteisfunktio on funktio $g : Y \to X$, jolla $g(f(x)) = x$ kaikilla $x \in X$ ja $f(g(y)) = y$ kaikilla $y \in Y$. Funktion $f$ käänteisfunktiota merkitään $f^{-1}$. Funktion on oltava bijektio, jotta sillä olisi käänteisfunktio.
Käänteisluku (engl. Reciprocal)
Luvun käänteisluku on 1 jaettuna luvulla. Siten esimerkiksi luvun 4 käänteisluku on 1/4. Käänteisluku on se luku, jolla annettu luku on kerrottava, jotta saataisiin 1.
Käänteisluvun käänteisluku on alkuperäinen luku.
Katso myös Reaaliluku, Kompleksiluvun käänteisluku.
Käänteisluku, Käänteisalkio, Kertolaskun käänteisalkio (engl. Multiplicative inverse)
Luvun käänteisalkio on se luku, jolla alkuperäinen luku on kerrottava, jotta saataisiin tulokseksi kertolaskun neutraalialkio.
Jos kertolaskun neutraalialkio on 1, niin alkion $a$ käänteisalkio $a'$ on se alkio, jolla $aa' = a'a = 1$. Luvulla 0 ei ole käänteisalkiota. Joukossa $\mathbb{N}$ vain luvulla 1 on käänteisalkio. Joukossa $\mathbb{Z}$ vain luvuilla 1 ja $-1$ on käänteisalkio. Sen sijaan joukoissa $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ alkion $a \neq 0$ käänteisalkio on $1/a$.
Katso myös Ykkösalkio, Kertolaskun neutraalialkio, Kertolasku, Käänteis-, Jakolasku, Joukko, Kunta, Jakaminen.
Käänteismatriisi (engl. Inverse matrix)
Matriisin $A$ käänteismatriisi $A^{-1}$ , jos se on olemassa, toteuttaa yhtälön \[ A A^{-1} = A^{-1} A = I, \] missä $I$ on yksikkömatriisi.
$2 \times 2$-matriisin $A = \left[ \begin{array}{cc} a & b\\ c & d \end{array} \right]$ käänteismatriisi $A^{-1}$ voidaan laskea kaavalla \[ A^{-1} = \frac{1}{a d-b c}\left[ \begin{array}{cc} d & -b \\ -c & a \end{array} \right], \] mikäli $ad-dc \neq 0$. Jos $ad-bc = 0$, niin käänteismatriisia ei ole olemassa.
Katso myös Käänteis-, Determinantti, Ortogonaalinen matriisi, Matriisi.
Käänteisväittämä (engl. Logical inverse, Inverse statement)
\newcommand{\implies}{\Rightarrow} Väittämän $ A \implies B $ -- $A$:sta seuraa $B$ -- käänteinen väittämä on $\overline{A} \implies \overline{B}$ eli ei-$A$:sta seuraa ei-$B$.
Katso myös Käänteis-, Käänteinen, Kontrapositio.
Kääntyvä (engl. Invertible)
Jokin on kääntyvä, jos sille voidaan muodostaa käänteisalkio. Erityisesti neliömatriisi on kääntyvä, jos sillä on käänteismatriisi eli jos sen determinantti on eri kuin nolla.
Katso myös Käänteis-.
Kääntyvä matriisi, Säännöllinen matriisi (engl. Invertible matrix)
Neliömatriisi, jolla on käänteismatriisi. Käänteismatriisi on olemassa jos ja vain jos matriisin determinantti ei ole nolla. Säännöllistä matriisia kutsutaan myös kääntyväksi matriisiksi.
Katso myös Determinantti, Neliömatriisi.
Kääntää (engl. Invert)
Etsiä alkion käänteisalkio. Kääntäminen kahdesti antaa tulokseksi alkuperäisen alkion.
Katso myös Käänteis-.
Königsbergin sillat (engl. Konigsberg bridge problem, Konigsberg)
Kuuluisa ongelma, jossa kysytään, onko mahdollista tehdä kiertokävely Königsbergin kaupungissa ylittämällä kaikki kaupungissa olevat seitsemän siltaa vain kerran ja palaamalla takaisin paikkaan, josta kävelylle lähdettiin. Euler osoitti verkkoteorian avulla, että tämä ei ole mahdollista.
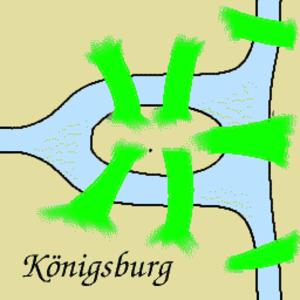
Katso myös Eulerin kierros, Verkkoteoria, Verkko.
