M (engl. M)
Megan, miljoonaa tarkoittavan etuliitteen, lyhenne. Esimerkiksi 1 m tarkoittaa yhtä metriä, mutta 1 Mm tarkoittaa yhtä megametriä eli miljoonaa metriä.
m (engl. m)
Metrin lyhenne.
Pieni kirjain m on myös millin, yhtä tuhannesosaa tarkoittavan etuliitteen, lyhenne. Siten esimerkiksi 1 s tarkoittaa yhtä sekuntia, mutta 1 ms tarkoittaa yhtä millisekuntia eli sekunnin tuhannesosaa.
Katso myös Metri.
Maalijoukko, Arvojoukko, Funktion maalijoukko (engl. Codomain)
Funktion $f \colon A \rightarrow B$ maalijoukko on joukko $B$ eli niiden arvojen joukko, joita funktion voidaan periaatteessa ajatella saavan.
Funktio on surjektio, jos se saa kaikki arvot maalijoukossaan eli $fA=B$.
Kuvauksen $f \colon \mathbb{R} \rightarrow \mathbb{R}, x \mapsto x^2$, maalijoukko on $\mathbb{R}$, mutta $f$ ei saa esimerkiksi arvoa $-1$ missään pisteessä. Kuvauksen $f$ kuvajoukko on väli $[0, \infty)$.
Katso myös Kuvaus, Funktio, Kuvaus, Kuvajoukko, Joukko, Lähtöjoukko, Funktion kuvajoukko, Määrittelyjoukko, Funktio.
Maclaurinin sarja (engl. Maclaurin series)
Maclaurinin sarja on Taylorin sarjan erikoistapaus muotoa \[ f(x)=f(0)+f\prime(0)x+f\prime\prime(0)x^{2}/2+f\prime\prime\prime(0)x^{3}/3!+... +f^{(n-1)}(0)x^{n-1}/(n-1)!+R_{n}. \] (Tämä on Taylorin sarja pisteessä $a=0$.) Maclaurinin lause kertoo, millä ehdoilla funktiolla $f$ on tällainen sarjaesitys. Yllä $R_{n}$ on jäännöstermi, joka voidaan esittää samoin kuin Taylorin sarjan jäännöstermi.
Katso myös Potenssisarja, Taylorin sarja, Virhetermi, Jäännöstermi.
Mahdollisuus, Sattuma (engl. Chance)
Jokin tapahtuu sattumalta, jos sen tapahtumista ei voi ennustaa varmasti, vaan voidaan puhua ainoastaan sen tapahtumisen todennäköisyydestä.
Jonkin tapahtumisen mahdollisuus on sen tapahtumisen todennäköisyys. Sanaa käytetään myös kuvaamaan tilaisuutta tehdä jotakin.
Katso myös Riski, Tapahtuma, Todennäköisyys, Otosavaruus, Ominaisuus, Määrite.
Mahdottoman tapauksen todennäköisyys (engl. Probability of null event, Probability of impossible event)
Koska tapahtuma $\emptyset$ ei sisällä yhtään alkeistapausta, niin $p(\emptyset)=0$.
Katso myös Tyhjä joukko, Todennäköisyys.
Mahtavuus (engl. Cardinality)
Joukon mahtavuus on luku, joka kertoo joukon alkioiden lukumäärän. Äärellisen joukon mahtavuus on aina luonnollinen luku. Numeroituvan äärettömän joukon mahtavuus on $\aleph_{0}$ ("alef-nolla"). Pienin sitä suurempi mahtavuus on $\aleph_{1}$ ("alef-yksi"). Reaalilukujen joukon mahtavuus on $2^{\aleph_{0}}$ ja se on suurempi kuin $\aleph_{0}$. Väitettä $2^{\aleph_{0}} = \aleph_{1}$ kutsutaan kontinuumihypoteesiksi. Se on osoitettu riippumattomaksi joukko-opin aksioomista.
Joukon $A$ mahtavuutta voidaan merkitä $n(A)$, $|A|$ tai $\overline{A}$.
Katso myös Perusluku, Joukko, Alef-nolla, Ominaisuus, jonka arvot ovat diskreettejä.
Maili (engl. Mile)
Englantilainen pituusyksikkö, joka on yhtä suuri kuin 1760 jaardia eli 5280 jalkaa eli 1609,344 metriä.
Katso myös Jalka.
Mailia tunnissa (engl. Mile per hour)
Nopeusyksikkö. 1 mph tarkoittaa yksi maili tunnissa eli 1,609 kilometriä tunnissa eli 0,447 metriä sekunnissa.
Katso myös mph.
Maksimaalinen (engl. Maximal)
Olla jonkin maksimi tai suurin mahdollinen esimerkki jostakin.
Katso myös Minimaalinen, Ideaali, Ihanne.
Maksimi (engl. maximum)
Jonkin suurin mahdollinen arvo.
Maksimikohta on piste, jossa funktio saa suurimman arvonsa.
Paikallinen maksimi ei välttämättä ole funktion kaikkein suurin arvo, mutta se on suurempi kuin maksimikohdan ympäristössä saadut arvot.
Yhden muuttujan funktion derivaatan nollakohta on lokaali maksimikohta, jos funktion toinen derivaatta on tässä kohdassa negatiivinen.
Katso myös Kaltevuus, Minimi, Derivaatta, Gradientti, Ääriarvo.
Maksimoida (engl. Maximize, Maximise)
Tehdä jokin niin suureksi kuin mahdollista.
Katso myös Minimoida.
Malli (engl. Model)
Matemaattinen malli, joka toimii tietyllä tarkkuudella samalla tavalla kuin todellisuus. Mallin perusteella voidaan ratkaista tutkittavan ilmiön tilaan liittyviä ongelmia. Esimerkiksi yksinkertaisin malli muuttujan sijainnille on muuttujan otoskeskiarvo. Mikäli muuttuja riippuu muiden muuttujien arvosta, voidaan muuttujaa mallittaa regressiomallin $$ \hat Y = f(X_1, X_2, ... X_p) $$ avulla.
Mandelbrotin joukko (engl. Mandelbrot set)
Niiden pisteiden $c$ joukko, joilla iteroitu kuvaus $z \mapsto z^2+c$ ei hajaannu äärettömyyteen. Mandelbrotin joukko on fraktaali.

Katso myös Fraktaali.
Mantissa (engl. Mantissa)
Luvun kymmenkantaisen logaritmin desimaaliosa. Esimerkiksi luvuilla $20$ ja $200$ on sama mantissa $0.3010\ldots$, koska $\log(20) = 1.3010\ldots$ ja $\log(200) = 2.3010\ldots$.
Katso myös Murtoluku, Eksponentti, Logaritmi.
Markovin epäyhtälö (engl. Markov's inequality)
Jos $X$ on satunnaismuuttuja, jolla on äärellinen odotusarvo, niin tällöin kaikilla $a>0$ pätee \[ \mathbb{P}(|X| \geq a) \leq \frac{ \mathbb{E} |X|}{a}. \] Katso myös Jensenin epäyhtälö ja Chebyshevin epäyhtälö.
Katso myös Erisuuruus, Chebyshevin epäyhtälö, Jensenin epäyhtälö, Epäyhtälö.
Markovin ketju (engl. Markov chain)
Stokastinen prosessi, jonka määrittelee jono satunnaismuuttujia $X_t$, $t = 0, 1, 2, \ldots$, joilla on ominaisuus \[ \mathrm{P}(X_{t+1} = r \mid X_0 = t_0, X_1 = t_1, \ldots, X_t = r_t) = \mathrm{P}(X_{t+1} = r \mid X_t = r_t). \] Toisin sanoen, tulevaisuuden tapahtuman todennäköisyys riippuu ainoastaan nykyisyydestä, ei menneisyydestä.
Satunnaiskävely on esimerkki Markovin ketjusta.
Katso myös Tilastotiede, Ehdollinen todennäköisyys, Satunnaismuuttuja.
Massakeskipiste, Painopiste (engl. Barycentre, Center of mass, Centre of mass)
Kohdissa $(x_{i}, y_{i}, z_{i})$ sijaitsevista pistemassoista $m_{i}$ koostuvan kappaleen massakeskipiste eli painopiste on $(\bar{x}, \bar{y}, \bar{z})$, missä $\bar{x} = \frac{\sum_i x_im_i}{\sum_i m_i}$, jne.
Jos kappaleen $V$ massatiheys pisteessä $(x, y, z)$ on $p(x, y, z)$ ja kappaleen kokonaismassa on $M$, niin sen massakeskipiste eli painopiste on $(\bar{x}, \bar{y}, \bar{z})$, missä $\bar{x} = \frac{\int_V x p dV}{M}$, jne.
Karkeasti sanoen on kaksiulotteisen kappaleen massakeskipiste se piste, josta tuettuna kappale pysyy vaakatasossa, kun taas kolmiulotteisen kappaleen massakeskipiste on se piste, joka jää aina kohtisuoraan kappaleen kiinnityspisteen alapuolelle kiinnitettiinpä kappale roikkumaan mistä pisteestä tahansa.
Katso myös Keskipiste, Pyramidin massakeskipiste, Ympyränkaaren massakeskipiste, Puolipallonkuoren massakeskipiste, Puolipallon massakeskipiste, Kolmion massakeskipiste, Pyörähdyskappaleen massakeskipiste, Ympyrän sektorin massakeskipiste, Kartion vaipan massakeskipiste, Kartion massakeskipiste, Tasoalueen massakeskipiste.
Matemaattinen päättely (engl. Mathematical reasoning)
Päättely, jossa käsitellään lukuja, kuvioita, tms. sekä tehdään täsmällisiä väittämiä ja johtopäätöksiä niiden ominaisuuksista ja suhteista. Tällainen päättely voi olla melko yksityiskohtainen olematta välttämättä tarpeeksi perusteellinen, jotta sitä voisi kutsua todistukseksi.
Matematiikan historia (engl. History of maths)
Matematiikan osa-alue, joka käsittelee sitä, miten tietämyksemme matematiikasta on aikojen kuluessa kehittynyt, sekä ihmisiä, jotka ovat tähän kehitykseen vaikuttaneet.
Matematiikka (engl. Mathematics)
Lukujen ja abstraktien rakenteiden tutkiminen kaikkein yleisimmässä mielessä.
Katso myös Analyysi, Alkeismatematiikka, Soveltava matematiikka, Uusi matematiikka.
Matematiikka ja tietojenkäsittely (engl. Maths and Computing)
Tietojenkäsittelytieteellä on läheinen yhteys matematiikkaan. Matematiikkaa tarvitaan usein tutkittaessa, miten laskennallinen prosessi toimii tai mikä on tehokkain tapa tehdä jokin asia.
Modernissa matematiikassa voidaan toisaalta usein käyttää tietokoneita asioiden helpottamiseksi, esimerkiksi likimääräisten ratkaisujen löytämisessä, algebrallisten lausekkeiden muokkaamisessa tai jopa sellaisten monimutkaisten todistusten tarkastamisessa, jotka ovat liian pitkiä käsin tehtäviksi.
Katso myös Sovellus, Kryptografia, Kryptologia.
Matriisi (engl. Matrix)
Neliön tai suorakaiteen muotoinen, yleensä suurten hakasulkujen ympäröimä joukko lukuja. Matriisien yhteen- ja kertolaskua varten on omat sääntönsä. Lineaarimuunnosten esittäminen matriisien avulla on kätevää näitä sääntöjä käyttämällä.
Esimerkiksi yhtälöryhmä \begin{eqnarray*} x + 2y + 3z &=& 1\\ 2x + 5y + 7z &=& 2\\ x + 4y &=& 3\\ \end{eqnarray*} voidaan esittää yhtenä matriisiyhtälönä \[ \mathbf{Ax} = \mathbf{B}, \] missä \[ \mathbf{A} = \left[ \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 5 & 7 \\ 1 & 4 & 0 \end{array} \right ]\mbox{,}\quad \mathbf{x} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right ]\quad\mbox{ja}\quad \mathbf{B} = \left[ \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right ]. \]
Matriiseilla voidaan helposti esittää monia useista komponenteista koostuvia fysikaalisia suureita. Esimerkiksi kiinteän kappaleen hitausmomentit eri pyörähdysakselien suhteen voidaan esittää $3 \times 3$- matriisina.
Katso myös Nollamatriisi, Yhtälöryhmä, Lineaarinen yhtälöryhmä, Diskreetti matematiikka, Kolmiomatriisi, Taulukko, Peilausmatriisi, Rotaatiomatriisi, Kiertomatriisi, Determinantti, Matriisin normi, Matriisin transpoosi, Harva matriisi, Sarakeavaruus, Neliömatriisi, Riviavaruus, Käänteismatriisi, Hermitoitu matriisi, Täydennetty matriisi, Nauhamatriisi, Kanoninen muoto, Cayley-Hamiltonin lause, Karakteristinen yhtälö, Karakteristinen polynomi, Kofaktori, Cramerin sääntö, Matriisin dimensio, Ominaisvektori, Alkeismatriisi, Hessen matriisi, Jacobin matriisi, Lineaarialgebra.
Matriisin aste (engl. Rank of a matrix, Rank)
Lineaarisesti riippumattomien rivien (tai sarakkeiden) lukumäärä matriisissa.
Yhtäpitävästi, matriisin kuva-avaruuden dimensio.
Katso myös Ominaisuus, jonka arvot ovat diskreettejä.
Matriisin dimensio (engl. Dimension of a matrix)
Matriisin dimensio on sen rivien (tai yhtäpitävästi, sarakkeiden) virittämän aliavaruuden dimensio. Tämä on sama kuin matriisin lineaarisesti riippumattomien rivien (tai yhtäpitävästi, sarakkeiden) lukumäärä.
Joskus matriisin dimensiolla tarkoitetaan matriisin tyyppiä. Tällöin $m \times n$- matriisin dimensio on $m \times n$.
Katso myös Ydin, Lineaarinen riippumattomuus, Dimensio, Ulottuvuus, Vektoriavaruus, Sarakeavaruus, Riviavaruus, Matriisi.
Matriisin normi (engl. Norm of a matrix)
$n \times m$-matriisin $A$ normi määritellään kaavalla \[ \| A \| = \max_{v\in\mathbb{R}^n, v\neq 0} \frac{\| A v \| } { \| v \| }. \] Toisin sanoen, $\| A \|$ on suurin arvoista, jotka saadaan jakamalla vektorin $A v$ normi vektorin $v$ normilla jokaisella nollasta eroavalla $\mathbb{R}^n$:n vektorilla $v$.
Katso myös Reaaliluku, Vektorin normi, Matriisi.
Matriisin operaattorinormi (engl. Subordinate matrix norm, Operator matrix norm, Subordinate or operator matrix norm)
Matriisin operaattorinormi määritellään kaavalla $$ \| A \| = \max_{|\bar v| = 1} | A \bar v | = \max_{\bar v \neq 0} \frac{| A \bar v|}{|\bar v|}.$$ Yllä on oletettu, että yhtälön keski- ja oikeassa jäsenessä on ennalta määritelty normi, josta operaattorinormi riippuu. Yleisimmin tämä ennalta määritelty normi on euklidinen normi.
Matriisin transpoosi (engl. Transpose of a matrix)
Olkoon $A$ matriisi, jossa rivillä $i$ sarakkeessa $j$ on alkio $a_{i,j}$. Matriisin $A$ transpoosi on matriisi $A^T$, jossa alkio $a_{i,j}$ on rivillä $j$ sarakkeessa $i$.
Esimerkiksi matriisin $\left ( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right )$ transpoosi on matriisi $ \left ( \begin{array}{cc} 1 & 3 \\ 2 & 4 \end{array} \right ).$
Katso myös Unitaarinen matriisi, Symmetrinen matriisi, Ortogonaalinen matriisi, Matriisi, Normaali matriisi, Vinosymmetrinen matriisi, Hermiittinen matriisi.
Mediaalikolmio (engl. Medial triangle)
Kolmio, jonka kärjet ovat annetun kolmion sivujen keskipisteet.
Katso myös Kolmio, Keskijana, Mediaani, Keskipiste.
Mediaani (engl. Median, Median of data)
Yrityksessä on 7 henkilöä, joiden palkat ovat:
- Pomo 5000
- Kanslisti 1300
- Työntekijä 1 1700
- Työntekijä 2 1500
- [] Työntekijä 3 1400
- Työntekijä 4 1200
- Työntekijä 5 1200
Mediaani on muuttujanarvo, joka jakaa tilastoaineiston kahteen yhtä suureen osaan. Mikäli havaintoja on pariton määrä, mediaani on suuruusjärjestykseen järjestetyssä aineistossa keskimmäiseen havaintoon liittyvä muuttujanarvo. Mikäli havaintoja on parillinen määrä, mediaani on suuruusjärjestykseen järjestetyssä aineistossa kahteen keskimmäiseen havaintoon liittyvien muuttujanarvojen keskiarvo. Otosmediaani on arvio (estimaatti) muuttujan jakauman mediaanille, joka jakaa jakauman kahteen yhtä suuren osaan.
Katso myös Paikantamistunnusluku, Keskiluku, Moodi, Tyyppiarvo, Kvartiili, Neljännespiste, Verrata, Laatikko ja viikset -kuvio.
Mediaani, Keskijana (engl. Median, Median of a triangle)
Jana, joka yhdistää kolmion kärjen ja sen vastaisen sivun keskipisteen. Kolmion kolme mediaania leikkaavat toisensa samassa pisteessä ja tämä piste on kolmion painopiste.
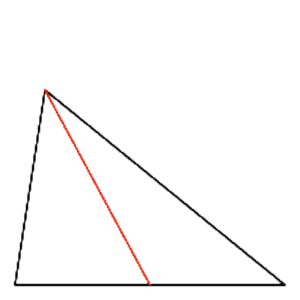
Katso myös Mediaalikolmio, Painopiste, Kolmion massakeskipiste.
Mega (engl. Mega)
Etuliite, joka tarkoittaa miljoonaa eli $10^{6}$. Megalle käytetään merkkiä M, esimerkiksi 1 MHz on miljoona hertziä.
Tietojenkäsittelyssä laskettaessa tavujen lukumäärää mega tarkoittaa lukua $2^{20}$ eli 1048576.
Megatavu (engl. Megabyte)
$2^{20} = 1048576$ tavua.
Katso myös Tavu.
Menelausin lause (engl. Menelaus' theorem)
Olkoon $ABC$ kolmio. Jatketaan kolmion sivuja $AB$, $BC$ ja $CA$ äärettömyyteen ja piirretään suora $L$. Jos $L$ leikkaa sivun $BC$ pisteessä $X$, sivun $CA$ pisteessä $Y$ ja sivun $AB$ pisteessä $Z$, pätee yhtälö \[ \frac{\mathrm{BX}}{\mathrm{XC}} \cdot \frac{\mathrm{CY}}{\mathrm{YA}} \cdot \frac{\mathrm{AZ}}{\mathrm{ZB}} = -1. \]
Katso myös Lause, Kolmio, Suhde, Suorien leikkauspiste.
Meridiaani, Pituuspiiri (engl. Meridian)
Maapallon napojen kautta kulkeva isoympyrä.
Nollapituuspiiri on Greenwichin kautta kulkeva pituuspiiri.
Pituuspiirin sijaintia kuvaa sen pituusaste, joka on meridiaanin tason ja nollameridiaanin tason välinen kulma.
Katso myös Loksodromi, Isoympyrä.
Meripeninkulma (engl. Nautical mile)
Merenkulussa käytetty pituusyksikkö, alkuaan yhtä maapallon meridiaaniympyrän kaariminuuttia vastaava matka. Meripeninkulma on 1852 metriä.
Merkintätapa, Notaatio (engl. Notation)
Tapa, jolla kirjoitetaan asioita käyttäen kirjaimia, numeroita ja muita merkkejä.
Sopimus siitä, mitä asiaa merkitään milläkin merkillä.
Katso myös 12 tunnin kello, Kalenteri, Tangentin neliö, Sinin neliö, Tavu, Osoite, Kaarisulkeet, Sekantin neliö, Etumerkki, Paikkajärjestelmä, Verranto, Numero, Eksponentti, Desimaalipilkku, Kanoninen, $O(f(x))$, Kreikkalaiset kirjaimet, Lyhenne, Alaindeksi, Takaliite, Yläindeksi, Rivi, Valita, Tukkimiehen kirjanpito, Äärettömyys, Etumerkillä varustettu luku, Lukujärjestelmä, Kantaluku, Asymptoottinen kasvunopeus, Binomikerroin, Alef, Sarake, Ketjumurtoluku, Kroneckerin delta, Ellipsi, Yleistetty tulo.
Merkitsevin tai vähiten merkitsevä numero (engl. Significant figure, Most or least significant digit)
Kun luku kirjoitetaan tavalliseen tapaan, niin äärimmäisenä vasemmalla oleva numero on merkitsevin numero, koska se vaikuttaa eniten luvun suuruuteen. Äärimmäisenä oikealla oleva numero on vähiten merkitsevä numero, koska sen vaikutus luvun suuruuteen on vähäisin. Esimerkiksi luvussa 1507,54 merkitsevin numero on 1 ja vähiten merkitsevä numero on 4.
Katso myös Tarkkuus, Paikkajärjestelmä, Numero.
Merkitsevyystaso (engl. Significance level)
Hypoteesia testattaessa merkitsevyystaso on todennäköisyys, jolla nollahypoteesi hylätään virheellisesti.
Katso myös Nollahypoteesi, Todennäköisyys.
Merkitsevyystaso (engl. Significance level)
Hypoteesia testattaessa merkitsevyystaso on todennäköisyys, jolla nollahypoteesi hylätään virheellisesti.
Katso myös Nollahypoteesi, Todennäköisyys.
Meromorfinen (engl. Meromorphic)
Olkoon $D \subset \mathbb{C}$ alue eli avoin ja yhtenäinen kompleksitason $\mathbb{C}$ osajoukko. Kuvaus $f \colon D \rightarrow \bar{\mathbb{C}}$ on meromorfinen, mikäli se on analyyttinen lukuunottamatta niitä pisteitä, joissa sillä on napa.
Katso myös Analyyttinen funktio.
Mersennen alkuluku (engl. Mersenne prime)
Alkulukua, joka voidaan kirjoittaa muodossa $2^{n}-1$, sanotaan Mersennen alkuluvuksi. Monet Mersennen luvuista $M_{n}$ ovat alkulukuja, esimerkiksi luvut $M_2$, $M_3$, $M_5$, $M_7$ ja $M_{13}$. $M_{n}$ voi olla alkuluku vain silloin, kun $n$ on alkuluku. Kuitenkaan jokainen alkuluku $n$ ei anna Mersennen alkulukua. Esimerkiksi $M_{11}$ ei ole alkuluku. Mersennen alkulukuja tunnetaan 38 kappaletta, joista pienimmät ovat $2^{2}-1 = 3$, $2^{3}-1 = 7$, $2^{5}-1 = 31$, $2^{7}-1 = 127$ ja $2^{13}-1 = 8191$. Suurin tunnettu Mersennen alkuluku on $2^{13466917}-1$. Jos $2^{p}-1$ on alkuluku, niin $2^{p-1} (2^{p}-1)$ on täydellinen luku.
Katso myös Seitsemän, 7, Mersennen luku, Alkuluku.
Mersennen luku (engl. Mersenne number)
Kokonaisluku, joka on muotoa $M_{p} = 2^{p}-1$, missä $p$ on alkuluku. Jos tällainen luku on itsekin alkuluku, sitä sanotaan Mersennen alkuluvuksi. Jos $p$ on yhdistetty luku, niin $M_{p}$ on yhdistetty luku. Käänteinen väite ei päde.
Katso myös Seitsemän, 7, Mersennen alkuluku, Kokonaisluku.
Metri (engl. Metre, Meter)
Metrijärjestelmän perusyksikkö, jota käytetään pituuden mittaamiseen; sen lyhenne on m. Yksi metri on sata senttimetriä tai kilometrin tuhannesosa.
Metrijärjestelmän pituusyksikkö, jonka lyhenne on m. Se on määritelty useita kertoja. Ensimmäiseksi vuonna 1791 se määriteltiin Dunkerquen kautta kulkevan pituuspiirin neljäskymmenesmiljoonasosan pituutena.
Vuonna 1927 se määriteltiin platinan ja iridiumin seoksesta valmistetun standarditangon pituutena.
Vuonna 1963 se määriteltiin tietyissä olosuhteissa tapahtuvan kryptonatomiin liittyvän säteilyn aallonpituuden tiettynä monikertana.
Vuonna 1983 se määriteltiin sen matkan pituutena, jonka valo kulkee $\frac{1}{299792458}$ sekunnissa.
Katso myös m, SI-yksiköt, Senttimetri, Kilometri.
Metriikka (engl. Metric)
Mikä tahansa "etäisyysfunktio" $d(x,y)$, joka ottaa argumentikseen kaksi pistettä ja antaa tulokseksi ei-negatiivisen reaaliluvun ja toteuttaa seuraavat ehdot:
$d(x,y) = 0$ jos ja vain jos $x=y$,
$d(x,y) = d(y,x)$,
$d(x,y)+d(y,z) \geq d(x,z)$ (kolmioepäyhtälö).
Katso myös Kolmioepäyhtälö, Funktio, Kuvaus, Elliptinen geometria, Riemannin geometria, Metrinen avaruus.
Metrinen avaruus (engl. Metric space)
Metrinen avaruus on joukko $X$ varustettuna kuvauksella $d : X^2 \to \mathbb{R}$, joka toteuttaa ehdot
- $d(x,y) \geq 0$ ja $d(x,y)=0$ jos ja vain jos $x=y$,
- $d(x,y) = d(y,x)$,
- $d(x,z)\leq d(x,y)+d(y,z)$ kaikilla $x,y,z \in X$.
Jokainen metrinen avaruus on topologinen avaruus, jossa avoimia joukkoja ovat ne $X$:n osajoukot $U$, joiden jokainen piste $x \in U$ sisältyy avoimen palloon \[ B_\varepsilon (x) = \{ y \in X : d(x,y) \lt \varepsilon \} \subset U \] jollakin $\varepsilon \gt 0$.
Katso myös Kolmioepäyhtälö, Rajoitettu, Metriikka, Joukko, Normiavaruus, Täydellinen.
mg (engl. mg)
Milligramman lyhenne.
Katso myös Milligramma, Lyhenne.
MGF (engl. MGF)
Lyhenne momenttiemäfunktiolle.
Katso myös Eksponenttijakauma, Momenttiemäfunktio, Summan momenttiemäfunktio.
Mielivaltainen (engl. Arbitrary)
Jos muuttujan arvo on mielivaltainen, niin sitä koskevat matemaattiset tulokset ovat tosia kaikilla mahdollisilla muuttujan arvoilla. Joskus saatetaan olla erityisen kiinnostuneita tilanteesta, jossa muuttuja voi saada hyvin suuria tai hyvin pieniä arvoja. Tällöin sanottaisiin, että muuttujan arvo on "mielivaltaisen suuri" (tai pieni).
Katso myös Muuttuja.
Miinusmerkki (engl. Minus)
Merkki $-$, joka tarkoittaa vähentämistä tai vastalukua.
Katso myös Etumerkki.
Mikro- (engl. micro)
Etuliite, joka tarkoittaa yhtä miljoonasosaa eli $10^{-6}$. Mikrolle käytetään merkkiä $\mu$, esimerkiksi yksi $\mu \mathrm{m}$ eli mikrometri on metrin miljoonasosa.
Katso myös Lyhenne.
Mikrogramma (engl. Microgram)
Massan yksikkö, joka on yhtä suuri kuin gramman miljoonasosa. Mikrogramman lyhenne on $\mu\mathrm{g}$.
Katso myös Milligramma.
Mikrolitra (engl. Microlitre, Microliter)
Litran miljoonasosa.
Mikrometri (engl. Micrometer)
Laite hyvin pienten pituuksien tarkkaan mittaamiseen.
Katso myös Mikrometri.
Mikrometri (engl. Micrometre)
Metrin miljoonasosa eli millimetrin tuhannesosa.
Katso myös Mikrometri.
Miljardi (engl. Milliard)
Tuhat miljoonaa. Sama kuin amerikkalainen biljoona.
Katso myös Biljoona, 1 000 000 000 000, Kymmenen potenssit.
Miljoona, 1000000 (engl. 1 000 000, Million, 1000000)
Tuhat tuhatta eli $1000^{2}$
tai sadan kuutio eli $100^{3}$
tai kymmenen kuudes potenssi eli $10^{6}.$
Katso myös Biljoona, 1 000 000 000 000, Kymmenen potenssit.
Milli- (engl. Milli)
Etuliite, joka tarkoittaa yhtä tuhannesosaa. Millille käytetään merkkiä m, esimerkiksi yksi ms eli millisekunti on sekunnin tuhannesosa.
Katso myös Sentti.
Milligramma (engl. Milligram)
Gramman tuhannesosa. Milligramman lyhenne on mg.
Katso myös mg, Mikrogramma.
Millilitra (engl. Millilter, Millilitre)
Tilavuuden yksikkö, joka on yhtä suuri kuin litran tuhannesosa tai senttilitran kymmenesosa. Millilitran lyhenne on ml. Yksi millilitra on yhtä suuri kuin yksi kuutiosenttimetri.
Katso myös Tilavuus, ml, Kuutiosenttimetri.
Millimetri (engl. Millimeter, Millimetre)
Metrin tuhannesosa. Millimetrille käytetään merkintää mm.
Katso myös mm, Senttimetri.
Millisekunti (engl. Millisecond)
Sekunnin tuhannesosa. Millisekunnin lyhenne on ms.
Minimaalinen (engl. Minimal)
Joukon pienin alkio tai pienin mahdollinen esimerkki jostakin.
Katso myös Maksimaalinen.
Minimax (engl. Minimax)
Periaate, jonka mukaan päätöksenteossa pitäisi pyrkiä minimoimaan suurin mahdollinen (maksimaalinen) tappio. Tätä periaatetta pidetään usein tarpeettoman pessimistisenä.
Katso myös Algoritmi.
Minimi (engl. Minimum)
Jonkin pienin mahdollinen arvo.
Minimikohta on piste, jossa funktio saa pienimmän arvonsa. Paikallinen minimi ei välttämättä ole funktion kaikkein pienin arvo, mutta se on pienempi kuin minimikohdan ympäristössä saadut arvot.
Yhden muuttujan funktion derivaatan nollakohta on funktion paikallinen minimikohta, jos funktion toinen derivaatta on tässä kohdassa positiivinen
Katso myös Kaltevuus, Maksimi, Funktio, Kuvaus, Derivaatta, Gradientti, Ääriarvo.
Minimoida (engl. Minimise)
Tehdä jokin niin pieneksi kuin mahdollista.
Katso myös Maksimoida.
Minkowskin epäyhtälö (engl. Minkowski's inequality)
Olkoot $p \ge 1$, ja $(x_n)$ ja $(y_i)$ kompleksilukujonoja. Jos $\left( \sum_{n=1}^ \infty |x_n|^p \right)^{1/p}$ ja $\left( \sum_{n=1}^ \infty |y_n|^p \right)^{1/p}$ ovat olemassa, pätee \[ \left ( \sum_{n=1}^ \infty |x_n+y_n|^p \right)^{1/p} \leq \left( \sum_{n=1}^ \infty |x_n|^p \right)^{1/p} + \left( \sum_{n=1}^ \infty |y_n|^p \right)^{1/p}. \] Minkowskin epäyhtälö voidaan todistaa Hölderin epäyhtälön avulla.
Katso myös Erisuuruus, Epäyhtälö.
Minuutti (engl. Minute)
Ajan yksikkö. Yksi minuutti on 60 sekuntia tai 1/60 tuntia. Minuutti on myös kulman yksikkö; se on asteen kuudeskymmenesosa. Yksi kulmaminuutti on myös 60 kulmasekuntia. Minuutin lyhenne on min tai ".
1 min = 60 s (aika) ja 1" = 60"" (kulma).
Mitallinen funktio (engl. Measurable function)
Olkoon $(X,\sigma,m)$ mitta-avaruus ja $(Y,\tau)$ topologinen avaruus. Kuvaus $f \colon X \rightarrow Y$ on mitallinen, jos kaikilla avoimilla $U \subset Y$ pätee, että $f^{-1} U$ on mitallinen, eli sigma-algebran $\sigma$ jäsen.
Katso myös Funktio, Kuvaus, Mitta-avaruus.
Mitallinen joukko (engl. Measurable set)
Mitta-avaruuden $(X, \sigma, m)$ mitallisia osajoukkoja ovat ne joukon $X$ osajoukot, jotka ovat sigma-algebran $\sigma$ jäseniä.
Katso myös Joukko, Sigma-algebra.
Mitata, Mitta (engl. Measure, Measurement)
Mitata jotakin tarkoittaa saada selville, kuinka suuri se on. Löytää numeerinen arvo jollekin ominaisuudelle. Myös todennäköisyyttä voi mitata.
Katso myös Ympyrän kehän pituus.
Mitta, Mitata (engl. Measure, Measurement)
Mitata jotakin tarkoittaa saada selville, kuinka suuri se on. Löytää numeerinen arvo jollekin ominaisuudelle. Myös todennäköisyyttä voi mitata.
Katso myös Ympyrän kehän pituus.
Mitta-asteikko (engl. Scale)
Mitta-asteikko määrittelee muuttujien mittaustasoon liittyvät ominaisuudet. Tunnetuimmat mittauksessa käytetyt mitta-asteikot ovat:
- nominaali- eli luokitteluasteikko
- ordinaali- eli järjestysasteikko
- intervalliasteikko
- suhdeasteikko
Katso myös Pienennyskuvaus, Suhde, Suurennuskuvaus.
Mitta-avaruus (engl. Measure space)
Kolmikko $(X, \Gamma, m)$ on mitta-avaruus, jos $X$ on joukko, $\Gamma$ on sigma-algebra joukossa $X$ ja $m$ on funktio $\Gamma \rightarrow [0, \infty)$, joka toteuttaa seuraavan ehdon:
Jos $\mathcal{U}$ on numeroituva kokoelma joukon $\Gamma$ alkioita, niin pätee \[ \Sigma_{V \in \mathcal{U}} m(V) = m(\bigcup_{V \in \mathcal{U}} V). \]
Katso myös Avaruus, Sigma-algebra, Mitallinen funktio.
Mittaaminen (engl. Mensuration)
Geometristen kuvioiden kulmien, pinta-alojen ja pituuksien suuruuden selvittäminen.
MKSA-järjestelmä (engl. Metric unit, Metric system)
Mittayksikköjärjestelmä, jonka perusyksiköt ovat metri, kilogramma, sekunti ja ampeeri. Luvun 10 monikertojen avulla saadaan perusyksiköistä johdettua uusia mittayksiköitä, jotka ovat suurempia tai pienempiä kuin perusyksiköt.
Katso myös Yksikkö, Senttimetri.
ml (engl. ml)
Millilitran, tilavuuden yksikön, lyhenne.
Katso myös Millilitra, Lyhenne.
mm (engl. mm)
Millimetrin lyhenne.
Katso myös A (paperikoot), Lyhenne, Millimetri.
$\mod$
Lyhenne sanasta modulo.
Katso myös Kongruentit luvut, Modulo, Lyhenne, Vektorin normi.
Modulaariaritmetiikka (engl. Modular arithmetic, Modulo arithmetic)
"Aritmetiikka modulo $n$" on aritmetiikkaa, jossa laskun jokaisessa vaiheessa poistetaan kaikki mahdolliset luvun n monikerrat ja tarkastellaan vain jakojäännöksiä. Jos esimerkiksi halutaan laskea yhteen luvut 5 ja 7 modulo 9, niin $5+7 = 12$, mutta summasta poistetaan 9 ja saadaan $5+7 = 3$ modulo 9.
Katso myös Modulo, Lukuteoria, Ekvivalenssiluokka, Kiinalainen jäännöslause, Kongruenssi, Eulerin $\varphi$-funktio, Josefuksen ongelma.
Moduli (engl. Module)
Olkoon $R$ rengas. $R$-moduli on Abelin ryhmä $M$, jossa on määritelty kertolasku $* \colon R \times M \rightarrow M$, joka toteuttaa seuraavat ehdot:
- $(ab) * c = a * (b * c)$ kaikilla $a,b \in R$ ja $c \in M$.
- $a * (b + c) = a* b + a * c$ ja $(a + b) * c = a * c + b * c$ kaikilla $a \in R$, $b,c \in M$.
- $1 * a = a$ kaikilla $a \in M$, kun $1$ on renkaan $R$ kertolaskun neutraalialkio.
$(\mathbb{Q},+)$ on $(\mathbb{Z}, +, \cdot)$-moduli, kertolaskuna tavallinen kertolasku.
Kuten tavallisenkin kertolaskun kohdalla, myös modulien kertolaskumerkki $*$ jätetään usein kirjoittamatta.
Jos siis $r \in R$ ja $a \in M$, merkitään $r a=r * a$.
Yllä on määritelty vasen $R$-moduli. Oikea $R$-moduli on muutoin samanlainen, mutta kertolaskussa renkaan alkio kirjoitetaan oikealle ja modulin alkio vasemmalle. Tällöin myös ehto 1 korvataan ehdolla
- $c * (a b) = (c * a ) * b$ kaikilla $c \in M$ ja $a,b \in R$.
Katso myös Abelin ryhmä, Rengas.
Modulo (engl. Modulo)
Kahden luvun sanotaan olevan kongruentteja modulo $x$, jos jaettaessa nämä luvut luvulla $x$ on jakojäännös molemmissa jakolaskuissa sama.
Katso myös Modulaariaritmetiikka, Jakojäännös, $\mod$, Funktio, Kuvaus, Binäärinen kuvaus, Kaksipaikkainen kuvaus.
Momenttiemäfunktio (engl. Moment generating function)
Jos $X$ on jakauma, sen momenttiemäfunktio on \[ M_X ( \theta ) = E ( e^{ \theta X } ) . \]
Tämä merkitsee, että $M(0)=1, M^{\prime } (0) = E(X) , M^{(n)} (0) = E(X^n ) , $ mitä voidaan käyttää varianssin löytämiseen.
Katso myös Funktio, Kuvaus, MGF, Summan momenttiemäfunktio.
Mongen lause (engl. Monge's theorem)
Olkoot $A$, $B$ ja $C$ tason kolme ympyrää, joista yksikään ei sijaitse kokonaan toisen sisällä. Olkoot $P$ ympyröiden $A$ ja $B$ yhteisten ulkotangenttien leikkauspiste, $Q$ ympyröiden $B$ ja $C$ yhteisten ulkotangenttien leikkauspiste ja $R$ ympyröiden $C$ ja $A$ yhteisten ulkotangenttien leikkauspiste. Tällöin pisteet $P$, $Q$ ja $R$ sijaitsevat samalla suoralla.
Monikerta (engl. Multiple)
Annetun luvun monikerta on luku, joka on jaollinen kyseisellä luvulla. Eräitä luvun 2 monikertoja ovat luvut 2, 4, 6, 8, 10 ja 12. Eräitä luvun 5 monikertoja ovat luvut 5, 10, 15, 20, 25, 30 ja 35.
Katso myös Yhteinen monikerta, Lukuteoria, Pienin yhteinen monikerta, Tekijä, Kokonaisluku.
Monikulmio (engl. Polygon)
Tasokuvio, jonka reuna koostuu janoista.
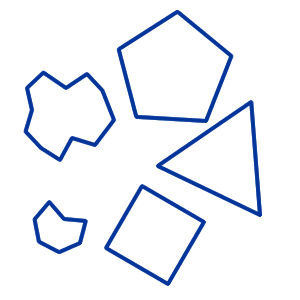
Katso myös Tasainen monitahokas, Viisikulmio, Kahdeksankulmio, $n$-kulmio, Kuusikulmio, Seitsemänkulmio, Kolmio, Nelikulmio, Sisäkulma, Ulkokulma, Euklidinen geometria, Lävistäjä, Konkaavi monikulmio, Konveksi monikulmio, Diagonaali, Särmä, Kuvio, Kulmio.
Monikulmioluku (engl. Polygonal number, Figurate number)
Yleisnimitys kolmioluvuille, neliöluvuille, viisikulmioluvuille, kuusikulmioluvuille, ... eli luvuille, jotka esittävät kunkin monikulmion muodostavien tietynlaisten pistekuvioiden pisteiden lukumääriä.
Katso myös Neliöluku, Kolmioluku, Kokonaisluku.
Monikulmion kulmat (engl. Angles in a polygon)
Jatkamalla monikulmion sivuja tai piirtämällä monikulmion kärkien kautta kulkevia uusia suoria voidaan määritellä useita erilaisia monikulmion kulmia, esimerkiksi sisä- ja ulkokulmat.
Monikulmion ympäri piirretty ympyrä (engl. Circumscribed circle, Circumcircle)
Ympyrä, joka kulkee monikulmion, esimerkiksi kolmion, kaikkien kärkien kautta.
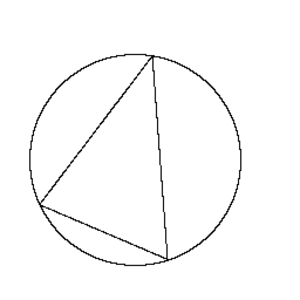
Katso myös Ympyrä, Piirtää ympyrä monikulmion ympäri, Kolmioon liittyvät ympyrät.
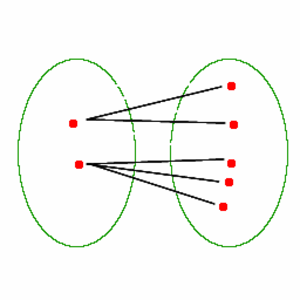
Monikäsitteinen (engl. One to many)
Vastaavuus, jossa yhteen olioon saattaa liittyä useita olioita.
Monitahokas (engl. Polyhedra, Polyhedron)
Kolmiulotteinen kappale, jonka sivut ovat tasopintoja ja reunat ovat suoria.
Kolmiulotteinen kappale, jonka kaikki tahkot ovat monikulmioita. Jos jokainen tahko on täsmälleen saman muotoinen ja kokoinen ja täsmälleen sama määrä tahkoja kohtaa jokaisessä kärjessä, niin monitahokasta sanotaan säännölliseksi.
Ainoat säännölliset monitahokkaat ovat Platonin monitahokkaat eli säännölliset 4-, 6-, 8-, 12- ja 20-tahokkaat.
Katso myös Tasainen monitahokas, Eulerin yhtälö, Kappale, Avaruusgeometria, Oktaedri, Kuusitahokas, Heksaedri, Tetraedri, Pyramidi, Särmiö, Prisma, Lävistäjä, Säännöllinen monitahokas, Konveksi monitahokas, Platonin kappaleet, Diagonaali, Dodekaedri, Ikosaedri.
Monitahokkaan pinta-ala (engl. Surface area)
Monitahokkaan kaikkien tahkojen pinta-alojen summa.
Katso myös Pinta-ala, Pallovyöhykkeen ala.
monitulkintainen (engl. Ambiguous)
Jokin asia on monitulkintainen, jos ei ole täysin selvää, mitä se tarkoittaa. Esimerkiksi "tilaa säästävä ratkaisu" voisi tarkoittaa joko että jokin ratkaisu säästää tilaa tai kehotustä tilata säästävä ratkaisu. Matematiikassa yritetään välttää moniselitteisyyttä niin paljon kuin mahdollista ja käytetään asioiden merkityksen selventämiseksi erityisiä merkintätapoja ja merkkejä.
Katso myös Looginen ominaisuus.
Monoidi (engl. Monoid)
Pari $(G,*)$ on monoidi, jos $G$ on joukko ja $*$ on laskutoimitus $G \times G \rightarrow G$, joka toteuttaa seuraavat ehdot:
- Kaikilla $a,b,c \in G$ pätee $(a * b) * c = a * (b * c)$.
- On olemassa sellainen $e \in G$, että kaikilla $a \in G$ pätee $a * e = e * a = a$.
Voidaan todistaa, että määritelmässä esiintyvä alkio $e$ on yksikäsitteinen, ja sitä kutsutaan monoidin neutraalialkioksi.
Pari $(\mathbb{N},+)$ on monoidi.
Kaikkien suomen kielen aakkosista muodostettavien äärellisten merkkijonojen joukko yhdessä tyhjän merkkijonon kanssa on monoidi. Laskutoimituksena tässä monoidissa on merkkijonojen laittaminen peräkkäin, esimerkiksi $hien*osto=hienosto$ ja $(talvi * kunnossa) * pito = talvi * (kunnossa * pito) = talvikunnossapito$. Neutraalialkiona on tyhjä merkkijono.
Katso myös Neutraalialkio, Ryhmä.
Monomi (engl. Monomial)
Monomorfismi (engl. Monomorphism)
Injektiivinen homomorfismi.
Katso myös Injektiivinen, Homomorfismi, Morfismi.
Monotoninen (engl. Monotone)
Funktio $f$ on monotonisesti kasvava jollakin välillä, jos se toteuttaa ehdon $a \leq b \Rightarrow f(a) \leq f(b)$ kaikilla $a$ ja $b$, jotka ovat kyseisellä välillä.
Monotoninen jono (engl. Monotonic sequence)
Monotoninen jono $u_{n}$ on joko
1) vähenevä eli $u_{n} \leq u_{n-1}$ pätee kaikilla $n$
tai
2) kasvava eli $u_{n} \geq u_{n-1}$ pätee kaikilla $n$.
Katso myös Jono, Aidosti monotoninen jono, Vähenevä jono, Kasvava jono.
Monte Carlo -menetelmä (engl. Monte Carlo method)
Menetelmä, missä monimutkaisia numeerisia ongelmia ratkaistaan simuloimalla, toisin sanoen tekemällä suuri määrä satunnaiskokeita, joiden perusteella ratkaisu määritetään. Esimerkiksi epäsymmetrisissä todennäköisyyskentissä tapahtuman A todennäköisyys voidaan ratkaista tekemällä suuri määrä kokeita, jolloin tapahtuman A todennäköisyys saadaan niiden kokeiden suhteellisena osuutena, joissa A on tapahtunut: \[ P(A) = \frac{n(A)}{n} . \] Esimerkiksi nastaa heitettäessä tulos voi olla "piikki alas" tai "piikki ylös". Todennäköisyys $$ P("piikki ylös") $$ voidaan määrätä heittämällä nastaa tuhansia kertoja ja tutkimalla niiden tapausten suhteellista osuutta, joissa piikki on tullut ylöspäin. Tulos ei välttämättä päde toiselle erilaiselle nastalle. Menetelmän nimi tulee Monte Carlossa olevan pelikasinon mukaan, missä pelaajien rahat jaetaan uudelleen satunnaiskokeiden avulla.
Moodi, Tyyppiarvo (engl. Mode)
Yrityksessä on 7 henkilöä, joiden palkat ovat:
- Pomo 5000
- Kanslisti 1300
- Työntekijä 1 1700
- Työntekijä 2 1500
- Työntekijä 3 1400
- Työntekijä 4 1200
- Työntekijä 5 1200
Luokan oppilaiden silmien väri on: sininen, sininen, sininen, sininen, sininen, harmaa, harmaa, harmaa, vihreä, ruskea, ruskea, ruskea. Silmien värin moodi on sininen (frekvenssi 5): oppilaat ovat tyypillisesti sinisilmäisiä.
Moodi eli tyyppiarvo on luokitellussa aineistossa käytetty paikantamistunnusluku. Luokittelu- ja järjestysasteikolla moodi on siihen luokkaan liittyvä muuttujanarvo, jossa on eniten havaintoja (kyseessä tyypillinen muuttujanarvo). Mikäli kyseessä on luokiteltu aineisto (intervalli- tai suhdeasteikon muuttuja), moodi määritellään yleensä sen luokan luokkakeskukseksi, jossa on eniten havaintoja. Eräissä aineistoissa voi olla kaksi tai useampia moodeja (luokan frekvenssi oleellisesti suurempi kuin viereisten luokkien frekvenssi).
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Paikantamistunnusluku, Keskiluku, Mediaani, Verrata.
Morfismi (engl. Morphism)
Struktuurin säilyttävä kuvaus.
Jatkuvat kuvaukset ovat topologisten avaruuksien välisiä morfismeja. Ryhmähomomorfismit ovat ryhmien välisiä morfismeja. Lineaarikuvaukset ovat modulien välisiä morfismeja. Kuvaukset ovat joukkojen välisiä morfismeja.
Sanaa morfismi käytetään erityisesti kategoriateoriassa. Kategoriateoria on abstrakti aksiomaattinen teoria, jossa peruskäsitteitä ovat objekti ja morfismi. Esimerkiksi topologiset avaruudet (objektit) ja jatkuvat kuvaukset (morfismit) toteuttavat kategoriateorian aksioomat, samoin kuin ryhmät (objektit) ja ryhmähomomorfismit (morfismit).
Katso myös Kuvaus, Isomorfismi, Funktio, Kuvaus, Homomorfismi, Automorfismi, Epimorfismi, Monomorfismi, Diffeomorfismi, Endomorfismi, Groupoidi, Homeomorfismi, Kategoria, Isomorfia, Funktio.
Morsen aakkoset (engl. Morse code)
Tapa esittää tavallisen aakkoston kirjaimet sekä muutama erikoismerkki pisteiden ja viivojen eli pitkien ja lyhyiden äänen tai valon sykäyksien muodostamien jonojen avulla.
mph (engl. mph)
Lyhenne sanoista "miles per hour" eli mailia tunnissa. Nopeusyksikkö, jota käytetään Yhdysvalloissa ja yhä Iso-Britanniassakin.
Katso myös Mailia tunnissa.
Muistinumero (engl. Carry)
Kun lukuja lasketaan yhteen allekkain ja sarakkeen summa on ainakin 10, niin kymmenten lukumäärä on muistinumero, joka on siirrettävä yhteenlaskettavaksi seuraavaan sarakkeeseen. Vastaavasti kun lukuja kerrotaan allekkain numero kerrallaan ja kahden numeron tulo on kaksinumeroinen, niin kymmenten lukumäärä on muistinumero, joka on lisättävä välittömästi vasemmalle siitä sarakkeesta, johon kyseisten numeroiden tulo varsinaisesti on kirjoitettava.
Muistinäppäin (engl. Memory)
Laskimen näppäin, joka mahdollistaa näytöllä näkyvän luvun tallentamisen myöhempää käyttöä varten.
Katso myös Laskin.
Multiplikatiivinen (engl. Multiplicative)
Kertolaskuun liittyvä.
Lukuteoriassa: Funktio $f$, joka toteuttaa ehdon $f(a b) =f(a) f(b)$ kaikille yhteistekijättömille $a$ ja $b$.
Jos ehto $f(a b)=f(a) f(b)$ pätee kaikille $a,b$, on funktio täysin multiplikatiivinen.
Katso myös Keskenään jaottomat luvut.
Murtoluku (engl. Fraction)
Tapa kirjoittaa lukuja, erityisesti lukuja, jotka eivät ole kokonaislukuja, kahden luvun välisenä osamääränä. Nämä kaksi lukua ovat yleensä kokonaislukuja, mutta niiden ei tarvitse olla; joskus ne voivat olla murtolukuja tai jopa desimaalilukuja.
Katso myös Murtolukujen yhteenlasku, Aritmetiikka, Laskento, Yhteinen nimittäjä, Sekaluku, Prosenttiosuus, Osoittaja, Murtoluvun supistaminen, Rationaaliluku, Aito murtoluku, Epämurtoluku, Samanarvoiset murtoluvut, Kymmenmurtoluku, Nimittäjä, Alennus, Yksikkömurtoluku, Supistumaton murtoluku, Ketjumurtoluku, Mantissa.
Murtolukujen kertolasku (engl. Multiplying fractions)
Kun halutaan kertoa keskenään kaksi murtolukua, kirjoitetaan ne rinnakkain. Kerrotaan murtolukujen osoittajat keskenään ja nimittäjät keskenään. Osoittajien tulo on murtolukujen tulon osoittaja ja nimittäjien tulo on murtolukujen tulon nimittäjä.
Lasketaan esimerkiksi $\frac{2}{3} \cdot \frac{4}{5}$. Kun kerrotaan murtolukujen osoittajat keskenään, saadaan $2 \cdot 4 = 8$, ja kun kerrotaan nimittäjät keskenään, saadaan $3 \cdot 5 = 15$. Siten $\frac{2}{3} \cdot \frac{4}{5} = \frac{2 \cdot 4}{3 \cdot 5} = \frac{8}{15}$.
Murtolukujen yhteenlasku (engl. Adding fractions)
Kahden murtoluvun yhteen laskemiseksi niille on löydettävä yhteinen nimittäjä. Kun tämä on tehty, voidaan molemmat murtoluvut kirjoittaa muodossa, jossa nimittäjänä on löydetty yhteinen nimittäjä. Sitten yksinkertaisesti lasketaan yhteen murtolukujen osoittajat. Tulosta on ehkä sievennettävä.
Esimerkki: \[ \frac{1}{2} + \frac{1}{3}. \] Ensin etsitään yhteinen nimittäjä: 6 on yhteinen nimittäjä, koska 6 on jaollinen sekä luvulla 2 että luvulla 3. Nyt kirjoitetaan molemmat murtoluvut muodossa, jossa 6 on nimittäjänä: $\frac{1}{2}$ on $\frac{3}{6}$ ja $\frac{1}{3}$ on $\frac{2}{6}$. Nyt on laskettava \[ \frac{3}{6} + \frac{2}{6}, \] joka on $\frac{3+2}{6}$ eli $\frac{5}{6}$.
Katso myös Yhteenlasku, Yhteinen nimittäjä, Murtoluku.
Murtoluvun supistaminen (engl. Simplify a fraction)
Murtoluvun supistaminen tarkoittaa, että jaetaan murtoluvun osoittaja ja nimittäjä jollakin niiden yhteisellä tekijällä. Esimerkiksi murtoluvun $\frac{2}{6}$ osoittajalla ja nimittäjällä on yhteinen tekijä 2, joten jakamalla osoittaja ja nimittäjä luvulla 2 saadaan $\frac{1}{3}$.
Katso myös Supistaminen, Murtoluku.
Murtoviiva (engl. Broken line)
Muunnos, Kuvata, Muuntaa, Muuttaa joksikin (engl. Transform)
Muuttaa joukko kuvioita tai lukuja tai olioita toisiksi kuvioiksi, luvuiksi tai olioiksi jonkin säännön mukaisesti.
Katso myös Fourier'n muunnos.
Muuntaa (engl. Convert)
Muuttaa jotakin muodosta toiseen; vaihtaa tapaa, jolla ilmaistaan jotakin. Esimerkiksi luku voidaan muuntaa murtoluvusta (10/4) desimaaliluvuksi (2,5).
Katso myös Supistaminen.
Muuntaa, Kuvata, Muuttaa joksikin, Muunnos (engl. Transform)
Muuttaa joukko kuvioita tai lukuja tai olioita toisiksi kuvioiksi, luvuiksi tai olioiksi jonkin säännön mukaisesti.
Katso myös Fourier'n muunnos.
Muutosnopeus (engl. Rate of change)
Jonkin muutosnopeus tarkoittaa sitä, miten nopeasti se muuttuu ajan kuluessa.
Esimerkiksi paikan muutosnopeus tarkoittaa sitä, miten kauas lähtöpisteestä siirrytään tietyn ajan kuluessa. Tämä voidaan selvittää jakamalla kuljettu matka siihen kuluneella ajalla, jolloin saadaan paikan keskimääräinen muutosnopeus. Jos tarkasteltavan ajanjakson pituus lähestyy nollaa, niin keskimääräinen muutosnopeus lähestyy arvoa, jota kutsutaan hetkelliseksi muutosnopeudeksi. Tämä kertoo, kuinka nopeasti suure muuttuu tietyllä hetkellä. Paikan muutosnopeutta kutsutaan yleensä vain nopeudeksi.
Samalla periaatteella voidaan tarkastella monen asian muutosnopeutta, kuten pituuden, tilavuuden, korkeuden, nopeuden, jne.
Katso myös Hetkellinen muutosnopeus, Derivaatta, Ominaisuus, jonka arvot ovat jatkuvia.
Muuttaa joksikin, Kuvata, Muuntaa, Muunnos (engl. Transform)
Muuttaa joukko kuvioita tai lukuja tai olioita toisiksi kuvioiksi, luvuiksi tai olioiksi jonkin säännön mukaisesti.
Katso myös Fourier'n muunnos.
Muuttuja (engl. Variable)
Arkikielessä muuttuja on jokin joka muuttuu. Se on suure, joka voi saada eri arvoja. Se on vakion vastakohta.
Lausekkeen paikka, jonka täyttää kirjain tai muu merkki ja jonka kohdalle ajatellaan voitavan sijoittaa jokin olio, usein luku.
Katso myös Algebra, Vakio, Tuntematon, Parametri, Identiteetti, Kaikilla, Mielivaltainen, Funktion argumentti, Korvaaminen, Sijoittaminen, sijoitus, Infinitesimaalinen, Kaksiulotteinen, Jokaisella, Satunnaismuuttuja.
Myriadi (engl. Myriad)
10000. Sanaa käytetään yleensä osoittamaan mitä tahansa suurta lukumäärää.
Katso myös Kymmenen potenssit.
Myötäpäivään (engl. Clockwise)
Kierto samaan suuntaan kuin kellon viisarit eli kierto ylhäältä oikealle, sitten alas, sitten vasemmalle ja sitten taas ylös.
Matematiikassa kiertosuuntaa myötäpäivään sanotaan negatiiviseksi kiertosuunnaksi. (Maapallo kiertää myötäpäivään, kun sitä katsellaan Etelänavan yläpuolelta.)

Katso myös Kulma, Symmetriakeskus, Kierto, Vastapäivään, Kierron muuttaminen vastakkaissuuntaiseksi, Kiertosuunta.
Määrite, Ominaisuus (engl. Attribute)
Sellainen tiedonpalanen tai ilmaisu, joka kertoo oliosta muutakin kuin vain sen, mikä olio on kyseessä. Esimerkiksi koko tai väri voi olla olion ominaisuus.
Katso myös Affiini, Algebrallinen, Yksikäsitteinen tekijöihin jako, Kanoninen, Sattuma, Mahdollisuus, Satunnainen, Karteesinen, Alternoida, Vaativuus, Suure, Uskottavuus.
Määritelmä (engl. Definition)
Täsmällinen kuvaus siitä, mitä tarkoitetaan tietyllä sanalla, ilmaisulla tai merkillä.
Katso myös Ehto.
Määrittelyjoukko, Lähtöjoukko (engl. Domain)
Funktion $f \colon A \rightarrow B$ määrittelyjoukko on $A$. Toisin sanoen, funktion $f$ määrittelyjoukko on niiden pisteiden joukko, joissa $f$ on määritelty. Määrittelyjoukkoa kutsutaan myös lähtöjoukoksi.
Englannin kielen sana "domain" voi tarkoittaa myös aluetta eli euklidisen avaruuden avointa ja yhtenäistä osajoukkoa.
Katso myös Injektio, Funktio, Kuvaus, Komplementtijoukko, Joukko, Bijektio, Surjektio, Maalijoukko, Arvojoukko, Funktion maalijoukko, Kokonaisalue, Homotopia, Cauchyn integraalilause.
Määrittää (engl. Determine)
Sanaa "määrittää" käytetään tavallisesti silloin, kun etsitään jonkin muuttujan arvoa tiettyjen ehtojen vallitessa. Muuttujan määrittäminen tarkoittaa sen arvon tai lausekkeen löytämistä.
Katso myös Perustelu.
Määrärätyn integraalin laskusääntöjä (engl. Definite integral identities)
\[ \int _a^b f(x) dx + \int_b^c f(x) dx = \int_a^c f(x) dx . \] \[ \int_a^b f(x) dx = - \int_b^a f(x) dx . \] \[ \int_a^b cf(x) dx = c \int _a^b f(x) dx . \]
Katso myös Integrointisääntö.
Määrätty integraali (engl. Definite integral)
Integraali, jonka integroimisvälin päätepisteet ovat reaalilukuja. Määrätty integraali on reaaliluku, ei funktio. Esimerkiksi \[ \displaystyle{\int_{1}^{2}} \mathrm{x}^2 \mathrm{dx} \] on määrätty integraali.
Katso myös Integraali, Integraalifunktio, Määräämätön integraali.
Määräämätön (engl. Indefinite)
Prosessi voi jatkua määräämättömästi, jos ei ole olemassa tiettyä pistettä, jossa sen pitäisi päättyä.
Määräämätön integraali, Integraalifunktio (engl. Indefinite integral)
Funktion $f$ integraalifunktio eli määräämätön integraali, jota merkitään \[\int f(x)\,dx,\] on mikä tahansa funktio $F$, jonka derivaatta $F'$ on funktio $f$.
Katso myös Integraali, Määrätty integraali.
Möbiuksen nauha (engl. Mobius band, Mobius strip)
Päättymätön pinta, jolla on vain yksi puoli. Sellaisen voi tehdä pitämällä kiinni pitkän kapean paperiliuskan päistä, kääntämällä toisen liuskan pään ympäri ja liittämällä sitten liuskan päät yhteen.
Möbiuksen nauha on nimetty saksalaisen matemaatikon August Möbiuksen (1790-1868) mukaan.
Katso myös Möbius.
Möbius (engl. August Möbius, Möbius)
August Möbius (1790--1868) oli saksalainen matemaatikko. Hänet muistetaan nykyään pääasiassa Möbiuksen nauhasta, joka on nimetty hänen mukaansa, vaikka tosiasiassa Möbiuksen nauhan keksi matemaatikko nimeltä Listing. Möbius tutki astronomiaa sekä trigonometrisia yhtälöitä, geometriaa ja projektiivista geometriaa. Möbius-kuvaus on nimetty hänen mukaansa. Hän oli kiinnostunut topologiasta ja työskenteli kartan värittämiseen liittyvien kysymysten parissa.
Katso myös Topologia, Möbiuksen nauha.