T-jakauma, Studentin t-jakauma (engl. Student's t-distribution, t-distribution)
Keskiarvotesteissä käytetty jakauma. Jakauman nimi johtuu siitä, että sen esitti 1900-luvun alussa Guinness-panimon laaduntarkkailusta vastaava pääkemisti William S. Gosset salanimellä "Student". Mikäli käytössä on otos $X_i, i=1,n$ normaalisti jakautuneesta perusjoukosta jonka odotusarvo on $ \mu $, noudattaa suure $$ \mathrm{t} = \frac{\bar{\mathrm{x}} - \mu } {\mathrm{s} / \sqrt{\mathrm{n}}} , $$ missä $$ \mathrm{s}^2 = \sum _{\mathrm{i}=1} ^{\mathrm{n}} \frac{ ( \mathrm{x}_{\mathrm{i}} - \bar{\mathrm{x}} ) ^{2} } {\mathrm{n}-1} , $$ t-jakaumaa vapausasteilla $n-1$. t-jakauma on symmetrinen ja muistuttaa muodoltaan normaalijakaumaa. t-jakauma kuvaa normaalisti jakautuneesta perusjoukosta poimitun otoksen otoskeskiarvon vaihtelua, kun vaihtelun mittana käytetään poimitun otoksen perusteella arvioitua keskiarvon hajontaa. Vapausasteiden lukumäärä ottaa huomioon käytettävissä olevan tiedon tarkkuuden. Kun havaintoja (vapausasteita) on vähän, otoksesta arvioitu keskihajonta on epätarkka, ja t-jakauman hännät ovat voimakkaammat kuin normaalijakauman hännät. Kun havaintojen lukumäärä (vapausasteiden lukumäärä) kasvaa, keskihajonnalle tehdyn arvion tarkkuus kasvaa ja t-jakauma lähestyy normaalijakaumaa.
Katso myös Normaalijakauma, t-taulukko, Vapausaste, Jakauma, T-testi, F-jakauma, Gaussin jakauma.
t-taulukko (engl. t-table)
Sarake n kertoo vapausasteiden lukumäärän; t-arvot ovat taulukon runko-osassa (etsi ensimmäinen t-arvo, joka on pienempi kuin mittaamasi t-arvo); todennäköisyys selviää taulukon yläriviltä.
Todennäköisyyttä, joka on pienempi kuin 0.05, pidetään yleensä merkitsevänä.
| n | .25 | .20 | .15 | .10 | .05 | .025 | .02 | .01 | .005 | .0025 | .001 | .0005 |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 15.89 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | .816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 4.849 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | .765 | .978 | 1.250 | 1.638 | 2.353 | 3.182 | 3.482 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | .741 | .941 | 1.190 | 1.533 | 2.132 | 2.776 | 2.999 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | .727 | .920 | 1.156 | 1.476 | 2.015 | 2.571 | 2.757 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | .718 | .906 | 1.134 | 1.440 | 1.943 | 2.447 | 2.612 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | .711 | .896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.517 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | .706 | .889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.449 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | .703 | .883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.398 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | .700 | .879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.359 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | .697 | .876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.328 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | .695 | .873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.303 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | .694 | .870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.282 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | .692 | .868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.264 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | .691 | .866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.249 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | .690 | .865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.235 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | .689 | .863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.224 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | .688 | .862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.214 | 2.552 | 2.878 | 3.197 | 3.611 | 3.922 |
| 19 | .688 | .861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.205 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | .687 | .860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.197 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | .663. | .859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.189 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | .686 | .858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.183 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | .685 | .858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.177 | 2.500 | 2.807 | 3.104 | 3.485 | 3.768 |
| 24 | .685 | .857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.172 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | .684 | .856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.167 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | .684 | .856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.162 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | .684 | .855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.15 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | .683 | .855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.154 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | .683 | .854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.150 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | .683 | .854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.147 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | .681 | .851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.123 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | .679 | .849 | 1.047 | 1.295 | 1.676 | 2.009 | 2.109 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | .679 | .848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.099 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | .678 | .846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.088 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | .677 | .845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.081 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 1000 | .675 | .842 | 1.037 | 1.282 | 1.646 | 1.962 | 2.056 | 2.330 | 2.581 | 2.813 | 3.098 | 3.300 |
| inf. | .674 | .841 | 1.036 | 1.282 | 1.64 | 1.960 | 2.054 | 2.326 | 2.576 | 2.807 | 3.091 | 3.291 |
Katso myös T-jakauma, Studentin t-jakauma, T-testi.
T-testi (engl. t-test, Student's t-test, t test)
Yleisnimitys kaikille niille testeille, joissa päätöksenteko perustuu t-jakaumaan. Testisuure on muotoa $$ t= \frac{d-d_o} {s_d} $$ ja testiin liittyvä nollahypoteesi $ H_o: E(d) = d_o $. Testisuure mittaa otoksen perusteella lasketun estimaatin $ d $ etäisyyttä nollahypoteesin mukaisesta arvosta $ d_o $. Mittana käytetään otoksen perusteella $d$:n hajonnalle laskettua estimaattia $s_d $. Mikäli nollahypoteesi on tosi ja mikäli $d$ on jakautunut normaalisti, testisuure noudattaa t-jakaumaa $s_d$:n vapausasteilla. Nollahypoteesin voimassaollessa testisuure saa tyypillisesti lähellä nollaa olevia arvoja ja suuria arvoja kun nollahypoteesi ei pidä paikkaansa. T-testistä on versioita eri tilanteisiin.
- Keskiarvon t-testi
- Keskiarvojen erotuksen t-testi
- Parittaisten mittausten t-testi
Katso myös t-taulukko, Nollahypoteesi, Tilastollinen testi, T-jakauma, Studentin t-jakauma.
Tahko (engl. Face)
Tahko on kappaleen litteä pinta.
Esimerkiksi kuutiossa on 6 tahkoa.
Kaksi tahkoa leikkaavat toisesa pitkin kappaleen särmää, kolme tahkoa tai useampikin kohtaavat toisensa kappaleen kärjessä.
Kolmiulotteisen kappaleen ulkopuolen särmien rajaama alue.
Katso myös Tasainen monitahokas, Kappale, Avaruusgeometria, Kuvio.
Tai (engl. or)
Kaksipaikkainen looginen operaattori, joka antaa tulokseksi totuusarvon 'epätosi', jos molemmat argumentit ovat epätosia, ja muussa tapauksessa totuusarvon 'tosi'.
Tälle operaattorille käytetään merkintää $\vee$.
Katso myös Looginen operaattori, Ja.
Taikaneliö (engl. Magic square)
Taulukko lukuja, jotka on kirjoitettu neliön muotoon siten, että jokaisen rivin, jokaisen sarakkeen sekä neliön kahden lävistäjän lukujen summa on aina sama. Tämä summa tunnetaan nimellä taikavakio.
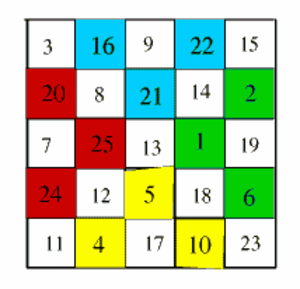
Katso myös Epätaikaneliö.
Takagin käyrä, van der Waerdenin käyrä (engl. Blancmange curve)
Takagin käyrä määritellään kaavalla \[ y(x) = \sum_{k=0}^{\infty} \frac{f(2^kx)}{2^k}, \] missä $f$ on ns. sahanteräfunktio. Käyrä tunnetaan myös van der Waerdenin käyränä. Takagin käyrä on esimerkki käyrästä, joka ei ole derivoituva missään pisteessä.
Takaliite (engl. Suffix)
Yksittäinen kirjain tai numero, joka kirjoitetaan muuttujan jälkeen alaindeksiksi kertomaan, mikä muuttujien joukon muuttujista kyseinen muuttuja on.
Katso myös Merkintätapa, Notaatio, Kulmio.
$\tan(-x)$
$\tan (-x) = -\tan x$.
Katso myös Trigonometrinen identiteetti, Pariton funktio.
$\tan(2x)$
Tangenttifunktion kaksinkertaiselle kulmalle pätee \[ \tan(2x) = \frac{2\tan(x)}{1-\tan^2(x)}. \]
Katso myös $\tan$, Kaksinkertaisen kulman kaava.
$\tan(x/2)$
\[ \tan \left( \frac{x}{2} \right ) = \pm \sqrt{ \frac{1 - \cos(x)}{ 1 + \cos(x)}} = \frac{\sin(x)}{1 + \cos(x)} = \frac{1 - \cos(x)}{\sin(x)}. \]
Katso myös $\tan$, $\sin$, Puolikkaan kulman kaava, Neliöjuuri, $\cos$, Kosini.
$\tan(x+180^\circ)$
$\tan(x+180^\circ)=\tan(x+\pi)=\tan(x)$.
Katso myös Trigonometrinen identiteetti.
$\tan(x+90^\circ)$
$\tan(x+90^\circ)=\tan(x + \frac{\pi}{2})= \frac{-1}{\tan(x)}$.
Katso myös Trigonometrinen identiteetti.
$\tan$
Tangenttifunktion lyhenne.
$\tan x$ tarkoittaa kulman $x$ tangenttia eli suorakulmaisen kolmion kulman, jonka suuruus on $x$, vastaisen kateetin suhdetta viereiseen kateettiin. Se on sama kuin $\sin x/\cos x$.
Katso myös $\arctan$, Tangenttifunktio, Tangentin neliö, Tangentin ja kosinin välinen yhteys, Trigonometrinen yhtälö, Lyhenne, Kotangentti, $\tan(2x)$, $\cot(2x)$, $\tan(x/2)$.
Tangentin ja kosinin välinen yhteys (engl. Tan squared plus one)
Kaikilla $x$:n arvoilla pätee \[\tan^{2}(x)+1 = \sec^{2}(x)=\frac{1}{\cos^2x}.\]
Tangentin neliö (engl. Tangent squared)
Merkintä $\tan^{2}(x)$ tarkoittaa samaa kuin $[\tan(x)]^{2}$.
Katso myös $\tan$, Merkintätapa, Notaatio.
Tangentin tarkkoja arvoja (engl. Particular values of tan)
$\tan 0^{\circ} = 0$,
$\tan 30^{\circ} = \tan \frac{\pi}{6} = \frac{1}{\sqrt{3}}$,
$\tan 45^{\circ} = \tan \frac{\pi}{4} = 1$,
$\tan 60^{\circ} = \tan \frac{\pi}{3} = \sqrt{3}$,
$\tan 180^{\circ} = \tan \pi = 0$.
Katso myös Trigonometristen funktioiden tarkat arvot.
Tangentti (engl. Tangent, Tangent line)
Suora, joka koskettaa annettua käyrää, esimerkiksi ympyrää täsmälleen yhdessä pisteessä. Tangentti on käyrää kahdessa pisteessä leikkaavan suoran raja-asento, kun leikkauspisteet lähenevät toisiaan niin, että ne lopulta yhtyvät samaksi pisteeksi.
Ympyrän tangentti muodostaa aina suoran kulman kosketuspisteestä piirretyn säteen tai halkaisijan kanssa.

Katso myös Kolmion tangenttikolmio, Tangenttivektori, Ympyrä, Jänne, Suora, Derivaatta, Sekantti.
Tangenttifunktio (engl. Tangent, Tangent function)
Jos suorakulmaisessa kolmiossa yhden kulman suuruus on $x$, niin kulman $x$ tangentti on $x$:n vastaisen kateetin suhde viereiseen kateettiin. $x$:n tangentti on yhtä suuri kuin $\sin x/\cos x$.
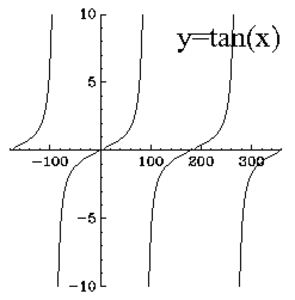
Katso myös $\tan$, Trigonometrinen yhtälö, Trigonometria, Suora kulma, $\sin$, Trigonometrinen funktio, $\cos$, Kosini.
Tangenttitaso (engl. Tangent plane)
Pinnan tangenttitaso annetussa pisteessä on taso, joka on pinnan kanssa yhdensuuntainen ja koskettaa sitä kyseisessä pisteessä. Tangenttitaso on pintaa pitkin jotain käyrää leikkaavan tason raja-asento, kun leikkauskäyrä surkastuu pisteeksi.
Katso myös Taso, Analyyttinen avaruusgeometria.
Tangenttivektori (engl. Tangent vector)
Käyrän tai pinnan tangenttivektori annetussa pisteessä on vektori, joka on käyrän kyseiseen pisteeseen piirretyn tangenttisuoran suuntainen tai jonkin pinnan kyseiseen pisteeseen piirrettyyn tangenttitasoon sisältyvän suoran suuntainen.
Katso myös Vektori, Yksikkötangenttivektori, Piste, Yhdensuuntainen, Tangentti, Käyrä, Normaalivektori, Sivunormaalivektori.
$\tanh(2x)$
Kaikilla $x$ on voimassa \[ \tanh(2x) = \frac{2\tanh(x)}{1 + \tanh(x)^2}. \]
Katso myös $\tanh(x+y)$.
$\tanh(x+y)$
Kaikilla $x,y$, joilla $\tanh(x)\tanh(y) \neq -1$, pätee \[ \tanh(x+y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}. \]
Katso myös $\tanh(2x)$.
Tapahtuma (engl. Event)
Tapahtuma on mikä tahansa otosavaruuden osajoukko satunnaiskokeessa. Jos satunnaiskoe on nopanheitto, niin otosavaruus on silloin silmälukujen joukko $\{ 1, 2, 3, 4, 5, 6 \}$. Tapahtumia ovat tässä tapauksessa esimerkiksi seuraavat:
- Silmäluku on $6$ eli osajoukko $\{ 6 \}$.
- Silmäluku on parillinen eli osajoukko $\{ 2, 4, 6 \}$.
- Silmäluku on pienempi kuin $4$ eli osajoukko $\{ 1, 2, 3 \}$.
Todennäköisyyslaskennassa tapahtuma on mikä tahansa otosavaruuden osajoukko. Tapahtuman $A$ sanotaan sattuvan, jos kokeen tulos $\omega$ on osajoukossa $A$ eli $\omega \in A$.
Katso myös Sattuma, Mahdollisuus, Valita, Riippumattomat tapahtumat, Otosavaruus, Boolen epäyhtälö.
Tarkka arvo (engl. Exact)
Numeroarvo on tarkka, jos se esittää täsmälleen sitä lukua, mitä pitääkin. Laskun tarkka vastaus saattaa sisältää neliöjuuria tai muita irrationaalilukuja. Se ei ole pyöristetty desimaaliluku.
Katso myös Differentiaaliyhtälö.
Tarkkuus (engl. Accuracy)
Arvioidun suureen tarkkuus ilmoittaa, miten paljon arvio luultavasti enintään poikkeaa todellisesta arvosta. Jos tarkkuuden sanotaan olevan 10 %, niin arvio poikkeaa todellisesta arvosta enintään 10 %.
Katso myös Merkitsevin tai vähiten merkitsevä numero, Estimaatti, Ominaisuus, jonka arvot ovat jatkuvia.
Tasa-arvokäyrä (engl. Contour)
Tasainen jakauma (engl. Uniform distribution)
Välillä $[a,b]$ tasaisen jatkuvan jakauman tiheysfunktio on $f(x) = 1/(b-a)$, missä $b-a$ on satunnaismuuttujan $X$ mahdollisten arvojen muodostaman välin $[a,b]$ pituus.
Äärellisen diskreetin tasaisen jakauman eli symmetrisen jakauman tapauksessa kunkin arvon todennäköisyys on $P(X=t) = 1/n$, missä $n$ satunnaismuuttujan X mahdollisten arvojen lukumäärä.
Katso myös Jakauma, Tasaisen jakauman odotusarvo, Diskreetti tasainen jakauma, Jatkuva tasainen jakauma.
Tasainen monitahokas (engl. Uniform polyhedron)
Tasainen monitahokas on monitahokas, jonka tahkot muodostavat jokaisen kärjen ympärille samanlaisen kuvion. Olettaen, että jokainen särmä saa olla vain kahden tahkon yhteinen särmä, on olemassa 75 tasaista monitahokasta. Kaikki nämä yhtä lukuun ottamatta voidaan määrätä Wythoffin symbolin avulla. Tasaisen monitahokkaan kärjet sijaitsevat pallon pinnalla. Tämän pallon keskipiste on monitahokkaan painopiste. Ne kärjet, jotka voidaan yhdellä särmällä yhdistää annetun kärjen kanssa, sijaitsevat ympyrällä.
Katso myös Ympyrä, Tahko, Pallo, Monikulmio, Monitahokas, Platonin kappaleet, Kuutio, Säännöllinen heksaedri.
Tasainen suppeneminen (engl. Uniform convergence)
Olkoon $Y$ metrinen avaruus ja $f_i \colon X \rightarrow Y$, $i \in \mathbb{N}$ jono kuvauksia. Kuvausjono $(f_i)$ suppenee tasaisesti kohti kuvausta $f \colon X \rightarrow Y$, mikäli kaikilla $\epsilon \gt 0$ on olemassa $i_0\in \mathbb{N}$ siten, että kaikilla $x \in X$ pätee $d(f_i(x),f(x)) \lt \epsilon$ aina, kun $i>i_0$.
Jos $Y$ on normiavaruus, voidaan kuvausten $X \rightarrow Y$ joukossa määritellä normi kaavalla $|f|=\sup_{x \in X} |f(x)|$. Tällöin tasainen suppeneminen on sama asia kuin suppeneminen em. normin mielessä.
Katso myös Suppeneminen, Konvergenssi.
Tasaisen jakauman odotusarvo (engl. Mean of a uniform distribution)
Jos tasaisen jakauman päätepisteet ovat $a$ ja $b$, on jakauman odotusarvo $(a+b)/2$.
Katso myös Tasainen jakauma, Keskiarvo, Aritmeettinen keskiarvo.
Tasaisesti jatkuva (engl. Uniformly continuous)
Olkoot $(X,d)$ ja $(Y,d')$ metrisiä avaruuksia. Kuvaus $f \colon X \rightarrow Y$ on tasaisesti jatkuva, mikäli kaikilla $\epsilon>0$ on olemassa $\delta>0$ siten, että aina kun $x,y \in X$ ja $d(x,y) \lt \delta$, tällöin myös $d(f(x),f(y))<\epsilon$.
Vertaa jatkuva.
Kuvaus $f \colon \mathbb{R} \rightarrow \mathbb{R}$, $x \mapsto 2x$ on tasaisesti jatkuva.
Kuvaus $g \colon \mathbb{R} \rightarrow \mathbb{R}$, $x \mapsto x^2$ on jatkuva, mutta ei tasaisesti jatkuva.
Jos $X$ on kompakti metrinen avaruus ja $Y$ on metrinen avaruus, jokainen jatkuva kuvaus $X \rightarrow Y$ on tasaisesti jatkuva.
Tasajako (engl. Equal partitioning)
Jako yhtä suuriin osiin.
Kymmenen voidaan jakaa viiteen kahden jäsenen ryhmään, kahteen viiden jäsenen ryhmään tai kymmeneen yhden jäsenen ryhmään. Kaksitoista voidaan jakaa tasan vieläkin useammalla eri tavalla. Se voidaan jakaa kolmeen neljän jäsenen ryhmään, neljään kolmen jäsenen ryhmään, kuuteen kahden jäsenen ryhmään, kahteen kuuden jäsenen ryhmään tai kahteentoista yhden jäsenen ryhmään.
Katso myös Ositus.
Tasakulmainen (engl. Equiangular)
Tasakulmaisen kuvion kaikki kulmat ovat yhtä suuria. Esimerkiksi suorakulmio on tasakulmainen.
Tasakylkinen (engl. Isosceles)
Jokin, jonka kaksi sivua ovat yhtä pitkiä, on tasakylkinen. Yleensä puhutaan tasakylkisistä kolmioista, mutta myös puolisuunnikas voi olla tasakylkinen; tällöin sen kaksi erisuuntaista sivua ovat yhtä pitkät.
Katso myös Tasakylkinen puolisuunnikas, Tasakylkinen kolmio, Tasasivuinen.
Tasakylkinen kolmio (engl. Isosceles triangle)
Kolmio, jossa on kaksi yhtä pitkää sivua. Kolmatta sivua sanotaan kolmion kannaksi.
Katso myös Tasakylkinen, Kolmio.
Tasakylkinen puolisuunnikas (engl. Isosceles trapezium, Isosceles trapezoid)
Puolisuunnikas, jonka kaksi erisuuntaista sivua ovat yhtä pitkät.
Katso myös Tasakylkinen, Puolisuunnikas.
Tasasivuinen (engl. Equilateral)
Monikulmio on tasasivuinen, jos sen kaikki sivut ovat yhtä pitkät.
Jos kolmio on tasasivuinen, on se välttämättä myös tasakulmainen, mutta sama ei päde muiden monikulmioiden tapauksessa.
Katso myös Yhtäsuuri, Tasakylkinen, Sama.
Tasasivuinen kolmio (engl. Equilateral triangle)
Kolmio, jonka kaikki sivut ovat yhtä pitkät. Tasasivuisen kolmion jokaisen kulman suuruus on $60^{\circ}$.

Katso myös Erisivuinen kolmio, Möbius, Khi-toiseen taulukko, Napoleonin kolmiot, Kolmio, Suorakulmainen kolmio, Teräväkulmainen kolmio, Tylppäkulmainen kolmio.
Tasasivuisen hyperbelin eksentrisyys (engl. Eccentricity of a rectangular hyperbola)
Tasasivuisen hyperbelin eksentrisyys $e$ on $\sqrt{2}$.
Katso myös Hyperbelin eksentrisyys.
Tasasivuisen hyperbelin johtosuora (engl. Directrix of a rectangular hyperbola)
Jos tasasivuisen hyperbelin asymptootit ovat $x$- ja $y$-akselit ja hyperbeli kulkee pisteen $(c,c)$ kautta, niin sen johtosuorat ovat $x + y = \pm c \sqrt{2}$.
Katso myös Hyperbelin johtosuora.
Tasasivuisen hyperbolin yhtälö (engl. Equation of a rectangular hyperbola)
Jos tasasivuisen hyperbelin asymptootit ovat $x$- ja $y$-akselit ja se kulkee pisteen $(c,c)$ kautta, niin sen yhtälö on $xy=c^{2}$.
Katso myös Hyperbelin yhtälö, Kartioleikkauksen yhtälö.
Taso (engl. Plane)
Taso on tasainen pinta, jonka mitkä tahansa kaksi pistettä yhdistävä suora sijaitsee kokonaan kyseisessä tasossa.
Katso myös Tason vektorimuotoinen yhtälö, Tangenttitaso, Kompleksitaso, Kaksiulotteinen, Avaruusgeometria, Samassa tasossa oleva, Jordanin käyrälause, Euklidinen taso, Koordinaattitaso, Affiini taso, Analyyttinen avaruusgeometria, Kahden tason välinen kulma, Ekliptika.
Tasoalueen massakeskipiste (engl. Centre of mass of a lamina)
Suorien $x=a$, $x=b$ sekä $x$-akselin ja käyrän $y=f(x)$ rajoittaman tasoalueen massakeskipiste on piste $(\bar{x}, \bar{y})$, missä $\bar{x} = \int_a^b xf(x) dx / \int_a^b f(x)dx$ ja $\bar{y} = \int_a^b \frac{1}{2}f(x)^2 dx / \int_a^b f(x) dx$.
Katso myös Kolmion massakeskipiste, Puoliympyrän massakeskipiste, Ympyrän sektorin massakeskipiste, Massakeskipiste, Painopiste.
Tason neljännes (engl. Quadrant)
Tason osa, jota rajoittaa kaksi suoraa, jotka leikkaavat toisensa suorassa kulmassa. Esimerkiksi suorakulmaisessa koordinaatistossa tason osa, jonka pisteiden sekä $x$- että $y$-koordinaatti ovat positiivisia, on neljännes.

Katso myös Kuvio.
Tason vektorimuotoinen yhtälö (engl. Vector equation of a plane)
Tason, joka sisältää pisteen $\overline{a}$, ja joka on vektorien $\overline{b}$ ja $\overline{c}$ suuntainen, yhtälö on $\overline{x} = \overline{a}+t \overline{b}+u \overline{c}$, missä parametrit $t$ ja $u$ voivat olla mitä tahansa reaalilukuja.
Huomaa, että vektorit $b$ ja $c$ eivät saa olla yhdensuuntaisia. Vaihtoehtoisesti, jos on annettu piste $A$, sen paikkavektori $ \overline{a}$ ja tason normaalivektori $ \overline{n}$, niin vektoria $ \overline{n}$ vastaan kohtisuorassa olevan ja pisteen $A$ kautta kulkevan tason yhtälö vektorimuodossa on $(\overline{r}- \overline{a}) \cdot \overline{n} = 0$.Katso myös Vektori, Suoran vektorimuotoinen yhtälö, Taso, Yhtälö, Tason yhtälö.
Tason yhtälö (engl. Equation of a plane)
Jos taso ei ole pystysuora, niin sen yhtälö on muotoa $z = mx + ny + c$ ja se leikkaa $z$-akselin kohdassa $z=c$.
Tavallisempaa on kirjoittaa tason yhtälö vektorien avulla seuraavasti. Jos on annettu piste $A$ paikkavektorina $\mathbf{a}$ ja normaalivektori $\mathbf{n}$, niin pisteen $A$ kautta kulkevan vektoria $\mathbf{n}$ vastaan kohtisuoran tason yhtälö on \[ n_{1}x + n_{2}y + n_{3}z + d = 0, \] missä $d = -\mathbf{a}\cdot \mathbf{n}$.
Katso myös Tason vektorimuotoinen yhtälö, Kahden tason leikkaus, Annetun kolmen pisteen kautta kulkeva taso, Pinnan tangenttitason yhtälö, Yhtälö, Suoran ja tason leikkauspiste.
Tasoverkko (engl. Planar graph)
Verkko, joka voidaan piirtää tasoon siten, että mitkään verkon kaksi viivaa eivät leikkaa toisiaan.
Katso myös Verkkoteoria, Verkko.
Tau (engl. Tau)
Kreikkalainen kirjain $\tau$ (pieni kirjain) tai $T$ (iso kirjain) lausutaan tau ja sen äänneasu on sama kuin suomen t-kirjaimen.
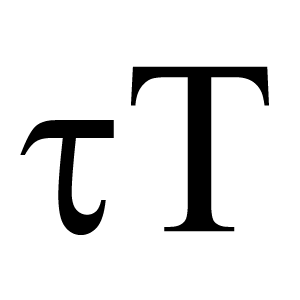
Katso myös Kreikkalaiset kirjaimet.
Taulukko (engl. Array)
Joukko lukuja tai muuta tietoa, joka esitetään tietyssä muodossa, yleensä ruudukkona. Esimerkiksi $$ \left( \begin{array}{ccc} 1 & 3 & 5 \\ 2 & 6 & 1 \\ 2 & 8 & 9 \end{array} \right) $$ Matriisit ja vektorit ovat esimerkkejä taulukoista.
Katso myös Matriisi.
Taulukkolaskenta (engl. Spreadsheet)
Tietokoneohjelma, joka näyttää monenlaisia (usein taloudellisia) aineistoja riveinä ja sarakkeina sekä sallii käsitellä ja laskea uudelleen näitä tietoja. Usein aineiston osat saattavat riippua muista osista, joten jos yhtä osaa muutetaan, suuri määrä arvoja saatetaan laskea uudelleen.
Katso myös Tietokone.
Tautokroni (engl. Tautochrone)
Käyrä, jolla on seuraava ominaisuus: jos kappale liikkuu käyrää pitkin painovoiman vaikutuksesta, niin aika, jonka kappale tarvitsee päästäkseen käyrän päätepisteeseen ei riipu siitä pisteestä, mistä lähdettiin liikkeelle. Tautokronikäyrä on sykloidi.
Katso myös Käyrä.
Tautologinen (engl. Tautologous, Logically equivalent)
Kaksi lausetta ovat tautologiset eli loogisesti yhtäpitävät, jos joko molemmat ovat tosia tai molemmat ovat epätosia olkoot niiden argumentit mitä hyvänsä. Tällöin merkitään $ P \equiv Q $ tai $ P \iff Q $.
Katso myös Logiikka, Kontrapositio.
Tavu (engl. Byte)
Tietojenkäsittelyssä kahdeksan bittiä.
Katso myös Kilotavu, Bitti, Megatavu, Merkintätapa, Notaatio, Nibble.
Taylorin sarja (engl. Taylor series)
Muotoa \[ f(x+a)=f(a)+f'(a)x+f''(a)x^{2}/2+f'''(a)x^{3}/3!+... +f^{(n-1)}(a)x^{n-1}/(n-1)!+R_{n} \] olevaa potenssisarjaa kutsutaan Taylorin sarjaksi. Taylorin lause kertoo, millä ehdoilla funktiolla $f$ on tällainen sarjaesitys. Yllä $R_{n}$ on jäännöstermi. Se voidaan kirjoittaa useassa eri muodossa ja se saa yleensä pieniä arvoja, kunhan $n$ on tarpeeksi suuri.
Katso myös Analyyttinen funktio, Potenssisarja, Maclaurinin sarja, Jäännöstermin Cauchyn lauseke, Virhetermi, Jäännöstermi, Funktion $(1-x)^{-1}$ sarjakehitelmä, Jäännöstermin integraalilauseke, Lagrangen jäännöstermi.
Tekijä, Jakaja (engl. Divisor)
Luvun $n$ jakaja eli tekijä on luku, jolla $n$ on jaollinen.
Yleensä sekä luku $1$ ja luku $n$ itse lasketaan luvun $n$ tekijöiksi. Alkuluku on sellainen positiivinen kokonaisluku, jonka ainoat tekijät ovat $1$ ja luku itse. Lukua $1$ ei yleensä kuitenkaan pidetä alkulukuna. Alkulukuina pidetään siis sellaisia lukuja, joilla on tasan kaksi eri tekijää.
Katso myös Yhteinen tekijä, Lukuteoria, Alkuluku, Kokonaisluku, Aito jakaja.
Tekijä (engl. Factor)
Luku on toisen luvun tekijä, mikäli se jakaa tasan tuon toisen luvun. Esimerkiksi luvun $20$ tekijät ovat $1$, $2$, $5$, $10$ ja $20$. Luvun $23$ tekijät ovat $1$ ja $23$.
Luku on toisen luvun tekijä, jos se jakaa tasan tuon toisen luvun. Esimerkiksi $7$ on luvun $21$ tekijä, koska $21 = 7 \cdot 3$.
Polynomi on toisen polynomin tekijä, jos se jakaa tasan tuon toisen polynomin. Esimerkiksi $x-1$ on polynomin $x^2-1$ tekijä, koska $x^2-1 = (x-1)(x+1)$.
Katso myös Monikerta, Lukuteoria, Alkutekijä, Yhteinen tekijä, Kokonaisluku.
Tekijätopologia (engl. Quotient topology)
Olkoon $X$ topologinen avaruus ja $\cong$ ekvivalenssirelaatio avaruudessa $X$. Olkoon $X/\cong$ kaikkien $\cong$-ekvivalenssiluokkien joukko ja $pr \colon X \rightarrow X/\cong$ kuvaus $x \mapsto [x]$.
Avaruuden $X/\cong$ tekijätopologian muodostavat ne joukot $U \subset X/\cong$, joille $pr^{-1} U$ on avoin.
Joukko $X /\cong$ yhdessä tekijätopologian kanssa muodostaa tekijäavaruuden.
Määritellään reaaliakselilla ekvivalenssirelaatio $\cong$, jolle $x \cong y$ jos ja vain jos $x-y \in \mathbb{N}$. Nyt tekijäavaruus on homeomorfinen yksikköympyrän kanssa.
Katso myös Topologia, Ekvivalenssirelaatio.
Teoreettinen keskiarvo, Odotusarvo (engl. Expectation)
Odotusarvolla on alunperin tarkoitettu odotettavissa olevaa voittoa pelissä $$ E(x) = \sum_1^k x_i \cdot P(x_i), $$ missä $x_i$ on voitto ja $ P(x_i) $ ko. voiton todennäköisyys.
Odotusarvo on myös satunnaismuuttujan teoreettinen keskiarvo. Mikäli samasta joukosta poimitaan äärettömän monta otosta ja jokaisesta otoksesta lasketaan jokin tilastollinen suure, on suureen keskiarvo näissä otoksissa suureen odotusarvo.
Mikäli muuttuja on diskreetti, sen odotusarvo on $$ E(x) = \sum_1^k x_i \cdot P(x_i). $$ Jatkuvan satunnaismuuttujan odotusarvo on vastaavasti $$ E(x) = \int x \cdot f(x) dx. $$
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Todennäköisyys, Lineaarisen funktion odotusarvo.
Teoria (engl. Theory)
Matematiikassa ja logiikassa teoriaksi sanotaan joukkoa väittämiä, jotka on todistettu lähtien samoista oletuksista, joita sanotaan teorian aksioomiksi.
Luonnontieteissä teoriaksi sanotaan joukkoa ideoita, joita on menestyksellisesti käytetty ennustusten tekemiseen pitkälle aikavälille, ja jotka on todettu hyödyllisiksi.
Termi (engl. Term)
Esimerkiksi lausekkeessa 3x + 4y + 2z osat 3x, 4y ja 2z ovat termejä.
Yksi yhteenlaskettavista luvuista summassa tai sarjassa. Sanaa termi käytetään myös yleisemmässä merkityksessä tarkoittamaan osaa algebrallisesta lausekkeesta.
Katso myös Lauseke, Kerroin, Korvaaminen, Sijoittaminen, sijoitus, Jono, Virhetermi, Jäännöstermi.
Terävä (engl. Acute)
Teräväkärkinen. Terävä kulma on kulma, joka on pienempi kuin suora kulma ($90^{\circ}$). Teräväkulmaisen kolmion kaikki kolme kulmaa ovat teräviä kulmia.
Terävä kulma (engl. Acute angle)
Kulma, joka on suoraa kulmaa pienempi, on terävä kulma.
Katso myös Kulma, Kupera kulma, Suora kulma, Teräväkulmainen kolmio, Tylppä kulma.
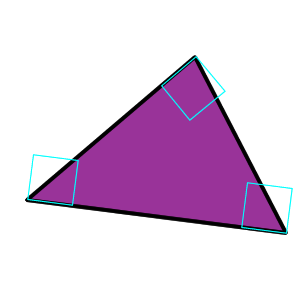
Teräväkulmainen kolmio (engl. Acute triangle)
Kolmiota, jonka kaikki kolme kulmaa ovat teräviä kulmia, sanotaan teräväkulmaiseksi kolmioksi.
Katso myös Terävä kulma, Kolmio, Tasasivuinen kolmio, Tylppäkulmainen kolmio.
Tessellaatio, Laatoitus (engl. Tessellation)
Tason peittäminen kuvioilla, jotka eivät mene päällekkäin. On olemassa kolme mahdollista tason laatoitusta, joissa käytetään identtisiä säännöllisiä monikulmioita. Nämä ovat säännöllisistä kuusikulmioista, neliöistä ja tasasivuisista kolmioista koostuvat laatoitukset. Käyttämällä erilaisia säännöllisiä monikulmioita tai epäsäännöllisiä kuvioita saadaan paljon useampia laatoituksia. Joillakin laatoituksilla on kiertosymmetriaa, mutta ei kaikilla.

Katso myös Arkhimedeen laatoitus, Laatoitus.
Testifunktio (engl. Test function)
Analyysissä funktioilla on ominaisuuksia, joiden määritelmissä viitataan muihin funktioihin. Tämä tapahtuu usein niin, että funktiolla $f$ on (määritelmän nojalla) jokin ominaisuus $P$, mikäli kaikille jonkun luokan funktioille $g$ pätee, että parilla $(f,g)$ on jokin ominaisuus $Q$.
Tällaisissa määritelmissä funktioita $g$ kutsutaan testifunktioiksi.
Usein testifunktioiden joukko on sileiden kompaktikantajaisten funktioiden joukko.
Tetra (engl. Tetra)
Neljää tarkoittava etuliite.
Tetraedri (engl. Triangle-based pyramid, Triangular pyramid, Tetrahedron)
Pyramidi, jonka pohjakin on kolmio; nelitahokas.
Katso myös Pyramidi, Kolmio, Bangin lause, Ympäripiirretty pallo, Monitahokas, Platonin kappaleet, 4, Neljä.
Tetraedriluku (engl. Tetrahedral number)
Tetraedriluvut ovat lukuja, jotka saadaan tarkastelemalla pisteistä muodostettua tetraedrin muotoista kappaletta. Muodostetaan pisteistä esimerkiksi kolmio, jonka jokainen sivu muodostuu kolmesta pisteestä, asetetaan sen päälle kolmio, jonka jokaisella sivulla on kaksi pistettä ja sen päälle kolmio, jonka jokaisella sivulla on yksi piste. Tällöin on pisteistä muodostettu tetraedri. Tässä tapauksessa pisteiden kokonaismäärä on (kolmas kolmioluku) + (toinen kolmioluku) + (ensimmäinen kolmioluku) $= 6+3+1 = 10$.
Yleisesti, $n$:s tetraedriluku on yhtä suuri kuin $n$:n ensimmäisen kolmioluvun summa. Tämä on sama kuin neljäs luku vasemmalta lukien Pascalin kolmion $n+2$:lla rivillä.
Binomikaavan avulla voidaan osoittaa, että $n$:s tetraedriluku on ${n+2\choose 3} = \frac{(n+2)(n+1)n}{6}$.
Ainoat luvut, jotka ovat sekä tetraedrilukuja että neliöitä, ovat 4 ($= 2^{2} = T_{2}$) ja 19600 ($= 140^{2} = T_{48}$).
Katso myös Kaksikymmentä, 20, Tiu, Valita, Kolmioluku, Pascalin kolmio, Kokonaisluku.
Tetromino (engl. Tetromino)
Neljän identtisen neliön järjestäminen tasossa siten, että ne on liitetty toisiinsa reuna reunaa vasten. On olemassa viisi mahdollista tetrominoa.
Theta (engl. Theta)
Kreikkalainen kirjain $\theta$ (pieni kirjain) tai $\Theta$ (iso kirjain) lausutaan teeta. Sen äänneasu on suunnilleen sama kuin suomen t-kirjaimen, mutta se on kovempi.
Pientä kirjainta $\theta$ käytetään usein merkitsemään tuntematonta kulmaa, kaksiulotteisessa napakoordinaatistossa olevaa kulmaa tai pallokoordinaatistossa pisteen paikkavektorin ja $z$-akselin välistä kulmaa tai paikkavektorin ja $xy$-tason välistä kulmaa. Tilastotieteessä sitä käytetään merkitsemään yleistä populaatioparametria.

Katso myös Kreikkalaiset kirjaimet.
Tietokone (engl. Computer)
Elektroninen laite, joka kykenee suorittamaan yksinkertaisia laskutoimituksia ja tekemään yksinkertaisia loogisia päätelmiä miljoonia (tai jopa miljardeja) kertoja ihmistä nopeammin.
Katso myös Babbage, Taulukkolaskenta.
Tiheys (engl. Density)
Tilastollinen testi (engl. Statistical test)
Päätössääntö, jolla otosaineiston perusteella (puutteellisen tiedon vallitessa) päätellään voiko aineistoon liittyvä väite (nolla-hypoteesi) pitää paikkansa vai ei. Tilastotieteessä on lähes lukematon määrä eri tilanteisiin kehitettyjä testejä. Tilastollista testausta voidaan lähestyä myös seuraavalla tavalla: Testissä tutkija esittää testisuureen avulla aineistolle nollahypoteesiin liittyvän kysymyksen (väitteen) ja kysyy mitä mieltä aineisto on väitteestä. Päätöksentekoa varten tutkijan on tunnettava, millaisia vastauksia aineisto antaa kun väite (nollahypoteesi) pitää paikkansa. Ts. testisuureen jakauman nollahypoteesin voimassa ollessa. Mikäli vastaus on lähellä odotettua, tutkija toteaa aineiston tukevan sille esitettyä väitettä ja että se näin voi hyvinkin pitää paikkansa. Mikäli vastaus poikkeaa selvästi odotetusta (menee kriittisen rajan ulkopuolelle), tutkija toteaa, että väite ei voi pitää paikkaansa. Tilastollinnen testi on siis poissulkevaa päättelyä. Pienet erot jäävät huomaamatta, mutta suuret huomataan. Kuinka suuria poikkeamia testissä huomataan, riippuu käytettävissä olevasta tiedon määrästä (havaintojen lukumäärästä).
Katso myös Varianssianalyysi, T-testi, Keskiarvojen erotuksen t-testi, Keskiarvon t-testi, Parittaisten otosten t-testi, F-jakauma.
Tilastollinen tunnusluku, Tunnusluku (engl. Statistic)
Teoriassa mikä tahansa tilastoaineistosta laskettu suure (tai kokoelma suureita) on tunnusluku. Myös graafista esitystä, kuten histogammi, voidaan kutsua tunnusluvuksi. Kaikki edellä määritellyt suureet eivät tietenkään ole mielenkiintoisia, vaan yleensä keskitytään sellaisiin tunnuslukuihin, jotka tehokkaasti tiivistävät otoksessa olevan informaation muutamaan lukuun. Paljon käytettyjä tunnuslukuja ovat esimerkiksi keskiarvo, varianssi, korrelaatiokerroin, kvarttiilit, mediaani, ... Otosaineistosta laskettuna tunnusluku on satunnaissuure, jonka arvo riippuu siitä mikä otos perusjoukosta on valittu. Otoksesta laskettuja tunnuslukuja merkitään tilastotieteessä latinalaisilla kirjaimilla, jotta ne paremmin erottuisisivat vastaavista teoreettisista parametreista, joita yleensä merkitään kreikkalaisilla kirjaimilla.
Katso myös Korrelaatiokerroin, Vaihtelevuus, Korrelaatiokerroin, Luottamusväli, Kvartiilivälin pituus, Kvartiili, Neljännespiste, Otostunnusluku, Keskihajonta, Tilastotiede, Harhaton estimaattori, Varianssi, Vaihteluväli, Korrelaatio, Kovarianssi.
Tilastotiede (engl. Statistics)
Tilastotiede "Statistics" - "State Arithmetics" on alunperin tarkoittanut tiedettä, joka tutkii valtion tilaa - esim. "Mistä valtio voi saada verotuloja?" Nykyjään tilastotiede on tieteenala, joka tutkii kaikkea numeerisen tiedon hankintaa, kuvaamista ja analysointia, sekä päätöksentekoa epävarmuuden vallitessa.
Katso myös Alkeismatematiikka, Jakauma, Tunnusluku, Tilastollinen tunnusluku, Verrata, Markovin ketju.
Tilavuus (engl. Volume)
Kolmiulotteisen avaruuden määrä, jonka olio vie tilaa. Tilavuuden dimensio on $L^{3}$ ja sen yksikkö metrijärjestelmässä on m$^{3}$.
Katso myös Pinta-ala, Pyörähdyskappaleen tilavuus, Pint, Millilitra, Senttilitra, Ominaisuus, jonka arvot ovat jatkuvia, Cavalierin lause, Tiheys.
Tiu, Kaksikymmentä, 20 (engl. 20, Twenty)
20 kappaletta on kansanomaisesti tiu.
20 on neljäs tetraedriluku.
Ikosaedrin sivutahkojen ja säännöllisen dodekaedrin kärkien lukumäärä.
20 on puolitäydellinen luku.
$\phi(20) = 8, \quad d(20) = 6, \quad \sigma(20) = 42$.

Katso myös Kymmenen monikerta, Tetraedriluku.
Tiukka lineaarijärjestys, Tiukka täydellinen järjestys (engl. Strict total ordering)
Olkoon $A$ joukko. $\lt \subset A \times A$ on tiukka lineaarijärjestys, mikäli on voimassa:
- Jos $a \lt b$ ja $b \lt c$, niin $a \lt c$ kaikilla $a,b,c \in A$.
- Kaikilla $a,b \in A$ pätee täsmälleen yksi ehdoista
- $a = b$,
- $a \lt b$,
- $a \gt b$.
Katso myös Tiukka osittaisjärjestys.
Tiukka osittaisjärjestys (engl. Strict partial ordering)
Olkoon $A$ joukko. $\lt \subset A \times A$ on tiukka osittaisjärjestys, mikäli on voimassa:
- Jos $a \lt b$ ja $b \lt c$, niin $a \lt c$ kaikilla $a,b,c \in A$.
- $a \lt a$ ei päde millään $a \in A$.
- $a \lt b$ ja $b \lt a$ eivät päde yhtä aikaa millään $a, b \in A$.
Katso myös Osittaisjärjestys, Tiukka lineaarijärjestys, Osittainen järjestys, Tiukka täydellinen järjestys.
Tiukka täydellinen järjestys, Tiukka lineaarijärjestys (engl. Strict total ordering)
Olkoon $A$ joukko. $\lt \subset A \times A$ on tiukka lineaarijärjestys, mikäli on voimassa:
- Jos $a \lt b$ ja $b \lt c$, niin $a \lt c$ kaikilla $a,b,c \in A$.
- Kaikilla $a,b \in A$ pätee täsmälleen yksi ehdoista
- $a = b$,
- $a \lt b$,
- $a \gt b$.
Katso myös Tiukka osittaisjärjestys.
Todennäköinen (engl. Probable, Likely)
Tapahtuma on todennäköinen, jos sillä on hyvä mahdollisuus tapahtua.
Todennäköisyyden aksioomat (engl. Axiomatic probability)
Olkoot $\Omega$ alkeistapausten joukko ja $\mathcal{F}$ kokoelma (ns. $\sigma$-algebra) joukon $\Omega$ osajoukkoja eli tapahtumia. Kuvaus $\mathbf{P}$ joukolta $\mathcal{F}$ reaalilukujen joukolle $\mathbb{R}$ on todennäköisyys, jos se toteuttaa seuraavat kolme aksioomaa:
1) $0 \leq \mathbf{P}(A) \leq 1$ kaikilla $A \in \mathcal{F}$,
2) $\mathbf{P}(\Omega) = 1$,
3) Jos $A_1,A_2, \ldots \in \mathcal{F}$ on jono pareittain pistevieraita tapahtumia, niin pätee \[ \mathbf{P} \left( \bigcup_i A_i \right) = \sum_i \mathbf{P}(A_i). \]
Todennäköisyys (engl. Probability)
Todennäköisyys on tapahtumaan (kokeen tulokseen) liitetty luku (mitta), joka kertoo, miten yleinen (todennäköinen) on kyseinen tapahtuma. Mikäli kaikki tulosvaihtoehdot ovat samanarvoisia (symmetrisiä) todennäköisyys esitetään yleensä murtolukuna - suotuisien tulosvaihtoehtojen lukumäärän suhteena kaikkiin mahdollisiin tulosvaihtoehtoihin. $$ \textrm{P(tapahtuma)} = \frac{\textrm{(suotuisat tulosvaihtoehdot)}} {\textrm{(kaikki mahdolliset tulokset)}}. $$ Eräs tapa mitata todennäköisyyttä, on suorittaa suuri määrä kokeita, jolloin tapahtuman todennäköisyys on $$ \textrm{P(tapahtuma)} = \frac{\textrm{(Onnistumisten lukumäärä)}} {\textrm{(Kokeiden lukumäärä)}} = \frac{\textrm{(k)}} {\textrm{(n)}} $$
Katso myös Tshebyshevin epäyhtälö, Leikkauksen todennäköisyys, Mahdottoman tapauksen todennäköisyys, Yhdisteen todennäköisyys, Varman tapauksen todennäköisyys, Vedonlyöntisuhde, Klassinen todennäköisyys, Yhtä todennäköinen, Sattuma, Mahdollisuus, Valita, Odotusarvo, Teoreettinen keskiarvo, Otosavaruus, Boolen epäyhtälö, Merkitsevyystaso, Merkitsevyystaso, Ominaisuus, jonka arvot ovat jatkuvia, Ehdollinen todennäköisyys, Uskottavuus.
Todistaa vääräksi (engl. Disprove)
Todistaa, että jokin väite ei ole tosi. Tämä voidaan usein tehdä etsimällä vastaesimerkki.
Katso myös Vastaesimerkki, Perustelu.
Todistamaton (engl. Unproved)
Asia, jota ei vielä ole todistettu.
Jotkut kuuluisat otaksumat ovat osoittautuneet hyvin vaikeiksi todistaa, ne säilyvät todistamattomina pitkän aikaa. Tällainen on esimerkiksi Goldbachin otaksuma.
Katso myös Looginen ominaisuus, Goldbachin otaksuma.
Toiminta (engl. Action)
Ryhmän $G$ (vasen) toiminta avaruudessa $X$ on kuvaus $\tau \colon G \times X \rightarrow X$, joka toteuttaa ehdot $\tau(e,x)=x$ kaikilla $x \in X$, ja $\tau(a,\tau(b,x))=\tau(a b,x)$ kaikilla $a,b \in G$, $x \in X$.
Usein toimintaa merkitään lyhyesti $ax=\tau(a,x)$.
Oikea toiminta on samankaltainen, kuvaus vain määritellään $X \times G \rightarrow X$.
Ryhmä $G$ toimii itsessään kuvauksella $G \times G \rightarrow G$; $(g,x) \mapsto gx$. Toinen ryhmän toiminta itsessään, konjugointi, voidaan määritellä kaavalla $(g,x) \mapsto g x g^{-1}$.
Ryhmä $G$ toimii konjugoimalla myös kaikkien $G$:n osajoukkojen tai aliryhmien joukossa kuvauksella $(g,A) \mapsto g A g^{-1}$.
Joukon $X$ kaikkien permutaatioiden ryhmä $S_X$ toimii $X$:ssä kuvauksella $(p,x) \mapsto p(x)$.
Katso myös Kuvaus, Stabilisaattori, Funktio.
Toinen derivaatta (engl. Second derivative)
Jos funktio $y$ derivoidaan kahdesti, kutsutaan tulosta funktion $y$ toiseksi derivaataksi. Funktion $y$ toista derivaattaa merkitään $\frac{\mathrm{d}^2 y}{\mathrm{d}x^2}$.
Esimerkiksi, jos $y = 5 x^3 + 6 x^2 + x + 4$, niin \[ \frac{\mathrm{d}y}{\mathrm{d}x} = 15x^2 + 12x + 1 \] ja \[ \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} = 30x + 12. \]
Katso myös Differentiaali- ja integraalilaskenta, Korkeamman kertaluvun derivaatta, Derivaatta, Toisen derivaatan numeerinen approksimointi, Käännepiste.
Toisen asteen lauseke (engl. Quadratic expression)
Lauseke, joka sisältää muuttujan neliön, mutta ei sitä korkeampia potensseja.
Katso myös Polynomi.
Toisen asteen yhtälö (engl. Quadratic equation)
Yhtälö, joka ilmoittaa, että jokin toisen asteen polynomi on yhtä suuri kuin nolla.
Toisen asteen yhtälö voidaan aina kirjoittaa muodossa $ax^{2}+bx+c = 0$. Esimerkiksi $5x^{2}+3x+10 = 0$ ja $10x^{2}+7 = 3x^{2}+11x$ ovat toisen asteen yhtälöitä..
Katso myös Neliöksi täydentäminen, Toisen asteen yhtälön ratkaisu.
Toisen asteen yhtälön ratkaisu (engl. Quadratic equation solution, Quadratic formula)
Toisen asteen yhtälön $ax^2+bx+c=0$ ratkaisut ovat \[\frac{ -b+\sqrt{b^{2}-4ac} }{2a}\] ja \[\frac{ -b-\sqrt{b^{2}-4ac} }{2a}\]. Tämä nähdään täydentämällä yhtälön vasen puoli neliöksi.
Katso myös Neliöksi täydentäminen, Toisen asteen yhtälö, Ratkaisu.
Toisen derivaatan numeerinen approksimointi (engl. Numerical second derivative)
Funktion $f$ toinen derivaatta $f''$ pisteessä $x$ on likimain $$\frac{f(x+h) - 2f(x) + f(x-h)}{h^2},$$ kun $h$ on hyvin pieni positiivinen reaaliluku.
Katso myös Likiarvo, Derivaatan numeerinen approksimointi, Toinen derivaatta.
Toisen kertaluvun differentiaaliyhtälö (engl. Second order differential equation)
Differentiaaliyhtälö, jossa esiintyy tuntemattoman funktion toinen derivaatta, mutta ei korkeampia derivaattoja.
Katso myös Differentiaaliyhtälö, Karakteristinen yhtälö, Legendren differentiaaliyhtälö.
Toisen lajin elliptinen integraali (engl. Elliptic integral of the second kind)
Elliptinen integraali muotoa \[ \int_{0}^{x} \sqrt{\frac{1-k^2t^2}{1-t^2}} dt,\] missä $k$ on elliptinen moduuli.
Katso myös Elliptinen integraali.
Toisensa poissulkeva (engl. Mutually exclusive)
Kaksi väittämää ovat toisensa poissulkevia, jos siitä, että toinen on tosi, seuraa, että toinen ei ole tosi.
Topologia (engl. Topology)
Topologia on kappaleiden sellaisten ominaisuuksien tutkimista, jotka eivät muutu, kun kappaleita venytetään ja väännetään, mutta ei revitä eikä liimata. Esimerkiksi rinkelin yksireikäisyys on tällainen ominaisuus: jos rinkeliä väännetään, mutta ei revitä, sen reikä ei katoa tai muutu kahdeksi reiäksi.
Topologia tutkii sellaisia ominaisuuksia, kuten kappaleen reikien lukumäärä, avaruuden dimensio ja kuvauksen jatkuvuus, jotka eivät muutu, kun kappaleita väännetään ja venytetään, mutta ei revitä eikä liimata.
Solmuteoria on topologian ala, joka tutkii, millä tavoin umpinainen narusilmukka voi olla solmussa.
Topologinen avaruus on pari $(X, \tau)$, missä $X$ on joukko ja $\tau$ on topologia eli sellainen kokoelma joukon $X$ osajoukkoja, joka toteuttaa seuraavat ehdot:
- $\emptyset \in \tau$ ja $X \in \tau$.
- Jos $U,V \in \tau$, niin $U \cap V \in \tau$.
- Jos $\mathcal{U} \subset \tau$, niin $\bigcup \mathcal{U} \in \tau$.
Yksi topologisen avaruuden käsitteen tarkoituksista on päästä määrittelemään kuvausten jatkuvuus hyvin yleisessä kontekstissa. Jos $(X,\tau)$ ja $(Y, \tau')$ ovat topologisia avaruuksia, niin kuvaus $f \colon X \rightarrow Y$ on jatkuva, mikäli kaikilla $x \in X$ ja kaikilla $U \in \tau'$, joilla $f(x) \in U$, on olemassa sellainen $V \in \tau$, että $x \in V$ ja $fV \subset U$.
Reaaliakseli voidaan ajatella topologisena avaruutena $(\mathbb{R},\tau)$, missä $\tau$ määritellään niin, että sen muodostavat joukot tyyppiä $]a,b[$, missä $a,b \in \mathbb{R}$, sekä näiden yhdisteet. Kun reaaliakselille ajatellaan tämä topologia, on edellä annettu yleinen jatkuvuuden käsite sama kuin tavanomainen reaalifunktioiden jatkuvuuden käsite.
Katso myös Möbius, Joukko, Topologinen ryhmä, Avoin joukko, Tekijätopologia, $N_2$, Tulotopologia, Relatiivitopologia, Algebrallinen topologia, Ekvivalentti, Yhtäpitävä.
Topologinen monisto (engl. Topological manifold)
Topologinen avaruus $X$ on $n$-ulotteinen topologinen monisto, jos $X$ on Hausdorff ja kaikilla $x \in X$ on ympäristö, joka on homeomorfinen avaruuden $\mathbb{R}^n$ kanssa.
Topologisen moniston määritelmässä on hiukan häilyvyyttä.
Joskus monistoiksi lasketaan myös reunalliset monistot. Reunallisessa monistossa jokaisella pisteellä on ympäristö, joka on homeomorfinen joko avaruuden $\mathbb{R}^n$ kanssa tai avaruuden $\{ (x_1, \dots, x_n) \in \mathbb{R}^n | x_1 \ge 0 \}$ kanssa.
Toisinaan taas monistoilta vaaditaan vielä lisäksi ominaisuus $N_2$, eli että monistolla on numeroituva kanta. Toisinaan numeroituvan kannan vaatimusta lievennetään niin, että riittää, että jokaisella moniston yhtenäisellä komponentilla on ominaisuus $N_2$, eli että monisto on parakompakti.
Termiä topologinen monisto käytetään, jotta se erottuisi sileistä monistoista eli differentiaalimonistoista.
Katso myös Hausdorff-avaruus, Hausdorffin avaruus, $N_2$, Homeomorfinen.
Topologinen ryhmä (engl. Topological group)
Kolmikko $(X, \tau, *)$ on topologinen ryhmä, jos $(X, \tau)$ on topologinen avaruus, ja $(X, *)$ on ryhmä, ja lisäksi funktiot
- $* \colon X \times X \rightarrow X; (a,b) \mapsto a * b$
- $()^{-1} \colon X \rightarrow X; a \mapsto a^{-1}$
Katso myös Topologia, Ryhmä, Lien ryhmä, Analyyttinen ryhmä.
Torus (engl. Torus)
Munkkirinkilän muotoinen kappale tai tällaisen kappaleen pinta, joka on ikäänkuin polkupyörän sisäkumi tai pelastusrengas.
Katso myös Kappale.
Totaalinen järjestys, Lineaarijärjestys (engl. Total ordering)
Olkoon $X$ joukko. Relaatio $\le \subset X \times X$ on totaalinen järjestys, mikäli seuraavat ehdot pätevät
- $x \le x$ kaikilla $x \in X$.
- Jos $x \le y$ ja $y \le z$, niin tällöin $x \le z$ kaikilla $x,y,z \in X$.
- Kaikilla $x,y \in X$ pätee $x \le y$ tai $y \le x$.
Katso myös Osittaisjärjestys, Osittainen järjestys.
Totalisti rajoitettu, Prekompakti (engl. Totally bounded)
Metrinen avaruus on prekompakti, jos jokaista lukua $\epsilon \gt 0$ kohti voidaan löytää äärellinen määrä avoimia $\epsilon$-säteisiä palloja, jotka peittävät koko avaruuden. Täydellinen metrinen avaruus on prekompakti jos ja vain jos se on jonokompakti tai vain kompakti.
Katso myös Rajoitettu, Kompakti.
Totuustaulu, Totuustaulukko (engl. Truth table)
Luettelo, johon on merkitty loogisen konnektiivin (esimerkiksi JA, EI, TAI) argumenttien kaikki mahdolliset totuusarvot sekä onko kyseinen yhdistelmä tosi vai epätosi.
Totuustaulukko, Totuustaulu (engl. Truth table)
Luettelo, johon on merkitty loogisen konnektiivin (esimerkiksi JA, EI, TAI) argumenttien kaikki mahdolliset totuusarvot sekä onko kyseinen yhdistelmä tosi vai epätosi.
$\tr$
Matriisin jäljen lyhenne. Siis $\mathrm{tr}(A)$ tarkoittaa neliömatriisin $A$ jälkeä.
Transformaatio (engl. Transformation)
Geometrisen olion, kuten tason, transformaatio on injektiivinen kuvaus joukosta $S$ joukkoon $S$, missä $S$ on olion muodostavien pisteiden joukko. Esimerkkejä transformaatioista ovat kierrot, peilaukset, suurennukset ja siirrot. Myös algebrallisille oliolle voidaan määritellä transformaatioita eli injektiivisiä kuvauksia oliojoukkojen välillä. Mille tahansa olioille voidaan määritellä transformaatioita.
Katso myös Perspektiivinen affiinikuvaus, Funktio, Kuvaus, Kiintopiste, Geometrinen muunnos.
Transformaatioryhmä (engl. Transformation group)
Kokoelma transformaatioita, jotka muodostavat ryhmän, jonka laskutoimitus on transformaatioiden yhdistäminen. Esimerkiksi kolmen kierron, jotka ovat $0^{\circ}$:een, $120^{\circ}$:een ja $240^{\circ}$:een kierto tietyn pisteen ympäri, muodostama joukko varustettuna laskutoimituksella, joka on kuvausten yhdistäminen, on ryhmä.
Katso myös Ryhmä, Geometrinen muunnos.
Transitiivinen (engl. Transitive)
Relaatio $\sim$ on transitiivinen, jos se toteuttaa ehdon $x \sim y$ ja $y \sim z \Rightarrow x \sim z$ kaikilla $x$, $y$ ja $z$, jotka kuuluvat relaation $\sim$ määrittelyjoukkoon.
Joukon $X$ kuvausten ryhmä $G$ on transitiivinen, jos kaikilla joukon $X$ alkiolla $x$ ja $y$ on olemassa $G$:n alkio $g$ siten, että $g(x) = y$.
Katso myös Järjestys, Intransitiivinen, Järjestetty.
Transkendenttinen (engl. Transcendental)
Luku on transkendenttinen, jos se ei ole minkään kokonaislukukertoimisen polynomiyhtälön juuri.
Transkendenttinen funktio on funktio $y=f(x)$, jota ei voida kirjoittaa $x$:n ja $y$:n polynomina.Transkendenttinen käyrä on käyrä, jonka yhtälössä esiintyy transkendenttisia funktioita.
Katso myös Transsendenttinen luku, Transsendenttifunktio, Algebrallinen luku.
Transpositio, Vaihto, Vaihdos (engl. Transposition)
Permutaatio, jossa kahden alkion paikat vaihtuvat keskenään.
Katso myös Parillinen permutaatio, Pariton permutaatio, Permutaatio.
Transsendenttifunktio (engl. Transcendental function)
Funktio $y=f(x)$ on transsendenttifunktio, jos sitä ei voida kirjoittaa muodossa \[ \sum _{0 \le i,j \le n } a_{ij} x^i y^j = 0 . \]
Katso myös Transkendenttinen, Funktio, Kuvaus, Algebrallinen funktio.
Transsendenttinen luku (engl. Transcendental number)
Luku, joka ei ole minkään kokonaislukukertoimisen polynomin nollakohta. Esimerkkejä transsendenttisista luvuista ovat $e$, $\pi$ ja Liouvillen luku.
Katso myös Algebrallinen, Irrationaaliluku, Transkendenttinen, Neperin luku, $e$, Pii, $\pi$, Liouvillen luku, Liouvillen vakio.
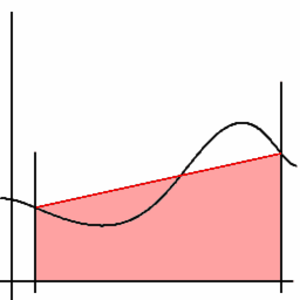
Trapetsisääntö (engl. Trapezium rule, Trapezoid rule)
Eräs numeerisen integroinnin menetelmä. Menetelmä saadaan integroimalla suora, jonka arvot välin päätepisteissä ovat yhtä suuret kuin funktiolla $f(x)$: \[ \int_{a}^{b} f(x)dx \approx \frac{1}{2}(b-a)(f(a)+f(b)). \]
Tästä saadaan yleisemmin: \[ \int_a ^b y dx \approx \frac{1}{2} h[( y_0 + y_n ) + 2( y_1 + y_2 + \ldots + y_{n-1} ) ], \] missä pisteet $a=x_{0}, x_{1}, \ldots, x_{n-1}, x_{n}=b$ jakavat välin $[a,b]$ tasaisesti $n$:ään yhtä pitkään $h=(b-a)/n$:n pituiseen osaan ja $y_{i}=y(x_{i})$.
Katso myös Sääntö, Keskipistesääntö, Simpsonin sääntö.
Trigonometria (engl. Trigonometry)
Kolmioiden sivujen ja kulmien mittalukujen välisten yhteyksien selvittely, erityisesti trigonometrisia funktioita käyttäen.
Katso myös Tangenttifunktio, Trigonometrinen yhtälö, Sini, Kosini, Geometria, Trigonometrinen funktio, Analyyttinen avaruusgeometria.
Trigonometrian Pythagoraan lause (engl. Sine squared plus cos squared)
Trigonometrinen funktio (engl. Circular function, Trigonometric function)
Funktio, jonka argumentti on kulma, jonka toinen kylki on $x$-akseli ja toinen kylki origosta alkava puolisuora. Funktion arvo on tämän toisen kyljen ja yksikköympyrän leikkauspisteen koordinaatti, tällaisen koordinaatin käänteisluku tai koordinaattien suhde. Trigonometrisia funktioita ovat siis sini-, kosini-, tangentti-, kotangentti-, sekantti- ja kosekanttifunktiot.
Katso myös Tangenttifunktio, Trigonometrinen yhtälö, Trigonometrinen identiteetti, Trigonometria, Sini, Funktio, Kuvaus, Kotangentti, Kosini, Sekanttifunktio, Arkusfunktio, Hyperbolinen funktio, Kosekantti.
Trigonometrinen identiteetti (engl. Trigonometric identity)
Yhtälö, jossa esiintyy trigonometrisia funktioita. Esimerkiksi $\sin(x+y)=\sin x\cos y+\sin y\cos x$.
Katso myös Yhteenlaskukaava, $\tan(-x)$, $\cos(-x)$, $\sin(-x)$, $\sin(x+180^{\circ})$, Identiteetti, Puolikkaan kulman kaava, $a\cos(x) + b\sin(x)$, Tulokaava, Trigonometrinen funktio, Kosinilause, $\sin(x+90^\circ)$, $\cos(x + 90^\circ)$, $\cos(x+180^\circ)$, $\tan(x+180^\circ)$, $\tan(x+90^\circ)$, De Moivren kaava, Kaksinkertaisen kulman kaava, Summakaava.
Trigonometrinen yhtälö (engl. Trigonometric equation)
Yhtälö, joka sisältää muuttujan trigonometrisiä funktioita. Tällaisilla yhtälöillä on usein äärettömän monta ratkaisua, koska trigonometriset funktiot ovat jaksollisia. Esimerkiksi yhtälön $\sin x = 0$ ratkaisut ovat muotoa $x = n\pi$, missä $n$ on mikä tahansa kokonaisluku.
Katso myös $\tan$, Tangenttifunktio, Trigonometria, $\sin$, Trigonometrinen funktio, $\cos$, Kosini, Yhtälö.
Trigonometristen funktioiden approksimointi (engl. Small angle approximation)
Jos kulma $x$ mitataan radiaaneissa, ja se on hyvin pieni, voidaan tehdä seuraavat approksimaatiot: \[ \sin x \approx x \] \[ \cos x \approx 1 - \frac{x^2}{2} \] \[ \tan x \approx x \]
Katso myös Likiarvo.
Trigonometristen funktioiden tarkat arvot (engl. Particular values of trigonometric functions)
Trigonometristen funktioiden arvot ovat hyvin yksinkertaisia kulmien $0^{\circ}$, $30^{\circ}$, $45^{\circ}$, $60^{\circ}$, $90^{\circ}$ ja $180^{\circ}$ tapauksissa.
Katso myös Kosinin tarkkoja arvoja, Tangentin tarkkoja arvoja, Sinin tarkkoja arvoja, Reaaliluku.
Triviaali, Ilmeinen, Itsestään selvä (engl. Trivial)
Jokin on triviaali, jos on hyvin ilmeistä, onko se totta vai epätotta. Usein suuri joukko väittämiä sisältää joitakin triviaaleja väittämiä.
Joskus tätä sanaa käytetään liian paljon. Pitäisi sanoa jonkin olevan itsestäänselvä vain, jos se todella on sitä, ei silloin jos se vain näyttää siltä tai emme jaksa vaivautua todistamaan sitä.
Katso myös Looginen ominaisuus.
Trokoidi (engl. Trochoid)
Vierintäkäyrä, jonka ympyrän kiinnitetty piste piirtää ympyrän vieriessä pitkin suoraa tai toisen ympyrän kehää. Ympyrän kiinnitetty piste voi sijaita ympyrän kehällä tai ympyrän sisällä.
Katso myös Ympyrä, Vierintäkäyrä, Hyposykloidi, Hypotrokoidi.
Tshebyshevin epäyhtälö (engl. Tchebychev's Theorem)
Jos $X$ on satunnaismuuttuja ja $g(x)$ on muuttujan $x$ ei-negatiivinen funktio, niin $ \mathrm{P(g(X)} \geq \mathrm{k)} \leq \frac{\mathrm{E(g(X))}}{\mathrm{k}}, $ eli todennäköisyys sille, että $g(x)$ on suurempi tai yhtä suuri kuin $k$, on pienempi tai yhtä suuri kuin satunnaismuuttujan $g(X)$ odotusarvo jaettuna luvulla $k$.
Katso myös Lause, Todennäköisyys.
Tuhat, 1000 (engl. 1000, Thousand)
Tukkimiehen kirjanpito (engl. Tally)
Yksinkertainen tapa laskea asioita; kirjoitetaan yksi pystyviiva jokaista asiaa kohti kunnes päästään viidenteen asiaan. Tällöin vedetään vaakasuora viiva neljän pystysuoran viivan yli. Sen jälkeen toistetaan sama menettely aloittamalla uusi pystysuorien viivojen ryhmä. Tämä tekee viiden ryhmien laskemisen melko helpoksi, ja voidaan nähdä kuinka monta asiaa on laskettu.
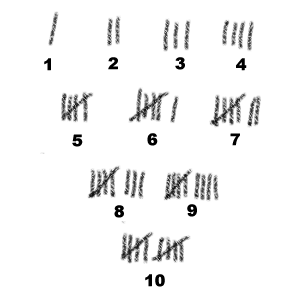
Katso myös Merkintätapa, Notaatio.
Tulo (engl. Product)
Tulos, joka saadaan kertomalla keskenään kaksi tai useampaa suuretta. Esimerkiksi lukujen 3 ja 4 tulo on 12 ($3 \cdot 4 = 12$) sekä lukujen 2, 3 ja 5 tulo on 30 ($2 \cdot 3 \cdot 5 = 30$)
Katso myös Kertolasku, Pisteen potenssi ympyrän suhteen, Vektoritulo, Ristitulo, Pistetulo, Vandermonden determinantti, Skalaaritulo, Sisätulo, Vektorien tensoritulo, Yleistetty tulo, Ääretön tulo.
Tulokaava (engl. Product formula)
Trigonometrinen identiteetti, joka ilmaisee kahden trigonometrisen funktion, joista toisen argumentti on $x$ ja toisen $y$, tulon toisten trigonometristen funktioiden avulla, joiden argumentteina ovat $x+y$ ja $x-y$.
Katso myös Trigonometrinen identiteetti, $\cos(x)\cos(y)$.
Tulon derivointisääntö (engl. Product rule)
Funktioiden $f(x)$ ja $g(x)$ tulon $f(x)g(x)$ derivointisääntö on \[ \frac{\mathrm{d}}{\mathrm{dx}}(f g) = g\frac{\mathrm{d}f}{\mathrm{dx}} + f \frac{\mathrm{d}g}{\mathrm{dx}}. \]
Katso myös Derivointisääntö, Sääntö, Leibnizin sääntö, Osamäärän derivointisääntö, Osittaisintegrointi.
Tulon nollasääntö (engl. Zero property)
Jos $a \cdot b = 0$, niin ainakin toinen luvuista $a$ ja $b$ on $=0$.
Tuloste, Arvo (engl. Output)
Funktion $f \colon A \rightarrow B$ arvo pisteessä $a \in A$ on $f(a)$, eli se arvojoukon alkio, jonka $f$ liittää pisteeseen $a$.
Tietokoneohjelman tuloste on se tieto, jonka ohjelma on tuottanut ohjelman suorituksen päättyessä. Tietojenkäsittelytieteessä usein ajatellaan, että ohjelman syötteet ja tulosteet ovat luonnollisia lukuja.
Sanaa tuloste käytetään yleensä sellaisen (ei-interaktiivisen) tietokoneohjelman yhteydessä, joka saa syötteen pelkästään suorituksen alkaessa ja palauttaa tulosteen kerralla ohjelman suorituksen päättyessä.
Arkikielessä mitä tahansa ohjelman tulostamaa dataa (näyttölaitteelle tai paperille) kutsutaan tulosteeksi.
Katso myös Kuvajoukko, Funktion kuvajoukko.
Tulotopologia (engl. Product topology)
Olkoot $(X, \tau)$ ja $(Y, \tau')$ topologisia avaruuksia. Tällöin joukossa $X \times Y$ voidaan määritellä tulotopologia, jonka kannan muodostavat kaikki joukot tyyppiä $U \times V$, missä $U \in \tau$ ja $V \in \tau'$.
Jos $(X_i,\tau_i)$, $i \in I$ on kokoelma topologisia avaruuksia, voidaan määritellä joukossa $\times_{i \in I} X_i$ tulotopologia, jonka kannan muodostavat kaikki joukot tyyppiä $\times_{i \in I} U_i$, missä $U_i \in \tau_i$ kaikilla $i$, ja $U_i \neq X_i$ äärellisen monella $i$.
Tulotopologia avaruudessa $\mathbb{R} \times \mathbb{R}$ on sama kuin tason tavanomainen topologia.
Katso myös Topologia.
Tunnusluku, Tilastollinen tunnusluku (engl. Statistic)
Teoriassa mikä tahansa tilastoaineistosta laskettu suure (tai kokoelma suureita) on tunnusluku. Myös graafista esitystä, kuten histogammi, voidaan kutsua tunnusluvuksi. Kaikki edellä määritellyt suureet eivät tietenkään ole mielenkiintoisia, vaan yleensä keskitytään sellaisiin tunnuslukuihin, jotka tehokkaasti tiivistävät otoksessa olevan informaation muutamaan lukuun. Paljon käytettyjä tunnuslukuja ovat esimerkiksi keskiarvo, varianssi, korrelaatiokerroin, kvarttiilit, mediaani, ... Otosaineistosta laskettuna tunnusluku on satunnaissuure, jonka arvo riippuu siitä mikä otos perusjoukosta on valittu. Otoksesta laskettuja tunnuslukuja merkitään tilastotieteessä latinalaisilla kirjaimilla, jotta ne paremmin erottuisisivat vastaavista teoreettisista parametreista, joita yleensä merkitään kreikkalaisilla kirjaimilla.
Katso myös Korrelaatiokerroin, Vaihtelevuus, Korrelaatiokerroin, Luottamusväli, Kvartiilivälin pituus, Kvartiili, Neljännespiste, Otostunnusluku, Keskihajonta, Tilastotiede, Harhaton estimaattori, Varianssi, Vaihteluväli, Korrelaatio, Kovarianssi.
Tuntematon (engl. Unknown)
Tuntematon suure yhtälössä on se, mikä halutaan saada selville; suuretta merkitään kirjaimella (muuttuja), kun yritetään löytää tapoja hyödyntää muita tiedossa olevia tosiasioita sen selvittämiseksi, mikä suure on. Yhtälöryhmissä saattaa esiintyä useampi kuin yksi tuntematon, mutta ajatus on sama.
Tunti (engl. Hour)
Tunti on ajan mittayksikkö. Yksi vuorokausi jakautuu 24 tuntiin ja yksi tunti 60 minuuttiin.
Tusina, 12, Kaksitoista (engl. 12, Twelve, a dozen)
Lukumäärän 12 ilmaisin on kansanomaisesti tusina. 12 on pienin kokonaisluku, joka voidaan kirjoittaa kahdella eri tavalla aitojen tekijöidensä tuloksi: 12 = 3 x 4 = 2 x 6.
12 on pienin runsas luku ja siten myös pienin ylirunsas luku.
12 on kuution ja säännöllisen oktaedrin särmien, dodekaedrin sivutahkojen ja säännöllisen ikosaedrin kärkien lukumäärä.
12 on kolmas viisikulmioluku.
?(12) = 4, d(12) = 6, ?(12)=28.

Tuuma (engl. Inch)
Englantilainen pituusyksikkö, joka on yhtä suuri kuin 2.54 cm. Yksi jalka on 12 tuumaa.
Tyhjä (engl. Null)
Jokin on tyhjä, jos se ei sisällä yhtään alkiota. Esimerkiksi tyhjä joukko on joukko, jossa ei ole yhtään alkiota.
Katso myös Nolla, Tyhjä joukko, Nollahypoteesi.
Tyhjä joukko (engl. Null set or empty set, Null set, Empty set)
Joukko, jossa ei ole yhtään alkiota. Tyhjää joukkoa merkitään symbolilla $\emptyset$. Joskus käytetään myös merkintää $\{ \}$.
Katso myös Mahdottoman tapauksen todennäköisyys, Tyhjä, Joukko, Osajoukko, Aito osajoukko.
Tylppä (engl. Obtuse)
Tylppä kulma on kulma, joka on suurempi kuin 90 astetta, mutta pienempi kuin 180 astetta.
Tylppäkulmainen kolmio on kolmio, jossa on tylppä kulma.

Katso myös Tylppäkulmainen kolmio.
Tylppä kulma (engl. Obtuse angle)
Tylppä kulma on kulma, joka on suurempi kuin suora kulma, mutta pienempi kuin oikokulma.
Katso myös Terävä kulma, Kulma, Kupera kulma, Suora kulma.
Tylppäkulmainen kolmio (engl. Obtuse triangle)
Tylppäkulmainen kolmio on kolmio, jonka yksi kulma on tylppä.
Katso myös Erisivuinen kolmio, Kolmio, Tylppä, Tasasivuinen kolmio, Teräväkulmainen kolmio.
Tyyppiarvo, Moodi (engl. Mode)
Yrityksessä on 7 henkilöä, joiden palkat ovat:
- Pomo 5000
- Kanslisti 1300
- Työntekijä 1 1700
- Työntekijä 2 1500
- Työntekijä 3 1400
- Työntekijä 4 1200
- Työntekijä 5 1200
Luokan oppilaiden silmien väri on: sininen, sininen, sininen, sininen, sininen, harmaa, harmaa, harmaa, vihreä, ruskea, ruskea, ruskea. Silmien värin moodi on sininen (frekvenssi 5): oppilaat ovat tyypillisesti sinisilmäisiä.
Moodi eli tyyppiarvo on luokitellussa aineistossa käytetty paikantamistunnusluku. Luokittelu- ja järjestysasteikolla moodi on siihen luokkaan liittyvä muuttujanarvo, jossa on eniten havaintoja (kyseessä tyypillinen muuttujanarvo). Mikäli kyseessä on luokiteltu aineisto (intervalli- tai suhdeasteikon muuttuja), moodi määritellään yleensä sen luokan luokkakeskukseksi, jossa on eniten havaintoja. Eräissä aineistoissa voi olla kaksi tai useampia moodeja (luokan frekvenssi oleellisesti suurempi kuin viereisten luokkien frekvenssi).
Katso myös Keskiarvo, Aritmeettinen keskiarvo, Paikantamistunnusluku, Keskiluku, Mediaani, Verrata.
Täydellinen (engl. Complete)
Metrinen avaruus on täydellinen, jos sen jokainen Cauchy-jono suppenee kohti jotakin avaruuden alkiota.
Normiavaruus on täydellinen, jos sitä vastaava luonnollisella metriikalla varustettu metrinen avaruus on täydellinen edellä mainitussa mielessä. Tällaista avaruutta kutsutaan Banach-avaruudeksi.
Logiikan päättelysysteemi on täydellinen, jos jokainen väite, joka systeemissä voidaan esittää, voidaan siinä todistaa tai kumota.
Katso myös Banachin avaruus, Cauchy-jono, Metrinen avaruus.
Täydellinen luku (engl. Perfect)
Luku on täydellinen, jos se on yhtä suuri kuin sitä itseään pienempien tekijöidensä summa. Esimerkiksi 6 ja 28 ovat täydellisiä lukuja, sillä $6 = 1+2+3$ ja $28 = 1+2+4+7+14$. Täydellisiä lukuja ei tunneta kovin montaa. On olemassa jo Eukleideen ajoista asti tunnettu kaava, joka tuottaa joitakin niistä; lasketaan yhteen luvun 2 peräkkäisiä potensseja, kunnes saadaan alkuluku, ja kerrotaan saatu summa viimeisellä luvulla, joka lisättiin summaan. Esimerkiksi $2^{0}+2^{1}+2^{2} = 1+2+4 = 7$, joka on alkuluku. Kerrotaan saatu summa 7 luvulla 4. Tulokseksi saadaan 28, joka on täydellinen luku. Kaikki tunnetut täydelliset luvut ovat parillisia.
Luku on täydellinen, jos se on yhtä suuri kuin tekijöidensä summa. Esimerkiksi 6 ja 28 ovat täydellisiä lukuja, sillä $6 = 1+2+3$ ja $28 = 1+2+4+7+14$. Seuraavat kaksi täydellistä lukua ovat 496 ja 8128. Täydellisiä lukuja ei tunneta kovin monta. Ensimmäiset viisi täydellistä lukua ovat 6, 28, 496, 8128 ja 33550336. Kaikki parilliset täydelliset luvut päättyvät kymmenjärjestelmässä kirjoitettuna numeroihin 6 tai 8, mutta nämä eivät vuorottele. Kaikki tunnetut täydelliset luvut ovat muotoa $2^{n-1} (2^{n}-1)$, missä $2^{n}-1$ on Mersennen alkuluku. Ei tiedetä, onko olemassa äärettömän monta täydellistä lukua. Ei myöskään tiedetä, onko olemassa parittomia täydellisiä lukuja.
Katso myös Aito jakaja.
Täydellinen luku (engl. Perfect number)
Positiivinen kokonaisluku on täydellinen, jos se on yhtä suuri kuin kaikkien tekijöidensä summa lukua itseään lukuunottamatta. Esimerkiksi luvun $6$ tekijät ovat $1$, $2$, $3$ ja $6$. Koska $1 + 2 + 3 = 6$, on luku $6$ täydellinen. Vastaavasti on luku $28 = 1+2+4+7+14$ myös täydellinen. Seuraavat kolme täydellistä lukua ovat $496$, $8128$ ja $33550336$. Täydellisiä lukuja ei tunneta kovin montaa.
Kymmenjärjestelmässä esitettyinä kaikki täydelliset luvut päättyvät joko lukuun $6$ tai lukuun $8$, mutta luvut $6$ ja $8$ eivät koskaan vuorottele. Kaikki täydelliset luvut ovat muotoa $2^{n-1}(2^{n}-1)$, missä $2^{n}-1$ on Mersennen alkuluku.
Sitä ei tiedetä, onko täydellisiä lukuja äärettömän monta tai onko olemassa paritonta täydellistä lukua.
Katso myös Aito jakaja, Lähes täydellinen luku.
Täydellinen nelikulmio (engl. Complete quadrilateral)
Kuvio, jonka määrittävät neljä suoraa, joista mitkään kolme eivät leikkaa samassa pisteessä, sekä näiden suorien kuusi leikkauspistettä.
Katso myös Kuvio.
Täydennetty matriisi (engl. Augmented matrix)
Yhtälöryhmän \begin{eqnarray*} a_{11}x_{1} + \ldots + a_{1n}x_{n} & = & b_{1}\\ . &&\\ . &&\\ a_{m1}x_{1} + \ldots + a_{m n}x_{n} & = & b_{m}\\ \end{eqnarray*} täydennetty matriisi on \[ \left( \begin{array}{cccc|c} a_{11} & a_{12} & \ldots & a_{1n} & b_1\\ . &&&&.\\ . &&&&.\\ a_{m1} & a_{m2} & \ldots & a_{m n} & b_m\\ \end{array}\right).\] (Tällaisessa matriisissa oikeanpuoleisen ja sitä edeltävän sarakkeen väliin kirjoitetaan usein pystyviiva tai pystykatkoviiva vastaamaan yhtälöryhmän yhtäsuuruusmerkkiä.)
Katso myös Matriisi.