Matematiikan verkkosanakirja

Voiman yksikön Newtonin lyhenne. Yksi Newton on yhtä suuri kuin kilogramma kertaa metri jaettuna sekunnilla toiseen eli 1 N = 1 kg m/s$^{2}$.

Katso myös Newton, Lyhenne.

Topologinen avaruus $X$ on $N_2$, mikäli on olemassa numeroituva kokoelma $\mathcal{U}$ avaruuden $X$ avoimia osajoukkoja, joka toteuttaa seuraavan ehdon: Jokainen avaruuden $X$ avoin joukko voidaan esittää yhdisteenä kokoelman $\mathcal{U}$ alkioista.

Toisin sanoen $X$ on $N_2$, mikäli avaruudella $X$ on numeroituva kanta.

Avaruus $X$ on $N_1$, mikäli jokaisella avaruuden $X$ pisteellä on numeroituva ympäristökanta.

Reaaliakseli varustettuna tavanomaisella topologiallaan on $N_2$, samoin kuin korkeampiulotteiset euklidiset avaruudet.

Numeroituva diskreetti avaruus on $N_2$, mutta ylinumeroituva diskreetti avaruus ei ole $N_2$.

Katso myös Topologia, Topologinen monisto, Numeroituva.

Lyhenne sanalle numero.

Katso myös Luku, Lyhenne.

Esimerkiksi nelikulmio on 4-kulmio.

Monikulmio, jossa on n kappaletta sivuja.

Katso myös Monikulmio, Kulmio.

Luvun $x$ $n$:s juuri on se luku, joka on korotettava potenssiin $n$, jotta saataisiin $x$.

Katso myös Kuutiojuuri, Neliöjuuri, Juuri.

Nabla on operaattori $\nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right)$. Siis \[ \nabla f(x,y,z) = \left( \frac{\partial f(x,y,z)}{\partial x}, \frac{\partial f(x,y,z)}{\partial y}, \frac{\partial f(x,y,z)}{\partial z} \right). \]

Katso myös Delta, Differentiaalioperaattori.

NAND on binäärinen looginen operaattori, joka ottaa syötteenään kaksi totuusarvoa (tosi tai epätosi), ja palauttaa totuusarvon. NAND palauttaa totuusarvon epätosi, jos ja vain jos molemmat lähtöarvot ovat tosia.

Katso myös Looginen operaattori.

Etuliite, joka tarkoittaa $10^{-9}$. Lyhennetään n. Esimerkiksi yksi nanometri (nm) on $10^{-9}$ metriä.

Katso myös Lyhenne.

Olkoon $f \colon U \rightarrow \overline\mathbb{C}$, missä $U \subset \mathbb{C}$. Piste $a \in U$ on napa, jos $f(a)=\infty$, mutta jollain $m \geq 0$ kuvaus $$ z \mapsto (z-a)^m f(z)$$ on analyyttinen pisteen $a$ jossain ympäristössä.

Katso myös Piste, Analyyttinen funktio.

Koordinaattijärjestelmä, jossa pisteen paikka ilmaistaan etäisyytenä kiinnitetystä viittauspisteestä (navasta) ja kulmana kiinnitetystä viittaussuorasta. Esimerkiksi tasossa viittauspiste (napa) on yleensä origo ja viittaussuora positiivinen x-akseli.

Katso myös Analyyttinen tasogeometria, Koordinaatisto.

Apuväline usempinumeroisten lukujen kertolaskujen laskemiseen. Sen keksi skotlantilainen matemaatikko John Napier (1550--1617). Laite koostuu sarjasta "luita", jotka sisältävät osan kertotauluista.

Annetun kolmion kullekin sivulle voidaan piirtää tasasivuinen kolmio, jonka sivun pituus on annetun kolmion kyseisen sivun pituus. Näitä kolmea kolmiota kutsutaan Napoleonin kolmioiksi.

Katso myös Napoleonin lause, Tasasivuinen kolmio, Fermat'n piste.

Jos piirretään minkä tahansa annetun kolmion jokaiselle sivulle tasasivuinen kolmio, niin näiden kolmen tasasivuisen kolmion keskipisteet muodostavat kolmion, joka on tasasivuinen.

Katso myös Lause, Napoleonin kolmiot.

Matriisi, jonka nollasta eroavat alkiot sijaitsevat päälävistäjän ympärillä. Esimerkiksi \[ \left( \begin{array}{ccccc} 1 & 2 & 0 & 0 & 0 \\ 6 & 4 & 1 & 0 & 0 \\ 0 & 7 & 2 & 5 & 0 \\ 0 & 0 & 3 & 1 & 9 \\ 0 & 0 & 0 & 3 & 1 \end{array} \right). \]

Katso myös Päälävistäjä, Matriisi.

Anglosaksinen massan yksikkö. Sen lyhenne on lb. Yksi naula on 16 unssia ja 14 naulaa on yksi stone. Yksi naula on noin 0,4535924 kg.

Jos $A$ on jokin väittämä, niin $A$:n vastakohtaa 'ei ole $A$' kutsutaan $A$:n negaatioksi.

Negatiivinen luku on luku, jonka arvo on pienempi kuin nolla. Negatiivisen luvun eteen kirjoitetaan miinusmerkki.

Esimerkiksi $-5$ on luku "miinus viisi", $-3,25$ on "miinus kolme pilkku kaksikymmentäviisi".

Pienempi kuin nolla.

Katso myös Positiivinen.

Horisontin alapuolelle muodostunut kulma.

Katso myös Kulma, Korkeuskulma.

Monikulmio, jossa on neljä sivua ja neljä kulmaa.

Katso myös Viisikulmio, Suunnikas, Neljäkäs, Puolisuunnikas, Suorakaide, Suorakulmio, Monikulmio, Aubelin lause, Konsyklinen, 4, Neljä.

Neliö on kuvio, jossa on neljä yhtä pitkää sivua ja neljä suoraa kulmaa.

Laskemme neliön jostakin kertomalla sen itsellään eli korottamalla sen toiseen potenssiin.

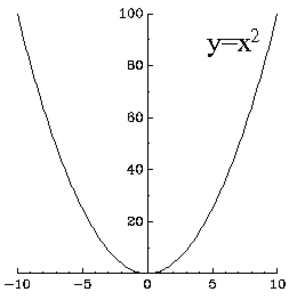
Katso myös Potenssiin korottaminen, Neliöluku, Neliöjuuri.

Luvun 9 neliöjuuria ovat 3 ja -3: $ \sqrt {9} = \pm 3 $

Luvun 25 neliöjuuria ovat 5 ja -5: $ \sqrt {25} = \pm 5 $

Kaikkien kokonaislukujen neliöjuuret eivät ole kokonaislukuja eivätkä negatiivisten lukujen neliöjuuret edes reaalilukuja.

Annetun luvun neliöjuuri on luku, joka itsellään kerrottuna antaa tulokseksi alkuperäisen luvun. Luvun $x$ neliöjuurelle käytetään merkintää $ \sqrt {\mathrm{x}} $ .

Jotta neliöjuuren arvo olisi yksikäsitteisesti määrätty, asetetaan Suomessa nykyisin lisäehto: neliöjuuren arvoksi kelpaa vain ei-negatiivinen luku.

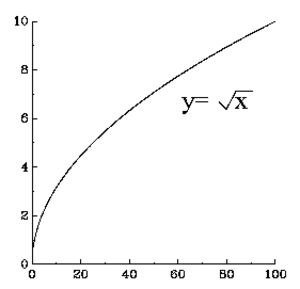
Katso myös Juurimerkki, Neliöksi täydentäminen, $n$:s juuri, Korottaa toiseen, Laskea neliö jostakin, Neliöluku, Juuri, Neliö, $\cos(x/2)$, $\sin(x/2)$, $\tan(x/2)$, Luvun 2 neliöjuuri on irrationaalinen.

Toisen asteen polynomin muuntaminen ensimmäisen asteen polynomin neliön ja vakion summaksi. Toisen asteen yhtälön ratkaisu perustuu neliöksi täydentämiseen.

Pyritään ratkaisemaan yhtälö $ax^2+bx+c=0$, missä $a \neq 0$. Se on sama kuin \[x^2+{b\over a}x+{c\over a}=0.\]

Huomataan, että \[\left(x+{b\over 2a}\right)^2=x^2+{b\over a}x+{b^2\over 4a^2}.\] Siis \[\left(x+{b\over 2a}\right)^2-{b^2\over 4a^2}+{c\over a}=0,\] joten \[\left(x+{b\over 2a}\right)^2={b^2\over 4a^2}-{c\over a}\] ja \[x={-b\pm\sqrt{b^2-4ac}\over 2a}\].

Katso myös Toisen asteen yhtälö, Neliöjuuri, Toisen asteen yhtälön ratkaisu.

Luku on neliöluku, jos se on kahden yhtä suuren kokonaisluvun tulo. Esimerkiksi \begin{eqnarray*} 1 &=& 1 \times 1 \\ 4 &=& 2 \times 2 \\ 9 &=& 3 \times 3 \\ 16 &=& 4 \times 4 \\ 25 &=& 5 \times 5 \end{eqnarray*} ovat neliölukuja.

Katso myös Kuutioluku, Korottaa toiseen, Laskea neliö jostakin, Neliöjuuri, Kolmioluku, Kahden neliön erotus, Neliö, Monikulmioluku.

$n$:n ensimmäisen positiivisen kokonaisluvun neliöiden summa on \[ \sum _{r=1}{n} r^2 = \frac{1}{6}n(n+1)(2n+1) \]

Katso myös Peräkkäisten kuutioiden summa, Sarja.

Matriisi, jossa on sama määrä rivejä ja sarakkeita.

Katso myös Jälki, Säännöllinen matriisi, Singulaarinen matriisi, Lävistäjämatriisi, Ortogonaalinen matriisi, Matriisi, LU-hajotelma, Normaali matriisi, Kääntyvä matriisi, LDU-hajotelma.

Yksi neliömetri on kymmenentuhatta neliösenttimetriä.

Yksi neliömetri on miljoonasosa neliökilometriä.

Yksi neliömetri on sellaisen neliön pinta-ala, jonka sivujen pituus on yksi metri. Neliömetrin lyhenne on $m^{2}.$

Neliömetri on pinta-alan yksikkö SI-järjestelmässä.

Katso myös Pinta-ala, Pinta-alayksikkö, SI-yksiköt, Hehtaari.

Jos neliön sivun pituus on $a$, neliön pinta-ala on $a^2$.

Pyramidi, jossa on yksi neliönmuotoinen tahko (pyramidin pohja) ja neljä kolmionmuotoista tahkoa.

Katso myös Neliöpohjaisen pyramidin tilavuus, Pyramidi, Kolmio.

Neliöpohjaisen pyramidin, jonka korkeus on $h$ ja pohjan sivun pituus $x$, tilavuus on $x^{2} h/3$.

Katso myös Neliöpohjainen pyramidi.

Luonnollinen luku on neliövapaa, jos se ei ole jaollinen minkään ykköstä suuremman luonnollisen luvun neliöllä.

Neljä on toinen neliöluku, sillä $2^2 = 2 \cdot 2 = 4$. (Huomaa myös, että $2 + 2 = 4$.)

Neljä on ensimmäinen tetraedriluku ja ensimmäinen yhdistetty luku.

Neljä on pienin luku, joka on alkuluvun neliö

Neljä on tetraedrin, yksinkertaisimman mohitahokkaan, tahkojen ja kärkien lukumäärä.

Neljä on ainoa sellainen yhdistetty luku $n$, joka ei jaa lukua $(n-1)!$.

$\phi(4) = 2, \quad d(4) = 3, \quad \sigma(4) = 7$.

Katso myös Tetraedri, Nelikulmio.

• Lävistäjät puolittavat toisensa ja leikkaavat suorassa kulmassa.
• Neljäkkäällä on kaksi symmetriasuoraa.
• Kiertosymmetrian aste on kaksi.
• Vastakkaiset kulmat ovat yhtä suuret.
• Vastakkaiset sivut ovat yhdensuuntaiset.

Erityinen nelikulmio; suunnikas, jonka kaikki sivut ovat yhtä pitkät.

Katso myös Suunnikas, Puolisuunnikas, Suorakaide, Suorakulmio, Nelikulmio.

Jokainen tason kartta voidaan värittää neljällä värillä siten, että kahta vierekkäistä maata ei väritetä samalla värillä.

Katso myös Lause, Neljän värin ongelma.

Onko olemassa sellaista pisteiden ja näitä yhdistävien janojen muodostamaa tason verkkoa, jonka pisteiden värittäminen vaatii vähintään viisi väriä, kun värittäminen tehdään siten, että mitkään kaksi janalla yhdistettyä pistettä eivät saa samaa väriä? Yhtäpitävästi voidaan kysyä, onko olemassa sellaista tason karttaa, jonka värittäminen vaatii vähintään viisi väriä, kun värittäminen tehdään siten, että mitkään kaksi vierekkäistä maata eivät saa samaa väriä?

Matemaatikot Appel ja Haken esittivät vuonna 1976 todistuksen, jonka mukaan jokaisen tällaisen verkon värittämiseen riittää neljä väriä. Todistuksessaan he joutuivat käyttämään tietokonetta lukuisten mahdollisten vaihtoehtojen tarkistamiseen. Tämän vuoksi jotkut matemaatikot eivät hyväksyneet heidän todistustaan. Appelin ja Hakenin todistuksen oikeellisuus onnistuttiin kuitenkin tarkistamaan tietokoneen avustuksella vuonna 2004.

Toisenlaisilla pinnoilla värittämiseen vaadittavien värien lukumäärä on eri. Esimerkiksi tooruksen pinnalla lukumäärä on seitsemän.

Katso myös Verkkoteoria, Neljän värin lause, Verkko.

Polynomi, joka sisältää muuttujansa neljännen potenssin, mutta ei sitä korkeampia potensseja.

Katso myös Polynomin tekijöihinjako, Polynomi, Elliptinen integraali.

Ala- ($Q_1$), keski- ($Q_2$) ja ylä- ($Q_3$) kvartiili ovat tunnuslukuja, jotka jakavat tilastoaineiston 4 yhtä suureen osaan. Ala-kvartiilin ($Q_1$) alapuolella on neljännes, keski-kvartiilin ($Q_2$) alapuolella puolet ja ylä-kvartiilin ($Q_3$) alapuolella kolme neljäsosaa aineistosta. Keski-kvartiilia kutsutaan yleensä mediaaniksi ja merkitään $Md$:llä.

Katso myös Kvartiilivälin pituus, Mediaani, Tunnusluku, Tilastollinen tunnusluku, Laatikko ja viikset -kuvio.

Luvun neljäs potenssi saadaan kertomalla luku itsellään ja kertomalla näin saatu tulos vielä kerran itsellään. Luvun $a$ neljäs potenssi on siis $a \cdot a \cdot a \cdot a$. Tätä merkitään $a^4$.

Neljän yhtä suuren luvun tulo; luvun neliön neliö.

Katso myös Luku.

Kokonaiseen tarvitaan neljä neljäsosaa.

14 on kolmen pienimmän neliöluvun summa ($14 = 1 + 4 + 9$), joten se on kolmas (neliö)pyramidiluku.

$\phi(14) = 6, d(14) = 4, \sigma(14) = 24$.

Neperin luku on matematiikassa usein esiintyvä vakio, jonka tarkkaa arvoa ei voida ilmaista äärellisenä desimaalilukuna. Sen likiarvo on 2,718281828.

On olemassa täsmälleen yksi reaaliluku $a$, jolle pätee $\frac{d}{dx}a^x = a^x$ kaikilla $x \in \mathbb{R}$. Tätä lukua kutsutaan Neperin luvuksi ja sitä merkitään kirjaimella $e$. Sen likiarvo on $2,718281828$.

Luvun $e$ laskemiseksi on olemassa useita kaavoja. Esimerkiksi \[ e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{1}{n!}. \]

Pätee myös \[ e = \lim_{n \to \infty} (1 + \frac{1}{n})^{n}. \]

Katso myös Vakio, Transsendenttinen luku, Hyperbolinen kosini, Hyperbolinen sini.

Ensimmäisen lajin Besselin funktioiden tiettyjä yksinkertaisia kombinaatioita kutsutaan toisen lajin Besselin funktioiksi ja merkitään $Y_n(z)$. Ne ovat Besselin yhtälön ratkaisuja.

Katso myös Funktio, Kuvaus, Bessel Friedrich Wilhelm, Besselin yhtälö, Besselin funktio (ensimmäinen laji), Besselin funktio (kolmas laji), Hankelin funktio.

Laskutoimituksen neutraalialkio on alkio, joka ei muuta laskutoimituksessa muita alkioita. Esimerkiksi 1 on kertolaskun neutraalialkio, koska luvulla 1 kertominen ei muuta mitään lukua. Yhteenlaskun neutraalialkio on 0, koska lisättäessä luku 0 mihin tahansa lukuun ei luku muutu.

Katso myös Nolla-alkio, Yhteenlaskun neutraalialkio, Ykkösalkio, Kertolaskun neutraalialkio, Monoidi, Yksikkömatriisi, Binäärinen kuvaus, Alkio, Kaksipaikkainen kuvaus, Identiteettimatriisi.

Voiman yksikkö SI-järjestelmässä, sen lyhenne on N. Yksi newton on yhtä suuri kuin voima, joka antaa 1 kg:n massalle kiihtyvyyden 1 m/s$^{2}$. Newton on myös kimmoisuusmoduulin yksikkö SI-järjestelmässä.

Katso myös N, SI-yksiköt.

Nibble on tietojenkäsittelytieteessä käytettävä informaation mittayksikkö. Yksi nibble on neljä bittiä, eli sen avulla voidaan esittää yksi vaihtoehto kuudestatoista.

Katso myös Tavu.

Olkoon $R$ rengas. $x \in R$ on nilpotentti, mikäli $x^n=0$ jollain $n$.

Neliömatriisi $A$ on nilpotentti, jos $A^n=0$ jollain $n$, missä $A^n$ tarkoittaa matriisin $A$ kertomista $n$ kertaa itsensä kanssa.

Katso myös Lineaarikuvaus, Lineaarimuunnos.

Kahden pelaajan peli, jossa pelaajat vuorotellen poistavat jotkut tai kaikki tulitikut tulitikkukasoista, joita on tietty määrä.

Katso myös Peli.

Murtoluku on luku, joka ilmoittaa luvun $1$ tasaosien lukumäärän. Nimittäjä kertoo, kuinka moneen yhtä suureen osaan $1$ tällöin on jaettu. Nimittäjä kirjoitetaan murtoluvussa viivan alapuolelle. Esimerkiksi murtoluvun $\frac{3}{7}$ nimittäjä on $7$ ja murtoluvun $\frac{2}{11}$ nimittäjä on $11$.

Katso myös Yhteinen nimittäjä, Osoittaja, Aito murtoluku, Epämurtoluku, Murtoluku, Yksikkömurtoluku, Kokonaisluku.

Luku, joka on jaollinen numeroidensa summalla. Esimerkiksi $1729$ on Harshadin luku, koska $1729 = 19 \cdot 91$ ja $19 = 1 + 7 + 2 + 9$. Harshadin lukuja kutsutaan myös Nivenin luvuiksi.

Kun ilmaistaan jonkin luvun likiarvo, on kerrottava myös tarkkuus, jolla likiarvo on oikea.

Katso myös Likimääräinen, Lyhenne.

Luku, joka ei muuta mitään lukua, kun se lisätään toiseen lukuun. Lukusuoralla nolla sijaitsee lukujen -1 ja +1 puolivälissä. Se on tyhjän joukon alkioiden lukumäärä. Sen merkki on 0.

Luku, joka laskettaessa vastaa ei yhtään niitä, joita ollaan laskemassa.

Luku, joka voidaan lisätä mihin tahansa lukuun ilman, että kyseinen luku muuttuu (eli yhteenlaskun neutraalialkio).

Luku, joka ei muutu kerrottaessa sitä muilla luvuilla.

Huomaa, että jos jaetaan jokin luku nollalla, tulos ei ole luku. Se on määrittelemätön tai joskus sen voidaan ajatella olevan ääretön.

Jos kerrotaan jokin luku nollalla, tulos on nolla. Jos lisätään lukuun tai vähennetään siitä nolla, luku ei muutu.

Jokaisessa kunnassa on oltava alkio, joka vastaa lukua nolla, koska kunnassa on oltava yhteenlaskun neutraalialkio.

Monen funktion arvo pisteessä 0 on erikseen määritelty tai se on määrittelemätön.

$0^{0}$ on määrittelemätön. $0!$ määritellään sopimuksella $0! = 1$.

Nolla on sekä reaaliluku että rationaaliluku.

Katso myös Polynomin nollakohta, Tyhjä.

Luku, joka ei muuta mitään lukua, jos se lasketaan yhteen tämän kanssa. Tavallisessa lukujärjestelmässä tämä luku on 0; siksi yhteenlaskun neutraalialkiota kutsutaan joskus nolla-alkioksi.

Alkio $e$, joka toteuttaa ehdon $a+e = e+a = a$ jokaiselle joukon alkiolle $a$. Joukoissa $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ ja $\mathbb{C}$ yhteenlaskun neutraalialkio on 0. Ryhmän neutraalialkiota yhteenlaskun suhteen saatetaan kutsua myös nolla-alkioksi.

Katso myös Vasta-alkio, Neutraalialkio.

Tilastollisessa päätöksenteossa aineistolle esitettävään kysymykseen (testiin) liittyvä oletus. Nollahypoteesi on muotoiltava niin, että testisuureen jakauma nollahypoteesin voimassa ollessa tunnetaan. Näin jakauman perusteella voidaan laskea, miten todennäköistä on se, että nollahypoteesi pitää paikkansa. Tilastollinen päätöksenteko perustuu tähän todennäköisyyteen.

Katso myös Vastahypoteesi, Vaihtoehtoinen hypoteesi, Kriittinen arvo, T-testi, Tyhjä, Merkitsevyystaso, Merkitsevyystaso.

Niiden pisteiden joukko, joissa annettu funktio saa arvon 0, on funktion nollakohtien muodostama joukko.

Katso myös Ydin, Joukko.

Kahden toisiaan sivuavan käyrän välinen kulma; kulma, jonka suuruus on $0^{\circ}$.

Katso myös Kulma.

Matriisi, jonka kaikki alkiot ovat nollia.

Katso myös Matriisi.

Peli, missä toinen pelaaja voittaa sen mitä toinen pelaaja häviää. (Välissä ei ole pelinjärjestäjää, joka ottaa omansa joka pelistä.)

Katso myös Peli.

Vektori, jonka pituus on 0. Sen suunta on määrittelemätön.

Katso myös Vektori, Yksikkövektori, Vektorin normi.

Menetelmä, jolla diskreetti Fourier'n muunnos voidaan laskea nopeasti. On siis laskettava \[ F_j = \sum_{k=0}^{n-1} f_k \omega_{n}^{jk}, \] missä $\omega_{n} = e^{-2\pi i/n}$ ja $j = 0, 1, \ldots, n-1$. Nopealla Fourier'n muunnoksella tähän tarvitaan $O(n\log_{2}(n))$ laskutoimitusta: Olkoot $m = n/2$ ja \[ F^{\mathrm{even}}_{j} = \sum_{k=0}^{m-1} f_{2k} \omega_{m}^{jk} \] ja \[ F^{\mathrm{odd}}_{j} = \sum_{k=0}^{m-1} f_{2k+1} \omega_{m}^{jk}. \] Tällöin \[ F_{j} = F^{\mathrm{even}}_{j} + \omega_{n}^{j} F^{\mathrm{odd}}_{j} \] kaikilla $j =0, 1, \ldots, n-1$. Tässä $F^{even}$ ja $F^{odd}$ ovat $m = n/2$ pisteen diskreettejä Fourier'n muunnoksia. Tätä menetelmää voidaan nyt soveltaa rekursiivisesti tarvittavien laskutoimitusten määrän vähentämiseksi.

Katso myös Diskreetti Fourier'n muunnos, FFT.

Suure, joka ilmaisee kuinka kovalla vauhdilla jokin liikkuu ja mihin suuntaan. Nopeudella on sekä suuruus että suunta, joten se on vektorisuure. Nopeuden suuruus on sama kuin vauhti.

Vektorisuure, joka ilmaisee kuinka kovalla vauhdilla jokin liikkuu ja mihin suuntaan. Se on paikan muutosnopeus.

Katso myös Ominaisuus, jonka arvot ovat jatkuvia.

Kuutio, jonka kullakin sivulla on eri määrä pisteitä eli eri silmäluku, yleensä yhdestä kuuteen. Tavallisessa arpakuutiossa kuution vastakkaisten sivujen silmälukujen summa on 7.

Arpakuutioita käytetään usein todennäköisyyteen liittyvissä kysymyksissä ja ongelmissa, koska reilua noppaa heitettäessä on kukin kuudesta silmäluvusta yhtä mahdollinen.

Suora, joka on kohtisuorassa annettua suoraa tai tasoa vastaan.

Katso myös Suora, Normaalivektori, Analyyttinen avaruusgeometria, Osittaisderivaatta.

Jos $G$ on ryhmä, $a \in G$ ja $H \subset G$, merkitään $aH=\{ ah \mid h \in H\}$ ja $Ha=\{ ha \mid h \in H\}$.

Ryhmän $G$ aliryhmä $H$ on normaali, jos $aH=Ha$ kaikilla $a \in G$.

Abelin ryhmän kaikki aliryhmät ovat normaaleja.

Katso myös Ryhmä, Aliryhmä, Jäännösluokkaryhmä, Syklinen ryhmä, Normalisaattori, Yksinkertainen ryhmä, Konjugaattiluokka.

Neliömatriisia $A$ kutsutaan normaaliksi, jos $A \bar{A}^{T} = \bar{A}^{T}A$. Tässä $\bar{A}$ on matriisi, jonka alkiot ovat matriisin $A$ alkioiden kompleksikonjugaatit.

Katso myös Unitaarinen matriisi, Matriisin transpoosi, Lävistäjämatriisi, Ortogonaalinen matriisi, Liittoluku, Neliömatriisi, Kompleksikonjugaatti, Hermiittinen matriisi.

Teoreettinen jatkuva todennäköisyysjakauma, jonka tiheysfunktio on \[ f(x,\mu ,\sigma ^2 ) = \frac{1}{{\sqrt {2\pi \sigma ^2 } }} \cdot e^{\left( { - \frac{1}{2}\frac{{\left( {x - \mu } \right)^2 }}{{\sigma ^2 }}} \right)} \, = \,\frac{1}{{\sigma \sqrt {2\pi } }} \cdot e^{\left( { - \frac{1}{2}\left( {\frac{{x - \mu }}{\sigma }} \right)^2 } \right)} \] Summan jakauma.

Otoskeskiarvon jakauma. Otoskeskiarvo lasketaan muuttujanarvojen summan avulla, ja näin otoskeskiarvo noudattaa suurissa otoksissa (ainakin likimäärin) normaalijakaumaa, olipa perusjoukon jakauma lähes mikä tahansa.

Mittausvirheen jakauma. Mittausvirheet muodostuvat usean osavirheen summana ja näin ne yleensä noudattavat normaalijakaumaa.

Luonnossa on runsaasti muuttujia (ei sentään kaikki), jotka noudattavat (ainakin likimääräisesti) normaalijakaumaa - mistä jakauman nimi.

Mikäli ilmiöön vaikuttavat tekijät (impulssit) ovat kerrannaisia, noudattaa muuttuja logNormaali-jakaumaa.

Katso myös Jatkuva satunnaismuuttuja, Kellokäyrä, Jakauma, Keskiarvo, Aritmeettinen keskiarvo, T-jakauma, Studentin t-jakauma, Varianssi, Eksponenttifunktio, Standardi normaalijakauma, Keskeinen raja-arvolause, Virhefunktio, Gauss, Gaussin.

Annettuun käyrän tai pinnan pisteeseen piirretty normaalivektori on vektori, joka on kohtisuorassa käyrää tai pintaa vastaan kyseisessä pisteessä.

Katso myös Vektori, Yksikkönormaalivektori, Tangenttivektori, Piste, Kohtisuora, Käyrä, Normaali, Suora, Sivunormaalivektori.

Olkoon $G$ ryhmä ja $H$ ryhmän aliryhmä. Sanomme, että aliryhmän $H$ normalisaattori $N(H)=\{ g \in G \mid g^{-1}Hg=H\}$.

$N(H)$ on suurin ryhmän $G$ aliryhmä, joka sisältää $H$:n normaalina aliryhmänään.

Katso myös Joukko, Ryhmä, Aliryhmä, Normaali aliryhmä, Stabilisaattori, Sentralisaattori.

Vektoriavaruus $V$ yli kunnan $\mathbb{R}$, jossa on määritelty normi eli kuvaus $|\cdot| \colon V \rightarrow \mathbb{R}$, joka toteuttaa seuraavat ehdot:

• $|v| \ge 0$ kaikilla $v \in V$.
• $|a||v|=|av|$ kaikilla $a \in \mathbb{R}$, $v \in V$.
• $|v+w| \le |v| + |w|$ kaikilla $v,w \in V$.

Normiavaruudessa voidaan määritellä metriikka kaavalla $d(x,y)=|x-y|$.

Katso myös Vektoriavaruus, Lipschitz-ehto, $\ell^p$-avaruus, Metrinen avaruus.

Tapa, jolla kirjoitetaan asioita käyttäen kirjaimia, numeroita ja muita merkkejä.

Sopimus siitä, mitä asiaa merkitään milläkin merkillä.

Katso myös 12 tunnin kello, Kalenteri, Tangentin neliö, Sinin neliö, Tavu, Osoite, Kaarisulkeet, Sekantin neliö, Etumerkki, Paikkajärjestelmä, Verranto, Numero, Eksponentti, Desimaalipilkku, Kanoninen, $O(f(x))$, Kreikkalaiset kirjaimet, Lyhenne, Alaindeksi, Takaliite, Yläindeksi, Rivi, Valita, Tukkimiehen kirjanpito, Äärettömyys, Etumerkillä varustettu luku, Lukujärjestelmä, Kantaluku, Asymptoottinen kasvunopeus, Binomikerroin, Alef, Sarake, Ketjumurtoluku, Kroneckerin delta, Ellipsi, Yleistetty tulo.

Määrättyjä lukuja ennemmin kuin merkkejä ja symboleja koskeva. Usein numeeriset menetelmät ovat likimääräismenetelmiä, joita käytetään, kun tarkan vastauksen löytäminen olisi liian vaikeaa tai kestäisi liian kauan.

Yksi merkeistä, joita käytetään lukujen esittämiseen. Arabialaiset numerot ovat 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9. Roomalaisiin numeroihin kuuluvat I (yksi), V (viisi), X (kymmenen), L (viisikymmentä), C (sata), D (viisisataa) ja M (tuhat). On olemassa myös monia muita numerojärjestelmiä, joita käytetään muissa maissa.

Katso myös Arabialaiset numerot, Roomalaiset numerot, Merkintätapa, Notaatio.

Jokin luvuista $0$ -- $9$. Käytetään luvussa esittämään arvoa, joka riippuu numeron paikasta. Esimerkiksi luvussa $1923$

• numero $1$ esittää lukua $1000$,
• numero $9$ esittää lukua $900$,
• numero $2$ esittää lukua $20$,
• numero $3$ esittää lukua $3$.

Katso myös Merkitsevin tai vähiten merkitsevä numero, Desimaaliluku, Benfordin laki, Kymmenjärjestelmän luku.

Selvittää äärellisen joukon alkioiden lukumäärä.

Laskemisen voi tehdä siten, että luettelee luonnollisia lukuja luvusta yksi alkaen samalla kun käy läpi joukon alkiot. Näin tulee samalla numeroineeksi joukon alkiot eli asettaneeksi ne yksi-yhteen -vastaavuuteen jonkin luonnollisten lukujen joukon alkusegmentin kanssa. Joissakin tapauksissa voi myös äärettömän joukon alkiot numeroida periaatteessa samalla tavoin, jolloin saadaan yksi-yhteen -vastaavuus niiden ja kaikkien luonnollisten lukujen välillä.

Joidenkin, mutta ei kaikkien, äärettömien joukkojen ominaisuus. Ääretöntä joukkoa sanotaan numeroituvaksi, jos sen alkiot voidaan laittaa yksi yhteen -vastaavuuteen luonnollisten lukujen kanssa. Cantor todisti ensimmäisenä, että reaalilukujen joukko ei ole numeroituva.

Ääretöntä joukkoa $X$ kutsutaan numeroituvaksi, jos on olemassa bijektio $X \to \mathbb{N}$ tai yhtäpitävästi bijektio $X \to \mathbb{Z}$.

Katso myös Cantor, Ylinumeroituva, Bijektio, $N_2$, Numeroituva yhdiste.

Numeroituva yhdiste on numeroituvan joukkojen kokoelman yhdiste. Jos siis $U_1, U_2, U_3, \dots$ ovat joukkoja, on $\bigcup_{i=1}^{\infty} U_i$ niiden numeroituva yhdiste.

Katso myös Yhdiste, Numeroituva.

Esimerkiksi virtuaalinen työ on työ, joka olisi tehty voimalla, jota ei todellisuudessa ollut olemassa.

Virtuaalinen kuva on olemassa tietokoneen muistissa, mutta ei nähtävänä.

Ei todellinen.

Verbit "osoittaa" ja "näyttää" tarkoittavat matematiikassa samaa kuin verbi "todistaa".

Katso myös Perustelu.