Matematiikan verkkosanakirja

Kaikilla reaaliluvuilla $x$ pätee Eulerin kaava \[ \exp(ix)=\cos(x)+i\sin(x). \]

Katso myös $\exp$, $\sin$, $\cos$, Kosini, $e^{x+iy}$.

Kaikilla reaaliluvuilla $x$ ja $y$ pätee \[ e^{x + i y} = e^x ( \cos(y) + i\sin(y)). \]

Katso myös $\sin$, $\cos$, Kosini, $e^{ix}$.

Neperin luku on matematiikassa usein esiintyvä vakio, jonka tarkkaa arvoa ei voida ilmaista äärellisenä desimaalilukuna. Sen likiarvo on 2,718281828.

On olemassa täsmälleen yksi reaaliluku $a$, jolle pätee $\frac{d}{dx}a^x = a^x$ kaikilla $x \in \mathbb{R}$. Tätä lukua kutsutaan Neperin luvuksi ja sitä merkitään kirjaimella $e$. Sen likiarvo on $2,718281828$.

Luvun $e$ laskemiseksi on olemassa useita kaavoja. Esimerkiksi \[ e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{1}{n!}. \]

Pätee myös \[ e = \lim_{n \to \infty} (1 + \frac{1}{n})^{n}. \]

Katso myös Vakio, Transsendenttinen luku, Hyperbolinen kosini, Hyperbolinen sini.

Toiminta $G \times X \rightarrow X$ on efektiivinen, jos kaikilla $g \in G, g \neq e$, olemassa sellainen $x \in X$, että $gx \neq x$. Toisin sanoen jokainen $g$, joka ei ole neutraalialkio, liikuttaa jotakin joukon $X$ pistettä.

Efektiivisyyden kanssa ekvivalentti ehto on se, että ehdosta $\forall x \in X gx = g'x$ seuraa $g=g'$. Efektiivinen toiminta voidaan mieltää joukon $X$ permutaatioryhmän jonkun aliryhmän toimintana.

Ehdollisen todennäköisyyden tapauksessa kysytään: Miten tapahtuman $A$ todennäköisyys muuttuu, jos saamme tietää tapahtuman $B$ sattuneen?

Silloin kun kaikki alkeistapaukset ovat yhtä todennäköisiä, on tapahtuman $A$ todennäköisyys \[ P(A) = \frac{\text{tapahtumalle } A \text{ suotuisten alkeistapausten lukumäärä }}{ \text{kaikkien alkeistapausten lukumäärä}}. \]

Lisätiedon vaikutus on, että sen saatuamme olemme kiinnostuneita ainoastaan tapahtumalle $B$ suotuisista alkeistapauksista. Tällöin todennäköisyys on \[ P(A \text{ kun } B \text{ on jo sattunut}) = \frac{ \text{tapahtumille } A \text{ ja } B \text{ suotuisten alkeistapausten lukumäärä}}{\text{tapahtumalle } B \text{ suotuisten alkeistapausten lukumäärä}}. \]

Tämä voidaan ilmaista lyhyemmin kaavalla \[ P(A \mid B) = \frac{P(A \cap B)}{P(B)}, \] missä $P(A \mid B)$ on tapahtuman $A$ todennäköisyys ehdolla, että tapahtuma $B$ on jo sattunut.

Kun $\mathbb{P}(B) \gt 0$, määritellään tapahtuman $A$ todennäköisyys ehdolla $B$ kaavalla \[ \mathbb{P}(A \mid B) = \frac{ \mathbb{P}(A \cap B)}{ \mathbb{P}(B)}. \]

Katso myös Riippumattomat tapahtumat, Todennäköisyys, Bayesin kaava, Bayesin lause, Markovin ketju.

Se, mitä vaaditaan, jotta jokin asia olisi tosi. Esimerkiksi eräs ehto sille, että nelikulmio on neliö, on että kaikki sen sivut ovat yhtä pitkiä, ja toinen ehto on, että kaikki sen kulmat ovat yhtä suuria.

Katso myös Määritelmä, Aksiooma, Lipschitz-ehto, Rajoite, Rajoitusehto, Dirichlet'n ehdot.

Looginen operaattori, joka antaa tulokseksi 'tosi', jos sen argumentti on epätosi ja 'epätosi', jos sen argumentti on tosi. Ilmaisulle EI($A$) käytetään merkintää $\neg A$ tai $\sim A$.

Katso myös Looginen operaattori.

Seuraavissa tapauksissa luvut ovat erisuuria:

$1 \neq 2,$

$5 \neq 109.$

Tässä tapauksessa luvut ovat yhtäsuuret:

$4 = 4.$

Kaksi lukua ovat erisuuria, mikäli ne eivät ole yhtäsuuria, eli toinen luku on suurempi kuin toinen.

Erisuuruusmerkkiä käytetään toisinaan ilmaisemaan, että kaksi asiaa ovat eri kokoisia, toisinaan, että ne ovat eri asioita. Yleensä tästä ei aiheudu sekaannusta, mutta esimerkiksi kaksi janaa voivat olla yhtä pitkiä olematta sama jana. Vastaava ongelma liittyy yhtä suuruusmerkkin.

$x^2 \neq x$, jos $x \neq 0$ ja $x \neq 1$.

Erisuuruusmerkillä ilmaistaan, että kaksi matemaattista oliota eivät ole samoja. Erisuuruusmerkillä voidaan myös ilmaista, että jokin yhtälö ei päde.

Olkoon $f,g \colon \mathbb{R} \rightarrow \mathbb{R}$. Tällöin $f \neq g$ tarkoittaa, että $f$ on eri funktio kuin $g$, eli $f(x) \neq g(x)$ vähintään yhdessä pisteessä $x \in \mathbb{R}$.

Jos $I$ ja $J$ ovat janoja tasossa, $I \neq J$ tarkoittaa, että $I$ on eri jana kuin $J$. Tässä tapauksessa on mahdollista, että $I$ ja $J$ ovat yhtä pitkiä. Jos $\ell$ on funktio, joka liittää janaan sen pituuden, tarkoittaa $\ell(I) \neq \ell(J)$, että janat $I$ ja $J$ ovat eri mittaiset.

Suurempi tai yhtäsuuri kuin 0.

Ei-negatiivisten reaalilukujen joukko koostuu niistä reaaliluvuista $x$, joilla $x \geq 0$. Tämä joukko sisältää luvun 0, toisin kuin aidosti positiivisten reaalilukujen joukko.

Katso myös Suurempi tai yhtäsuuri kuin, Joukko.

Taso, jossa Maan rata kiertää Auringon. Tai Auringon näennäinen vuotuinen rata Maasta katsottuna.

Katso myös Taso, Ympyrä.

Vektorikenttää $f$ sanotaan konservatiiviseksi (tai eksaktiksi), jos jokaisella umpinaisella polulla $C$ pätee \[ \int _C f \cdot d\bar{s} = 0, \] toisin sanoen, vektorikentän $f$ integraali umpinaisen polun ympäri on nolla. Tämä pätee jos ja vain jos on olemassa sellainen skalaarikenttä $\phi$, että $f = - \nabla \phi$. Skalaarikenttää $\phi$ kutsutaan vektorikentän $f$ potentiaaliksi.

Katso myös Kunta, Käyräintegraali.

Lauseketta $P(x,y)dx+Q(x,y)dy$ kutsutaan eksaktiksi differentiaaliksi, jos on olemassa sellainen funktio $f(x,y)$, että $df(x,y) = P(x,y)dx+Q(x,y)dy$. Tämä pätee täsmälleen silloin, kun \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}. \]

Katso myös Differentiaali, Osittaisderivaatta.

Kartioleikkaus voidaan määritellä niiden pisteiden $P$ joukkona, joiden etäisyys kiinteästä pisteestä $S$ on vakiosuhteessa pisteen $P$ etäisyyteen kiinteästä suorasta $N$. Tätä vakiosuhdetta kutsutaan kartioleikkauksen eksentrisyydeksi.

Ellipsin tapauksessa eksentrisyys mittaa sitä, kuinka paljon ellipsi poikkeaa ympyrästä.

Katso myös Parabelin eksentrisyys, Ellipsin eksentrisyys, Hyperbelin eksentrisyys, Ominaisuus, jonka arvot ovat jatkuvia, Kartioleikkaus.

Eksistenssikvanttori on symboli $\exists$, joka luetaan "on olemassa" tai "jollakin". Jos $P$ on ominaisuus, niin $\exists x P(x)$ tarkoittaa, että on olemassa sellainen olio, jolla on ominaisuus $P$.

Vertaa käsitteeseen "Universaalikvanttori".

Väite $\exists x (5 = 3+x)$ on tosi, koska voidaan valita $x=2$.

Väite $\exists x ( x \cdot 0 = 5)$ on epätosi, sillä ei ole olemassa lukua, joka kerrottuna nollalla antaisi tulokseksi luvun viisi.

Katso myös Universaalikvanttori.

Annetun kulman eksplementtikulma on se kulma, joka annettuun kulmaan lisättynä tuottaa $360$ asteen kulman.

Katso myös Kulma.

Jos kahden kulman summa on $360^{\circ}$, ovat kulmat toistensa eksplementtikulmia.

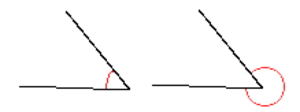
Katso myös Kulma, Kupera kulma.

Yhtälöä sanotaan eksplisiittiseksi, jos sen toinen puoli sisältää pelkän muuttujan ja tämä muuttuja ei esiinny yhtälön toisella puolella. Esimerkiksi yhtälö $a = b(c-d)+c(b+e)$ on muuttujan $a$ suhteen eksplisiittinen.

Katso myös Implisiittinen.

Luku, joka kertoo, kuinka monta kertaa jotakin lukua on kerrottava itsellään. Esimerkiksi $3^{2}$ tarkoittaa $3 \cdot 3$ eli $3$ korotettuna potenssiin $2$. Tässä $2$ on eksponentti.

Muotoa $a^b$ olevassa lausekkeessa luku $b$ on eksponentti.

Katso myös Eksponentti, Merkintätapa, Notaatio, Potenssien laskusäännöt.

Potenssiinkorotuksessa potenssin osoittava luku. Esimerkiksi potenssiinkorotuksessa $2^5$ on luku $5$ eksponentti.

Katso myös Eksponentti, Mantissa.

Lausekkeessa $a^b$ luku $a$ on korotettu potenssiin $b$. Lukua $b$ sanotaan tässä yhteydessä myös eksponentiksi ja lukua $a$ kantaluvuksi.

Eksponenttifunktio on funktio, joka korottaa luvun $e$ argumenttinsa osoittamaan potenssiin. Toisin sanoen, eksponenttifunktion arvo pisteessä $x$ on $e^{x}$. Myös merkintää $\exp(x)$ käytetään. Vakio $e \approx 2,718281828\dots $ on ns. Neperin luku.

Eksponenttifunktio on luonnollisen logaritmifunktion $\ln(x)$ käänteisfunktio.

Eksponenttifunktioiksi kutsutaan myös funktioita $a^x$, missä $a$ on mikä tahansa positiivinen reaaliluku.

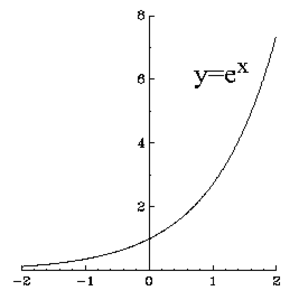
Katso myös Eksponenttifunktion yhteenlaskukaava, $\exp$, Potenssiin korottaminen, Laskutoimitus, Normaalijakauma, $\ln$, Eksponenttifunktio differentiaaliyhtälön ratkaisuna, Gaussin jakauma, Hyperbolinen kosini, Hyperbolinen sini.

Eksponenttifunktio $e^x$ voidaan määritellä differentiaaliyhtälön \[ \frac{\mathrm{d}f}{\mathrm{d}x}(x) = f(x), \quad f(0) = 1 \] yksikäsitteisenä ratkaisuna eli sinä funktiona $f(x)$, joka toteuttaa tämän differentiaaliyhtälön.

Katso myös Eksponenttifunktion derivaatta, Eksponenttifunktio, Ensimmäisen kertaluvun differentiaaliyhtälö.

\[ \frac{\mathrm{d}}{\mathrm{dx}} \mathrm{exp(x)} = \mathrm{exp(x)} . \]

Katso myös $\exp$, Eksponenttifunktio differentiaaliyhtälön ratkaisuna.

\[ \int e^x \mathrm{d}x = e^x + C. \]

Katso myös $\exp$.

Kaikilla reaaliluvuilla $x$ pätee \[ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots + \frac{x^n}{n!} + \ldots = \sum_{n=0}^{\infty} \frac{x^n}{n!}. \]

Katso myös $\exp$.

Kaikilla kompleksiluvuilla $x$ ja $y$ pätee $e^{x+y} = e^{x} e^{y}$.

Katso myös Lause, Eksponenttifunktio.

Perättäisten tapahtumien väliaikojen jakauma.

Eksponenttijakauma on jatkuva jakauma tiheysfunktiona $$f(x) = \lambda e^{-\lambda x},$$ missä $\lambda \gt 0$ on vakio. Eksponenttijakauman odotusarvo on $1 / \lambda$ js varianssi on $1 / \lambda^2$.

Eksponenttijakauma on gammajakauman erikoistapaus.

Katso myös MGF, Gammajakauma.

Käyttää funktion tunnettuja arvoja funktion arvojen arvioimiseksi sen alueen ulkopuolella, jossa funktion arvot jo tunnetaan.

Lineaarinen ekstrapolointi on kyseessä silloin, kun funktion arvioimiseksi sen arvojen oletetaan olevan suoralla.

Katso myös Interpoloida.

Päiväntasaaja on Maapallon keskellä molemmista Navoista yhtä kaukana kulkeva ympyräviiva. Päiväntasaaja jakaa Maapallon pohjoiseen ja eteläiseen pallonpuoliskoon (eli puolipalloon).

Geometriassa ekvaattori on se pyörähdyspinnan akselia vastaan kohtisuora ympyrä, joka jakaa pinnan kahteen yhtenevään osaan.

Katso myös Puolipallo.

Relaatio $\sim$ on ekvivalenssirelaatio joukossa $S$, jos

• $a \sim a$ (refleksiivisyys),
• $a \sim b \Rightarrow b \sim a$ (symmetrisyys),
• $a \sim b \mbox{ja} b \sim c \Rightarrow a \sim c$ (transitiivisuus)

ovat voimassa kaikilla $a, b, c \in S$.

Alkion $a \in S$ ekvivalenssiluokka relaation $\sim$ suhteen on joukko $\{ x \in S : x \sim a \}$.

Ekvivalenssiluokat muodostavat joukon osituksen.

Katso myös Modulaariaritmetiikka, Ositus, Joukko, Ekvivalenssirelaatio.

Joukon $S$ relaatio $R$ on ekvivalenssirelaatio, jos sillä on seuraavat kolme ominaisuutta:

- $R$ on refleksiivinen eli $a R a$ pätee kaikilla $a \in S$.

- $R$ on symmetrinen eli oletuksesta $a R b$ seuraa $b R a$ kaikilla $a, b \in S$.

- $R$ on transitiivinen eli oletuksista $a R b$ ja $b R c$ seuraa $a R c$ kaikilla $a, b, c \in S$.

Katso myös Ositus, Tekijätopologia, Ekvivalenssirelaation projektio, Ekvivalenssiluokka, Ryhmän konjugoidut alkiot.

Olkoon $R$ joukossa $X$ määritelty ekvivalenssirelaatio. Tällöin ekvivalenssirelaation liittyvä projektio on kuvaus $\pi \colon X \rightarrow X/R$, joka kuvaa jokaisen alkion $x$ sen määräämälle ekvivalenssiluokalle $[x]$.

Katso myös Kuvaus, Ekvivalenssirelaatio, Funktio.

Kaksi väitettä $A$ ja $B$ ovat ekvivalentit, jos $A$:sta voidaan todistaa $B$ ja $B$:stä voidaan todistaa $A$.

Kaksi yhtälöä ovat ekvivalentit, jos niillä on täsmälleen sama ratkaisujoukko.

Kaksi normia ovat ekvivalentit, jos ne määrittelevät saman topologian. Toisin sanoen, $\| \cdot \|_1$ ja $\| \cdot \|_2$ ovat ekvivalentit, jos on olemassa sellaiset vakiot $c$ ja $d$, että $\| x \|_1 \le c\| x \|_2$ ja $\| x \|_2 \le d\| x \|_1$ kaikilla $x$. Äärellisulotteisen vektoriavaruuden kaikki normit ovat keskenään ekvivalentteja. Ääretönulotteisessa vektoriavaruudessa voi sen sijaan olla useita eri normeja.

Polkujen ekvivalenssi: Katso käsite "Polku".

Katso myös Samanarvoiset murtoluvut, Topologia.

Poistaa muuttuja yhtälöstä tai yhtälöryhmästä, tavallisesti korvaamalla se jollakin, joka on sen kanssa yhtäpitävä.

$\ell^p$-avaruus on normiavaruus, jonka alkioita ovat äärettömät reaali- tai kompleksilukujonot $(x_1, x_2, \dots)$, joille $\sum_{i=1}^\infty |x_i|^p \lt \infty$.

Jonon $(x_1, x_2, \dots)$ normi määritellään kaavalla $$ |(x_1, x_2, \dots)|_p = (\sum_{i=1}^\infty |x_i|^p)^{1/p}.$$

Se, että yllä määritelty kaavan todella antaa normin, seuraa Hölderin epäyhtälöstä. Jos $p=\infty$, normi määritellään kaavalla $|x|_\infty = \sup_i |x_i|$.

Katso myös Vektoriavaruus, Normiavaruus, Hölderin epäyhtälö.

Kuvio, joka näyttää litistetyltä ympyrältä. Se voidaan muodostaa leikkaamalla ympyräkartio vinosti tasolla Ellipsin näköisiä kuvioita sanotaan elliptisiksi.

Ellipsi on litistetty ympyrä.

Täsmällisesti ellipsi voidaan määritellä seuraavasti. Kun kiinteät pisteet $A$ ja $B$ sekä positiivinen vakio $k$ on annettu, niin ellipsi on niiden pisteiden $P$ joukko, joilla pisteiden $A$ ja $P$ sekä pisteiden $B$ ja $P$ välisten etäisyyksien summa on vakio $k$. Pisteet $A$ ja $B$ ovat ellipsin polttopisteet.

Ellipsi voidaan myös määritellä niiden pisteiden $(x,y)$ joukkona, jotka toteuttavat yhtälön $p(x-a)^{2}+q(y-b)^{2} = r$, missä $(a,b)$ on ellipsin keskipiste ja $p$, $q$, $r$ ovat positiivisia vakioita.

Ellipsin pisintä halkaisijaa kutsutaan ellipsin isoksi akseliksi ja lyhintä halkaisijaa pieneksi akseliksi. Iso akseli ja pieni akseli ovat aina kohtisuorassa toisiaan vastaan. Jos $m$ on puolet ison akselin pituudesta ja $n$ on puolet pienen akselin pituudesta, niin ellipsin pinta-ala on $\pi mn$.

Katso myös Ympyrä, Soikio, Ovaali, Ellipsin polttopiste, Ellipsin pinta-ala, Kartioleikkaus, Ellipsin johtosuora, Elliptinen integraali.

Ellipsi tarkoittaa litistetyn ympyrän muotoisen kuvion lisäksi kolmen pisteen jonoa ($\ldots$), jolla osoitetaan, että jotakin on jätetty lauseesta tai lausekkeesta pois. Matematiikassa ellipsiä käytetään yleisesti muun muassa desimaalilukujen, summien, sarjojen ja matriisien esityksissä. Kirjoitetaan esimerkiksi \[ 3.14159 \ldots, \quad 1+2+3+ \ldots +n, \quad 1+\frac{1}{2!}+\frac{1}{3!}+ \ldots, \quad \left( \begin{array}{ccc} 1 & 0 & ... \\ 0 & 1 & ... \\ \vdots & \vdots & \vdots \end{array} \right). \]

Katso myös Merkintätapa, Notaatio.

Ellipsin eksentrisyys $e$ on $ \lt 1$ ja toteuttaa yhtälön $b^{2} = a^{2}(1-e^{2})$, missä $a$ ja $b$ ovat ellipsin puoliakselit.

Katso myös Eksentrisyys.

Jos ellipsin keskipiste on origo, eksentrisyys on $e$ ja puolipääakseli $a$ on $x$-akselin suuntainen, niin ellipsin johtosuorat ovat $x = \pm \frac{a}{e}$.

Katso myös Ellipsi, Suora.

Jos ellipsin keskipiste on $(a,b)$, ja x-suuntaisen akselin pituus on $c$, ja y-suuntaisen akselin pituus on $d$, on ellipsillä parametrisoitu yhtälö $x=a+c\cos(t), y=b + d\sin(t)$.

Katso myös Ellipsin yhtälö.

Jos ellipsin ison akselin pituus on $2a$ ja pikkuakselin pituus on $2b$, niin ellipsin pinta-ala on $\pi ab$. Huomaa, että jos $a=b$, niin ellipsi on ympyrä ja saadaan tavallinen ympyrän pinta-alan kaava.

Katso myös Ympyrän pinta-ala, Ellipsi.

Olkoot $A$ ja $B$ kaksi tason pistettä. Niiden pisteiden $P$ joukko, joilla pisteiden $A$ ja $P$ sekä pisteiden $B$ ja $P$ välisten etäisyyksien summa on vakio, on ellipsi. Pisteet $A$ ja $B$ ovat ellipsin polttopisteet.

Jos ellipsin keskipiste on $(0,0)$, eksentrisyys on $e$ ja iso akseli on $x$-akselin suuntainen sekä pituudeltaan $2a$, niin ellipsin polttopisteet ovat $(ae,0)$ ja $(-ae,0)$.

Katso myös Piste, Ellipsi.

Jos ellipsin keskipiste on $(0,0)$ ja sen toinen akseli on $x$-akselin suuntainen ja pituudeltaan $2a$ ja toinen akseli $y$-akselin suuntainen ja pituudeltaan $2b$, niin ellipsin yhtälö on \[ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1. \]

Katso myös Kartioleikkauksen yhtälö, Ellipsin parametrisoitu yhtälö, Yhtälö.

Kolmiulotteinen kappale, jonka kaikki tasoleikkaukset ovat ellipsejä.

Ellipsoidilla on kolme symmetria-akselia. Nämä ovat laskevassa pituusjärjestyksessä ellipsoidin isoakseli, keskiakseli ja pikkuakseli.

Jos ellipsoidin keskipiste on origo ja sen akselit ovat $x$-, $y$- ja $z$-akselien suuntaiset, niin sen yleinen yhtälö on \[\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1.\]

Katso myös Kappale, Pyörähdysellipsoidi.

Ellipsoidin, jonka ison akselin, keskiakselin ja pienen akselin pituudet ovat $2a$, $2b$ ja $2c$, tilavuus on $\frac{4}{3} \pi abc$.

Riemannin geometria on geometria, jossa kahden pisteen välisen etäisyyden antaa Riemannin etäisyysfunktio tavallisen Pythagoraan etäisyysfunktion sijaan. Riemannin geometriaa voi ajatella pallon pintana, jossa "suorat" ovat ympyröitä pallon pinnalla. Tällainen geometria on tärkeässä osassa yleisessä suhteellisuusteoriassa.

Riemannin geometriaa kutsutaan myös elliptiseksi geometriaksi.

Katso myös Metriikka.

Integraali muotoa \[ \int f ( x, \sqrt{R} ) dx, \] missä $R$ on muuttujan $x$ kolmannen tai neljännen asteen polynomi ja $f$ on argumenttiensa rationaalifunktio.

Kukin elliptinen integraali voidaan kirjoittaa jonkin alkeisfunktion monikertojen ja elliptisten integraalien kolmen perustyypin summana.

Elliptisiä integraaleja käytettiin ensimmäisen kerran etsittäessä ellipsin ympärysmittaa.

Katso myös Ellipsi, Integraali, Kuutiollinen polynomi, Kolmannen asteen polynomi, Neljännen asteen polynomi, Rationaalilauseke, Rationaalifunktio, Ensimmäisen lajin elliptinen integraali, Toisen lajin elliptinen integraali, Kolmannen lajin elliptinen integraali.

Struktuurin (ryhmän, renkaan, jne.) $G$ endomorfismi on homomorfismi $G \rightarrow G$.

Katso myös Homomorfismi, Lineaarikuvaus, Automorfismi, Morfismi, Lineaarimuunnos.

Diofantoksen yhtälö on yhtälö, jossa ratkaistavat tuntemattomat ovat kokonaislukuja. Ensimmäisen asteen eli lineaarinen Diofantoksen yhtälö on sellainen Diofantoksen yhtälö, jossa muuttujia on vain laskettu yhteen ja kerrottu vakioilla, ei kerrottu keskenään eikä korotettu mihinkään potenssiin. Esimerkiksi $x+y = 5$ on ensimmäisen asteen Diofantoksen yhtälö, mutta $x^{2}+y = 1$ ei ole.

Katso myös Diofantoksen yhtälö.

Differentiaaliyhtälö, jossa esiintyy tuntemattoman funktion ensimmäinen derivaatta, mutta ei korkeampia derivaattoja. Esimerkiksi $f'(x) = f(x)$ on ensimmäisen kertaluvun differentiaaliyhtälö.

Katso myös Differentiaaliyhtälö, Eksponenttifunktio differentiaaliyhtälön ratkaisuna.

Palautuskaava, jossa jonon $(u_n)$ jäsen $u_n$ määritellään sitä jonossa edeltävän jäsenen $u_{n-1}$ avulla. Esimerkiksi \[ u_{n} = (1 + 2u_{n-1})(2 - 3u_{n-1}) \] on ensimmäisen kertaluvun palautuskaava, mutta \[ u_{n} = 1 + 2u_{n-1} + 3u_{n-2} \] ei ole.

Katso myös Ensimmäisen kertaluvun rekursioyhtälön ratkaisu, Palautuskaava.

Ensimmäisen kertaluvun rekursioyhtälön $u_{n+1}=au_{n}+f(n)$ ratkaisut ovat \[ \left \{ \begin{array}{cc} u_n = a^n u_0, & f(n)=0 \\ u_n = A a^n + v_n & f(n) \neq 0 \end{array} \right , \] kun $v_n$ on joku yksittäinen ratkaisu. Tämä pätee, kun $a \neq 1$. Kun $a=1$, pätee \[ u_n = u_0 + \sum _{i=0} ^{n-1} f(i) . \]

Katso myös Ratkaisu, Palautuskaava, Ensimmäisen kertaluvun palautuskaava.

Elliptinen integraali muotoa \[ \int_{0}^{x} \frac{dt}{\sqrt{(1-t^2)(1-k^2 t^2)}}, \] missä $k$ on elliptinen moduuli.

Katso myös Elliptinen integraali.

Entropia on systeemin epäjärjestyksen määrän mitta. Entropia liittyy systeemin pyrkimykseen päätyä tilaan, jossa kaikenlaiset erot ovat tasoittuneet. Hyvin järjestäytyneen, harvoin esiintyvän tilan entropia on siis pieni, kun taas järjestäytymättömän, usein esiintyvän tilan entropia on suuri.

Termodynamiikan toisen päälauseen mukaan entropian määrä maailmankaikkeudessa pyrkii keskimäärin aina lisääntymään, toisin sanoen luonto siirtyy järjestäytyneistä tiloista vähemmän järjestäytyneisiin tiloihin (kappaleet kuluvat ja hajoavat, kuumat kappaleet jäähtyvät ja kylmät lämpenevät ympäristön lämpötilaan, ...).

Surjektiivinen homomorfismi.

Katso myös Homomorfismi, Morfismi.

Episykliksi kutsutaan sitä ympyrää, joka episykloidia piirrettäessä vierii pitkin toisen ymyrän kehää.

Katso myös Ympyrä, Episykloidi.

Vierintäkäyrä, jonka ympyrän kehän kiinnitetty piste piirtää tämän ympyrän vieriessä toisen kiinnitetyn ympyrän kehää pitkin. Jos näiden kahden ympyrän ympärysmitat ovat verrannolliset, niin vierintäkäyrä on suljettu ja sykloidin ja kiinnitetyn ympyrän leikkauspisteiden lukumäärä on äärellinen.

Katso myös Episykli, Pistevierintäkäyrä.

Kreikan aakkoston kirjain $\epsilon$ (pieni kirjain).

Pientä epsilonia käytetään usein analyysissä merkitsemään suuretta, joka voi saada mielivaltaisen pieniä positiivisia arvoja.

Katso myös Kreikkalaiset kirjaimet.

Symboleja $\epsilon$ ja $\delta$ käytetään yleisesti analyysissä esittämään lukuja, jotka lähestyvät nollaa. Epsilon-delta- analyysillä viitataan usein tilanteisiin, joissa molemmat luvut lähestyvät nollaa samanaikaisesti.

Katso myös Analyysi, Raja-arvo.

Ei jatkuva. Funktiota sanotaan epäjatkuvaksi jossakin pisteessä, jos sen arvo muuttuu äkillisesti (eli hyppää) kyseisessä pisteessä. Tällaisessa pisteessä on funktion kuvaajassa aukko.

Katso myös Jatkuva, Paloittain jatkuva, Jatkuvuus.

Murtoluku, jonka osoittaja on suurempi kuin nimittäjä, esimerkiksi 4/2 tai 22/7.

Katso myös Osoittaja, Aito murtoluku, Murtoluku, Nimittäjä.

Integraali, jossa toinen tai molemmat integroimisrajat ovat äärettömiä tai integroitavan funktion arvo jossakin integroimisvälin pisteessä on ääretön tai määrittelemätön.

Katso myös Integraali.

Nopan sanotaan olevan epäreilu, jos jokaisen silmäluvun saaminen ei ole yhtä todennäköistä.

Jos monen nopanheiton jälkeen on paljon kolmosia ja viitosia, mutta vähän muita silmälukuja, on syytä epäillä, että noppa ei ole symmetrinen vaan epäreilu ja harhainen.

Ei reilu; harhainen. Mahdolliset alkeistapaukset eivät ole yhtä todennäköisiä.

Katso myös Harhainen, Reilu, Harhaton.

Kuvion, jolla ei ole symmetriaa, sanotaan olevan epäsymmetrinen.

Katso myös Symmetria.

Epäsäännöllinen monikulmio on monikulmio, joka ei ole säännöllinen. Vastaavasti, mikä tahansa epäsäännöllinen muoto tai olio on muoto tai olio, joka ei ole säännöllinen.

Katso myös Säännöllinen.

$4 \times 4$-epätaikaneliö on neliö, johon luvut 1 -- 16 on järjestetty niin, että neljän rivin, neljän sarakkeen ja kahden lävistäjän lukujen summat muodostavat kymmenen peräkkäisen kokonaisluvun jonon.

Vastaavalla tavalla määriteltyjä $2 \times 2$ tai $3\times 3$-kokoisia epätaikaneliöitä ei ole olemassa, mutta suurempikokoisia epätaikaneliöitä on olemassa useita, esimerkiksi \[ \begin{array}{rrrr} 1 &13& 3& 12 \\ 15 & 9& 4& 10 \\ 7 & 2 &16 & 8 \\ 14 & 6& 11 & 5 \end{array} \]

Katso myös Taikaneliö.

Ei tarkka.

Toden vastakohta.

Katso myös Looginen ominaisuus, Epätosi propositiolause, Falsum.

Symbolia $\bot$ ("falsum") käytetään usein logiikassa merkitsemään propositiolausetta, joka on määritelmän mukaan aina epätosi.

Katso myös Epätosi, Väärä.

Väittämä kahdesta luvusta tai lukumäärästä, joita verrataan toisiinsa. Väittämä kertoo, että luvut tai lukumäärät eivät ole yhtä suuria tai että toinen niistä on suurempi tai pienempi kuin toinen.

Erityisiä merkkejä käytetään osoittamaan asioita, jotka ovat yhtä suuria ($=$), suurempia ($>$), pienempi ($<$), yhtä suuria tai suurempia ($\ge$) tai yhtä pieniä tai pienempiä ($\le$) kuin jokin toinen asia.

Esimerkiksi $8<9$, $7>5$, $12<15$, $6 = 3+3$.

Katso myös Algebra, Kolmioepäyhtälö, Lisääminen puolittain epäyhtälöön, Epäyhtälön kertominen puolittain, Minkowskin epäyhtälö, Chebyshevin epäyhtälö, Jensenin epäyhtälö, Boolen epäyhtälö, Markovin epäyhtälö, Hölderin epäyhtälö, Aritmeettisen ja geometrisen keskiarvon välinen epäyhtälö, Cauchy-Schwarzin epäyhtälö, Rajoite, Rajoitusehto, Yhtäsuuruus.

Jos $x0$, niin $xa

Jos $xya$.

Katso myös Lisääminen puolittain epäyhtälöön, Erisuuruus, Suurempi kuin, Lause, Pienempi kuin, Epäyhtälö.

Lyhenne englannin sanasta equation (yhtälö).

Katso myös Lyhenne, Yhtälö.

Menetelmä alkulukujen löytämiseen. Sen keksi kreikkalainen matemaatikko Eratosthenes noin 230 eKr. Valitaan joukko luonnollisia lukuja ja poistetaan niistä luvut, jotka ovat jaollisia luvulla 2, paitsi luku 2. Seuraavaksi poistetaan luvut, jotka ovat jaollisia luvulla 3, paitsi luku 3, sitten luvulla 5 jaolliset luvut (paitsi 5), sitten 7:llä jaolliset (paitsi 7), sitten 11:llä jaolliset (paitsi 11), jne. Kun on poistettu kaikkien joukon suurimman luvun neliöjuurta pienempien alkulukujen monikerrat, joukossa jäljellä olevat luvut ovat alkulukuja.

Pál Erdös (1913-1996) oli unkarilainen matemaatikko. Hän teki enimmäkseen töitä sellaisten, yleensä lukuteorian ja kombinatoriikan, ongelmien parissa, joiden esittäminen on helppoa, mutta ratkaiseminen vaikeaa. Hän oli erittäin tuottelias ja kirjoitti paitsi yksin myös yhdessä monien muiden kanssa suuren määrän tutkimuksia. Tästä on saanut alkunsa Erdös-luvun käsite: Matemaatikon Erdös-luku on yksi suurempi kuin hänen kirjoituskumppaniensa pienin Erdös-luku. Kaikkien yhdessä Erdösin kanssa tutkimuksen kirjoittaneiden Erdös-luku on 1, joten heidän kirjoituskumppaniensa Erdös-luku on 2, jne. Erdösillä ei ollut omaa kotia, vaan hän kantoi vähäisen omaisuutensa matkalaukussaan ja matkusti ympäri maailmaa asuen matemaatikkotuttaviensa luona. Saapuessaan hän ilmoitti: "Aivoni ovat avoinna." Tällä hän tarkoitti olevansa valmis tekemään matematiikkaa.

Merkintä $erf(z)$ tarkoittaa virhefunktiota \[ \frac{2}{\sqrt{\pi}} \int_{0}^{z} e^{-s^2} ds. \]

Katso myös Lyhenne, Integraali, Virhefunktio.

Erikoinen pallonpinta on differentiaalimonisto, joka on homeomorfinen moniston $S^n$ kanssa (kun $S^n$:lle oletetaan sen tavallinen differentioituva struktuuri), mutta ei diffeomorfinen sen kanssa.

Joukot $A$ ja $B$ ovat erilliset eli pistevieraat, jos niiden leikkaus on tyhjä eli ei ole olemassa alkiota, joka kuuluu molempiin joukkoihin. Tällöin merkitään $A \cap B = \emptyset$. Yleisemmin on joukkojen kokoelma $C$ erillinen, jos mitkä tahansa kaksi $C$:n eri joukkoa ovat pistevieraat.

Katso myös Yhdiste, Jordanin käyrälause, Joukko.

Joukon $X$ permutaatioita $A$ ja $B$ kutsutaan erillisiksi, jos kaikilla $x \in X$ pätee joko $A(x) = x$ tai $B(x) = x$. Huomaa, että tällöin $A \circ B = B \circ A$ eli permutaatiot $A$ ja $B$ kommutoivat.

Esimerkiksi permutaatiot $(0,1,2,3) \mapsto (1,0,2,3)$ ja $(0,1,2,3) \mapsto (0,1,3,2)$ ovat erilliset.

Katso myös Permutaatio.

Jos $E_{1}$ ja $E_{2}$ ovat erillisiä tapauksia eli $ \mathrm{p(E}_1 \cap \mathrm{E}_2 ) = \mathrm{p(} \emptyset ) = 0. $ niin $ \mathrm{p(E}_1 \cup \mathrm{E}_2 ) = \mathrm{p(E}_1 ) + \mathrm{p(E}_2 ) $.

Jos $E_{1}, E_{2}, ..., E_{n}$ ovat parittain erillisiä ja jos lisäksi jokainen perusjoukon S alkio kuuluu johonkin kokoelman joukkoon $E_{k}$, niin $p(E_{1})+p(E_{2})+...+p(E_{n})$ = 1.

Katso myös Komplementin todennäköisyys, Yhdisteen todennäköisyys.

Kolmio, jossa kaikki sivut ovat eripituisia ja kaikki kulmat erisuuruisia.

Katso myös Kolmio, Tasasivuinen kolmio, Tylppäkulmainen kolmio.

Seuraavissa tapauksissa luvut ovat erisuuria:

$1 \neq 2,$

$5 \neq 109.$

Tässä tapauksessa luvut ovat yhtäsuuret:

$4 = 4.$

Kaksi lukua ovat erisuuria, mikäli ne eivät ole yhtäsuuria, eli toinen luku on suurempi kuin toinen.

Erisuuruusmerkkiä käytetään toisinaan ilmaisemaan, että kaksi asiaa ovat eri kokoisia, toisinaan, että ne ovat eri asioita. Yleensä tästä ei aiheudu sekaannusta, mutta esimerkiksi kaksi janaa voivat olla yhtä pitkiä olematta sama jana. Vastaava ongelma liittyy yhtä suuruusmerkkin.

$x^2 \neq x$, jos $x \neq 0$ ja $x \neq 1$.

Erisuuruusmerkillä ilmaistaan, että kaksi matemaattista oliota eivät ole samoja. Erisuuruusmerkillä voidaan myös ilmaista, että jokin yhtälö ei päde.

Olkoon $f,g \colon \mathbb{R} \rightarrow \mathbb{R}$. Tällöin $f \neq g$ tarkoittaa, että $f$ on eri funktio kuin $g$, eli $f(x) \neq g(x)$ vähintään yhdessä pisteessä $x \in \mathbb{R}$.

Jos $I$ ja $J$ ovat janoja tasossa, $I \neq J$ tarkoittaa, että $I$ on eri jana kuin $J$. Tässä tapauksessa on mahdollista, että $I$ ja $J$ ovat yhtä pitkiä. Jos $\ell$ on funktio, joka liittää janaan sen pituuden, tarkoittaa $\ell(I) \neq \ell(J)$, että janat $I$ ja $J$ ovat eri mittaiset.

Väittämä kahdesta luvusta tai lukumäärästä, joita verrataan toisiinsa. Väittämä kertoo, että luvut tai lukumäärät eivät ole yhtä suuria tai että toinen niistä on suurempi tai pienempi kuin toinen.

Erityisiä merkkejä käytetään osoittamaan asioita, jotka ovat yhtä suuria ($=$), suurempia ($>$), pienempi ($<$), yhtä suuria tai suurempia ($\ge$) tai yhtä pieniä tai pienempiä ($\le$) kuin jokin toinen asia.

Esimerkiksi $8<9$, $7>5$, $12<15$, $6 = 3+3$.

Katso myös Algebra, Kolmioepäyhtälö, Lisääminen puolittain epäyhtälöön, Epäyhtälön kertominen puolittain, Minkowskin epäyhtälö, Chebyshevin epäyhtälö, Jensenin epäyhtälö, Boolen epäyhtälö, Markovin epäyhtälö, Hölderin epäyhtälö, Aritmeettisen ja geometrisen keskiarvon välinen epäyhtälö, Cauchy-Schwarzin epäyhtälö, Rajoite, Rajoitusehto, Yhtäsuuruus.

Määrä, jonka jokin suure on suurempi tai pienempi kuin toinen suure. Verrattaessa keskenään muita asioita erotukset saattaisivat kertoa jonkin asian olevan isompi tai pienempi, paksumpi tai ohuempi, pitempi tai lyhyempi, kylmempi tai lämpimämpi, korkeampi tai matalampi jne. Usein ollaan kiinnostuneita annetun lukujonon lukujen välisten erotusten muodostamasta jonosta.

Katso myös Erotusjono, Aritmeettisen jonon erotus, Vähennyslasku, Vähentäminen, Verrata, Vandermonden determinantti.

Annetun jonon erotusten jono on jono, joka muodostetaan jonon kahden peräkkäisen jäsenen erotuksista. Aritmeettisen jonon erotusten jono on vakiojono. Kolmiolukujen jonon 1, 3, 6, 10, $\dots$ erotusten jono on 1, 2, 3, 4, $\dots$

Katso myös Erotus, Aritmeettinen jono, Kolmioluku, Jono.

Relaatio $\le \subset A \times A$ on joukon $A$ esijärjestys, jos se toteuttaa ehdot

• $a \le a$ kaikilla $a \in A$
• Jos $a \le b$ ja $b \le c$ niin $a \le c$ kaikilla $a,b,c \in A$.

Vertaa osittaisjärjestykseen.

Katso myös Osittaisjärjestys, Osittainen järjestys.

Estimaattorin arvo otoksessa eli otoksen perusteella tehty arvio perusjoukon (jakauman) tuntemattomalle parametrille.

Estimaattia merkitään yleensä roomalaisella kirjaimella (esimerkiksi $m$ ja $s$), kun taas tuntematonta estimoitavaa parametria merkitään kreikkalaisella kirjaimella (esimerkiksi $\mu$ ja $\sigma$). Toisinaan estimaattia merkitään kirjoittamalla kreikkalaisen kirjaimen päälle hattu (esimerkiksi $\hat\mu$ ja $\hat{\sigma^2}$).

Katso myös Tarkkuus, Pyöristys, Interpoloida.

Kreikkalainen kirjain $\eta$ (pieni kirjain) tai $H$ (iso kirjain), lausutaan "eeta".

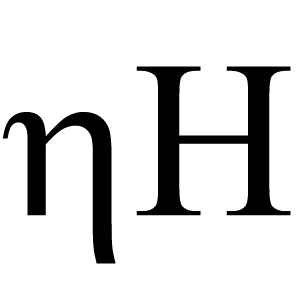
Katso myös Kreikkalaiset kirjaimet.

Luvun sanotaan olevan etumerkillä varustettu, jos sen edessä on plus- tai miinusmerkki.

Luku, jonka edessä on plus- tai miinusmerkki.

Esimerkiksi $-5$, $+11$, $-9$, $+14$, $-6$, $+56$, $-2$, $\dots$

Katso myös Merkintätapa, Notaatio, Reaaliluku.

Laskimen näppäin, joka vaihtaa näytöllä näkyvän luvun negatiivisesta positiiviseksi tai päin vastoin. Sitä merkitään yleensä $\pm$ tai $+/-$.

Katso myös Laskin.

Joko plus ($+$) tai miinus ($-$). Kertoo, onko luku positiivinen vai negatiivinen.

Katso myös Plus, Merkintätapa, Notaatio, Miinusmerkki.

Kahden olion välinen etäisyys kertoo, kuinka kaukana ne ovat toisistaan.

Katso myös Pisteen etäisyys suorasta, Pisteen etäisyys tasosta.

Tason pisteiden $(x,y)$ ja $(u,v)$ välinen etäisyys on \[ \sqrt{(x-u)^{2} + (y-v)^{2}}. \] Avaruuden pisteiden $(x,y,z)$ ja $(u,v,w)$ välinen etäisyys on \[ \sqrt{(x-u)^{2}+(y-v)^{2}+(z-w)^{2}}. \]

Katso myös Lause, Pisteen etäisyys suorasta, Analyyttinen tasogeometria, Pisteen etäisyys tasosta, Analyyttinen avaruusgeometria.

Eukleideen aksioomat ovat ne viisi perusoletusta, joiden varaan Eukleiden rakensi geometriansa. Ne ovat seuraavat:

• Mitkä tahansa kaksi pistettä voidaan yhdistää janalla.
• Jokaista janaa voidaan jatkaa loputtomasti kumpaankin suuntaan.
• Kaikki suorat kulmat ovat yhteneviä.
• Kun piste ja jana on annettu, on olemassa täsmälleen yksi ympyrä, jonka keskipiste ja säde nämä ovat.
• Annetun pisteen kautta kulkee täsmälleen yksi annetun suoran suuntainen suora.

Viimeinen aksiooma tunnetaan myös Playfairin aksioomana. Se on riippumaton muista aksioomista ja sitä voidaan muuttaa, jolloin saadaan erilaisia, epäeuklidisia geometrioita. Alun perin se esitettiin erilaisessa, mutta yhtäpitävässä, muodossa:

Jos on annettu suorat $A$ ja $B$ sekä ne leikkaava suora $C$ ja jos suoran $C$ samalle puolelle muodostuneiden sisäkulmien summa on pienempi kuin kaksi suoraa kulmaa, niin suorat $A$ ja $B$ leikkaavat toisensa tällä puolella suoraa $C$.

Katso myös Aksiooma.

Menetelmä, jolla löydetään kahden eri luvun suurin yhteinen tekijä:

1) Jaa suurempi numero pienemmällä.

2) Jos jako menee tasan, niin suurin yhteinen tekijä on pienempi luku. Muussa tapauksessa lukujen suurin yhteinen tekijä on sama kuin pienemmän luvun ja jakojäännöksen suurin yhteinen tekijä, joten toista kohta 1) näillä kahdella luvulla.

Etsitään esimerkiksi $\mathrm{syt}(17,20)$:

Koska $20/17 = 1 + 3/17$ on jakojäännös $3$, joten $\mathrm{syt}(17,20) = \mathrm{syt}(17,3)$.

Koska $17/3 = 5 + 2/3$, on jakojäännös $2$, joten $\mathrm{syt}(17,20) = \mathrm{syt}(3,2)$.

Koska $3/2 = 1 + 1/2$, on jakojäännös $1$, joten $\mathrm{syt}(17,20) = \mathrm{syt}(2,1)$.

Koska $2/1 = 2$, menee jako tasan, joten $\mathrm{syt}(17,20) = 1$.

Katso myös Algoritmi, Suurin yhteinen tekijä.

Eukleideen aksioomat ovat ne viisi perusoletusta, joiden varaan Eukleiden rakensi geometriansa. Ne ovat seuraavat:

• Mitkä tahansa kaksi pistettä voidaan yhdistää janalla.
• Jokaista janaa voidaan jatkaa loputtomasti kumpaankin suuntaan.
• Kaikki suorat kulmat ovat yhteneviä.
• Kun piste ja jana on annettu, on olemassa täsmälleen yksi ympyrä, jonka keskipiste ja säde nämä ovat.
• Annetun pisteen kautta kulkee täsmälleen yksi annetun suoran suuntainen suora.

Viimeinen aksiooma tunnetaan myös Playfairin aksioomana. Se on riippumaton muista aksioomista ja sitä voidaan muuttaa, jolloin saadaan erilaisia, epäeuklidisia geometrioita. Alun perin se esitettiin erilaisessa, mutta yhtäpitävässä, muodossa:

Jos on annettu suorat $A$ ja $B$ sekä ne leikkaava suora $C$ ja jos suoran $C$ samalle puolelle muodostuneiden sisäkulmien summa on pienempi kuin kaksi suoraa kulmaa, niin suorat $A$ ja $B$ leikkaavat toisensa tällä puolella suoraa $C$.

Katso myös Aksiooma.

Rengas $R$, jossa voidaan määritellä jakolaskualgoritmi. Toisin sanoen, jos $\alpha, \beta \in R$ ja $\beta \neq 0$, niin on olemassa sellainen $\gamma \in R$, että $N (\alpha - \beta \gamma) \lt N (\beta)$ pätee sopivalla renkaan $R$ normilla $N$.

Katso myös Rengas, Gaussin kokonaisluvut, Gaussin luvut.

Eukleides (n. 300 - 260 eKr.) oli kreikkalainen matemaatikko ja kuuluisa geometrian töistään ja erityisesti kirjastaan Alkeet.

Hän laati pisteitä, suoria ja tasoja käsittelevän geometrian järjestelmän tiettyjen oletusten varaan. Nämä oletukset ovat seuraavat:

• Mitkä tahansa kaksi pistettä voidaan yhdistää janalla.
• Jokaista janaa voidaan jatkaa loputtomasti kumpaankin suuntaan.
• Kaikki suorat kulmat ovat yhteneviä.
• Kun piste ja jana on annettu, on olemassa täsmälleen yksi ympyrä, jonka keskipiste ja säde nämä ovat.
• Annetun pisteen kautta kulkee täsmälleen yksi annetun suoran suuntainen suora.

Eukleides (n. 300--260 eKr.) oli se kreikkalainen matemaatikko, joka kirjoitti kuuluisan geometrian oppikirjan Alkeet. Hän kuvaili tässä kirjassaan taso- ja avaruusgeometrian säännöt ja työskentelymenetelmät, jotka ovat yhä nykyäänkin käytössä ja joita ei kyseenalaistettu kuin vasta 1800-luvun lopulla.

Alkeissa Eukleides todisti monia tärkeitä tuloksia, kuten Pythagoraan lauseen ja sen tosiasian, että alkulukuja on ääretön määrä, Platonin monitahokkaiden ominaisuudet, jne.

Katso myös Euklidinen geometria.

Eukleidekseen liittyvä. Erityisesti geometrisia olioita saatetaan kutsua euklidisiksi, jos ne on määritelty euklidisessa avaruudessa tai euklidisella tasossa eli tavallisessa "litteässä" tasossa, jossa euklidisen geometrian aksioomat ovat voimassa.

Katso myös Euklidinen geometria.

$n$-ulotteinen euklidinen avaruus on kaikkien sellaisten $n$-alkioisten vektorien joukko, joiden jokainen alkio on reaaliluku.

$n$-ulotteista euklidista avaruutta merkitään symbolilla $\mathbb{R}^{n}$.

Euklidinen avaruus on sekä vektoriavaruus että sisätuloavaruus.

Katso myös Vektoriavaruus, Sisätuloavaruus.

Tavallinen tason tai avaruuden geometria. On olemassa myös muunlaisia geometrioita, jotka tutkivat suorien ja pisteiden ominaisuuksia pallon pinnalla, satulapinnalla tai avaruudessa, joka on samalla tavoin kaareva.

Katso myös Kulma, Eukleides, Euklidinen, Ympyrä, Monikulmio, Suora, Geometria, Aksiomaattinen geometria, Kuvio.

Avaruudessa $\mathbb{R}^n$ määritellään euklidinen normi asettamalla \[ \| (x_1, \dots, x_n) \| = (x_1 ^2 + \ldots + x_n^2)^{1/2}. \] Euklidinen normi antaa pisteen tavallisen etäisyyden origosta.

Yleisemmin euklidinen normi voidaan määritellä sisätuloavaruudessa kaavalla $\| v \| = ( v \cdot v)^{1/2}$.

Katso myös Pistetulo, Skalaaritulo, Sisätulo, Frobeniuksen normi.

Rengas $R$, jossa voidaan määritellä jakolaskualgoritmi. Toisin sanoen, jos $\alpha, \beta \in R$ ja $\beta \neq 0$, niin on olemassa sellainen $\gamma \in R$, että $N (\alpha - \beta \gamma) \lt N (\beta)$ pätee sopivalla renkaan $R$ normilla $N$.

Katso myös Rengas, Gaussin kokonaisluvut, Gaussin luvut.

Euklidinen taso on reaalilukujen järjestettyjen parien muodostama joukko, jossa kahden pisteen välinen etäisyys on niiden euklidinen etäisyys. Tason pisteitä voidaan ajatella vektoreina, joilla on kaksi komponenttia. Euklidista tasoa merkitään $\mathbf{R}^{2}$.

Euklidinen taso on euklidisen avaruuden erikoistapaus, kaksiulotteinen euklidinen avaruus.

Katso myös Taso.

Euler-Mascheronin vakio $\gamma$ on \[ \gamma = \lim _{n \to \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln(n) \right). \] Sen arvo on likimain $0.5772156649 \ldots$.

Euler-Mascheronin vakio tulee esille monien integraalien yhteydessä. Sitä, onko Eulerin vakio rationaaliluku vai irrationaaliluku, ei tiedetä.

Katso myös Vakio.

Eulerin funktio $\varphi(n)$ antaa niiden positiivisten kokonaislukujen $k$ määrän, jotka ovat pienempiä kuin $n$ ja joilla ei ole yhteisiä tekijöitä luvun $n$ kanssa eli $\mathrm{syt}(k,n) = 1$. Eulerin funktio on multiplikatiivinen eli \[ \varphi(mn) = \varphi(m)\varphi(n) \] on voimassa kaikilla $m,n$, joilla $\mathrm{syt}(m,n) = 1$.

Katso myös 15, Viisitoista, Modulaariaritmetiikka, Funktio, Kuvaus, Kokonaisluku, Eulerin lause, Fermat-Eulerin lause.

Kaava $e^{ix} = \cos x + i \sin x$, missä $i$ on imaginaariyksikkö eli luvun $-1$ neliöjuuri. Erikoistapauksena saadaan $e^{i\pi} = -1$.

Katso myös Lause, Kompleksiluku.

Eulerin kierros on sellainen Eulerin kulku, joka päättyy samaan pisteeseen kuin josta se alkoi.

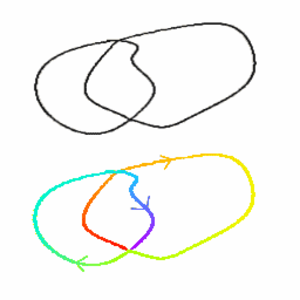
Katso myös Königsbergin sillat, Eulerin kulku.

Eulerin kulku annetussa verkossa on sellainen kulku, jossa jokainen verkon viiva esiintyy täsmälleen kerran.

Katso myös Eulerin kierros, Verkkoteoria, Verkko.

Jos $n$ on luonnollinen luku ja $a$ on sellainen kokonaisluku, että $\mathrm{syt}(n,a) =1$, niin $a^{\varphi(n)}-1$ on jaollinen luvulla $n$. Tässä $\varphi(n)$ on Eulerin $\varphi$-funktio.

Katso myös Keskenään jaottomat luvut, Lause, Eulerin $\varphi$-funktio, Fermat'n pieni lause.

Eulerin lukuja eli sekanttilukuja ovat luvut $E_i$, jotka esiintyvät funktioiden $\mathrm{sech}(x)$ ja $\mathrm{sec}(x)$ potenssisarjakehitelmissä \[ \mathrm{sech}(x) = 1 - \frac{E_1}{2!}x^2 + \frac{E_2}{4!}x^4 - \frac{E_3}{6!}x^6 + \ldots \] ja \[ \mathrm{sec}(x) = 1 + \frac{E_1}{2!}x^2 + \frac{E_2}{4!}x^4 + \frac{E_3}{6!}x^6 + \ldots. \]

Katso myös $\sec$, Potenssisarja, $\sech$.

Eulerin menetelmä on yksinkertainen, mutta hitaasti suppeneva, menetelmä differentiaaliyhtälön $\frac{dy}{dx} = f(x,y)$, $y(x_0) = y_0$, numeeriseksi ratkaisemiseksi: Olkoon $h$ positiivinen vakio. Lähdetään alkuehdosta $y(x_0) = y_0$ ja määritellään rekursiivisesti \[ x_{i+1} = x_i + h, \quad y_{i+1} = y_i + h f(x_i, y_i). \] Tällöin differentiaaliyhtälön ratkaisun arvo pisteessä $x_i$ on likimain $y_i$.

Kolmion kärjistä ortosentriin piirrettyjen janojen keskipisteitä kutsutaan Eulerin pisteiksi.

Katso myös Ortosentri, Feuerbachin ympyrä, Yhdeksän pisteen ympyrä.

Kolmion ortosentri $H$, painopiste $G$, ympäripiirretyn ympyrän keskipiste $O$ ja yhdeksän pisteen ympyrän keskipiste $N$ sijaitsevat samalla suoralla. Tätä suoraa kutsutaan Eulerin suoraksi. Tällä suoralla pätee \[ OG : GN : NH = 2 : 1 : 3. \]

Katso myös Ortosentri, Kolmion ympäri piirretyn ympyrän keskipiste, Painopiste.

Euler-Mascheronin vakio $\gamma$ on \[ \gamma = \lim _{n \to \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln(n) \right). \] Sen arvo on likimain $0.5772156649 \ldots$.

Euler-Mascheronin vakio tulee esille monien integraalien yhteydessä. Sitä, onko Eulerin vakio rationaaliluku vai irrationaaliluku, ei tiedetä.

Katso myös Vakio.

Jos monitahokkaassa ei ole aukkoja (eli se on yhdesti yhtenäinen), niin pätee Eulerin lauseeksikin kutsuttu yhtälö \[ V - E + F = 2, \] missä $V$ on monitahokkaan kärkien, $E$ särmien ja $F$ sivutahkojen lukumäärä.

Katso myös Lause, Monitahokas.

Euroopan yhteisvaluutan rahayksikkö.

Katso myös Sentti.

Eksponenttifunktion lyhenne. $\exp(x)$ tarkoittaa eksponenttifunktion arvoa pisteessä $x$ eli $\exp(x) = e^{x}$.

Katso myös Lyhenne, Eksponenttifunktion derivaatta, Eksponenttifunktio, $\ln$, Funktion $e^{ax}$ integraalifunktio, $e^{ix}$, Eksponenttifunktion integraalifunktio, Eksponenttifunktion potenssisarja.