Matematiikan verkkosanakirja

Yleisimmin käytetyt paperikoot muodostavat ns. A-sarjan. Kokoja merkitään A1, A2, A3 jne. Koot on määritelty seuraavasti:

Jokainen koko on suorakaide, jonka sivut ovat suhteessa $1:\sqrt{2}$. A0:n ala on 1 m$^{2}$, A1:n puolet tästä, A2:n neljäsosa jne.

Koot ovat siis:

A0 $= 841 \times 1189$ mm;

A1 $ = 594 \times 841$ mm;

A2 $= 420 \times 594$ mm;

A3 $= 297 \times 420$ mm;

A4 $= 210 \times 297$ mm;

A5 $= 148 \times 210$ mm;

A6 $= 105 \times 148$ mm;

A7 $= 74 \times 105$ mm;

A8 $= 52 \times 74 $mm;

A9 $= 37 \times 52 $mm;

A10 $= 26 \times 37$ mm.

Paperikoon A$n$ leveys on $2^{-1/4-n/2}$ m ja korkeus $2^{1/4-n/2}$ m. Kokoja on pyöristetty alaspäin, jotta varmistuisi, että kaksi A4-paperia olisivat yhdessä hiukan pienemmät kuin yksi A3-paperi jne.

Katso myös mm.

Päättelyä, joka etenee seurauksista syihin, kutsutaan a posteriori -päättelyksi. Väittämiä, joiden totuus tai epätotuus voidaan selvittää havainnoimalla ja tekemällä kokeita, kutsutaan a posteriori -väittämiksi.

Katso myös A priori.

Perustelua, joka etenee syystä seuraukseen, kutsutaan a priori -perusteluksi. Deduktiivinen päättely on siis a priori -päättelyä. Väittämiä, joiden totuus tai epätotuus voidaan ratkaista vetoamatta kokeisiin tai havaintoihin, kutsutaan a priori -väittämiksi.

Katso myös A posteriori.

$a \cdot \cos(x) + b \cdot \sin(x) = r \cdot \cos(x-t)$, missä $r = \sqrt{a^{2}+b^{2}}$, $\cos(t) = a/r$ ja $\sin(t) = b/r$.

Samalla tavoin $ a \cdot \cos(x) + b \cdot \sin(x) = r \cdot \sin(x+u)$, missä $r = \sqrt{a^{2}+b^{2}}$, $\cos(u) = b/r$ ja $\sin(u) = a/r$.

Katso myös Trigonometrinen identiteetti.

Vain tavallisista kirjain- ja numeromerkeistä koostuva. Tätä sanaa käytetään usein tietokoneohjelmissa tai puhuttaessa tietokoneen näppäimistön näppäimistä.

Merkkejä $\{$ ja $\}$ käytetään joskus kaavoissa tarkoittamaan samaa asiaa kuin kaarisulkeilla; sulkeiden sisään merkitty osa selvitetään ensin.

Joskus käytetään yhtä aikaa sekä aaltosulkeita että kaarisulkeita, kun olisi liian sekavaa käyttää paljon kaarisulkeita. Esimerkiksi \[ \{(x^{2}+y^{2})(z+x)-(z^{2}+y)^{2}\}^{2}. \] Kaarisulkeita käytetään erityisesti joukon määrittelyssä. Esimerkiksi positiivisten kokonaislukujen joukko voidaan merkitä $\{x\in{\mathbb{Z}}|x>0\}$.

Aaltosulut ovat symbolit $\{$ ja $\}$. Niitä käytetään yleensä merkitsemään joukkoja. Esimerkiksi $\{ 1,2,3,4\}$ on joukko, joka sisältää alkiot $1,2,3,4$. Joukko $\{ x \in A \mid P(x)\}$ on joukon $A$ osajoukko, joka sisältää ne $A$:n alkiot, joilla on ominaisuus $P$.

Toisinaan aaltosulkuja käytetään osoittamaan laskujärjestystä samaan tapaan kuin tavallisiakin sulkuja. Tällöin kaavassa on useita sisäkkäisiä sulkuja, ja aaltosulut ovat ulompana kuin tavalliset ja hakasulut, esim. $\{ 1 + [ 2 + (3+4) ]\}$.

Katso myös Kaarisulkeet.

Pinta-alan yksikkö. Yksi aari on sata neliömetriä. Yksi hehtaari on sata aaria.

Katso myös Pinta-ala, Pinta-alayksikkö, Hehtaari.

Muinainen laskuväline.

Antiikin kreikkalaiset ja roomalaiset käyttivät laskutoimitusten apuna kiviä, joita sijoitettiin vaakasuoralle alustalle kaiverretuille viivoille. Viivat edustivat ykkösiä, kymmeniä, satoja jne. Nykyisin monissa maissa käytetään yhä samalla periaatteella toimivia helmitauluja, joissa viivat ja kivet on korvattu vaakasuorilla tangoilla, joihin on kiinnitetty renkaita.

Ryhmä $(G,+)$ on Abelin ryhmä, jos se toteuttaa lisäksi ehdon

• Kaikilla $a,b \in G$ pätee $a + b = b + a$.

Abelin ryhmän laskutoimitusta merkitään yleensä $+$-merkillä. Abelin ryhmän neutraalialkiota merkitään yleensä merkillä $0$, ja alkion $a$ käänteisalkiota $-a$.

Pari $(\mathbb{Z}, +)$ on Abelin ryhmä.

Pari $(\mathbb{R} \setminus \{0\}, \cdot)$ on Abelin ryhmä.

Kääntyvät $n \times n$-matriisit muodostavat matriisien kertolaskun suhteen ryhmän, joka ei ole Abelin ryhmä.

Katso myös Vaihdannainen, Kommutatiivinen, Ryhmä, Moduli.

Abskissa on $x$-koordinaatti karteesisessa koordinaattijärjestelmässä

Katso myös Ordinaatta, Karteesinen koordinaatisto.

Abstrakti algebra tutkii joukkoja, joissa on määritelty laskutoimituksia. Joukon $G$ laskutoimitus tarkoittaa tässä yhteydessä funktiota $* \colon G \times G \rightarrow G$, joka toteuttaa joitakin yhteen- ja kertolaskun laskusäännöistä tuttuja ehtoja, esimerkiksi sen, että

• $a * (b * c ) = (a * b) * c$.

Esimerkkejä joukoista, joissa on määritelty laskutoimituksia ovat monoidit, ryhmät, renkaat, kunnat, modulit ja vektoriavaruudet.

Katso myös Algebra, Ryhmä.

Ackermannin funktio $f \colon \mathbb{N}^2 \rightarrow \mathbb{N}$ määritellään seuraavasti: $$ \left\{ \begin{array}{l} f(0,b) = b+1 \\ f(a+1,0) = f(a,1) \\ f(a+1,b+1) = f(a, f(a+1,b)) \end{array} \right. $$ Tämä funktio kasvaa aivan hirvittävän nopeasti, kun $a$ ja $b$ kasvavat.

Katso myös Funktio, Kuvaus.

Latinan kielinen ilmaisu, jolla tarkoitetaan, että jokin asia on keksitty tai tehty pelkästään tiettyä tarkoitusta varten; suunnittelematta; ilman mitään erityistä syytä, että se olisi pitänyt tehdä juuri kyseisellä tavalla.

Yhteenlaskun kanssa tekemisissä oleva. Esimerkiksi additiivinen vakio on vakio, joka jossain kaavassa on lisättävä johonkin.

Affiini kuvaus on mikä tahansa sellainen tason kuvaus itselleen, jossa yhdensuuntaisten suorien kuvat ovat edelleen yhdensuuntaisia suoria.

Katso myös Affiini geometria, Affiini taso, Ominaisuus, Määrite.

Geometria, joka tarkastelee niitä kuvioiden ja avaruuden ominaisuuksia, jotka eivät muutu affiineissa kuvauksissa eli kuvauksissa jotka säilyttävät suorat suorina ja yhdensuuntaiset yhdensuuntaisina.

Se geometrian osa, joka tutkii ominaisuuksia, jotka säilyvät affiineissa kuvauksissa.

Katso myös Affiini, Geometria.

Affiini muunnos on mikä tahansa lineaarimuunnosten ja siirtokuvausten kombinaatio.

Affiini muunnos kuvaa suorat suoriksi siten, että yhdensuuntaiset suorat kuvautuvat yhdensuuntaisiksi suoriksi ja epäyhdensuuntaiset suorat kuvautuvat epäyhdensuuntaisiksi suoriksi.

Katso myös Geometrinen muunnos.

Tason kuvaa affiinissa muunnoksessa kutsutaan affiiniksi tasoksi.

Katso myös Affiini, Taso.

Aidosti monotoninen jono $u_{n}$ on joko

1) aidosti vähenevä eli $u_{n} \lt u_{n-1}$ pätee kaikilla $n$

tai

2) aidosti kasvava eli $u_{n} \gt u_{n-1}$ pätee kaikilla $n$.

Katso myös Monotoninen jono.

Aidosti positiivisten reaalilukujen joukko koostuu vain niistä reaaliluvuista $x$ , joilla $x \gt 0$. Se ei sisällä lukua 0, toisin kuin ei-negatiivisten reaalilukujen joukko.

Aidosti positiivinen funktio saa vain aidosti positiivisia arvoja, eikä sillä siis ole negatiivisia arvoja eikä nollakohtia.

Katso myös Suurempi kuin, Joukko.

Merkki $\Rightarrow$ tarkoittaa "jos ... niin ...". $A\Rightarrow B$ voidaan lukea "jos $A$ niin $B$" tai "$A$:sta seuraa $B$".

$\Rightarrow$ voidaan ajatella loogisena operaattorina, joka antaa tulokseksi "epätosi", jos ensimmäinen argumentti on tosi ja toinen epätosi, muussa tapauksessa tulos on "tosi".

""A:sta seuraa B"" tarkoittaa, että jos A on tosi, myöskin B:n on oltava tosi. Saman voi ilmaista sanomalla, että A on B:lle riittävä ehto.

Esimerkiksi $x \gt 0 \Rightarrow x \gt -1$. Jos nimittäin $x \gt 0$, on tällöin myös välttämättä $x \gt -1$.

Matematiikassa väitteen $a \Rightarrow b$ totuus määräytyy pelkästään lauseiden $a$ ja $b$ totuusarvojen perusteella. Väite $a \Rightarrow b$ on epätosi pelkästään silloin, kun väite $a$ on tosi ja $b$ epätosi, ja tosi kaikissa muissa tapauksissa.

Tällainen tulkinta merkille $\Rightarrow$ vangitsee syy-seuraussuhteesta matemaattisen päättelyn kannalta olennaiset piirteet. Se ei kuitenkaan vastaa täysin arkiajattelun "jos...niin...", päättelyitä, sillä väitteen $a \Rightarrow b$ totuus ei vaadi minkäänlaista sisäistä syy-seuraussuhdetta lauseiden $a$ ja $b$ totuudelle. Erityisesti, jos $a$ on epätosi lause, on $a \Rightarrow b$ tosi, oli $b$ mikä lause tahansa. Siis esimerkiksi "Kuu on juustoa $\Rightarrow$ Lehmät lentävät" on tosi väite.

Katso myös Jos, Perustelu, Johtopäätös, Siksi, implikaationuoli, Seurata jostakin, Olla seuraus, Kontrapositio.

Joukko aikajärjestykseen järjestettyjä havaintoja.

Tosiasioita tai muuta tietoa kerättynä yhteen myöhempää käyttöä tai tutkimusta varten. Usein dataa voidaan esittää tai havainnollistaa kuvioilla, kaavioilla ja taulukoilla. Tietojenkäsittelyssä dataksi kutsutaan mitä tahansa automaattiseen käsittelyyn sopivaa aineistoa. Sana "data" on monikkomuoto latinan sanasta "datum".

Katso myös Poikkeava havainto, Äärihavainto, Joukko, Luokiteltu aineisto, Luokka-arvoinen aineisto.

Luvun jakaja, joka ei ole luku itse.

Katso myös Tekijä, Täydellinen luku, Jakaja.

Murtoluku, joka on pienempi kuin 1 eli murtoluku, jonka osoittaja on pienempi kuin nimittäjä. Esimerkiksi 2/5, 3/4, 1/3, 4/7 ja 18/19.

Katso myös Sekaluku, Osoittaja, Epämurtoluku, Murtoluku, Nimittäjä.

Joukko $A$ on joukon $B$ aito osajoukko, jos $A$ on joukon $B$ osajoukko ja $A$ on eri joukko kuin $B$.

Katso myös Tyhjä joukko, Osajoukko.

Yksittäinen ajanhetki vastakohtana ajanjaksolle, jolla on alku ja loppu.

Jokin geometriseen kuvioon tai tilanteeseen tai fysikaaliseen kappaleeseen liittyvä erityinen suora kuten symmetria-akseli, koordinaattiakseli tai pyörähdysakseli.

Katso myös $z$-akseli, $y$-akseli, $x$-akseli, Särmiön akseli, Lieriön akseli, Suoran ja akselin leikkauspiste, Kartion akseli, Pyramidin akseli, Kiertosymmetrian akseli, Pyörähdysakseli, Suora, Karteesinen koordinaatisto, Koordinaattiakseli, Liittoakseli, Symmetria-akseli.

Geometria, jonka teoreemat johdetaan annetuista kyseisen geometrian aksioomista loogisen päättelyn avulla. Euklidinen geometria on esimerkki aksiomaattisesta geometriasta.

Katso myös Aksiooma, Euklidinen geometria.

Perusoletus, joka on keskeinen kehitettävän teorian kannalta. Yleensä matematiikassa pyritään muotoilemaan aksioomat tietylle matematiikan osalle, esimerkkinä euklidisen geometrian aksioomat. Aksioomien joukko pyritään pitämään mahdollisimman pienenä, ja yleensä yritetään löytää aksioomia, joiden totuus on ilmeinen.

Vaihtamalla yhtä aksioomaa saadaan usein kehitettyä täysin erilainen teoria; esimerkiksi muuttamalla euklidisen geometrian paralleelliaksioomaa saadaan geometrioita, jotka pätevät pallon tai satulan pinnalla, mutta eivät tasolla.

Katso myös Ehto, Oletus, Eukleideen aksioomat, Valinta-aksiooma, Postulaatti, Aksiomaattinen geometria, Eukleideen postulaatit.

Pieni kirjain tai numero, joka kirjoitetaan alemmaksi kuin tavalliset merkit.

Merkinnässä $M_i$ muuttuja $i$ on alaindeksi.

Katso myös Merkintätapa, Notaatio.

Matriisi, jonka kaikki päälävistäjän yläpuolella olevat alkiot ovat nollia.

Katso myös Kolmiomatriisi, LU-hajotelma, LDU-hajotelma.

Luku $x$ on reaalilukujoukon $S$ alaraja, jos $x$ on pienempi tai yhtä suuri kuin jokainen joukon $S$ luku.

Katso myös Infimum, Suurin alaraja, Reaaliluku.

Heprean kielen aakkoston ensimmäinen kirjain, $\aleph$. Kirjainta $\aleph$ käytetään myös tiettyjen äärettömien lukujen (ns. kardinaalilukujen) merkkinä.

Katso myös Merkintätapa, Notaatio.

Symbolia $\aleph_{0}$ käytetään merkitsemään luonnollisten lukujen joukon kokoa (kardinaliteettia). Symboli luetaan "alef-nolla".

Katso myös Mahtavuus.

Alennus on määrä, joka vähennetään hinnasta, tavallisesti jonkin myymiseksi nopeammin. Alennus voi olla jokin tietty rahamäärä kuten 3 euroa tai se voi olla prosentti- tai murtoluku kuten 50 % tai 1/3.

Katso myös Prosenttiosuus, Murtoluku.

Kauppojen alennusmyynneissä tavaroiden hinnat ovat alennettuja. Alkuperäisestä hinnasta on otettu rahaa pois, tavarat maksavat vähemmän. Myydäkseen tavaroita kauppiaat usein lupaavat kiinteän summan, joka otetaan pois kaikista hinnoista, esimerkiksi 5 euroa. Tällöin kaikki tavarat maksavat 5 euroa vähemmän.

Toisinaan kauppiaat alentavat hintoja kiinteällä prosentilla, esimerkiksi 10%:lla. Tällöin hinnasta otetaan pois 10 senttiä jokaista euroa kohti.

Alentaa jotakin, yleensä rahamäärää, tarkoittaa tehdä se pienemmäksi.

Katso myös Vähetä, Vähentyä.

Kreikkalainen kirjain $\alpha$ (pieni kirjain) tai $A$ (iso kirjain), lausutaan alfa. Äänneasu on sama kuin suomen a-kirjaimen.

Katso myös Kreikkalaiset kirjaimet.

Se osa matematiikkaa, joka käyttää merkkejä esittämään suureita, jotka saattavat olla tunnettuja tai tuntemattomia. Se on perusmatematiikan haara, joka yleistää aritmetiikan käyttämällä muuttujia, jotka saavat arvokseen lukuja. Tästä matematiikan haarasta kirjoitti ensimmäisenä Diofantos Aleksandrialainen 200-luvulla jKr. Algebraa käytettiin antiikin Babyloniassa, Egyptissä ja Intiassa. Eurooppaan algebra välittyi islamilaisen kulttuurin kautta.

Katso myös Algebrallinen, Lauseke, Boolen algebra, Parametri, Polynomi, Erisuuruus, Alkeismatematiikka, Muuttuja, Funktio, Kuvaus, Prosentti, Funktion kuvaaja, Analyyttinen tasogeometria, Koordinaatti, Jono, Abstrakti algebra, Vektorialgebra, Algebrallinen käyrä, Algebrallinen funktio, Algebrallinen topologia, Epäyhtälö, Yhtälö, Algebran peruslause, Graafi.

Algebraan liittyvä.

Reaali- tai kompleksluku $ w $ on algebrallinen, jos se on sellaisen polynomiyhtälön nollakohta, jonka kertoimet ovat rationaalilukuja. Siten kaikki rationaaliluvut ovat algebrallisia lukuja samoin kuin kaikki rationaalilukujen $n$:nnännet juuret. Luvut, jotka eivät ole algebrallisia, ovat transkendenttilukuja. Esimerkiksi $\pi$ ja $e$ ovat transkendenttilukuja.

Katso myös Algebra, Polynomin nollakohta, Transsendenttinen luku, Ominaisuus, Määrite.

Funktio $y(x)$, joka voidaan kirjoittaa yhtälönä \[ p_{0}(x)y^{0}+p_{1}(x)y^{1}+p_{2}(x)y^{2} +\ldots+p_{n-1}(x)y^{n-1} +p_{n}(x)y^{n}=0, \] missä kukin $p_{i}(x)$ on muuttujan $x$ polynomi.

Katso myös Algebra, Funktio, Kuvaus, Transsendenttifunktio.

Käyrä, jonka yhtälö sisältää ainoastaan algebrallisia funktioita.

Katso myös Algebra, Käyrä, Yhtälö.

Kunnan laajennus suuremmaksi kunnaksi, jonka jokainen alkio on algebrallinen pienemmän kunnan suhteen.

Katso myös Kuntalaajennus.

Lukua, joka on kokonaislukukertoimisen polynomiyhtälön juuri, kutsutaan algebralliseksi.

Esimerkiksi $\sqrt{5}+3$ on algebrallinen luku, koska se on yhtälön $x^2 - 6 x + 4 = 0$ juuri. Luku $\pi$ sen sijaan ei ole algebrallinen, koska se ei ole minkään kokonaislukukertoimisen polynomiyhtälön juuri.

Kompleksiluku voi olla algebrallinen. Esimerkiksi $i$ on yhtälön $1+x^{2} = 0$ juuri.

Kaikki rationaaliluvut ovat algebrallisia, mutta kaikki reaali- tai kompleksiluvut eivät ole.

Lukua, joka ei ole algebrallinen, kutsutaan transsendentaaliseksi.

Katso myös Transkendenttinen, Reaaliluku.

Algebrallinen topologia käyttää algebran menetelmiä topologian ongelmien tutkimiseen, usein konstruoimalla tutkittavana olevia topologisia avaruuksia vastaavia ryhmiä sekä kyseisten avaruuksien välisiä jatkuvia kuvauksia vastaavia ryhmien välisiä homomorfismeja.

Katso myös Algebra, Avaruus, Topologia, Ryhmä, Homomorfismi.

Kunta $k$ on algebrallisesti suljettu, jos sen polynomirenkaan $k[x]$ jokaisella polynomilla on nollakohta $k$:ssa.

Jokaisella kompleksilukukertoimisella astetta $N \ge 1$ olevalla polynomilla \[ p(z)=a_{0}+a_{1}z+a_{2}z^{2}+...+a_{N-1}z^{N-1}+z^{N} \] on nollakohta; toisin sanoen, $p(w) = 0$ pätee jollakin kompleksiluvulla $w$.

Katso myös Algebra, Argand, Lause, Yhtälön juuri, Polynomifunktio, Kompleksiluku.

Yksiselitteinen menetelmä jonkin, yleensä matemaattisen, tehtävän suorittamiseksi tai ratkaisemiseksi. Esimerkiksi Eukleideen algoritmi antaa jonon toimintaohjeita kahden luvun suurimman yhteisen tekijän löytämiseksi.

Katso myös Binäärihaku, Eukleideen algoritmi, Diskreetti matematiikka, Kuplalajittelu, Vaihtolajittelu, Hajoita ja hallitse, Lajittelualgoritmi, Minimax, Lineaarinen haku.

Jos $V$ on $F$-vektoriavaruus, joukko $A \subset V$ on avaruuden $V$ aliavaruus, mikäli seuraava ehto toteutuu

• $ax+by \in A$ kaikilla $x,y \in A$, $a,b \in F$.

Katso myös Vektoriavaruus.

Olkoon $(K,+,\times)$ kunta. Joukko $A \subset K$ on kunnan $K$ alikunta, jos $A$ sisältää alkiot $0$ ja $1$, ja on suljettu yhteen-, vähennys-, kerto- ja jakolaskun suhteen.

Tällöin joukko $A$ on kunta, laskutoimituksina kunnan $K$ laskutoimitusten rajoittumat joukkoon $A$.

Katso myös Kunta.

Joukon pienin alkio on alkio, joka on pienempi tai yhtä suuri kuin joukon muut alkiot.

Olkoon $R$ rengas ja $S \subset R$. Sanomme, että $S$ on renkaan $R$ alirengas, jos se toteuttaa seuraavat ehdot:

• $1 \in S$.
• Jos $a,b \in S$, myös $a-b \in S$ ja $ab \in S$.

Jos $S$ on renkaan $(R,+_R,*_R)$ alirengas, on kolmikko $(S,+_S,*_S)$ rengas, missä $a +_S b = a+_R b$ ja $a *_S b = a *_R b$ kaikilla $a,b \in S$.

Katso myös Rengas.

Olkoon $G$ ryhmä. Sanomme, että $H \subset G$ on ryhmän $G$ aliryhmä, jos se toteuttaa seuraavat ehdot

• Jos $a,b \in H$, niin $a * b \in H$.
• Jos $a \in H$, niin $a^{-1} \in H$.
• Jos $e$ on ryhmän $G$ neutraalialkio, $e \in H$.

Jos $H \subset G$ on ryhmän $(G, *_G)$ aliryhmä, on pari $(H, *_H)$ ryhmä, laskutoimituksenaan $a *_H b = a *_G b$ kaikilla $a,b \in H$.

$\mathbb{Z}$ on ryhmän $(\mathbb{R}, +)$ aliryhmä.

$\{x \in \mathbb{R} \mid x>0\}$ on ryhmän $(\mathbb{R} \setminus \{0\}, \cdot)$ aliryhmä.

Katso myös Ryhmä, Normaali aliryhmä, Homomorfismin ydin, Normalisaattori, Stabilisaattori, Cauchyn ryhmälause, Kommutaattorialiryhmä, Lagrangen lause.

Alkeellinen voi tarkoittaa yksinkertaista tai helppoa. Joskus se tarkoittaa, että tiettyä tarkoitusta (esimerkiksi todistusta) varten tarvittava matematiikka käsittelee aihepiirin perusasioita.

Katso myös Looginen ominaisuus.

Eukleideen suuri antiikin matematiikan kokonaisesitys.

Olkoon $D$ alue. Polku $\psi : [a,b] \rightarrow D $ on polun $\phi : [a,b] \rightarrow D$ alkeisdeformaatio, jos on olemassa pisteet $a = x_0 \lt x_1 \lt \ldots \lt x_n = b$ ja alueen $D$ konveksit avoimet osajoukot $C_0, \dots, C_{n-1}$, joille pätee $\phi(x_i)=\psi(x_i)$ kaikilla $i=0,\dots, n$ ja $\phi[x_i,x_{i+1}], \psi[x_i, x_{i+1}] \subset C_i$ kaikilla $i=0, \dots, n-1$.

Jos $f$ on kompleksianalyyttinen, pätee tällöin \[ \int_{\phi} f(z) dz =\int_{\psi} f(z) dz. \]

Vertaa käsitteeseen "homotooppinen".

Katso myös Funktio, Kuvaus.

Algebra, geometria, lukuteoria jne. Ei sisällä differentiaali- ja integraalilaskentaa.

Katso myös Aritmetiikka, Laskento, Algebra, Lukuteoria, Kombinatoriikka, Tilastotiede, Matematiikka, Geometria.

Matriisia $A$ kutsutaan alkeismatriisiksi, jos matriisin $B$ kertominen matriisilla $A$ suorittaa matriisiin $B$ jonkin alkeisrivitoimituksen tai jonkin alkeissaraketoimituksen. Toisin sanoen, jos matriisi $AB$ saadaan matriisista $B$ joko vaihtamalla kaksi $B$:n riviä tai saraketta keskenään tai kertomalla jokin $B$ rivi tai sarake vakiolla tai kertomalla jokin rivi tai sarake vakiolla ja lisäämällä se johonkin toiseen riviin tai sarakkeeseen, on $A$ alkeismatriisi.

Katso myös Matriisi.

Joukon jäsen.

Merkintä $x \in S$ tarkoittaa, että alkio $x$ on joukossa $S$ eli $x$ on joukon $S$ alkio. Merkintä $x \notin S$ tarkoittaa, että $x$ ei ole joukon $S$ alkio.

Katso myös Neutraalialkio, Kommutoida, Sisältää, Jäsen, Kuulua joukkoon, Joukko, Osajoukko, Ryhmän alkion kertaluku, Harva matriisi, Kommutaattori, Konjugaattiluokka, Ryhmän konjugoidut alkiot, Sivuluokka, Alkio.

Joukon jäseniä eli alkioita ovat ne oliot, jotka kuuluvat joukkoon.

Katso myös Joukko, Alkio.

Alkuluku on luku, jolla on täsmälleen kaksi tekijää: 1 ja luku itse.

Positiivinen kokonaisluku, jonka ainoat positiiviset tekijät ovat 1 ja luku itse.

Katso myös Yksitoista, 11, 13, Kolmetoista, Jaottomuus, Alkutekijä, Tekijä, Yhdistetty luku, Mersennen alkuluku, Fermat'n alkuluku, Dirichlet'n lause, Pseudoalkuluku, Riemannin zeta-funktio, Sophie Germainin alkuluku, Bertrandin otaksuma, Fermat'n pseudoalkuluku, Cauchyn ryhmälause, Jakaja, Kryptografia, Kryptologia, Aritmetiikan peruslause.

Otaksuma, joka sanoo, että alkulukukaksosia eli sellaisia alkulukupareja, joiden erotus on 2, on ääretön määrä. Tätä ei ole todistettu.

Katso myös Otaksuma, Konjektuuri.

Niiden alkulukujen, jotka ovat pienempiä tai yhtä suurin kuin $n$, lukumäärä on likimain $n/\log(n)$.

Itse asiassa, jos $p(n)$ on niiden alkulukujen, jotka ovat pienempiä tai yhtäsuuria kuin $n$, lukumäärä, niin \[ \frac{\mathrm{p(n)}}{\mathrm{n/log(n)}} \to 1 \text{ kun } \mathrm{n} \to \infty. \]

Lause, jonka mukaan $\pi(x)$, lukua $x$ pienempien alkulukujen lukumäärä, on asymptoottisesti yhtä suuri kuin $x/ \log x$. Yhtäpitävästi, $n$:s alkuluku on asymptoottisesti yhtä suuri kuin $n \log n$.

Yleisempi Landaulta (1900) peräisin oleva muotoilu on \[ \pi _k(x) \sim \frac{x}{ \text{log} x} \frac{ ( \text{log} ( \text{log} x ) )^k}{(k-1)!}, \] missä $\pi _k(x)$ on niiden lukua $x$ pienempien lukujen määrä, joilla on $k$ eri alkulukutekijää.

Katso myös Lause, Asymptoottisesti ekvivalentti.

Algoritmi, jonka avulla voidaan selvittää, onko annettu kokonaisluku alkuluku vai ei.

Luvun alkutekijä on luvun tekijä, joka on alkuluku.

Katso myös Alkuluku, Tekijä.

Menetelmä, jolla kertolasku voidaan laskea kynällä ja paperilla.

Katso myös Kertolasku.

Vuorotella kahden arvon välillä. Esimerkiksi jono $0,1,0,1,\dots$ alternoi.

Katso myös Vastakohtaiset kulmat, Vastahypoteesi, Vaihtoehtoinen hypoteesi, Ominaisuus, Määrite.

Lyhenne latinankielisistä sanoista "ante meridiem". Ilmaus tarkoittaa aikaa ennen keskipäivää eli aikaa keskiyöstä keskipäivään.

Amerikassa käytetään paperikokojärjestelmää, joka ei ole yleisesti käytössä muualla. Se sisältää paperikoot 'letter', 'legal', 'executive' ja 'ledger/tabloid', kuten myös A-, B-, C-, D- ja E-paperikoot teknisille piirustuksille. Amerikkalainen paperin standardikoko A teknisille piirustuksille on 216 mm $\times$ 279 mm.

Sana tai ilmaisu, joka saadaan toisesta sanasta tai ilmaisusta laittamalla siinä olevat kirjaimet toisenlaiseen järjestykseen.

Usein, erityisesti epämuodollisissa päättelyissä, voidaan saada tietoa jostakin tekemällä rinnastus jonkin muun kanssa eli sanomalla, että nämä kaksi asiaa ovat jollakin tavalla samanlaisia. Esimerkiksi kuvan piirtämisen ja kirjan kirjoittamisen välillä on analogia. Nämä kaksi toimintoa ovat hyvin erilaisia, mutta niillä on myös paljon yhteistä, mikä tarkoittaa, että jos tiedetään jotain jommastakummasta, sitä voidaan soveltaa myös toiseen.

Erityisesti tietokonetekniikassa sekä muunlaisessa teknologiassa laitetta sanotaan analogiseksi, jos se käyttää fysikaalisia suureita lukujen tai toisten fysikaalisten suureiden esittämiseen. Esimerkiksi elohopealämpömittari on analoginen, koska siinä elohopeapatsaan pituus esittää lämpötilaa, mutta digitaalikello ei ole.

Katso myös Digitaalinen.

Se matematiikan osa-alue, jossa käytetään hyödyksi raja-arvon ja jatkuvuuden käsitteitä. Esimerkiksi differentiaali- ja integraalilaskenta tai päättymättömät sarjat kuuluvat matemaattiseen analyysiin.

Katso myös Differentiaali- ja integraalilaskenta, Matematiikka, Raja-arvo, Sarja, Epsilon-delta -analyysi.

Jos on olemassa funktio $F(x)$, jolle pätee $F'(x) = f(x)$ kaikilla $a \le x \le b$, niin \[ \int_{a}^{b} f(x)dx = F(b)-F(a). \]

Derivointi on siten integroinnille käänteinen laskutoimitus.

Reaalimuuttujan tapaus: Olkoon $F$ jatkuvasti derivoituva suljetulla välillä $[a,b]$ ja olkoon $F' = f$. Silloin $\int_a^b f(x)dx$ on olemassa ja \[ \int_a^b f(x)dx = F(b)-F(a). \]

Kompleksimuuttujan tapaus: Olkoon $D$ alue ja $f : D \to \mathbb{C}$ jatkuva. Jos $F'=f$ ja $\varphi : [a,b] \to D$ on polku, niin \[ \int_{\varphi} f(z)dz = F(\varphi(b))-F(\varphi(a)). \]

Katso myös Differentiaali- ja integraalilaskenta, Lause.

Olkoon $D \subset \mathbb{C}$ alue eli avoin yhtenäinen joukko. Kuvaus $f \colon D \rightarrow \mathbb{C}$ on holomorfinen, jos sillä on kompleksinen derivaatta kaikissa pisteissä.

Katso myös Derivoituva, Differentioituva, Kokonainen funktio, Analyyttisen jatkeen yksikäsitteisyys, Riemannin poistuvan erikoispisteen lause, Cauchyn integraalilause.

Kolmiulotteinen geometria, joka käyttää koordinaatteja kolmiulotteisten kappaleiden tilavuuksien, pinta-alojen ja kulmien laskemiseen.

Katso myös Kulma, Vektori, Tangenttitaso, Trigonometria, Taso, Normaali, Suora, Etäisyyskaava, Analyyttinen tasogeometria, Analyyttinen geometria, Koordinaatti, Lieriökoordinaatit, Sylinterikoordinaatit, Suuntakulmat.

Kompleksiluvuilla määritelty funktio on analyyttinen, mikäli se on differentioituva. Se voidaan esittää Taylorin sarjana minkä tahansa pisteen suhteen.

Katso myös Derivoituva, Differentioituva, Funktio, Kuvaus, Meromorfinen, Napa, Taylorin sarja, Kompleksiluku, Liittofunktiot.

Geometrian laji, joka kuvaa pisteitä, suoria ja kuvioita koordinaattien avulla. Analyyttinen geometria käyttää hyväksi algebraa näihin olioihin liittyvien asioiden todistamiseksi.

Katso myös Karteesinen, Analyyttinen tasogeometria, Analyyttinen avaruusgeometria.

Topologinen ryhmä, jossa kertolasku ja käänteisalkion ottaminen ovat jatkuvia ja sileitä.

Katso myös Jatkuva, Ryhmä, Topologinen ryhmä, Lien ryhmä, Sileä kuvaus, Jatkuvuus.

Kaksiulotteinen geometria, joka käyttää koordinaatteja tasokuvioiden pituuksien, kulmien ja pinta-alojen laskemiseen.

Katso myös Algebra, Vektori, Etäisyyskaava, Koordinaattitaso, Karteesinen koordinaatisto, Koordinaattiakseli, Analyyttinen geometria, Koordinaatti, Napakoordinaatit, Kartioleikkaus, Analyyttinen avaruusgeometria.

Oletetaan, että $f$ ja $g$ ovat jossain alueessa määriteltyjä kompleksianalyyttisiä funktioita ja että $f|A = g|A$ jollain $A$, joka sisältää itsensä kasautumispisteen. Tällöin $f=g$ koko määrittelyalueessa.

Jos valitaan $g=0$, nähdään, että ei-vakion analyyttisen funktion nollakohdat ovat erakkopisteitä.

Katso myös Lause, Holomorfinen, Analyyttinen.

Olkoot $A$, $B$ ja $C$ avaruuden pisteitä, jotka eivät sijaitse samalla suoralla. Tällöin on olemassa täsmälleen yksi taso, joka kulkee pisteiden $A$, $B$ ja $C$ kautta. Tälle tasolle kuuluvat täsmälleen ne pisteet, jotka ovat muotoa $$(1-s-t) A + s B + t C,$$ kun $s$ ja $t$ käyvät läpi kaikki reaalilukuarvot. Edellä laskutoimituksissa avaruuden pisteet on samaistettu paikkavektoreidensa kanssa.

Katso myös Tason yhtälö.

Jokin asia on anomaalinen eli poikkeava, jos se ei noudata yleistä mallia tai säännönmukaisuutta.

Katso myös Looginen ominaisuus.

Derivoinnille käänteinen operaatio. Etsiessämme antiderivaattaa yritämme päästä käyrän gradientin kaavasta itse käyrän kaavaan. Osoittautuu, että tämä on sama asia kuin integraalifunktion etsiminen. Tämän seikan todistaminen on tosin hankalaa.

Funktion $f$ antiderivaatta on differentioituva funktio $F$, jolle pätee $F^{\prime}=f$ kaikkialla funktion $f$ määrittelyalueessa.

Katso myös Integraali, Derivaatta.

Kvanttimekaniikassa operaattoreiden $A$ ja $B$ antikommutaattori $[A,B]^{-1} = AB + BA$.

Katso myös Operaattori, Binäärinen kuvaus, Kommutaattori, Kaksipaikkainen kuvaus.

Laskutoimitus $*$ on antikommutatiivinen, jos $a*b = - b*a$ pätee kaikilla $a$ ja $b$.

Vektorien ristitulo on esimerkki tällaisesta laskutoimituksesta.

Katso myös Laskutoimitus, Vaihdannainen, Kommutatiivinen, Vektoritulo, Ristitulo.

Relaatio $R \subset X \times X$ on antisymmetrinen, jos $a R b$ ja $b R a$ yhdessä implikoivat $a=b$.

Katso myös Symmetrinen.

Geometrinen konstruktiotehtävä, jossa etsitään ympyrää, joka sivuaa kolmea muuta annettua ympyrää.

Aputulos, jota käytetään jonkin tärkeämmän teoreeman eli lauseen todistuksessa. Lauseen todistuksen yhteydessä saatetaan todistaa useitakin lemmoja.

Katso myös Zornin lemma.

Merkit 1, 2, 3, 4, 5, 6, 7, 8, 9 ja 0. Näitä käytetään lähes kautta maailman lukujen merkitsemiseen.

Katso myös Numero.

Mikä tahansa yhtenäinen osa käyrää viivaa; erityisesti ympyrän kehän yhtenäinen osa.

Katso myös Ympyrä, Puoliympyrä, Käyrä, Jänne, Sekantti, Konsyklinen.

Arkuskosinin, kosinin käänteisfunktion, lyhenne. $\arccos x$ tarkoittaa kosinin käänteisfunktion arvoa pisteessä $x$ eli sitä 0:n ja $\pi$:n välillä olevaa lukua, jonka kosini on $x$.

Silloin tällöin arkuskosinille käytetään myös lyhennettä acos.

Kosinifunktion käänteisfunktion lyhenne. Jos $-1\le x \lt 1$, niin $\arccos x$ on se ehdon $0\le y\le \pi$ toteuttava luku $y$, jolle $\cos y=x$. Laskimissa ja tietokoneohjelmissa $\arccos$:n tilalla käytetään joskus merkintää ACOS tai acos.

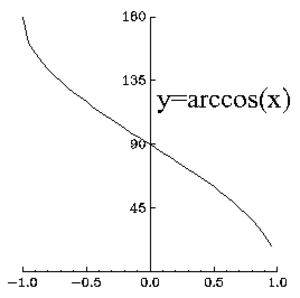
Katso myös Lyhenne, $\arccos$-funktion derivaatta, $\arccos$-funktion integraalifunktio, $\arcsin$.

\[ \frac{\mathrm{d}}{\mathrm{d}x}arccos(x) = \frac{-1}{\sqrt{1-x^2}}. \]

Katso myös $\arccos$.

\[ \int \arccos(x) \mathrm{d}x = x \arccos(x)-\sqrt{1-x^2}+C. \]

Katso myös $\arccos$.

Kosekantin käänteisfunktion merkintä. arccosec$(x)$ on se ehdon $-\pi/2\le y\le \pi/2$ toteuttava luku $y$, jolle $\csc(y)=x$.

Katso myös Lyhenne, Arkuskosekantti, $\csc$.

Kotangenttifunktion käänteisfunktion merkintä. arccot $x$ on se ehdon $0 \lt y \lt \pi$ toteuttava luku $y$, jolle $\cot y=x$.

Katso myös Lyhenne, Arkuskotangentti, $\arccot$-funktion derivaatta, $\arccot$-funktion integraalifunktio.

\[ \frac{\mathrm{d}}{\mathrm{d}x}arccot(x) = \frac{-1}{1+x^2}. \]

Katso myös $\arccot$.

\[ \int arccot(x) \mathrm{d}x = x arccot(x)+\frac{1}{2} \ln(1+x^2)+C. \]

Katso myös $\arccot$, $\ln$.

Hyperbolisen kosekantin käänteisfunktion eli funktion "area cosecans hyperbolica" lyhenne. $\mathrm{arcosech}(x)$ tarkoittaa hyperbolisen kosekantin käänteisfunktion arvoa pisteessä $x$ eli lukua, jonka hyperbolinen kosekantti on $x$.

Katso myös Lyhenne, $\arcosech$-funktion derivaatta, $\arcosech$-identiteetti.

Kun $x \neq 0$, niin \[ \frac{\mathrm{d}}{\mathrm{d}x} arcosech(x) = - \frac{1}{x \sqrt{1 + x^2}}. \]

Katso myös $\arcosech$.

Kun $x>0$, niin \[arcosech(x) = \ln \left( \frac {1 + \sqrt{1+x^2}}{x} \right). \] Kun $x<0$, niin \[arcosech(x) = - \ln \left( \frac {1 + \sqrt{1+x^2}}{-x} \right).\]

Katso myös $\arcosech$, $\ln$.

Hyperbolisen kosinin käänteisfunktion (eli area cosinus hyperbolicus -funktion) merkintä. arcosh $x$ on se ei-negatiivinen luku $y$, jolle $\cosh y=x$.

Katso myös Lyhenne, $\arcosh$-funktion derivaatta, $\arcosh$-funktion integraalifunktio, Hyperbolisen kosinin käänteisfunktio.

\[ \frac{\mathrm{d}}{\mathrm{d}x}arcosh(x) = \frac{1}{\sqrt{x^2 - 1}}. \]

Katso myös $\arcosh$.

\[ \int arcosh(x)\mathrm{d}x = x arcosh(x)-\sqrt{x^2-1}+C. \]

Katso myös $\arcosh$.

Kaikilla $x \geq 1$ pätee \[arcosh(x) = \ln \left( x + \sqrt{x^2 - 1} \right). \]

Katso myös Identiteetti, Hyperbolisen kosinin käänteisfunktio.

Hyperbolisen kotangentin käänteisfunktion lyhenne. $\mathrm{arcoth x}$ tarkoittaa hyperbolisen kotangentin käänteisfunktion arvoa pisteessä $x$ eli sitä lukua, jonka hyperbolinen kotangentti on $x$.

Katso myös Lyhenne, $\arcoth$-funktion derivaatta, $\arcoth$-identiteetti, $\arcoth$-funktion integraalifunktio.

Kun $|x| \gt 1$, niin \[ \frac{\mathrm{d}}{\mathrm{d}x} arcoth(x) = \frac{1}{1-x^2}. \]

Katso myös $\arcoth$.

\[ \int \arccoth(x)\mathrm{d}x=x \arcoth(x) + \frac{1}{2} \ln ( x^2-1) + C. \]

Katso myös $\arcoth$, $\ln$.

Kaikilla $x$, joilla $|x| \gt 1$, pätee \[ \mathrm{arccoth}(x) = \frac{1}{2} \ln \left( \frac{x+1}{x-1} \right).\]

Katso myös $\arcoth$, $\ln$.

Sekanttifunktion käänteisfunktion lyhenne. $\mathrm{arcsec}(x)$ on se ehdon $-\pi \le y \le \pi$ toteuttava luku $y$, jolle $\sec y=x$.

Katso myös Lyhenne, $\sec$, Arkussekantti, $\arcsec$-funktion derivaatta.

\[ \frac{\mathrm{d}}{\mathrm{d}x} \arcsec(x) = \frac{1}{x \sqrt{x^2-1}}. \]

Katso myös $\arcsec$.

Sinifunktion käänteisfunktion lyhennysmerkintä. $\arcsin(x)$ on se luku $-1 \le y \le 1$, jolla pätee $\sin(y) = x$.

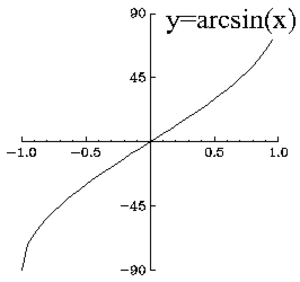
Katso myös $\arccos$, Lyhenne, Arkussini, $\arcsin$-funktion derivaatta, $\arcsin$-funktion integraalifunktio.

\[ \frac{\mathrm{d}}{\mathrm{d}x} \arcsin(x) = \frac{1}{\sqrt{1-x^2}}. \]

Katso myös $\arcsin$.

\[ \int \arcsin(x) \mathrm{d}x = x \arcsin(x) + \sqrt{1-x^2} + C. \]

Katso myös $\arcsin$.

Tangenttifunktion käänteisfunktio. $\arctan x$ on se luku $y$, $-\pi/2\lt y \pi/2$, jolle $\tan y=x$. Voidaan merkitä myös $\tan^{-1}(x)$ tai (joissain laskimissa ja tietokoneohjelmissa) atan $x$.

Katso myös $\tan$, Kotangentti, Arkusfunktio, $\arctan$.

Tangenttifunktion käänteisfunktion lyhennysmerkintä. $\mathrm{arctan}(x)$ on se luku $y$, jolla pätee $\tan(y) = x$.

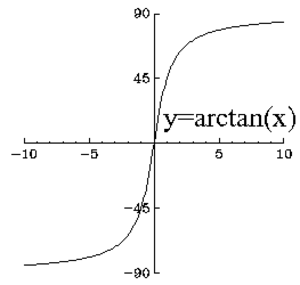
Katso myös $\arctan$, Lyhenne, $\arctan$-funktion derivaatta, $\arctan$-funktion integraalifunktio, $\arctan$-funktion potenssisarja.

\[ \frac{\mathrm{d}}{\mathrm{d}x} \arctan(x) = \frac{1}{1+x^2}. \]

Katso myös $\arctan$.

\[ \int \arctan(x) \mathrm{d}x = x \arctan(x) - \frac{1}{2} \ln (1+x^2) + C. \]

Katso myös $\ln$, $\arctan$.

Kaikilla $x$, joilla $|x|<1$, pätee \[arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - ... + (-1)^{n} \frac{x^{2n+1}}{2n+1} + ... \]

Katso myös $\arctan$, Gregoryn sarja.

Käänteisiä hyperbolisia funktioita ovat arsinh(x), arcosh(x), artanh(x) ja arcoth(x). Nämä ovat toisinaan hyödyllisiä laskettaessa integraaleja sijoitusmenetelmän avulla.

Katso myös Hyperbolinen funktio, Hyperbolisen kosinin käänteisfunktio, Hyperbolisen sinin käänteisfunktio.

Kompleksiluvun argumentti eli lukua esittävän paikkavektorin ja $x$-akselin välinen positiiviseen kiertosuuntaan laskettu kulma.

Katso myös Kompleksiluvun argumentti, Lyhenne.

Jean Robert Argand (1768--1822). Sveitsiläinen matemaatikko. Muistetaan kompleksilukujen geometrisesta tulkinnastaan, missä kompleksiluku $i$ tulkitaan $90^{\circ}$ kierroksi, sekä kompleksiluvun itseisarvon käsitteestä. Hänen paras työnsä koski algebran peruslausetta.

Katso myös Kompleksitaso, Kompleksiluvun moduli, Kompleksiluku, Algebran peruslause.

Aritmeettinen jono on sellainen äärellinen tai ääretön lukujono, jossa kahden peräkkäisen luvun erotus on aina sama. Esimerkiksi jono 1, 5, 9, 13, 17 on aritmeettinen lukujono, koska kahden peräkkäisen luvun erotus on aina sama eli 4. Tätä lukua sanotaan jonon erotukseksi.

Katso myös Erotusjono, Aritmeettisen jonon erotus, Aritmeettinen sarja, Geometrinen jono, Jono.

Lukujen $x_1, x_2, \ldots, x_n$ aritmeettinen keskiarvo on \[ \bar{x} = \frac{1}{n} \sum x_i . \] Tunnetuin intervalli- ja suhdeasteikolla käytetty paikantamistunnusluku. Muuttujanarvojen painopiste.

Katso myös Normaalijakauma, Korrelaatiokerroin, Odotusarvo, Teoreettinen keskiarvo, Paikantamistunnusluku, Keskiluku, Moodi, Tyyppiarvo, Verrata, Harhaton keskiarvo, Tasaisen jakauman odotusarvo, Lineaarinen funktio ja keskiarvo, Aritmeettisen ja geometrisen keskiarvon välinen epäyhtälö, Keskeinen raja-arvolause, Variaatiokerroin, Poikkeama, Gaussin jakauma, Geometrinen keskiarvo, Keskiverto.

Jono aritmeettisia laskutoimituksia, joita voidaan suorittaa niin monta kertaa kuin halutaan. Jos niitä on tarkoitus toistaa jatkuvasti yhä uudelleen, prosessia kutsutaan usein iteraatioksi.

Katso myös Kaprekarin jono, Iterointi.

Jono, jonka $n$:s jäsen saadaan laskemalla yhteen jonkin aritmeettisen jonon $n$ ensimmäistä jäsentä. Esimerkkinä tästä ovat kolmioluvut; $n$:s kolmioluku saadaan laskemalla yhteen $n$ ensimmäistä luonnollista lukua.

Katso myös Aritmeettinen jono, Sarja.

Lukujen $a_1, a_2, \ldots, a_n$ aritmeettisen ja geometrisen keskiarvon välillä vallitsee epäyhtälö \[ \frac{\sum _{i=1}^{n} a_{i}}{n} \geq \sqrt[n]{\prod_{i=1}^{n} a_{i}}. \] Toisin sanoen, lukujen $a_1, a_2, \ldots, a_n$ aritmeettinen keskiarvo on aina suurempi tai yhtä suuri kuin niiden geometrinen keskiarvo.

Katso myös Erisuuruus, Lause, Keskiarvo, Aritmeettinen keskiarvo, Epäyhtälö, Geometrinen keskiarvo, Keskiverto.

Jos lukujonossa kahden peräkkäisen termin erotus on aina sama, niin lukujonoa kutsutaan aritmeettiseksi lukujonoksi. Peräkkäisten termien erotusta kutsutaan jonon erotukseksi.

Katso myös Verrannollisuus, Erotus, Aritmeettinen jono.

Jokainen kokonaisluku $n \gt 1$ voidaan kirjoittaa alkulukujen tulona ja tämä tulo on alkulukujen järjestystä vaille yksikäsitteinen.

Katso myös Aritmetiikka, Laskento, Alkuluku, Lause.

Matematiikan osa-alue, joka käsittelee lukuja ja niillä tehtäviä laskutoimituksia.

Katso myös Laskin, Murtoluku, Alkeismatematiikka, Luonnollinen luku, Aritmetiikan peruslause.

Tason laatoitus säännöllisin monikulmioin siten, että jokaista monikulmion kärkeä ympäröi sama kuvio, jossa on ainakin kahdenlaisia monikulmioita.

Erilaisia Arkhimedeen laatoituksia on kahdeksan kappaletta. Niissä käytetään

- kolmioita ja kaksitoistakulmioita,

Katso myös Laatoitus, Tessellaatio.

Veteen laitettuun kappaleeseen kohdistuu noste, joka on yhtä suuri kuin kappaleen syrjäyttämän vesimäärän paino.

Kelluva kappale syrjäyttää siis vettä painonsa verran, kun taas upoksissa oleva kappale syrjäyttää vettä tilavuutensa verran.

Seuraavaa pinta-aloja koskevaa tulosta sanotaan joskus Arkhimedeen lauseeksi:

Katso myös Arkhimedes, Lause, Lieriö, Pallovyöhykkeen ala.

Monitahokas, jonka kaikki sivutahkot ovat säännöllisiä monikulmioita, ja saman kärkiluvun omaavat monikulmiot ovat keskenään yhteneviä.

Arkhimedeen monitahokkaita eli puolisäännöllisiä monitahokkaita on kolmeatoista lajia, kun mukaan ei lasketa särmiöitä ja antiprismoja, jotka myös ovat puolisäännöllisiä.

Jotkut Arkhimedeen monitahokkaat saadaan katkaisemalla eli leikkaamalla kärjet pois säännöllisistä monitahokkaista. Esimerkiksi katkaistu kuutio on kuutio, jonka kärjet on leikattu pois siten, että neliönmuotoisista tahkoista tulee säännöllisiä kahdeksankulmioita ja tahkot, joita muodostuu pois leikattujen kärkien paikoille, ovat tasasivuisia kolmioita.

Katso myös 13, Kolmetoista, Catalanin monitahokkaat.

Spiraali, jonka yhtälö napakoordinaateissa on $r = a\theta$, missä $a$ on reaaliluku.

Katso myös Spiraali.

Kreikkalainen matemaatikko (287--212 eKr.), joka asui Syrakusassa. Muutamia hänen kirjojaan on säilynyt. Ne käsittelevät vaikeita kaksi- ja kolmiulotteisen geometrian ongelmia sekä muita matematiikan ja fysiikan aloja, kuten dynamiikkaa.

Katso myös Arkhimedeen lause.

Trigonometrisen funktion käänteisfunktio. Niitä merkitään $\arcsin x$, $\arccos x$, $\arctan x$ tai $\sin^{-1} x$, $\cos^{-1} x$, $\tan^{-1} x$.

Katso myös $\arctan$, Arkuskosekantti, Arkussini, Arkussekantti, Arkuskotangentti, Arkuskosini, Trigonometrinen funktio.

Kosekanttifunnktion käänteisfunktio. Sitä merkitään $\mathrm{arccosec}(x)$ tai $\mathrm{cosec}^{-1}(x)$.

Katso myös $\arccosec$, Arkusfunktio, $\csc$.

Kosinifunktion käänteisfunktio. Sitä merkitään $\arccos(x)$ tai $\cos^{-1}(x)$. Funktion arvojoukko on $[0,\pi]$.

Katso myös Arkusfunktio.

Kotangentin käänteisfunktio. Sitä merkitään $\mathrm{arccot}(x)$ tai $\cot^{-1}(x)$. Funktion arvojoukko on avoin väli $(0,\pi)$.

Katso myös $\arccot$, Arkusfunktio, $\cot$.

Sekanttifunktion käänteisfunktio. Sitä merkitään $\mathrm{arcsec}(x)$ tai $\sec^{-1}(x)$.

Katso myös $\arcsec$, $\sec$, Arkusfunktio.

Sinifunktion käänteisfunktio. Sitä merkitään $\arcsin(x)$ tai $\sin^{-1}(x)$. Funktion määrittelyjoukko on väli $[-1,\,1]$ ja arvojoukko väli $[-\pi/2,\,\pi/2]$.

Katso myös Sini, Arkusfunktio, $\arcsin$.

Kuutio, jonka kullakin sivulla on eri määrä pisteitä eli eri silmäluku, yleensä yhdestä kuuteen. Tavallisessa arpakuutiossa kuution vastakkaisten sivujen silmälukujen summa on 7.

Arpakuutioita käytetään usein todennäköisyyteen liittyvissä kysymyksissä ja ongelmissa, koska reilua noppaa heitettäessä on kukin kuudesta silmäluvusta yhtä mahdollinen.

Hyperbolisen sinifunktion käänteisfunktion lyhennysmerkintä. $arsinh(x)$ on se luku $y$, jolla pätee $\sinh(y)=x$.

Katso myös Lyhenne, $\arsinh$-funktion derivaatta, $\arsinh$-funktion integraalifunktio, Hyperbolisen sinin käänteisfunktio.

\[ \frac{\mathrm{d}}{\mathrm{d}x}arsinh(x) = \frac{1}{\sqrt{x^2+1}}. \]

Katso myös $\arsinh$.

\[ \int arsinh(x) \mathrm{d}x = x arsinh(x) - \sqrt{1+x^2}+C. \]

Katso myös $\arsinh$.

Kaikilla luvuilla $x$ pätee \[ \mathrm{arsinh}(x) = \ln \left( x+\sqrt{x^2+1} \right). \]

Katso myös Hyperbolisen sinin käänteisfunktio.

Hyperbolisen tangenttifunktion käänteisfunktion lyhennysmerkintä. $artanh(x)$ on se luku $y$, jolla pätee $\tanh(y)=x$.

Katso myös Lyhenne, $\artanh$-funktion derivaatta, $\artanh$-identiteetti, $\artanh$-funktion integraalifunktio, $\artanh$-funktion potenssisarja.

\[ \frac{\mathrm{d}}{\mathrm{d}x}artanh(x) = \frac{1}{1-x^2}. \]

Katso myös $\artanh$.

\[ \int artanh(x) \mathrm{d}x = x artanh(x) + \frac{1}{2} \ln (1-x^2)+C. \]

Katso myös $\ln$, $\artanh$.

Kaikilla $x$, joilla $|x|<1$, pätee \[artanh(x) = x + \frac{x^3}{3} + \frac{x^5}{5} + ... + \frac{x^{2n+1}}{2n +1 } + ... \]

Katso myös $\artanh$.

Kaikilla $x$, joilla $|x|<1$, pätee \[artanh(x) = \frac{1}{2} \ln \left( \frac{1+x}{1-x} \right). \]

Katso myös $\artanh$.

Sanalla arvo tarkoitetaan matematiikassa yleensä lukua tai muuta oliota, joka on jonkin muuttujan paikalla. Lausekkeelle tai funktiolle saadaan arvo sijoittamalla jotkin arvot sen muuttujien paikalle.

Funktion $f \colon A \rightarrow B$ arvo pisteessä $a \in A$ on $f(a)$, eli se arvojoukon alkio, jonka $f$ liittää pisteeseen $a$.

Tietokoneohjelman tuloste on se tieto, jonka ohjelma on tuottanut ohjelman suorituksen päättyessä. Tietojenkäsittelytieteessä usein ajatellaan, että ohjelman syötteet ja tulosteet ovat luonnollisia lukuja.

Sanaa tuloste käytetään yleensä sellaisen (ei-interaktiivisen) tietokoneohjelman yhteydessä, joka saa syötteen pelkästään suorituksen alkaessa ja palauttaa tulosteen kerralla ohjelman suorituksen päättyessä.

Arkikielessä mitä tahansa ohjelman tulostamaa dataa (näyttölaitteelle tai paperille) kutsutaan tulosteeksi.

Katso myös Kuvajoukko, Funktion kuvajoukko.

Funktion $f \colon A \rightarrow B$ maalijoukko on joukko $B$ eli niiden arvojen joukko, joita funktion voidaan periaatteessa ajatella saavan.

Funktio on surjektio, jos se saa kaikki arvot maalijoukossaan eli $fA=B$.

Kuvauksen $f \colon \mathbb{R} \rightarrow \mathbb{R}, x \mapsto x^2$, maalijoukko on $\mathbb{R}$, mutta $f$ ei saa esimerkiksi arvoa $-1$ missään pisteessä. Kuvauksen $f$ kuvajoukko on väli $[0, \infty)$.

Katso myös Kuvaus, Funktio, Kuvaus, Kuvajoukko, Joukko, Lähtöjoukko, Funktion kuvajoukko, Määrittelyjoukko, Funktio.

Sanoa tai olettaa, että kaksi asiaa ovat yhtä suuret. Esimerkiksi joskus asetetaan samoiksi kertoimet, mikä tarkoittaa, että oletetaan $x$:ien kokonaismäärän olevan sama yhtälön molemmilla puolilla, $x$:n neliöiden kokonaismäärän olevan sama yhtälön molemmilla puolilla, jne.

Askelfunktio on funktio, jonka kuvaaja koostuu erillisistä vaakasuorista viivasegmenteistä. Funktio $\mathrm{int}(x)$, jonka arvo pisteessä $x$ on reaaliluvun $x$ kokonaislukuosa, on esimerkki askelfunktiosta.

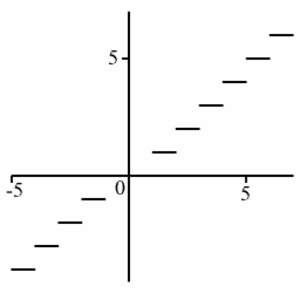
Katso myös Funktio, Kuvaus, Suurin lukua pienempi kokonaisluku, Heavisiden askelfunktio.

Laskutoimitus on liitännäinen, silloin, kun ei ole väliä, mihin sulkeet sijoitetaan, kun toimitus esiintyy kahdesti peräkkäin jossakin lausekkeessa.

Laskutoimitus $\circ$, jolla \[ a \circ (b \circ c)=(a \circ b) \circ c \] on voimassa kaikilla mahdollisilla $a, b, c$.

Kulmien suuruutta mitataan asteina. Jos jaetaan mikä tahansa ympyrä 360:een yhtä suureen osaan keskipisteen kautta kulkevien suorien avulla, niin jokaisen kahden vierekkäisen suoran muodostaman kulman koko on yksi aste. Ympyrässä on siis 360 astetta.

Kulman yksikkö. Ympyrässä on 360 astetta.

Katso myös Kulma, Uusaste, Graadi, Polynomin aste.

Litteä ympyrän tai puoliympyrän muotoinen väline kulmien mittaamiseen ja piirtämiseen.

Katso myös Geometria.

Kun kiinteän mittaista janaa liikutetaan siten, että sen päät koskettavat toisiaan vastaan kohtisuorassa olevia akseleita, niin jana piirtää kuvion, jota kutsutaan astroidiksi.

Astroidin parametrimuotoinen yhtälö on $x=a\cos^3 t$, $y=a\sin^3 t$.

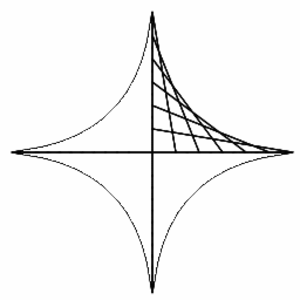
Katso myös Käyrä, Verho, Verhokäyrä.

Käyrän asymptootti on suora, jota käyrä lähestyy origosta kauemmas siirryttäessä, mutta johon käyrä ei kuitenkaan missään yhdy.

Esimerkiksi käyrän $y=1/x$ asymptootteja ovat sekä $x$-akseli että $y$-akseli.

Katso myös Asymptoottinen, Käyrä, Suora, Hyperbelin yhtälö.

Käyrää tai pintaa sanotaan asymptoottiseksi, jos sillä on asymptoottina suora tai taso.

Yleisesti johonkin objektiin liittyvä asymptoottinen objekti ilmaisee objektin olemusta tilanteessa, jossa jokin parametri lähestyy ääretöntä.

Kahden funktion $f$ ja $g$ sanotaan olevan asymptoottisesti yhtä suuret, jos \[\lim_{x\to\infty}\frac{f(x)}{g(x)}=1.\]

Katso myös Asymptootti.

Satunnaismuuttujajonon $Z_i$ asymptoottinen jakauma on niiden jakaumien rajajakauma, kun $i$ kasvaa rajatta.

Katso myös Jakauma.

Olkoot $(a_n)$ ja $(b_n)$ äärettömiä lukujonoja. Sanomme, että $(a_n)$ kasvaa korkeintaan yhtä nopeasti kuin $(b_n)$, $(a_n) = O(b_n)$, jos on olemassa sellainen vakio $M$, että $a_n \le M b_n$ riittävän suurilla indeksin $n$ arvoilla.

Jos $(a_n)=O(b_n)$ ja $(b_n)=O(a_n)$, jonot $(a_n)$ ja $(b_n)$ kasvavat yhtä nopeasti. Tällöin merkitään $(a_n)=\Theta(b_n)$. Jos $(a_n)=O(b_n)$, mutta $(b_n) \neq O(a_n)$, jono $(b_n)$ kasvaa nopeammin kuin $a_n$. Tällöin merkitään $(a_n)=o(B_n)$.

Luokat $O, o$ ja $\Theta$ voidaan määritellä yhtäpitävästi myös tutkimalla lausekkeen $\frac{a_n}{b_n}$ arvoa, kun $n$ lähenee ääretöntä. Jos kyseinen lauseke on ylhäältä rajoitettu, $(a_n)=O(b_n)$. Jos kyseinen lauseke lähenee nollaa, $(a_n)=o(b_n)$. Jos taas on olemassa positiiviset vakiot $c,C$, joille $c \lt \frac{a_n}{b_n} \lt C$, pätee $(a_n)=\Theta(b_n)$.

Katso myös Järjestys, $O(f(x))$, Merkintätapa, Notaatio, Asymptoottisesti ekvivalentti.

Hajaantuvaa sarjaa $s_n(x) = a_0 + \frac{a_1}{x} + \frac{a_2}{x^2} + \ldots + \frac{a_n}{x^n}$ kutsutaan funktion $f(x)$ asymptoottiseksi sarjaksi, jos \[ \lim_{|x| \to \infty} x^n [ f(x) - s_n(x) ] = 0 \] on voimassa kaikilla $n$.

Katso myös Asymptoottisesti ekvivalentti, Sarja.

Funktiot $f,g \colon \mathbb{R}_+ \rightarrow \mathbb{R}$ ovat asymptoottisesti ekvivalentteja, jos $$\lim_{x \rightarrow \infty} \frac{f(x)}{g(x)}=1.$$

Katso myös Asymptoottinen kasvunopeus, Alkulukulause, Asymptoottinen sarja.

Tila-avaruuden pisteiden joukko, jota kohti lähellä kulkevat radat suppenevat ja joka on stabiili.

Katso myös Joukko.

Jos annetun nelisivukkaan kullekin sivulle piirretään neliö, niin silloin vastakkaisille sivuille piirrettyjen neliöiden keskipisteet yhdistävät kaksi janaa ovat yhtä pitkät ja kohtisuorassa toisiaan vastaan.

Katso myös Lause, Nelikulmio.

Laite, joka kertoo lä kellonajan luomalla varjon alustalle, johon on merkitty luvut kuten kellotaulussa.

Funktio $f$ on automorfinen annetun transformaatioryhmän suhteen kompleksitason alueessa $D$, jos 1) $f$ on analyyttinen alueessa $D$ napoja lukuunottamatta ja 2) $T(z)$ kuuluu alueeseen $D$ kaikilla annetun transformaatioryhmän alkioilla $T$ ja alueen $D$ alkioilla $z$ ja pätee $f(T(z)) = T(f(z))$ - toisin sanoen, kukin transformaatio säilyttää $f$:n toiminnan.

Katso myös Funktio, Kuvaus, Automorfismi.

Luku $n$, jonka neliö päättyy lukuun $n$. Esimerkiksi $5$ on automorfinen luku, koska sen neliö $5^2 = 25$ päättyy lukuun $5$.

Katso myös 6, Kuusi, Kokonaisluku.

Kuvaus $f \colon A \rightarrow A$ on automorfismi, mikäli se on isomorfismi. Automorfismi on siis isomorfismi joukolta itselleen.

Kuvaus $f \colon \mathbb{Z} \rightarrow \mathbb{Z}$, $x \mapsto -x$ on ryhmän $(\mathbb{Z}, +)$ automorfismi.

Katso myös Kuvaus, Isomorfismi, Homomorfismi, Endomorfismi, Morfismi, Galois'n ryhmä, Automorfinen funktio, Isomorfia, Funktio.

Kolmiulotteinen joukko, jossa asiat voivat sijaita tai tapahtumat tapahtua.

Katso myös Otosavaruus, Mitta-avaruus, Algebrallinen topologia.

Avaruusgeometria tutkii kolmiulotteisia geometrisia olioita kuten palloja, kuutioita, jne.

Katso myös Katkaistu kartio, Taso, Tahko, Tetraedri, Pyramidi, Särmiö, Prisma, Lieriö, Kartio, Pallo, Sivutahkoverkko, Geometria, Monitahokas, Platonin kappaleet, Kuutio, Säännöllinen heksaedri.

Jos $(X, \tau)$ on topologinen avaruus, niin silloin topologian $\tau$ jäsenet ovat $X$:n avoimet osajoukot.

Jos reaaliakseli varustetaan sen tavanomaisella topologialla, avoimia joukkoja ovat kaikki avointen välien yhdisteet.

Katso myös Joukko, Topologia, Suljettu joukko.

Olkoon $X$ topologinen avaruus ja $A \subset X$. Kokoelma $\mathcal{U}$ avaruuden $X$ avoimia osajoukkoja on joukon $A$ avoin peite, mikäli kaikilla $x \in A$ on olemassa sellainen $V \in \mathcal{U}$, että $x \in V$.

Olkoon $\mathcal{U}$ joukon $A$ avoin peite, ja $\mathcal{V} \subset \mathcal{U}$. Tällöin $\mathcal{V}$ on peitteen $\mathcal{U}$ alipeite, mikäli $\mathcal{V}$ on joukon $A$ peite.

Katso myös Joukko, Kompakti.

Väli, joka ei sisällä päätepisteitään. Esimerkiksi niiden pisteiden $x$ joukko, joilla $0 \lt x \lt 1$, on avoin väli. Avointa väliä, jonka päätepisteet ovat $a$ ja $b$, merkitään $]a,b[$ tai $(a,b)$. Muotoa $(-\infty,b)$, $(a, \infty)$ ja $(-\infty, \infty)$ olevat välit ovat myös avoimia, mutta ne eivät ole rajoitettuja, kuten väli muotoa $(a,b)$.

Katso myös Suljettu väli, Väli.