Matematiikan verkkosanakirja

Charles Babbage (1792--1871) teki pioneerityötä logiikassa ja tietojenkäsittelyssä. Hänen mekaanisen laskukoneensa, Differenssikoneen, jäljennös on nähtävissä Lontoon Science Museumissa. Isompi kone, varsinainen tietokone (Analyyttinen kone), ei koskaan valmistunut. Babbagen koneet sisältävät piirteitä, joita käytetään vielä nykyäänkin tietokoneiden suunnittelussa, ja ne olivat teoriassa kykeneviä suorittamaan minkä tahansa matemaattisen laskelman huomattavalla nopeudella.

Katso myös Logiikka, Tietokone.

Muinainen sivilisaatio. Babylonialaiset ja muut nuolenpääkirjoitusta kirjoittaneet käyttivät lukujärjestelmää, joka on sekoitus kymmenkantaista ja 60-kantaista lukujärjestelmää. Meidän järjestelmämme ajan ja kulmien mittaamiseen, joissa käytetään luvun 60 monikertoja ja tekijöitä, ovat todennäköisesti peräisin babylonialaisten järjestelmästä.

Stefan Banach (1892-1945) oli puolalainen matemaatikko. Hänet muistetaan parhaiten nimeään kantavista Banach-Tarskin paradoksista ja Banachin avaruuden käsitteestä.

Banach työskenteli abstraktin joukko-opin, integraaliyhtälöiden, mittateorian, funktionaalianalyysin ja monen muunkin matematiikan alan parissa. Hänen panoksensa aksiomaattisen joukko-opin tutkimukseen oli erityisen tärkeä.

Katso myös Banachin-Tarskin paradoksi, Banachin avaruus, Banachin algebra.

Banachin avaruus, jonka normi toteuttaa epäyhtälön $\| x y \| \leq \| x \| \cdot \| y \|$.

Katso myös Banachin avaruus, Banach.

Normilla varustettu, täydellinen vektoriavaruus, jonka kerroinkunta on reaalilukujen tai kompleksilukujen joukko. Euklidinen avaruus on eräs esimerkki Banachin avaruudesta.

Katso myös Vektoriavaruus, Täydellinen, Banach, Banachin algebra, Hilbertin avaruus.

Valinta-aksiooman ja ei-mitallisten joukkojen teorian avulla voidaan osoittaa, että jos $\mathrm{B(1)}$ on 1-säteinen pallo ja $\mathrm{B(2)}$ on 2-säteinen pallo, niin on olemassa joukot $\mathrm{C_1}, \ldots, \mathrm{C_n}$ ja $\mathrm{D_1}, \ldots, \mathrm{D_n}$, joille pätee \[ \mathrm{B(1)}=\mathrm{C_1} \cup \mathrm{C_2} \cup ... \cup \mathrm{C_n}\] ja \[ \mathrm{B(2)}=\mathrm{D_1} \cup \mathrm{D_2} \cup ... \cup \mathrm{D_n}\] ja joukko $\mathrm{C_k}$ on isometrinen joukon $\mathrm{D_k}$ kanssa kaikilla $k$:n arvoilla. Nämä joukot ovat fraktaaleja. Niiden tilavuuksia ei voida laskea samalla tavalla kuin 'tavallisten' joukkojen tilavuuksia.

Katso myös Paradoksi, Valinta-aksiooma, Banach, Fraktaali.

Jos tetraedrin kaikilla tahkoilla on sama ympärysmitta, niin silloin tahkot ovat yhdenmuotoisia kolmioita.

Katso myös Lause, Tetraedri.

Thomas Bayes (1702--1761), englantilainen matemaatikko ja teologi, muistetaan pääasiassa Bayesin kaavasta sekä bayesilaisesta tilastollisesta päättelystä, joka on Bayesin kaavan motivoima. Hän julkaisi tutkimuksia todennäköisyyslaskennasta, differentiaali- ja integraalilaskennan loogisesta perustasta sekä asymptoottisista sarjoista.

Katso myös Bayesiläinen päättely, Bayesin kaava, Bayesin lause.

Tilastollinen päättely, joka perustuu Bayesin lauseeseen. Oletetaan tutkittavan satunnaismuuttujan noudattavan ns. a priori -jakaumaa. Kokeiden suorittamisen jälkeen tästä jakaumasta lasketaan ns. a posteriori -jakauma soveltamalla Bayesin lausetta.

Katso myös Bayes, Bayesin kaava, Bayesin lause.

Olkoon $\{ A_1, A_2, \ldots, A_n \}$ perusjoukon $\Omega$ ositus. Bayesin kaava on kaava \[ P(A_k \mid B) = \frac{P(B \mid A_k) P(A_k)}{\sum_{i=1}^{n} P(A_i)P(B \mid A_i)}, \] $k = 1, 2, \ldots, n$.

Katso myös Bayes, Lause, Bayesiläinen päättely, Ehdollinen todennäköisyys.

Olkoon $\{ A_1, A_2, \ldots, A_n \}$ perusjoukon $\Omega$ ositus. Bayesin kaava on kaava \[ P(A_k \mid B) = \frac{P(B \mid A_k) P(A_k)}{\sum_{i=1}^{n} P(A_i)P(B \mid A_i)}, \] $k = 1, 2, \ldots, n$.

Katso myös Bayes, Lause, Bayesiläinen päättely, Ehdollinen todennäköisyys.

Olkoon annettu joukko satunnaislukuja, jotka voivat olla mielivaltaisen suuria. Näiden lukujen ensimmäisten numeroiden esiintymisfrekvenssi ei noudata tasaista jakaumaa, kuten voisi olettaa. Sen sijaan kaikkein todennäköisimmin esiintyy numero 1 (todennäköisyys likimain 0,30), toiseksi todennäköisimmin esiintyy numero 2 (todennäköisyys likimain 0,18), kolmanneksi todennäköisimmin esiintyy numero 3 (todennäköisyys likimain 0,12), jne.

Katso myös Numero, Frekvenssi, Satunnainen.

Jakob Bernoulli (1654-1705) oli sveitsiläinen matemaatikko ja Johann Bernoullin veli. Hän työskenteli analyysin, mekaniikan, äärettömien sarjojen ja käyrien parissa. Bernoullin luvut on nimetty hänen mukaansa.

Katso myös Bernoullin luvut, Bernoulli Johann.

Johann Bernoulli (1667-1748) oli sveitsiläinen matemaatikko, Daniel Bernoullin isä ja Jakob Bernoullin veli. Hän opiskeli (silloin uutta) differentiaali- ja integraalilaskentaa ja keksi l'Hospitalin sääntönä tunnetun raja-arvojen laskusäännön. Hän työskenteli myös muun muassa differentiaaliyhtälöiden integroinnin, sarjojen summauksen ja variaatiolaskennan parissa.

Katso myös Ketjukäyrä, L'Hospitalin sääntö, Bernoulli Jakob, Brakistokroni, Variaatiolaskenta.

Satunnaiskoe, jossa on vain kaksi tulosvaihtoehtoa: $1$ ja $0$ (kyllä - ei tai onnistuminen - epäonnistuminen). Tulosvaihtoehtojen todennäköisyydet ovat $P(1)=p$ ja $P(0)=1-p$.

Katso myös Satunnaismuuttuja.

Bernoullin lukuja ovat funktion $x/(e^{x}-1)$ potenssisarjakehitelmässä esiintyvien termien $x^{n}/n!$ kertoimet. Kyseinen kehitelmä on \[ 1 - \frac{1}{2}x + \frac{1}{6} \frac{\mathrm{x}^2}{2!} - \frac{1}{30} \frac{\mathrm{x}^4}{4!} + \frac{1}{42} \frac{\mathrm{x}^6}{6!} - .... \] joten Bernoullin luvut ovat $1$, $-1/2$, $1/6$, $-1/30$, $1/42$, jne.

Katso myös Jono, Bernoulli Jakob.

Otaksuma (konjektuuri), että lukujen $n$ ja $2n$ välistä löytyy aina alkuluku olipa $n \ge 2$ mikä tahansa luonnollinen luku.

Katso myös Alkuluku, Otaksuma, Luonnollinen luku, Konjektuuri.

Friedrich Wilhelm Bessel (1784-1846) oli tähtitieteilijä ja matemaatikko. Hän teki merkittävän työn määrittäessään tähtien paikkoja, ratoja ja etäisyyksiä Auringosta. Hänen mukaansa nimetyt Besselin funktiot muodostavat funktioluokan, jota tarvitaan kolmen toisiaan puoleensa vetävän kappaleen liikkeen analysoimisessa.

Katso myös Besselin yhtälö, Besselin funktio (ensimmäinen laji), Besselin funktio (toinen laji), Neumannin funktio, Besselin funktio (kolmas laji), Hankelin funktio.

Kertalukua $n, n \neq 0$ oleva ensimmäisen lajin Besselin funktio $J_{n}(z)$ määritellään kaavalla \[J_n(z) = \frac{1}{\pi} \int_0^{\pi}\cos(nt - z\sin(t))\mathrm{d}t. \] Kun $n$ on positiivinen kokonaisluku, niin yllä oleva on yhtäpitävä määritelmän \[J_n(z) = \sum_{r=0}^{\infty}\frac{(-1)^r}{r!\Gamma(n+r+1)} \left(\frac{z}{2}\right)^{n+2r} \] kanssa. Nämä funktiot esiintyvät aaltoyhtälön sylinterikoordinaateissa ilmaistussa ratkaisussa ja toteuttavat Besselin yhtälön.

Katso myös Funktio, Kuvaus, Bessel Friedrich Wilhelm, Besselin yhtälö, Besselin funktio (toinen laji), Neumannin funktio, Besselin funktio (kolmas laji), Hankelin funktio.

Kolmannen lajin Besselin funktioita on kahdenlaisia: \[ H_n^{(1)}(z)=J_n(z)+iY_n(z) \] ja \[ H_n^{(2)}(z)=J_n(z)-iY_n(z), \] missä $J_n$ ja $Y_n$ ovat ensimmäisen ja ja toisen lajin Besselin funktioita. Kolmannen lajin Besselin funktiot ovat Besselin yhtälön ratkaisuja.

Katso myös Funktio, Kuvaus, Bessel Friedrich Wilhelm, Besselin yhtälö, Besselin funktio (ensimmäinen laji), Besselin funktio (toinen laji), Neumannin funktio.

Ensimmäisen lajin Besselin funktioiden tiettyjä yksinkertaisia kombinaatioita kutsutaan toisen lajin Besselin funktioiksi ja merkitään $Y_n(z)$. Ne ovat Besselin yhtälön ratkaisuja.

Katso myös Funktio, Kuvaus, Bessel Friedrich Wilhelm, Besselin yhtälö, Besselin funktio (ensimmäinen laji), Besselin funktio (kolmas laji), Hankelin funktio.

Besselin yhtälöksi kutsutaan differentiaaliyhtälöä \[z^2 \frac{\mathrm{d}^2 y}{\mathrm{d}z^2} + z\frac{\mathrm{d}y}{\mathrm{d}z}+ (z^2 - n ^2)y = 0. \]

Katso myös Bessel Friedrich Wilhelm, Besselin funktio (ensimmäinen laji), Besselin funktio (toinen laji), Neumannin funktio, Besselin funktio (kolmas laji), Hankelin funktio, Yhtälö.

Kreikkalainen kirjain $\beta$ (pieni kirjain) tai $B$ (iso kirjain), lausutaan beeta. Äänneasu on sama kuin suomen b-kirjaimen.

$\beta$:lla merkitään joskus betajakaumaa.

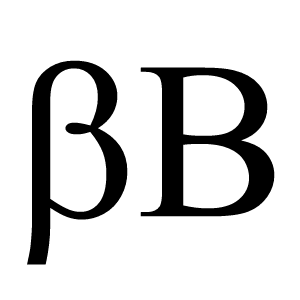
Katso myös Kreikkalaiset kirjaimet, Betajakauma.

Betafunktio parametreinaan $p$ ja $q$ määritellään kaavalla \[\mathrm{B}(p,q) = \int_0^1 x^{p-1}(1-x)^{q-1}\mathrm{d}x. \] Se voidaan määritellä myös kaavalla \[ \mathrm{B}(p,q) = \frac{\Gamma(p)\Gamma(q)}{\Gamma (p+q)}, \] missä $\Gamma(t)$ on gammafunktio.

Katso myös Funktio, Kuvaus, Gammafunktio.

Jatkuva jakauma, joka on määritelty välillä $(0, 1)$ ja jonka tiheysfunktio on \[ f(x) = \frac{1}{\mathrm{B}(m,n)} x^{m-1} (1- x)^{n-1}, \] missä $\mathrm{B}(m,n)$ on betafunktio ja $m, n$ ovat positiivisia.

Katso myös Jakauma, Beta.

Jakson kahdentumispiste (bifurkaatiopiste) on sellainen systeemin parametrien joukko, jossa systeemin käyttäytyminen muuttuu kvantitatiivisesti. Jokin systeemi voi esimerkiksi olla stabiili arvoilla $k \lt 1$ ja epästabiili arvoilla $k \gt 1$, missä $k$ on systeemin parametri. Tällöin $k = 1$ on jakson kahdentumispiste.

Katso myös Piste.

Funktio on bijektiivinen, jos se on sekä injektiivinen että surjektiivinen.

Katso myös Surjektiivinen, Bijektio, Injektiivinen.

Bijektio tarkoittaa kuvausta, joka on sekä injektio että surjektio. Bijektioita ovat täsmälleen ne kuvaukset, joilla on käänteiskuvaus.

Katso myös Surjektiivinen, Kuvaus, Isomorfismi, Yksi yhteen kuvaus, Yksi yhteen vastaavuus, Kuvajoukko, Bijektiivinen, Lähtöjoukko, Funktion kuvajoukko, Duaali, Numeroituva, Määrittelyjoukko, Duaaliavaruus, Isomorfia, Funktio.

Bilateraalisesti symmetrinen kuvio voidaan leikata kahteen identtiseen osaan, jotka ovat toistensa peilikuvia.

Suoraa, jota pitkin kaksiulotteinen kuvio on leikattu, kutsutaan symmetriasuoraksi.

Tasoa, jota pitkin kolmiulotteinen kuvio on leikattu, kutsutaan symmetriatasoksi.

Katso myös Peilaussymmetria.

Kahden muuttujan lauseke, joka on lineaarinen kummankin muuttujan suhteen. Toisin sanoen, lauseke, jossa muuttujia on kerrottu vakioilla tai toinen toisillaan, mutta kumpaakaan muuttujaa ei ole korotettu neliöön tai mihinkään muuhun potenssiin.

Esimerkiksi $6x+2y+4xy+2$ on bilineaarinen lauseke.

Katso myös Lauseke.

Olkoot $V$ ja $W$ vektoriavaruuksia kerroinkuntana $\mathbf{F}$. Tällöin funktiota $\varphi : V \times W \to \mathbf{F}$ kutsutaan bilineaariseksi muodoksi, jos se on lineaarinen kummankin muuttujan suhteen erikseen. Toisin sanoen, jos kiinnitetään piste kummasta tahansa vektoriavaruudesta, niin tuloksena saadaan toisen muuttujan suhteen lineaarinen kuvaus.

Esimerkiksi, jos $V = W = \mathbf{F}^n$, niin kuvaus $\varphi(v,w) = \sum_{i=1}^n v_iw_i$ on bilineaarinen muoto.

Jos $v_1, \ldots, v_n$ on $V$:n kanta ja $w_1, \ldots, w_m$ on $W$:n kanta, niin liitämme bilineaariseen kuvaukseen $\varphi$ matriisin $A$ asettamalla $A_{ij}= \varphi(v_i, w_j)$. Tällöin $\varphi(x,y)$ voidaan laskea kaavalla \[ \varphi (x,y) = \sum_{i=1}^n \sum_{j=1}^m x_i y_j A_{ij} = x ^{T} Ay. \] Avaruuksille $V$ ja $W$ voidaan aina löytää sellaiset kannat, että muodon $\varphi$ matriisi on \[ \left( \begin{array}{cc} I_r & 0 \\ 0 & 0 \end{array} \right), \] missä $I_r$ on $r \times r$-identiteettimatriisi.

Katso myös Kuvaus, Surkastunut, Kunta, Vektoriavaruus, Pistetulo, Skalaaritulo, Sisätulo, Funktio.

Miljoona miljoonaa eli $10^{12}$ eli 1000000000000.

Amerikanenglannin sana billion tarkoittaa samaa kuin suomen miljardi eli lukua $10^{9}.$ Monet kääntäjät ovat tästä tietämättömiä ja aiheuttavat sekaannusta.

Katso myös Miljoona, 1000000, Kymmenen potenssit, Miljardi.

Lyhenne sanasta binääri tai binäärinen.

Katso myös Lyhenne.

Binomiksi kutsutaan lauseketta, joka sisältää kaksi termiä, joiden välissä on $+$ tai $-$.

Binomikaava kertoo, mitä tapahtuu, kun binomi korotetaan annettuun potenssiin. Kehitelmää ja sarjaa, johon binomikaava johtaa, kutsutaan binomikehitelmäksi ja binomisarjaksi. Binomijakauman määrittelevä kaava on yhteydessä binomikehitelmään.

Katso myös Lauseke, Erisuuri, Ei sama kuin, Binomijakauma, Binomikaava.

Onnistumiskertojen lukumäärän jakauma riippumattomissa toistokokeissa. Jakauman pistetodennäköisyysfunktio on \[ P(r) = \left( \begin{array}{c} \mathrm{n} \\ \mathrm{r}\end{array} \right ) \mathrm{p}^{\mathrm{r}} \mathrm{(1-p)}^{\mathrm{n-r}} \] missä $ \left ( \begin{array}{c} \mathrm{n} \\ \mathrm{r} \end{array} \right )$ on nk. binomikerroin. Binomijakauman odotusarvo on $n \cdot p$ ja varianssi $n \cdot p \cdot q$.

Katso myös Binomi, Jakauma, Binomikerroin.

\[ ( x + y )^{n} = \sum_{i=0}^{n} {n \choose i} x^{i} y^{n-i} = x^{n} + nx^{n-1} y + {n \choose 2} x^{n-2} y^2 + ... + nxy^{n -1} + y^{n} \]

Kaikilla luonnollisilla luvuilla $n$ ja kaikilla kompleksiluvuilla $x, y$ pätee \[ (x+y)^n= \sum_{r=0}^{n} {n \choose r} x^ry^{n-r}. \] Tämä voidaan todistaa induktiolla käyttämällä Pascalin kolmion perustana olevaa kaavaa \[ {{n+1} \choose r} = {n \choose r} + {n \choose {r-1}}. \]

Katso myös Lause, Valita, Binomi.

Merkintä ${p \choose q}$ tarkoittaa lukua $\frac{p!}{q! (p-q)!}$. Myös merkintää $^{p}C_{q}$ käytetään. Tällaisia lukuja kutsutaan binomikertoimiksi siksi, että ne esiintyvät binomikehitelmissä. Esimerkiksi: \[ (x + y)^4 = {4 \choose 0} x^4 + {4 \choose 1} x^3 y+ {4 \choose 2} x^2 y^2 + {4 \choose 3} xy^3 + {4 \choose 4} y^4 \] \[ = x^4 + 4 x^3 y + 6 x^2 y^2 + 4 xy^3 + y^4. \]

Binomikerroin ${p \choose q}$ esiintyy Pascalin kolmiossa rivillä $p$ paikassa $q$ vasemmalta laskettuna. (Huomaa, että laskeminen aloitetaan nollasta.)

Katso myös Kerroin, Valita, Kombinaatio, Merkintätapa, Notaatio, Binomijakauma, Binomikertoimien summa, Binomikerrointen laskusääntöjä.

\[ {n \choose k} = {n \choose{n-k}} \] \[ {n \choose n} = 1 \] \[ {n \choose 0} = 1 \] \[ {n \choose 1} = n \] \[ {n \choose k} + {n \choose {k+1}} = {{n+1} \choose {k+1}} \]

Katso myös Lause, Binomikerroin.

\[ {n \choose r} + {n \choose {r+1}} = {{n+1} \choose {r+1} }. \]

Katso myös Identiteetti, Binomikerroin.

Hakumenetelmä tiedon hakemiseen järjestetystä tietojoukosta, jossa toistuvasti verrataan joukon keskimmäistä alkiota etsittävään alkioon, jotta saadaan selville, kummalla puolella keskimmäistä alkiota etsittävä alkio sijaitsee, ja sitten unohdetaan joukon toinen puolikas.

Katso myös Algoritmi, Lineaarinen haku.

Lukujärjestelmä, jonka kantaluku on 2. Binäärilukujärjestelmässä jokainen luku ilmaistaan numerojen 0 ja 1 avulla.

Katso myös Desimaali, Kolmijärjestelmä, Lukujärjestelmä, Kantaluku.

Informaatioteoriassa suure \[h = - \sum_i p(i) \log_2(p(i)), \] missä $p(i)$ on lähteen lähettämän symbolin $i$ todennäköisyys.

Funktio, joka kuvaa annetun joukon alkioparin saman joukon alkioksi. Esimerkiksi yhteenlasku ja kertolasku ovat binäärisiä kuvauksia.

Luonnollisten lukujen vähennyslasku ei ole binäärinen kuvaus, koska kahden luonnollisen luvun erotus ei välttämättä ole luonnollinen luku. Esimerkiksi $1-2 = -1$ ei ole luonnollinen luku.

Katso myös Yhteenlasku, Modulo, Kertolasku, Laskutoimitus, Neutraalialkio, Jakolasku, Vaihdannainen, Kommutatiivinen, Vähennyslasku, Vähentäminen, Rengas, Antikommutaattori, Groupoidi, Jakaminen.

Jos $A$ ja $B$ ovat joukkoja, niin $R \subseteq A \times B$ on binäärinen (2-paikkainen) relaatio joukkojen $A$ ja $B$ välillä.

Katso myös Joukko.

Binääriluku: joko $0$ tai $1$. Sanaa bitti käytetään lähinnä tietojenkäsittelyssä.

Katso myös Tavu, Lyhenne.

Suljettu konveksi käyrä, jonka leveys on vähintään 1, voi sisältää ympyrän, jonka halkaisija on 2/3.

Ison-Britannian koodi- ja salakirjoituskeskuksen päämaja toisen maailmansodan aikana. Kuuluisa onnistuneista yrityksistä murtaa saksalaisten Enigma-koneiden tuottama koodi. Alan Turing työskenteli siellä muiden englantilaisten matemaatikkojen kanssa.

Jos $f$ on suljetulla välillä $[a,b]$ jatkuva funktio, $f(a) \neq f(b)$ ja $k$ on pisteiden $f(a)$ ja $f(b)$ välissä oleva luku, on $f(c) = k$ jollakin $a \lt c \lt b$.

Katso myös Lause, Funktio, Kuvaus, Jatkuva, Jatkuvuus.

Struktuuri, jonka muodostavat joukko $S$ sekä kaksi vaihdannaista ja liitännäistä laskutoimitusta $+$ ja $\times$, jotka toteuttavat seuraavat ehdot.

1) Kummallakin laskutoimituksella on neutraalialkio joukossa $S$, ja nämä alkiot eivät ole samoja.

2) Kumpikin laskutoimitus noudattaa osittelulakia toisen suhteen.

3) Jokaisella joukon $S$ alkiolla on yksi ja sama käänteisalkio joukossa $S$ kummankin laskutoimituksen suhteen.

Huomaa, että laskutoimitukset $+$ ja $\times$ eivät ole aivan samat kuin tavallisten lukujen yhteen- ja kertolasku. Tällaista algebraa käytetään paljon logiikassa ja joukko-opissa.

Katso myös Algebra.

Mille tahansa tapahtumille $A_1, A_2, \dots$, \[ \mathbb{P} \left( \bigcup_i A_i \right) \leq \sum_i \mathbb{P}(A_i). \]

Katso myös Erisuuruus, Tapahtuma, Todennäköisyys, Epäyhtälö.

Robert Boyle (1627--1691), irlantilainen fyysikko ja kemisti, joka muistetaan Boylen laista. Boylen laki kuvailee ideaalikaasun. Pitkällä sarjalla ilmapumpun avulla tehtyjä kokeita hän osoitti, että ääni ei kulje tyhjiön läpi, ja että liekit tarvitsevat ilmaa. Hän myös selvitti ilman elastiset ominaisuudet. Hän oivalsi, että tyhjiö voi olla olemassa, ja että ei ole kaiken täyttävää "eetteriä" (ajatus, jota ei pystytty lopullisesti kumoamaan seuraaviin 300 vuoteen). Hän kirjoitti vähemmän menestyksekkäästi optiikasta. Hän oli Royal Societyn perustajajäsen ja eräs ensimmäisistä, joka sovelsi matemaattisia menetelmiä kemiaan ja fysiikkaan.

Intialainen matemaatikko, joka eli vuosina 598-665. Hänen ansioikseen luetaan nollan ja negatiivisten lukujen tuominen aritmetiikkaan. Hänen tärkein kirjansa oli hindulaisen tähtitieteen ja matematiikan runollinen esitys. Hän teki töitä pääasiassa toisen asteen yhtälöiden ja yhtälöryhmien yleisten ratkaisujen etsimisen parissa.

Olkoot $(0,H)$ ja $(L,0)$ kaksi pistettä. Polkua $(x,r(x))$, jota pitkin kappale liukuu pisteestä $(0,H)$ kitkattomasti pisteeseen $(L,0)$ lyhyimmässä mahdollisessa ajassa, kutsutaan brakistokroniksi. Kyseinen polku ei ole suora, vaan pisteiden $(0,H)$ ja $(L,0)$ kautta kulkeva sykloidi.

Katso myös Bernoulli Johann, Sykloidi.

Kartioleikkauksen ympärille piirretyn kuusikulmion päälävistäjät (vastakkaiset kulmat yhdistävät suorat) leikkaavat samassa pisteessä.

Logaritmi järjestelmässä, jonka kantaluku on 10. Luvun $x$ kymmenkantainen logaritmi on se luku, jonka ilmaisemaan potenssiin 10 on korotettava, jotta saataisiin $x$.

Katso myös Logaritmi.

Millä luvuilla $n$ pätee, että $n!+1$ on jonkin luvun $m$ neliö eli $m^2$? Edellä $n! = 1 \cdot 2\cdot \ldots \cdot n$ on luvun $n$ kertoma.

Luvut $4$, $5$ ja $7$ ovat ongelman ainoat tunnetut ratkaisut.

Katso myös Kertoma.

Kolmiossa $ABC$ on kaksi sellaista sisäpistettä $X$ ja $Y$, joilla on ominaisuudet \[ \angle BAX = \angle CBX = \angle ACX = \angle ABY = \angle BCY = \angle CAY = \omega. \] Pisteitä $X$ ja $Y$ kutsutaan kolmion $ABC$ Brocardin pisteiksi ja kulmaa $\omega$ Brocardin kulmaksi.

Brocardin kulma $\omega$ on yksikäsitteinen ja se toteuttaa ehdon $\cot(\omega) = \cot(A) + \cot(B) + \cot(C)$.

Olkoon $B^n = \{ x \in \mathbb{R}^n \mid \|x\| \le 1 \}$. Brouwerin kiintopistelause sanoo, että mikäli kuvaus $f : B^n \rightarrow B^n$ on jatkuva, niin sillä on kiintopiste.

Katso myös Kiintopistelause.

Hyvin pieni hiukkanen joutuu nesteessä satunnaisliikkeeseen, koska siihen osuu jatkuvasti nestemolekyylejä. Tätä satunnaisliikettä kutsutaan Brownin liikkeeksi sen ensimmäisenä havainneen tiedemiehen mukaan. Samaa nimeä käytetään liikettä kuvaavista matemaattisista malleista.

Vakio, jota merkitään kirjaimella $B$ ja joka on kaikkien alkulukukaksosten käänteislukujen summa: \[ B = \left( \frac{1}{3}+ \frac{1}{5} \right) + \left( \frac{1}{5}+ \frac{1}{7} \right) + \left( \frac{1}{11}+ \frac{1}{13} \right) + \left( \frac{1}{17}+ \frac{1}{19} \right) + \left( \frac{1}{29}+ \frac{1}{31} \right) + ... \]

(Huomaa, että luku $5$ esiintyy kahdessa alkulukukaksosparissa, joten sen käänteisluku esiintyy myös kahdesti yllä olevassa summassa. Jotkut matemaatikot jättävät toisen niistä pois.)

Brunin vakion likiarvo on $1.9021605820$. Se, että yllä oleva sarja suppenee, osoittaa että alkulukukaksoset ovat harvassa verrattuna tavallisiin alkulukuihin, joiden käänteislukujen summa hajaantuu. Yllä olevan sarjan suppeneminen ei kuitenkaan kerro sitä, onko alkulukukaksosia äärellinen vai ääretön määrä.

Katso myös Vakio.

Oletetaan, että lattialle on aseteltu yhdensuuntaisia suoria siten, että kahden vierekkäisen suoran etäisyys on aina $1$. Jos lattialle tipautetaan neula, jonka pituus on $1$, niin todennäköisyys, että neula asettuu poikittain jonkin suoran päälle, on $\frac{2}{\pi}$.

Katso myös Koe, Pii, $\pi$.