PDF

11. Analyysistä tulee täsmällistä 1800-luvulla

1700-luku oli ollut matemaattisessa analyysissä villin keksimisen aikaa; menetelmät toimivat ja se riitti, loogisten perusteiden pitävyyttä ei juuri kyselty. 1800-luvulle tultaessa kriittisemmät ja enemmän täsmällisyyttä korostavat tutkimusasenteet alkoivat saada jalansijaa. Kompleksilukujen parempi ymmärtäminen johti niiden käyttöön ja kompleksimuuttujan funktioteorian syntyyn. - Tässä käsitellään muutamaa analyysin kehitykseen keskeisesti vaikuttanutta matemaatikkoa. Heistä useiden ansiot ulottuvat muillekin matematiikan aloille.

11.1 Cauchy

Täsmällisyyden pioneeri analyysissä on (Gaussin ohella) ranskalainen Augustin Cauchy (1789-1857). Hän oli École Polytechniquen kasvatti, alkoi uransa insinöörinä, mutta siirtyi pian matematiikkaan ja mm. École Polytechniquen opettajaksi. Cauchyn École Polytechniquelle kirjoittamaan oppikirjasarjaan kuuluva Cours d'analyse (1821) perustuu jokseenkin nykyaikaiseen raja-arvon määritelmään, jossa $\delta$ ja $\epsilon$ eivät kuitenkaan vielä eksplisiittisesti esiinny, ja sarjojen suppenemisen tarkkaan tutkimiseen. Raja-arvon Cauchy määritteli sanallisesti:

''Jos muuttujan peräkkäiset arvot lähestyvät rajatta kiinteätä arvoa niin, että ne lopulta eroavat tästa miten vähän tahansa, niin mainittua kiinteää arvoa kutsutaan muiden arvojen raja-arvoksi.''

Jatkuvuuden Cauchy määritteli siten, että muuttuja $f(x+\alpha)- f(x)$ tulee mielivaltaisen pieneksi, kun muuttuja $\alpha$ pienenee rajatta. Usean muuttujan funktion raja-arvon suhteen Cauchy erehtyi. Hän oletti funktion, joka on kunkin muuttujansa suhteen jatkuva olevan itsekin jatkuva. Jatkuvien funktioiden väliarvolauseen, Bolzanon lauseen, Cauchy todisti konstruoimalla vähenevän ja kasvavan jonon (X_n), (x_n), x_n<X_n, siten että f(x_n) ja f(X_n) ovat erimerkkiset ja $X_n-x_n=\frac{1}{m}(X_{n-1}-x_{n-1})$. Jonot suppenevat kohti yhteistä raja-arvoa x, ja jatkuvuus takaa, että f(x)=0.

Sarjojen suppenemisen systemaattinen tutkiminen ja ylipäänsä suppenemisen tärkeyden oivaltaminen on paljolti Cauchyn ansiota. Suppenemisen juuri- ja suhdetestit esiintyvät hänellä, samoin sarjojen tulon antava Cauchyn kertosääntö. Cauchy yritti todistaa Newtonin binomisarjakehitelmän pätevyyden seuraavasti: Jos

$$\phi(a)=1+ax+\frac{a(a-1)}{2!}x^2+\dots,$$

niin kertosääntö antaa $\phi(a+b)=\phi(a)\phi(b)$. Mutta Cauchyn jatkuville funktioille todistaman tuloksen perusteella tällaisen funktionaaliyhtälön ratkaisuja ovat funktiot $\phi(a)=\phi(1)^a$. Koska $\phi(1)=1+x$, on $\phi(x)=(1+x)^a$. Binomisarjan selvitti lopullisesti Abel v. 1826.

Funktion y = f(x) differentiaali dy on Cauchylle luku $f'(x)\,dx$, missä dx on äärellinen luku. Funktion integraalin määritelmää Cauchy ei perustanut antiderivaattaan. Hän määritteli integraalin $\int_a^b f(x)dx$ summien

$$S_n = (x_1 - a)f(a) + (x_2 -x_1)f(x_1) +\dots + (b -x_n)f(x_n)$$

raja-arvoksi, kun välin $(a,\,b)$jakovälien (x_i,x_i+1) pituudet lähestyvät nollaa. Integraalin Cauchy, joka ei tuntenut tasaisen jatkuvuuden käsitettä, väitti olevan laskettavissa aina, kun f on jatkuva. Näin määritellyn integraalin ja antiderivaatan yhteyden osoittamiseen Cauchy käytti todistamaansa differentiaalilaskennan väliarvolausetta,

$$f(x)- f(y)=f'(\xi)(x-y),$$

jonka erikoistapauksen oli tosin esittänyt Michel Rolle (1652-1719) yli sata vuotta aikaisemmin, ja väliarvolauseen yleistystä

$$\frac{f(x)-f(y)}{g(x)-g(y)}=\frac{f'(\xi)}{g'(\xi)}.$$

Useissa Cauchyn päättelyissä olennaisen Cauchyn yleisen suppenemisehdon, sen, että lukujonon a_n suppenemiselle on välttämätöntä ja riittävää erotuksen |a_n+p-a_n| pienuus suurilla n:n ja kaikilla p:n arvoilla, oli kyllä havainnut myös tsekkiläinen hengenmies Bernhard Bolzano (1781-1848), jonka aikaansa edellä oleva tuotanto jäi pitkään laajemmalti tuntemattomaksi. Vuonna 1817 julkaisemassaan kirjasessa, siis ennen Caychya, Bolzano esitti ensimmäisenä täsmällisessä muodossa nykyaikaisen jatkuvuuskäsitteen: f on jatkuva, jos se muuttuu niin, että $f(x+\omega)-f(x)$ voidaan tehdä pienemmäksi kuin mikä hyvänsä annettu suure, kun han vain $\omega$ tehdään niin pieneksi kuin halutaan. - Cauchyn suppenemisehdon todistaminen onnistuu vain, jos reaaliluvun käsite on täsmällisesti määritelty.

Tasaisen suppenemisen käsite jäi ilmeisesti vielä Cauchylle jonkin verran epämääräiseksi, vaikka hänen myöhemmissä kirjoituksissaan siihen viittaavia seikkoja onkin. Tasaisen suppenemisen määritelmän ensimmäisenä esittäjänä pidetään englantilaista fyysikkoa George Stokesia (1819-1903).

Cauchy on (jälleen Gaussin ohella, joka ei kuitenkaan aikalaisille julkaissut tuloksiaan) funktioteorian, eli kompleksilukumuuttujan kompleksilukuarvoisten funktioiden tutkimuksen perustaja. Jo Euler ja d'Alembert olivat joutuneet hydrodynamiikassa tekemisiin osittaisdifferentiaaliyhtälöparin

$$\frac{\partial_u}{\partial_x} = \frac{\partial_v}{\partial_y}... ...-\frac{\partial_u}{\partial_y} = \frac{\partial_v}{\partial_x}$$

kanssa, mutta Cauchy totesi näiden yhtälöiden, sittemmin Cauchyn-Riemannin yhtälöinä tunnettujen, merkityksen kompleksilukumuuttujan z=x+iy funktion w(z) =u(z) + iv(z)derivoituvuudelle. Cauchy tutki derivoituvien kompleksifunktioiden eli analyyttisten funktioiden tason käyriä pitkin muodostettuja integraaleja; vuonna 1825 hän esitti funktioteoriassa keskeisen merkityksen omaavan Cauchyn integraalilauseen, jonka mukaan tällaisen funktion yhdesti yhtenäistä aluetta G ympäröivää umpinaista käyrää ${\cal C}$ pitkin laskettu integraali aina häviää. Lause on - ainakin jatkuvan derivaatan omaavien funktioiden tapauksessa yksinkertainen seuraus taso- ja käyräintegraaleja yhdistävästä Greenin kaavasta:

$$\begin{split} \int_{\mathcal{C}}f(t)\,dt &=\int_{\mathcal{C}}... ...rac{\partial u}{\partial x}\right) \,dx\,dy\\ &=0. \end{split}$$

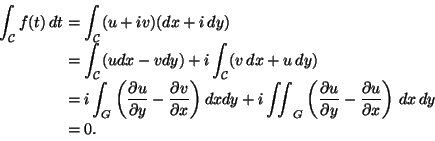
Kuusi vuotta myöhemmin Cauchy osoitti, etä analyyttinen funktio voidaan kehittää potenssisarjaksi, jonka suppenemissäde on kehityskeskuksen ja funktion lähimmän erikoispisteen etäisyys. Cauchy on Eulerin jälkeen kaikkien aikojen tuotteliaimpia matemaatikkoja. Hänen tutkimuksensa koskevat useimpia matematiikan aloja (esim. determinanttien teoria nykymuodossaan on suurelta osin hänen työtään, ja tavallisten sekä osittaisdifferentiaaliyhtälöiden teoriassa hänen panoksensa on merkittävä), ja niiden runsaus ja laajuus sai Ranskan tiedeakatemian määräämään julkaisusarjansa artikkelien enimmäispituuden neljäksi sivuksi. Vuoden 1830 vallankumouksen yhteydessä katolinen ja poliittisilta mielipiteiltään vanhoillinen Cauchy joutui jättämään Ranskan; hän oleskeli maanpaossa mm. Prahassa. Ei ole kuitenkaan mitään todisteita Cauchyn ja Bolzanon mahdollisista yhteyksistä.

11.2 Abel, Jacobi, Dirichlet

Norjassa Finnöyn saarella lähellä Stavangeria syntynyt Niels Henrik Abel (1802-29) on yksi niistä (onneksi verraten harvoista) ensi luokan matemaatikoista, joiden elämä on jäänyt (keuhkotaudin vuoksi) traagisen lyhyeksi. Abel oli köyhä ja saapui Euroopan periferiasta. Tämä lienee osasyy siihen, että häntä kohdeltiin tieteellisissä keskuksissa useammin kuin kerran tylysti. Gauss ei vastannut hänen kirjeisiinsä, eikä Ranskan akatemia suostunut ottamaan hänen käsikirjoitustaan vastaan, ''koska käsialasta ei saanut selvää''. Abel elätti itseään mm. yksityistunteja antamalla. Uutinen Abelin nimityksestä professoriksi Berliiniin saapui Norjaan vasta Abelin kuoleman jälkeen. Abel oli ensimmäisiä, jotka oivalsivat suppenemisen tärkeyden päättymättömillä sarjoilla operoitaessa (''matematiikassa ei ole yhtäkään sarjaa, jonka suppeneminen olisi pitävästi osoitettu!''). Hänet muistetaan kuitenkin parhaiten jo Cardanon ajoista jatkuneiden korkeampaa kuin neljättä astetta olevien algebrallisten yhtälöiden algebrallisten ratkaisujen etsimisen lopettajana; viidennen asteen yhtälön yleisen algebrallisen ratkeamattomuuden Abel todisti jo 19-vuotiaana. (Hiukan puutteellisemman viidennen asteen yhtälön ratkeamattomuustodistuksen oli jo ennen Abelia esittänyt italialainen lääkäri Paolo Ruffini, 1765-1822.)

Abel tutki elliptisiä integraaleja ja oivalsi Legendreltä huomaamatta jääneen elliptisen integraalin käänteisfunktion kaksijaksoisuuden. Saman havainnon tekivät Abelista riippumatta Gauss ja saksalainen Carl Jacobi (1804-51), joka myös kehitteli näiden käänteisfunktioiden, elliptisten funktioiden, teoriaa pitemmälle. Jacobilta ovat peräisin elliptisten funktioiden ja trigonometristen funktioiden sukulaisuuteen viittaavat elliptisten funktioiden merkinnät sn, cn ja dn. - Abel kiinnitti myös huomiota integraaleihin $\int\frac{1}{\sqrt{P(x)}}\,dx,$ joissa P on korkeampaa kuin neljättä astetta oleva polynomi, ja näiden käänteisfunktioihin eli Abelin funktioihin. Jacobi puolestaan osoitti, että vastaavanlaisia käänteisfunktioita voi tutkia myös, kun muuttujia on useampia.

Jacobin ansioita on myös (alkuaan Cauchyn käyttöönottaman) n:n muuttujan n:n funktion systeemin funktionaalideterminantin eli Jacobin determinantin merkityksen oivaltaminen ja funktionaalideterminanttien systemaattinen teoria - Jacobi halusi pitää tavallisiakin determinantteja n:n muuttujan n:n lineaarifunktion systeemin funktionaalideterminanttina.

Saksalainen, vaikkakin ranskalaista sukua oleva Peter Lejeune Dirichlet (1805-59) oli Gaussin seuraaja Göttingenin yliopistossa; hänen postuumeina julkaistut lukuteorian luentonsa popularisoivat ja täydensivät Gaussin vaikeasti luettavaa Disquisitiones Arithmeticæ -teosta. Dirichlet'n tunnetuin lukuteoreettinen tulos kertoo, että jos a:lla ja b:llä ei ole yhteisiä tekijöitä, niin aritmeettisessa jonossa a_n=an+b on äärettömän monta alkulukua. Dirichlet'n keksintöä on myös sinänsä yksinkertaisen laatikkoperiaatteen tai kyyhkyslakkaperiaatteen (jos n+1 esinettä sijoitetaan n:ään laatikkoon, niin ainakin yhdessä laatikossa on enemmän kuin yksi esine) monipuolinen käyttökelpoisuus lukuteoriassa. Analyytikkona Dirichlet kehitti mm. Fourier'n trigonometrisia sarjoja. Dirichlet oli ensimmäinen vakavasti Fourier-sarjan suppenemista tutkinut matemaatikko. Fourier-sarjojen yhteydessä Dirichlet johtui moderniin funktion määritelmään:

Jos muuttuja y liittyy muuttujaan x siten, että aina kun x:lle annetaan jokin lukuarvo, on olemassa sääntö, jonka perusteella y saa yksikäsitteisen lukuarvon, niin y:n sanotaan olevan x:n funktio.

Esittämänsä määritelmän mukaisesti Dirichlet antoi esimerkin funktiosta, jolla ei ole analyyttistä lauseketta: kun x on rationaalinen, niin y = c, ja kun x on irrationaalinen, niin $y=d\ne c$. Toisaalta Dirichlet osoitti, että kohtuullisen säännöllisen funktion f Fourier-sarjan rajafunktio on yleensä f, ja että sarjan summa pisteissä, joissa funktio on epäjatkuva, mutta omaa toispuoliset raja-arvot, sarjan summa on raja-arvojen keskiarvo. - Käsite sarjan ehdollinen suppeneminen on peräisin Dirichlet'ltä.

Dirichlet'n probleema on potentiaaliteorian keskeinen ongelma: alueen G reunalla määritellyn funktion jatkaminen G:hen siten, että jatko toteuttaa Laplacen differentiaaliyhtälön. Probleeman yhteydessä Dirichlet esitti Dirichlet'n periaatteen nimellä tunnetun osittain puutteellisen variaatioperiaatteen, joka tuli näyttelemään tärkeää osaa funktioteorian kehityksessä 1800-luvun jälkipuoliskolla. Periaate sanoo, että Dirichlet'n probleeman ratkaseva funktio minimoi integraalin $\int_G \vert\nabla f\vert^2\,dV$ kaikkien G:n reunalla annettuun funktioon yhtyvien funktioiden joukossa. Dirichlet ja periaatetta käyttäneet muutkin matemaatikot eivät selvittäneet, onko minimointitehtävällä varmasti ratkaisu. Asian selvitti lopullisesti vasta Hilbert vuonna 1899.

11.3 Riemann

Dirichlet'n seuraaja Göttingenissä - joka 1800-luvulla ja 1900-luvun alussa oli maailman merkittävimpiä matemaattisia tutkimuskeskuksia - oli Bernhard Riemann (1826-66), erittäin omaperäinen ja modernin matematiikan kehitykseen syvästi vaikuttanut tutkija. Abelin tavoin Riemann kuoli ennenaikaisesti keuhkotautiin.

Riemannin väitöskirja (1851) käsitteli kompleksimuuttujan funktioita. Se sisälsi mm. Riemannin kuvauslauseen, jonka mukaan jokainen yhdesti yhtenäinen tasoalue voidaan yksikäsitteisesti ja konformisesti, siis mikroskooppisella tasolla yhdenmuotoisuuskuvauksena, kuvata mille hyvänsä muulle samanlaiselle alueelle jonkin analyyttisen funktion avulla, ja vallankumouksellisen idean analyyttisten funktioiden, kuten $\sqrt{z}$:n, monikäsitteisyyden poistamisesta siten, että funktion määrittelyjoukkona pidetään tasoalueen sijasta sen päällä mahdollisesti useana kerroksena lepäävää pintaa. Tästä oivalluksesta alkunsa saanut Riemannin pintojen teoria on sittemmin johtanut analyysin ja topologian monipuoliseen vuorovaikutukseen ja vaikuttanut ratkaisevasti siihen, että topologiasta on kehittynyt oma elinvoimainen matematiikan haaransa. Riemannin merkittäviä saavutuksia analyysin alalla on Cauchyn integraalia paljon käyttökelpoisempi Riemannin integraali, jonka Riemann kehitti Fourier-sarjojen tutkimuksen yhteydessä mahdollistamaan epäjatkuvien funktioiden integroinnin. Riemannin perusidea oli korvata Cauchyn käyttämä arvo f(x_i) integraalia määrittelevissä summissa $\sum f(x_i)(x_{i+1}-x_i)$ mielivaltaisella arvolla $f(\overline x_i)$, missä $x_i\le \overline x_i\le x_{i+1}$. Integroituvuuden ehdoksi muodostuu summan $\sum O_i(x_{i+1}-x_i)$, missä O_i on f:n kokonaisoskillaatio välillä $[x_i,\,x_{i+1}]$, lähestyminen nollaa jaon tihentyessä. Tasaisesti jatkuva funktio on Riemannin mielessä integroituva. Tasainen jatkuvuus ei vielä ollut käsitteenä selkiintynyt Riemannin aikaan. Toisaalta Riemann saattoi antaa esimerkin funktiosta, jolla on äärettömän tiheässä epäjatkuvuuskohtia, mutta joka kuitenkin on integroituva. Riemannin integraalin nykyinen esitystapa, jossa tarkastellaan integroimisjoukon jakoon liittyviä funktion ala- ja yläsummia

$$\begin{split} \sum m_i(x_{i+1}-x_i),&\quad \sum M_i(x_{i+1}-x... ...} f(x),&\quad M_i=\sup_{x_i\le x\le x_{i+1}} f(x), \end{split}$$

on peräisin ranskalaiselta Gaston Darboux'lta (1842-1917). - Riemann esitti luennoillaan myös esimerkin jatkuvasta funktiosta, jolla ei ole derivaattaa missään. (Tällaisen 1800-luvun funktiokäsitteen perusteita järkyttäneen funktion oli ensimmäisenä konstruoinut Bolzano, mutta muiden Bolzanon töiden tapaan sen kohtalona oli ollut jäädä huomaamatta tieteen keskuksissa.) Matematiikan kuuluisin avoin kysymys on (kun Fermat'n suuren lauseen ongelma nyt on selvitetty) Riemannin hypoteesi. Riemann arveli, että kompleksiluvun $s=\sigma + i\tau$ funktion $\zeta(s)=1+2^{-s}+3^{-s}+\dots,$ ns. Riemannin $\zeta$-funktion, kaikki ei-reaaliset nollakohdat ovat suoralla $\sigma= \frac 12$. Riemannin hypoteesi on yhä todistamatta; sillä olisi monia mielenkiintoisia seurauksia lukuteorian alalla.

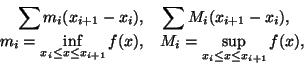
Vaikka Riemann oli nerokas matemaatikko, häntä ei voi varsinaisesti pitää täsmällisyyden apostolina: hänen tutkimusotteensa perustui yleensä geometris-fysikaaliseen intuitioon. Esim. (sinänsä oikean) Riemannin kuvauslauseen todistus perustui puutteelliseen Dirichlet'n periaatteeseen. - Riemannin puhtaasti geometrisista ansioista myöhemmin.

11.4 Weierstrass

1800-luvun jälkipuoliskon matemaattisen analyysin keskeisen hahmon Karl Weierstrassin (1815-97) tie matematiikan huipulle oli mutkallinen. Epäonnistuneiden juridiikan opintojen jälkeen Weierstrass hankki oppikoulunopettajan pätevyyden ja toimi pikkukaupungeissa matematiikan opettajana, kunnes matemaattinen maailma hänet ''löysi'' 1854. Elämäntyönsä pääosan Weierstrass teki sitten Berliinin yliopistossa.

Weierstrassin asenne matematiikkaan oli jossain määrin Riemannin asenteen vastakohta. Weierstrass pyrki vapauttamaan analyysin kaikesta intuitiivisesta, saattamaan sen vastaansanomattoman vankalle aritmeettiselle pohjalle. Juuri Weierstrass mm. huomautti Riemannille Dirichlet'n periaatteen virheellisyydestä. Weierstrassin ohjelmaa, analyysin aritmetisointia, toteutti hänen lisäkseen runsas joukko oppilaita, jotka usein julkaisivat omissa nimissään oikeastaan mestarin käsialaa olevia tuloksia.

Weierstrass vei loppuun Cauchyn aloittaman differentiaali- ja integraalilaskennan perusteiden lujittamisen ottamalla täysin huomioon tasaisen suppenemisen merkityksen mm. eri rajaprosessien järjestyksen vaihdossa. Nykyanalyysin "epsilonistiikka" on varsinaisesti Weierstrassin koulukunnan vakiinnuttamaa. Luennoidessaan 1861 Berliinin teknillisessä korkeakoulussa Weierstrass esitti jatkuvuuden määritelmän seuraavasti:

Jos on mahdollista määrittää h:lle sellainen raja $\delta$, että kaikille h:n arvoille, joiden itseisarvo on pienempi kuin $\delta$, f(x+h)-f(x) on pienempi kuin mielivaltainen suure $\epsilon$, joka voi olla miten pieni tahansa, niin argumentin äärettömän pieniä muutoksia vastaavat funktionarvojen äärettömän pienet muutokset.

Analyyttisten funktioiden teorian lähtökohdaksi Weierstrass määritteli potenssisarjat; funktioteorian keskeiseksi työkaluksi muodostui analyyttinen jatkaminen: potenssisarjakehitelmän pätevyysaluetta laajennetaan ottamalla käyttöön uusi kehityskeskus ja alkuperäisen suppenemisympyrän ulkopuolelle ulottuva uusi suppenemisympyrä. Analyyttisen jatkamisen kautta jokainen potenssisarja tulee määrittelemään mahdollisimman laajassa alueessa yleensä monikäsitteisen analyyttisen konfiguraation. - Funktioteorian perusteisiin Weierstrass johtui elliptisten ja Abelin funktioiden tutkimuksista, joita hän harjoitti opettajantyönsä ohessa ja joista ensimmäiset julkaistiin koulujen vuosikertomuksissa.

11.5 Irrationaalilukujen luokat ja reaalilukujen täsmällinen määrittely

Reaalilukujen jakautuminen rationaalisiin ja irrationaalisiin oli periaatteessa tunnettua jo pythagoralaisten ajoista. Vuonna 1844 ranskalainen Joseph Liouville (1809-82) osoitti, että kaikki irrationaaliluvut eivät ole ($\sqrt 2$:n tavoin) algebrallisia lukuja eli jonkin kokonaislukukertoimisen polynomin P nollakohtia. Liouvillen esittämä konstruktio ei-algebrallisten eli transkendenttisten lukujen olemassaololle oli varsin komplisoitu, mutta muutamat esimerkit ovat melko yksinkertaisia. Esimerkiksi luku $0{,}1001000100001\dots$ on transkendenttiluku. Vuonna 1873 ranskalainen Charles Hermite (1822-1901) onnistui osoittamaan, että Neperin luku e on transkendenttinen; $\pi$:n suhteen saman asian todisti kymmenen vuotta myöhemmin saksalainen Ferdinand Lindemann (1852-1939). Lindemannin todistus osoitti lopullisesti, että antiikin probleema ympyrän neliöimisestä euklidisin työvälinein on mahdoton ratkaista.

Monien matemaattisen analyysin loogisten vaikeuksien keskeinen syy oli itse luvun käsitteen epämääräisyys. Irrationaaliluku voitiin käsittää rationaalilukujen jonon raja-arvoksi, mutta toisaalta raja-arvon määritelmä jo edellytti, että raja-arvokandidaatti oli olemassa ja siis määritelty. Cauchy ja Bolzano olivat pyrkineet määrittelemään jonon suppenemisen pelkästään sen termien avulla (Cauchyn kriteeri), ja Bolzano oli lisäksi pyrkinyt määrittelemään reaaliluvut rationaalilukujonojen avulla, mutta vasta vuonna 1872 tällainen määrittely onnistui tyydyttävällä tavalla. Määritelmän esittivät toisistaan riippumatta ranskalainen Charles Méray (1835-1911), joka oli jo aikaisemmin kiinnittänyt huomiota mainittuun ristiriitaisuuteen, sekä Weierstrass oppilaansa Eduard Heinen (1821-81) ja tämän yhteistyökumppanin Georg Cantorin (1845-1918) kanssa.

Lukujonoihin perustuvan reaaliluvun määrittelyn rinnalle syntyi samana vuonna, 1872, suoremmin reaaliluvun geometriseen mielikuvaan ja Eudoksoksen klassiseen suhdeoppiin kytkeytyvä Richard Dedekindin (1831-1916) määritelmä. Sen mukaan reaaliluvun määrittelee jokainen Dedekindin leikkaus, rationaalilukujen joukon jako kahdeksi yhteisalkiottomaksi osajoukoksi A ja B, missä jokainen joukon A luku on jokaista joukon B lukua pienempi. Leikkaukset, joissa A:ssa on suurin tai B:ssä pienin luku, vastaavat rationaalilukuja.

Alkuun - Etusivu - Edellinen - Seuraava