12. Geometria 1600-1800-luvuilla

Geometria ei 1700-luvulla edistynyt samalla tavalla kuin analyysi. Sen sijaan 1800-luku merkitsi geometriassakin perusteiden selventymistä ja kokonaan uusien metodien esiin tuloa. Eri kehityskulkujen samanaikaisuus ja päällekkäisyys tekee vaikeaksi johdonmukaisen kuvan antamisen muista kuin epäeuklidisen geometrian syntyyn johtaneista tapahtumista.

12.1 Projektiivisen geometrian alkuvaiheet

Projektiivisen geometria, olennaisesti kuvioiden projektioissa säilyviä ominaisuuksia tutkivan geometrian haaran, aloittajana pidetään ranskalaista arkkitehtiä Gerard Desarguesia (1593-1662). Hänen aikanaan kovin vähälle huomiolle jääneessä teoksessaan Brouillon projet d'une atteinte aux événements des rencontres d'un cone aved un plan (Luonnos yritykseksi käsitellä tapahtumia kartion ja tason kohdatessa, 1639) esiintyi omaperäisen kasviopillisen terminologian alla myöhemmin projektiivisessa geometriassa tyypillisiä käsitteitä kuten äärettömän kaukaiset pisteet, joissa yhdensuntaiset suorat leikkaavat. Desarguesin nimi on parhaiten säilynyt Desarguesin lauseessa, jonka mukaan ''perspektiivisessä asemassa'' sijaitsevien kolmioiden (joiden vastinkärkien kautta kulkevat suorat leikkaavat samassa pisteessä) vastinsivujen jatkeiden leikkauspisteet ovat samalla suoralla.

Desarguesilla oli yksi oppilas, Blaise Pascal. Pascal todisti jo 16-vuotiaana, että kartioleikkauksen sisään piirretyn kuusikulmion vastakkaisten sivujen jatkeiden leikkauspisteet ovat samalla suoralla. Pascalin ajattelu oli nimenomaan projektiivista. Lause on suhteellisen helppo todistaa, jos kartioleikkaus on ympyrä. Pascal päätteli, että teoreeman sisältämät leikkausominaisuudet säilyvät projisoitaessa, joten lause on tosi yleisille kartioleikkauksille.

Gaspard Mongen perustaman ranskalaisen geometrian koulukunnan huomattavin edustaja oli Jean-Victor Poncelet (1788-1867). Projektiivisen geometrian itsenäisenä tieteenalana on saanut alkunsa hänen tutkimuksistaan.

Poncelet osallistui pioneeriupseerina Napoleonin Venäjän-retkeen ja jäi vangiksi; geometriset pääajatuksensa hän kehitti sotavankeudessa Saratovissa. Poncelet osoitti, että tasogeometrian väittämissä on yleensä mahdollista vaihtaa sanat piste ja suora keskenään lauseen totuusarvon muuttumatta. Tätä duaalisuusperiaatetta sovelsi järjestelmällisesti Poncelet'n kilpailija Joseph Diaz Gergonne (1771-1859). Poncelet täydensi geometristen objektien valikoimaa ideaalisilla ja imaginaarisilla olioilla (suora leikkaa aina ympyrän, joko reaalisissa tai imaginaarisissa pisteissä), ja edisti siten matematiikan abstrahoitumista. - Poncelet'n on alkujaan myös alkeisgeometrian kaunis tulos yhdeksän pisteen ympyrästä: kolmion korkeusjanojen kantapisteet, sivujen keskipisteet ja korkeusjanojen leikkauspisteen ja kolmion kärkien välisten janojen keskipisteet ovat kaikki samalla ympyrällä.

12.2 Synteettinen ja analyyttinen geometria

Poncelet'n metodit olivat yleensä synteettisiä, analyysin keinoja käyttämättömiä. Puhtaaksiviljellyimmissä muodoissaan synteettiset metodit esiintyivät sveitsiläissyntyisellä mutta pääosin Berliinissä toimineella Jakob Steinerilla (1796-1863), joka mm. keksi inversion eli ympyräpeilauksen merkityksen. Poncelet ja Steiner kehittivät menetelmiä euklidisten tehtävien ratkaisemiseksi harppia ja viivoitinta vähemmin välinein. Italialainen Lorenzo Mascheroni (1750-1800) oli 1797 osoittanut, että euklidiset konstruktiot voidaan tehdä pelkällä harpilla (jos suora katsotaan piirretyksi, kun kaksi sen pistettä on saatu konstruoiduksi). Poncelet ja Steiner osoittivat, että konstruktiot voidaan tehdä myös pelkällä viivoittimella, jos käytössä on lisäksi yksi kiinteä ympyrä ja sen keskipiste. Vasta vuonna 1927 tuli tietoon, että Mascheronin tuloksen oli jo 1672 anonyymisti julkaissut tanskalainen Georg Mohr (1640-97) unohduksiin joutuneessa kirjasessa Euclides danicus.

Puhtaasti Eukleideen järjestelmään pohjautuva geometria sai jonkinverran täydennyksiä sekin. Italialainen Giovanni Ceva (1647-1734) julkaisi kolmion ''merkillisiä pisteitä'' koskevia tietoja yhtenäistävän lauseen Cevan lauseen, 1678. Englantilaisen Robert Simsonin (1687-1768) nimi liittyy mielenkiintoiseen kolmion Simsonin suoraan, vaikka ensimmäinen kirjallinen tieto kyseisen suoran löytymisestä on vasta vuodelta 1797. Euler julkaisi ''Eulerin suoraa'' koskevan tuloksen 1765.

Analyyttiseltä kannalta geometriaa tutki mm. Julius Plücker (1801-68). Hän keksi - samanaikaisesti eräiden muiden geometrikkojen kanssa - hyödylliset homogeeniset koordinaatit. Kun tason pistettä merkittiin kolmikkona , poistui äärettömän kaukaisen pisteen erikoisasema ja pisteen ja suoran duaalisuus kävi ilmeiseksi. Yhtälö pu + qv + rw = 0 esittää sekä kaikkia pisteen kautta kulkevia suoria että kaikkia kolmikon määrittämän suoran pisteitä. Plücker yleisti duaalisuuden myös avaruuteen (jossa tasot ja pisteet ovat toistensa ja suorat itsensä duaaleja); saman ohjelman toteutti ranskalainen Michel Chasles (1793-1880). Chasles käytti ensimmäisenä vektoreihin liittyviä suuntajanoja. Yleiseen n-ulotteiseen avaruuteen analyyttisen geometrian yleisti ensimmäisenä monipuolinen englantilainen juristi ja matemaatikko Arthur Cayley (1821-95). Cayleyn työkaluina olivat determinantit; kun suoran yhtälö tason homogeenisissa koordinaateissa lausuttuna on

12.3 Epäeuklidinen geometria

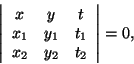
Eukleideen viidennen postulaatin eli paralleeliaksiooman mahdollinen riippuvuus muista aksioomista askarrutti lukuisia matemaatikkoja yli 2000 vuoden ajan. Klaudios Ptolemaios, Proklus, Nasir Eddin al-Tusi ja Omar Khaijjam yrittivät todistaa postulaattia teoreemana. 1700-luvulla italialainen jesuiitta Girolamo Saccheri (1667-1733) pyrki todistamaan postulaattia epäsuorasti. Hänen lähtökohtanaan oli nelikulmio, jossa on kaksi suoraa kulmaa ja kaksi yhtä pitkää sivua. Paralleelipostulaatin kanssa yhtäpitävää on, että nelikulmion muut kaksi kulmaa, jotka joka tapauksessa ovat yhtä suuret, ovat suoria. Saccheri oletti kulmat tylpiksi tai teräviksi ja johti seurauksia. Tylpän kulman tapaus johti ristiriitaan (ainakin jos suorat ovat äärettömän pitkiä), mutta terävän kulman tapaus jäi epäselväksi, vaikka Saccheri ilmoittikin päätyneensä myös tässä tapauksessa ristiriitaan. Itse asiassa Saccheri tuli johtaneeksi suuren määrän myöhemmin syntyneeseen epäeuklidiseen geometriaan kuuluvia teoreemoja.

Saccherin päättelyiden kanssa samansuuntaista työtä tekivät sveitsiläissyntyinen Johann Lambert (1728-77) ja Legendre. Lambert lähti liikkeelle nelikulmiosta, jonka kolme kulmaa ovat suoria. Oletusta, jonka mukaan neljäs kulma olisi terävä, ei Lambert onnistunut kumoamaan, ja luopui paralleeliaksiomaa koskevan tutkimuksensa julkaisemisesta. Lambertin ystävät painattivat tutkimuksen Die Theorie der Parallelinien kuitenkin kirjoittajan kuoleman jälkeen 1777. Legendren suositun oppikirjan Éléments de Géométrie (1794) (jonka katsottiin korvaavan Eukleideen Alkeet) eri painoksissa oli laajoja paralleelipostulaatin tarkasteluja. Tekemällä avaruuden äärettömyyttä koskevan lisäoletuksen Legendre osoitti, että kolmion kulmien summa ei ylitä :ta ja että jos on olemassa kolmio, jonka kulmasumma on , niin kaikkien kolmioiden kulmasumma on , jolloin myös paralleelipostulaatti on tosi. Viimeinen Legendren toimittama painos ilmestyi 1833.

1810-luvulla Gauss vakuuttui mahdollisuudesta korvata paralleelipostulaatti jollakin muulla olettamuksella geometrian järjestelmän silti sortumatta. Koska hän ei julkaissut ajatuksiaan, luetaan epäeuklidinen geometria kahden vakiintuneiden tieteellisten keskusten ulkopuolella toimineen matemaatikon ansioksi. Toinen heistä on venäläinen Nikolai Ivanovits Lobatsevski (1792-1856), ''Geometrian Kopernikus'', Moskovasta 800 km itään sijaitsevan Kasanin yliopiston rehtori. Lobatsevski oli uskonut löytäneensä todistuksen paralleelipostulaatille ja julkaissutkin sellaisen, mutta vuosien 1826 ja 1829 välillä hänelle kävi selväksi, että ristiriidaton geometrian järjestelmä on luotavissa myös siten, että annetun suoran ulkopuolella olevan pisteen kautta oletetaan kulkevaksi useita eri suoria, jotka eivät leikkaa annettua suoraa. Lobatsevskin kirjoitukset levisivät varsin hitaasti, mutta ne tulivat kuitenkin esim. Gaussin tietoon. Vaikka Gauss yksityiskirjeissä kiittikin Lobatsevskia, hän ei ottanut julkisesti kantaa tämän tuloksiin.

Toinen epäeuklidisen geometrian keksijä, unkarilainen (oikeastaan Transsilvanian Koloszvárissa, nykyisen Romanian Cluj'ssa syntynyt) upseeri János Bolyai (1802-60) oli myös kosketuksissa Gaussiin, sillä hänen isänsä Farkas (Wolfgang) Bolyai (1775-1856), itsekin paralleeliaksiooman todistusyrityksiä harrastanut matematiikanopettaja, oli ollut Gaussin opiskelutoveri Göttingenissä. Isän kieltelyistä huolimatta poikakin innostui paralleelipostulaatista ja onnistui kehittämään geometrian, jossa annetun pisteen kautta kulkee äärettömän monta annetun suoran kanssa yhdensuuntaista suoraa. János Bolyain ilmeisesti jo vuonna 1823 valmistunut tutkimus julkaistiin 1832 Farkas Bolyain Tentamen Juventutem studiosam in elementa matheseos puræ introducendi -nimisen geometrisen kirjan 26-sivuisena liitteenä nimellä Appendix scientiam spatii absolute veram exhibens (Lobatsevski julkaisi oman teoriansa 1829 Kasanissa venäjäksi ja 1840 Berliinissä saksaksi). Gauss kieltäytyi jälleen kommentoimasta: ''Jos kehuisin tätä työtä, kehuisin itseäni, koska olen ajatellut samoin jo monen vuoden ajan.'' Tämä Gaussin tunnustus ja samanaikainen prioriteetin kiisto samoin kuin saksankielisen version ilmestyminen Lobatsevskin työstä masensivat János Bolyain niin, että hän ei myöhemmin enää julkaissut varteenotettavia matemaattisia töitä.

Epäeuklidisen geometrian todellisen merkityksen oivalsi vasta Riemann, jonka kuuluisa, Gaussin antamaan aiheeseen pohjautuva dosentinväitöskirja Ueber die Hypothesesen, welche der Geometrie zu Grunde liegen (1854). Riemann tarkasteli geometrioita, joissa suorat eivät välttämättä ole äärettömiä, ja joissa oletus, jonka mukaan suoran ulkopuolella olevan pisteen kautta ei voi piirtää ollenkaan suoran kanssa yhdensuuntaista suoraa. Riemannin työ sisälsi kauaskantoisen ohjelman: geometrian tutkimuskohde ei ole avaruuden pisteiden, suorien ja tasojen joukko, vaan yleiset n-ulotteiset monistot, joiden ominaisuudet määräytyvät monistolla määritellystä metriikasta, joka voi muuttua siirryttäessä pisteestä toiseen. Riemannin avaruuskäsitys on mm. yleisen suhteellisuusteorian perustana. Riemann esitti yksinkertaisen mallin geometriasta, jossa kaikki suorat leikkaavat: pallo ja isoympyrät. Myöhemmin italialainen Eugenio Beltrami (1835-1900) löysi samanlaisen mallin Lobatsevskin ja Bolyain geometrialle; kyseessä oli pseudopallo-niminen pyörähdyspinta.

Epäeuklidisen geometrian voi katsoa vapauttaneen geometria. Tuli mahdolliseksi rakentaa erilaisiin aksioomajärjestelmiin nojautuvia geometrioita, ja kysymys siitä, minkälainen geometria vallitsee reaalimaailmassa siirtyi fysiikan puolelle.

12.4 Klein ja Erlangenin ohjelma

Felix Klein (1849-1925) oli 1800-luvun lopun ja 1900-luvun alun keskeinen matemaattinen organisaattori Saksassa. Hän aloitti uransa Plückerin assistenttina ja toimi suurimman osan elämäänsä Göttingenissä.

1870-luvulla Klein oli jonkin aikaa Erlangenin yliopiston professorina. Hänen siellä 1872 pitämänsä virkaanastujaisesitelmä tunnetaan Erlangenin ohjelman nimellä. Klein havaitsi, että algebran piirissä syntynyt ryhmän käsite oli sopiva struktuuri kuvaamaan erilaisia geometrisia järjestelmiä. Kutakin geometrista systeemiä karakterisoi tietty tarkasteltavan avaruuden transformaatioiden eli bijektiivisten kuvausten ryhmä; kyseisen systeemin tutkiminen tarkoittaa sellaisten ominaisuuksien selvittämistä, jotka säilyvät invariantteina ryhmän transformaatioissa. Euklidista metristä geometriaa esim. vastaa tason translaatioiden, peilausten ja kiertojen ryhmä. Erlangenin ohjelman vaikutukset ovat yhä nähtävissä mm. nykyisissä geometrian oppikursseissa. Kleinilta on peräisin epäeuklidisen geometrian ns. hyperbolinen malli, jossa tasoa vastaa ympyräkiekko D, suoria vastaavat ympyrän kehää vastaan kohtisuorat ympyrät ja äärettömän kaukaista pistettä vastaa ympyrän kehä.

Kleinin keskeinen asema 1800-luvun lopun matemaattisessa elämässä antoi hänelle loistavat lähtökohdat kirjoittaa 1800-luvun matematiikan historiasta. Kleinin vanhoilla päivillään Göttingenissä pitämiin luentoihin perustuva Entwicklung der Mathematik im 19. Jahrhundert (1926-27) on harvoja todellisen eturivin matemaatikon kirjoittamia matematiikan historiaa käsitteleviä teoksia. Se on erittäin luettavaa tekstiä edelleen.

Alkuun - Etusivu - Edellinen - Seuraava