PDF

10. Ranskan vallankumouksen ajan matematiikkaa

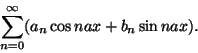
1700- ja 1800-lukujen taite oli etenkin Ranskassa matemaattisesti aktiivista aikaa. Lagrangen toiminta ajoittuu osaksi Ranskan vallankumouksen aikaan, ja useat seuraavassa käsiteltävät matemaatikot aloittivat työnsä jo ennen vallankumousta. Gauss liittyy Ranskan vallankumoukseen vain ajallisesti. Aikakauden keskeinen poliittinen ja sotilaallinen hahmo Napoleon Bonaparte (1769-1821) lienee ainoa matematiikan historiaan nimensä jättänyt hallitsija: Napoleonin lause sanoo, että kolmion sivut kantoima piirrettyjen tasasivuisen kolmioiden painopisteet kärkinä piirretty kolmio on tasasivuinen.

10.1 Monge ja École Polytechnique

Enimmältään itse oppinsa hankkinut Gaspard Monge (1746-1818) tunnetaan matematiikassa ennen muuta analyyttisen geometrian ja differentiaaligeometrian kehittäjänä ja deskriptiivisen geometrian keksijänä. Tämän erityisesti tekniikan kehitykselle tärkeän matematiikan alan Monge keksi nuorena toimiessaan sotilasoppilaitoksen piirtäjänä - linnoituslaitteiden piirustamisessa pitkät numerolaskutr korvannut deskriptiivinen geometria olikin aluksi tarkkaan varjeltu ranskalainen tai oikeastaan nimenomaan Mézièresin pioneeriakatemian sotasalaisuus. Monge julkaisi metodinsa vasta vuonna 1795. Ranskan vallankumoukseen Monge otti innokkaasti osaa ja joutui samalla moniin keskeisiin tehtäviin, mm. laivastoministeriksi. Ns. direktoriohallituksen aikana vuonna 1795 perustettiin, paljolti Mongen ansiosta, Pariisiin teknillinen korkeakoulu École Polytechnique, jossa Monge sittemmin toimi opettajana ja huomattavan geometrisen koulukunnan perustajana.

Mongen deskriptiivinen geometria oli synteettinen menetelmä. Mongen ansiot analyyttisen geometrian alalla olivat myös merkittävät. Häneltä ovat olennaisesti peräisin mm. suoran yhtälöt kolmiulotteisessa avaruudessa. Mongea pidetään myös yhtenä differentiaaligeometrian perustajista.

Polyteknillinen koulu viitoitti tekniikan kehityksen myötä tarpeelliseksi tulleen korkeamman teknisen opetuksen suuntaviivoja, mutta samalla se muodostui Ranskan ehdottomaksi matemaattiseksi keskukseksi. Sen ensimmäisiä opettajia olivat Mongen ohella mm. Lagrange, Laplace ja Legendre. École Polytechniquen rinnalle perustettiin pian opettajanvalmistusta varten École Normale, jonka opettajakuntaan on myös kuulunut joukko Ranskan merkittävimpiä matemaatikkoja (ikivanhan Sorbonnen, Pariisin yliopiston, merkitys matematiikan kannalta oli 1700- ja 1800-luvuilla vähäinen). École Polytechniquen ja École Normalen oppikirjoiksi kirjoitetut teokset olivat 1800-luvun matematiikan oppikirjojen ehdotonta huippua.

10.2 Fourier

Mongen ystäviä ja työtovereita niin École Polytechniquessa kuin Napoleonin Egyptin-sotaretkelläkin oli Joseph Fourier (1768-1830) (Monge oli Napoleonin perustaman Egyptin instituutin johtaja ja Fourier sen sihteeri; Fourier julkaisi retken aikana kootun tieteellisen materiaalin). Hän teki vallankumouksellisen ja paljon vastustusta synnyttäneen huomion: jokainen funktio f, ei välttämättä edes jatkuva, voidaan esittää trigonometrisena sarjana, Fourier-sarjana

$$\sum_{n=0}^{\infty} (a_n\cos nax + b_n\sin nax).$$

Fourier'n pääteos Théorie Analytique de la Chaleur (Analyyttinen lämpöteoria, 1822), jossa trigonometrisia sarjoja käytetään osittaisdifferentiaaliyhtälöiden reuna-arvotehtävien ratkaisuun, ei ollut kaikin puolin loogisesti moitteeton; sen epätäsmällisyydet olivat yksi keskeisiä 1800-luvulla läpiviedyn analyysin täsmällistyttämisohjelman alkusyitä.

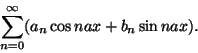
Fourierin sarjakehitelmän lähtökohtana oli stabiilin lämpötilajakauman etsiminen alueessa $\{(x,\,y)\vert<x<\pi,\,0<y\}$. Jakauma tottelee Laplacen yhtälöä

$$\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}=0$$

ja reunaehtoja $u(0,\,y)=u(\pi,\,y)=0$, $u(x,\,0)=\phi(x)$. Jos ratkaisua etsitään muodossa $u(x,\,y)=f(x)g(y)$, saadaan muotoa $u(x,\,y)=e^{-ny}\sin nx$, n=1, 2, 3,... olevia yksittäisratkaisuja ja niiden superpositiona yleisempi ratkaisu $u(x,\,y)=\sum_{n=1}^{\infty}b_ne^{- ny}\sin nx$, missä b_n:t ovat vakioita. Jos vakiot voidaan määrittää niin, että

$$\sum_{n=1}^{\infty}b_n\sin nx=\phi(x),$$

ratkaisu on valmis. Fourier päätyi jokseenkin heuristisen, pitkälti $\phi$:n Taylorin kehitelmään perustuvan päättelyn jälkeen siihen, että kertoimet toteuttavat toisen kertaluvun differentiaaliyhtälön, joka viimein johtaa kertoimien lausekkeeseen

$$b_n=\frac{2}{\pi}\int_0^{\pi}\phi(x)\sin(nx)\,dx.$$

Tämän saatuaan hän totesi samaan päädyttävän olettamalla $\phi$:lle trigonometrinen kehitelmä ja käyttämällä ''ortogonaalisuusehtoja''

$$\int_0^{\pi}\sin kx\sin nx\,dx=0,\ {\rm jos}\ k\ne n.$$

Koska kertoimien lauseke edellyttää vain ''käyrän alle jäävää pinta-alaa'', ja koska $\phi$:n jaksollisuus vähintäänkin tuo helposti mukanaan epäjatkuvuuskohtia, Fourierin sarja synnytti tarpeen tarkastella integrointia ja yleisemminkin analyysin prosesseja myös epäjatkuvien funktioiden maailmassa. Fourierin sarjan suppeneminen ja sen rajafunktion käyttäytyminen ei ole ongelmatonta. Näiden kysymysten selvittelystä tuli yksi merkittävimpiä analyysin kehitykseen 1800-luvulla vaikuttaneita tekijöitä.

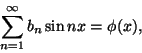
Fourier otti käyttöön määrätyn integraalin rajojen nykyisen merkinnän

$$\int_a^bf(x)\,dx.$$

Euler oli merkinnyt

$$\int f(x)\,dx\left[\displaystyle{x=a \atop x=b}\right].$$

10.3 Laplace ja Legendre

Myös Pierre Simon Laplace (1749-1827), ''Ranskan Newton'', alkoi matemaattisen uransa sotakoulun opettajana. Hänkin osallistui vallankumouksen ja Napoleonin hallinnon aikana yhteiskunnallisiin toimiin, olipa kuusi viikkoa sisäministerinäkin, joskin huonolla menestyksellä. Napoleon joutui nimittäin erottamaan Laplacen todettuaan, että hän ''toi infinitesimaalien hengen hallintoon''. Adrien Marie Legendre (1752-1833) pysytteli enimmäkseen sivussa yhteiskunnallisista tehtävistä lukuun ottamatta metrijärjestelmäprojektia, johon osallistuivat myös Lagrange, Monge ja Laplace. Kymmenjärjestelmään perustuvat mittayksiköt olivat valmiit vuonna 1799.

Laplace kirjoitti kaksi suurteosta: Théorie analytique des probabilités (1812) ja Mécanique céleste (viisi osaa, 1799-1825). Edellinen on matemaattisen analyysin keinovaroja täydellisesti hyväksi käyttävä todennäköisyyslaskennan kokonaisesitys. Siihen sisältyy useita huomattavia keksintöjä, kuten Laplacen muunnos

$${\cal L}f(s)= \int_0^{\infty}e^{-sx}f(x)\,dx,$$

joka on tärkeä mm. differentiaaliyhtälöitä ratkaistaessa, ja pienimmän neliösumman menetelmä havaintovirheiden eliminoimiseksi. Menetelmän oli ensimmäisenä esittänyt Legendre, mutta ilman todistusta. Monumentaalinen taivaanmekaniikan kokonaisesitys luo yleiskuvan Newtonin oppien mukaisesta aurinkokunnan fysiikasta. Teos tuo matematiikkaan potentiaalifunktion (joka tosin oli ollut tuttu Lagrangellekin), Laplacen operaattorin

$$\Delta =\dfrac{\partial^2}{\partial x^2}+\dfrac{\partial^2}{\partial y^2}+ \dfrac{\partial^2}{\partial z^2}$$

ja Laplacen differentiaaliyhtälön $\Delta u = 0$, jonka ratkaisut ovat potentiaalifunktioita.

Legendre kirjoitti hyviä ja suosittuja oppikirjoja mm. geometriasta ja integraalilaskennasta. Matemaattinen fysiikka saa kiittää häntä useista matemaattisista apuneuvoista, kuten monissa yhteyksissä tarpeellisista Legendren funktioista, jotka ovat differentiaaliyhtälön

(1 - x²)y"-2xy'+n(n +1)y=0

ratkaisuja. Legendre systematisoi tyyppiä

$$\int R(x,\sqrt{s(x)})\,dx,$$

missä R on rationaalifunktio ja s kolmannen tai neljännen asteen polynomi, olevien integraalien teoriaa. Hän osoitti, että nämä integraalit voidaan aina palauttaa yhteen muutamista ns. Legendren normaalimuodoista, joista tärkeimmät ovat

$$F(k,\phi)=\int_0^{\phi}\frac {dx}{\sqrt{1-k^2\sin^2x}}$$

ja

$$E(k,\phi)=\int_0^{\phi}\sqrt{1-k^2\sin^2x}\,dx.$$

Funktioiden E ja F arvoja on taulukoitu. Näiden ns. elliptisten integraalien teoria oli tärkeä tutkimuskohde 1800-luvulla; elliptisten integraalien tutkimuksen merkitys yleisen kompleksimuuttujan funktioiden teorian synnylle on suuri.

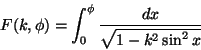
Legendren työt myös lukuteorian alalla ovat merkittäviä. Tunnettuja ovat hänen neliölukujen jakojäännöksiä koskevat tuloksensa, joiden yhteydessä syntyi Legendren symboli (p|q), joka on +1 tai -1sen mukaan, onko p jonkin neliön jakojäännös modulo alkuluku q vai ei. Legendre esitti myös empiiristen havaintojen perusteella syntyneen alkulukuhypoteesin, jonka mukaan n:ää pienempien alkulukujen lukumäärä $\pi(n)$ lähestyy asymptoottisesti arvoa

$$\frac{n}{\log n},$$

kun n kasvaa. Tämän alkulukujen sattumanvaraiselta näyttävän jakautumisen kannalta yllättävän hypoteesin todistus onnistui vasta vuonna 1896 ranskalaiselle Jacques Hadamardille (1865-1963) ja belgialaiselle Charles de la Vallée Poussinille (1866-1962); venäläinen Pafnuti Tsebysev (1821-94) oli tällä välin ehtinyt osoittaa, että raja-arvo

$$\lim_{n\to\infty} \pi(n)\frac{\log n}{n}$$

on olemassa. - Legendre todisti Fermat'n suuren lauseen hypoteesin oikeaksi tapauksessa n=5.

10.4 Gauss

Carl Friedrich Gauss (1777-1855), ''matemaatikkojen kuningas'', syntyi työläisperheeseen Braunschweigissa lähellä Hannoveria (tasan 50 vuotta Newtonin kuoleman jälkeen); vanhempien vastustuksesta huolimatta varhaiskypsä poika pääsi opintielle mm. hallitsevan herttuan tuella. Gauss epäröi klassisen filologin ja matemaatikon elämänurien välillä 18-vuotiaana, jo sitä ennen keksittyään pienimmän neliösumman menetelmän, 10 vuotta ennen Legendrea. Uranvalinta selvisi, kun Gauss keksi, että säännöllinen 17-kulmio on konstruoitavissa harpin ja viivoittimen avulla - jo antiikin ajoista jatkunut tasogeometrian tutkimus oli siihen mennessä selvittänyt säännöllisen p-kulmion piirtämisen parittomilla p:n arvoilla vain tapauksissa p=3 ja p=5.

Newtonin tapaan Gaussinkin periaate oli julkaista tutkimustuloksiaan säästeliäästi: hänen sinetissäänkin on tunnuslause Pauca sed matura, 'vähän mutta kypsää'. Gaussin jälkeensä jättämien muistiinpanojen tutkimus on osoittanut, että hän on itsenäisesti tehnyt monia merkittäviä muiden matemaatikkojen nimiin kirjattuja keksintöjä.

17-kulmion konstruoitavuutta koskeneen tiedonannon jälkeen Gaussin seuraava julkaisu oli 1799 ilmestynyt väitöskirja, joka sisälsi hyväksyttävän todistuksen algebran peruslauseelle (termi on peräisin Gaussilta). (Täsmällinen todistus vaatisi tietysti täsmällisen reaaliluvun määritelmän, jota Gaussin aikaan ei vielä ollut.) Todistusta olivat aikaisemmin yrittäneet d'Alembertin ohella Euler ja Lagrange. Myöhemmin Gauss palasi aiheeseen ja esitti lauseelle kaikkiaan kolme erilaista uutta todistusta. Gaussin menestys algebran peruslauseen todistuksessa kytkeytyy hänen havaintoonsa mahdollisuudesta esittää kompleksilukuja graafisesti tason vektoreina. (Saman havainnon tekivät samoihin aikoihin itsenäisesti norjalainen maanmittari Caspar Wessel (1745-1818) ja sveitsiläinen kirjanpitäjä Jean Robert Argand (1768-1822); kompleksilukujen graafista esitystä kutsutaan toisinaan Argandin diagrammiksi.) Polynomiyhtälön P(x+iy)=0 kanssa yhtäpitävä yhtälö Q(x,y)+iR(x,y)=0 toteutuu käyrien Q(x,y)=0 ja R(x,y)=0leikkauspisteessä; Gauss osoitti, että nämä käyrät aina sijaitsevat niin, että leikkauspisteen täytyy olla olemassa.

Gaussin tunnetuin matemaattinen teos on kaksi vuotta väitöskirjan jälkeen (1801) ilmestynyt lukuteoriaa käsittelevä Disquisitiones arithmeticæ. Kirjassa otetaan käyttöön lukukongruenssin käsite ja merkintä $a\equiv b \pmod{p}$, todistetaan myös Legendren keksimä ja Eulerin ennakoima kvadraattinen resiprositeettilause

(p|q)(q|p)=(-1)^(p-1)(q-1)/4

ja annetaan välttämätön ja riittävä ehto säännöllisen monikulmion konstruoitavuudelle euklidisin työkaluin (sivuluvun on oltava luvun 2 potenssin ja Fermat'n alkulukujen tulo). - Kvadraattisen resiprositeettilauseen laajennus korkeampien potenssien jäännöksiä koskevaksi johti Gaussin tutkimaan jaollisuuskysymyksiä, jotka koskevat kompleksisisia kokonaislukuja eli Gaussin kokonaislukuja a + ib, missä a ja b ovat kokonaislukuja. Gauss tunsi ilmeisesti myös alkulukuhypoteesin, vaikkei siitä koskaan mitään julkaissutkaan.

Gaussin pitkäaikaisin virka-asema oli Göttingenin observatorion johtajan tehtävä. Samaan aikaan hän toimi Göttingenin yliopiston matematiikan professorina. Gauss pysyi Göttingenissä loppuikänsä, huolimatta monista tarjotuista paikoista eri akatemioissa.

Tähtitieteen pariin Gauss joutui miltei sattumalta: 1. tammikuuta 1801 tehtiin ensimmäiset havainnot pikkuplaneetta Cereksestä. Koska havaintoja oli vähän ja ne olivat epävarmoja (Ceres oli siirtynyt yhteensä vain $3^{\circ}$), tuntui mahdottomalta määrittää uuden taivaankappaleen rataa, mutta Gauss, poikkeuksellisen taitava laskija, suoriutui tehtävästä menestyksellä. Laskelmien sivutuotteena syntyi metodi ratalaskujen suorittamiseksi vain harvojen havaintojen perusteella. Gaussin tähtitieteellinen pääteos Theoria motus corporum clestium vuodelta 1809 sisältää monia matemaattisen tilastotieteen perusasioita; nimitys Gaussin käyrä muistuttaa Gaussin tuotannon tästä puolesta.

Gauss osallistui monella tavoin käytäntöä suoraan palvelevaan työhön. Hän mm. suunnitteli ja johti Hannoverin vaaliruhtinaskunnan kolmiomittauksen raskaine kenttätöineen (Hannover on jokseenkin tasaista maastoa, mikä ei ole eduksi kolmiomittaukselle) ja osallistui vanhoilla päivillään aktiivisesti sähkölennättimen keksimiseen. Käytännön geodesia kytkeytyi Gaussilla myös teoriaan. 1820-luvulla hän teki perustavia tutkimuksia pintojen differentiaaligeometriasta. Gaussin ansiota on erityisesti huomion kiinnittäminen pinnan sisäisiin, ulkopuolisesta kolmiulotteisesta avaruudesta riippumattomiin ominaisuuksiin; tällainen ominaisuus on esim. pinnan kokonaiskaarevuus eli sen Gaussin kaarevuus.

Gaussin elinaikanaan julkaisematta jättämät muistiinpanot osoittavat, että hän oli edennyt huomattavan pitkälle kompleksimuuttujan funktioteorian suuntaan: hän tunsi elliptisten integraalien käänteisfunktioiden, ns. elliptisten funktioiden tärkeän perusominaisuuden, kaksijaksoisuuden, ja Cauchyn integraalilauseen, jonka mukaan kompleksimuuttujan analyyttisen funktion integraali pitkin tason sulkeutuvaa käyrää häviää. Sen sijaan Gauss julkaisi itse hypergeometrista sarjaa

$$\begin{split} F(x;a,b,c)= &1+\frac{ab}{c}x+\frac{a(a+1)b(b+1)... ...ac{a(a+1)(a+2)b(b+1)(b+2)}{3!c(c+1)(c+2)}x^3+\cdots \end{split}$$

koskevan tutkimuksensa. Tutkimukseen liittynyt täsmällinen todistus sille, että sarja suppenee, on ensimmäinen varsinainen sarjan konvergenssitodistus matematiikan historiassa.

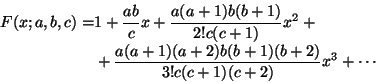
Gaussin julkaisemattomista muistiinpanoista ja kirjeenvaihdosta käy ilmi, että hän oli perillä epäeuklidisen geometrian perusteista jo ennen Bólyaita ja Lobatsevskia. Gauss yritti selvittää avaruuden geometrista rakennetta myös empiirisesti mittaamalla suurten kolmioiden kulmasummaa. Virhearvioiden rajoissa nämä mittaukset eivät osoittaneet, että kulmasumma olisi muuta kuin 180$^{\circ}$.

Alkuun - Etusivu - Edellinen - Seuraava