PDF

9. Analyysin nopea kehitys 1700-luvulla

Infinitesimaalilaskennan keksiminen sysäsi matemaattisen analyysin erittäin nopeaan kehitykseen. Uusia menetelmiä käytettiin osin kritiikittömästi ja teorioiden loogisiin perusteisiin ehdittiin kiinnittää niukasti huomiota. Tekniseltä kannalta differentiaali- ja integraalilaskenta saavutti 1700-luvulla monin osin nykyisen tason.

9.1 Bernoullin veljekset

Alankomaista 1500-luvun lopulla Sveitsin Baseliin siirtynyt Bernoullin suku on matematiikan historian merkittävimpiä. Siihen kuuluu tusinan verran ensi luokan tiedemiehiä. Suvun matemaatikoista kuuluisimmat ovat veljekset Jakob (1654-1705) ja Johann (1667-1748) Bernoulli. (Erikielisissä lähteissä etunimet kirjoitetaan myös esim. Jacques ja Jean tai James ja John.) Bernoullin veljekset olivat Leibnizin oppilaita, työtovereita ja myös kilpailijoita. He vaikuttivat merkittävästi siihen, että differentiaali- ja integraalilaskenta levisi juuri Leibnizin luomassa muodossa.

Jakob Bernoulli esitti Bernoullin epäyhtälön 1+nx < (1+x)ⁿ, todisti harmonisen sarjan hajaantuvaksi (Oresmen aikaisempi todistus oli unohdettu) ja tutki erilaisia käyriä differentiaali- ja integraalilaskentaa käyttäen. Jakob Bernoulli pohti myös sarjaa

$$\sum\frac{1}{n^2},$$

jonka hän tiesi suppenevaksi majoranttisarjan

$$\sum \frac{1}{n(n-1)}$$

perusteella. Sana integraali on Jakob Bernoullin vuonna 1690 käyttöön ottama. Leibniz, joka oli käyttänyt integraalilaskennasta nimitystä calculus summatorius, omaksui myöhemmin myös integraali-sanan.

Leibniz ja Bernoullit tutkivat paljon ns. brakistokroniongelmaa. Tarkoitus oli löytää käyrä, jota pitkin painovoiman vaikutuksen alaisena liikkuva kappale siirtyisi nopeimmin pisteestä A pisteeseen B, joka ei ole suoraan A:n alapuolella. Jakob Bernoullin onnistui ensimmäisenä osoittaa, että kyseinen kaari on sykloidin kaari. Brakistokroniongelmasta katsotaan saaneen alkunsa variaatiolaskennan, matematiikan haaran, joka etsii ääriarvotehtäviin vastaukseksi funktioita eikä vain luvuin ilmaistavia ääriarvokohtia. Itse asiassa Newton oli tässäkin ensimmäinen keksijä: hän ratkaisi jo aikaisemmin ongelman, jossa etsittiin sellaisen kappaleen muotoa, jonka vastus väliaineessa olisi mahdollisimman pieni.

Jakob Bernoullin pitkään ansiolistaan kuuluvat vielä napakoordinaattien käyttöönotto ja ns. Bernoullin differentiaaliyhtälön y'+p(x)y=q(x)yⁿratkaisu, joka tosin onnistui samaan aikaan myös Leibnizille ja Johann-veljelle. Jakob Bernoulli kirjoitti myös ensimmäisen varsinaisen todennäköisyyslaskentaa käsittelevän monografian Ars conjectandi, joka tosin ilmestyi vasta postuumina 1713 (Huygens oli tosin julkaissut vuonna 1657 asiaa käsittelevän vihkosen De ratiociniis in ludo aleae.) Bernoullin teos sisältää kombinatoriikan alkeiden systemaattisen esityksen, induktiotodistuksen binomikaavalle, ns. Bernoullin lukujen (jotka esiintyvät mm. peräkkäisten kokonaislukujen parillisten potenssien summan lausekkeessa) määrittelyn ja todennäköisyyslaskennan suurten lukujen lain.

Johann Bernoulli oli monesti vanhemman veljensä kilpailija ja kiistakumppani ja lopulta myös tämän seuraaja professorina Baselissa. Johann toimi jonkin aikaa yhteistyössä ranskalaisen markiisin Guillaume l'Hôspitalin (1661-1704) kanssa: Bernoulli, yksi noin neljästä tuolloin maailmassa differentiaali- ja integraalilaskentaa osanneista, opetti markiisille uutta analyysiä ja lupasi, palkkiota vastaan, antaa tämän käyttöön tekemänsä uudet matemaattiset keksinnöt. Näihin kuului mm. l'Hôspitalin sääntönä tunnettu havainto

$$\lim_{x\to a}\frac{f(x)}{g(x)} =\frac{f'(a)}{g'(a)},$$

jos f(a)=g(a)=0. Itse asiassa l'Hôspital ja Johann Bernoulli eivät puhu raja-arvosta, vaan $\frac{0}{0}$-tyyppisen lausekkeen arvosta. Säännön ja muut Bernoullilta oppimansa asiat markiisi julkaisi 1696 teoksessa Analyse des infiniment petits, joka siten on ensimmäinen differentiaalilaskennan oppikirja. Teoksen merkitys koko seuraavana vuosisatana oli suuri, vaikka monet sen premissit (kuten että äärettömän vähän toisistaan eroavat suureet ovat samoja tai että käyrät koostuvat äärettömän lyhyistä janoista) eivät nykyään vakuutakaan. Johann Bernoullin omallakin nimellä julkaistu tuotanto on laaja: se käsittää mm. variaatiolaskentaa, differentiaaligeometriaa, ensimmäisen havainnon trigonometristen funktioiden ja eksponenttifunktion yhteydestä ja nykyisen funktion merkitsemistavan ennakoinnin (Bernoulli merkitsi x:n funktiota symbolilla $\phi x$).

Johann Bernoulli oli Leibnizin aggressiivisimpia puolustajia differentiaali- ja integraalilaskennan prioriteettikiistassa. Hänen poikansa Daniel Bernoulli (1700-82) oli erittäin monipuolinen luonnontieteilijä, jonka matemaattiset tulokset liittyvät ennen muuta osittaisdifferentiaaliyhtälöihin.

9.2 Englannin matematiikkaa 1700-luvulla

Vaikka Newtonin ja hänen perintönsä dominoiva vaikutus kahlitsikin matematiikan kehitystä Englannissa, ei 1700-luku kuitenkaan muodosta matemaattista tyhjiötä Brittein saarilla. Merkittäviä brittimatemaatikkoja 1700-luvun alkupuolella olivat ranskalaissyntyinen, uskonnollisen vainon takia Englantiin muuttanut ja suurimman osan elämäänsä köyhyydessä viettänyt Abraham de Moivre (1667-1754) ja skotlantilainen Colin Maclaurin (1698-1746), Newtonin oppilas.

De Moivre kuuluu todennäköisyyslaskennan uranuurtajiin: hänen tuotannossaan esiintyy ensi kerran virhefunktio e^-x2 ja sen yhteys binomijakaumaan, ja hänen teoksensa Doctrine of Chances (1718) on Jakob Bernoullin Ars conjectandin ohella ensimmäinen todennäköisyyslaskennan systemaattinen esitys. De Moivre käytti edeltäjiään luontevammin kompleksilukuja. Kaava

$$(\cos x + i\,\sin x)^n = \cos nx + i\,\sin nx,$$

de Moivren kaava, ei esiinny eksplisiittisesti de Moivrella, mutta kylläkin lähes ekvivalentissa muodossa. Sen sijaan de Moivren aikalaisen ja Newtonin kolmannen asteen käyriä koskeneiden tutkimusten täydentäjän James Stirlingin (1692-1770) mukaan Stirlingin kaavana tunnettu approksimaatio

$$n!\approx \sqrt{2\pi n}n^ne^{-n}$$

on itse asiassa de Moivren keksintöä, työkalu binomijakauman kertoimien tarkastelussa. De Moivre on myös vakuutusmatematiikan pioneereja.

Maclaurinin nimi tunnetaan nykyisin Maclaurinin sarjasta

$$f(x)=f(0) + f'(0)x + \frac{1}{2} f''(0)x^2 +\dots$$

Itse asiassa sarjan oli julkaissut englantilainen Brook Taylor (1685-1731) aikaisemmin yleisemmässä, Taylorin sarjan muodossa jo 1715, ja jo skotlantilainen James Gregory (1638-75) oli käyttänyt sitä erikoistapauksissa. Myös Newton ja Johann Bernoulli olivat tunteneet sarjan. - Taylorin, Maclaurinin ja Newtonin formulaatioissa f:n derivaattojen paikalla on vastaavia fluksioiden osamääriä.

Maclaurinin todelliset ansiot ovat korkeamman asteen käyrien tutkimuksessa (jonka oli pannut alulle Newton) ja siitä, että hän kirjoitti yhden ensimmäisistä Newtonin differentiaali- ja integraalilaskentaa esittelevistä oppikirjoista, teoksen Treatise of Fluxions (1742). Kirjassaan Maclaurin pyrki esittämään analyysiä ''antiikin täsmällisyydellä''. Maclaurin puolusti Newtonia Englannissa virinneessä polemiikissa, joka koski uuden analyysin perusteiden pitävyyttä. Vastapuolta edusti tunnettu filosofi, irlantilainen piispa George Berkeley (1685-1753), joka asetti - aiheellisesti - kyseenalaisiksi tarpeen mukaan nolliksi tai nollasta poikkeaviksi käsitetyt äärettömän pienet suureet (''ghosts of departed quantities'') ja otaksui analyysin antamien oikeiden tulosten johtuvan sattumasta ja toisensa kumoavista virheistä. Yhtä lailla kriittinen Berkeley oli leibnizilaista analyysiä kohtaan. - Maclaurin kirjoitti myös suositun, postuumina ilmestyneen, mutta kuuteen painokseen yltäneen algebran oppikirjan Treatise of Algebra (1748), jossa ensi kerran esiintyy kahden ja kolmen tuntemattoman lineaarisen yhtälöryhmän ratkaisukaava, Cramerin sääntö; nimensä tämä sääntö sai sveitsiläisestä Gabriel Cramerista (1704-52), joka käytti yhtälöissään indeksoituja kertoimia ja sai säännön säännöllisyyden näin paremmin näkyviin vuonna vuonna 1750 ilmestyneessä tutkielmassaan.

Maclaurinin pitäytymisen klassisiin menetelmiin on katsottu haitanneen matematiikan kehitystä Englannissa. - Maclaurin sairastui kuolettavasti osallistuessaan 1745 Edinburghin puolustukseen kapinoivia skotteja vastaan.

9.3 Euler

Yksi kaikkien aikojen merkittävimpiä matemaatikkoja on Leonhard Euler (1707-83). Hän oli Bernoullien tapaan kotoisin Baselista Sveitsistä ja Johann Bernoullin oppilas. Euler, kuten useat muutkin 1700-luvun merkittävät matemaatikot, teki elämäntyönsä tiedeakatemioissa, joita hallitsijat perustivat eri maiden hovien yhteyteen. Euler toimi pisimpään Pietarissa Pietari Suuren aloitteesta perustetussa tiedeakatemiassa. Pietariin nuoren Eulerin houkuttelivat sinne jo aikaisemmin asettuneet Johann Bernoullin pojat Daniel ja nuorena kuollut Nicolaus Bernoulli (1695-1726). Myös Berliinissä Fredrik Suuren perustamassa vastaavanlaisessa akatemiassa Euler vietti pitkähkön ajanjakson, ennen kuin Katariina Suuri kutsui hänet takaisin Pietariin. Euler on haudattu Pietariin, Aleksanteri Nevskin luostarin hautausmaalle.

Eulerin tuotteliaisuus on lähes käsittämätön. Vaikka hän menetti näön toisesta silmästään alle 30-vuotiaana ja sokeutui kokonaan 17 vuotta ennen kuolemaansa, hän kirjoitti ja saneli jatkuvasti matematiikkaa, keskimäärin 800 sivua vuodessa. Elinaikanaan Euler julkaisi yli 500 tutkimusta, ja julkaistavaa riitti vielä 40 vuodeksi Eulerin kuoleman jälkeen; kaikkiaan Eulerin julkaisujen määräksi on laskettu 856. Eulerin ensimmäinen tieteellinen julkaisu ilmestyi, kun hän oli 19-vuotias. Se käsitteli kysymystä laivan mastoista. Eulerin koottujen teosten julkaiseminen on yhä kesken. Ne tulevat lopulta käsittämään 72 vankkaa osaa; tähän ei vielä kuulu usean tuhannen kirjeen laajuinen kirjeenvaihto eivätkä aiemmin julkaisemattomat käsikirjoitukset ja päiväkirjat. Eulerin mukaan nimettyjä käsitteitä ja lauseita löytyy matematiikasta kymmenittäin. - Eulerilla oli 13 lasta.

Eulerin kirjoitukset käsittelevät jokseenkin kaikkia silloisen matematiikan ja fysiikan aloja, ja paitsi tieteellisiä tutkimuksia niihin kuuluu oppikirjoja ja yleistajuisia esityksiä. Tieteellisen popularisoinnin esikuvia on Eulerin Kirjeitä eräälle saksalaiselle prinsessalle (1760-61). Euler on luonut suuren osan vakiintunutta matematiikan merkintäkoneistoa: mm. luonnollisen logaritmijärjestelmän kantaluvun merkintä e (Euler todisti, että e on irrationaalinen ja tarkasteli ensimmäisenä logaritmeja eksponentteina), ympyrän kehän ja halkaisijan suhde $\pi$, imaginaariyksikkö $i=\sqrt{-1}$, funktiomerkintä f(x) (vuodelta 1734), kolmion sivujen ja kulmien standardimerkinnät a, b, c; A, B, C, summamerkki $\sum$, binomikertoimen merkintä $${p\choose q}$$ (itse asiassa Euler kirjoitti $${\left[\frac{p}{q}\right]}$$), kolmion sisään ja ympäri piirrettyjen ympyröiden säteiden standardimerkinnät r, R ovat kaikki Eulerin käyttöönottamia ja vakiinnuttamia, vaikka $\pi$-merkintää olikin jo ehtinyt aikaisemmin käyttää muuan englantilainen William Jones (1675-1749).

Paitsi puhtaasti merkintöjen alalla Eulerin lukuisat oppikirjat, kuten Introductio in analysin infinitorum (1748), Institutiones calculi differentialis (1755) ja Institutiones calculi integralis (1768-74) ja saksankielinen Vollständige Anleitung zur Algebra (1770) loivat monin osin yhä vallitsevan korkeamman matematiikan yliopisto-opetuksen standardin. Introductio kokosi uuden analyysin peruskäsitteet funktiokäsitteen ympärille. Eulerille ei funktio kuitenkaan vielä ollut aivan lopullisesti täsmentynyt, vaan hän määritteli sen milloin muuttujista ja vakioista mielivaltaisesti kootuksi lausekkeeksi, milloin koordinaatistoon piirretyn mielivaltaisen (''vapaallla kädellä piirretyn'') käyrän havainnollistamaksi riippuvuudeksi. - Kaikki Eulerin päättelyt eivät olleet korrekteja: geometrisen sarjan summakaavasta Euler päätteli suoraviivaisesti, että

$$\dots x^{-2} + x^{-1} + 1 + x + x^2+\dots = \frac{\frac{1}{x}}{1-\frac{1}{x}}+\frac{1}{1-x}=0\,!$$

Useimmissa tapauksissa Eulerin intuitio johti kuitenkin hänet oikeaan tulokseen, vaikka päättelyaskelet olisivatkin olleet vajavaisia.

Eulerin tärkein työkalu olivat joka tapauksessa sarjat. Esimerkiksi yhtälön

$$\frac{\sin\sqrt x}{\sqrt x}=1-\frac{x}{3!}+\frac{x^2}{5!}-\dots=0.$$

ratkaisuja ovat $x_1=\pi^2$, $x_2=(2\pi)^2$, ...Mutta algebrallisen yhtälön $1+a_1x+\dots+a_nx^n=0$ juurille x₁, x₂, ..., x_npätee

$$1+a_1x+a_2x^2+\dots+a_nx^n=\left(1-\frac{x}{x_1}\right)\left(1- \frac{x}{x_2}\right)\dots\left(1-\frac{x}{x_n}\right)$$

ja

$$\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_n}=-a_1.$$

Jos tämän oletettaisiin pätevän myös ''ääretönasteisiin'' polynomeihin, saataisiin

$$\frac{1}{\pi^2}+\frac{1}{(2\pi)^2}+\frac{1}{(3\pi)^2}+\dots=-\left(- \frac{1}{3!}\right),$$

joten

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\dots=\frac{\pi^2}{6}.$$

Saatuaan tietää Eulerin tuloksen Johann Bernoulli toivoi veljensä olevan elossa - Jakob Bernoulli oli omistanut paljon tarmoa epäonnistuneisiin yrityksiinsä laskea kokonaislukujen neliöiden käänteislukujen summaa. Samanlaisin päättelyin Euler johti sittemmin Riemannin $\zeta$-funktiona tunnetuksi tulleen sarjan

$$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}$$

arvon parillisilla kokonaisluvuilla s. Arvolla s=1 $\zeta(s)$ on hajaantuva harmoninen sarja. Euler todisti, että sarjan n:nnen osasumman ja luvun $\ln n$ erotus lähenee raja-arvoa $\gamma$; tätä lukua sanotaan Eulerin vakioksi. Euler keksi mm. yhteyden

$$\zeta(s)=\prod_{p}\frac{1}{1-p^{- s}},$$

missä tulo ulotetaan kaikkiin alkulukuihin p.

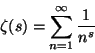
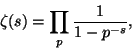
Esimerkkinä Eulerin päättelystä tarkastellaan vielä eksponenttifunktion perusominaisuuksien johtoa. Jos $\varepsilon$ on ''äärettömän pieni luku'', niin $a^{\varepsilon}=1+k\varepsilon$, missä k on a:sta riippuva vakio. Jos nyt x on äärellinen luku, niin $N=\frac{x}{\varepsilon}$ on ''äärettömän suuri luku''. Silloin

$$\begin{split}a^x &= a^{N\varepsilon}=(1+k\varepsilon)^N=\left... ...x^2+\frac{1}{3!}\frac{N(N-1)(N-2)}{N^3}k^3x^3+\dots \end{split}$$

Koska N on äärettömän suuri, on

$$\frac{N-1}{N}=\frac{N-2}{N}=\dots=1,$$

joten

$$a^x=1+\frac{kx}{1!}+\frac{k^2x^2}{2!}+\frac{k^3x^3}{3!}+\dots$$

Kun tässä asetetaan x=1, saadaan

$$a=1+k+\frac{k^2}{2!}+\frac{k^3}{3!}+\dots$$

Merkitäään nyt e:llä arvoa k=1 vastaavaa a:ta. Silloin

$$e=1+\frac{1}{2!}+\frac{1}{3!}+\dots$$

Aikaisemman nojalla on edelleen $e^x=\left(1+\frac{x}{N}\right)^N$.

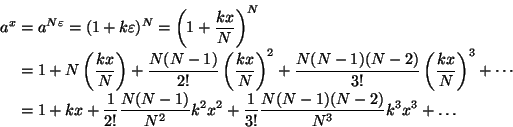
Euler operoi kompleksiluvuilla vapaasti. Eulerin kaava

$$e^{ix}= \cos x + i\,\sin x$$

(jonka keksijänä voinee pitää de Moivrea) oli hänelle keskeinen käsite mm. logaritmifunktion ominaisuuksien selvittelyssä: Euler selvitti matemaatikkoja pitkään askarruttaneen kysymyksen negatiivisten lukujen logaritmeista ja totesi logaritmifunktion monikäsitteisyyden. Euler on usean muuttujan anlyysin pioneereja. Kaksinkertaisen integraalin muuttujanvaihtokaava on hänen esittämänsä. Eulerin vaikutus näkyy myös mm. tavallisissa differentiaaliyhtälöissä ja variaatiolaskennassa. Differentiaaliyhtälöiden teorian vakiintunut asioiden esittämisen järjestys ja monet tekniikat, kuten integroivien tekijöiden käyttö ja vakiokertoimisten lineaaristen yhtälöiden ratkaisukaavat periytyvät häneltä. Variaatiolaskennan keskeinen integraalin

$$I(y)=\int_a^bF(x,\,y,\,y')\,dx$$

maksimoivan funktion y=y(x)välttämätön ehto

$$\frac{\partial F}{\partial y}-\frac{d}{dx}\left( \frac{\partial F}{\partial y'}\right)=0$$

on sekin nimeltään Eulerin yhtälö.

Analyysin ohella Eulerin merkitys näkyy jokseenkin kaikilla matematiikan alueilla. Euler kehitti huomattavasti lukuteoriaa: hän osoitti Fermat'n olettamuksen kaikkien lukujen 2²ⁿ + 1 eli Fermat'n lukujen jaottomuudesta vääräksi, julkaisi ensimmäisen todistuksen ns. Fermat'n pienelle lauseelle, jota hän myös yleisti sittemmin Eulerin funktioksi nimetyn (nimitys on Gaussin) lukuteoreettisen funktion $\phi$ avulla ( $\phi(n) = n$:ää pienempien sellaisten kokonaislukujen määrä, joilla ei ole yhteisiä tekijöitä n:n kanssa), osoitti alkulukujen käänteisluvuista muodostuvan sarjan hajaantuvaksi, todisti Fermat'n suuren lauseen hypoteesin todeksi eksponentilla n=3jne. Geometriaan Euler jätti mm. kolmion merkillisiä pisteitä yhdistävän Eulerin suoran ja yhdesti yhtenäisen monitahokkaan kärkien, särmien ja sivutahkojen määriä v, e ja s sitovan Eulerin kaavan v - e + s = 2. Myös toisen asteen pintojen, kartioleikkausten kolmiulotteisen analogian, ominaisuuksien selvittely kuuluu Eulerin ansioluetteloon.

Yksi Eulerin kuuluisimpia töitä on ns. Königsbergin siltaongelman ratkaisu vuodelta 1736. Tehtävää - on konstruoitava kävelyreitti, joka ylittäisi Itä-Preussin Königsbergissä (nykyisin paremmin tunnettu Kaliningradina) olevat Pregel-joen seitsemän siltaa, kunkin vain kerran - ja sen ratkaisua, jossa tällainen reitti osoitetaan mahdottomaksi, voi luonnehtia lähinnä ajanvietematematiikaksi, mutta toisaalta katsotaan, että Eulerin ratkaisu on antanut alkusysäyksen kahdelle sittemmin merkittävälle matematiikan alalle, topologialle ja verkkoteorialle. Eulerin polku on sellainen verkon sivuista koostuva tie, jossa kukin sivu esiintyy tasan yhden kerran.

9.4 Ranskan valistusajan matemaatikkoja

Huomattavimmat 1700-luvun puolivälin ranskalaismatemaatikot olivat Alexis Claude Clairaut (1713-65) ja Jean le Rond d'Alembert (1717-83). Edellinen - eräs kaikkien aikojen varhaiskypsimpiä matemaatikkoja - luki kymmenvuotiaana l'Hôspitalia ja julkaisi teini-ikäisenä merkittävän kolmiulotteista analyyttistä geometriaa käsittelevän teoksen ja valittiin erivapaudella jo 18-vuotiaana Ranskan tiedeakatemian jäseneksi. - Clairaut lienee käynyt Suomessakin kuuluisan, maapallon muotoa selvitelleen Maupertuis'n meridiaaninmittausretkikunnan mukana. Hänen myöhempi maapallon muotoa käsittelevä teoksensa sisältää differentiaaliyhtälöiden teoriaa kehittäneitä tuloksia, mm. differentiaalin Mdx+Ndyeksaktisuusehdon

$$\frac{\partial M}{\partial y}= \frac{\partial N}{\partial x}.$$

Löytölapsi (etunimi Jean le Rond viittaa samannimiseen pariisilaiskirkkoon, jonka portaille korkeasukuinen (markiisitar) äiti oli pojan hylännyt; aatelinen isä kustansi sittemmin pojan elatuksen ja koulutuksen) d'Alembert oli monipuolinen tiedemies ja filosofi, alkuperäiseltä koulutukseltaan juristi. Lakitieteen opinnot suoritettuaan d'Alembert aikoi vielä opiskella lääkäriksi. Koska matematiikan harrastus oli haitaksi opinnoille, d'Alembert talletti matemaattiset kirjansa erään ystävänsä luokse. Vähin erin hän kuitenkin haki ne takaisin, jätti lääketieteen ja rupesi ammatikseen matemaatikoksi ja filosofiksi. d'Alembertin pitkäaikainen toimi oli Ranskan Tiedeakamian pysyvän sihteerin tehtävä; hän oli aikansa merkittävimpiä tiedepoliittisia vaikuttajia. Fredrik II kutsui Eulerin akatemiaansa d'Alembertin neuvosta, samoin myöhemmin Lagrangen.

D'Alembert oli keskeisessä asemassa valistusfilosofien suurteoksen, Denis Diderot'n (1713-84) julkaiseman 28-osaisen Encyclopédien toimituksessa ja vastasi sen matematiikkaa ja luonnontieteitä käsittelevistä artikkeleista. Ensyklopedia - artikkelissa d'Alembert mm. esitti modernin käsityksensä infinitesimaalilaskennan perustamisesta täsmälliselle raja-arvon käsitteelle : d'Alembert ymmärsi nykyaikaiseen tapaan raja-arvon suureeksi, jota muuttuva suure lähestyy niin, että suureen ja raja-arvon erotus tulee pienemmäksi kuin mikä hyvänsä ennalta annettu suure. D'Alembert pyrki löytämään todistuksen algebran peruslauseelle (jonka mukaan jokaisella polynomilla on ainakin yksi kompleksinen nollakohta); ranskalaisella kielialueella tämä keskeinen teoreema tunnetaan d'Alembertin lauseena. Sen todistus onnistui paremmin Gaussille.

D'Alembert on Eulerin ja Daniel Bernoullin ohella osittaisdifferentiaaliyhtälöiden tutkimuksen aloittajia: hän tutki mm. värähtelevän kielen liikettä (ongelma, joka on synnyttänyt poikkeuksellisen paljon matemaattista teoriaa ja joka oli monen kiistan aiheena 1700-luvun johtavien matemaatikkojen kesken), ja johtui osittaisdifferentiaaliyhtälöön

$$\frac{\partial^2u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2}.$$

Tälle värähtely-yhtälölle d'Alembert löysi ratkaisun

u(x,t) = f(x+t) + g(x-t);

tässä f ja g ovat mielivaltaisia funktioita.

9.5 Lagrange

1700-luvun jälkipuoliskon merkittävin ranskalaismatemaatikko on Joseph Louis Lagrange (1736-1813), Eulerin ohessa koko vuosisadan suurimpia. Puoliksi italialainen Lagrange syntyi ja opiskeli Torinossa, jonka tykistöakatemian matematiikan professoriksi hänet nimitettiin jo 19-vuotiaana. Samoin kuin Eulerin, Lagrangenkin työnantajina olivat hallitsijat. Fredrik Suuri kutsui hänet Eulerin seuraajaksi Berliinin tiedeakatemiaan, jossa hän vaikutti 20 vuotta, ja 1787 Ludvig XVI kutsui hänet Ranskaan akateemikon tehtäviin. Lopun elämäänsä Lagrange toimi Pariisissa. Lagrange kärsi masennuksesta, erityisesti Ranskaan muutettuaan.

Lagrangen tutkimusote oli kriittisempi kuin useimpien hänen aikansa matemaatikkojen. Analyysin loogisten perusteiden aukkoja Lagrange pyrki paikkaamaan suuressa teoksessaan Théorie des fonctions analytiques (1797) sarjakehitelmien avulla: jos funktion f Taylorin sarja

$$f(x) = a_0 + a_1(x-x_0)+a_2(x-x_0)^2 +\dots$$

tunnetaan, f:n derivaatat voidaan ilmaista kertoimien avulla: f'(x₀)= a₁, f"(x₀) =2a₂ jne. Lagrange teki näistä relaatioista derivaattojen määritelmän, uskoen päässeensä eroon infinitesimaalisista suureista. Itse asiassa sana derivaatta, (jolle aikanaan on suomen kieleen tarjottu sananmukaista käännöstä 'johdos'), tuli ensi kertaa käyttöön vasta tässä yhteydessä. Valitettavasti määritelmä toimii vain suppenevan Taylorin sarjan omaavien funktioiden yhteydessä. Vastaesimerkki f(x)=e^-1/x2, $x\ne 0$, f(0)=0 on esimerkki funktiosta, jonka kaikki derivaatat origossa häviävät ja jonka sarjakehitelmä on nollafunktion kehitelmä, mutta joka ei kuitenkaan ole nolla origon ulkopuolella. Lagrangekaan ei aina ottanut huomioon suppenemisongelmia, joiden mukana välttämättä seuraa kysymys raja-arvosta. - Usein käytettävät derivaattojen merkinnät f'(x), f''(x) jne. ovat peräisin Lagrangelta, samoin ensimmäinen lauseke Taylorin sarjan jäännöstermille.

Lagrangen tutkimukset käsittelivät mekaniikkaa (Lagrangen funktio ja liikeyhtälöt; monumentaaliteos Mécanique analytique (1788), mekaniikan aksiomaattinen esitys ''ilman yhtäkään kuvaa'') ja differentiaaliyhtälöitä (ns. epähomogeenisten lineaaristen yhtälöiden ratkaiseminen parametrien variointimenetelmällä on hänen keksintöään), variaatiolaskentaa, yhtälöiden numeerista ratkaisemista, lukuteoriaa (mm. todistus Fermat'n väittämälle, että jokainen kokonaisluku voidaan esittää enintän neljän neliön summana, Pellin yhtälön yleinen ratkaisu) ja algebraa. Viimeksi mainitulla alalla Lagrange kuuluu ryhmäkäsitteen ennakoijiin. Hän tutki algebrallisen yhtälön ratkeavuuden ja sen juurien permutaatio-ominaisuuksien yhteyksiä ja johtui mm. keskeiseen teoreemaan, jonka mukaan (nykyisin käsittein) äärellisen ryhmän aliryhmän kertaluku on ryhmän kertaluvun tekijä. Tämä tulos tunnetaan nimellä Lagrangen lause. Usean muuttujan sidotun ääriarvon määrittäminen apumuuttujien, Lagrangen kertoimien, avulla on hänen keksintöään.

Ranskan vallankumouksen aikana Lagrange toimi puheenjohtajana komiteassa, joka suunnitteli metrijärjestelmän. Lagrange ajoi läpi suhdeluvun 10, vaikka luvulla 12 oli paljon kannatusta.

Alkuun - Etusivu - Edellinen - Seuraava