1600-lukua voidaan pitää eräänä matematiikan historian suurista käännekohdista. Tuolloin syntyivät nykymatematiikan keskeiset metodit, differentiaali- ja integraalilaskenta, jota myös kutsutaan infinitesimaalilaskennaksi, ja analyyttinen geometria. Edellisen synty liitetään yleensä Newtoniin ja Leibniziin, jälkimmäisen Descartesiin.
Suuret keksinnöt eivät kuitenkaan syntyneet yhtäkkiä. Noin sadan vuoden ajalta ennen Newtonin ja Leibnizin aikaa löytyy päättelyitä, joissa on nähtävissä matemaattiselle analyysille tunnusomaisia piirteitä. Infinitesimaalilaskentaa enmnkoinut Arkhimedeen Metodi oli tuolloin tuntematon, mutta ajan yleisenä henkenä oli antiikin työlään ekshaustiomenetelmän korvaaminen nopeammin tuloksiin johtavilla, joskin loogisesti vähemmän pitävillä metodeilla.
Ensimmäisiä infinitesimaalisten päättelyjen esittäjiä oli Stevin, joka v. 1586 ilmestyneessä teoksessaan De Beghinselen der Weeghconst perusteli käsitystään kolmion muotoisen kappaleen painopisteen sijainnista mediaanilla ajattelemalla kolmion sisään piirrettyjä pieniä suunnikkaita, joiden pitemmät sivuparit olivat kolmion sivujen suuntaisia. Kunkin tällaisen painopiste oli suunnikkaan keskikohdassa, joten kolmiokin tuli tasapainottumaan pitkin kutakin mediaaniaan.
Infinitesimaalisia pinta-alan- ja tilavuudenmääritysmenetelmiä käytti huomattavalla menestyksellä tähtitieteen suurmies Johannes Kepler (1571-1630). Ympyrän ja ellipsin alat Kepler laski täyttämällä kuviot pienillä kolmioilla, joiden kantojen annettiin kutistua äärettömän pieniksi.
Keplerin planeettaliikettä koskeva toinen laki -
auringosta planeettaan piirretty vektori piirtää samassa
ajassa aina saman pinta-alan, perustui kuitenkin virheelliseen
infinitesimaalipäättelyyn. Kepler oletti havaintojen
perusteella, että planeetan nopeus kunakin hetkenä on
kääntäen verrannollinen sen auringosta A laskettuun
etäisyyteen r. Jos radan pisteiden P ja Q välinen kaari
jaetaan osakaariin ![]() ,
niin planeetan välillä PQkäyttämä aika on likimain
,
niin planeetan välillä PQkäyttämä aika on likimain
Hyvä viinivuosi 1612 inspiroi Keplerin
käyttämään samoja menetelmiä useiden
pyörähdyskappaleen muotoisten viinitynnyrien tilavuuksien
laskemiseksi. Tulokset ja avoimiksi jääneet kysymykset
julkaistiin 1615 teoksena Nova stereometria doliorum
vinariorum. - Esimerkkinä Keplerin integrointitavoista on
toruksen tilavuuden laskeminen. Olkoon toruksen sisäympyrän
säde b ja leikkausympyrän a. jos torus viipaloidaan
paloiksi ''putkea'' vastaan kohtisuorilla tasoilla, niin yhden
tällaisen palan tilavuus on likimain
Galileo Galilei (1564-1642) ei ollut varsinaisesti matemaatikko, mutta hän teki varteenotettavia havaintoja ''äärettömän pienistä'' ja ''äärettömän suurista'' suureista. Galilei mm. kiinnitti huomiota ''eri kertalukua'' oleviin äärettömän pieniin suureisiin. - Galilei havaitsi ensimmäisenä sen äärettömän joukon perusominaisuuden, että osajoukossa voi olla ''yhtä monta'' alkiota kuin perusjoukossa: ''On olemassa yhtä monta neliölukua kuin itse lukujakin.''
Galilein oppilaista oli matemaatikkona kuuluisin
Bonaventura Cavalieri (1598-1647),
jesuiitta ja Bolognan
professori. Cavalierin ''integrointimenetelmät'' olivat Keplerin
käyttämiä täsmällisempiä ja johtivat tulokseen
useammin. Kepler laski yhteen mittalukuja, jotka liittyvät
pieniin, mutta samaa ulotteisuutta kuin tutkittava kuvio oleviin
osiin. Cavalierin perusajatus oli muodostaa vastaavuus kahden
kuvion tai kappaleen infinitesimaalisten osien välillä; jos
toiseen kuvioon liittyvä mittaluku oli tunnettu, toisen
mittaluku saatiin selville. Cavalierin periaate sanoo,
että jos kahden kappaleen kaikki tasoleikkaukset ovat yhtä
suuret, kappaleilla on sama tilavuus. Periaatteen nojalla esim. r-säteinen ympyrä pohjana piirretyn h-korkuisen kartion
tilavuus voidaan laskea vertaamalla kappaletta samankorkuiseen
yksikköneliöpohjaiseen pyramidiin, jonka tilavuus on
Cavalierin pääteos Geometria indivisibilibus
continuorum (1635) vaikutti suuresti infinitesimaalilaskennan
kehitykseen. Teos sisältää tuloksen, joka on
yhtäpitävä kaavan
![]() .
Etäisyydellä x kappaleiden kärjistä
oleva pohjien suuntainen taso leikkaa kartiosta ympyrän, jonka
ala on
.
Etäisyydellä x kappaleiden kärjistä
oleva pohjien suuntainen taso leikkaa kartiosta ympyrän, jonka
ala on
![]() ja pyramidista neliön, jonka ala
on
ja pyramidista neliön, jonka ala
on
![]() .
Tästä seuraa, että kartion tilavuus on
.
Tästä seuraa, että kartion tilavuus on
![]() .
.
kanssa. Kaavan (1)
Cavalieri totesi oikeaksi arvoilla
![]() vertaamalla
suunnikkaan sivun suuntaisten janojen potenssien ja
lävistäjän suunnikkaasta erottamien kolmioiden kannan
suuntaisten janojen potenssien summia.
vertaamalla
suunnikkaan sivun suuntaisten janojen potenssien ja
lävistäjän suunnikkaasta erottamien kolmioiden kannan
suuntaisten janojen potenssien summia.
Cavalierin päättely tapauksessa n=2 on suunnilleen
seuraava, modernisoiduin merkinnöin. Tarkastellaan tason
ensimmäisessä neljänneksessä olevaa yksikköneliötä,
jonka yksi kärki on origossa ja jonka lävistäjä on suora
y=x. Jos lasketaan y-akselin suuntaisten janojen neliöiden
summa, saadaan (symmetriaa hyväksi käyttäen)
Tapauksessa n=3 päättely on jo mutkikkaampi
(merkitään y=1-x):
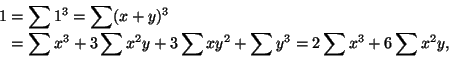
René Descartes eli
latinalaistetulla nimellä
Cartesius (1596-1650) oli nuorempana seikkailija ja
myöhemmin kuuluisa filosofi. Matematiikalle hän omistautui
vain ajoittain. Hänen matemaattinen pääteoksensa La
Géométrie ilmestyi sekin suuren filosofisen teoksen
Discours de la Méthode (1637) liitteenä. Vaikka
analyyttistä geometriaa pidetäänkin Descartesin
keksintönä kuten termit karteesinen koordinaatisto ja
karteesinen tulo osoittavat, ei La Géométrie juuri
muistuta nykyistä analyyttistä geometriaa koordinaatistoineen,
käyrän yhtälöineen ja funktion kuvaajineen. Descartesin
päätavoite oli algebran ja geometrian riippuvuuden
osoittaminen ja algebran hyödyksi käyttäminen geometrian
tutkimisessa. Descartesin metodi geometriassa oli antaa jokaiselle
tehtävän osalle, tunnetulle tai tuntemattomalle, symboli,
johtaa symbolien välille riittävä määrä algebrallisia
yhtälöitä ja ratkaista tuntematon. Algebrallinen symbolismi
oli Descartesin teoksessa ensi kertaa lähes sama kuin nykyisin
käytössä oleva, ainoina poikkeuksina se, että Descartes
kirjoitti aa symbolin a2 sijasta,
![]() merkinnän
merkinnän
![]() sijasta ja että yhtäsuuruusmerkki (
sijasta ja että yhtäsuuruusmerkki (
![]() takaperin) oli erilainen kuin nykyisin. Merkintöjä a3,
a4 jne. hän kyllä käytti. Aakkosten alkupään
kirjaimien varaaminen tunnetuille ja loppupään tuntemattomille
suureille on myös Descartesin innovaatio.
takaperin) oli erilainen kuin nykyisin. Merkintöjä a3,
a4 jne. hän kyllä käytti. Aakkosten alkupään
kirjaimien varaaminen tunnetuille ja loppupään tuntemattomille
suureille on myös Descartesin innovaatio.
La Géométrie sisältää myös Descartesin merkkisäännön: polynomiyhtälön positiivisten ja negatiivisten (eli Descartesin terminologiassa ''väärien'') juurten määrä voidaan päätellä polynomin peräkkäisten kertoimien eri- ja samanmerkkisyydestä: positiivisia juuria on (enintään) yhtä paljon kuin kertoimien jonossa on merkinvaihdoksia ja negatiivisia juuria on enintään yhtä paljon kuin kertoimien jonossa on peräkkäisten samanmerkkisten kertoimien pareja.
Ruotsin kuningatar Kristiina kutsui Descartesin 1649 Tukholmaan filosofianopettajakseen. Poikkeuksellisen kylmä talvi 1650 ja kello viideltä aamulla pidetyt oppitunnit olivat Descartesille liikaa; hän sairastui ja kuoli.
Analyyttisen geometrian peruskäsitteet keksi itsenäisesti Pierre de Fermat (1601-65), vapaa-aikoinaan matematiikkaa tutkinut toulouselainen juristi. Selvemmin kuin Descartes Fermat oivalsi, että kahden muuttujan yhtälö määrittelee uran eli tasokäyrän. ''Aina, kun lopullisessa yhtälössä esiintyy kaksi tuntematonta, kyseessä on ura. Toisen [tuntemattoman janan] päätepiste piirtää suoran tai käyrän viivan.'' Hän myös tunnisti kaikki kahden muuttujan toisen asteen polynomit kartioleikkausten yhtälöiksi. Fermat'n analyyttinen geometria, kirjattuna teokseen Ad locus planos et solidos isagoge, tuli julki vasta 1679, Fermat'n kuoleman jälkeen, kuten suurin osa hänen muustakin tuotannostaan.
Fermat kuuluu matematiikan historian suuriin nimiin.
Tämä perustuu paitsi hänen geometrian ja analyysin alalla
saavuttamiinsa tuloksiin myös monipuolisiin lukuteorian
tuloksiin. Fermat kehitti todistusmenetelmän, jota hän nimitti
''äärettömäksi laskeutumiseksi'' (eräänlainen
takaperoinen induktio), ja todisti sen avulla mm., että ei ole
olemassa yhtälön
x4+y4= z4 toteuttavia
positiivisia kokonaislukuja x, y, z.
Fermat ilmoitti (Diofantoksen
Arithmetican käännöksen marginaaliin
tekemässään
lisäyksessä) osaavansa todistaa saman tuloksen silloinkin, kun
eksponenttina on mielivaltainen kokonaisluku ![]() .
Tämä
Fermat'n suuren lauseen tai viimeisen teoreeman
nimellä tunnettu hypoteesi on yli 300 vuoden ajan kiehtonut
sekä ammatti- että amatöörimatemaatikkoja. Saksalainen
amatöörmatemaatikko ja lääkäri
Paul Wolfskehl
lahjoitti vuosisadan vaihteessa huomattavan palkinnon, joka oli
tarkoitus antaa tietyt kriteerit täyttävälle Fermat'n
ongelman ratkaisulle. Palkinto luovutettiin kesällä 1997
englantilaiselle
Andrew Wilesille (1953-), joka oli kaksi vuotta
aikaisemmin lopullisesti ratkaissut ongelman. Vaikka
palkintosäätiö menetti lähes koko omaisuutensa Saksan
1920-luvun suurinflaatiossa, oli palkinto 75
.
Tämä
Fermat'n suuren lauseen tai viimeisen teoreeman
nimellä tunnettu hypoteesi on yli 300 vuoden ajan kiehtonut
sekä ammatti- että amatöörimatemaatikkoja. Saksalainen
amatöörmatemaatikko ja lääkäri
Paul Wolfskehl
lahjoitti vuosisadan vaihteessa huomattavan palkinnon, joka oli
tarkoitus antaa tietyt kriteerit täyttävälle Fermat'n
ongelman ratkaisulle. Palkinto luovutettiin kesällä 1997
englantilaiselle
Andrew Wilesille (1953-), joka oli kaksi vuotta
aikaisemmin lopullisesti ratkaissut ongelman. Vaikka
palkintosäätiö menetti lähes koko omaisuutensa Saksan
1920-luvun suurinflaatiossa, oli palkinto 75![]() 000 Saksan
markkaa.
000 Saksan
markkaa.
Fermat'n ilman todistusta ilmoittamista tuloksista useimmat ovat lopulta osoittautuneet oikeiksi. Poikkeuksen tekee Fermat'n väite, jonka mukaan kaikki muotoa 22n+1 olevat luvut, ns. Fermat'n luvut, olisivat alkulukuja. Itse asiassa nämä luvut ovat muutamaa poikkeusta lukuunottamatta yhdistettyjä, ja nykyisen tietämyksen mukaan alkulukuja vain, kun n=0, 1, 2, 3 tai 4. Ns. Fermat'n pieni lause, jonka mukaan ap-1-1 on jaollinen p:llä aina, kun p on alkuluku eikä a ole jaollinen p:llä, on sekin peräisin Fermat'lta, mutta lauseen todistukset ovat myöhemmältä ajalta.
Osoitetaan Fermat'n äärettömän laskeutumisen
menetelmällä, että yhtälöllä
Pierre Fermat sekä hänen maanmiehensä
Blaise Pascal (1623-62) ja
Giles Personne de Roberval
(1602-75) kykenivät kukin johtamaan kaavan
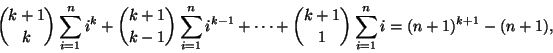

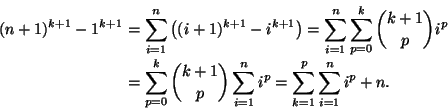
Fermat selvitti potenssin integroinnin vielä omalla
tavallaan: Jos halutaan laskea käyrän y=xn alle
jäävän alueen ala, 0:n ja pisteen suoran x=a välissä,
jaetaan väli ![]() pisteillä Ea, E2a, ..., missä
E<1. Approksimoidaan alaa suorakaiteilla, joiden kanta on
Eka-
Ek+1a ja korkeus (Eka)n. Suorakaiteiden yhteinen ala on
pisteillä Ea, E2a, ..., missä
E<1. Approksimoidaan alaa suorakaiteilla, joiden kanta on
Eka-
Ek+1a ja korkeus (Eka)n. Suorakaiteiden yhteinen ala on
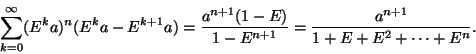
Englantilainen John Wallis (1616-1703), 53 vuotta Oxfordin yliopiston matematiikan proferssorina toiminut, oli varsinaisesti negatiivisten ja murtolukumuotoisten eksponenttien käyttöönottaja. Häneltä on mm. konventio x0=1. Wallis esitti 1656 ilmestyneessä teoksessaan Arithmetica Infinitorum, että kaava ( 2) pätee murtolukueksponenteillekin. Hänen päättelynsä perustui Pascalin kolmion rivien interpoloimiseen. Se oli varsin spekulatiivinen ja hyväksyttävissä vain, kun n on kokonaisluvun käänteisluku. Sitovamman perustelun yleistä rationaalieksponenttia vastaavassa tapauksessa esitti Fermat. Wallisin päättely on silti mielenkiintoinen osoittaessaan, miten intuitio ohjaa matemaattista keksimistä. Newton seurasi Wallisia luodessaan teorialleen keskeisen binomisarjan.
Wallis päätteli numeerisen evidenssin perusteella,
että suhde
Paraabelin ![]() kvadratuuria hyväksi
käyttäen 20-vuotias (ja sittemmin unohdettu) englantilainen
William Neil (1637-70) esitti 1657 ensimmäisen
täsmällisen käyrän pituuden määrityksen. Kyseessä
oli ns. semikuubinen paraabeli, jonka yhtälö on y2
= x3. Käyrän pituus s välillä
kvadratuuria hyväksi
käyttäen 20-vuotias (ja sittemmin unohdettu) englantilainen
William Neil (1637-70) esitti 1657 ensimmäisen
täsmällisen käyrän pituuden määrityksen. Kyseessä
oli ns. semikuubinen paraabeli, jonka yhtälö on y2
= x3. Käyrän pituus s välillä ![]() ,
,
![]() on likimain
on likimain
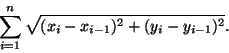
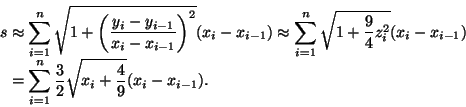
Samoin kuin Wallis tuli palvelleeksi Newtonia, Leibniz
hyödynsi Pascalin havaintoa ympyränkaareen liittyvästä
''karakteristisesta kolmiosta''. Olkoon O yksikköympyrän
keskipiste, A kehän piste, C A:n projektio x-akselilla,
MLK pieni suorakulmainen kolmio, jonka hypotenuusa ML sivuaa
ympyrää pisteessä A ja jonka kateetit KL ja MK ovat
x- ja y-akselien suuntaiset. Silloin kolmiot AOC ja LMKovat yhdenmuotoiset. Jos AO=r ja AC=y,
![]() ,
KL=dx, niin
,
KL=dx, niin
![]() .
Näistä havainnoista Pascal johti
olennaisesti kaavaa
.
Näistä havainnoista Pascal johti
olennaisesti kaavaa
Matemaattisen analyysin historiassa differentiaalilaskenta astuu esiin vasta integraalilaskennan jälkeen, toisin kuin aineen alkeisopetuksessa nykyisin. Ensimmäiset infinitesimaaliset tangentinmääritykset tehtiin vuoden 1630 vaiheilla, analyyttisen geometrian luojien toimesta. Fermat'n maksimiperiaate oli ensimmäisiä analyyttisiä tangentinmäärityksiä: löytääkseen funktion fmaksimikohdan Fermat kirjoitti yhtälön f(x + E) = f(x), jakoi yhtälön puolittain E:llä, asetti E=0 ja ratkaisi x:n. Raja-arvon käsite ei ollut Fermat'lle tuttu, mutta hänen menettelynsä on ilmeistä sukua erotusosamaarän raja-arvon määritykselle.
Ensimmäinen Fermat'n käsittelemä
ääriarvotehtävä oli janan AB jakaminen janoiksi AC,
CB niin, että
![]() on mahdollisimman suuri. Jos
AB=a, AC=x ja C' on toinen C:n lähellä oleva piste
niin, että CC'=e, niin
on mahdollisimman suuri. Jos
AB=a, AC=x ja C' on toinen C:n lähellä oleva piste
niin, että CC'=e, niin
![]() eli
eli
![]() eli
eli
![]() eli
eli
![]() .
Kun nyt asetetaan e=0, saadaan ratkaisu
.
Kun nyt asetetaan e=0, saadaan ratkaisu
![]() ,
eli todetaan, että annetun piirin omaavista
suorakaiteista neliö on alaltaan suurin.
,
eli todetaan, että annetun piirin omaavista
suorakaiteista neliö on alaltaan suurin.
Vastaavalla tavalla Fermat ratkaisi käyrän tangentin
tai oikeastaan sivuamispisteen ja x-akselin välisen tangentin
osan projektion x-akselilla eli alitangentin. Olkoon
käyrä y=xn ja P sen piste. P:n kautta piirretty
tangentti leikkaa x-akselin pisteessä T; P:n projektio
x-akselilla on N. Jos N' on toinen x-akselin piste,
NN'=e ja P' on se käyrän y=xn piste, jonka projektio
P' on, ja vielä P:n kautta piirretty tangentti leikkaa
suoran P'N' pisteessä S ja P:n kautta piirretty
x-akselin suuntainen suora pisteessä R, ja TN=t, P'R=d,
niin kolmioiden PNT ja SRP yhdenmuotoisuuden perusteella
![]() .
Mutta
y+d=(x+e)n=xn+nxn-1e+ e:n korkeampia potensseja, joten
.
Mutta
y+d=(x+e)n=xn+nxn-1e+ e:n korkeampia potensseja, joten
![]() .
Siis
.
Siis
![]() .
.
Fermat esitti valon liikettä koskevan variaatioperiaatteen, Fermat'n periaatteen, jonka mukaan valo valitsee aina sellaisen etenemistien, jota pitkin pääsee nopeimmin pisteestä toiseen. Heijastumiseen sovellettuna tämä johti helposti heijastuslakiin, jonka mukaan tulo- ja lähtökulmat ovat samat, ja väliaineesta toiseen siirtyvän valon kohdalla Snellin lakiin.
Descartes puolestaan konstruoi käyrälle annettuun pisteeseen normaalin vaatimalla, että yhtälöllä, jonka määrittelevät käyrä ja leikkauspisteen kautta kulkeva ympyrä, on kaksoisjuuri leikkauspisteessä. Kun lisäksi vaaditaan, että ympyrän keskipiste on annetulla suoralla, saadaan käyrän normaali leikkauspisteen kautta piirretyn ympyrän säteen suunnasta.
Descartesin menetelmällä paraabelin y=x2tangentti pisteessä ![]() löytyisi seuraavasti. Pisteen
löytyisi seuraavasti. Pisteen
![]() kautta kulkevan ja piste
kautta kulkevan ja piste ![]() keskipisteenä
olevan ympyrän säde r toteuttaa ehdon
r2=(b-a)2+a4. Jos
tämän ympyrän yhtälöstä
(x-b)2+y2=r2 ja
paraabelin yhtälöstä y=x2 eliminoidaan y, saadaan
yhtälö
(x-b)2+x4-
(b-a)2-a4=(x-a)(x+a-2b)+(x-a)(x3+x2a+xa2+a3)=0. Jotta aolisi yhtälön kaksoisjuuri, on oltava
2a-2b+4a3=0 eli
b-a=2a3. Pisteen P kautta kulkevan normaalin kulmakerroin on
keskipisteenä
olevan ympyrän säde r toteuttaa ehdon
r2=(b-a)2+a4. Jos
tämän ympyrän yhtälöstä
(x-b)2+y2=r2 ja
paraabelin yhtälöstä y=x2 eliminoidaan y, saadaan
yhtälö
(x-b)2+x4-
(b-a)2-a4=(x-a)(x+a-2b)+(x-a)(x3+x2a+xa2+a3)=0. Jotta aolisi yhtälön kaksoisjuuri, on oltava
2a-2b+4a3=0 eli
b-a=2a3. Pisteen P kautta kulkevan normaalin kulmakerroin on
![]() .
Tästä saadaan tangentin
kulmakertoimeksi 2a, niin kuin pitääkin. - Descartes piti
normaalin ja tangentin määritystä suurimpana saavutuksenaan:
''Uskallan sanoa, että tämä [normaalin määritys] ei ole
pelkästään hyödyllisin ja yleisluontoisin geometrian
probleema niiden joukossa, jotka osaan ratkaista, vaan myös
niiden joukossa, joita koskaan ole toivonut osaavani ratkaista.''
.
Tästä saadaan tangentin
kulmakertoimeksi 2a, niin kuin pitääkin. - Descartes piti
normaalin ja tangentin määritystä suurimpana saavutuksenaan:
''Uskallan sanoa, että tämä [normaalin määritys] ei ole
pelkästään hyödyllisin ja yleisluontoisin geometrian
probleema niiden joukossa, jotka osaan ratkaista, vaan myös
niiden joukossa, joita koskaan ole toivonut osaavani ratkaista.''
Fermat'n ja Descartesin esittämiä komplisoituja
tangentinmääritysmenetelmiä yksinkertaistivat hollantilainen
Johann Hudde (1628-1704) ja flaamilainen
René François de Sluse (1622-85).
He johtivat laskennallisempia
menetelmiä tangentinmäärityksessä esiintyvien
kaksoisjuurten määrittämiseksi. Hudden menetelmä oli
seuraavanlainen. Olkoon
Erotusosamäärän raja-arvon idea tulee sen sijaan
selvästi esiin Newtonin cambridgeläisen opettajan
Isaac Barrow'n (1630-77)
1660-luvulla pitämissä luennoissa,
joissa tangentti tulkitaan kahden lähekkäin olevan käyrän
pisteen kautta kulkevan suoran raja-asennoksi, kun pisteet ovat
lähellä toisiaan. Tämä raja-asento voitiin laskea
jättämällä korkeamman kertaluvun infinitesimaalit pois.
Barrow esitti myös ensimmäisenä, että sellaisen käyrän
C1, joka esittää toisen käyrän C2, x-akselin ja
y- akselin suuntaisten suorien rajoittaman alueen pinta-alaa,
tangentti saadaan suoraan käyrän C2 avulla. Barrow esitti
tämän asian, joka on olennaisesti sama kuin differentiaali- ja
integraalilaskennan peruslause, pelkästään geometrisena
totuutena. Asiaan sisältyvää funktioiden relaatiota hän ei
käsitellyt, joten hänen tulostaan ei varsinaisesti voi
pitää integraalilaskennan peruslauseena.
Tangentinmäärityksiä tehtiin myös mekaanisin
perustein. Näin toimi mm. Roberval: jos käyrän ajatellaan
syntyvän massapisteen liikkuessa, on pisteen hetkellisen
nopeuden suunta tangentin suunta. Jos käyrä voidaan tulkita
kahden eri liikkeen yhdistelmäksi (kuten sykloidi, jossa
yhdistyvät translaatio ja rotaatio, kumpikin vakionopeuksisena),
voidaan tangentti määrittää nopeuksien yhteenlaskun
periaatteella. Kun paraabeli tulkitaan sellaisen pisteen
liikkeenä, jonka etäisyys polttopisteestä ja johtosuorasta
on sama, voidaan paraabelin tangentin suunta saada
polttopisteestä pois suuntautuvan ja johtosuoraa vastaan
kohtisuorassa olevien yhtä pitkien vektorien summana. Tästä
nähdään heti, että paraabelin tangentti puolittaa
polttosäteen ja johtosuoraa vastaan piirretyn kohtisuoran
välisen kulman.
Alkuun
- Etusivu
- Edellinen
- Seuraava
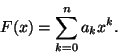
Muodostetaan
uusi polynomi G kertomalla F:n kertoimet aritmeettisen jonon
a, a+b, a+2b, ..., a+nb luvuilla. Siis
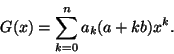
Silloin F:n kaksoisjuuri eon G:n juuri: jos
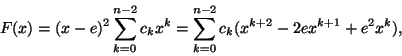
ja jos Ak=a+kb, niin
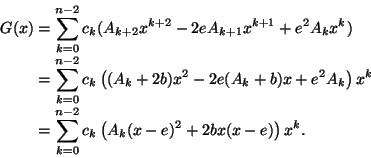
Jos
a=0 ja b=1, niin
G(x)=xF'(x); Hudden sääntö tulee
määrittäneeksi polynomin derivaatan puhtaasti algebrallisen
manipulaation tuloksena.
Matematiikkalehti Solmu
2000-09-07