PDF

6. Renessanssi

Renessanssin (''uudelleensyntymisen'') kiinnostus antiikkiin innosti edelleen myös antiikin matemaattisten klassikkojen käännöksiin. Kaupan tarpeet ja uusi tekniikka, kirjapainotaito, synnyttivät entistä paljon laajalevikkisemmän matemaattisen kirjallisuuden, laskuopit. Renessanssin aikana tehtiin ensimmäiset todella antiikin matematiikkaa pitemmälle menevät uudet keksinnöt, nimenomaan algebran alalla.

6.1 Painettuja laskuoppeja

Keskiajan lopulla Euroopan matematiikan painopiste oli yliopistojen ulkopuolella. Tosin Pariisin yliopistossa oli vuodesta 1336 voimassa sääntö, jonka mukaan tutkintoa ei myönnetty muuta kuin niille opiskelijoille, jotka valaehtoisesti tunnustivat kuunnelleensa Eukleideen Alkeiden ensimmäisiä kirjoja koskeneita luentoja.

Yleensä itseoppineet laskumestarit levittivät tietoa käytännön elämään kuten kauppaan, kirjanpitoon ja merenkulkuun liittyvästä aritmetiikasta ja algebrasta. Kirjapainotaidon keksiminen 1400-luvun keskivaiheilla ei välittömästi merkinnyt kovin suurta mullistusta matematiikassa. 1400-luvun merkittävin matemaatikko, saksalainen Johannes Müller alias Regiomontanus (1436-76) tosin omisti Nürnbergissä kirjapainon, mutta ennenaikainen kuolema esti häntä toteuttamasta laajoja suunnitelmiaan kääntää tärkeimmät matematiikan klassikkojen teokset suoraan kreikasta latinaksi ja painaa ne. (Konstantinopolin luhistuminen v. 1453 oli saanut monet siellä olleet oppineet siirtymään länteen, ja mukana oli tullut runsaasti kreikkalaisia käsikirjoituksia.) Regiomontanuksen omista töistä on tärkein De triangulis omnimodis, ensimmäinen eurooppalainen systemaattinen trigonometrian esitys. Se ilmestyi painosta vasta 1533. Sisällöltään se vastaa nykyistä trigonometrian peruskurssia, mutta esitys on täysin verbaalista. Nykyistä merkintätapaa ei vielä ollut. Itse sana trigonometria tuli käyttöön vasta 1500-luvun jälkipuoliskolla.

Kirjapainotaito teki 1400-luvun loppupuolella mahdolliseksi tuottaa lisääntyneen kaupan tarpeisiin kirjoitettuja laskuoppeja: ensimmäinen tällainen oli anonyymin tekijän Trevison aritmetiikka vuodelta 1478. Saksassa vaikuttanut laskuoppien kirjoittaja Adam Riese (1492-1559) on jättänyt saksan kieleen täsmällisyyttä ilmentävän puheenparren nach Adam Riese (vrt. ''Elon laskuopin mukaan''). Hiukan edistyneempiä aritmetiikan oppikirjoja kirjoittivat mm. italialainen Luca Pacioli (1445[?]-1509[?]) ja ranskalainen Nicolas Chuquet. Paciolin laajalle levinnyt teos Summa de aritmetica ei juuri sisältänyt enempää kuin Fibonaccin 300 vuotta vanhempi kirja. Chuquetin (ranskankielinen!) käsikirjoitus Triparty en la science des nombres (1484) sisälsi alkeellista symbolien käyttöä (esim. $\sqrt{14-\sqrt{180}}$ esiintyy muodossa $R)^2.14.\overline{m}.R)^2180$; yhteen- ja vähennyslaskun merkkeinä käytettiin melko yleisesti kirjaimia p (plus = enemmän) ja m (minus = vähemmän), käsitteli negatiivisia lukuja ja esitteli ensi kertaa suurten lukujen nimitykset biljoona, triljoona jne. Nykyaikaisia piirteitä alkoi yleisemminkin tulla esiin: 1500-luvun alkupuolen laskuopeista löytyy hajanaisia plus- ja miinusmerkkien sekä yhtäläisyysmerkkien esiintymiä (=-merkin ensimmäinen käyttäjä, englantilainen Robert Recorde, 1520-58, perusteli kahden vaakasuoran viivan valintaa vanhanaikaisella englannilla ''bicause noe .2. thynges can be moare equalle''), negatiivisia kertoimia, juurimerkkejä jne. +-merkki on luultavasti muotoutunut $\&$-symbolista, - saattaa olla m-kirjaimen korruptoitunut muoto. Ensi kerran nämä merkit ovat nykyisessä käytössä Johann Widmanin (s. n. 1460) vuonna 1489 ilmestyneessä laskuopissa. Nykyinen juurimerkkimme on itse asiassa r-kirjaimesta muodostunut; r on sanan radix alkukirjain; samaa etymologiaa on esim. retiisi. Se ilmestyi ensi kerran saksalaisen Christoff Rudolffin algebran oppikirjassa vuonna 1525.

Renessanssin matematiikasta puhuttaessa ei sovi unohtaa taiteen ja geometrian, etenkin avaruusgeometrian yhteyksiä. Perspektiivin vähittäinen tulo maalaustaiteeseen todistaa taiteilijoiden kiinnostuksesta geometriaan. Renessanssin suurista taiteilijoista esimerkiksi Albrecht Drer (1471-1528) ja Leonardo da Vinci (1452-1519) olivat myös kelpo matemaatikoita. Drerin 1514 valmistuneessa Melancholia-kuparipiirroksessa esiintyy ensimmäisiä kertoja länsimailla taikaneliö, joita etenkin kiinalaiset olivat konstruoineet jo ainakin ajanlaskun ensimmäisillä vuosisadoilla. Drerin neliö on

$$\begin{array}{cccc} 16&3&2&13 \\ 5&10&11&8 \\ 9&6&7&12 \\ 4&15&14&1\\ \end{array}$$

(huomaa vuosiluku alarivillä!).

6.2 Kolmannen ja neljännen asteen yhtälöiden ratkaisu

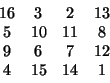
Aikaisemmat aritmetiikan ja algebran oppikirjat jätti varjoon italialaisen lääkärin, matemaatikon ja paavin henkilökohtaisen astrologin Geronimo tai Girolamo Cardanon (1501-76) vuonna 1545 ilmestynyt teos Ars Magna, joka sisälsi raportin ensimmäisistä todella merkittävistä matemaattisista edistysaskeleista sitten antiikin (ars magna = suuri taito tarkoitti algebraa vastakohtana vähempiarvoiselle aritmetiikalle). Kysymyksessä olivat kolmannen ja neljännen asteen yhtälöiden algebralliset ratkaisukaavat. Luca Pacioli oli Omar Khaijamin tavoin pitänyt kolmannen asteen yhtälön ratkaisemista mahdottomana tai ainakin yhtä vaikeana kuin ympyrän neliöinti.

Kertomus ratkaisukaavojen keksimisen ja julkaisun vaiheista kuuluu matematiikan historian värikkäimpiin. - Värikäs oli Cardanon elämäkin, johon sisältyi niin palvelusta astrologina ja lääkärinä Euroopan hoveissa kuin kidustusta inkvisition käsissä ja kirkonkirous Jeesuksen horoskoopin julkaisemisen takia. Säilyttääkseen astrologin maineensa Cardano tiettävästi lakkasi syömästä, kun hänen itselleen ennustamansa kuolinpäivä lähestyi, ja kuolikin sitten oikea-aikaisesti.

Kolmannen asteen yhtälön ratkaisukaavan keksi ilmeisesti Bolognan yliopiston matematiikan professori Scipione del Ferro (1465-1526). Hän ei julkaissut tulostaan, mutta ilmaisi sen kuitenkin oppilaalleen, matemaattisesti keskinkertaiselle Antonio Maria Fiorille. Noin vuonna 1535 oli myös itseoppinut matemaatikko Niccolo Tartaglia (1500[?]-57) keksinyt tai saanut selville ratkaisukaavan. Tartaglian kerskuttua tiedollaan järjestettiin 22. helmikuuta 1535 Fiorin ja Tartaglian kesken julkinen yhtälönratkaisukilpailu. Se päättyi Tartaglian kiistattomaan voittoon, sillä toisin kuin Tartaglia, Fior hallitsi ratkaisukaavan vain yhtä yhtälön kertoimien merkkien kombinaatiota vastaavassa tapauksessa, tapauksessa x³+px=q, mutta ei tapauksessa x³=px+q. Häikäilemätön Cardano onnistui vuonna 1539 perättömien lupausten avulla hankkimaan kaavan Tartaglialta, joka ehdottomasti vaati Cardanoa pitämään tiedon salassa. Tartaglia oli varovasti kätkenyt informaationsa runomuotoon (''Quando che'l cubo con le case appresso/ Se oggualia a qualche numero discreto/ Trovan dui altri, differenti in esso/ ...''), mutta Cardano pääsi siitä selville. Kun kaavat piakkoin tulivat julki Ars Magnassa, syntyi kiivas riita, jonka yhteydessä Cardano syytti Tartaglian itse asiassa varastaneen Ferron kaavan.

Cardanoa tuki syntyneessä polemiikissa hänen oppilaansa Luigi Ferrari
(1522-65). Cardanolta oli joskus kysytty ratkaisua ongelmaan, joka johti neljännen asteen yhtälöön. Cardano ei osannut tehtävää ratkaista, mutta hän pani Ferrarin tutkimaan asiaa. Tämä keksikin ratkaisumenetelmän (jonka eräässä vaiheessa on osattava ratkaista kolmannen asteen yhtälö), ja myös sen Cardano julkaisi Ars Magnassa. - Cardano ei pyrkinyt väittämään kolmannen ja neljännen asteen yhtälöiden ratkaisukaavoja omikseen, vaan tunnusti asianmukaisesti niiden alkuperän. Kolmannen asteen yhtälön ratkaisukaavoja kutsutaan silti yhä Cardanon kaavoiksi, neljännen asteen yhtälön ratkaisukaavoja taas Ferrarin kaavoiksi. - Cardanon nimi elää myös tekniikassa: kardaaninivel on nimetty hänen mukaansa.

Cardanon kaavojen johtamiseksi tarkastellaan kolmannen asteen yhtälöä muodossa

x³+px+q=0,

johon yleisestä muodosta x³+ax²+bx+c=0 aina päästään sijoituksella $x=y-\frac{a}{3}$. Merkitään x=u+v. Jos lisäksi vaaditaan, että 3uv=-p, saadaan yhtälö muotoon

u³+v³+q=0.

Tällöin y=u³ toteuttaa toisen asteen yhtälön

$$y-\frac{p^3}{27}\frac{1}{y}+q=0,$$

joka voidaan ratkaista. Saadaan

$$y=-\frac{q}{2}\pm\sqrt{\frac{q^2}{4}+\frac{p^3}{27}},$$

josta

$$x=u+v=\root 3\of{-\frac{q}{2}+ \sqrt{\frac{q^2}{4}+\frac{p^3}... ...\root3\of{-\frac{q}{2}-\sqrt {\frac{q^2}{4}+\frac{p^3}{27}} }.$$

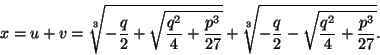
Ferrarin kaavoihin päästään muotoa

x⁴+2ax²+bx+c=0

olevasta yhtälöstä. Se täydennetään neliöksi

(x²+a)²=a²-bx-c.

Tuodaan mukaan parametri y, joka toteuttaa yhtälön

$$\begin{split} (x^2+a+y)^2&=(x^2+a)^2+2y(x^2+a)+y^2\\ &=(a^2-bx-c)+2y(x^2+a)+y^2\\ &=2yx^2- bx+a^2-c+2ay+y^2. \end{split}$$

Pyritään nyt valitsemaan y niin, että yhtälön oikea puoli on täydellinen neliö (px+q)². Näin on, jos kyseisen oikean puolen muodostavan toisen asteen polynomin diskriminantti on 0. Tämä johtaa y:n kolmannen asteen yhtälöön b²-8y(y²+2ay+a²-c)=0. Kun tämä kolmannen asteen yhtälö ratkaistaan Cardanon kaavoilla, yhtälön molemmat puolet ovat neliöitä, ja juurenoton jälkeen jää x:n ratkaisemiseksi enää toisen asteen yhtälö.

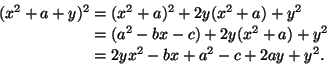
Kolmannen ja neljännen asteen yhtälöiden ratkaisukaavojen keksimisen suurin merkitys lienee siinä, että nyt saatettiin havaita uutta löydettävää vielä olevan jäljellä. Antiikin viisaat eivät olleet vielä rakentaneet matematiikkaa valmiiksi. Cardanon ja Ferrarin kaavat eivät sinänsä ole kovin hyödyllisiä: käytännössä kolmannen ja neljännen asteen yhtälöiden ratkaisut haetaan approksimaatioista, kuten oli osattu tehdä jo Cardanon aikanakin.

Cardanon kaavat johtavat silloin, kun yhtälön kaikki kolme juurta ovat reaalisia, tilanteeseen, jossa reaalijuuret esiintyvät kahden kompleksiluvun, itse asiassa kahden liittokompleksiluvun kuutiojuurten erotuksina. Tämä ns. casus irreducibilis jäi Cardanolle epäselväksi, vaikka hän siihen huomiota kiinnittikin. (Kompleksilukuja käyttävä nykymatemaatikko selvittää ongelman helposti.)

Cardano käsitteli negatiivisten lukujen neliöjuuria toisen asteen yhtälön tapauksessa (''jaa luku 10 kahteen osaan, joiden tulo on 40''), mutta vähän myöhemmin Raffael Bombelli (1526[?]-73) huomasi eräissä konkreettisissa tapauksissa kuten yhtälössä x³=15x + 4, jolla on ilmeinen ratkaisu x=4 ja Cardanon kaavojen mukainen ratkaisu $x=\root 3 \of {2+\sqrt{-121}}+\root 3 \of{2-\sqrt{-121}}$, että jos ''liittoluvuista'' otetut kuutiojuuret oletetaan toistensa ''liittoluvuiksi'', kaavat toimivat sellaisinaan. Bombelli otti käyttöön nimitykset piu di meno ja meno di meno, jotka vastaavat nykymerkintöjä i ja -i, ja näille mm. kaavoja $i\cdot i=(-i)\cdot (-i)=-1$ vastaavat laskusäännöt. Jos $\root 3 \of {2+\sqrt{-121}}=a+b\sqrt {-1}$, niin a³-3ab²=2 ja $(3a^2b-b^3)\sqrt {- 1}=\sqrt {-121}$. Näistä nähdään, että voidaan kirjoittaa $\root 3\of{1-\sqrt {-121}}=a-b\sqrt {-1}$ ja edelleen $5=\root 3\of{125}=a^2+b^2$. Kun tästä ratkaistu a² sijoitetaan yhtälöön 3a²b-b³=11, saadaan 15b-4b³=11. Nyt b=1 ja a=2. Cardanon kaavan kahden kolmannen juuren summa on todellakin 2a=4.

Bombellin Algebra ilmestyi v. 1572. Imaginaarilukujen todellinen luonne selvisi kuitenkin vasta vähitellen seuraavien kolmen vuosisadan kuluessa.

Kolmannen ja neljännen asteen yhtälöiden ratkaisun ydin on tehtävän palauttamisessa alemmanasteisen yhtälön, resolventtiyhtälön, ratkaisemiseen. Ikävä kyllä viidennen ja korkeamman asteen yhtälöiden tapauksessa vastaavalla tavalla konstruoidut resolventtiyhtälöt tulevat olemaan korkeampaa astetta kuin alkuperäinen yhtälö.

6.3 Viète ja Stevin

1500-luvun lopun merkittävin ja monipuolisin matemaatikko oli ranskalainen juristi ja hallintomies Francois Viète eli Vieta (1540-1603). Viète teki palveluksia Ranskan hallitsijoille mm. salakirjoituksia selvittämällä; espanjalaisten käyttämän salakirjoituksen avaaminen oli näille niin yllättävää, että kuningas Filip II syytti ranskalaisia mustaan magiaan turvautumisesta.

Viète oli flaamilaissyntyisen, mutta enimmäkseen Hollannissa toimineen insinöörin Simon Stevinin (1548-1620) ohella innokkaimpia desimaalilukujen käytön puoltajia. Tarkoissa laskutoimituksissa käytettiin tuolloin yhä babylonialais - hellenistisen tradition mukaisesti seksagesimaalimurtolukuja. Desimaalimerkintä ei heti vakiintunut nykyiselleen. Viètellä esiintyi mm. merkintöjä

$$141{,}421,\frac{356,24}{}$$

($200\,000$-säteisen ympyrän sisään piirretyn neliön sivu) ja

$$314{,}159{,}\frac{265,35}{1,000,00}$$

($100\,000$-säteisen puoliympyrän kehä). Stevin julkaisi 1585 flaaminkielisen kirjan De Thiende (Kymmenesosasta), jossa esiteltiin laskeminen desimaaleilla, mutta merkinnässä jokaista numeroa seurasi rengastettu numero, joka osoitti, mistä kymmenesosasta oli kysymys.

Kauaskantoisin Vièten uudistuksista oli kirjainten käyttö tunnettujen ja tuntemattomien suureiden merkinnässä. Kirjassaan In artem analyticem isagoge (Johdatus analyysin taitoon, 1591) Viète merkitsi vokaaleilla tuntemattomia suureita ja konsonanteilla tunnettuja. Aivan täysin nykyaikaisia eivät Vièten käyttämät symbolit kuitenkaan vielä olleet: osa kaavoissa tarvittavista merkinnöistä oli sanallisia. Esimerkiksi yhtälön A³+BA=CA²+D Viète kirjoitti ''A cub + B plano in A æ quatur C in A quad + D solido''. Vièten eri aikalaisten kirjoituksissa esiintyvät yhteensä jokseenkin kaikki nykyiset symbolit, mutta yhtä aikaa ne tulivat käyttöön vasta seuraavan vuosisadan puolella

Algebrassa Viète havaitsi osan yhtälöiden juurien ja kertoimien välisistä yhteyksistä (kuten että juurien summan vastaluku on lähinnä korkeimman tuntemattoman potenssin kerroin), mutta koska hän hyväksyi vain positiiviset juuret, teoria jäi vaillinaiseksi. Polynomiyhtälön kertoimet juurien avulla lausuvia kaavoja kutsutaan edelleen Vièten kaavoiksi.

Kolmannen asteen yhtälön x³+px+q=0 Viète ratkaisi sijoituksella

$$x=\frac{p}{3z}-z.$$

Sijoituksen jälkeen yhtälö muuttuu z³:n toisen asteen yhtälöksi

$$z^6-qz^3-\frac{p^3}{27}=0.$$

Trigonometriaa Viète edisti mm. tyyppiä

$$\sin A+\sin B=2\sin \frac{1}{2}(A+B)\cos\frac{1}{2}(A-B)$$

olevilla kaavoilla, tangenttilauseella

$$\frac{\tan\frac{A+B}{2}}{\tan\frac{A-B}{2}}=\frac{a+b}{a-b}$$

ja $\sin x$:n ja $\cos x$:n potenssien mukaan etenevillä $\sin kx$:n ja $\cos kx$:n kehitelmillä

$$\begin{split} \sin kx = &k \cos^{k-1} x \sin x - \frac{k(k-1)... ...dot 2 \cdot 3 \cdot 4} \cos^{n-4} x \sin^4 x- \dots \end{split}$$

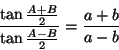
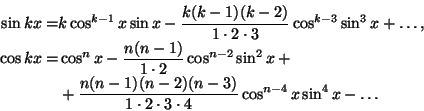
Viète osasi valjastaa trigonometrian algebran palvelukseen: hän johti trigonometriseen sijoitukseen perustuvan kolmannen asteen yhtälön ratkaisukaavan: mielivaltaiselle kulmalle $\alpha$ pätee

$$\cos^3\alpha =\frac{3}{4}\cos\alpha+\frac{1}{4}\cos3\alpha=0.$$

Olkoon ratkaistavana yhtälö

x³+px+q=0.

Merkitään x=ny; ratkaistava yhtälö on nyt $y^3=- \frac{p}{n^2}y-\frac{q}{n^3}$. Valitaan n niin, että $-\frac{p}{n^2}=\frac{3}{4}$. Etsitään $\alpha$, jolle $\cos 3\alpha=-\frac{4q}{n^3}=- \frac{q}{2}\sqrt{- \frac{27}{p^3}}$. Tämä voidaan tehdä, jos Cardanon kaavoissa neliöjuuren alla oleva suure $\frac{p^3}{27}+\frac{q^2}{4}$ on positiivinen, eli juuri Cardanon casus irreducibiliksen tapauksessa. Nyt $x=\frac{1}{n}\cos\alpha$ on alkuperäisen kolmannen asteen yhtälön ratkaisu. Kaikki ratkaisut saadaan ottamalla huomioon eri mahdolliset $\alpha$:n valinnat.

Kuuluisaksi tuli Vièten antama yllättävä trigonometrinen ratkaisu flaamilaisen Adriaen van Roomenin (1561-1615) esittämälle 45. asteen yhtälölle.

$$y^{45}-45y^{43}+945y^{41}-12300y^{39}+\cdots+95634y^5- 3795y^3+45y=C,$$

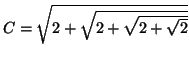missä esim. $C=\sqrt {2+\sqrt {2+\sqrt {2+\sqrt 2}}}$. Viete tunnisti, että yhtälön vasen puoli on $2\sin\phi$:n esitys luvun $y=2\sin\frac{\phi}{45}$ avulla ja löysi yhtälön 23 positiivista ratkaisua. Vièteltä periytyy myös ensimmäinen $\pi$:n analyyttinen lauseke, päättymätön tulo

$$\frac 2{\pi} = \sqrt{\frac 12}\sqrt{\frac 12 + \frac 12\sqrt{\frac 12}} \times\dots,$$

joka on yksinkertaisesti johdettavissa ympyrän sisään piirrettyjen 2ⁿ-kulmioiden alojen raja-arvosta. Jos A_n on yksikköympyrän sisään piirretyn n-kulmion ala, niin

$$\frac{A_{n}}{A_{2n}}= \frac{\frac{n}{2}\sin\frac{2\pi}{n}}{\frac{2n}{n}\sin\frac{2\pi}{2n}} =\cos \frac{2\pi}{2n}.$$

Kun otetaan huomioon, että A₄=2, $\cos\frac{\pi}{4}=\frac{1}{\sqrt 2}$, $\lim_{n\to\infty}A_{2^n}=\pi$ ja $\cos\frac{x}{2}=\sqrt {\frac{1}{2}(1+\cos x)}$, saadaan Vièten relaatio.

6.4 Logaritmien keksiminen

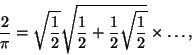
Astronomia ja merenkulku tarvitsevat varsin mutkikkaita trigonometrisia numerolaskuja. Pitkien kertolaskujen muuttamiseksi helpommiksi yhteen- ja vähennyslaskuiksi kehittyi 1500-luvulla, löytöretkien vuosisadalla, ns. prostafairesis-menetelmä. Se perustui tyyppiä

$$2\sin A\cos B = \sin(A + B) +\sin(A- B)$$

oleviin kaavoihin ja trigonometrisiin taulukkoihin.

Originelli skotlantilainen tilanomistaja, Merchistonin paroni John Napier (Neper) (1550-1617) (jonka julkaisutuotantoon kuuluu mm. aikanaan tavattoman suuren levikin saanut numerologinen todistus sille, että paavi on Antikristus, mutta myös käyttökelpoisia pallotrigonometrian kaavoja) keksi lyhemmän tavan. Jos tarkastelee geometrisen jonon termejä, huomaa, että jonon kahden termin tulo esiintyy jonossa paikalla, jonka järjestysnumero saadaan laskemalla yhteen alkuperäisten termien järjestysluvut. Napier keksi ottaa käyttöön jonon, jonka termit ovat hyvin lähellä toisiaan. Tällaisen jonon hän sai valitsemalla suhdeluvuksi luvun $1-10^{-7} = 0,\!9999999$. Desimaalien välttämiseksi Napier kertoi jonon luvut luvulla 10⁷. Lukua N vastaava Napierin logaritmi $L={\rm Nap\,log\,}N$ on siten luku, jolle pätee

N = 10⁷(1 -10^-7)^L.

Kahden luvun N₁ ja N₂tulolle saadaan

N₁N₂10^-7=10⁷(1- 10^-7)^L₁+L₂,

joten logaritmien tulosääntö ei sellaisenaan sovi Napierin logaritmeille. Napierin logaritmien ja ''Neperin luvun'' evälinen yhteys selittyy siitä, että (1 - 10^-7)¹⁰⁷on likimain 1/e.

Logaritmitaulukkojensa luvut Napier laski geometrisista sarjoista monimutkaisella interpolaatiomenettelyllä. Ensimmäisessä vaiheessa Napier vähensi luvusta 10000000 sen kymmenesmiljoonasosan, erotuksesta jälleen kymmenesmiljoonasosan jne., kunnes sadan vähennyksen jälkeen tullaan lukuun
9999900,000495. Tämän luvun Napier-logaritmi on 100. Lineaarinen ekstrapolaatio näyttää, että luvun 9999900 Napier-logaritmi on 100,000495. Tämän jälkeen Napier alkaa vähentää luvusta 10000000 sen sadastuhannesosan, erotuksesta samoin jne. Erotukset ovat jälleen geometrisen jonon lukuja, ja niiden Napier-logaritmit 100,000495:n monikertoja. 50:n vähennyksen jälkeen ollaan luvussa 9995001,224804 (Napier teki tässä kolmanteen desimaaliin vaikuttavan laskuvirheen), jonka Napier-logaritmi on $50\cdot 100{,}000495 =5000{,}024753$. Ekstrapolointi antaa luvun 9995000 Napier-logaritmiksi 5001,250175. Nyt Napier rakentaa vielä 21-rivisen ja 69-sarakkeisen taulukon, jossa kukin luku on yllä oleva luku vähennettynä kahdestuhannesosallaan ja samalla vasemmalla oleva luku vähennettynä sadasosallaan. Tällöin kunkin sarakkeen alin luku on suunnilleen sama kuin seuraavan sarakkeen ylin luku ja taulukon oikeaan alakulmaan tulee luku 4998609,4019. Kun vielä ekstrapoloidaan luvun 9900000 Napier-logaritmiksi taulukon vasemmanpuoleisen sarakkeen avulla (jonka Napier-logaritmit ovat 5001,250175:n monikertoja) 100503,223, saadaan p:nnellä rivillä ja q:nnessa sarakkeessa olevan luvun Napier-logaritmiksi $(p-1)\cdot 5001{,}25+(q-1)\cdot 100503{,}22$. - Koska Napier tähtäsi itse asiassa kulmien sinien logaritmeihin ja hänen kehyksenään oli suorakulmainen kolmio, jonka hypotenuusa on 10⁷, kuvailtu prosessi antoi mahdollisuuden laskea sinien logaritmit $30^{\circ}$:n ja $90^{\circ}$:n väliltä. Pienempiin kulmiin pääsee käsiksi kaavan $\sin 2\theta=2\sin\theta\sin(90^{\circ}-\theta)$avulla.

Napier perusteli menetelmäänsä geometris-dynaamisella tarkastelulla. Jos piste D liikkuu tasaisella nopeudella 10⁷ pitkin puolisuoraa $O\infty$ ja piste C liikkuu pitkin janaa AB, jonka pituus on 10⁷ niin, että sen nopeus jokaisella ajan hetkellä on CB, ja jos x=OD, y=CB, niin ajan t funktiona on x=10⁷t ja y'=-y, $\ln y(t)=-t+C$, $C=\ln 10^7$. Tästä saadaan $x=10^7\ln\frac{10^7}{y}$. Interpolaatio-approksimaation takia Napierin logaritmit eivät olleet aivan tasan edellisen kaavan mukaisia.

Kreikan sanoista logos 'suhde' ja arithmos 'luku' kokoon pantu sana logaritmi on Napierin käyttöön ottama, samoin kuin pilkun tai pisteen käyttö desimaalierottimena. Aluksi Napier oli kutsunut näitä lukuja keinotekoisiksi luvuiksi.

Napier julkaisi ideansa ja logaritmitaulukkonsa 1614 teoksessa Mirifici logarithorum canon descriptio ensi sijassa helpottamaan trigonometrisia laskuja. Lukujen logaritmien sijasta hän puhuikin sinien logaritmeista. Seuraavana vuonna lontoolainen professori (ilmeisesti ensimmäinen matematiikan professori Englannissa) Henry Briggs (1561-1639) kiinnostui logaritmeista. Hän vieraili Napierin luona Skotlannissa, ja yhteisymmärryksessä Napier ja Briggs päätyivät muunnettuun järjestelmään, jossa kantalukuna olisi 10. Briggs julkaisi 1624 lukujen 1 - 20$\,$000 ja 90$\,$000 - 100$\,$000 14-desimaaliset 10-kantaiset logaritmitaulut. Briggsin taulukko perustui lukujen $\sqrt {10}$, 10^1/4, 10^1/8, ..., 10^1/254 laskemiseen peräkkäisillä neliöjuurenotoilla. Logaritmit levisivät yleiseen käyttöön hämmästyttävän nopeasti. Keplerin mielestä logaritmit pidensivät taähtitieteilijän iän kaksinkertaiseksi.

Napierin ja Briggsin rinnalla kunnia logaritmien keksimisestä kuuluu myös sveitsiläiselle kojeiden rakentajalle Jobst Bürgille (1552-1632), jonka itsenäisesti jo 1588 keksimä logaritmikäsite tuli julkisuuteen vasta 1620. Bürgin logaritmit perustuivat luvun 1,0001 potensseihin: luvun 10⁸(1+10^-4)ⁿ Bürgin logaritmi on 10n.

Myös luonnolliset logaritmit, siis kantalukuun eperustuvat, ilmaantuivat matematiikkaan vuoden 1620 paikkeilla, vaikka niiden tärkeys havaittiinkin vasta myöhemmin, differentiaali- ja integraalilaskennan kehityttyä tarpeeksi.

Logaritmien yhteys matemaattiseen analyysiin alkaa belgialaisen jesuiitan Gregóire de San Vincentin vuoden 1620 paikkeilla tekemästä havainnosta, jonka mukaan (taas nykyaikaistetun puhetavan mukaan) suorakulmaisen hyperbelin xy=1, x-akselin ja suorien x=a, x=b rajaaman alueen ala on sama kuin hyperbelin, x-akselin ja suorien x=ta ja x=tb rajaaman alueen. Asian toteaa helposti approksimoimalla alueita esim. n:n suorakaiteen muodostamilla porraskuvioilla: edellisen alueen tapauksessa i:nnen suorakaiteen korkeus on t kertaa jälkimmäisen alueen vastaavan suorakaiteen korkeus, kun taas jälkimmäisessä tapauksessa suorakaiteiden kannat ovat tkertaa edellisen tapauksen suorakaiteiden kannat. Tästä seuraa, että hyperbelin määrittämällä pinta-alalla on logaritminen yhteenlaskuominaisuus - sittemmin onkin selvinnyt, että kuvattu ala on $\ln\frac{b}{a}$.

Alkuun - Etusivu - Edellinen - Seuraava