Pelkkää tylsyyttä odotettavissa?

Jukka Liukkonen
Mat. yo. evp.

Lokeromalli

Pallot ja lokerot kuuluvat todennäköisyyslaskennan harrastajan perussettiin. Palloja heitellään lokeroihin sattumanvaraisesti ja lasketaan todennäköisyyksiä. Tässä artikkelissa palloja on $n$ kappaletta ja lokeroita $m$ kappaletta. Sekä pallot että lokerot voidaan erottaa toisistaan; periaatteessa niiden kylkiin voidaan maalata yksilölliset tunnisteet. Lokerot muodostavat lokerikon, jossa on $m-1$ väliseinää.

\[\begin{align*} \text{Pallot:\ } & {\beta}\,{\in}\,\{1,\ldots,n\} \\ \text{Lokerot:\ } & \ell\,{\in}\,\{1,\ldots,m\} \end{align*}\]

Olkoot kaikki pallot jo lokerikossa. Erilaiset palloasetelmat samastetaan kokonaislukujonojen

\[\mathbf{\mu} = (\ell_1,\ldots,\ell_n),\;\; 1\le\ell_{\beta}\le m,\]

kanssa. Niitä kutsutaan mikrotiloiksi. Jono tulkitaan niin, että pallo ${\beta}$ on lokerossa $\ell_{\beta}$.

Makrotilat ovat lukumääräjonoja

\[\mathbf{M} = (k_1,\ldots,k_m),\;\; k_1+\ldots+k_m=n.\]

Luku $k_\ell\ge 0$ ilmoittaa, kuinka monta palloa on lokerossa $\ell$. Yhteen makrotilaan liittyy yleensä monta mikrotilaa.

Pallon ${\beta}$ osumistodennäköisyys lokeroon $\ell$ oletetaan pallosta ja lokerosta riippumattomaksi vakioksi $1/m$. Silloin mikrotilojen todennäköisyydet ovat keskenään samat.

Esimerkki. Kolme palloa P1, P2 ja P3 sijoitetaan kahteen lokeroon L1 ja L2. Kaikki mahdolliset mikro- ja makrotilat ovat:

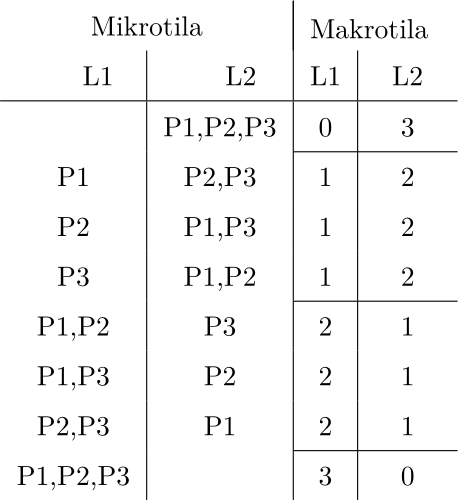
Esimerkiksi makrotila $(1,2)$ koostuu mikrotiloista $(1,2,2)$, $(2,1,2)$ ja $(2,2,1)$. Tällöin sanotaan, että makrotilan $(1,2)$ multiplisiteetti on 3. Mikrotilojen todennäköisyydet ovat keskenään samat, joten makrotilan todennäköisyys saadaan jakamalla sen multiplisiteetti kaikkien mikrotilojen lukumäärällä eli kaikkien makrotilojen multiplisiteettien summalla. Multiplisiteetit ja todennäköisyydet ovat:

Lukijalle saattaa tulla mieleen Pascalin kolmion potenssia 3 vastaava rivi.

Variaatiot, permutaatiot ja kombinaatiot

Tarkoituksena on selvittää, montako erilaista $k$-alkioista osajoukkoa on $n$-alkioisella joukolla $A$. Kysymystä lähestytään helpommin ratkaistavan ongelman kautta: montako $k$-alkioista jonoa voidaan muodostaa joukon $A$ alkioista, kun yksi alkio saa esiintyä jonossa vain kerran? Tilastotieteen termein kysymyksessä on otanta ilman takaisinpanoa. On syytä muistaa, että joukosta puhuttaessa alkioiden keskinäisellä järjestyksellä ei ole väliä. Sitä vastoin jonon alkioiden järjestyksellä on ratkaiseva merkitys. Jonojen lukumäärän laskemiseksi lähdetään liikkeelle seuraavalla tavalla:

Jonon ensimmäiseksi alkioksi kelpaa mikä tahansa $n$ alkiosta.
Jokaista ensimmäisen alkion valintaa kohti jäljellä on $n{-}1$ mahdollista seuraajaa. Tällöin $2$-alkioisia erilaisia jonoja on $n(n{-}1)$ kappaletta.
Jokaista kaksialkioista jonoa kohti on $n{-}2$ vaihtoehtoa kolmanneksi alkioksi, joten $3$-alkioisia erilaisia jonoja on kaikkiaan $n(n{-}1)(n{-}2)$ kappaletta.

Jatkamalla jonon pidentämistä alkio kerrallaan havaitaan, että erilaisten $k$-alkioisten jonojen, joukon $A$ $k$-variaatioiden, lukumäärä on

\[(n)_k := n\cdot(n-1)\cdot\ldots\cdot(n-k+1).\]

Erityisesti $n$-alkioisia erilaisia jonoja, joukon $A$ permutaatioita, on

\[(n)_n = n\cdot(n-1)\cdot\ldots\cdot2\cdot 1\]

kappaletta. Tälle tulolle on aikojen kuluessa vakiintunut merkintä

\[n! := 1\cdot2\cdot\ldots\cdot(n-1)\cdot n.\]

Joukko, joka koostuu $n$ alkiosta, voidaan siis järjestää jonoksi $n!$ eri tavalla. Lukumäärää $n!$ kutsutaan $n$-kertomaksi. Yleisesti on sovittu, että $0!=1$. Laventamalla tulolla $(n{-}k)!$ voidaan kirjoittaa

\[(n)_k = \frac{n\cdot\ldots\cdot(n-k+1)\cdot(n-k)\cdot\ldots\cdot 1}{(n-k)\cdot\ldots\cdot 1} = \frac{n!}{(n-k)!}\,.\]

Jos $k$-alkioisia erilaisia osajoukkoja on $x$ kappaletta, ja edellä todetun mukaisesti jokainen näistä joukoista voidaan järjestää jonoksi $k!$ eri tavalla, $k$-variaatioiden lukumäärä on $x\cdot k!$, mutta toisaalta se on $n!/(n{-}k)!$. Yhtälöstä

\[x\cdot k! = \frac{n!}{(n-k)!}\]

ratkaistaan

\[x = \frac{n!}{k!\,(n-k)!}\,.\]

Näin monta $k$-alkioista osajoukkoa, $k$-kombinaatiota, on $n$-alkioisella joukolla. Kombinaatioiden lukumäärää merkitään vakiintuneen tavan mukaisesti

\[{{n}\choose{k}} := \frac{n!}{k!\,(n-k)!}\,.\]

Merkintä luetaan “$n$ yli $k$:n”. Lukuja ${{n}\choose{k}}$ sanotaan binomikertoimiksi, sillä tunnetusti

\[(a+b)^n = \sum_{k=0}^n{{n}\choose{k}}a^kb^{n-k}.\]

Tämä binomikaavaksi kutsuttu identiteetti jätetään tässä todistamatta. Kaava todistetaan ja sitä havainnollistetaan esimerkein Wikipedia-sivulla [6]. Solmussa binomikaavaa on käsitellyt mm. Pekka Alestalo [3]. Kun $a=b=1$, binomikaavasta nähdään binomikertoimien summa:

\[\sum_{k=0}^n{{n}\choose{k}} = 2^n.\]

Binomikertoimien avulla saadaan selville makrotilojen lukumäärä. Ratkaistavana on siis tehtävä, monellako tavalla luku $n$ voidaan esittää $m$ ei-negatiivisen kokonaisluvun $k_1,\ldots,k_m$ summana. Luku $k_\ell$ ajatellaan jonoksi, jossa on $k_\ell$ kappaletta ykkösiä. Summa $k_1+\ldots+k_m$ koostuu silloin ykkösistä, joita on $n$ kappaletta, ja plusmerkeistä, joita on $m-1$ kappaletta. Montako tällaista jonoa on olemassa? Jos plusmerkin jommallakummalla puolella ei ole ykköstä, sillä kohdalla on tyhjä lokero, ja summassa $k_1+\ldots+k_m$ vastaavasti nolla. Ykkösten ja plusmerkkien jonossa on kaikkiaan $n+m-1$ paikkaa. Niistä voidaan valita paikat $m-1$ plusmerkille

\[{{n+m-1}\choose{m-1}} = {{n+m-1}\choose{n}}\]

eri tavalla. Yhtälö johtuu binomikertoimien symmetriasta.

Erilaisia makrotiloja on

\[{{n+m-1}\choose{n}}\]

kappaletta.

Multinomikertoimet

Makrotila $(k_1,\ldots,k_m)$, missä $k_1{+}\ldots{+}k_m{\,=\,}n$, koostuu yhdestä tai useammasta mikrotilasta. Tarkan lukumäärän eli makrotilan multiplisiteetin laskemiseksi päätellään seuraavasti:

Valittaessa $k_1$ palloa lokeroon $1$ erilaisia vaihtoehtoja on ${{n}\choose{k_1}}$ kappaletta.
Kun lokeroon $1$ on pallot valittu, mahdollisia valintoja lokeron $2$ palloiksi on ${{n-k_1}\choose{k_2}}$ kappaletta. Siis kahden ensimmäisen lokeron sisältö voidaan valita ${{n}\choose{k_1}}{{n-k_1}\choose{k_2}}$ eri tavalla.
Jokaista jo tehtyä valintaa kohti lokeron 3 pallot voidaan valita jäljellä olevien $n{-}k_1{-}k_2$ pallon joukosta ${{n-k_1-k_2}\choose{k_3}}$ eri tavalla. Kolmen ensimmäisen lokeron sisällöiksi on täten ${{n}\choose{k_1}}{{n-k_1}\choose{k_2}}{{n-k_1-k_2}\choose{k_3}}$ erilaista vaihtoehtoa.

Jatkamalla samaan tyyliin loppuun asti havaitaan, että vaaditut ehdot täyttäviä palloasetelmia on kaikkiaan

\[\begin{split} &{{n}\choose{k_1}}{{n-k_1}\choose{k_2}}{{n-k_1-k_2}\choose{k_3}}\ldots{{k_m}\choose{k_m}} \\[1ex] &\phantom{xxx}=\frac{n!}{k_1!\,(n-k_1)!}\cdot\frac{(n-k_1)!}{k_2!\,(n-k_1-k_2)!} \\[1ex] &\phantom{xxx}\phantom{xxx}\phantom{=}\cdot\frac{(n-k_1-k_2)!}{k_3!\,(n-k_1-k_2-k_3)!}\cdot\ldots \\[1ex] &\phantom{xxx}\phantom{xxx}\phantom{=}\cdot\frac{k_m!}{k_m!\,0!} \\[1ex] &\phantom{xxx}=\frac{n!}{k_1!\cdot k_2!\cdot\ldots\cdot k_m!}\,. \end{split}\]

Viimeinen yhtälö saadaan supistamalla joka kohdassa tulon osamäärämuotoisen tekijän nimittäjästä ja seuraavan tekijän osoittajasta yhteinen tekijä pois. Lukuja

\[{{n}\choose{k_1,\ldots,k_m}} := \frac{n!}{k_1!\cdot k_2!\cdot\ldots\cdot k_m!}\]

sanotaan multinomikertoimiksi, sillä

\[(x_1+\ldots+x_m)^n = \!\!\sum_{\substack{k_1+\ldots+k_m=n \\ k_1\ge0,\ldots,k_m\ge0}}\!\! {{n}\choose{k_1,\ldots,k_m}}\;x_1^{k_1}\ldots x_m^{k_m}.\]

Yhtälön todistus sivuutetaan. Lukija voi niin halutessaan todistaa sen itse tai katsoa todistuksen Wikipediasta [8].

Makrotilan $\mathbf{M}\,{=}\,(k_1,\ldots,k_m)$ multiplisiteetti on

\[{{n}\choose{k_1,\ldots,k_m}}.\]

Esimerkki. Kun yhdeksän palloa sijoitetaan kolmeen lokeroon, makrotilan $(0,9,0)$ multiplisiteetti on

\[{{9}\choose{0,9,0}} = \frac{9!}{0!\cdot 9!\cdot 0!} = 1.\]

Hajanaisemman tilan $(4,4,1)$ multiplisiteetti on paljon suurempi:

\[{{9}\choose{4,4,1}} = \frac{9!}{4!\cdot 4!\cdot 1!} = \frac{5\cdot6\cdot7\cdot8\cdot9}{2\cdot3\cdot4} = 5\cdot6\cdot7\cdot3 = 630.\]

Eniten levällään on tila $(3,3,3)$, jonka multiplisiteetti on

\[{{9}\choose{3,3,3}} = \frac{9!}{3!\cdot 3!\cdot 3!} = 5\cdot6\cdot7\cdot8 = 1680.\]

Näyttää siltä, että mitä tasaisempi pallojakauma, sitä suurempi multiplisiteetti.

Multiplisiteettien vertailua

Binomi on erikoistapaus multinomista, ja binomikertoimet ovat samalla multinomikertoimia:

\[{{n}\choose{k}} = {{n}\choose{k,\,n-k}}.\]

Binomikertoimista muodostetun Pascalin kolmion keskellä näyttää olevan huomattavasti suurempia lukuja kuin kolmion laidoilla. Seuraavaksi osoitetaan, että näin todella on, ja vastaava tulos pätee kaikille multinomikertoimille.

Kokonaislukujen jakoyhtälö kertoo, että jaettaessa kokonaisluku toisella saadaan osamäärä ja jakojäännös, jotka ovat kokonaislukuja ja määräytyvät yksikäsitteisesti jaettavasta ja jakajasta. Kun pallojen lukumäärä $n$ jaetaan lokeroiden lukumäärällä $m$, jakoyhtälön nojalla on olemassa yksikäsitteiset kokonaisluvut $q{\ge}0$ (osamäärä) ja $r{\ge}0$ (jakojäännös), joille

\[r<m \quad\text{ja}\quad n = qm+r.\]

Lause. Edellä määritellyin merkinnöin

\[{{n}\choose{k_1,\ldots,k_m}} \le {{n}\choose {\;\underbrace{q+1,\ldots,q+1}_\text{$r$ kpl},\underbrace{q,\ldots,q}_\text{$m-r$ kpl}\;}}.\]

Yhtäsuuruus on voimassa täsmälleen silloin, kun $\{k_1,\ldots,k_m\}\subset\{q,\,q+1\}$.

Todistus. Jos $\{k_1,\ldots,k_m\}\,{\subset}\,\{q,\,q+1\}$, jakoyhtälön yksikäsitteisyyden nojalla jonossa $(k_1,\ldots,k_m)$ pitää esiintyä $q$ tasan $m{-}r$ kertaa ja $q{+}1$ tasan $r$ kertaa. Tällöin multinomikertoimet ovat yhtäsuuret.

Olkoon ($\ast$) $\{k_1,\ldots,k_m\}\,{\not\subset}\,\{q,\,q+1\}$. Kaikki luvut $k_h$ eivät voi olla isompia kuin $q$, sillä muulloin olisi $n=k_1{+}\ldots{+}k_m \ge m(q{+}1) = qm{+}m > qm{+}r$. Toisaalta, jos kaikki luvut $k_h$ olisivat pienempiä kuin $q{+}1$, oletuksen ($\ast$) nojalla eräs niistä olisi aidosti pienempi kuin $q$, ja silloin olisi $n=k_1{+}\ldots{+}k_m<mq\le qm{+}r$. Täten eräs luvuista $k_h$ on korkeintaan $q$, ja eräs toinen luvuista $k_h$ on vähintään $q+1$. Oletuksen ($\ast$) nojalla on siis välttämättä olemassa indeksit $i,j\in\{1,\ldots,m\}$, joille $k_i{>}k_j+1$. Merkinnät voidaan olettaa valituiksi niin, että $i{=}1$ ja $j{=}2$ (muulloin vaihdetaan merkinnät, ja pelkkä merkintöjen vaihtaminen ei muuta taustalla olevaa tilannetta). Tällöin $k_1{>}k_2+1$, ja

\[\begin{split} {{n}\choose{k_1,k_2,\ldots,k_m}} &= \frac{1}{k_1!\,k_2!}\,\frac{n!}{k_3!\,\ldots\,k_m!} \\[1ex] &< \frac{1}{(k_1-1)!\,(k_2+1)!}\,\frac{n!}{k_3!\,\ldots\,k_m!} \\[1ex] &= {{n}\choose{k_1-1,k_2+1,\ldots,k_m}}. \end{split}\]

Epäyhtälö keskellä johtuu siitä, että

\[\begin{split} \frac{1}{k_1!\,k_2!} &= \frac{k_2+1}{k_1}\,\frac{1}{(k_1-1)!\,(k_2+1)!} \\[1ex] &< \frac{k_1}{k_1}\,\frac{1}{(k_1-1)!\,(k_2+1)!} \\[1ex] &= \frac{1}{(k_1-1)!\,(k_2+1)!}\,. \end{split}\]

Jono $(k_1-1,k_2+1,\ldots,k_m)$ on “tasaisempi” kuin alkuperäinen jono $(k_1,k_2,\ldots,k_m)$. Jatkamalla tasoittamista tarvittaessa päädytään lopulta jonon

\[(\;\underbrace{q+1,\ldots,q+1}_\text{$r$ kpl},\underbrace{q,\ldots,q}_\text{$m-r$ kpl}\;)\]

permutaatioon.

Tämä oli ns. laiskan matemaatikon induktiotodistus, joka tarvittaessa voidaan kirjoittaa viralliset muotovaatimukset täyttäväksi täydelliseksi induktioksi.

Multinomikerroin

\[{{n}\choose{k_1,\ldots,k_m}}\]

ja samalla makrotilan $\mathbf{M}{\,=\,}(k_1,\ldots,k_m)$ multiplisiteetti suurenee, kun jonoa $\mathbf{M}$ tasoitetaan kasvattamalla sen pieniä lukuja ja pienentämällä vastaavasti suuria lukuja, kunnes ollaan tilanteessa, jossa jonon luvut poikkeavat toisistaan korkeintaan yhdellä.

Edellä saatu tulos kertoo sen, että Pascalin kolmiossa ja sen monilotteisessa vastineessa, jota ehkä voitaisiin kutsua Pascalin $m$-simpleksiksi, luvut ovat suurimmillaan keskellä ja pienenevät laitoja kohti. Pienenemisen voimakkuudesta tulos ei sano mitään. Asiaa on helpointa tutkia lähtemällä liikkeelle tilanteesta $m=2$. Seuraaviin kuviin on piirretty tekijällä $2^{-n}$ skaalatut binomikertoimet $2^{-n}{{n}\choose{k}}$ pylväinä pallomäärillä $n\in\{10,60,1000\}$.

**Kuva 1.** Pallojen lukumäärä $n{=}10$.

**Kuva 2.** Pallojen lukumäärä $n{=}60$.

**Kuva 3.** Pallojen lukumäärä $n{=}1000$.

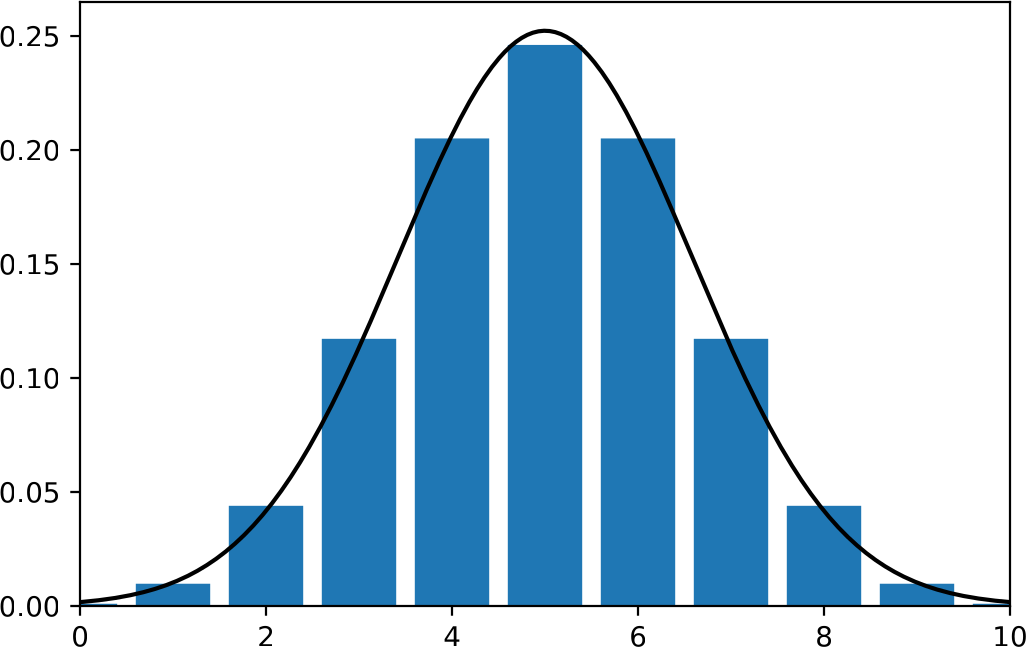
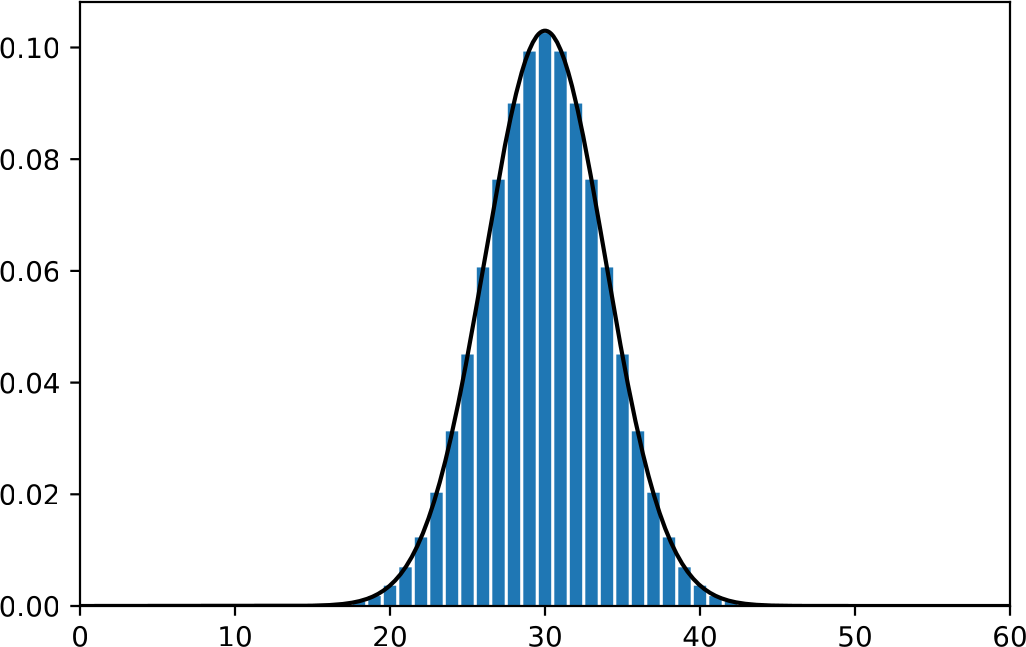
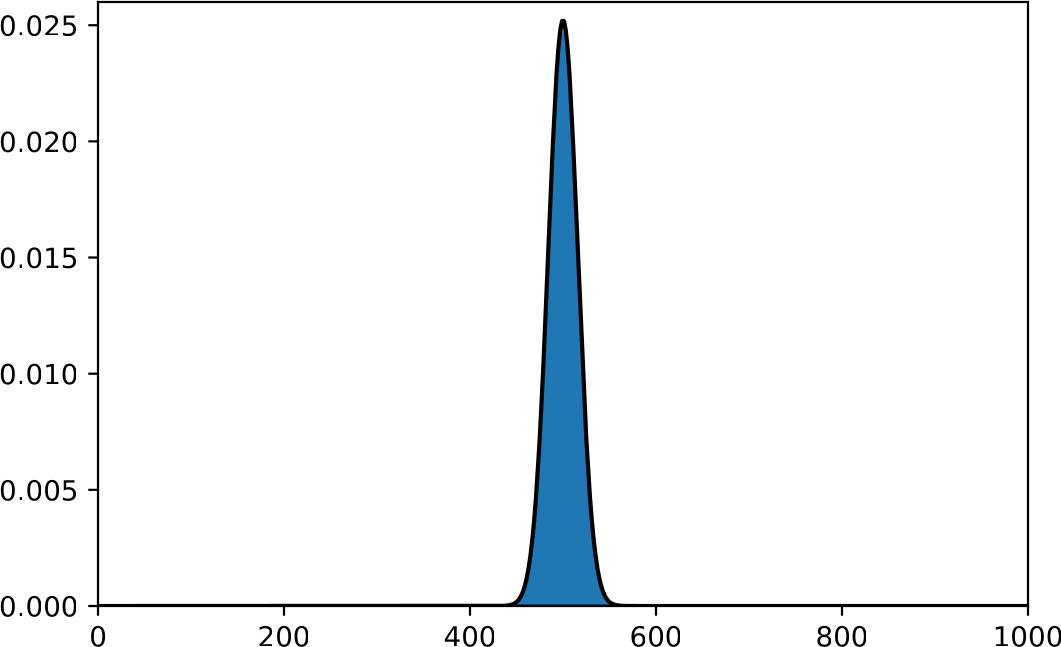
Pylväät erottuvat kunnolla toisistaan vain ensimmäisessä kuvassa. Skaalauksesta johtuen pylväiden pituuksien summa on tasan 1. Silloin ne ilmoittavat suoraan pylvääseen liittyvän kahden lokeron makrotilan todennäköisyyden. Näitä todennäköisyyksiä sanotaan binomitodennäköisyyksiksi, ja pylväikkö on kuva binomijakaumasta [5]. Kuviin on vertailun vuoksi piirretty myös pylväikköön sovitetun normaalijakauman N$(n/2,\,n/4)$ tiheysfunktion kuvaaja [9]. Jakauman odotusarvo $n/2$ ja varianssi $n/4$ ovat samat kuin binomijakaumalla, jota tällä tavoin approksimoidaan normaalijakauman avulla [1], [2]. Kuvien perusteella normaalijakaumasta saadaan erinomaisia likiarvoja binomitodennäköisyyksille, kun $n$ on suuri. Jakaumia on esitelty Wikipediassa sivulla [10].

Todennäköisyys näyttää keskittyvän sitä voimakkaammin jakauman keskelle, mitä suurempi $n$ on kyseessä. Kun $n$ on oikein suuri, esimerkiksi $n=10^{23}$, jakauma on arvatenkin laihtunut äärimmäisen ohueksi piikiksi¹ odotusarvon $5\cdot10^{22}$ kohdalle, ohueksi suhteessa odotusarvoon. Tämä tarkoittaa, että kumpaankin lokeroon hyvin tarkkaan tasaisesti jakautuneet makrotilat ovat lähestulkoon ainoat mahdolliset. Muiden tilojen todennäköisyys on häviävän pieni. Valtava enemmistö makrotiloista on siis sellaisia, jotka eivät käytännössä “milloinkaan” toteudu. Seuraavassa kappaleessa tämä ilmaistaan täsmällisesti.

Tasaisen jakauman musertava ylivoima

Kun epäsymmetristä kolikkoa, jolle kruunan todennäköisyys on ${p}$, heitetään $n$ kertaa, tuloksen kruuna esiintymiskertojen lukumäärää kuvaa binomijakauma $\text{Bin}(n,{p})$. Sen odotusarvo $\mu_n$ ja varianssi $\sigma_n^2$ ovat tunnetusti [5]

\[\mu_n = n{p},\quad \sigma_n^2 = n{p}(1-{p}).\]

Sama jakauma kuvaa makrotiloja, kun kruuna tulkitaan niin, että pallo osuu tiettyyn kiinteään lokeroon L. Silloin klaava vastaa tilannetta, jossa pallo sujahtaa johonkin muuhun lokeroon. Merkillepantavaa on, että keskihajonnan ja odotusarvon suhde lähestyy nollaa pallojen lukumäärän kasvaessa rajatta:

\[\frac{\sigma_n}{\mu_n} = \frac{\sqrt{n{p}(1-{p})}}{n{p}} = \frac{\sqrt{1-{p}}}{\sqrt{n{p}}} \xrightarrow[n\to\infty]{} 0.\]

Suurilla pallomäärillä binomijakaumaan liittyvät todennäköisyydet ovat hyvin tarkkaan samoja kuin vastaavan odotusarvon ja varianssin omaavaan normaalijakaumaan liittyvät todennäköisyydet. Lokeroon L kertyneiden pallojen lukumäärää merkitään $X_n$. Jakauman kaventumista tutkittaessa $X_n$ oletetaan normaalijakautuneeksi parametrein $\mu_n$ ja $\sigma_n^2$. Normaalijakaumista tiedetään, että parametrein $\mu$ ja $\sigma^2$ normaalijakautuneen satunnaismuuttujan arvoista

$68{,}2689\,\%$ sijoittuu välille $[\mu-\sigma,\mu+\sigma]$,
$95{,}4500\,\%$ sijoittuu välille $[\mu-2\sigma,\mu+2\sigma]$,
$99{,}7300\,\%$ sijoittuu välille $[\mu-3\sigma,\mu+3\sigma]$,
$99{,}9937\,\%$ sijoittuu välille $[\mu-4\sigma,\mu+4\sigma]$,

ja niin edelleen. Välin $[-4\sigma_n,4\sigma_n]$ ulkopuolelle sijoittuvat pallomäärät $X_n$ ovat siis hyvin, hyvin harvinaisia. Lisäksi välin pituuden $8\sigma_n$ suhde odotusarvoon eli symmetrisen jakauman tapauksessa jakauman keskikohtaan $\mu_n$ lähestyy nollaa, kun pallojen määrä $n$ kasvaa rajatta. Tämähän merkitsee juuri sitä, että pallojen lisääntyessä jakauma kapenee kapenemistaan ja näyttää lopulta pelkältä odotusarvon kohdalle pystytetyltä ohuelta piikiltä.

Jakauman hoikistumisilmiö toistuu jokaisen lokeron kohdalla erikseen. Artikkelin alussa tehdyn oletuksen mukaan pallon osumistodennäköisyys tiettyyn lokeroon on vakio ${p}=1/m$. Silloin kunkin lokeron piikki osuu pallomäärän $\mu_n=n{p}=n/m$ kohdalle.

Edellä sanottua kannattaa maistella hetki. Kaikki mikrotilat ovat yhtä todennäköisiä. Makrotilojen todennäköisyysvarallisuus keskittyy lähes kokonaan äärimmäisen harvalle kapitalistimakrotilalle, joille yhteistä on se, että pallot ovat hyvin tarkkaan tasaisesti jakautuneet lokeroperheen jäsenten kesken. Mitähän Karl Marx sanoisi tästä?

Tuloksen täsmällinen muotoilu

Edellä tehdyissä päättelyissä turvauduttiin osittain geometriseen mielikuvaan ja jätettiin paljon välivaiheita pois. Lopputulostakaan ei esitetty kuin mielikuvan tasolla. Kaikki vaadittava työ voidaan kyllä tehdä ehdottoman täsmällisesti yksityiskohtia myöten. Se ei ole edes vaikeaa henkilölle, joka on hankkinut tietämystä ja kokemusta differentiaali- ja integraalilaskennan sekä todennäköisyyslaskennan alkeiskurssilla yliopistotasolla. Päättelyt jäivät hieman hatariksi, mutta lausuttakoon kuitenkin lopputulos täsmällisesti.

Olkoon $X_{n,\ell}$ pallojen määrä lokerossa $\ell$ pallojen kokonaismäärän ollessa $n$. Kun satunnaismuuttujan $X_{n,\ell}$ odotusarvoa merkitään $\mu_{n,\ell}=n/m$, muuttujan suhteellinen poikkeama odotusarvosta määritellään kaavalla

\[{\cal D}[X_{n,\ell}] := \left|\frac{X_{n,\ell}-\mu_{n,\ell}}{\mu_{n,\ell}}\right|.\]

Lause. Olkoot $\epsilon$ ja $\delta$ kaksi positiivista reaalilukua. Silloin on olemassa sellainen positiivinen kokonaisluku $n_0$, että kaikilla $n>n_0$ on voimassa

\[{\mathbb P}\left\{{\cal D}[X_{n,\ell}] <\delta\text{\;kaikilla $\ell=1,\ldots,m$}\right\} > 1-\epsilon.\]

Merkintä ${\mathbb P}\{\ldots\}$ tarkoittaa tapahtuman $\{\ldots\}$ todennäköisyyttä.

Lokerikon pallomäärien jakauma saadaan niin lähelle tasaista jakaumaa kuin halutaan niin suurella todennäköisyydellä kuin halutaan, kunhan palloja otetaan mukaan peliin tarpeeksi suuri määrä.

Merkitys maailmankaikkeudelle

Ludwig Boltzmannin mukaan eristetyn termodynaamisen systeemin mikrotilat ovat keskenään yhtä todennäköisiä. Kun systeemi elää, sen mikrotila matemaattisella vääjäämättömyydellä ajautuu porukkaan, siis makrotilaan, jossa on eniten vaihtoehtoja tarjolla. Tuo porukka, kuten edellä todettiin, on tasaisten jakaumien sangen tylsä seurapiiri. Vääjäämättömyyttä kutsutaan nimellä termodynamiikan toinen pääsääntö. Maailmankaikkeus on eristetty termodynaaminen systeemi. Pallot eivät todellisuudessa ole palloja, vaan maailmankaikkeuden pienen pieniä rakennusosasia. Lokerotkaan eivät oikeasti ole lokeroita, vaan noiden vähäisten hiukkasten tiloja; hiukkanen on aina jossakin tilassa. Jos tilaksi käsitetään esimerkiksi paikka ja liikemäärä, hiukkasten tasainen jakautuminen eri tilojen kesken merkitsee melkoista sekamelskaa, systeemin makrotilaa, josta parhaallakaan hahmottamiskyvyllä ei ole mahdollista löytää minkäänlaista rakennetta.²

Todennäköisyyslakien mukaan maailma on siis pikkuhiljaa muuttumassa universaaliksi, tasaiseksi, mielenkiinnottomaksi mössöksi. Prosessia kutsutaan lämpökuolemaksi [7]. Älä kuitenkaan heitä kirvestäsi kaivoon: lämpökuolema ei tule vielä huomenna. Odotellessa on hyvä tutustua sellaisten suurhenkilöiden kuin Rudolf Clausius, Ludwig Boltzmann (mainittiinkin jo), J. Willard Gibbs, John von Neumann ja Claude Shannon aikaansaannoksiin. En suinkaan vähättele listalta pois jääneitä. Tämä oli vain satunnaisotos sieltä joukon kärkipäästä.

Viitteet

[1] Alestalo, Pekka: Presidentti-gallup. Solmu 3/2005.
https://matematiikkalehtisolmu.fi/2005/3/gallup.pdf

[2] Alestalo, Pekka: Normaalijakauman kertymäfunktiosta. Solmu 1/2006.
https://matematiikkalehtisolmu.fi/2006/1/alestalo.pdf

[3] Alestalo, Pekka: Binomikaava. Solmu 2/2013.
https://matematiikkalehtisolmu.fi/2013/2/binomi.pdf

[4] Liukkonen, Jukka: Yleistetyt funktiot eli distribuutiot. Solmu 1/2007.
https://matematiikkalehtisolmu.fi/2007/1/distribuutiot.pdf

[5] Wikipedia: Binomial distribution.
https://en.wikipedia.org/wiki/Binomial_distribution

[6] Wikipedia: Binomial theorem.
https://en.wikipedia.org/wiki/Binomial_theorem

[7] Wikipedia: Heat death of the universe.
https://en.wikipedia.org/wiki/Heat_death_of_the_universe

[8] Wikipedia: Multinomial theorem.
https://en.wikipedia.org/wiki/Multinomial_theorem

[9] Wikipedia: Normal distribution.
https://en.wikipedia.org/wiki/Normal_distribution

[10] Wikipedia: Probability distribution.
https://en.wikipedia.org/wiki/Probability_distribution

Alaviitteet

Kun $n$ kasvaa rajatta, jakaumasta muotoutuu kuuluisa Diracin delta -piikki [4].↩︎
Fyysikot älkööt menettäkö malttiaan tämän “kaiken teorian” takia.↩︎