Suorakulmio
Jukka Liukkonen
Mat. yo. evp.
Suora kulma ja suorakulmainen kolmio
Yksi mieltäni kauimmin askarruttaneista käsitteistä on suora kulma. Jos otan käsittelyyn L-kirjaimen muotoon väännetyn rautalanganpätkän ja vedän tuon ainoan kulman suoraksi, tuloksena ei suinkaan ole suora kulma, vaan suoran kulman tuhoutuminen. Mielestäni suoran kulman tulisi olla suora, siis sellainen, joka ei ole kulma ensinkään. Luku nolla on joskus keksitty ilmoittamaan jonkin olevaisen paljoutta silloin, kun tuota olevaista ei ole lainkaan. Siksi suoraksi väännetty rautalanka on mielestäni nollakulman ilmentymä. Mutta kun ei: matematiikan kaanonissa nollakulma tarkoittaa sitä kulmaa, jossa kulmaa eli äkillistä suunnanmuutosta on eniten. Siinä rautalangan päät osoittavat samaan suuntaan.
Geometrian luultavasti jumalallista alkuperää oleva nomenklatuuri on ymmärtääkseni asia, johon en pysty vaikuttamaan. Vaikka suora kulma ja nollakulma ovat mielestäni yksi ja sama asia, jatkan perinteisellä linjalla. Elämän helppoudellakin on oma merkityksensä. Olkoon siis suora kulma yhtä kuin kohtisuora kulma, sellainen \(90\) asteen tai \(\pi/2\) radiaanin suuruinen kulma. Kolmioista tai muista monikulmioista puhuessani tarkoitan kulmilla vain kärkikulmia, en niitä 180 asteen kulmia, joita on ylinumeroituvasti ääretön määrä kärkipisteiden väleissä. Tässäkin noudatan vakiintunutta puhetapaa. Yhdestä periaatteestani en kuitenkaan luovu: kutsun suorakulmaiseksi kolmioksi ainoastaan sellaista kolmiota, jonka kaikki kulmat ovat suoria. Ehdottomasti! Mitä järkeä on siinä, että kolmiota, jonka kulmista alle 34 % on suoria, kutsutaan suorakulmaiseksi? Sehän on yhtä hölmöä kuin jos pianon, viulun ja sellon muodostamaa kokonaisuutta kutsuttaisiin pianotrioksi. Tuota ... tämä ei tainnut olla osuva vertaus.
Olen piirtänyt aidon suorakulmaisen kolmion kuvaan 1. En viitsi merkitä kulmiin niitä tuttuja väkäsiä, suoran kulman merkkejä, sillä kaikki tämän artikkelin kulmiot ovat suorakulmioita.
Suoraan kulkeminen kaareutuvalla pinnalla
Opiskelijariennoista kotiutuessani minulla oli joskus vaikeuksia kulkea suoraan. Nyt jälkikäteen ymmärrän, että hankaluudet johtuivat maapallon pinnan kaareutumisesta. En ollut perehtynyt kaareutuvien pintojen geometriaan tarpeeksi syvällisesti. En yksinkertaisesti edes tiennyt, mitä suoraan kulkeminen kaareutuvalla pinnalla tarkkaan ottaen tarkoittaa.
Newtonin inertialain mukaan kappale jatkaa suoraviivaista liikettä vakionopeudella, ellei siihen vaikuta mitään voimia. Voiman vaikutus ilmenee kiihtyvyytenä. Sekä nopeus \(\mathbf{v}\) että kiihtyvyys \(\mathbf{a}\) ovat vektorisuureita, ts. niillä on suuruus ja suunta. Jos \(\mathbf{v}\) ja \(\mathbf{a}\) ovat yhdensuuntaiset, siis saman- tai vastakkaissuuntaiset, liike säilyy suoraviivaisena. Liikkeen suunta muuttuu täsmälleen silloin, kun \(\mathbf{a}\) on erisuuntainen kuin \(\mathbf{v}\). Kiihtyvyysvektori \(\mathbf{a}\) voidaan jakaa nopeusvektorin suuntaiseen komponenttiin \(\mathbf{a}_{||}\) ja sitä vastaan kohtisuoraan komponenttiin \(\mathbf{a}_{\perp}\):
\[\mathbf{a} = \mathbf{a}_{||}+\mathbf{a}_{\perp}\,,\quad \mathbf{a}_{||} = \frac{\mathbf{a}\mathbf{\cdot}\mathbf{v}}{\mathbf{v}\mathbf{\cdot}\mathbf{v}}\,\mathbf{v},\quad \mathbf{a}_{\perp} = \mathbf{a}-\mathbf{a}_{||}\,.\]
Liike on suoraviivaista, jos ja vain jos \(\mathbf{a}_{\perp}=\mathbf{0}\).
Seuraavaksi ajatellaan, että piste liikkuu kolmiulotteisessa euklidisessa avaruudessa \({\mathbb E}^3\) kaareutuvaa kaksiulotteista pintaa \(S\) pitkin. Tuo pinta voisi olla esimerkiksi pallon pinta. Koska pinta kaareutuu, liike ei yleensä ole suoraviivaista kolmiulotteisessa avaruudessa asustavan kolmiulotteisen tarkkailijan näkökulmasta. Entäpä jos liikettä tarkkailee pinnalla asustava kaksiulotteinen tarkkailija Lettu? Hän ei pääse irtaantumaan pinnasta eikä suoraan havaitse kolmatta ulottuvuutta.
Keskinopeus on paikan muutos jaettuna aikavälin pituudella. Paikan muutos on vektori. Se on sitä enemmän pinnan \(S\) suuntainen, mitä lyhyempi on aikaväli. Hetkellinen nopeus saadaan raja-arvona, kun aikavälin pituus kutistetaan nollaan. Täten pinnalla tapahtuvan liikkeen nopeusvektori on aina pinnan suuntainen. Tuon nopeusvektorin Lettu havaitsee. Kiihtyvyysvektorin komponentti \(\mathbf{a}_{\perp}\) jaetaan pinnan suuntaiseen komponenttiin \(\mathbf{a}_{\perp}^{||}\) ja pintaa vastaan kohtisuoraan komponenttiin \(\mathbf{a}_{\perp}^{\perp}\). Silloin
\[\mathbf{a}_{\perp} = \mathbf{a}_{\perp}^{||} + \mathbf{a}_{\perp}^{\perp}\,,\quad \mathbf{a} = \mathbf{a}_{||}+\mathbf{a}_{\perp}^{||} + \mathbf{a}_{\perp}^{\perp}\,.\]
Kummankin yhtälön oikealla puolella esiintyvät vektorit ovat kohtisuorassa toisiaan vastaan.1 Vain pinnan suuntaiset komponentit \(\mathbf{a}_{||}\) ja \(\mathbf{a}_{\perp}^{||}\) näyttäytyvät Letun havaintomaailmassa. Siitä johtuen Lettu pitää liikettä suoraviivaisena, jos \(\mathbf{a}_{\perp}^{||}=0\). Toisin sanoen: liike pinnalla on suoraviivaista täsmälleen silloin, kun kiihtyvyysvektorin nopeusvektoria vastaan kohtisuora komponentti on kohtisuorassa myös pintaa vastaan. Tällöin liikkuvalla pisteellä ei ole pinnan suuntaista kiihtyvyyttä muissa suunnissa kuin mahdollisesti liikkeen ja samalla liikeradan suunnassa.
Letun havaintomaailman geometriaa voidaan pitää pinnan \(S\) sisäisenä geometriana. Nopeusvektorin \(\mathbf{v}\) itseisarvoa \({\left|\mathbf{v}\right|}\) sanotaan vauhdiksi tai ratavauhdiksi. Liikerataa pitkin voidaan kulkea myös tasaisella vauhdilla, esimerkiksi yksikön suuruisella vauhdilla. Onkin yksinkertaisempaa määritellä pinnan sisäisessä geometriassa suorat viivat eli geodeesit tasavauhtisen liikkeen avulla:
Määritelmä. Pintaa pitkin tasaisella vauhdilla liikkuvan pisteen liikerata on geodeesi, jos liikkeen kiihtyvyysvektori on kohtisuorassa pintaa vastaan.
Pallopinnalla geodeesit ovat isoympyrän kaaria tai niiden pätkiä. Isoympyrällä tarkoitetaan pallon keskipisteen kautta kulkevan tason ja pallopinnan leikkausympyrää. Täten kaikki pituuspiirit ovat geodeeseja, mutta leveyspiireistä ainoastaan päiväntasaaja on geodeesi. Isoympyrä kokonaisuudessaan on maksimaalinen geodeesi siinä mielessä, että ei ole pidempää geodeesia, johon isoympyrä sisältyisi aitona osana.
Monikulmiot pinnoilla
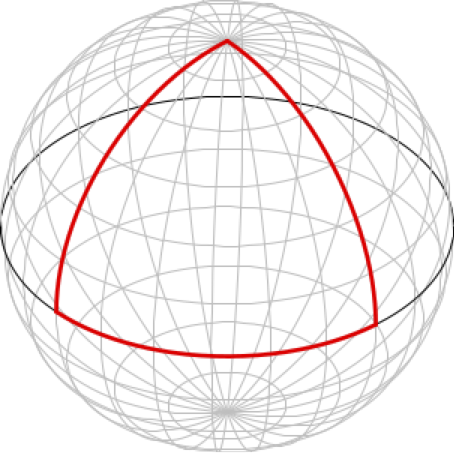
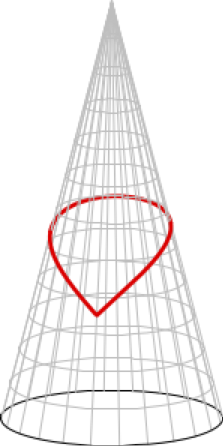
Tasomonikulmion peräkkäisiä kärkiä yhdistävät sivut ovat janoja, tason suoria viivoja. Pinnalla \(S\) monikulmion sivuilta vaaditaan, että ne ovat geodeeseja. Kuvan 1 esittämän pallokolmion sivut kulkevat isoympyröitä pitkin, joten pallokolmio on ihan laillinen monikulmio. Samoin ovat kuvien 2 ja 3 esittämät suorakulmiot.
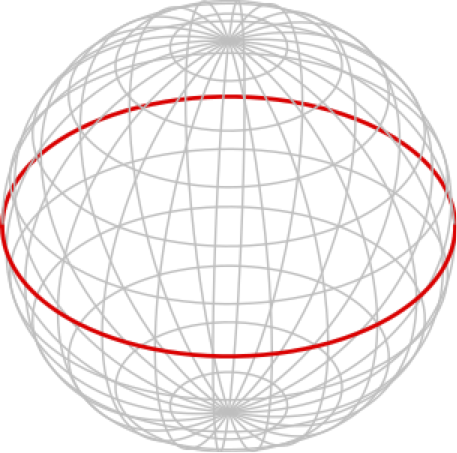
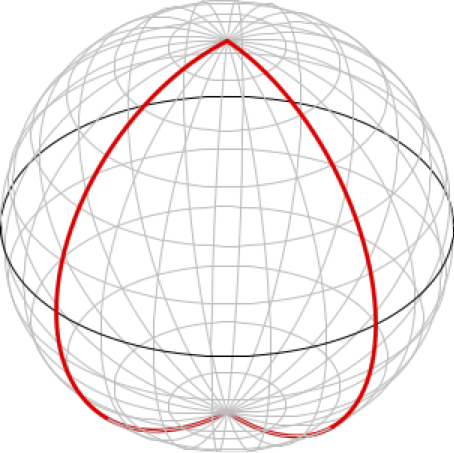
Pallopinnalle saadaan täten piirrettyä suorakulmaiset nolla-, kaksi- ja kolmikulmiot. Suorakulmaisen yksikulmion piirtämistä varten siirrytään kartiopinnalle. Piirtämisen ideaa on havainnollistettu kuvissa 4 ja 5. Jos kartion terävä kärki häiritsee, se voidaan tarvittaessa korvata tasaisen pyöreällä huipulla, joka saumattoman sileästi liittyy muuhun kartioon. Myös kaksi- ja kolmikulmaiset suorakulmiot voidaan toteuttaa kartiopinnalla. Mitenköhän ne saadaan aikaan?
Järjestyksessä seuraavana on suorakulmainen nelikulmio. Sitä kutsutaan myös suorakaiteeksi syystä, jota en milloinkaan ole ymmärtänyt. Mikä ihmeen kaide? Ei mene minun pirtaani, ei sitten millään. Kuvassa 6 paistattelee säännöllinen suorakulmainen tasonelikulmio eli neliö. Siinä on neljä yhtä pitkää sivua. Neliöt ovat nykyisin hurjissa hinnoissa varsinkin pääkaupunkiseudulla. Matemaatikoilla on erinomainen tilaisuus vaurastua myymällä neliöitä. Toisaalta norjalaisen Niels Henrik Abelin (1802–1829) esimerkki osoittaa, että matematiikan kirkkaimmat helmet hioutuvat vaatimattomissa, suorastaan kurjissa olosuhteissa. Yliopistojen rahoituksesta vastaavat poliittiset päättäjät tietävät tämän varsin hyvin.

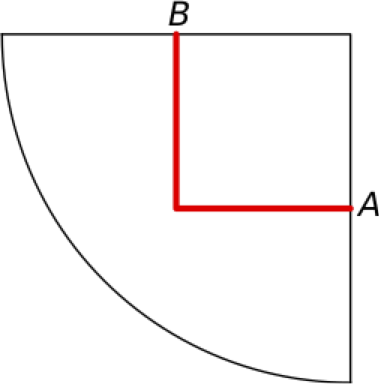
Suorakulmaisen nelikulmion kulmien summa on \(360^\circ\) eli täysi ympyrä. Onko silloin mahdollistakaan, että suorakulmaisessa monikulmiossa olisi enemmän kulmia kuin neljä, esimerkiksi viisi? Ongelmaa voidaan lähestyä käänteisesti ajattelemalla kolmiulotteiseen avaruuteen suljettu murtoviiva, jossa on viisi suoraa kulmaa kuten kuvassa 7. Sen jälkeen aletaan miettiä, millaisella pinnalla kyseinen murtoviiva saattaisi poukkoilla. Luonnonvoimat voidaan valjastaa mielikuvituksen avuksi: murtoviiva väännetään rautalangasta, kastetaan saippualiuokseen ja kas, saippuakalvo asettuu kauniisti kaareutuvaksi rautalangan reunustamaksi pinnaksi. Ajatuksissa pintaa jatketaan hieman laajemmalle, jolloin rautalanka ei enää ole reunalla. Huomaa, että avaruuden \({\mathbb E}^3\) jana on aina geodeesi, sijaitsipa se millä pinnalla tahansa. Miksi?
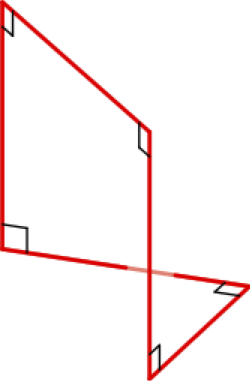
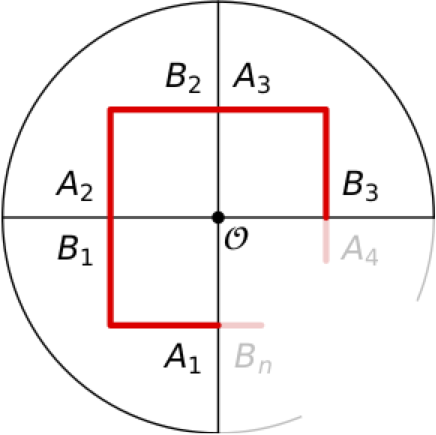
Rautalangasta vääntämällä on mahdollista tuottaa \(n\)-suorakulmioita myös kulmamäärillä \(n>5\). En halua artikkelin loppuosasta saippuaoopperaa, joten palaan kartiomallin pohdintaan. Onnistuisiko suorakulmion tuottaminen suurilla kulmamäärillä, jos sivusta auki leikatun kartion vaippaa jatkettaisiin ruuvimaisesti itsensä päälle niin, että huippukulmasta tulisi reilusti isompi kuin täysi ympyrä? Sen jälkeen ylileveä helma pliseerattaisiin kuin hame ja liimattaisiin halkio umpeen. Vekkihameen teräviä vekkejä ei saa syntyä, vaan helman tulee kaareutua sileästi. No, onnistuuhan se! Pinnan ja monikulmion konstruktio selitetään tarkemmin kuvan 8 yhteydessä. Näin ollen jokaista ei-negatiivista kokonaislukua \(n\) kohti on olemassa pinta, jolle voidaan piirtää suorakulmainen \(n\)-kulmio.
Poincarén kiekko
Kolmas ja matemaattisesti ehkä yksinkertaisin ja kaunein tapa tuottaa monikulmaisia suorakulmioita on piirtää ne eräälle pinnalle, joka ei mahdu kolmiulotteiseen euklidiseen avaruuteen, mutta kuusiulotteiseen avaruuteen \({\mathbb E}^6\) se ainakin mahtuu. Onneksi tuo pinta on mahdollista projisoida tason avoimeksi origokeskiseksi yksikkökiekoksi
\[B(0,1) := \{(x,y)\in{\mathbb E}^2\,\mid\,x^2+y^2<1\}\]
ja vieläpä konformisti, so. kulmien suuruudet säilyttäen. Etäisyydet tuossa projektiossa pakosti muuttuvat. Kuuluisa Mercatorin karttaprojektio [2] on tässä mielessä samanlainen. Ennen ihmepinnan tarkempaa esittelyä puhutaan hetki kaarevuudesta.
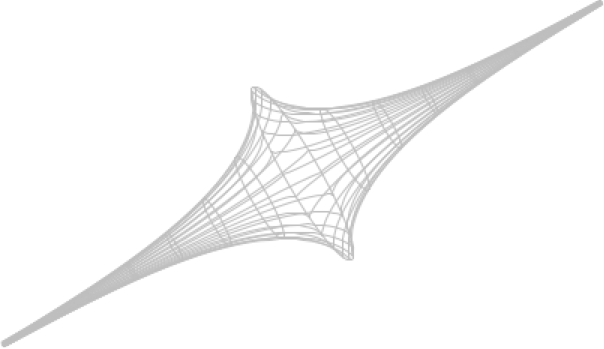
Kaksiulotteisen pinnan jokaiseen pisteeseen liittyy tietty reaaliluku, jota sanotaan kaarevuudeksi tuossa pisteessä. Kaarevuuden täsmällistä määritelmää ei ole tarkoituksenmukaista esittää tässä. Kaarevuuden etumerkistä saadaan vihje asettamalla pisteeseen pintaa sivuava tangenttitaso. Pallopinta jää kokonaan tangenttitason toiselle puolelle ja koskettaa tasoa vain sivuamispisteessä. Tämä on tyypillistä positiivisesti kaareutuvalle pinnalle. Tasoa sivuava tangenttitaso on taso itse. Tason kaarevuus on nolla. Myös ympyräpohjaisen lieriön kaarevuus on nolla. Tangenttitaso sivuaa lieriötä suoraa pitkin, ja symmetria-akselin suunnassa auki leikattu lieriö voidaan levittää tasoon. Pinnan \(z=y^2-x^2\) voidaan ajatella syntyvän siten, että \(xz\)-tason suuntaista alaspäin aukeavaa paraabelia liu’utetaan pitkin \(yz\)-tasossa sijaitsevaa ylöspäin aukeavaa paraabelia. Pinta on esimerkki satulapinnasta. Kun satulapinnan johonkin pisteeseen asetetaan tangenttitaso, pinta karkaa tason kummallekin puolelle heti sivuamispisteen välittömässä läheisyydessä, toisin kuin esimerkiksi lieriön pinta. Satulapinnalla on negatiivinen kaarevuus.
Pallopinta näyttää täsmälleen samalta kaikista pinnan pisteistä katsottuna. Pallon kaarevuuden on siis oltava sama positiivinen vakio jokaisessa pisteessä. Samasta syystä tason kaarevuus on nolla kaikkialla, samoin lieriön kaarevuus. Satulapinnan \(z=y^2-x^2\) negatiivinen kaarevuus vaihtelee pisteestä toiseen. Herää kysymys, onko olemassa pintaa, jolla on yksi ja sama negatiivinen kaarevuus kaikkialla. Kuvaan 9 piirretty, pseudopalloksi nimetty pinta [5] on melkein tällainen, mutta siinä on terävä reunus. Hyväksytäänkö pseudopallo vai ei riippuu siitä, mitä pinnalta vaaditaan. Jos pinnan on oltava sileä kaikkialla ja jokaista maksimaalista geodeesia pitkin pitää voida kulkea loputtomiin vakiovauhdilla ilman, että “pudotaan pinnalta pois”, pseudopallo ei riitä. Ratkaisuksi keksittiin jo 1800-luvulla hyperbolinen taso \({\mathbb H}^2\). Paikallisesti pseudopallo ja \({\mathbb H}^2\) ovat samankaltaisia, mutta kokonaisuuksina, globaalilta rakenteeltaan, ne ovat ratkaisevasti erilaisia. Hyperbolinen taso on kappaleen alussa mainittu ihmepinta. Sen epäeuklidista geometriaa esitellään artikkelissa [3] mm. virkatun mallin avulla.
Sitkeän kansanvalistustyön seurauksena kansalaiset tietävät jo korkeammasta matematiikastakin jotakin — luultavasti ainakin sen, että topologi, tuo puolisokea matemaatikon alalaji, ei erota kahvikuppia munkkirinkilästä. Yliopiston kahvilassa posliinikuppia hampaantyngillään järsivä topologi pitää hyperbolista tasoakin avoimena kiekkona. Yllätys, yllätys: pseudopallon ja kiekon välisen eron topologi huomaa heti.
Poincarén2 mallissa [4] hyperbolinen taso \({\mathbb H}^2\) projisoidaan yksikkökiekoksi \(B(0,1)\) siten, että geodeeseja vastaavat kiekon reunaympyrän kohtisuoraan kohtaavat ympyränkaaret ja rajatapauksina kiekon lävistäjät; muut geodeesit ovat näiden maksimaalisten geodeesien pätkiä. Projektio säilyttää kulmat: kahden geodeesin välinen kulma pinnalla \({\mathbb H}^2\) on sama kuin niitä vastaavien kaarien välinen tavallinen euklidinen kulma Poincarén kiekolla. Erityisesti suorat kulmat Poincarén kiekolla ja hyperbolisella tasolla vastaavat toisiaan. Kuvaan 10 on piirretty geodeeseja ja niistä muodostettu säännöllinen seitsenkulmainen suorakulmio.
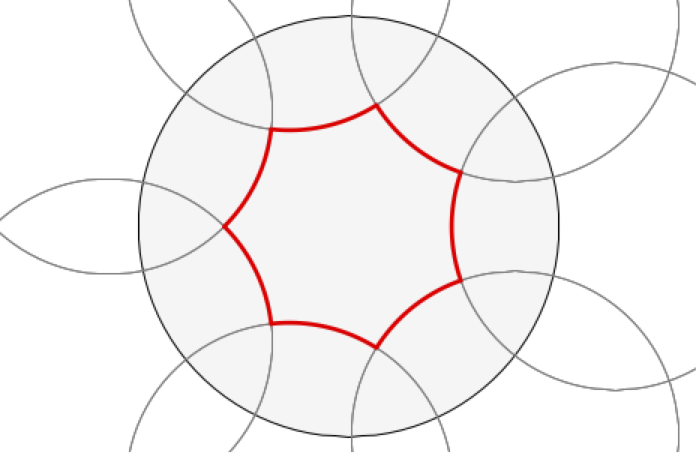
Kahden pisteen välinen etäisyys kiekosta mitattuna on täysin erilainen kuin vastinpisteiden etäisyys pinnalla \({\mathbb H}^2\). Hyperbolisen metriikan pituuselementin \(\text{d}s\) neliö kiekon tavallisten \(xy\) -koordinaattien ja \(r\theta\) -napakoordinaattien avulla lausuttuna on
\[\text{d}s^2 = \frac{4(\text{d}x^2+\text{d}y^2)}{\left(1-x^2-y^2\right)^2} = \frac{4(\text{d}r^2 + r^2\,\text{d}\theta^2)}{\left(1-r^2\right)^2}\,.\]
Jälkimmäistä kaavaa ja integraalilaskentaa käyttäen voidaan laskea, että Poincarén kiekon reuna on hyperbolisen metriikan mielessä äärettömän kaukana origosta. Euklidisen \(r\)-säteisen origokeskisen ympyrän kehältä on sädettä pitkin hyperbolista matkaa origoon peräti
\[\rho := \ln\frac{1+r}{1-r}\]
yksikköä, kun \(r<1\). Pituuselementin napakoordinaattiesityksestä saadaan lisäksi laskettua hyperbolinen pituus \(\lambda\) origokeskiselle ympyräviivalle, jonka hyperbolinen säde on \(\rho\):
\[\lambda = \pi(\text{e}^\rho-\text{e}^{-\rho}) \approx \pi\text{e}^\rho.\]
Tässä \(\text{e}\approx 2{,}718\) on Neperin luku. Jos \(\rho\) olisi ympyrän euklidinen säde, ympyrän kehän pituus olisi \(2\pi\rho\). Origokeskisen \(\rho\)-säteisen ympyrän kehän pituus hyperbolisessa metriikassa on noin \(\pi\text{e}^\rho\), kun \(\rho\) on suuri. Silloin hyperbolinen kehä on pituudeltaan \(\text{e}^\rho/(2\rho)\) -kertainen euklidiseen verrattuna. Kun \(\rho=10\), pituuksien suhde on noin \(1100\). Kun \(\rho=100\), suhde on noin \(1,34\cdot 10^{41}\). Tästä johtuu hyperbolisen avaruuden virkattujen pannulappumallien voimakas poimuttuminen.
Hyperbolisen kehän rajun venymisen takia ei tunnu aivan mahdottomalta tosiasia, että vakiokaarevuuden omaava pinta \({\mathbb H}^2\) välttämättä pursuaa ulos avaruudesta \({\mathbb E}^3\). Tämän ja hieman enemmänkin on suuri matemaatikko David Hilbert (1862–1943) todistanut vuonna 1901. Muita aiheeseen liittyviä tuloksia ovat todistaneet mm. Kaunis mieli -elokuvastakin tuttu matemaatikko ja talousnobelisti John Nash (Nashin upotuslauseet 1950- ja 60-luvulla), Danilo Blanuša (isometrinen upotus \({\mathbb H}^2\to{\mathbb E}^6\), vuosi 1955) ja Èmil’ Renol’dovich Rozendorn (isometrinen immersio \({\mathbb H}^2\to{\mathbb E}^5\), vuosi 1960).
Poincarén mallin yhteenveto. Pistejoukkona (ja topologisena avaruutena) hyperbolinen pinta \({\mathbb H}^2\) voidaan ajatella kaksiulotteiseksi kiekoksi \(B(0,1)\). Kiekon avaruudesta \({\mathbb E}^2\) perimä euklidinen metriikka (so. mitta etäisyydelle) antaa kiekon kaarevuudeksi nolla. Kaarevuuden kuitenkin halutaan olevan \({-1}\) koko kiekossa. Euklidinen metriikka on siis korvattava jollain toisella metriikalla. Jo 1800-luvulla keksittiin hyperbolinen metriikka, jolla kaarevuustavoite toteutuu. Jos tällä toisella metriikalla varustettu kiekko halutaan sijoittaa sileästi kaareutuvaksi kaksiulotteiseksi pinnaksi euklidiseen avaruuteen \({\mathbb E}^n\) niin, että (sopivasti venytetyn ja vanutetun) kiekon avaruudelta \({\mathbb E}^n\) perimä euklidinen metriikka pintaa pitkin yhtyy kiekon hyperboliseen metriikkaan, avaruudessa pitää olla tarpeeksi ulottuvuuksia: \({\mathbb E}^2\) ja \({\mathbb E}^3\) eivät riitä, mutta \({\mathbb E}^6\) todistetusti riittää. Poincarén kiekkomalli on kuitenkin sikäli kätevä, että pinnan \({\mathbb H}^2\) geodeesit näyttäytyvät kiekon reunaympyrän kohtisuoraan leikkaavina ympyränkaarina. Lisäksi kahden tällaisen ympyränkaaren välinen euklidinen kulma on yhtä suuri kuin vastaavien geodeesien välinen hyperbolinen kulma pinnalla \({\mathbb H}^2\). Kun tiedetään, mitä Poincarén kiekolla tapahtuu, tiedetään samalla, mitä hyperbolisella pinnalla tapahtuu. Kiekko toimii ikkunana ihmepinnalle.
Viitteet
[1] Lehtinen, Matti: Matematiikan historian luentoja. Päivitetty 11.11.2014.
https://matematiikkalehtisolmu.fi/2000/mathist/histluennot.pdf
[2] Rasila, Antti: Mercatorin kartta. Solmu 1/2007.
https://matematiikkalehtisolmu.fi/2007/1/mercator.pdf
[3] Schroderus, Riikka: Hyperbolisesta geometriasta. Solmu 3/2015.
https://matematiikkalehtisolmu.fi/2015/3/hyperbolisesta_geometriasta.pdf
[4] Wikipedia: Poincaré disk model.
https://en.wikipedia.org/wiki/Poincare_disk_model
[5] Wikipedia: Pseudosphere.
https://en.wikipedia.org/wiki/Pseudosphere
Alaviitteet
Nollavektorin ajatellaan olevan kohtisuorassa kaikkia muita vektoreita vastaan.↩︎
Matematiikan viimeiseksi yleisneroksikin sanottu Henri Poincaré vaikutti Ranskassa vuosina 1854–1912. Hänen jälkeensä matematiikka on paisunut niin laajaksi tieteenalaksi, että sitä ei yksi ihminen pystyne kokonaisuudessaan hallitsemaan.↩︎