pdf  Solmu 3/2021

---

Ympyrän sisään piirrettyä

Markku Halmetoja

Kiitos Donald Knuth’in¹, lapsuuden harppiharjoitukset on nyt mahdollista tuottaa muutamalla koodirivillä paljon parempina kuin ne onnistuvat paperille tuhertamalla. Koululaisena näitä piirustaessa selvisi kuitenkin,

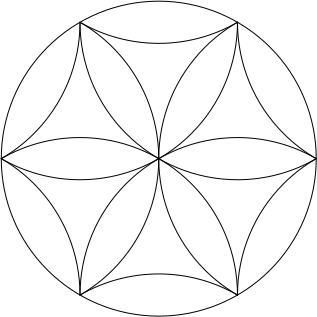
että ympyrän kehä voidaan jakaa kolmeen ja kuuteen yhtäsuureen osakaareen. Niiden vastaisista jänteistä muodostuu ympyrän sisään piirretty tasasivuinen kolmio ja säännöllinen kuusikulmio. Piirtäminen siis onnistuu antiikin kreikkalaisen ihanteen mukaisesti “geometrisesti oikein”, eli pelkästään harppia ja viivainta (ja kynää!) käyttäen.

Kreikkalaisille matematiikka oli geometriaa. Heillä ei ollut käytettävissään nykyaikaista reaalilukujen teoriaa eikä algebrallisia menetelmiä yhtälöiden käsittelemiseen. Ongelma katsottiin ratkaistuksi ainoastaan silloin, kun se voitiin piirtää harppia ja viivainta käyttäen. Piirtäminen tapahtui ensisijaisesti ajattelemalla: mietittiin algoritmi miten kuvio syntyisi jos se piirrettäisiin ja todistettiin menettelytapa oikean tuloksen antavaksi matemaattisten objektien määritelmiin, niitä koskeviin todistamattomina hyväksyttyihin peruslauseisiin eli aksioomiin ja aikaisemmin todistettuihin teoreemiin perustuen. Eukleides² systematisoi aikakaudellaan tunnetun alkeisgeometrian tällaiseksi aksioomiin ja määritelmiin perustuvaksi yhtenäiseksi esitykseksi noin 2300 vuotta sitten. Vaikka hänen järjestelmänsä oli osin puutteellinen ja epäselvä, geometriaa opetettiin kautta maailman pääosin hänen Elementa-teokseensa pohjautuen aina 1900-luvun ensimmäiselle puoliskolle asti. Siihen perustunut kouluopetus oli Suomessakin ainoa eksaktiin ajatteluun johtanut polku. Hilbert³ viimeisteli eukleidisen geometrian aksioomat lopulliseen muotoon vuonna 1899 ilmestyneessä teoksessaan Grundlagen der Geometrie. Nyttemmin matematiikasta kiinnostuneet voivat tutustua suomen kielellä sekä Eukleideen aksioomiin että Hilbertin niihin tekemiin täsmennyksiin hiljattain julkaistusta teoksesta [1]. Geometriaa opitaan myös valtakunnallisessa kilpavalmennuksessa, sillä se on vakioaihe matematiikka-olympialaisissa ja muissakin kilpailuissa. Solmun arkistossa on paljon geometriaan liittyvää aineistoa ja antikvariaateistakin saattaa löytyä vanhoja geometrian oppikirjoja.

Ympyrän sisään piirretyt säännölliset monikulmiot olivat yksi antiikin matemaatikoiden mielenkiinnon kohteista. Jos kärkiä on \(n\) kappaletta, niin monikulmio jakautuu \(n\):ksi tasakylkiseksi keskuskolmioksi, joiden huippukulmat ovat ympyrän keskipisteessä ja kyljet säteen mittaisia. Huippukulman suuruus on asteina \(\frac{360^{\circ}}{n}\) ja radiaaneina \(\frac{2\pi}{n}\). On selvää, että jos säännöllinen \(n\)-kulmio on piirretty, voidaan keskuskolmioiden huippukulmat puolittamalla (se tehdään harpilla ja viivaimella) saada aikaan säännöllinen \(2n\)-kulmio. Siksi parittoman määrän kärkipisteitä omaavat monikulmiot ovat erityisen kiinnostavia. Antiikin matemaatikot tunsivat (siis osasivat piirtää) niistä kolme: tasasivuisen kolmion, säännöllisen viisikulmion sekä säännöllisen 15-kulmion. (Luonnollisesti he osasivat piirtää myös neliön.) Noin parituhatta vuotta myöhemmin Gauss⁴ onnistui todistamaan, että konstruktio on mahdollinen, jos ja vain jos kärkien lukumäärä on muotoa \(n=2^{2^{k}} + 1\) oleva alkuluku tai tällaisten eri alkulukujen tulo. Näitä lukuja kutsutaan Fermat’n⁵ luvuiksi, ja tähän (2021) mennessä niistä tiedetään alkuluvuiksi ainoastaan viisi ensimmäistä:

\[\begin{aligned} F_{0} & = 2^{2^{0}}+1 = 3, \\ F_{1} & = 2^{2^{1}}+1 = 5,\\ F_{2} & = 2^{2^{2}}+1 = 17,\\ F_{3} & = 2^{2^{3}}+1 = 257,\\ F_{4} & = 2^{2^{4}}+1 = 65537. \end{aligned}\]

Ennen asian täydellisempää käsittelyä, Gauss onnistui 19-vuotiaana konstruoimaan säännöllisen 17-kulmion, mikä teki häneen niin suuren vaikutuksen, että hän laati siitä uutisen sanomalehteen. Myöhemmin hän halusi hautakiveensä veistettävän tämän monikulmion, mutta kivenveistäjä kieltäytyi, sillä hän ei olisi saanut sitä erottumaan ympyrästä. Kiveen ei taltalla ja vasaralla syntynyt riittävän terävää viivaa.

Ilmeisesti Gaussin tulosten innoittamina Richelot⁶ konstruoi säännöllisen 257-kulmion ja Hermes⁷ käytti kymmenen viimeistä elinvuottaan 65537-kulmion piirtämiseen. Hänen papereitaan säilytetään Göttingenin yliopiston matematiikan laitoksen ullakolla arkussa ([3]).

Yliopiston algebran kurssilla selvitetään, mitä yleensä voidaan piirtää harpilla ja viivaimella. Kurssilla tuskin konkreettisesti piirretään, sillä asia liittyy algebrassa tutkittavaan kuntateoriaan. Gaussin monikulmioita koskevan tuloksen ymmärtäminen on merkittävästi tätä yleistä teoriaa vaativampaa.

Tässä kirjoituksessa tutkimme eräitä säännöllisiä, ympyrän sisään piirrettyjä monikulmioita likimain lukion oppimäärän mukaisesti. Pidämme selviönä, että ympyrän kehällä on \(n(\geq 3)\) pistettä, jotka jakavat sen \(n\):ksi saman suuruiseksi osakaareksi riippumatta siitä voidaanko pisteet löytää muinaiskreikkalaiseen tapaan. Perehdymme erityisesti viisikulmioon, sillä sen kauniita ominaisuuksia on suhteellisen helppo löytää. Sen kerrotaan lävistäjineen olleen Pythagoraan⁸ koulukunnan ilmeisesti salassa pidetty tunnusmerkki, sillä siihen sisältyy lukuisia irrationaalisia suhteita. Niiden olemassaolo oli ristiriidassa koulukunnan julkilausutun opinkappaleen kanssa; sen mukaan kaikki oli esitettävissä kokonaislukujen suhteina. Lävistäjien muodostama tähtikuvio lienee ollut tunnettu jo muinaisessa Babyloniassa noin 4000 vuotta sitten eli 1500 vuotta ennen Pythagorasta ([2]). Ennen viisikulmioon ryhtymistä, ympyrän sisällä kun ollaan, katsomme erään nykylukiossa unhoon jääneen antiikin aarteen.

Olkoon \(ABCD\) jännenelikulmio, siis nelikulmio, jonka kärjet ovat ympyrän kehällä. Valitaan lävistäjältä \(BD\)

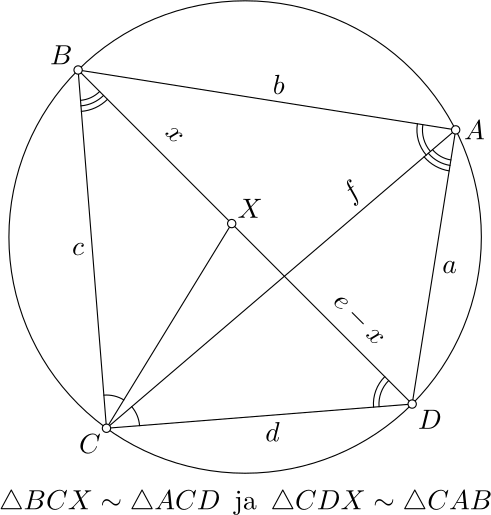
piste \(X\) siten, että \(\angle XCB = \angle DCA\). Tällöin myös \(\angle DCX = \angle ACB\), joten sopivia kehäkulmia tarkkailemalla havaitaan kuvion alareunaan kirjatut yhdenmuotoisuudet. Vastinsivuista saadaan kuvion merkinnöin verrannot

\[x:a = c:f\quad\mathrm{ja}\quad (e-x):b = d:f,\]

joista seuraa Ptolemaioksen⁹ teoreema:

\[ac + bd = ef.\]

Jännenelikulmion lävistäjien tulo on vastakkaisten sivujen tulojen summa.

Viisikulmioon päästään mukavimmin 10-kulmion kautta, sillä se saadaan siitä samalla tavalla kuin tasasivuinen kolmio kuusikulmiosta. Kuviossa on yksi 10-kulmion keskuskolmio. Sen huippukulma \(\alpha = 36^{\circ}\) ja kantakulmat \(2\alpha = 72^{\circ}\). Kantakulman puolittaja jakaa keskuskolmion kahdeksi tasakylkiseksi kolmioksi.

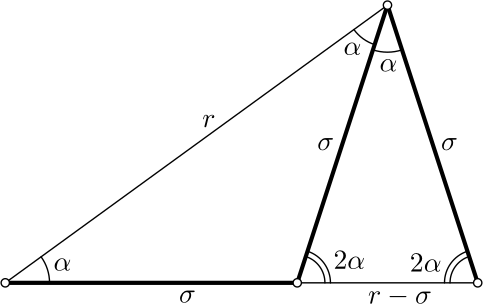
Yhdenmuotoisista kolmioista (tai kulmanpuolittajalauseen avulla) saadaan verranto

\[r:\sigma = \sigma:(r-\sigma).\]

Se kertoo, että ympyrän säde jakaantuu kultaisen leikkauksen suhteessa ja että jaossa saatu suurempi osa on etsitty kymmenkulmion sivu. Siksi tätä kolmiota on myös kutsuttu kultaiseksi kolmioksi. Verrannosta seuraa

\[\sigma = \tfrac{1}{2}(\sqrt{5}-1)r,\]

ja se on helppo piirtää antiikin välineillä. Itse asiassa peruskoulun oppimäärä saattaa riittää seuraavan ohjelman toteuttamiseen:

1. Piirretään suora ja sille normaali.

2. Erotetaan niiden leikkauspisteestä toiselle suoralle säde \(r\) ja toiselle \(2r\).

3. Yhdistetään näin saatujen janojen päätepisteet, jolloin kuvio täydentyy suorakulmaiseksi kolmioksi. Sen hypotenuusan pituus on \(r\sqrt{5}\).

4. Vähennetään hypotenuusasta \(r\) ja puolitetaan erotus. Se on kysytty kymmenkulmion sivu \(\sigma\).

Ottamalla \(\sigma\) harpin kärkien väliin, saadaan ympyrän kehälle kymmenen pistettä ja sama määrä yhtäpitkiä osakaaria. Kolmion kulmien kosineille saadaan kosinilauseen avulla viisikulmion tutkimisen kannalta mukavat arvot:

\[\cos{36^{\circ}} = \tfrac{1}{4}(\sqrt{5}+1)\quad\mathrm{ja}\quad\cos{72^{\circ}} = \tfrac{1}{4}(\sqrt{5}-1).\]

Esimerkiksi viisikulmion sivun pituus

\[\begin{aligned} S &= \sqrt{r^{2} + r^{2} - 2rr\cos{72^{\circ}}}\\[4pt] &= r\sqrt{2 -\tfrac{1}{2}(\sqrt{5}-1)}\\[4pt] &= \tfrac{1}{2}r\sqrt{10 - 2\sqrt{5}}. \end{aligned}\]

Viisikulmion lävistäjät rajoittavat kuvion osoittamalla tavalla pienemmän viisikulmion. Jos tätä ei ole aikaisemmin nähnyt, kannattaa pysähtyä miettimään, miksi sen sivut ovat keskenään yhtä pitkiä ja kaikki kulmat yhtäsuuria. Pythagoralaiset olivat tässä pohjattoman äärellä, sillä tämän pienemmän viisikulmion lävistäjät rajoittavat vielä pienemmän viisikulmion eikä tällä tavalla saatavien viisikulmioiden määrälle näy loppua. Ehkä se lisäsi kuvion mystisyyttä.

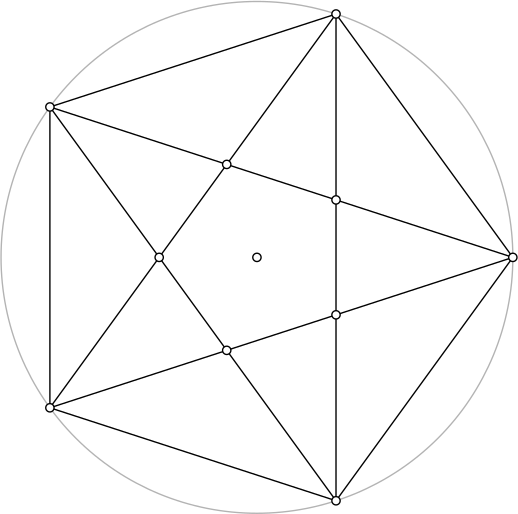
Edellä tuli mainittua, että viisikulmioon liittyy irrationaalisia suhteita. Aktiivinen lukija saa nyt tilaisuuden tutkia niitä ja paria muutakin kulmiota. Useimmat seuraavista kysymyksistä ovat “katso-ja-näe” tyyppiä, eli pitkiä laskutoimituksia ei tarvita. Aluksi sovitaan merkinnöistä, sillä kaunista kuviota ei viitsi sotkea kirjaimilla. Olkoot siis viisikulmion sivu \(= S\), lävistäjä \(= l\), lävistäjien rajaaman pienemmän viisikulmion sivu \(= s\) ja sakaran sivujana \(=a\). Tällöin \(l = a+s+a\).

1. Määritä a) \(S:l\),\(\,\,\,\,\quad\) b) \(s:a\).

2. Määritä a) \(s:S\), \(\quad\) b) \((a+s):S\).

3. Osoita, että \[\frac{l}{S}-\frac{S}{l} = 1.\]

4. Koska viisikulmion lävistäjät rajaavat alkuperäisen kulmion sisään uuden viisikulmion, saadaan päättymätön jono toinen toistaan pienempiä viisikulmioita. Laske kaikkien viisikulmioiden alojen summa, kun isoimman ala on \(A\).

5. Ympyrän sisään piirretyn säännöllisen 7-kulmion sivu on \(s\) ja eripituiset lävistäjät \(a\) ja \(b\). Osoita, että \[\frac{1}{a} + \frac{1}{b} = \frac{1}{s}.\]

6. Määritä \(\cos 24^{\circ}\) tarkka arvo ja laske \(r\)-säteisen ympyrän sisään piirretyn säännöllisen 15-kulmion sivun pituus.

Kompleksilukujen vakiintuminen matemaattisen analyysin osaksi 1700-luvulta alkaen paljasti yllättävän yhteyden geometrisina objekteina pidettyjen monikulmioiden ja algebrallisten yhtälöiden välillä. Asian selvittämiseksi tarvitaan lukion oppimäärään kuulumattomat perustiedot kompleksiluvuista. Artikkelin [4] kaksi ensimmäistä kappaletta sisältää riittävän materiaalin, ks. myös [6]. Tärkein on de Moivren¹⁰ kaava:

Kaikilla \(\varphi\in\mathbb{R}\) ja \(n\in\mathbb{Z}\) \[(\cos{\varphi} + i\sin{\varphi})^{n} = \cos{n\varphi} + i\sin{n\varphi}.\]

Se on jäänyt tärkeämpien Eulerin¹¹ kaavojen varjoon, mutta sillä olisi arvokas pedagoginen merkitys jos se opittaisiin lukiossa. Se toimisi hyvänä johdantona matemaattisiin korkeakouluopintoihin. Kompleksilukujen perusominaisuudet de Moivren kaavaan asti kannattaisi siis sisällyttää lukion opetussuunnitelmaan. Sopiva sijainti olisi trigonometrian osuuden jatkona.

Jaetaan kompleksitason origokeskinen yksikköympyrä \(n\):ään yhtäsuureen osakaareen jakopisteillä

\[(\cos{\tfrac{2k\pi}{n}}{,}\sin{\tfrac{2k\pi}{n}}),\quad k\in\{0, 1, 2, \ldots, n-1\},\]

jotka voidaan kätevimmin esittää kompleksilukuina

\[\varepsilon_{k} = \cos{\tfrac{2k\pi}{n}} + i\sin{\tfrac{2k\pi}{n}}, \quad k\in\{0, 1, 2, \ldots, n-1\}.\]

Jakopisteet ovat kyseisen ympyrän sisään piirretyn \(n\)-kulmion kärkipisteet. Niistä \(\varepsilon_{0} =1\) sijaitsee pisteessä \((1,0)\) ja de Moivren kaavan mukaan kaikilla kyseeseen tulevilla \(k\):n arvoilla (itse asiassa kaikilla \(k\in\mathbb{Z}\))

\[\begin{aligned} \epsilon_{k}^{n} &=\big(\cos{\tfrac{2k\pi}{n}} + i\sin{\tfrac{2k\pi}{n}}\big)^{n}\\[4pt] &= \cos{\tfrac{2kn\pi}{n}} + i\sin{\tfrac{2kn\pi}{n}}\\[4pt] &= \cos{2k\pi} + i\sin{2k\pi} = 1 + 0 = 1. \end{aligned}\]

Tulos merkitsee sitä, että luvut \(\varepsilon_{k}\) ovat polynomiyhtälön \(z^{n}-1=0\) juuria. Jos merkitään lyhyesti \(\varepsilon_{1} = \varepsilon\), niin de Moivren kaavan mukaan yhtälön juuret voidaan myös kirjoittaa muotoon \(1, \varepsilon, \varepsilon^{2}, \varepsilon^{3}, \ldots,\varepsilon^{n-1}\). Koska yhtälön asteluku on \(n\), sillä on enintään \(n\) eri juurta, joten olemme löytäneet ne kaikki, ja mikä hienointa, ne sijaitsevat yksikköympyrän kehällä ympyrän sisään piirretyn säännöllisen \(n\)-kulmion kärkinä. Gaussin todistus monikulmioiden konstruoitavuudesta perustuu tähän havaintoon, mutta se on hyvin vaikea. Suomen kielellä se löytyy teoksesta [5]. Kärkipisteihin perustuu myös signaalinkäsittelyssä sovellettu diskreetti Fourier-muunnos käänteismuunnoksineen. Historiaa taaksepäin katsovalle nykyihmiselle tämä kaikki kertoo jotakin oleellista matematiikan luonteesta.

Lopuksi vielä eräs hauska huomio. Tarkastellaan yksikköympyrän sisään piirrettyjä säännöllisiä monikulmioita. Niistä ensimmäinen on tasasivuinen kolmio. Jos lasketaan sen yhdestä kärjestä muihin kärkiin piirrettyjen janojen pituuksien tulo, niin se havaitaan kulmien lukumääräksi: tulo on \(\sqrt{3}\cdot\sqrt{3} = 3\). Neliölle tämä tulo on \(\sqrt{2} \cdot2\cdot\sqrt{2}=4\). Viisikulmiollekin se nähdään, jos jaksaa hieman pyöritellä juurilausekkeita ja kuusikulmiolle \(1\cdot\sqrt{3}\cdot2\cdot\sqrt{3}\cdot1=6\). Tällainen säännönmukaisuus ei voi olla sattumaa. Osoita siis, että jos yksikköympyrän sisään piirretyn säännöllisen monikulmion yhdestä kärjestä piirretään janat kaikkiin muihin kärkiin, niin janojen pituuksien tulo on monikulmion kärkien lukumäärä.

Viitteet

[1] Matti Lehtinen: Geometriaa ja geometriasta, Eukleides-kirjat 2021.

[2] Carl Boyer: Tieteiden kuningatar, matematiikan historia osa I, Art House 2000.

[3] Boris Sjöberg: Från Euklides till Hilbert, Historien om matematikens utveckling under tvåtusen år, Åbo Akademis förlag 1996.

[4] Matti Lehtinen: Kaikki tarpeellinen kompleksiluvuista, https://matematiikkalehtisolmu.fi/2006/1/lehtinen.pdf.

[5] Kalle Väisälä: Lukuteorian ja korkeamman algebran alkeet, 2. painos, Otava 1961.

[6] Jerry Segercrantz: \(\sin{18^{\circ}}\) kolmella eri tavalla, https://matematiikkalehtisolmu.fi/2004/2/sin18.pdf.

Alaviitteet

1. Donald Knuth (1938–), amerikkalainen tietojenkäsittelyteoreetikko, TeX- ja METAFONT-ohjelmistojen kehittäjä.

2. Eukleides Aleksandrialainen (325–265), kreikkalainen matemaatikko.

3. David Hilbert, (1862–1943), saksalainen matemaatikko.

4. Carl Friedrich Gauss (1777–1855), saksalainen matemaatikko.

5. Pierre de Fermat (1601–1665), ranskalainen matemaatikko.

6. Friedlich Julius Richelot (1808–1875), saksalainen matemaatikko.

7. Johan Gustav Hermes (1846–1912), saksalainen matemaatikko.

8. Pythagoras Samoslainen (n. 570 – n. 490), kreikkalainen matemaatikko.

9. Claudius Ptolemaios (85–165), kreikkalainen astronomi ja matemaatikko.

10. Abraham de Moivre (1667–1754), ranskalainen matemaatikko.

11. Leonhard Euler (1707–1783), sveitsiläinen matemaatikko.