PDF

15. Todennäköisyyslaskenta: ajanvietteestä tiedettä

Todennäköisyyslaskentaan on viitattu lyhyesti useissa yhteyksissä edellä. Tarkastellaan todennäköisyyslaskennan kehitystä 20. vuosisadan alkuun mennessä hiukan kootummin.

15.1 Alku uhkapeleissä

Uhkapeleihin liittyvää laskentoa lienee harjoitettu pitkään. Cardano oli noin vuonna 1526 kirjoittanut noppapeleistä kirjan Liber de Ludo Aleæ., jossa esiintyy todennäköisyyksien kertolaskusääntö. Varsinaisen todennäköisyyslaskennan katsotaan saaneen alkunsa siitä, kun Chevalier de Mérénä tunnettu Antoine Gombaud (1607-84) esitti Pascalille kaksi kysymystä uhkapelistä. Näistä ensimmäinen koski peliä, joka koostuu pelieristä, joiden voittamiseen kummallakin pelaajalla on samat mahdollisuudet. Jos ensimmäisenä kuusi erää voittanut saa pelipanoksen, mutta peli joudutaan keskeyttämään tilanteessa, jossa toinen pelaaja on voittanut viisi ja toinen kolme erää, niin mikä on oikeudenmukainen tapa jakaa pelipanos? Kysymys oli ollut pohdinnan kohteena jo pitkään. Luca Pacioli oli ehdottanut jakosuhdetta 5:3, Tartaglia 2:1. Pascal ja Fermat käsittelivät ongelmaa kirjeenvaihdossaan ja päätyivät samaan ratkaisuun (7:1), edellinen Pascalin kolmiota hyödyntävällä rekursiopäättelyllä, jälkimmäinen alkeistapaukset laskevalla kombinatorisella päättelyllä. Toinen de Mérén kysymys koski kahden nopan heittoa. Monestako kahden nopan heitosta koostuvassa pelissä kannattaa lyödä vetoa sen puolesta, että heittosarjassa on kaksoiskuutonen? Pelurien nyrkkisäännön mukaan kysytty lukumäärä olisi $\frac{4}{6}\cdot 36=24$, mutta empiirinen kokemus asetti tämän kyseenalaiseksi.

Pascal sovelsi eräänlaista odotusarvon teoriaa teologiaan: ihminen voi elää joko niin kuin jumala olisi olemassa tai niin kuin jumalaa ei olisi olemassa. Jos jumalaa ei ole olemassa, elämäntavan valinta on merkityksetön. Jos taas jumala on olemassa, oikea elämäntapa johtaa pelastumiseen, väärä kadotukseen. Koska edellinen vaihtoehto on äärettömän paljon parempi kuin jälkimmäinen, oikean elämätavan valinnan tuottama odotusarvo on suurempi, vaikka jumalan olemassaolon todennäköisyys olisi pienikin.

Hollantilaisen Christiaan Huygensin kirjanen De Ratiociniis in AleæLudo ilmestyi 1657. Siinä tarkastelun pohjana on odotusarvo: jos pelissä on p mahdollisuutta voittaa summa a ja q mahdollisuutta voittaa summa b, peliin kannattaa sijoittaa summa $x=\frac{pa+qb}{p+q}$. Tätä periaatetta soveltaen Huygens osoitti, että 24 kaksoisnopanheiton pelissä ei kannata lyödä vetoa kaksoiskuutosen puolesta, mutta 25 heiton pelissä kylläkin.

15.2 Suurten lukujen laki ja normaalijakauma

Jakob Bernoulli yleisti Pascalin pelipanoksenjako-ongelman ratkaisua tilanteisiin, joissa voitto ja tappio eivät olleet symmetrisiä. Näin hän tuli määritelleeksi yleisen binomijakauman. Jos onnistumisen mahdollisuuksia on a ja epäonnistumisen b, niin todennäköisyys onnistua k kertaa n:stä yrityksestä on Bernoullin mukaan

$$\frac{{n\choose k}a^kb^{n-k}}{(a+b)^n}.$$

Bernoullin Ars Conjectandi (1713) laajensi todennäköisyyskäsitystä pelkistä nopan vaihtoehdoista arkitodellisuuteen. Bernoulli arveli, että absoluuttista varmuutta on monesti vaikea saavuttaa, mutta että moraalinen varmuus vallitsee silloin, jos arveltu asiaintila vallitsee 999 kertaa tuhannesta. Moraalisen varmuuden teoriaa Bernoulli sovelsi tilanteeseen, jossa toistuvilla havainnoilla päätellään jakauma. Jos mustien ja valkeiden kuulien on uurnassa r ja s kappaletta ja X on N:llä nostolla saatujen mustien kuulien määrä, niin Bernoulli päätteli, että tarpeeksi suurilla N:n arvoilla $\frac{X}{N}$poikkeaa luvusta $\frac{r}{r+s}$ vähemmän kuin $\frac{1}{r+s}$ vain harvemmin kuin kerran tuhannessa nostosarjassa. Bernoullin laskelmat osoittivat, että jos r=30 ja s=20, luvuksi N kelpaa ainakin 25$\,$550. Bernoullin pettymykseksi luku oli näin suuri, joten suurten lukujen lain soveltaminen käytäntöön ei näyttänyt kovin mielekkäältä.

Abraham De Moivre tarkensi Huygensin ja Bernoullin tuloksia. Jos onnistumisen ja epäonnistumisen mahdollisuuksien suhde on a:b=1:q, niin yritysten määrä, jossa ainakin yksi onnistuminen tapahtuu todennäköisemmin kuin nolla onnistumista, saadaan yhtälöstä $(1+\frac{1}{q})^x=2$. Kun q on suuri, $x\approx 0{,}7q$; kaksoiskuutosen tapauksessa q=35 ja x=24,5. De Moivre kehitteli binomitodennäköisyyden kaavaa arvioimalla bimomikertoimessa esiintyviä kertomatermejä. De Moivre päätyi symmetrisen binomijakauman tapauksessa tulokseen, jonka mukaan $\frac{n}{2}+t$:n onnistumisen todennäköisyys on noin $\frac{2}{\sqrt{2\pi n}} e^{-\frac{2t^2}{n}}.$ Edellisen kaavan synnyttämä käyrä approksimoi binomijakaumaa. De Moivre totesi käyrällä olevan käännepisteen kohdissa $\frac{1}{2}(n\pm\sqrt n)$ ja että enintään $\frac{1}{2}\sqrt n$:n poikkeama keskeltä sattui todennäköisyydellä 0,682688. De Moivre ei käsitellyt perusteellisesti epäsymmetristä jakaumaa. Hän totesi kuitenkin, että Bernoullin tutkimassa tapauksessa 25550 yritystä voitiin supistaa 6498:aan. - Ns. todennäköisyyslaskennan keskeinen raja-arvolause, jonka mukaan lähes mielivaltaisten muuttujien summa jakautuu yhteenlaskettavien määrän kasvaessa normaalijakauman mukaisesti, tuli esiin Laplacen tuotannossa 1800-luvun alussa. Lauseen todistus riittävän väljin odotuksin esitettiin vasta 1900-luvun puolella.

15.3 Tilastollinen päättely

Kysymystä siitä, missä määrin ilmiöstä tehdyistä havainnoista voidaan päätellä sen todennäköisyys, tutki vakavasti ensimmäisenä englantilainen Thomas Bayes (1702-61). Bayes otti käyttöön ehdollisen todennäköisyyden käsitteen ja johti kaavan

$$\frac{\int_a^bx^k(1-x)^{n-k}\,dx}{\int_0^1x^k(1-x)^{n-k}\,dx}$$

ilmaisemaan todennäköisyyttä, jolla toistokokeen onistumistodennäköisyys on välillä $(a,\,b)$, jos tiedetään, että n:ssä toistossa on onnistuttu k kertaa. Laplace julkaisi 1774 tuloksen, joka kertoi havainnon k onnistumista n:stä ilmaisevan, että onnistumistodennäköisyys poikkeaa $\frac{k}{n}$:stä enintään c:n verran todennäköisyydellä

$$\frac{2}{\sqrt {2\pi}}\int_0^{c/\sigma}e^{-\frac{u^2}{2}}\,du,$$

missä $\sigma^2=\frac{k(n-k)}{n^3}$. Laplace sovelsi tulosta käytäntöönkin. Pariisissa oli vuosien 1745 ja 1770 välillä syntynyt 251$\,$527 poikaa ja 241$\,$945 tyttöä. Laplace laski, että todennäköisyys, että poikien syntyminen olisi vähemmän todennäköistä kuin tyttöjen olisi $1{,}15\cdot 10^{-42}$, joten se, että poikia syntyy tyttöjä useammin, on moraalisesti varmaa.

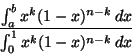
Toinen kysymyksenasettelu, jossa tilastollinen aineisto vaati matemaattista käsittelyä, liittyi tähtitieteellisiin havaintoihin. Useiden havaintojen sovittaminen mekaniikan malleihin johti tilanteisiin, joissa muutaman tuntemattoman määrittämiseksi oli käytettävissä lukuisia ei aivan yhteensopivia yhtälöitä. 1700-luvulla esitettiin erilaisia ratkaisuja yhtälöt parhaiten toteuttavan likimääräisratkaisun määrittämiseksi. Adrien-Marie Legendre julkaisi 1805 komeetan radanmääritystä käsittelevän tutkielmansa liitteenä tarkastelun, jossa usean muuttujan lineaaristen lausekkeiden arvon tulisi olla nolla eri muuttujayhdistelmillä. Legendre perusteli tasapainosyillä ratkaisua, jossa yhtälöihin parhaiten sopivaksi muuttujayhdistelmäksi valitaan se, joka tekee lausekkeiden arvojen neliöiden summan mahdollisimman pieneksi. Tehtävä voitiin helposti ratkaista differentiaalilaskennan avulla.

Gauss julkaisi oman versionsa pienimmän neliösumman menetelmästä vuonna 1809. Gauss kertoi käyttäneensä menetelmää jo vuodesta 1795. Gauss johti menetelmän huomattavasti seikkaperäisemmin kuin Legendre määrittämällä ensin havaintovirheen $\Delta$ jakaumafunktion $\phi$, jonka Gauss pystyi näyttämään olevan muotoa

$$\phi(\Delta)=\frac{h}{\sqrt{\pi}}e^{-h^2\Delta^2}.$$

Johto perustui oletukseen, että havaintoarvojen keskiarvo on todennäköisimmin oikea arvo.

Normaalijakauman irrotti havaintovirheiden teoriasta yleisempiin yhteyksiin belgialainen Adolphe Quetelet (1796-1874). Hän havaitsi normaalijakauman monenlaisissa ihmistä kuvaavissa tilastoissa. Erityisen sitova todistus normaalijakauman puolesta oli tilasto, jossa oli mitattu 5732 skotlantilaisen sotilaan rinnanympärys; ympärys jakautui normaalisti keskiarvona 40 tuumaa. Quetelet otti käyttöön käsitteen todennäköinen poikkeama. Se tarkoitti sitä matkaa normaalijakauman asteikolla keskikohdan molemmin puolin, joka piti sisällään puolet tapauksista.

Englantilainen Francis Galton (1822-1911) pyrki käyttämään Quetelet'n menetelmiä Darwinin periytymisopin todistamiseen. (Galton oli Darwinin serkku.) Erikokoisten herneiden jälkeläisten kokoa selvittäneet kokeet johtivat Galtonin regression ja korrelaation käsitteisiin. Galton päätteli korrelaation suuruuden pelkästään havaintopisteitä silmämääräisesti hyvin vastaavan suoran kulmakertoimesta. Keskihajonnan käsitteen samoin kuin pienimmän neliösumman käytön korrelaatiokertoimen määrityksessä toi tilastotieteeseen vuonna 1892 englantilainen Karl Pearson (1871-1936). Pearson esitti myös $\chi^2$-testin, joka toi mukanaan yleisen ajatusmallin nollahypoteesista ja sen säilyttämisestä tai kumoamisesta tilastollisen aineiston avulla. Toisen laajalti käytetyn testin, pienten otosten keskiarvon jakaumaan perustuvan t-testin eli Studentin testin kehitti 1900-luvun alussa englantilainen William Gosset (1876-1937). Gosset joutui pohtimaan pienten otosten keskiarvon käyttäytymistä toimiessaan Guinnesin panimon kemistinä. On arveltu, että Pearson pakotti Gossetin julkaisemaan tuloksensa salanimellä Student, koskei halunnut, että hänen perustamassaan ja toimittamassaan Biometrika-sarjassa esiintyisi tekijä, jonka taustaorganisaatio on panimo.

Alkuun - Etusivu - Edellinen - Seuraava