PDF

3. Muinaiskulttuurien matematiikasta

Nykymatematiikan monimutkainen ja abstrakti käsitemaailma pohjautuu perimmältään lukumäärää, kokoa ja muotoa koskeviin havaintoihin. Tieto siitä, miten nämä ovat saaneet systemaattista muotoa primitiivisten kansojen keskuudessa, on lähinnä epäsuorien todisteiden ja spekulaatioiden varassa. Alan tutkijat ovat mm. esittäneet teorioita laskemisen tai geometrian synnystä käytännön tarpeiden vaatimusten mukaan ja toisaalta ajatuksia matematiikan mahdollisesta rituaalis-uskonnollisesta alkuperästä.

Kielitieteellisen todistusaineiston avulla voidaan päätellä, että useimmissa kulttuureissa lukujen ilmaiseminen on perustunut tavalla tai toisella ihmisen ruumiinrakenteen kannalta luonnolliseen kymmen- tai viisijärjestelmään, mutta myös esim. kaksikymmenjärjestelmää (vaikkapa ranskan kielessä 80 on quatre-vingts 'neljä kertaa kaksikymmentä' ja 90 quatre-vingt-dix 'neljä kertaa kaksikymmentä ja kymmenen') ja kaksi- tai kolmejärjestelmää esiintyy. - Suomessa ja sen sukukielissä voi aavistella kymmenjärjestelmän alkua vaikkapa yksi, yhden - yhdeksän ja kaksi, kahden - kahdeksan -sanapareista.

Geometrista ornamentiikkaa tavataan jo kivikauden aikaisessa keramiikassa ja tekstiileissä - näin voitaisiin ajatella geometrian syntyneen ihmisen esteettisistä tarpeista. Maanviljelyksen ja maanomistuksen kehittyminen on tuonut mukanaan tarpeen mitata maata. Geometrian merkitys rituaaleissa tulee ilmi esim. varhaisimmissa intialaisissa matemaattisissa teksteissä, Sulvasutrissa, joissa käsitellään temppelien alttarien mittasuhteiden määrittämistä, tai ns. Deloksen ongelmassa eli kuution kahdentamisongelmassa, jonka perinteinen muotoilu koski kuutionmuotoista alttarikiveä.

Matematiikasta edes jossain määrin siinä mielessä kuin sana nykyisin ymmärretään voidaan ruveta puhumaan Egyptin, Mesopotamian, Intian ja Kiinan jokilaaksojen ensimmäisten suurten muinaiskulttuurien yhteydessä (amerikkalaiset maya- ja inkakulttuurit ovat ajallisesti myöhempiä ja maantieteellisesti kokonaan erossa matematiikan kehityksestä). Karkeasti ottaen kahta - kolmea vuosituhatta ennen ajanlaskumme alkua näissä kulttuureissa kehittyneet maanviljelys, keinokastelu sekä eriytynyt yhteiskuntajärjestys ja keskitetty hallinto edellyttivät melkoisessa määrin laskemista. Nykyään on luotavissa joltisenkin selkeä kuva kahden ensiksi mainitun kulttuurin matematiikasta; länsimaisen matematiikan kehitykselle on muinaiskulttuureista merkittävin vaikutus ollut Mesopotamian matematiikalla eli babylonialaisella matematiikalla.

3.1 Egyptin matematiikkaa

Egyptiläisessä hieroglyfikirjoituksessa käytettävä numeroiden merkintätapa on peräisin viimeistään noin vuodelta 3000 eKr. Sen periaate on sama kuin roomalaisten numeroiden: kullekin kymmenen potenssille on oma symbolinsa, joka toistetaan numeroa kirjoitettaessa tarpeellisen monta kertaa. Egyptiläisistä piirtokirjoituksista on löydetty jopa miljoonan suuruusluokkaa olevia lukuja. Noin 2000 eKr. numeromerkintä kehittyi nykyisempään suuntaan, kun ns. hieraattisessa kirjoitustavassa eri numeroita alettiin merkitä omilla symboleillaan.

Egyptiläisten ajanlasku oli verrattain kehittynyt. Vuodessa oli 12 30 päivän kuukautta ja 5 tasauspäivää. Rakennustaiteen tuotteet osoittavat nekin huomattavia matemaattisia taitoja. (Pyramidit; etenkin Kheopsin pyramidin mittasuhteisiin liittyvät myöhemmät matemaattiset spekulaatiot lienevät kuitenkin perusteettomia.) Tällaisten epäsuorien todisteiden lisäksi on käytettävissä muutamia suoraan egyptiläistä matematiikanharjoitusta valaisevia lähteitä, joista tärkeimmät ovat kaksi sisällöltään matemaattista papyruskääröä, ns. Rhindin papyrus, noin vuodelta 1650 eKr., ja ns. Moskovan papyrus noin vuodelta 1850 eKr.

Rhindin eli Ahmesin papyrus sisältää 85 etupäässä aritmeettista tehtävää vastauksineen ja eräitä laskemista helpottavia taulukoita. (Ahmes oli papyruksen kirjoittaja, joka kuitenkin vain kopioi luultavasti paljon vanhempaa tekstiä,Henry Rhind, 1833-63, puolestaan skottilainen pankkiiri ja keräilijä, joka osti papyruskäärön vuonna 1858 Luxorin basaarista. Papyruskäärö on n. 5 metriä pitkä ja vajaan metrin leveä; nykyään se on esillä British Museumissa Lontoossa.)

Rhindin papyruksen tietojen perusteella egyptiläisen aritmetiikan keskeisiä piirteitä ovat additiivisuus, kahdennukseen ja osittelulakiin perustuva kerto- ja jakolasku sekä yksikkömurtolukujen käyttö. Siten esim. kertolaskussa $69 \cdot 19 =69 \cdot (16 + 2 + 1)$ laskettiin 69 + 69 = 138, 138 + 138 =276, 276+ 276 = 552, 552 + 552 = 1104 ja 1104 + 138 + 69 = 1311. Egyptiläinen kertolasku perustui siis itse asiassa luvun binaariesitykseen. (On helppo todistaa, että jokainen positiivinen kokonaisluku n on summa $\sum_{j=0}^ka_j2^j$, $a_j\in\{0,\,1\}$.)

Murtoluvuista egyptiläiset käyttivät vain lukua $\frac{2}{3}$ ja muotoa $\frac{1}{n}$ olevia lukuja eli yksikkömurtolukuja. Yksikkömurtoluvun merkkinä oli nimittäjän numerosymboli, jonka päälle piirrettiin pieni soikio tai piste. Koska $\frac{1}{n}$:n kahdentaminen tuottaa luvun $\frac{2}{n}$, joka ei yleensä ollut sallittua muotoa, oli käytössä taulukkoja $\frac{2}{n}$:n lausumiseksi muodossa $\frac{1}{a}+\frac{1}{b}+\dots+\frac{1}{c}$. Rhindin papyrus sisältää tällaisen taulukon kaikille parittomille n:ille välillä $[5,\,101]$. (Triviaalia jakoa $\frac{2}{n}=\frac{1}{n}+\frac{1}{n}$ egyptiläiset eivät jostain syystä kelpuuttaneet!) - Englantilainen J. J. Sylvester osoitti 1800 -luvulla, että jokainen murtoluku voidaan esittää äärellisenä yksikkömurtolukujen summana ja esitti erään algoritmin, jolla tämä voidaan tehdä.

Oletetaan, että $\frac{k}{q}$ voidaan kirjoittaa eri yksikkömurtojen summaksi, kun k<p. Olkoon $\frac{1}{n}$ suurin yksikkömurto, joka on pienempi kuin $\frac{p}{q}$. Silloin

$$\frac{1}{n}<\frac{p}{q}<\frac{1}{n-1}$$

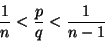
eli 0<np-q<p. Mutta

$$\frac{p}{q}=\frac{1}{n}+\frac{np-q}{nq}.$$

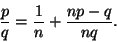
Koska $np-q<p,\, \frac{np-q}{nq}$ on eri yksikkömurtojen summa; koska $\frac{np-q}{nq}<\frac{1}{n}$, yksikään niistä ei ole $\frac{1}{n}$.

Egyptiläinen jakolasku: lasketaan esimerkiksi $\frac{19}{8}$. Se on luku, joka kerrottuna 8:lla antaa 19. Lasketaan $1\cdot 8=8$, $2\cdot 8=16$, $\frac{1}{2}\cdot 8=4$, $\frac{1}{4}\cdot 8=2$, $\frac{1}{8}\cdot 8=1$; koska 19=16+2+1, $\frac{19}{8}=2+\frac{1}{4}+\frac{1}{8}$.

Egyptiläisten kirjureiden laskennon oppikirjaksi ilmeisesti tarkoitettu Rhindin papyrus sisältää joukon tehtäviä, jotka on tulkittavissa ensimmäisen asteen yhtälöiksi x + ax = b, vieläpä siinä määrin abstraktissa muodossa, että tuntematon ei ole aivan konkreettinen määrä jotain hyödykettä, vaan abstraktimpi aha, 'kasa'. Yhtälön ratkaisu löydettiin menettelyllä, jota sittemmin on alettu kutsua nimellä positio falsi eli väärä sijoitus: tuntemattoman suuruus ''arvattiin'', laskettiin tätä arvausta vastaava ''yhtälön oikea puoli'' ja korjattiin arvausta tunnetun oikean puolen avulla.

Esim. ''Kasa ja $\frac{1}{7}$ kasaa on 19. Kuinka suuri on kasa?'' Jos kasa olisi 7, kasa ja $\frac{1}{7}$kasaa olisi 8; koska $19 =(2 + \frac{1}{4} + \frac{1}{8})\cdot 8$, tehtävän oikea vastaus $16+\frac{1}{2} + \frac{1}{8}$ saadaan, kun lasketaan $7\cdot \left(2 + \frac{1}{4} +\frac{1}{8}\right)= (1+2+4)\cdot\left(2 + \frac{1... ...}\right)+ \left(8+1+\frac{1}{2}\right)=\left(16+\frac{1}{ 2}+\frac{1}{8}\right)$.

Rhindin Papyrus sisältää vielä tarkistuksen, ts. ''todistuksen'': todellakin

$$16+\frac{1}{2}+\frac{1}{8}+\frac{1}{7}\cdot\left(16 +\frac{1}{2}+\frac{1}{8}\right)=19.$$

Egyptiläisten tuntemat algebralliset tehtävät rajoittuvat vain lineaarisiin yhtälöihin. Toisen tai korkeamman asteen yhtälöihin johtavia tehtäviä ei muinaisessa Egyptissä ilmeisesti tarvittu eikä hallittu.

Kreikkalainen historioitsija Herodotos (n. 484 - n. 425 eKr.) katsoi kreikkalaisten oppineen geometrian egyptiläisiltä, jotka olivat tarvinneet geometriaa maanmittaukseen: faarao oli alkuaan antanut ihmisille viljelysmaata, kullekin yhtä paljon, ja määrännyt maasta veron. Niilin tulvan jälkeen viljelypalstojen koko muuttui. Maanmittarit, geometrit eli köydenpingottajat, olisivat sitten määrittäneet uudet veroperusteet. Egyptiläisten varsinainen geometrinen tietämys on säilyneistä lähteistä päätellen ollut kuitenkin melko niukkaa. Erään Rhindin papyruksen tehtävän (numero 50) mukaan ympyrän ala olisi laskettu tavalla, joka vastaisi $\pi$:n arvoa $\frac{256}{81}=3,\!16 \dots$: ''Pyöreän pellon halkaisija on 9 ketiä. Mikä on sen pinta-ala? Ota halkaisijasta $\frac{1}{9}$, eli 1; jäännös on 8. Kerro 8 kertaa 8: tulos on 64. Siis ala on 64 setatia.''

Jos olisi $\pi\left(\frac{d}{2}\right)^2 = \left(\frac{8d}{9}\right)^2$, olisi $\pi=\frac{4\cdot 64}{81}=\frac{256}{81}$. Luonteva selitys tälle arviolle on verrata ympyrää neliöön, jonka sivu on d. Jos neliö jaetaan yhdeksään yhtenevään pikkuneliöön, niin näkee helposti, että ympyrän ala ei paljon poikkea alasta, joka on $\frac{7}{9}d^2=\frac{63}{81}d^2\approx\frac{64}{81}d^2=\left(\frac{8d}{9}\right)^2$. - Rhindin papyruksessa on muitakin likimääräiskaavoja: nelikulmio, jonka sivut ovat a, b, c ja d saa alakseen $\frac{a+c}{2} \cdot \frac{b+d}{2}$.

Epäsuorasti voidaan päätellä, että egyptiläisille olisi ollut tunnettua se, että yhdenmuotoisten kuvioiden alojen suhde on vastinsivujen suhteen neliö; asiaa ei tietenkään täsmällisesti formuloitu tai ''todistettu''. Mitään varsinaisia todisteita siitä, että egyptiläiset olisivat tunteneet esimerkiksi Pythagoraan lauseen sisällön, ei ole.

Ehkä yllättävin egyptiläistä geometriaa koskeva tieto löytyy Rhindin papyrusta parisataa vuotta vanhemmasta Moskovan papyruksesta: siinä lasketaan erään katkaistun neliöpohjaisen pyramidin tilavuus käyttäen selvästi oikeaa kaavaa $V=\frac{h}{3}(a^2+ab+b^2)$. (Kuviossa profiili katkaistusta pyramidista, luvut 4 ja 2 pohjan ja kannen särmänpituuksina ja 6 korkeutena sekä laskutoimitus, joka johtaa oikeaan tilavuuteen 56.) Tälle tulokselle osaa antaa arvoa, kun huomaa, että puolisuunnikkaan alan kaavan yleistykseen perustuvan virheellisen kaavan '' $V=h \cdot \frac{a^2+b^2}{2}$'' saattaa löytää vielä tällä vuosisadalla painetuista oppikirjoista. - Kaavoja sanan nykymielessä eivät egyptiläiset tosin kirjoittaneet: kaikki asiat esitettiin sanallisina toimintaohjeina ja konkreettisin numerolaskuin.

3.2 Babylonialainen matematiikka

Muinaiskulttuureista kehittynein matematiikka oli ilmeisesti Mesopotamiassa, nykyisen Irakin alueella. Tätä matemaattista kulttuuria on tapana kutsua babylonialaiseksi, vaikka aluetta vallitsivat ja matematiikkaa harjoittivat vuosituhansien aikana useat muutkin kansat sumerilaisista alkaen.

Babylonialaisen matematiikan yhdistävä ulkoinen piirre on nuolenpääkirjoitus. Koviksi poltettuja nuolenpääkirjoitusta sisältäviä savitauluja on löydetty tuhansittain, joukossa kolmisensataa sisällöltään matemaattista. Nämä taulut ajoittuvat kolmelle kaudelle, vuoden 2100 eKr. ympäristöön, vuosille 1800-1600 eKr. (Hammurabin aika) ja vuosille 600 eKr.$\,$-$\,$300 jKr.; mielenkiintoisimmat ovat keskimmäiseltä jaksolta.

Babylonialainen numeromerkintä välillä 1-59 noudatti samaa periaatetta kuin egyptiläisen hieroglyfikirjoituksenkin. Ykkösellä ja kymmenellä oli omat nuolenpäämerkkinsä, joita toistettiin tarvittava määrä. Suurempia lukuja merkittäessä käytettiin kuitenkin 60-kantaista paikkajärjestelmää. Siten esim. 60 merkittiin samalla merkillä kuin 1, 61 kahdella vierekkäisellä ykkösen merkillä jne. Käytössä oli siis 60-kantainen lukujärjestelmä eli seksagesimaalijärjestelmä. Merkintätapaa sovellettiin myös ykköstä pienempiin lukuihin. (Babylonialainen merkintätapa on yhä käytössä asteen tai tunnin jaossa minuuteiksi ja edelleen sekunneiksi.) ''Seksagesimaalipilkun'' ja nollan puuttuminen teki merkinnästä monitulkintaisen: ''22'' saattoi olla esim. $2\cdot 60 + 2 = 122$, $2\cdot 3600 + 2 = 7202$ tai $2 + \frac{2}{60}$. Nollaa tarkoittava symboli tuli osittain käyttöön muutamana ajanlaskumme alkua edeltävänä vuosisatana. Nollaa käytettiin kuitenkin vain muiden numeromerkkien välissä, ei luvun lopussa. Seksagesimaaliluvut esitetään nykyajan teksteissä niin, että eri 60:n potenssien kertoimet erotetaan pilkuilla ja ''ykkösten'' ja ''kuudeskymmenesosien'' väliä merkitään puolipisteellä; esimerkiksi $2,\,35,\,11;\,17=2\cdot 3600+35\cdot 60+11+\frac{17}{60}= 9311\,\frac{17}{60}.$

Babylonialaisten käytännöllinen numeromerkintä teki tarkat numerolaskut periaatteessa yhtä helpoiksi kuin nykyäänkin. Useat jakolaskut oli helppo palauttaa kertolaskuiksi, koska murtoluvut $\frac{1}{k}$, missä k on 60:n tekijä ovat yksinkertaisia seksagesimaalilukuja ( $\frac{1}{2}=0;30$, $\frac{1}{3}=0;20$, $\frac{1}{4}=0;15$, $\frac{1}{5}=0;12$, $\frac{1}{6}=0;10$, $\frac{1}{8}=0;7,30$ jne.)

Babylonialaiset kehittivät lisäksi taitavia algoritmisia menetelmiä. Esim. neliöjuuri $\sqrt{a}$saatettiin laskea approksimaation

$$\sqrt{a} = \sqrt{n^2+b} \approx n +\frac{b}{2n} = \frac{1}{2}\left(n + \frac{a}{n}\right)$$

avulla; tässä n² on suurin a:ta pienempi kokonaisluvun neliö. Toisessa menetelmässä lähdetään approksimaatiosta a₁; muodostetaan peräkkäin

$$b_1 = \frac{a}{a_1},\quad a_2=\frac{a_1 + b_1}{2},\quad b_2 = \frac{a}{a_2}\quad \textrm{jne.}$$

Näin saadaan muutaman askelen jälkeen sangen tarkka $\sqrt{a}$:n likiarvo. (Ei ole kuitenkaan olemassa todisteita siitä, että babylonialaiset olisivat ajatelleet prosessiin sisältyvää päättymättömän suppenevan lukujonon ideaa.)

Jo noin 4000 vuotta vanhat babylonialaiset tekstit osoittavat, että - toisin kuin egyptiläiset - babylonialaiset tunsivat toisen asteen yhtälön ratkaisumenetelmän. Se ei kylläkään esiinny yleispätevänä ratkaisukaavana, vaan numeeristen esimerkkien muodossa, mutta esimerkit ovat selvästi tunnistettavissa yleisen metodin opetusvälineiksi. Seuraavassa käytetään 60-järjestelmän numeroita siten, että paikkaerotin on pilkku ja desimaalierotin puolipiste. Eräässä tulkitussa savitaulussa kysytään neliön sivua, jos ala vähennettynä sivulla on 14,30 (eli $14\cdot 60+30=870$). Tehtävän ratkaisu on seuraava:

Ota puolet yhdestä, eli 0;30 ja kerro 0;30 0;30:llä, joka on 0;15; lisää tämä 14,30:een, joka on 14,30;15. Tämä on 29;30:n neliö. Lisää 0;30 29;30:een, ja tulos on 30 eli neliön sivu.

Selvästi kyseessä on yhtälön x²-px=q ratkaisukaavan

$$x=\sqrt{\left(\frac{p}{2}\right)^2+q}+\frac{p}{2}$$

käyttö, kun p=1 ja q=870. Huomattakoon myös, että alan ja sivunpituuden dimensioita ei oteta huomioon, vaan kummankin lukuarvot esiintyvät samassa yhtälössä. - Koska negatiiviset luvut eivät olleet käytössä, antiikin aikana toisen asteen yhtälöt saattoivat olla vain muotoa x²=px+q, x²+px=q ja x²+q=px, missä p ja q ovat positiivisia.

Babylonialaista yhtälönratkaisua vielä, nykysymbolein ja merkinnöin: määritä x, jolle x²+6x=16. Aseta y=x+6. Ratkaistavana on yhtälöryhmä

$$\left\{\begin{array}{rcl} y-x & = & 6 \\ xy & = & 16. \\ \end{array} \right.$$

Jos y=a+3 ja x=a-3, niin jälkimmäinen yhtälö on a²-9=16, josta a=5, x=2. - Tyyppiä 7x²+6x=1 olevaa yhtälöä ei sievennetty nykytapaan jakamalla x²:n kertoimella, vaan kertomalla koko yhtälö 7:llä: yhtälöksi saadaan (7x)²+6(7x)=7 eli y²+6y=7, josta y=1, $x=\frac{1}{7}$.

Babylonialaisessa matematiikassa esiintyy jopa korkeamman asteen polynomiyhtälöihin johtavia tehtäviä; sellaisia ratkaistiin erikoistapauksissa käyttämällä apuna mm. n³ +n²-taulukkoja. Taulukoiden avulla ratkaistiin myös korkolaskujen yhteydessä vastaan tulevia eksponenttiyhtälöitä.

Babylonialaisten matematiikka oli (kuten muidenkin muinaiskulttuurien matematiikka) voittopuolisesti algebrallis-algoritmista. Geometriasta lienee tunnettu ainakin Pythagoraan lause. Eräässä savitauluista puretussa tehtävässä kysytään, miten kauas 30 yksikköä pitkän sauvan alapää joutuu pystysuorasta seinästä, kun yläpäätä lasketaan 6 yksikköä. Pythagoraan lauseen mukainen ratkaisu on $\sqrt{30^2-(30-6)^2}=\sqrt{324}=18$.

Omalaatuisin todiste Pythagoraan lauseen tunnettuudesta Babyloniassa on luonteeltaan aritmeettinen, nimittäin paljon tutkittu ja monien selitysten kohteena ollut savitaulu nimeltään Plimpton 322. Siinä on seksagesimaalilukuja

$$\begin{array}{lll} 1;59,0,15 & 1,59 & 2,49 \\ 1;56,56,58,14,... ...,16 & 3,31,49 & 5,9,1 \\ \dots & \dots & \dots \\ \end{array}$$

Taulua tutkittaessa on paljastunut, että luvut ovat lukuja $(\frac{c^2}{ b^2},\,a,\,c)$, missä a²+b²=c² ja kolmikot $(a,\, b,\,c)$, ovat ns. Pythagoraan lukuja. Nämä saadaan kaavoista a=p²-q², b=2pq, c=p²+q². Plimpton-taulun luvut ovat alku taulukolle, jossa ovat kaikki tällaiset, arvoilla p<60 ja $1<\frac{p}{q}<1+\sqrt{2}$ saatavat luvut järjestettynä suureen $\frac{p^2+q^2}{2pq}$ mukaan.

Ympyrän kehän ja halkaisijan suhteelle annettiin tavallisimmin arvo 3, mutta eräistä teksteistä löytyy parempi likiarvo $3\frac{1}{8}$(säännöllisen kuusikulmion piirin suhde ympäri piirretyn ympyrän kehään on 0;57,36.)

Myös Raamatussa esiintyy ''$\pi$:n arvo 3'', kuten Ensimmäinen Kuningasten kirja (7:23) kertoo:

Hän [Salomo] teki myös meren, valetun, kymmentä kyynärää leveän reunasta reunaan, ympäriinsä pyöreän - - ja kolmenkymmenen kyynärän pituinen mittanuora ulottui sen ympäri.

Katkaistun pyramidin tilavuudelle löytyy babylonialaisista savitauluista sekä vääriä että oikeita laskutapoja. Yleisiä matemaattisia teoreemoja eivät babylonialaiset sen paremmin kuin egyptiläisetkään tietojemme mukaan tunteneet eivätkä todistaneet: heidän matematiikkansa oli (kuten ''insinöörimatematiikka'' nykypäivinäkin) kokoelma toimintaohjeita, ei niiden perusteluja.

Alkuun - Etusivu - Edellinen - Seuraava