pdf  Solmu 2/2023

---

Solmun 3/2022 tehtävien 11–20 ratkaisut

11. Säännöllisen 12-kulmion \(ABCDEFGHIJKL\) sisään sivuille \(AB\) ja \(GH\) piirretään neliöt \(ABPQ\) ja \(GHRS\) kuten alla olevassa kuvassa on esitetty. Osoita, että \(PQ\) ja \(RS\) ovat säännöllisen 6-kulmion vastakkaiset sivut.

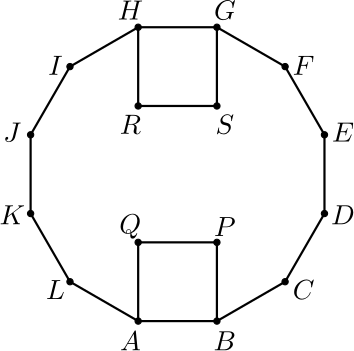
Ratkaisu. Säännöllisen 12-kulmion kulmien summa on

\[(12-2)\cdot 180^\circ=10\cdot 180^\circ=1800^\circ,\]

joten jokaisen kulman suuruus on

\[\frac{1800^\circ}{12}=150^\circ.\]

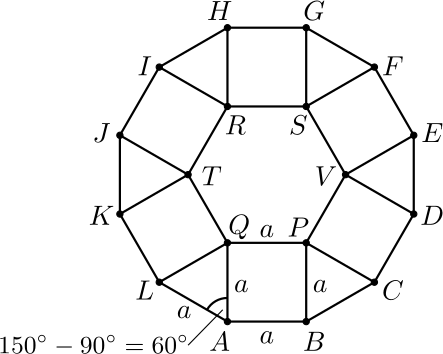
Kolmio \(LAQ\) on tasasivuinen, koska \(LA=LQ\) ja \(\angle LAQ=150^\circ-90^\circ=60^\circ\). Näin ollen \(\angle KLQ=150^\circ-60^\circ=90^\circ\), joten voidaan muodostaa neliö \(KLQT\) (ks. seuraava kuva, johon \(12\)-kulmion sisälle on lisätty piste \(T\)). Nyt

\[\angle PQT=360^\circ-90^\circ-60^\circ-90^\circ=120^\circ\]

ja \(PQ=QT\). Vastaavasti saadaan \(TR=RS\) ja \(\angle QTR=120^\circ\).

Symmetrisesti \(12\)-kulmion sisälle voidaan lisätä piste \(V\). Tällöin muodostuu 6-kulmio \(QPVSRT\), jonka sivut ovat yhtä pitkiä ja jokaisen kulman suuruus on \(120^\circ\). Näin ollen \(PQ\) ja \(RS\) ovat säännöllisen 6-kulmion vastakkaiset sivut.

12. Kahteen astiaan mahtuu kumpaankin 2 litraa nestettä. Ensimmäisessä astiassa on 2 litraa 100-prosenttista appelsiinimehua ja toisessa astiassa on 1 litra vettä. Puolet ensimmäisen astian appelsiinimehusta kaadetaan toiseen astiaan, jossa on vettä, ja neste sekoitetaan. Sekoitetusta nesteestä kaadetaan 1 litra takaisin ensimmäiseen astiaan. Menettely toistetaan: Ensimmäisestä astiasta kaadetaan 1 litra toiseen astiaan, neste sekoitetaan ja 1 litra sekoitettua nestettä kaadetaan takaisin ensimmäiseen astiaan. Kuinka monta prosenttia kummankin astian nesteestä on appelsiinimehua?

Ratkaisu. Ensimmäisen kaadon jälkeen ensimmäisessä astiassa on jäljellä 1 litra appelsiinimehua ja toisessa astiassa on 1 litra appelsiinimehua ja 1 litra vettä. Toisessa astiassa olevassa sekoitetussa nesteessä, jota on \(2\) litraa, on näin ollen puolet appelsiinimehua ja puolet vettä. Kun nyt toisesta astiasta kaadetaan 1 litra nestettä ensimmäiseen astiaan, tulee ensimmäiseen astiaan \(0{,}5\) litraa appelsiinimehua ja \(0{,}5\) litraa vettä siellä jo olevan \(1\) litran appelsiinimehun lisäksi. Tällöin sekoituksen jälkeen ensimmäisessä astiassa on \(1+0{,}5=1{,}5\) litraa appelsiinimehua ja \(0{,}5\) litraa vettä. Toisessa astiassa on \(0{,}5\) litraa appelsiinimehua ja \(0{,}5\) litraa vettä.

Tämän jälkeen menettely toistetaan. Toisessa kaadossa ensimmäisestä astiasta toiseen astiaan siirtyy \(0{,}75\) litraa appelsiinimehua ja \(0{,}25\) litraa vettä ja saman verran molempia jää ensimmäiseen astiaan. Tällöin toisessa astiassa on \(0{,}75+0{,}5=1{,}25\) litraa appelsiinimehua ja \(0{,}25+0{,}5=0{,}75\) litraa vettä. Kun sekoituksen jälkeen tästä kaadetaan puolet takaisin ensimmäiseen astiaan, niin toisesta astiasta siirtyy ensimmäiseen astiaan \(1{,}25:2=0{,}625\) litraa appelsiinimehua ja \(0{,}75:2=0{,}375\) litraa vettä. Saman verran eli \(0{,}625\) litraa appelsiinimehua ja \(0{,}375\) litraa vettä jää toiseen astiaan. Nyt ensimmäisessä astiassa on \(0{,}75+0{,}625=1{,}375\) litraa appelsiinimehua ja \(0{,}25+0{,}375=0{,}625\) litraa vettä.

Näin ollen ensimmäisen astian nesteestä appelsiinimehua on

\[\frac{1{,}375}{1{,}375+0{,}625}\cdot 100\ \%=\frac{1{,}375}{2}\cdot 100\ \%=68{,}75\ \%\]

ja toisen astian nesteestä appelsiinimehua on

\[\frac{0{,}625}{0{,}6255+0{,}375}\cdot 100\ \%=\frac{0{,}625}{1}\cdot 100\ \%=62{,}5\ \%.\]

13. Kolme vihkoa ja kaksi lyijykynää maksavat kirjakaupassa yhteensä 11,10 euroa. Viisi vihkoa ja neljä lyijykynää maksavat yhteensä 20,10 euroa. Mitä ovat yhden vihkon ja yhden lyijykynän hinnat?

Ratkaisu. Merkitään yhden vihkon hintaa \(V\):llä ja yhden lyijykynän hintaa \(K\):lla. Saadaan yhtälöpari

\[\begin{cases} 3V+2K=11{,}10\ \text{€},\\ 5V+4K=20{,}10\ \text{€}. \end{cases}\]

Kertomalla ensimmäinen yhtälö puolittain luvulla \(-2\) saadaan yhtälöpari

\[\begin{cases} -6V-4K=-22{,}20\ \text{€},\\ 5V+4K=20{,}10\ \text{€}, \end{cases}\]

josta laskemalla yhtälöt yhteen saadaan

\[-V=-2{,}10\ \text{€\quad eli\quad}V=2{,}10\ \text{€}.\]

Nyt alkuperäisen yhtälöparin ensimmäisestä yhtälöstä saadaan

\[2K=11{,}10\ \text{€}-3V=11{,}10\ \text{€}-3\cdot 2{,}10\ \text{€} =4{,}80\ \text{€},\]

joten \(K=2{,}40\ \text{€}\). Saatiin siis, että yhden vihkon hinta on \(2{,}10\) € ja yhden lyijykynän hinta on \(2{,}40\) €.

14. Luvuista \(1, 2, 3, 4, 5, 6, 7, 8\) valitaan kolme eri lukua ja lasketaan ne yhteen. Tämä tehdään kaikilla mahdollisilla kolmen luvun valinnoilla. Osa summista on parillisia ja osa on parittomia. Kumpi tulos on yleisempi, parillinen vai pariton summa?

Ratkaisu. Sekä parillisia että parittomia lukuja on neljä. Kolmen luvun summa on parillinen, jos kaikki kolme lukua ovat parillisia tai luvuista yksi on parillinen ja kaksi ovat parittomia. Kaikki kolme lukua ovat parillisia neljällä eri tavalla: \((2,4,6)\), \((2,4,8)\), \((2,6,8)\) ja \((4,6,8)\). Kaksi paritonta lukua voidaan valita kuudella eri tavalla: \((1,3)\), \((1,5)\), \((1,7)\), \((3,5)\), \((3,7)\) ja \((5,7)\), ja parillisia lukuja on neljä. Näin ollen tapoja valita kolme lukua niin, että luvuista yksi on parillinen ja kaksi ovat parittomia, on \(4\cdot 6=24\). Yhteensä tapoja valita kolme lukua niin, että lukujen summa on parillinen, on siis \(4+24=28\).

Kolmen luvun summa on pariton, jos kaikki kolme lukua ovat parittomia tai luvuista yksi on pariton ja kaksi ovat parillisia. Kaikki kolme lukua ovat parittomia neljällä eri tavalla: \((1,3,5)\), \((1,3,7)\), \((1,5,7)\) ja \((3,5,7)\). Kaksi parillista lukua voidaan valita kuudella eri tavalla: \((2,4)\), \((2,6)\), \((2,8)\), \((4,6)\), \((4,8)\) ja \((6,8)\), ja parittomia lukuja on neljä. Näin ollen tapoja valita kolme lukua niin, että luvuista yksi on pariton ja kaksi ovat parillisia, on \(4\cdot 6=24\). Yhteensä tapoja valita kolme lukua niin, että lukujen summa on pariton, on siis \(4+24=28\).

Näin ollen parillisia ja parittomia summia on yhtä monta.

15. Shakkiturnauksessa oli viisi osallistujaa. Jokainen osallistuja pelasi kerran jokaista muuta osallistujaa vastaan. Voitosta sai yhden pisteen, tasapelistä \(0{,}5\) pistettä ja häviöstä 0 pistettä. Turnauksen lopuksi havaittiin, että (i) turnauksen voittanut pelaaja ei pelannut yhtään tasapeliä, (ii) toiseksi tullut pelaaja ei hävinnyt yhtään peliä, (iii) kaikilla pelaajilla oli eri määrä pisteitä. Kuinka monta pistettä pelaajat saivat?

Ratkaisu. Koska pelaajia oli viisi, niin jokainen pelasi neljä peliä ja kaiken kaikkiaan pelejä pelattiin

\[\binom{5}{2}=\frac{5!}{2!\,3!}=10.\]

Näin ollen turnauksessa jaettiin yhteensä 10 pistettä. Ehtojen (i) ja (ii) perusteella turnauksen voittanut pelaaja hävisi toiseksi tulleelle pelaajalle. Näin ollen voittaja sai korkeintaan \(3\) pistettä. Koska hän ei pelannut yhtään tasapeliä, niin hänen pistemääränsä on kokonaisluku. \(1\) tai \(0\) eivät ole mahdollisia pistemääriä voittajalle, koska ehto (iii) ei voisi tällöin toteutua. Jos voittaja olisi saanut \(2\) pistettä, niin muut pelaajat olisivat saaneet turnauksessa yhteensä \(10-2=8\) pistettä. Tämä ei ole mahdollista, koska ehdon (iii) perusteella muiden pelaajien pistemäärät olisivat \(1{,}5\), \(1\), \(0{,}5\) ja \(0\), eli yhteensä \(3\) pistettä. Näin ollen voittaja sai \(3\) pistettä ja muut pelaajat saivat yhteensä \(10-3=7\) pistettä.

Muiden pelaajien kuin voittajan oli mahdollista saada yhteensä \(7\) pistettä vain siten, että he saivat mahdollisimman suuret pistemäärät, eli \(2{,}5\), \(2\), \(1{,}5\) ja \(1\) pistettä. Näin ollen pelaajien pistemäärät olivat paremmuusjärjestyksessä \(3\), \(2{,}5\), \(2\), \(1{,}5\) ja \(1\).

Tarkistetaan vielä, että tämä on mahdollinen tulos. Voittaja hävisi toiseksi tulleelle pelaajalle, mutta voitti kaikki muut kolme pelaajaa, joten hänen pistemääränsä oli \(3\cdot 1+0=3\). Toiseksi tullut pelaaja voitti ensimmäiseksi tulleen ja pelasi tasapelin muiden pelaajien kanssa, joten hänen pistemääränsä oli \(1+3\cdot 0{,}5=2{,}5\). Kolmanneksi tullut pelaaja hävisi voittajalle, pelasi tasapelin toiseksi ja neljänneksi tulleiden pelaajien kanssa ja voitti viidenneksi tulleen pelaajan, joten hänen pistemääränsä oli \(0+2\cdot 0{,}5+1=2\). Neljänneksi tullut pelaaja pelaaja hävisi voittajalle ja pelasi tasapelin muiden pelaajien kanssa, joten hänen pistemääränsä oli \(0+3\cdot 0{,}5=1{,}5\). Viidenneksi eli viimeiseksi tullut pelaaja pelasi tasapelin toiseksi ja neljänneksi tulleiden pelaajien kanssa ja hävisi muille, joten hänen pistemääränsä oli \(2\cdot 0+2\cdot 0{,}5=1\).

16. Positiivisen desimaaliluvun desimaalipilkku siirretään neljä paikkaa oikealle. Saatu luku on alkuperäisen luvun käänteisluku kerrottuna neljällä. Mikä on alkuperäinen luku?

Ratkaisu. Merkitään kysyttyä lukua \(n\):llä. Ehtojen perusteella

\[10\,000n=\frac{4}{n},\]

joten

\[n^2=\frac{4}{10\,000},\]

ja edelleen, koska luku \(n\) on positiivinen, saadaan

\[n=\sqrt{\frac{4}{10\,000}}=\frac{2}{100}=0{,}02.\]

17. Ratkaise yhtälöryhmä

\[\begin{cases} a+d=9,\\ ad+b=8,\\ bd+c=74,\\ cd=18, \end{cases}\]

kun \(a,b,c,d\) ovat kokonaislukuja.

Ratkaisu. Viimeisen yhtälön perusteella \(c\) ja \(d\) ovat samanmerkkiset, koska niiden tulo on positiivinen. Jos \(c\) ja \(d\) ovat negatiivisia, niin kolmannen yhtälön perusteella myös

\[b=\frac{74-c}{d}\]

on negatiivinen positiivisen luvun ja negatiivisen luvun osamääränä. Tällöin toisen yhtälön perusteella myös

\[a=\frac{8-b}{d}\]

on negatiivinen positiivisen luvun ja negatiivisen luvun osamääränä. Nyt \(a+d\) on kahden negatiivisen luvun summana negatiivinen, mikä on ristiriita ensimmäisen yhtälön kanssa.

Näin ollen \(c\) ja \(d\) ovat kummatkin positiivisia kokonaislukuja ja viimeisen yhtälön perusteella luvun \(18\) tekijöitä, joita ovat \(1\), \(2\), \(3\), \(6\), \(9\) ja \(18\).

Tarkastellaan kaikki mahdolliset tapaukset erikseen. Tapaustarkastelun alkuasetelma perustuu viimeiseen yhtälöön \(cd=18\).

Tapaus 1: Luvut \(c\) ja \(d\) eivät voi olla \(3\) tai \(6\), koska silloin viimeisen yhtälön perusteella jompi kumpi luvuista \(c\) ja \(d\) on \(3\) ja toinen on \(6\). Tällöin \(bd+c\) on jaollinen kolmella, mutta kolmas yhtälö \(bd+c=74\) ei voi toteutua, koska luku \(74\) ei ole kolmella jaollinen.

Tapaus 2: Jos \(c=1\), niin \(d=18\). Nämä eivät kelpaa, sillä kolmannen yhtälön perusteella

\[b=\frac{74-1}{18}=\frac{73}{18}=4\frac{1}{18},\]

joka ei ole kokonaisluku.

Tapaus 3: Jos \(c=2\), niin \(d=9\). Tällöin kolmannen yhtälön perusteella

\[b=\frac{74-2}{9}=\frac{72}{9}=8\]

ja toisesta yhtälöstä saadaan

\[a=\frac{8-8}{9}=\frac{0}{9}=0.\]

Lisäksi ensimmäinen yhtälö

\[a+d=0+9=9\]

toteutuu.

Tapaus 4: Jos \(c=9\), niin \(d=2\). Nämä eivät kelpaa, sillä kolmannen yhtälön perusteella

\[b=\frac{74-9}{2}=\frac{65}{2}=32\frac{1}{2},\]

joka ei ole kokonaisluku.

Tapaus 5: Jos \(c=18\), niin \(d=1\). Nämä eivät kelpaa, sillä vaikka kolmannesta yhtälöstä

\[b=\frac{74-18}{1}=\frac{56}{1}=56\]

ja toisesta yhtälöstä

\[a=\frac{8-56}{1}=-48\]

saadaan kokonaisluvut, niin ensimmäinen yhtälö ei toteudu:

\[a+d=-48+1=-47\neq 9.\]

Ainoa kokonaislukuratkaisu yhtälöryhmälle saatiin tapauksessa 3:

\[\begin{cases} a=0,\\ b=8,\\ c=2,\\ d=9. \end{cases}\]

18. Kirppu on lukusuoralla kohdassa 0 valmiina hyppäämään. Jokaisella hypyllään kirppu liikkuu 3 tai 5 yksikköä joko vasemmalle tai oikealle. Kirpun tavoite on käydä jokaisen luvun \(1,\ldots,20\) kohdalla. Etsi jono, jossa on enintään 22 hyppyä ja joka toteuttaa vaaditun tavoitteen.

Ratkaisu. Esimerkiksi jono \(0,3,6,11,8,5,10,7,12,17,\) \(20,15,18,13,16,19,14,9,4,1,4,7,2\) täyttää vaatimukset.

19. Valitaan kuutiosta satunnaisesti neljä kärkeä. Kaikki mahdolliset neljän kärjen valinnat ovat yhtä todennäköisiä. Mikä on todennäköisyys, että valitut kärjet muodostavat tetraedrin? Entä mikä on todennäköisyys, että valitut kärjet muodostavat säännöllisen tetraedrin?

Ratkaisu. Kuutiossa on kahdeksan ja tetraedrissa on neljä kärkeä. Näin ollen tetraedrin kärjet voidaan valita kuution kärjistä

\[\binom{8}{4}=\frac{8!}{4!\,4!}=\frac{8\cdot 7\cdot 6\cdot 5}{4\cdot 3\cdot 2\cdot 1}=70\]

eri tavalla.

Jos valitut neljä kärkeä sijaitsevat samassa tasossa, niin ne eivät muodosta tetraedriä. Sellainen kärkinelikko muodostuu, kun kaikki valitut kärjet ovat kuution saman tahkon kärkiä. Tällaisia kärkinelikoita on yhteensä kuusi, joka on kuution tahkojen lukumäärä. Valitut neljä kärkeä sijaitsevat samassa tasossa myös silloin, kun kärkien kautta kulkeva taso on kuution halkaisija (ts. kuution kaksi vastakkaista särmää sijaitsevat kuution halkaisevassa tasossa). Tällaisiakin nelikoita on yhteensä kuusi. Näin ollen 70 erilaisesta kärkinelikosta \(6+6=12\) on sellaisia, jotka eivät muodosta tetraedria. Saadaan siis, että kärkinelikoista \(70-12=58\) on sellaisia, jotka muodostavat tetraedrin. Neljän kärjen satunnaisella valinnalla on tetraedrin muodostumisen todennäköisyys näin ollen

\[\frac{58}{70}=\frac{29}{35}\approx 0{,}83.\]

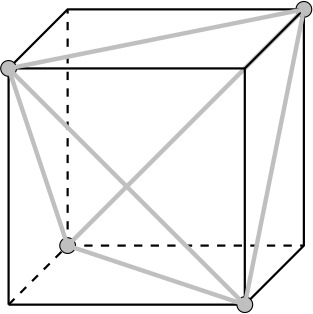
Säännöllinen tetraedri on mahdollista muodostaa kahdella eri tavalla. Valitaan ensin mikä tahansa kärki. Sen jälkeen valitaan jokaiselta kuution tahkolta, jonka kärkenä ensin valittu kärki on, tahkoneliön vastakkainen kärki. Näin valitut kolme kärkeä muodostavat yhdessä ensin valitun kärjen kanssa säännöllisen teraedrin (ks. alla oleva kuva, jossa tetraedrin kärjet ja särmät ovat vaaleanharmaita). Tetraedri on säännöllinen, koska sen kaikki särmät ovat kuution tahkojen halkaisijoita kärjestä vastakkaiseen kärkeen ja näin ollen ne ovat yhtä pitkiä.

Toinen säännöllinen tetraedri muodostuu valitsemalla kärjiksi loput kuution neljä kärkeä, jotka jäivät valitsematta ensimmäisen tetraedrin kärjiksi. Neljän kärjen satunnaisella valinnalla on säännöllisen tetraedrin muodostumisen todennäköisyys näin ollen

\[\frac{2}{70}=\frac{1}{35}\approx 0{,}03.\]

20. Neliön sivun pituus on \(6\) cm. Jokainen sivu on ympyrän halkaisija kuten alla olevassa kuvassa on esitetty. Ison ympyrän keskipiste on neliön keskipisteessä ja sen säde on neliön sivun pituinen. Laske alueiden I, II ja III pinta-alat.

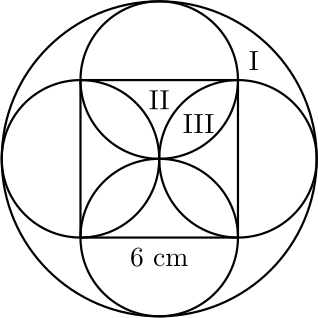
Ratkaisu. Ison ympyrän säde on 6 cm ja pienen ympyrän säde on 3 cm. Ison ympyrän pinta-ala on näin ollen \(36\pi\) cm\(^2\) ja pienen ympyrän pinta-ala on \(9\pi\) cm\(^2\). Neliön pinta-ala on \(36\) cm\(^2\).

Neljä pientä puoliympyrää peittävät neliön niin, että alueen III muotoiset neljä aluetta peittyvät kukin kaksi kertaa. Näin ollen alueen III pinta-ala on

\[\frac{4\cdot 0{,}5\cdot 9\pi - 36}{4}\ \text{cm}^2=(4{,}5\pi-9)\, \text{cm}^2 \approx 5{,}14\ \text{cm}^2.\]

Pienten ympyröiden yhteenlaskettu pinta-ala on

\[4\cdot 9\pi\ \text{cm}^2=36\pi\ \text{cm}^2,\]

joka on sama kuin ison ympyrän pinta-ala. Näin ollen pienten ympyröiden päällekkäiset alueen III muotoiset neljä aluetta ovat pinta-alaltaan täsmälleen yhtä suuret kuin ison ympyrän sisälle pienten ympyröiden ulkopuolelle jäävät alueen I muotoiset neljä aluetta. Saadaan siis, että alueen I pinta-ala on sama kuin alueen III pinta-ala, eli \((4{,}5\pi-9)\, \text{cm}^2 \approx 5{,}14\ \text{cm}^2\).

Alueen II pinta-ala saadaan laskettua esimerkiksi niin, että neliön pinta-alasta vähennetään kahden pienen puoliympyrän pinta-ala ja saatu pinta-ala jaetaan kahdella. Alueen II pinta-ala on siis

\[\frac{36 - 2\cdot 0{,}5\cdot 9\pi}{2}\ \text{cm}^2=(18-4{,}5\pi)\, \text{cm}^2 \approx 3{,}86\ \text{cm}^2.\]

Solmun 3/2022 tehtävien 1–10 ratkaisut julkaistiin edellisessä numerossa.

Lähde: KöMaL
Käännös ja sovitus suomeksi: Mika Koskenoja