Oppituntisuunnitelmia luvuista, yhtälöistä ja ongelmanratkaisusta
Neea Palojärvi
Tutkijatohtori ja yksi Integraalipäivien järjestäjistä, Helsingin yliopisto
Onko hakusessa valmiita oppituntisuunnitelmia matematiikan tunneille tai matematiikkakerhoon? Integraalipäivien kotisivuilta löytyy opettajien, tutkijoiden ja opiskelijoiden yhdessä tekemiä oppituntisuunnitelmia1 alakoulusta yliopistoon. Pääpaino on yläkoulun ja lukion oppitunneissa. Lähes kaikki suunnitelmat on julkaistu Nimeä 4.0 Kansainvälinen -lisenssillä, eli niitä saa muun muassa jakaa ja muunnella, kunhan muistaa muun muassa nimetä lähteen (ks. lisätietoa lisenssistä viitteestä [3].

Alla on esitelty kolme suunnitelmaa. Kaikki esiteltävät oppitunnit sisältävät yläkouluun suunnatun kokonaisuuden, kaksi viimeistä on suunnattu myös lukioon ja viimeinen edellisten lisäksi ammatilliseen koulutukseen.
Murtoluvuista ja äärettömästä
Merimies on kuollut ja perinnöksi on jäänyt aarrearkkuja (ks. [7]. Kun perintö yritetään jakaa vainajan toiveiden mukaisesti, se ei tunnu onnistuvan. Miten aarrearkut onnistutaan jakamaan testamentin määräämällä tavalla, kun mukaan lisätään yksi aarrearkku —ja lisätty arkku voidaan jaon jälkeen palauttaa takaisin? Entä kuinka suuri on mahdollisimman suuri lukua \(1\) pienempi reaaliluku? Tai kuinka “paljon” kokonaislukuja on rationaalilukuihin verrattuna?

Näitä kysymyksiä pohditaan oppitunnilla “Kokonaisluvut ja murtoluvut” [2]. Oppitunti (\(45\) min) on suunnattu peruskoulun 7. luokan oppilaille, oppitunnille tai matematiikkakerhoon. Tavoitteena on muun muassa, että oppilas ymmärtää oppitunnin jälkeen paremmin rationaalilukuja.
Vinkki: Kaipaisitko vielä haastavampaa materiaalia lukujen ominaisuuksista yläkoululaisten ylöspäin eriyttämiseen tai lukioon? Tutustu oppituntisuunnitelmaan “Ketjumurtoluvut” [4].
Yhtälöitä ja yhtälöryhmiä
Toukolan tehtaalla kuuluu kummia: Raaka-aineiden kulutus on lähtenyt käsistä. Onko tehtaan tuotanto vain kasvanut vai onko yövartija käyttänyt aineksia salaa betoniporsaiden valmistukseen? Oppitunnissa “Tonttutehdas lineaariyhtälöiden ratkaisussa” [5] selvitetään mysteeri lineaaristen yhtälöryhmän ratkaisemisen avulla!
\[\begin{cases} x+y+2z=130 \\ x+2y+z=150 \\ 2x+y+z=140 \end{cases}\]
Tämän yhtälöryhmän avulla selvitetään, onko yövartija ollut luvattomissa töissä betoniporsaiden parissa.
Lukion (pitkä tai lyhyt matematiikka tai matematiikkakerho, ainakin \(75\) min) oppitunnin tavoitteena on, että oppilas motivoituu lineaaristen yhtälöryhmien ratkaisemisen opiskeluun, näkee ne tuoreesta näkökulmasta, oppii niiden avulla ongelmanratkaisua, selventää käsitystään yhtälönratkaisusta ja kehittää valmiutta yleisten yhtälöryhmien ratkaisumenetelmien opiskeluun. Oppitunti koostuu edellä mainitusta motivoinnista, yhtälöryhmien ratkaisumenetelmien esittelystä esimerkkeineen ja harjoitustehtävistä.
Oppituntisuunnitelma sisältää myös yksinkertaisemman yläkouluun suunnatun version, jossa tutkitaan kahden yhtälön yhtälöpareja. Motivointina toimii yövartijan toimien sijaan kysymys, kuinka paljon puutarhatonttuja ja -pukkeja annetuista aineksista voidaan valmistaa.
Vinkki: Mikäli yhtälönratkaisusta kaipaa ylöspäin eriyttävää materiaalia tai kerhomateriaalia oppilaille, joille \(2\times2\)-matriisien kertolasku ja transponointi ovat jo tuttua, niin kannattaa tutustua oppituntisuunnitelmaan “Matriisit ja antennit” [6].
Toiminnallisia pisteitä ongelmanratkaisusta
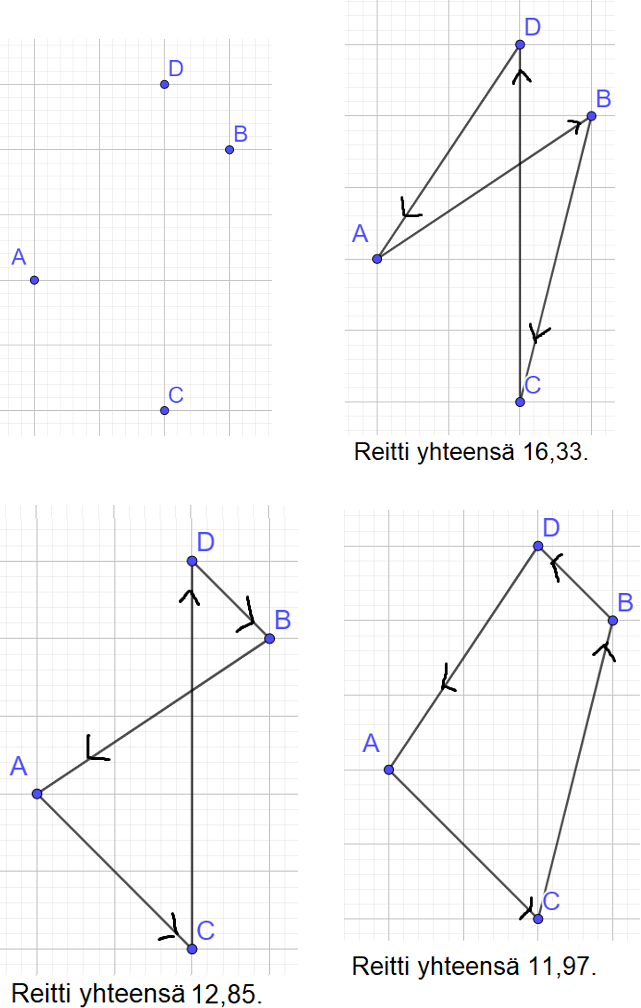
Onko lukuvuoden loppuun hakusessa asteen verran toiminnallisempi matematiikan oppitunti? Oppituntisuunnitelmassa “Vaikeat ongelmat, riittävän hyvän ratkaisun etsiminen, löytäminen ja hyväksyminen” on ratkaisu tähän!
Oppitunti (n. \(75\) min) koostuu opettajan alustuksesta aiheeseen, neljästä kiertopisteestä ja lopun yhteenvedosta. Oppimistavoitteena on muun muassa hahmottaa ongelmien ratkaisuavaruuksien suuruutta, tutkia strategioita ongelmien ratkaisemiseksi ja kehittää ongelmanratkaisutaitoja. Se on suunnattu yläkouluun, lukioon tai ammatilliseen oppilaitokseen, käsittelyn syvällisyys tapahtuu kohderyhmän mukaan. Materiaalissa on myös mukana diat alun johdantoon, pisteiden esittelyyn ja loppukoosteeseen.
Vinkki: Olisiko hakusessa toiminnallisia elementtejä ja oppiainerajat ylittäviä kokonaisuuksia sisältävä oppitunti? Tutustu oppituntiin “Tartuntatautien matematiikkaa” [1].
Eikö vielä tärpännyt?
Eivätkö edelliset kuitenkaan olleet aivan sitä, mitä haettiin? Saattaisiko jostain muusta Integraalipäivillä kehitellystä oppituntisuunnitelmasta olla apua? Tarjolla on esimerkiksi useampia oppiainerajat ylittäviä oppitunteja sekä oppituntisuunnitelmia matematiikkakerhoon.
Viitteet
[1] Viivi Aaltonen, Peppiina Laakso, Helena Konttinen & Mats Gyllenberg: “Tartuntatautien matematiikkaa”, laadittu keväällä 2021, luettu 27.2.2023,
https://blogs.helsinki.fi/integraalipaivat/files/2022/02/Tartuntatautien-matematiikkaa.pdf
[2] Henri Anttila, Harriet Beaver, Leila Kokko & Riikka-Liisa Vaara: “Oppitunnin suunnitelma: Kokonaisluvut ja murtoluvut”, laadittu keväällä 2022, luettu 27.2.2023,
https://blogs.helsinki.fi/integraalipaivat/files/2022/08/kokonaisluvut_murtoluvut.pdf
[3] Creative Commons: “Nimeä 4.0 Kansainvälinen (CC BY 4.0)”, luettu 27.2.2023,
https://creativecommons.org/licenses/by/4.0/deed.fi
[4] Anne-Maria Ernvall-Hytönen, Marko Hiltunen, Olga Kaliuta, Janina Kivimäki, Sari Pirkkalainen, Mikko Salminen & Erika Väänänen: “Ketjumurtoluvut”, laadittu keväällä 2023, luettu 27.2.2023,
https://blogs.helsinki.fi/integraalipaivat/files/2023/02/ketjumurtoluvut.pdf
[5] Jimmy Finnholm, Lena Gers, Piia Haapsaari, Ossi Mauno, Alexander Oiling & Roope Vehkalahti: “Tonttutehdas lineaariyhtälöiden ratkaisussa”, laadittu syksyllä 2022, luettu 27.2.2023,
https://blogs.helsinki.fi/integraalipaivat/files/2023/01/tonttutehdas.pdf
[6] Mats Gyllenberg, Sakari Salonen, Annina Jurvanen, Eeli Tamminen, Pirjo-Ritta Elo & Kerkko Luosto: “Matriisit ja antennit”, laadittu syksyllä 2022, luettu 27.2.2023,
https://blogs.helsinki.fi/integraalipaivat/files/2022/12/matriisit_ja_antennit.pdf
[7] Neea Palojärvi: “Aarrearkkujen jakoa”, Solmu 1/2018, 5–6,
https://matematiikkalehtisolmu.fi/2018/1/merimies.pdf
[8] Tarja Ylivuori, Aleksi Karhu, Mats Gyllenberg & Havu Miikonen: “Vaikeat ongelmat, riittävän hyvän ratkaisun etsiminen, löytäminen ja hyväksyminen”, laadittu syksyllä 2021, luettu 27.2.2023,
https://blogs.helsinki.fi/integraalipaivat/oppituntisuunnitelmia/vaikeat_ongelmat/