Harrastaja keksi yhden kiven laatoituksen
Hannu Korhonen
Katu- ja seinälaatoitukset ovat jaksollisia. Jaksottomat laatoitukset ovat olleet enemmän matemaatikkojen kuin rakentajien mielenkiinnon kohteina. Pitkään oli avoinna kysymys siitä, voidaanko taso laatoittaa jaksottomasti vain yhdellä laatalla. Pari sellaista laattaa on keksitty aikaisemmin [1]. Uusimman keksi englantilainen matematiikan harrastaja viime syksynä.
Uuden laatoituksen keksijä, matematiikan harrastaja, eläkkeellä oleva tulostinhuoltaja David Smith julkaisi tieteellisen artikkelin [2] kolmen matemaatikon kanssa avoimen julkaisemisen jakelualustalla Arxiv Forumilla 20. maaliskuuta 2023. Matemaatikkojen mukanaolo oli varmaan ehdottoman tarpeen, sillä artikkeli sisältää geometrisen kuvailun lisäksi myös todistuksen sille, että tästä uudesta laatasta voidaan tehdä useita erilaisia jaksottomia laatoituksia, mutta että siitä ei voida rakentaa minkäänlaista jaksollista laatoitusta.
Smith kertoo pohtineensa asiaa kymmenen vuotta [3]. “Olen aina puuhastellut kaikenlaisten muotojen parissa. Yhden kiven ongelmaan olen suorastaan hullaantunut”, sanoo Smith. “Pidin matematiikasta jo koulussa, mutta en suoriutunut siitä mitenkään loistavasti.” Keksintöä pidetään erityisen huomionarvoisena siksi, että se ei pohjaudu mihinkään aikaisemmin tunnettuun laatoitusideaan, vaan tuo mieleen pikemminkin aineen sisäisen rakenteen.
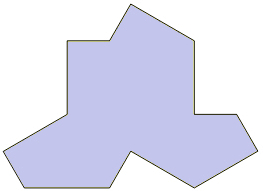
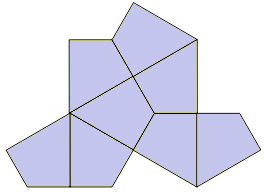
Alussa mainitun tiedeartikkelin kirjoittajat kutsuvat Smithin laattaa “hatuksi”. Hyvällä tahdolla sen muodossa voikin olla näkevinään hatun kuvun ja lierit (kuva 1, ylempi). Laatta on 13-kulmio. Se rakentuu kahdeksasta yhtenevästä pitemmän lävistäjänsä suhteen symmetrisestä nelikulmiosta (kuva 1, alempi). Nämä ovat vähän kapeampia kuin Penrosen “leijat”, terävä kulma on \(60^{\circ}\) ja kaksi muuta kulmaa suoria.
Suuret sanomalehdet tarttuivat aiheeseen nopeasti. New York Timesin viikkolehti kirjoitti siitä jo runsaan viikon kuluttua [3] sekä The Guardian [4] ja The Times [5] kahden viikon sisällä. Esimerkiksi Guardian luonnehti yhden kiven laatoitusta yhdeksi matematiikan kiehtovimmista mysteereistä. Median innostukseen vaikutti varmaankin se, että laatoitukset ovat visuaalisesti näyttäviä ja helposti ymmärrettävää tasogeometriaa, sekä toisaalta se, että näinkin konkreettiselta tuntuva ongelma oli askarruttanut matemaatikkoja jo kymmenien vuosien ajan. Ja ehkä vielä se, että idean keksijä oli maallikkoharrastaja eikä ammattimatemaatikko.
Tiedeyhdistysten verkkolehdet ja varsinaiset tiedelehdet olivat vielä nopeampia kuin sanomalehdet. Tieteen ja teknologian uutissivusto Phys.org kertoi artikkelista jo kolmen päivän kuluttua [6]. Uutinen oli lyhyt ja sisälsi lyhyen yhteenvedon siitä, mitä tason laatoitus tarkoittaa; muuten viitattiin alkuperäiseen tiedeartikkeliin. Wolfram-yhteisö tarttui aiheeseen vajaassa viikossa. Keskustelussa [7] analysoitiin tarkasti laatan muoto ja laatoitusmahdollisuuksia [8].
Smithin laatta – hattu – ei ole vain yksittäinen kiinteä geometrinen kuvio. Kuvion muotoa voidaan muuttaa jatkuvasti hatusta koveraksi kuusikulmioksi (kuva 3). IFLScience-uutissivuston artikkelin [9] mukaan ajatukselliset yhteydet ulottuvat myös puhtaan matematiikan ulkopuolelle. Esimerkiksi kvasikiteisten aineiden rakenteissa voidaan havaita samoja ominaisuuksia kuin jaksottomissa laatoituksissa. Samoilla ideoilla on sovelluksia myös käsipyyhkeiden kuvioinnista ja taittelusta häivehävittäjiin ja tieteiselokuvien muotoaan muuttaviin robotteihin.

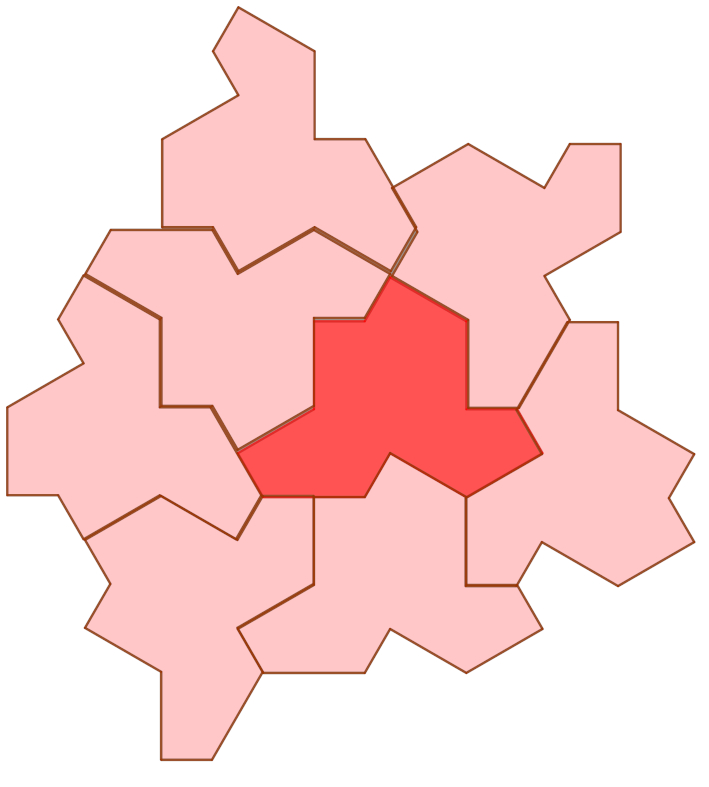
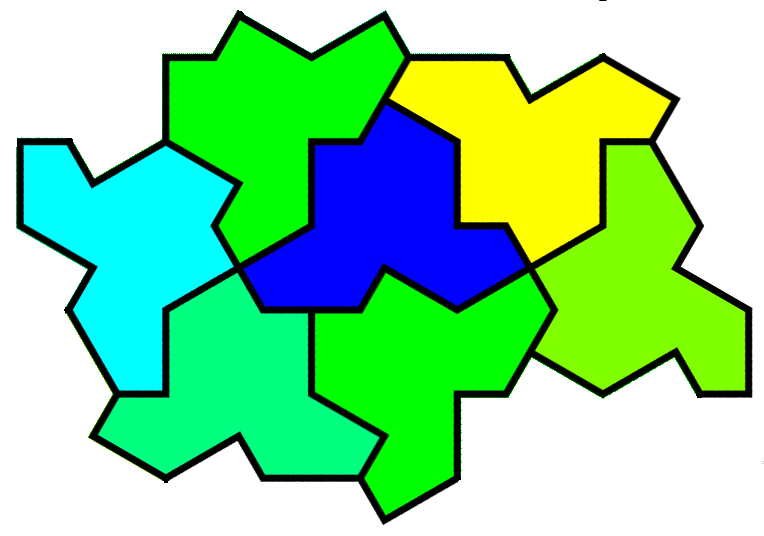
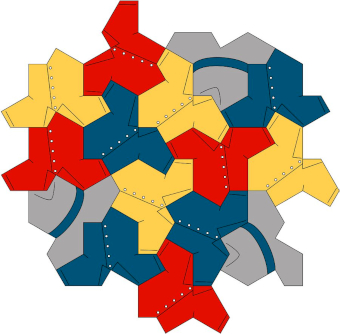
Quanta Magazine kuvasi perusteellisesti sen, miten tason peitto rakentuu hattulaatasta (kuva 4) [11]. Hattu ei kuitenkaan ole ainoa mielikuva, jonka Smithin laatta saattaa herättää tiedelehden toimittajassa [12] tai twiittaajassa [13] (kuva 5).


Lähteet ja lisää luettavaa
[1] Korhonen, Hannu (2022): Yhden kiven laatoitus. Solmu 2/2022 s. 4–6. Saatavissa myös
https://matematiikkalehtisolmu.fi/2022/2/yhden_kiven_ongelma.pdf
[2] Smith, David ym. (20.3.2023): An Aperiodic Monotile. Saatavissa osoitteesta
https://arxiv.org/pdf/2303.10798.pdf
[3] Roberts, Siobhan: Elusive ‘einstein’ solves a long-standing math problem. New York Times Weekly 29.3.2023.
https://www.npr.org/2023/03/31/1167297046/a-hobbyist-in-the-u-k-has-come-up-with-a-new-13-sided-shape-called-the-hat
[4] Cantor, Matthew: The miracle that disrupts order’: mathematicians invent new ‘einstein’ shape. The Guardian 4.4.2023 osoitteessa
https://www.theguardian.com/science/2023/apr/03/new-einstein-shape-aperiodic-monotile
[5] The Times: Retired yorkshireman solves elusive einstein tile maths problem.
https://www.thetimes.co.uk/article/retired-yorkshireman-solves-elusive-einstein-tile-maths-problem-vqw7xgt3p
[6] Yirka, Bob: A geometric shape that does not repeat itself when tiled. Phys.org 23.3.2023.
https://phys.org/news/2023-03-geometric-tiled.html
[7] Pegg, Ed (2023): Einstein problem solved. Wolfram Research osoitteessa
https://community.wolfram.com/groups/-/m/t/2856178
[8] Hat Tile App osoitteessa
https://cs.uwaterloo.ca/~csk/hat/app.html
[9] Spalding, Katie: This Brand New "Einstein" Tile Can Do Something No Other Shape Can Do. IFLScience 28.3.2023
https://www.iflscience.com/this-brand-new-einstein-tile-can-do-something-no-other-shape-can-do-68201
[10] Science News, YouTube-video
https://www.youtube.com/watch?v=ugnvucpcfPA
[11] Erica Klarreich, Erica: Hobbyist Finds Math’s Elusive ‘Einstein’ Tile. Quanta magazine 4.4.2023.
https://www.quantamagazine.org/hobbyist-finds-maths-elusive-einstein-tile-20230404/
[12] Conover, Emily: Mathematicians have finally discovered an elusive ‘einstein’ tile. Science News 24.3.2023.
https://www.sciencenews.org/article/mathematicians-discovered-einstein-tile
[13] Kaplan, Craig S.: Find another reflected turtle in an aperiodic tiling. Twitter 21.3.2023.
https://twitter.com/alytile/status/1638506055381708801?s=20