Onpas niitä paljon!
Neea Palojärvi
Helsingin yliopisto
Opetin viime syksynä Helsingin yliopistolla kombinatoriikan kurssia. Kurssilla muun muassa laskettiin erilaisten tapojen lukumääriä. Esimerkiksi tutkittiin, kuinka monella eri tavalla jokin määrä ihmisiä voidaan laittaa jonoon. Kurssin opettamisesta innostuneena kerroin kurssin tehtävistä myös sellaisille ystävilleni, sukulaisilleni ja tutuilleni, joilla ei ole matematiikan opiskelusta yliopistotaustaa. Osalla viimeisimmät matematiikan opinnot olivat kansakoulusta usean vuosikymmenen takaa, osalla toisen asteen opinnoista muutaman vuoden takaa. Heistä useampaa yhdisti hämmästys, kuinka paljon erilaisia tapoja on.
Tässä kirjoituksessa esitellään kolme kombinatoriikan kurssillani esiintynyttä tehtävää, joissa pohditaan eri asioiden lukumääriä. Tehtävät on valittu niin, että niissä on jotain konkreettista mukana ja tilannetta voi hahmotella esimerkiksi järjestelemällä kirjoja. Tätä voi tehdä vaikka yhdessä kavereiden kanssa! Kuten monesti matematiikan tehtävissä muutenkin, tehtävää yksinkertaisempien tilanteiden tutkiminen voi auttaa saamaan ajatuksesta kiinni. Tehtävät pyrkivät olemaan helpommasta vaikeampaan, mutta on toki varsin yksilöllistä, mitkä tehtävät kokee vaikeiksi. Alkuun pääsee peruskoulun tarjoamilla matematiikan tiedoilla, mutta korkeammasta matemaattisesta ajattelukyvystä on hyötyä. Erityisesti tehtävien vinkeissä ajattelu on pyritty kirjoittamaan melko selkeästi auki ja teksti niin, että aktiiviset ja taitavat ysiluokkalaisetkin saisivat siitä jotain irti.
Kirjojen järjestys
Tehtävä: Kirjahyllyyn laitetaan viisi matematiikan, neljä tietotekniikan, neljä fysiikan, kolme kemian ja kolme biologian kirjaa. Kuinka monella tavalla kirjat voidaan järjestää niin, että saman aineen kirjat ovat peräkkäin?
Vinkkejä tehtävän ratkaisuun: Tässä tehtävässä jokainen järjestys on eri, mikäli kirjat ovat eri järjestyksessä. Eli jos vasemmalla on ensin matematiikan kirja A ja sitten matematiikan kirja B, niin se on eri järjestys kuin jos vasemmalla olisi ensin kirja B ja sitten kirja A.
Kuten tekstin alussa mainittiinkin, kannattaa ensin miettiä yksinkertaisempia tilanteita. Mikä olisi vastaus, jos kysyttäisiinkin vain, kuinka monella eri tavalla kaksi matematiikan kirjaa voidaan laittaa eri järjestykseen hyllylle? Voit kokeilla tätä ihan oikeilla kirjoilla! Entä kaksi matematiikan kirjaa ja yksi fysiikan kirja? (Älä lue eteenpäin, jos et halua lukea edellisiin kysymyksiin vastauksia.) Ensimmäiseen kysymykseen vastaus on kaksi eri tapaa; voi olla, että toinen on vasemmanpuoleinen tai sitten päinvastoin. Jälkimmäiseen kysymykseen vastaus on neljä eri tapaa. Keksitkö tähän sellaiset perustelut, joiden avulla voidaan vakuuttua, että järjestyksiä on kahden matematiikan kirjan ja yhden fysiikan kirjan tapauksessa juuri tuon verran – ei yhtään enempää tai vähempää?
Esitetään nyt edelliselle kahden matematiikan kirjan ja yhden fysiikan kirjan tilanteelle yksi mahdollinen ratkaisutapa. Tarkastellaan ensin, kuinka monella eri tavalla yksi fysiikan kirja voi olla hyllyllä kahteen matematiikan kirjaan nähden. Koska matematiikan kirjojen on oltava peräkkäin, fysiikan kirjan on oltava joko niitä ennen tai niiden jälkeen. Tätä on havainnollistettu kuvassa 1. On kuitenkin vielä huomattava, että kummassakin näissä järjestyksissä matematiikan kirjojen paikat voivat vaihdella. Edellisessä kappaleessa on todettu, että ne voi laittaa kahteen eri järjestykseen. Eli kumpaakin kuvan 1 tilannetta kohti on täsmälleen kaksi eri matematiikan kirjojen järjestystä. Kaiken kaikkiaan kysyttyjä järjestyksiä on siis \(2\cdot 2=4\).
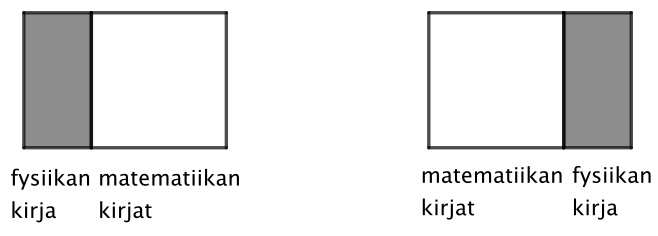
Pystyisitkö nyt yleistämään tilanteen ja vastaamaan alkuperäiseen kysymykseen? Halutessasi voit yrittää vielä pohtia joitain muita tehtävänannon tilannetta yksinkertaisempia tilanteita tai muilla sopivin tavoin yrittää hahmottaa tilannetta.
Tehtävän ratkaisu: Käytetään tässä ratkaisussa tunnettua merkintää \(n!=n(n-1)(n-2)\cdots 1\), joka on tässä määritelty kaikilla positiivisilla kokonaisluvuilla \(n\). Esimerkiksi on \(3!=3\cdot2\cdot1=6\).
Tarkastellaan ensin, kuinka monella eri tavalla eri aineet voivat olla, ja sitten, kuinka monella eri tavalla kirjat voidaan järjestää näiden aineiden sisällä.
Kirjoja on viidestä eri aineesta. Siispä vasemmanpuoleisin aine voidaan valita viidellä eri tavalla. Jäljellä on neljä ainetta, joista voidaan valita vasemmalta lukien toinen aine. Tämän jälkeen jäljellä on enää kolme ainetta, sitten kaksi ja oikeanpuoleisimman aineen kohdalla on enää yksi jäljellä. Siispä aineiden järjestämistapoja on \(5\cdot4\cdot3\cdot2\cdot1=5!\) erilaista, sillä esimerkiksi jokaista vasemmanpuoleista ainevalintaa kohti on aina neljä erilaista valintaa sen vieressä olevalle aineelle ja kukin näistä tuottaa erilaisen lopputuloksen.
Kuitenkin jokaisessa edellisistä järjestyksistä saman aineen kirjat voivat olla eri järjestyksissä. Vastaavalla tavalla kuin edellisessä kappaleessa on päätelty, voidaan todeta, että matematiikan kirjat voidaan järjestää \(5!\) eri tavalla, tietotekniikan \(4!\), fysiikan \(4!\), kemian \(3!\) ja biologian \(3!\) eri tavalla.
Yhteensä mahdollisia järjestystapoja on siis
\[5!\,5!\,4!\,4!\,3!\,3!=120\cdot120\cdot24\cdot24\cdot6\cdot6=298 \, 598\, 400.\]
Siis lähes \(300\) miljoonaa! Ei siis luultavasti kannata alkaa testaamaan tällaisella kirjamäärällä, mikäköhän kirjojen järjestys näyttäisi parhaimmalta hyllyssä.
Istumajärjestykset
Tehtävä: Illalliselle osallistuu kymmenen ihmistä, joista viisi juo viiniä ja viisi ei juo. He syövät illallisen pyöreän pöydän ympärillä ja asettuvat sen ympärille istumajärjestyksen mukaan niin, että mitkään kaksi viiniä juovaa eivät istu vierekkäin eivätkä mitkään kaksi henkilöä, jotka eivät juo viiniä, istu vierekkäin. Illallisen järjestäjä suunnittelee kirjoittavansa ylös kaikki mahdolliset edelliset vaatimukset toteuttavat istumajärjestykset ja valitsevansa niistä parhaimman.
Laske, kuinka monta erilaista istumajärjestystä on, ja kerro sen perusteella, kannattaako illallisen järjestäjän toteuttaa suunnitelmansa.
(Kaksi istumajärjestystä ovat samat, mikäli niissä jokaisen henkilön oikealla puolella istuva henkilö on kummassakin sama ja samoin vasemmalla puolella istuva.)
Vinkkejä tehtävän ratkaisuun: Kuten aiemminkin, tehtävää voi yrittää hahmottaa pienemmillä määrillä tai vaikka ilman lisäehtoja. Edellisessä tehtävässä käsiteltiin jo asioiden laittamista jonoihin eli tällaisia tilanteita osataan tutkia. Voisiko siis auttaa, jos ensin jättäisi kokonaan huomioimatta pöydän ympärillä istumisen ja keskittyisikin vain jonon tutkimiseen? Millaista jonoa kannattaisi tutkia, jotta siitä olisi hyötyä tämän tehtävän kannalta? (Älä lue eteenpäin, jos et halua tähän kysymykseen vastausta.)
Tutkittavissa istumajärjestyksissähän pitäisi joka toisen juoda viiniä ja joka toisen olla juomatta. Näin ollen olisi luonnollista tutkia sellaisia jonoja, joissa tämä ehto toteutuu. Voisiko joitain edellisessä tehtävässä esiintyneitä ajatustapoja soveltaa tämän tehtävän ratkaisuun? Vaikka nyt samalla tavalla toimivat (viiniä juovat tai eivät juovat) eivät ole vierekkäin kuten edellisessä kohdassa saman aineen kirjat, niin jonossa on kuitenkin samanhenkistä säännönmukaisuutta. Voit jälleen kerran tarvittaessa hahmotella tilannetta pienemmillä ihmismäärillä ja vaikka kokeilla kavereiden kanssa, kuinka monta erilaista jonoa löydätte. Kuinka monta sellaista jonoa, jossa joka toinen henkilö juo ja joka toinen ei juo viiniä, on, kun viisi ihmistä juo viiniä ja viisi ihmistä ei juo viiniä? Vastaus tähän kysymykseen löytyy tehtävän ratkaisun toisesta kappaleesta.
Tehtävässä kuitenkin kysyttiin istumajärjestyksiä, eikä jonoja. Alkuun voi hahmotella, mitä nämä rajoitukset oikein tarkoittavat ilman, että otetaan viinin juomista tai juomattomuutta huomioon. Esimerkiksi, jos pyöreän pöydän ympärillä esiintyy kolme eri ihmistä, niin kuinka monta erilaista istumajärjestystä on suluissa olevan tekstin perusteella (ei siis vielä tutkita viinin juomista tai juomattomuutta)? Vastaus näkyy kuvasta 2.
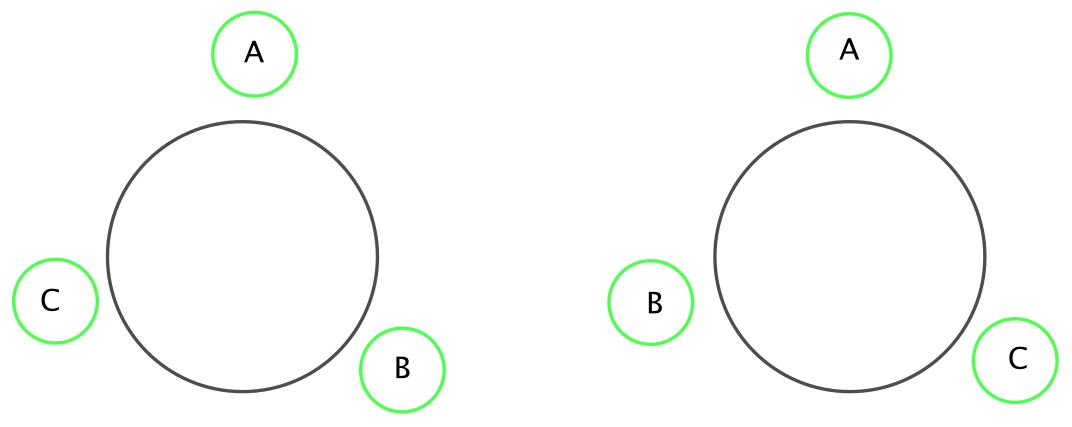
Erityisesti siis, kun ihmiset vain kiertävät ympäri pöytää myötä- tai vastapäivään (ks. kuva 3), niin tehtävänannon mukaan sama istumajärjestys säilyy. Mitä tapahtuu, jos tehdään ihan mikä tahansa sellainen muutos istumajärjestykseen, jota ei ole mahdollista saavuttaa alkuperäisen istumapaikkoja kiertämällä myötä- tai vastapäivään? Onko uusi istumajärjestys tehtävänannon tulkinnan mukaan silloin sama kuin alkuperäinen istumajärjestys? (Vastaus tähän löytyy seuraavasta kappaleesta.)
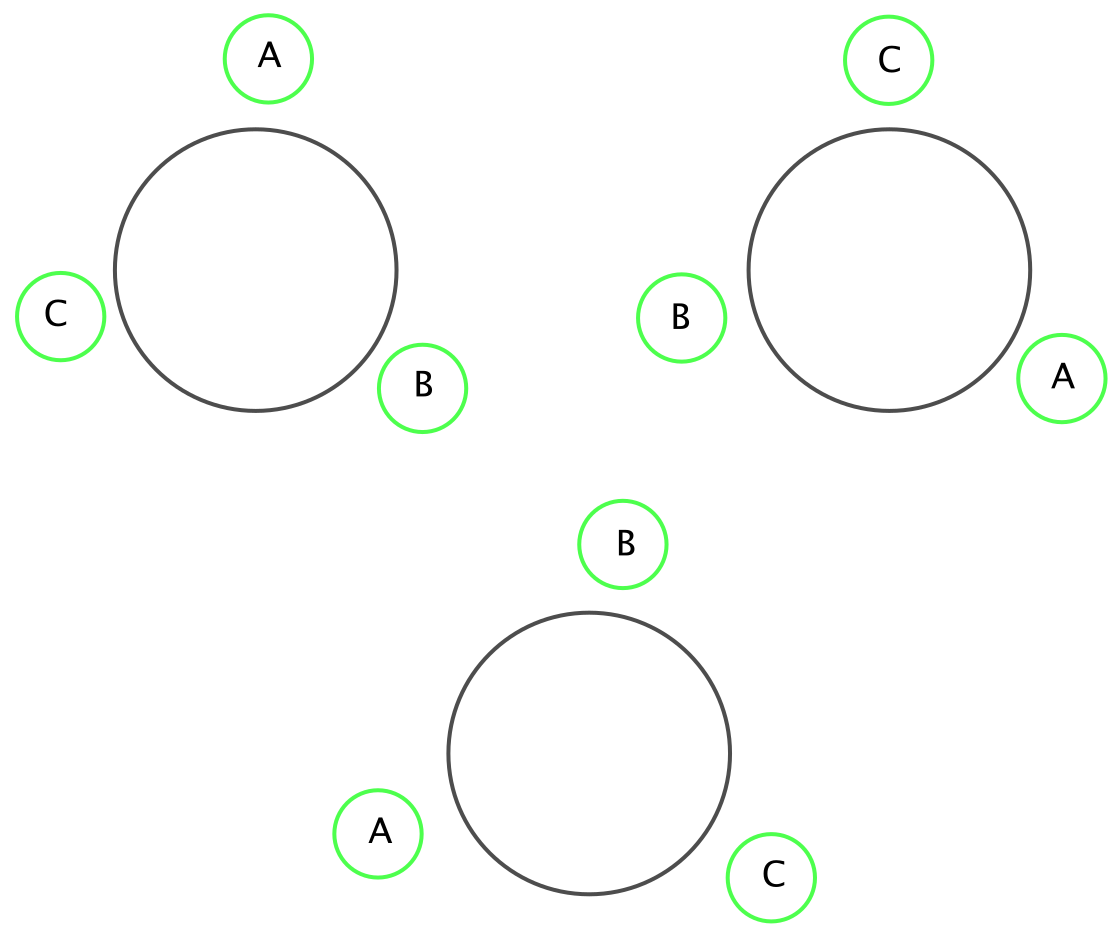
Vastaus edelliseen kysymykseen on, ettei istumajärjestys voi olla sama kuin alkuperäinen. Jos se nimittäin olisi, niin kaikilla olisi samat henkilöt oikealla ja vasemmalla puolella molemmissa istumajärjestyksissä. Kun tätä istumajärjestystä kierrettäisiin niin, että jokin henkilöistä istuisi samalla paikalla kuin alkuperäisessä istumajärjestyksessä, niin myös hänen vasemmalla puolellaan olevan pitäisi istua samalla paikalla kuin alkuperäisessä istumajärjestyksessä. Sama luonnollisesti pätisi myös tämän vasemmalla puolella olevalle ja niin edelleen. Siispä kaikkien olisi istuttava samoilla paikoilla kuin alkuperäisessä istumajärjestyksessä, mitä ei haluttu, koska tutkittavaa istumajärjestystä ei pitänyt saada aikaiseksi alkuperäistä istumajärjestystä kiertämällä.
Nyt on siis huomattu, että vain sellaiset tavat, joissa istumajärjestys saadaan toiseksi kiertämällä, ovat samoja. Jos siis pöydän ympärillä istuu kolme ihmistä, niin kuinka monta tämän istumajärjestyksen kanssa samanlaista istumajärjestystä on, kun istumajärjestystä kierretään? (Vastaus: Kolme, kukin saadaan kiertämällä vaikka myötäpäivään istumajärjestystä yhden askeleen eteenpäin.) Miten päättely yleistyy vaikka neljään, viiteen tai kymmeneen ihmiseen?
Kun edellinen, yhden istumajärjestyksen kanssa samanlaisten järjestysten lukumäärä on saatu selville, on aika yhdistää se aiempaan jonoajatteluun; tämähän on enää ainoa asia, mikä tehtävän ratkaisusta puuttuu. Miten jonossa olevat ihmiset voidaan laittaa istumaan päydän ympärille (miettimättä viinin juomista tai juomattomuutta)? Mitkä erilaiset jonot tuottavat samanlaiset istumajärjestykset? Voit esimerkiksi miettiä kolmen hengen muodostamia jonoja. Kuinka monta niitä on? Miten voit laittaa nämä jonot pöydän ympärille? Miten tämä vertautuu kuvassa 2 esitettyjen istumajärjestysten lukumäärään? Entä sitten siihen, että samanlaiset jonot saadaan, kun kierretään istumajärjestystä ympäri? (Vastaukset seuraavassa kappaleessa.)
Kolmen ihmisen jonojahan on \(3!=6\). Voidaan laittaa jonossa olevat ihmiset pöydän ympärille niin, että ensimmäinen istuu johonkin tiettyyn tuoliin, toinen sen vasemmalle puolelle ja kolmas tämän vasemmalle puolelle. Koska kiertämällä saadaan kuitenkin samanlaiset istumajärjestykset aikaan ja kaikki nämä tulevat erilaisissa jonoissa esiin, niin tulos pitää jakaa kolmella eli kiertojen lukumäärällä. Siispä erilaisia istumajärjestyksiä on kaksi. Miten tätä ajatusta voisi soveltaa tehtävänannon tilanteeseen?
Tehtävän ratkaisu: Tutkitaan tehtävää ensin sellaisessa tilanteessa, joka osataan jo edellisen kohdan pohjalta ratkaista. Ajatellaan siis tilannetta aluksi jonona eli ei oteta huomioon sitä, että ihmiset istuvat pyöreän pöydän ympärillä. (Lopullisessa tulkinnassa ajtellaan, että jonon toinen istuu jonon ensimmäisen vasemmalla puolella, kolmas toisen vasemmalla puolella kunnes lopulta viimeinen istuu ensimmäisen oikealla puolella, kun heidät laitetaan istumaan pöydän ympärille.)
Tässä jonossa ensimmäinen juo viiniä tai ei juo viiniä. Tälle valinnalle on siis kaksi eri vaihtoehtoa. Kun tämä on valittu, jonossa joka toisella on aina oltava tämä sama valinta eli he joko juovat viiniä tai eivät juo riippuen ensimmäisestä henkilöstä. Koska näitä henkilöitä on viisi, heidät voidaan laittaa \(5!\) eri järjestykseen. Toisaalta heidän välissään olevat henkilöt voidaan myös laittaa \(5!\) eri järjestykseen. Siispä pelkällä jonoajattelulla tapoja on \(2\cdot5!\,5!\).

Nyt on kuitenkin vielä huomioitava, että kun ihmiset laitetaan pöydän ympärille, niin kiertämällä istumajärjestystä pöydän ympäri saadaan uusi samanlainen istumajärjestys. Koska pöydän ympärillä on kymmenen paikkaa, niin tämä kierto voidaan tehdä kymmenellä eri tavalla. Lisäksi nämä käyvät läpi kaikki tavat saada kaksi samanlaista istumajärjestystä yhdestä istumajärjestyksestä, sillä muussa tapauksessa oikealla ja vasemmalla puolella olevat naapurit eivät säily. Siis edellisessä kappaleessa saatu tulos on vielä jaettavalla kymmenellä kysyttyjen istumajärjestysten lukumäärän saamiseksi:
\[\frac{2\cdot5!\,5!}{10}=4!\,5!=24\cdot120=2880.\]
Lähes \(3000\) istumajärjestyksen läpikäynti on työlästä, joten ehkä järjestäjän kannattaisi päättää sopiva istumajärjestys jollain muulla tavalla kuin käymälle kaikki järjestykset läpi.
Salasanojen lukumäärä
Tehtävä: Kuinka monta sellaista kahdeksan merkkiä pitkää salasanaa on, jotka koostuvat vain merkeistä a, b ja ! sekä jotka sisältävät jokaisen merkin ainakin kerran?
Vinkkejä tehtävän ratkaisuun: Kuten jo aiemmissa esimerkeissä huomattiin, voi tehtävän tutkiminen ilman lisäehtoja ja sen jälkeen lisäehtojen huomioiminen auttaa tehtävän ratkaisussa. Mikä voisi olla tässä tehtävässä se lisäehto, jota ilman tehtävää voisi aluksi miettiä? Miten tämän yksinkertaistuksesta pystyy muodostamaan ratkaisun kysyttyyn tehtävään? (Jos et halua nähdä yhtä mahdollisuutta vielä, älä siirry seuraavaan kappaleeseen.)
Yksi mahdollisuus on alkuun miettiä, kuinka monta sellaista salasanaa on, jotka koostuvat merkeistä a, b tai ! ilman mitään lisärajoituksia. Nythän kysyttyjen salasanojen lukumäärä saadaan, kun tuloksesta vähennetään ne salasanat, joista puuttuu jokin merkeistä a, b tai !. Kuinka monta salasanaa, jotka koostuvat merkeistä a, b, ! on? (Vastaus löytyy ratkaisun toisesta kappaleesta.)
Seuraavaksi olisi laskettava, kuinka monta sellaista jonoa on, josta puuttuu jokin merkeistä a, b tai !. Miten tämän voisi laskea? Miten voidaan soveltaa edellisen kappaleen laskuissa esitettyä ratkaisutapaa? Onko jotain erityistä otettava huomioon? Voi auttaa, että hahmottelee itselleen erilaisia salasanoja. Kun kaikki nämä havainnot yhdistää, onkin ratkaisu jo valmis.
Tehtävän ratkaisu: Lasketaan tämä lukumäärä laskemalla kaikki salasanat ja vähentämällä niistä ne salasanat, jotka eivät sisällä jotain merkeistä a, b tai !.
Lasketaan ensin kaikkien merkit a, b tai ! sisältävien salasanojen lukumäärä. Koska salasana on kahdeksan merkkiä pitkä ja kullekin merkille on kolme vaihtoehtoa, on kaikkia salasanoja \(3^8\).
Nyt on vielä vähennettävä sellaisten salasanojen, jotka eivät sisällä jotain merkeistä a, b tai !, lukumäärä. Huomataan, että tällöin siis kukin salasana koostuu korkeintaan kahdesta eri merkistä (ne kaksi muuta merkkiä) ja on kahdeksan merkkiä pitkä. Siispä sellaisia salasanoja, jotka eivät sisällä merkkiä a, on \(2^8\) kappaletta, sellaisia, jotka eivät sisällä merkkiä b, on myös \(2^8\) kappaletta ja sama pätee merkille !.
Nyt on kuitenkin vielä huomattava, että voi olla, ettei salasana sisällä myöskään kahta eri merkkiä. Esimerkiksi salasana aaaaaaaa ei sisällä merkkiä b, eikä merkkiä !. Se on siis laskettu edellisessä kappaleessa mukaan sekä silloin, kun tutkitaan salasanoja, jotka eivät sisällä merkkiä b että silloin, kun tutkitaan jonoja, jotka eivät sisällä merkkiä !. Näin ollen se on tullut laskettua edellä kahdesti. Siispä se on vähennettävä kerran. Koska salasana, joka ei sisällä mitä tahansa kahta merkkiä, on salasana joka sisältää vain yhden merkin, on tällaisia salasanoja kaiken kaikkiaan kolme kappaletta. Minkään muun tyyppisiä salasanoja ei ole laskettu mukaan useampaan kertaan. Siispä sellaisia salasanoja, jotka eivät sisällä jotain merkeistä a, b tai !, on \(3\cdot2^8-3\).
Nyt siis sellaisia kahdeksan merkin salasanoja, jotka koostuvat vain merkeistä a, b ja ! ja jotka sisältävät vähintään kerran kunkin merkeistä, on
\[\begin{align*} 3^8-\left(3\cdot 2^8-3\right) &=3^8-3\cdot2^8+3 =3\cdot\left(3^7-2^8+1\right)\\ &=3\cdot\left(2187-256+1\right) =3\cdot1932=5796 \end{align*}\]
kappaletta. Jo siis kolmella merkillä ja edellisillä rajoituksilla saa kohtuullisen paljon salasanoja aikaan. Pohdintatehtävänä voi olla, kuinka monta erilaista salasanaa saadaan aikaiseksi suuremmilla merkkimäärillä – joko lisärajoituksilla tai ilman.
Lopuksi
Edellisissä esimerkeissä näkyy hyvin, kuinka positiivisilla, ykköstä suuremmilla kokonaisluvuilla kerrottaessa tulo kasvaa nopeasti suureksi ja näin ollen edelliset vastauksetkin kasvavat melko nopeasti. Esimerkiksi, on jo
\[2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2=2^{10}=1024\]
ja \(2^{20}\) on yli miljoonan! Tai \(10!\) (eli “kuinka monella eri tavalla kymmenen ihmistä voi laittaa jonoon”) on \(3 \, 628\, 800\). Kannattaa siis edellisten esimerkkien valossakin olla hieman varovainen ennen kuin päättää alkaa käymään kaikkia erilaisia mahdollisia tapoja läpi laittaa eri asioita järjestykseen – edes silloin, kun asioita on verrattain pieni määrä.