Solmun tehtäviä
Tehtävät sopivat lukiolaisten lisäksi myös edistyneille yläkoululaisille.
1. Osoita, että jos reaaliluvut \(x\), \(y\) ja \(z\) toteuttavat yhtälön
\[\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1,\]
niin
\[\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}=0.\]
Määritä kaikki ehdon toteuttavat reaaliluvut.
2. Opri kirjoitti 2022 luvun listan seuraavasti: Listan kolmas luku on toinen luku jaettuna ensimmäisellä luvulla, listan neljäs luku on kolmas luku jaettuna toisella luvulla, ja niin edelleen, esimerkiksi listan 100. luku on 99. luku jaettuna 98. luvulla. Mikä on Oprin listan viimeinen luku, jos sen ensimmäinen luku on 20 ja toinen luku on 22?
3. Nelikulmion \(ABCD\) sivut \(AD\) ja \(DC\) ovat yhtä pitkät. Kulman \(DAB\) suuruus on \(\alpha\), kulman \(ABC\) suuruus on \(2\alpha\), kulman \(BCD\) suuruus on \(3\alpha\) ja kulman \(CDA\) suuruus on \(4\alpha\). Osoita, että sivu \(AB\) on kaksi kertaa niin pitkä kuin sivu \(AD\).
4. Olkoot \(x_1\) ja \(x_2\) yhtälön \(15x^2-21x+7=0\) reaalijuuret. Määritä lausekkeen
\[\frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{1}{x_1}+\frac{1}{x_2}\]
tarkka arvo.
5. Viisikulmion kaikki sivut ovat yhtä pitkiä ja kaksi sen kulmista ovat suoria. Kuinka suuria muut kolme kulmaa voivat olla?
6. Edel tekee puisia tikkuja, joiden pituus on kokonaisluku. Mitkään kolme tikkua eivät saa muodostaa kolmiota. Tikuissa on pituudeltaan 1 ja 10 olevat tikut ja pisimmän tikun pituus on 100. Kuinka monta tikkua Edel voi enintään tehdä?
7. Kahden kolminumeroisen luvun keskiarvo on luku, joka saadaan kirjoittamalla kyseiset luvut peräkkäin ja erottaen luvut desimaalipilkulla. Mitkä nämä kaksi lukua ovat?
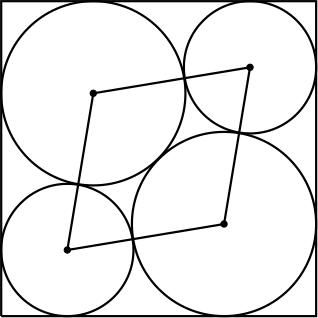
8. Yksikköneliön sisään piirretään neljä ympyrää kuten alla olevassa kuvassa on esitetty. Kaksi suurempaa ympyrää ovat samankokoiset ja samoin kaksi pienempää ympyrää ovat samankokoiset. Ympyrät sivuavat toisiaan ja neliön sivuja. Mikä on ympyröiden keskipisteet yhdistämällä muodostuvan vinoneliön pinta-ala?
9. Määritä kaikki positiiviset reaaliluvut \(x\), joille \(x+\dfrac{1}{x}\) on kokonaisluku ja \(x^3+\dfrac{1}{x^3}\) on alkuluku.
10. Mitkä luvuista \(1,\ldots,50\) voidaan lausua vähintään kahden peräkkäisen ei-negatiivisen kokonaisluvun summana?
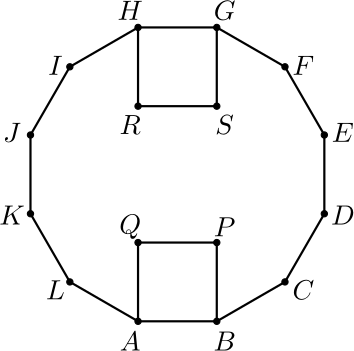
11. Säännöllisen 12-kulmion \(ABCDEFGHIJKL\) sisään sivuille \(AB\) ja \(GH\) piirretään neliöt \(ABPQ\) ja \(GHRS\) kuten alla olevassa kuvassa on esitetty. Osoita, että \(PQ\) ja \(RS\) ovat säännöllisen 6-kulmion vastakkaiset sivut.
12. Kahteen astiaan mahtuu kumpaankin 2 litraa nestettä. Ensimmäisessä astiassa on 2 litraa 100-prosenttista appelsiinimehua ja toisessa astiassa on 1 litra vettä. Puolet ensimmäisen astian appelsiinimehusta kaadetaan toiseen astiaan, jossa on vettä, ja neste sekoitetaan. Sekoitetusta nesteestä kaadetaan 1 litra takaisin ensimmäiseen astiaan. Menettely toistetaan: Ensimmäisestä astiasta kaadetaan 1 litra toiseen astiaan, neste sekoitetaan ja 1 litra sekoitettua nestettä kaadetaan takaisin ensimmäiseen astiaan. Kuinka monta prosenttia kummankin astian nesteestä on appelsiinimehua?
13. Kolme vihkoa ja kaksi lyijykynää maksavat kirjakaupassa yhteensä 11,10 euroa. Viisi vihkoa ja neljä lyijykynää maksavat yhteensä 20,10 euroa. Mitä ovat yhden vihkon ja yhden lyijykynän hinnat?
14. Luvuista \(1, 2, 3, 4, 5, 6, 7, 8\) valitaan kolme eri lukua ja lasketaan ne yhteen. Tämä tehdään kaikilla mahdollisilla kolmen luvun valinnoilla. Osa summista on parillisia ja osa on parittomia. Kumpi tulos on yleisempi, parillinen vai parioton summa?
15. Shakkiturnauksessa oli viisi osallistujaa. Jokainen osallistuja pelasi kerran jokaista muuta osallistujaa vastaan. Voitosta sai yhden pisteen, tasapelistä \(0{,}5\) pistettä ja häviöstä 0 pistettä. Turnauksen lopuksi havaittiin, että (i) turnauksen voittanut pelaaja ei pelannut yhtään tasapeliä, (ii) toiseksi tullut pelaaja ei hävinnyt yhtään peliä, (iii) kaikilla pelaajilla oli eri määrä pisteitä. Kuinka monta pistettä pelaajat saivat?
16. Positiivisen desimaaliluvun desimaalipilkku siirretään neljä paikkaa oikealle. Saatu luku on alkuperäisen luvun käänteisluku kerrottuna neljällä. Mikä on alkuperäinen luku?
17. Ratkaise yhtälöryhmä
\[\begin{cases} a+d=9,\\ ad+b=8,\\ bd+c=74,\\ cd=18, \end{cases}\]
kun \(a,b,c,d\) ovat kokonaislukuja.
18. Kirppu on lukusuoralla kohdassa 0 valmiina hyppäämään. Jokaisella hypyllään kirppu liikkuu 3 tai 5 yksikköä joko vasemmalle tai oikealle. Kirpun tavoite on käydä jokaisen luvun \(1,\ldots,20\) kohdalla. Etsi jono, jossa on enintään 22 hyppyä ja joka toteuttaa vaaditun tavoitteen.
19. Valitaan kuutiosta satunnaisesti neljä kärkeä. Kaikki mahdolliset neljän kärjen valinnat ovat yhtä todennäköisiä. Mikä on todennäköisyys, että valitut kärjet muodostavat tetraedrin? Entä mikä on todennäköisyys, että valitut kärjet muodostavat säännöllisen tetraedrin?
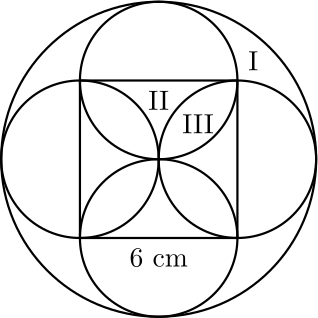
20. Neliön sivun pituus on 6 cm. Jokainen sivu on ympyrän halkaisija kuten alla olevassa kuvassa on esitetty. Ison ympyrän keskipiste on neliön keskipisteessä ja sen säde on neliön sivun pituinen. Laske alueiden I, II ja III pinta-alat.
Tehtävien ratkaisut julkaistaan Solmun tulevissa numeroissa.
Lähde: KöMaL
Käännös ja sovitus suomeksi: Mika Koskenoja