Yhden kiven laatoitus

Hannu Korhonen

Matematiikassa laatoittaminen (engl. tiling tai tessellation) tarkoittaa tason peittämistä kuvioilla, jotka eivät peitä toisiaan osittainkaan ja joiden väliin ei jää rakoja tai reikiä. Käytännössä useimmat seinä-, lattia- tai katulaatoitukset tehdään neliön tai suorakulmion muotoisista laatoista. Monilla muillakin kuvioilla laatoittaminen onnistuu (kuva 1). Laatoitus on jaksollinen, jos tasoa voidaan siirtää niin, että kuviointi ei muutu. Ongelmallisempia ovat laatoitukset, jotka eivät ole jaksollisia. Sellainen laatoitus onnistuu yhdelläkin laatalla.

Jaksollinen (engl. periodic) laatoitus on siirtosymmetrinen (kuva 1, kolme vasemmanpuoleista). Kuvio ei muutu, jos koko taso siirretään tiettyyn suuntaan tietyn matkan verran. Samalla kuviolla voi olla kaksikin toisistaan riippumatonta siirtosuuntaa ja muita näiden lineaariyhdistelmiä. Siirtosymmetrinen kuvio voi olla myös peilaus- tai kiertosymmetrinen. Penrosen tai Rissasen laatoista kootut ruusukuvioiset, kiertosymmetriset laatoitukset (kuva 1, kaksi oikeanpuoleista) ovat esimerkkejä jaksottomista (engl. aperiodic, non-periodic) laatoituksista [1], [2].

Sekä Penrosen että Rissasen laatoista voidaan tehdä sekä jaksollisia että jaksottomia laatoituksia. Penrosen laatoituksessa käytetään kahta erilaista laattaa ja Rissasen laatoituksessa useampia. Jaksottomaksi laatoitus voidaan pakottaa piirtämällä laattoihin kuvioita, joiden täytyy jatkua reunan yli seuraavalle laatalle, tai tekemällä laatan reunoihin koloja ja ulokkeita, jotka sallivat vain tietyt asennot. Useista laatoista kootuista jaksottomista tason peitoista on kirjoitettu paljon 1970-luvulta lähtien [5], [6], [7], [8].

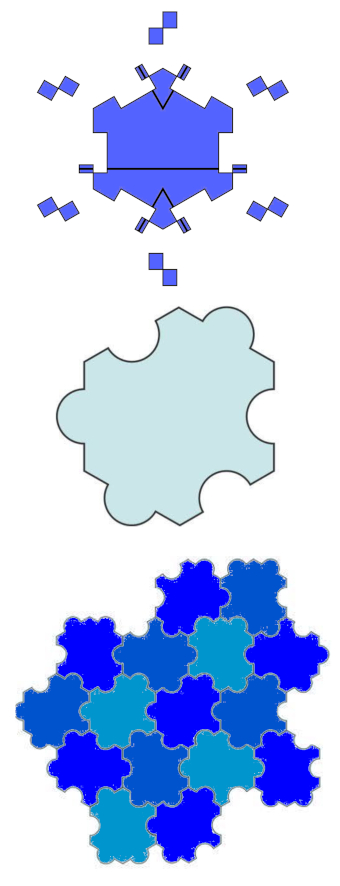
Pitkään oli avoinna kysymys, olisiko olemassa laatta, josta voitaisiin koota tason peitto, mutta joka ei sallisi jaksollisuutta. Tästä nimi “yhden kiven” ongelma (engl. ein-stein problem). Ensimmäinen ratkaisu keksittiin vasta kymmenkunta vuotta sitten [9]. Sitä ratkaisua ei voi luonnehtia tyylikkääksi, sillä “laatta” on monimutkainen eikä edes yhtenäinen (kuva 2, ylin).

Kuva 1: Kolme jaksollista (shakkilauta, Pythagoraan laatoitus ja Escherin Lintu/kala no 82) sekä kaksi jaksotonta laatoitusta (Penrose [3] ja Rissanen [4]).

Ihan tuore keksintö [10] on yhtenäinen kuvio, josta voidaan koota jaksoton ja vain jaksoton tason peitto (kuva 2, keskimmäinen osakuva). Viiteartikkeli sisältää myös todistuksen laatoituksen jaksottomuudelle. Jaksollisia laatoituksia (esimerkiksi kuva 1, kaksi vasemmanpuoleista) on helppo luoda matematiikkaohjelmilla, esimerkiksi Geogebralla [11], tai ohjelmoimalla. Sen sijaan jaksottoman laatoituksen rakentaminen on monivaiheisempaa.

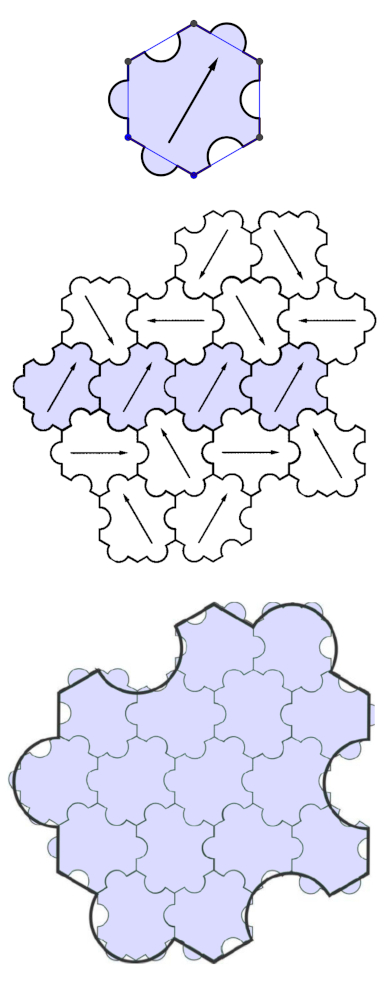
Kuva 2: Socolar-Taylor-laatta (ylin [9]), HexSeed-laatta (keskimmäinen [10]) ja osa jälkimmäisistä koottua laatoitusta (alin osakuva).

HexSeed-laatan rakenneperusta on säännöllinen kuusikulmio (kuva 3, ylin osakuva). Sen kolmelle sivulle tehdään puoliympyrän muotoiset lovet ja irrotetut palat siirretään ulokkeiksi muille sivuille. Tason peiton kokoamiseen johtava korvaussääntö muodostuu 16 toisiinsa liitetystä laatasta (kuva 3, keskimmäinen osakuva). Peruslaattojen kiertokulmat ovat 60 asteen kerrannaisia. Tuloskuvio on pääpiirteittäin peruslaatan muotoinen kohdistamisen määräävine lovineen ja ulokkeineen (kuva 3, alin osakuva).

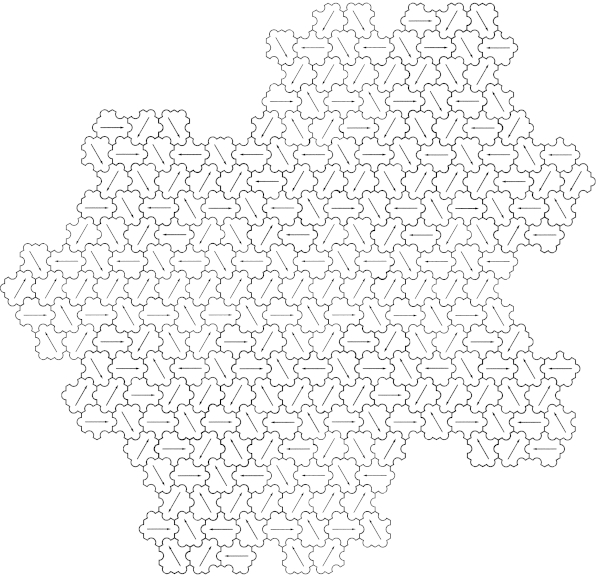
Kuva 3: HexSeed-peruslaatan rakenne ja sääntö, jonka mukaan laatoitus kootaan. Nuolet osoittavat peruslaatan suunnan.

Seuraavassa vaiheessa 16 peruslaatan muodostamia kuvioita liitetään vierekkäin saman korvaussäännön mukaan. Toisen korvauksen jälkeen kuviossa on 256 peruslaattaa (kuva 4). Näitä ryhmiä liitetään sitten taas toisiinsa samalla periaatteella. Tuloskuvioon sovelletaan samaa korvaussääntöä yhä uudestaan ja uudestaan. Seuraavissa korvauksissa syntyvissä kuvioissa on 4 096, 65 536, 1 048 576, …peruslaattaa. Peiton pinta-ala kasvaa 16-kertaiseksi jokaisella korvauskerralla. Koko taso peittyy, kun geometrista algoritmia jatketaan rajatta.

Kuva 4: HexSeed-laatoista rakentuva jaksoton tason peitto toisen korvauksen jälkeen.

Lähteitä ja lisäluettavaa

[1] Korhonen, Hannu: Sub Rosa, Dimensio 6/2018 s. 40–41.

[2] Korhonen, Hannu: Laatoitusten geometriaa, Dimensio 2019, osoitteessa https://dimensiolehti.fi/laatoitusten-geometriaa/

[3] Wikipedia-artikkeli Penrose tiling osoitteessa https://en.wikipedia.org/wiki/Penrose_tiling#/media

[4] Rissanen, Markus (2018): Basic Forms and Nature, From Visual Simplicity to Conceptual Complexity, väitöskirja, s. 245. Saatavissa osoitteesta https://taju.uniarts.fi/handle/10024/6275

[5] Gardner, Martin (1977): Mathematical Games. Extraordinary nonperiodic tiling that enriches the theory of tiles. Scientific American, Vol. 236, No. 1, pp. 110–121. Saatavissa osoitteesta https://web.ma.utexas.edu/users/radin/gardner.pdf

[6] Math & the Art of MC Escher (2012): Aperiodic Tessellations. Saatavissa osoitteesta https://mathstat.slu.edu/escher/index.php/Aperiodic_Tessellations

[7] Lindner, John F. (2017): ein Stein. Saatavissa osoitteesta https://woosterphysicists.scotblogs.wooster.edu/2017/11/01/ein-stein/

[8] Klaasen, Bernhard (2019): Forcing Nonperiodic Tilings with One Tile Using a Seed. Institute SCAI, Sankt Augustin, Germany. Saatavissa osoitteesta https://www.arxiv-vanity.com/papers/2109.09384/

[9] Socolar, Joshua ja Taylor, Joan (2011): An aperiodic hegonal tile, Journal of Combinatorial Theory, Series A 118, pp. 2207–2231, saatavissa osoitteesta https://www.sciencedirect.com/science/article/pii/S0097316511000859

[10] Gradit, Pierre ja Dongen, Vincent van (2022): A self-ruling monotile for aperiodic tiling, saatavissa osoitteesta https://arxiv.org/ftp/arxiv/papers/2201/2201.03079.pdf

[11] Geogebra-materiaali Pythagoraan laatoitus osoitteessa https://www.geogebra.org/m/fyfudqzs