Eduskuntavaalien suhteellisuusteoriaa – paikkajaosta ja sitä säätelevistä normeista

Jukka Liukkonen
Mat. yo. evp.

Johdanto

Suomessa järjestettiin ensimmäiset eduskuntavaalit vuonna 1907. Suomi oli tuolloin vielä Venäjän keisarikunnan autonominen suuriruhtinaskunta, joka vasta kymmenen vuotta myöhemmin, vuonna 1917, muuttui itsenäiseksi valtioksi. Eduskuntavaalit ovat alusta lähtien noudattaneet suhteellista vaalitapaa, so. edustajapaikat jakautuvat, tai niiden ainakin periaatteessa pitäisi jakautua, puolueille samalla tavalla kuin vaaleissa saadut äänet. Paikkojen jakaminen maantieteellisten vaalipiirien kesken tehdään sekin suhteellisuusperiaatetta noudattaen. Jaon perusteena on vaalipiirin alueella asuvien Suomen kansalaisten lukumäärä. Vaalien suhteellisuudesta ja vaalipiirijaosta on säädetty Suomen perustuslaissa ([2], 25 §).

Laskennallisesta näkökulmasta eduskuntavaalien toteutus perustuu kahteen johtavaan menetelmään. Eduskuntapaikkojen jaossa vaalipiireille käytetään Hare-Niemeyerin menetelmää. Kansanedustajien paikat vaalipiirin sisällä jaetaan puolueille¹ ja ehdokkaille D’Hondtin² menetelmällä.³

Varsinkin jälkimmäistä on kritisoitu sen takia, että pienissä vaalipiireissä pienten puolueiden on vaikeaa saada ehdokkaitaan eduskuntaan. Kritiikki on osittain perusteltua, mutta itse vaalipiirijako on ylivoimaisesti suurin syyllinen. Tämä on helppoa ymmärtää äärimmäisen esimerkin kautta: jos vaalipiirejä pienennettäisiin niin, että kustakin piiristä valittaisiin vain yksi kansanedustaja, ainoastaan suurin puolue saisi edustajanpaikan.

Äänten muuntaminen paikoiksi tarjoaa monenlaisia yllätyksiä. Pomminvarmaksi kuviteltu menetelmä saattaa joissain tilanteissa antaa järjen tai oikeustajun vastaisia tuloksia. Pekka Alestalo käsittelee erään tapauksen hauskassa Solmu-artikkelissaan [1].

Äänet, kvootit ja paikat

Artikkelin loppuosassa tarkastellaan yleistä tilannetta, jossa ${\Sigma}$ paikkaa jaetaan $P$ puolueen kesken äänimäärien $V_1,\ldots,V_P$ perusteella. Kaikki tässä mainitut luvut ovat positiivisia kokonaislukuja. Puolueiden $1,\ldots,P$ paikkamäärät $S_1,\ldots,S_P$ ovat ei-negatiivisia kokonaislukuja. Paikkojen ja äänien kokonaismäärät ovat

\[S = S_1+\ldots+S_P\,,\quad V = V_1+\ldots+V_P\,.\]

Lopullisen paikkajaon on toteutettava ehto $S={\Sigma}$. Vaatimus vaalien suhteellisuudesta tarkoittaisi ihannetilanteessa yhtälöiden

\[\frac{S_p}{{\Sigma}} = \frac{V_p}{V}\,,\quad p=1,\ldots,P\]

voimassaoloa. Kuitenkin kysymys on kokonaislukujen osamäärien yhtäsuuruudesta, ja sellainen toteutuu vain harvoissa poikkeustapauksissa. Puolueelle $p$ suhteellisuusperiaatteen mukaan siunaantuva täsmällinen paikkamäärä eli kvootti⁴ (engl. quota)

\[Q_p = \frac{V_p}{V}\,{\Sigma}\]

ei yleensä olekaan kokonaisluku. Periaatteen toteuttamispyrkimys merkitsee sellaisen paikkajaon etsimistä, että lukujonot

\[\mathbf{S} = (S_1,\ldots,S_P) \quad\text{ja}\quad \mathbf{Q} = (Q_1,\ldots,Q_P)\]

muistuttavat toisiaan mahdollisimman paljon. Ennen paikkojen laskemista on sovittava siitä, mitä tuo toisiaan muistuttaminen tarkoittaa.

Lukujonoja kutsutaan vastedes vektoreiksi. Kvoottivektorin $\mathbf{Q}$ ja paikkajaon $\mathbf{S}$ laskenta edellyttää äänisaalisvektorin

\[\mathbf{V} = (V_1,\ldots,V_P)\]

tuntemista. Varsinkin numeerisia vektoreita merkitään myös toisella tavalla, esimerkiksi

\[[\ 2{,}5\ \ 4{,}1\ \ {-1{,}7}\ \ 12{,}0\ \ 7{,}9\ \ 1{,}1\ ].\]

Vektorien nimet kirjoitetaan lihavoituina: $\mathbf{V}$. Niiden komponentit kuten myös muut skalaarit (so. luvut) kirjoitetaan lihavoimattomina: $V_p$. Vektorin nimi ilman lihavointia tarkoittaa vektorin komponenttien summaa, ellei asiayhteydestä ilmene muuta:

\[\mathbf{W} = (W_1,\ldots,W_P),\quad W = W_1+\ldots+W_P.\]

Hare-Niemeyerin menetelmä

Kvoottien summa on paikkojen kokonaismäärä:

\[Q_1+\ldots+Q_P = {\Sigma}.\]

Hare-Niemeyerin menetelmässä jokaiselle puolueelle $p$ annetaan aluksi kvootin $Q_p$ kokonaisosan ilmoittama määrä paikkoja. Tällöin yleensä muutama paikka jää jakamatta. Ne jaetaan murto-osien suuruuden perusteella. Puolueet asetetaan jonoon niin, että vastaavat murto-osat ovat laskevassa järjestyksessä, siis suurin ensin. Jonon alkupäästä lukien kullekin puolueelle annetaan yksi lisäpaikka, kunnes kaikki ${\Sigma}$ paikkaa on jaettu. Jonon häntäpään puolueet eivät saa lisäpaikkoja. Periaate on selitetty ilman matemaattisia symboleja vaalilain [3] 6 §:ssä.

Menetelmässä yksi paikka vastaa äänimäärää $V/{\Sigma}$, jota sanotaan Haren kvootiksi. Koko äänisaalis tulee käytetyksi, mutta ei välttämättä sillä tavalla kuin yksittäinen äänestäjä on halunnut: loppuvaiheessa ääniä siirrellään puolueilta toisille suhteellisuuden nimissä. Vähän ääniä saanut puolue saattaa jäädä ilman paikkaa. Tällöin tehdään suuri suhteellinen virhe, itse asiassa äärettömän suuri.

D’Hondtin menetelmä

Äänet voidaan käsittää valuutaksi, jolla puolueet ostavat paikkoja valtiolta. Paikkoja on myynnissä tasan ${\Sigma}$ kappaletta, ja valtio haluaa myydä ne kaikki mahdollisimman suurella kappalehinnalla, joka on sama kaikille puolueille. Kaupan jälkeen yhdelläkään puolueella ei ole tarpeeksi valuuttaa yhdenkään lisäpaikan ostamiseen. Paikan kappalehinta saadaan selville asettamalla kussakin puolueessa ehdokkaat heidän saamansa äänimäärän mukaiseen laskevaan järjestykseen. Jokaiselle ehdokkaalle annetaan vertausluku. Eniten ääniä saaneen vertausluku on koko puolueen $p$ äänimäärä $V_p$ eli $V_p/1$, toiseksi eniten ääniä saaneen vertausluku on $V_p/2$, kolmannen vertausluku on $V_p/3$ ja niin edelleen. Nimittäjät muodostavat lukujonon $(1,2,3,\ldots)$. Kun jokaisen puolueen jokaisella ehdokkaalla on vertausluku, heidät voidaan laittaa pitkään jonoon vertausluvun mukaiseen laskevaan järjestykseen. Kansanedustajiksi otetaan jonon alkupäästä ${\Sigma}$ ehdokasta. Edustajapaikan hinta on pienin vertausluku valituiksi tulleiden joukossa. Jos idea ei heti kirkastunut lukijalle, sitä kannattaa miettiä tovi. Periaate on selitetty vaalilain [3] 89 §:ssä.

Ehdokkaiden keskinäinen järjestys ratkaistaan arpomalla niissä tapauksissa, joissa kahdella saman puolueen ehdokkaalla on sama äänimäärä tai eri puolueiden ehdokkailla on sama vertausluku. Tästä on säädetty vaalilain [3] 90 §:ssä.

D’Hondtin menetelmässä kvootteja ei lasketa, eikä ääniä siirrellä puolueilta toisille. Ääniä jää tyypillisesti paljon käyttämättä. Paikan hinta voi tällöin olla selvästi pienempi kuin $V/{\Sigma}$. Puolue jää ilman edustajapaikkaa, jos sen kokonaisäänimäärä jää esimerkiksi yhden äänen vajaaksi paikan hinnasta.

Suhteellisuuden mittareita

Additiivisesta multiplikatiiviseen

Luvut $1$ ja $2$ ovat yhtä kaukana toisistaan absoluuttisessa mielessä kuin luvut $1000$ ja $1001$, mutta suhteellisessa mielessä $1$ ja $2$ ovat huomattavasti kauempana toisistaan kuin $1000$ ja $1001$. Luvun $1$ pitää kasvaa 100 % muuntuakseen luvuksi $2$, mutta siirtyminen luvusta $1000$ lukuun $1001$ merkitsee vain 0,1 %:n muutosta. Perinteisesti suhteelliset erot on muutettu absoluuttisiksi eroiksi logaritmifunktiolla: luvun $b$-kertaistuminen merkitsee sen $b$-kantaisen logaritmin lisäystä vakiolla $1$:

\[\log_b(bx) = \log_b(b)+\log_b(x) = 1 + \log_b(x)\]

riippumatta muuttujan $x > 0$ arvosta. Samassa tilanteessa $a$-kantainen logaritmi kasvaisi vakiotermillä $\log_a(b)$.

Additiivisen maailman $({\mathbb R},+,0)$ olioilla ja operaatioilla on vastine multiplikatiivisessa suhdemaailmassa $\big(\,]0,\infty[,\cdot,1\big)$. Siirtymän välittää eksponenttifunktio $u\mapsto e^u = \exp(u)$, ja siinä summa vaihtuu tuloksi, erotus osamääräksi, nolla ykköseksi, vastaluku käänteisluvuksi, vakiolla kertominen potenssiinkorotukseksi, aritmeettinen keskiarvo geometriseksi keskiarvoksi ja niin edelleen. Muunnoksen

\[{\cal M}:({\mathbb R},+,0)\to\big(\,]0,\infty[,\cdot,1\big)\]

toimintaperiaate ilmenee seuraavista esimerkeistä:

\[\begin{split} &{\cal M}(u) = e^u =: x,\quad {\cal M}(v) = e^v =: y,\\ &{\cal M}(0) = e^0 = 1,\quad {\cal M}(u+v) = e^{u+v} = e^u e^v = xy,\\ &{\cal M}(u-v) = e^{u-v} = \frac{e^u}{e^v} = \frac{x}{y}\,,\\ &{\cal M}(au) = e^{au} = (e^u)^a = x^a. \end{split}\]

Skalaarin m-itseisarvo

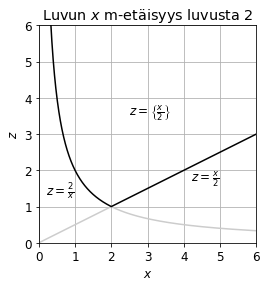
Suhdemaailman lukujen vertaaminen keskenään aloitetaan määrittelemällä multiplikatiivinen itseisarvo eli m-itseisarvo ${\left\{x\right\}}$ luvulle $x > 0$:

\[{\left\{x\right\}} = \left\{\begin{array}{rl} x\,, & x\ge 1 \\[1.5ex] \displaystyle\frac{1}{x}\,, & 0<x<1. \end{array}\right.\]

M-itseisarvolla on useita esityksiä; esimerkiksi

\[{\left\{x\right\}} = \max\left(x,\frac{1}{x}\right) = e^{|\ln x|} = a^{|\!\log_a(x)|},\]

kun $0<x$ ja $0<a\ne 1$. Havaitaan, että additiivisen maailman tutun identiteetin $|u-v|=|v-u|$ tapaan m-maailmassa pätee

\[{\left\{\frac{x}{y}\right\}} = {\left\{\frac{y}{x}\right\}}\,.\]

Suhdemaailmassa kahden (positiivisen) luvun “etäisyys” toisistaan on isomman suhde pienempään. Tällöin etäisyys kasvaa, kun isompi isonee tai pienempi pienenee. Oheisessa kuvassa $y=2$. Kun $x$ on hyvin pieni positiivinen luku, m-itseisarvo ${\left\{x\right\}}$ on hyvin suuri; itse asiassa

\[{\left\{x\right\}} = \frac{1}{x} \xrightarrow[x\to 0+]{} \infty,\]

kun $0<x<1$. Vaaleissa jotkut puolueet saattavat jäädä ilman paikkaa. Tätä tilannetta varten on kätevää sopia, että

\[{\left\{0\right\}} = \infty.\]

Vektorin normi ja m-normi

Itseisarvo voidaan yleistää vektoreille $\mathbf{u}=(u_1,\ldots,u_n)$ monilla eri tavoilla. Tällöin puhutaan vektorinormeista. Ne kuvaavat vektorisuureen suuruutta. Additiivisessa maailmassa eniten käytetty normi on kakkosnormi

\[\left\lVert\mathbf{u}\right\rVert_2 = \sqrt{u_1^2+\ldots+u_n^2}\,,\]

joka ilmoittaa vektorin Pythagoraan lauseen mukaisen pituuden $n$-ulotteisessa euklidisessa avaruudessa ${\mathbb R}^n$. Kakkosnormi, kuten kaikki normit, soveltuu myös vektoreiden eron mittaamiseen: vektorit $\mathbf{u}$ ja $\mathbf{v}$ muistuttavat toisiaan sitä enemmän, mitä lähempänä nollaa normin

\[\left\lVert\mathbf{u}-\mathbf{v}\right\rVert_2 = \sqrt{(u_1-v_1)^2+\ldots+(u_n-v_n)^2}\]

arvo on. Tässä $\mathbf{u}-\mathbf{v}=(u_1-v_1,\ldots,u_n-v_n)$.

Additiiviset normit muunnetaan muunnoksella ${\cal M}$ multiplikatiivisiksi m-normeiksi. Kun suhdemaailman vektori $\mathbf{x}$ viedään käänteismuunnoksella ${\cal M}^{-1}$ additiiviseen maailmaan vektoriksi $\ln\mathbf{x}:=(\ln x_1,\ldots,\ln x_n)$, lasketaan sen additiivinen kakkosnormi $\left\lVert\ln\mathbf{x}\right\rVert_2$ ja palataan muunnoksella ${\cal M}$ takaisin suhdemaailmaan, päädytään multiplikatiiviseen kakkosnormiin

\[\begin{split} {\left\{\!\!\left\{\mathbf{x}\right\}\!\!\right\}}_2 &= \exp\big(\left\lVert\ln\mathbf{x}\right\rVert_2\big) \\ &= \exp\left(\sqrt{(\ln x_1)^2 +\ldots+(\ln x_n)^2}\right). \end{split}\]

Vektorin m-normi on mitta sille, kuinka paljon vektori suhdemielessä poikkeaa ykkösvektorista

\[\mathbf{1}=(1,\ldots,1).\]

M-kakkosnormin mukainen vektoreiden $\mathbf{x}$ ja $\mathbf{y}$ multiplikatiivinen ero on

\[\begin{split} &{\left\{\!\!\left\{\frac{\mathbf{x}}{\mathbf{y}}\right\}\!\!\right\}}_2 = \exp\big(\left\lVert\ln(\mathbf{x}/\mathbf{y})\right\rVert_2\big) \\[1ex] &= \exp\left(\sqrt{(\ln x_1-\ln y_1)^2 +\ldots+(\ln x_n-\ln y_n)^2}\right). \end{split}\]

Vektoreiden osamäärä tulkitaan seuraavasti:

\[\frac{\mathbf{x}}{\mathbf{y}} = \left(\frac{x_1}{y_1},\ldots,\frac{x_n}{y_n}\right).\]

Laskutoimitukset tehdään vektoreille muutenkin komponenteittain, ellei toisin ilmoiteta. Myös tavanomaisten alkeisfunktioiden ($\ln$ ym.) arvot vektoreille lasketaan komponenteittain.

Normi- ja m-normiperheet

Additiivinen kakkosnormi on poiminta normiperheestä

\[\begin{split} \left\lVert\mathbf{u}\right\rVert_\kappa\hspace{0.9ex} &= \big(|u_1|^\kappa+\ldots+|u_n|^\kappa\big)^{1/\kappa},\; \kappa\ge 1, \\[1ex] \left\lVert\mathbf{u}\right\rVert_\infty &= \max\big({\left|u_1\right|},\ldots,{\left|u_n\right|}\big). \end{split}\]

Vastaavat multiplikatiiviset normit ovat

\[\begin{split} {\left\{\!\!\left\{\mathbf{x}\right\}\!\!\right\}}_\kappa\hspace{0.9ex} &= \exp\left(\left\lVert\ln\mathbf{x}\right\rVert_\kappa\right) \\[1ex] &= \exp\left(\big(|\ln x_1|^\kappa+\ldots+|\ln x_n|^\kappa\big)^{1/\kappa}\right), \\[1ex] &\phantom{xxi}\kappa\ge 1, \\[2ex] {\left\{\!\!\left\{\mathbf{x}\right\}\!\!\right\}}_\infty &= \exp\left(\left\lVert\ln\mathbf{x}\right\rVert_\infty\right) \\[1ex] &= \exp\Big(\!\max\big(|\ln x_1|,\ldots,|\ln x_n|\big)\Big) \\[1ex] &= \max\big({\left\{x_1\right\}},\ldots,{\left\{x_n\right\}}\big). \end{split}\]

Parametrilla $\kappa\in[1,\infty]$ säädellään vektorin komponenttien keskimääräisen arvon ja huippuarvon painotusta. Esimerkiksi siirtyminen vektorista $[1\ 1\ 7]$ vektoriin $[3\ 3\ 3]$ ei vaikuta normin $\left\lVert\cdot\right\rVert_1$ arvoon lainkaan (keskiarvo ei muutu), mutta $\left\lVert\cdot\right\rVert_\infty$ pienenee arvosta $7$ arvoon $3$ (huippuarvo muuttuu). Mitä suurempi $\kappa$, sitä enemmän normi mittaa pelkästään vektorin suurimpia komponentteja. Rajanormi $\left\lVert\cdot\right\rVert_\infty$ “näkee” ainoastaan suurimman komponentin.

Normia minimoitaessa on hyvä huomata, että additiivisen perheen normeista jokainen on itseisarvon ${\left|u_i\right|}\ge 0$ kasvava funktio, $i=1,\ldots,n$. Vastaavasti m-normeista jokainen on m-itseisarvon ${\left\{x_i\right\}}\ge 1$ kasvava funktio, sillä ${\left|\ln x_i\right|} = \ln{\left\{x_i\right\}}$.

Additiivisessa maailmassa erotuksen normi kuvastaa kahden vektorin, esimerkiksi paikkajako- ja kvoottivektorin, välisen eron suuruutta. Suhdemaailmassa eroa mitataan osamäärän m-normin avulla. Edustajapaikat jaetaan minimoimalla tavoitefunktiota

\[f_{\text{mul}}(\mathbf{S})={\left\{\!\!\left\{\mathbf{S}/\mathbf{Q}\right\}\!\!\right\}}_\kappa \quad\text{tai}\quad f_{\text{add}}(\mathbf{S})=\left\lVert\mathbf{S}-\mathbf{Q}\right\rVert_\kappa\]

sen mukaan, halutaanko korostaa suhteellisuutta vai ei.

Multiplikatiivisen tavoitefunktion lausekkeessa nähdään heti vaalien suhteellisuuden suurin ongelma: jokaisen puolueen pitää saada vähintään yksi paikka, muussa tapauksessa $f_{\text{mul}}(\mathbf{S})=\infty$. Yksi paikka on tultava, vaikka puolue olisi saanut vain yhden äänen. Ongelmaan ei ole siistiä ratkaisua. On pakko sopia periaatteesta, jolla vähiten ääniä saaneita puolueita jätetään ilman paikkaa. Samalla suhteelliselle vaalitavalle heitetään hyvästit näiden puolueiden osalta. Äänikynnysten kehittämiseen ei puututa tässä artikkelissa.

Paikkojen jakaminen puolueille

Muodollisesti kelvollisen paikkajaon $\mathbf{S}=(S_1,\ldots,S_P)$ on toteutettava seuraavat kriteerit:

\[\begin{split} \text{1)}\;\; &\text{$0 \le S_p \in {\mathbb Z}$ kaikilla $p=1,\ldots,P$}; \\ \text{2)}\;\; &S_1+\ldots+S_P = {\Sigma}. \end{split}\]

Tällaisten paikkajakojen joukossa ${\mathbb S}$ on

\[\binom{{\Sigma}+P-1}{{\Sigma}}\]

alkiota, sillä näin monella tavalla voidaan laittaa jonoon ${\Sigma}$ kpl paikkoja ja $P - 1$ kpl puoluerajoja. Äänestyksen jälkeen, kun äänisaalisvektori $\mathbf{V}$ on selvillä, paikat jaetaan puolueille etsimällä joukosta ${\mathbb S}$ alkio, joka parhaiten toteuttaa optimaaliselle paikkajaolle ennalta asetetut ehdot. Jos vaalipiirijako unohdetaan ja koko Suomi käsitetään yhdeksi vaalipiiriksi⁵, eduskuntavaaleissa $P=10$ ja ${\Sigma}=200$ ainakin suurin piirtein. Silloin mahdollisia paikkajakoja on noin $1{,}76\cdot 10^{15}$. Niiden läpikäyminen yksi kerrallaan on liian suuri työ. Tarvitaan tehokkaampi algoritmi paikkajaon optimoimiseksi.

Yleinen normiin perustuva paikkajakomenetelmä

Siirtyminen kvooteista paikkoihin merkitsee reaalilukujen korvaamista kokonaisluvuilla. Pyöristys alaspäin kokonaisluvuksi tehdään lattiafunktion (engl. floor) avulla. Lukujen kerrostalossa reaaliluvun $x$ lattia $\lfloor x\rfloor$ määritellään seuraavasti:

\[\lfloor x\rfloor = \max\{k\in{\mathbb Z}\mid k\le x\}.\]

Vektorille lattia muodostetaan komponenteittain. Samoin vektorien suuruusvertailut tehdään komponenteittain. Esimerkiksi

\[\begin{split} &\lfloor\mathbf{x}\rfloor = \big(\lfloor x_1\rfloor,\ldots,\lfloor x_n\rfloor\big),\\ &\mathbf{x}<\mathbf{y} \;\,\Leftrightarrow\;\, \text{$x_i<y_i$ kaikilla $i=1,\ldots,n$}. \end{split}\]

Jos paikkamäärien ei tarvitsisi olla kokonaislukuja, kvoottivektori olisi optimaalinen paikkajako. On melko yksinkertainen ja nopea tehtävä etsiä sellainen kokonaislukujono $\widetilde{\mathbf{S}}$, joka käytetyn normin tai m-normin mielessä vähiten eroaa jonosta $\mathbf{Q}$. Tutkittavia vaihtoehtoja on vähän, sillä väistämättä

\[\lfloor\mathbf{Q}\rfloor\le\widetilde{\mathbf{S}}\le\lfloor\mathbf{Q}+1\rfloor.\]

Vektori $\widetilde{\mathbf{S}}$, jota jatkossa kutsutaan näennäisratkaisuksi, ei vielä välttämättä kelpaa paikkajaoksi, sillä usein

\[\widetilde{S} = \widetilde{S}_1+\ldots+\widetilde{S}_P\ne {\Sigma}.\]

Siksi näennäisratkaisua on muutettava hieman. Muutetun vektorin $\mathbf{S}$ ja kvoottivektorin $\mathbf{Q}$ ero käytetyn normin tai m-normin mielessä on oltava minimaalinen ehdolla $\mathbf{S}\in{\mathbb S}$. Muutos tehdään lisäämällä näennäisratkaisuun keskenään samanmerkkisistä⁶ kokonaisluvuista koostuva, ehdon

\[W = W_1+\ldots+W_P = {\Sigma}-\widetilde{S}\]

toteuttava vektori $\mathbf{W}$. Optimaalisen vektorin $\mathbf{W}$, ja samalla optimaalisen paikkajaon

\[\mathbf{S}=\widetilde{\mathbf{S}}+\mathbf{W},\]

löytäminen brute force -menetelmällä, so. tutkimalla kaikki vaihtoehdot, ei normaalisti ole liian raskas tehtävä, sillä ${\left|W\right|}$ on pahimmillaan luokkaa “muutama”. Jos puolueita on kymmenen ja ${\left|W\right|}=4$, erilaisia vaihtoehtoja vektoriksi $\mathbf{W}$ on 715 kpl. Eduskuntavaaleja muistuttavissa tuhansissa testiajoissa ${\left|W\right|}$ ei ylittänyt arvoa 3. Raakaa laskentavoimaa vieroksuva lukija suunnitelkoon itse älykkään optimointialgoritmin.

Käytäessä läpi eri vaihtoehtoja saattaa paljastua, että optimaalisia paikkajakoja on useita. Optimointimenetelmää tai tavoitefunktiota voidaan pitää riittävän tarkkana, jos seuraava ehto on voimassa (transpositio tarkoittaa vektorin kahden komponentin vaihtamista keskenään):

Optimoinnin tarkkuusehto: jos $\mathbf{S}$ ja $\mathbf{S}'$ ratkaisevat optimointitehtävän, vektori $\mathbf{S}'$ saadaan vektorista $\mathbf{S}$ transpositioilla $S_r\leftrightarrow S_t$, missä $Q_r=Q_t$.

Ehdon tarkoittama tilanne syntyy, jos useampi puolue sattuu saamaan saman äänimäärän. Jotta paikkojen kokonaismääräksi saataisiin tasan ${\Sigma}$, jollekin näistä puolueista saatetaan joutua esimerkiksi antamaan yksi ylimääräinen paikka, jota se ei äänimäärällään ansaitsisi. Kyseiset puolueet ovat symmetrisessä asemassa keskenään niin, että on laskennan ja tavoitefunktion arvon kannalta yhdentekevää, mikä puolueista paikan saa. Käytännössä tällaiset tilanteet ratkaistaan arpomalla.

Hare-Niemeyer, D’Hondt ja normit

Edellisessä kappaleessa esitetty paikkajakomenetelmä lähtee liikkeelle näennäisratkaisun $\widetilde{\mathbf{S}}$ määrittämisestä. Näennäisratkaisu sijaitsee aina joukossa

\[\big\{ \mathbf{S}\,\;\big|\,\;\lfloor\mathbf{Q}\rfloor\le\mathbf{S}\le\lfloor\mathbf{Q}\rfloor+1 \big\},\]

josta käytetään tässä työnimeä kvoottivyö⁷. On ilmeistä, että normin $\left\lVert\mathbf{S}-\mathbf{Q}\right\rVert_\kappa$ minimointi kelvollisten paikkajakojen joukossa ${\mathbb S}$ johtaa kvoottivyössä sijaitsevaan ratkaisuun. Lukija voi tämän tarkistaa. Myös Hare-Niemeyerin tuottama ratkaisu sijaitsee kvoottivyössä. Niin ikään on ilmeistä, että nämä ratkaisut yhtyvät, vieläpä parametrista $\kappa$ riippumatta. Täten Hare-Niemeyerilla aikaansaatu paikkajako on samalla optimointitehtävän

\[\min_{\mathbf{S}\in{\mathbb S}}\left\lVert\mathbf{S}-\mathbf{Q}\right\rVert_\kappa\]

ratkaisu.

D’Hondtin menetelmän huolellinen analyysi paljastaa, että se ratkaisee optimointitehtävän

\[\min_{\mathbf{S}\in{\mathbb S}}\left\lVert\mathbf{S}/\mathbf{Q}\right\rVert_\infty\]

siitäkin huolimatta, että menetelmässä kvootit eivät eksplisiittisesti ole käytössä. Huomaa, että yleensä

\[\left\lVert\mathbf{S}-\mathbf{Q}\right\rVert_\infty \ne \left\lVert\mathbf{S}/\mathbf{Q}\right\rVert_\infty \ne {\left\{\!\!\left\{\mathbf{S}/\mathbf{Q}\right\}\!\!\right\}}_\infty\,.\]

Täten D’Hondtin menetelmän tavoitefunktio poikkeaa muista tässä artikkelissa käsitellyistä tavoitefunktioista.

Geometrinen menetelmä

Mikäli suhteellisuus on paikkajaon tärkein tavoite, paikkamäärien $S_p$ ja kvoottien $Q_p$ tulee olla mahdollisimman lähellä toisiaan m-normin mielessä. M-kakkosnormia käytettäessä tavoitefunktion

\[\begin{split} &f(\mathbf{S}) = {\left\{\!\!\left\{\frac{\mathbf{S}}{\mathbf{Q}}\right\}\!\!\right\}}_2 = \exp\big(\left\lVert\ln(\mathbf{S}/\mathbf{Q})\right\rVert_2\big) \\[1ex] &= \exp\left(\sqrt{(\ln S_1-\ln Q_1)^2 +\ldots+(\ln S_P-\ln Q_P)^2}\right) \end{split}\]

arvon tulee olla mahdollisimman pieni, mahdollisimman lähellä ykköstä. Paremman puutteessa tästä menetelmästä käytetään nimitystä geometrinen menetelmä.

Esimerkki. Suomen eduskuntavaaleissa vuonna 2019 puolueet saivat ääniä ja paikkoja seuraavasti [5]:

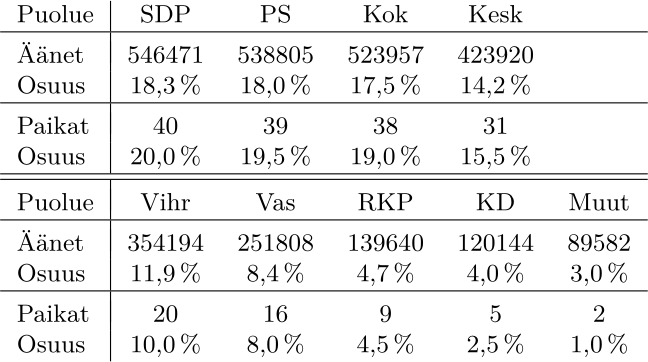
Jos koko valtakunta käsitettäisiin yhdeksi vaalipiiriksi, D’Hondtin, Hare-Niemeyerin ja geometrinen menetelmä antaisivat jokainen paikkajaoksi

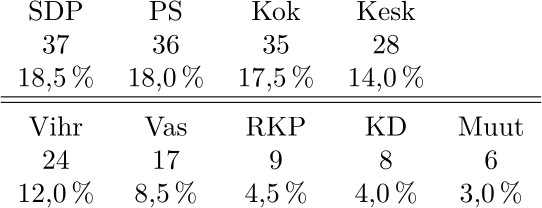
Myös optimoinnin välivaiheena syntyvä näennäisratkaisu $\widetilde{\mathbf{S}}$ yhtyisi tähän. Nykyinen vaalipiirijako hyödyttää puolueita seuraavasti (negatiivinen hyöty on haitta):

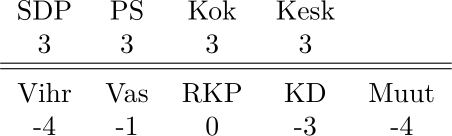
Esimerkiksi Kristillisdemokraateilla siirtyminen nykyisestä paikallisesti (suhteellisen) suhteellisesta vaalitavasta valtakunnallisesti suhteelliseen vaalitapaan olisi viime vaaleissa merkinnyt paikkamäärän muutosta 5:stä 8:aan eli 60 %:n kasvua.

Lienee selvää, että vaalipiireistä ei luovuta. Arvatenkin ehkä $40+39+38+31=148$ kansanedustajaa vastustaisi luopumista, ja korkeintaan $20+16+9+5+2=52$ kansanedustajaa poistaisi vaalipiirijaon. Pelin säännöistä päätetään pelin säännöillä! Tarkkaavainen lukija saattaa miettiä, onko tässä jokin periaatteellinen, looginen ristiriita. Ei siinä voi olla, sillä näin homma toimii käytännössä.

Kvoottivektorin

\[\begin{split} \mathbf{Q} &\approx [36{,}57\ \ 36{,}06\ \ 35{,}06\ \ 28{,}37\ \ 23{,}70\ \ 16{,}85 \\ &\phantom{xxxxxxxxxxxxxxxxxxxxxxxxx} 9{,}35\ \ 8{,}04\ \ 6{,}00] \end{split}\]

avulla saadaan laskettua valtakunnallinen mitta vuoden 2019 eduskuntavaalien suhteellisuudelle:

\[{\left\{\!\!\left\{\frac{\mathbf{S}_{2019}}{\mathbf{Q}}\right\}\!\!\right\}}_2 \approx 3{,}3926\,.\]

Ilman vaalipiirijakoa suhteellisuus olisi ollut

\[{\left\{\!\!\left\{\frac{\mathbf{S}}{\mathbf{Q}}\right\}\!\!\right\}}_2 \approx 1{,}0456\,.\]

Herää kysymys, onko perustuslakimme [2] kirjoitettu pilke silmäkulmassa vaalien suhteellisuusvaatimuksen osalta. $\Box$

Suosiiko D’Hondtin menetelmä suuria puolueita?

Hare-Niemeyerin menetelmä on additiivinen, geometrinen menetelmä on multiplikatiivinen ja D’Hondtin menetelmä additiivisen ja multiplikatiivisen sekoitus. Näitä kolmea verrattiin keskenään simuloimalla eduskuntavaaleja. Testiaineisto käsitti $100\,000$ satunnaisesti generoitua vaalitulosta. Generoinnin lähtökohtana oli vuoden $2019$ eduskuntavaalien tulos

\[\begin{split} \widehat{\mathbf{V}} &= (\widehat{V}_1,\ldots,\widehat{V}_9) \\ &= (546471,538805,523957,423920,354194,\\ &\hspace{20ex} 251808,139640,120144,89582), \\ {\Sigma}&= 200. \end{split}\]

Jokaiselle puolueelle $p=1,\ldots,P=9$ erikseen generoitiin uusi äänisaalis

\[V_p = \left\lfloor\text{rnd}\left(\frac{1}{2}\,,\;2\right)\widehat{V}_p\right\rfloor,\]

missä $\text{rnd}(1/2,\,2)$ on puoliavoimelle välille $[1/2,\,2\,[$ tasaisesti jakautunut satunnaisluku. Tämä tehtiin $100\,000$ kertaa, ja jokaisella kierroksella laskettiin paikat kaikilla kolmella menetelmällä.

Kierroksien joukossa oli 8885 sellaista, joissa kaikki kolme menetelmää antoivat saman paikkajaon. Muiden vastaavien kokeiden perusteella näyttää siltä, että menetelmien konsensus saavutetaan yleensäkin noin kymmenessä prosentissa vaaleista edellyttäen, että äänestystulokset on säädetty jokseenkin eduskuntavaalien äänisaalista $\widehat{\mathbf{V}}$ muistuttaviksi.

Paikkajakoja $\mathbf{S}\in\{\mathbf{S}_\text{H-N}, \mathbf{S}_\text{geo}, \mathbf{S}_\text{D'H}\}$ verrattiin kvootteihin $\mathbf{Q}$ laskemalla erotukset

\[\mathbf{S}-\mathbf{Q}.\]

Geometrisella keskiarvolla

\[\text{GM}(\mathbf{V}) := (V_1\ldots V_P)^{1/P}\]

keskitetyn äänisaalisvektorin luonnollisesta logaritmista

\[\ln\frac{\mathbf{V}}{\text{GM}(\mathbf{V})}\]

ja erotuksista $\mathbf{S}-\mathbf{Q}$ saatiin joka kierroksella pisteet

\[\left(\ln\frac{V_p}{\text{GM}(\mathbf{V})}\,,\; S_p-Q_p\right),\quad p=1,\ldots,P.\]

Nämä $100\,000\,P=900\,000$ pistettä piirrettiin koordinaatistoon läpikuultavalla värillä, vaalien läpinäkyvyyttä korostaen. Vaaka-akselilla vasemmalla ovat pienet, nollan kohdalla keskikokoiset ja oikealla suuret puolueet. Pystyakselilla on puolueen saaman paikkamäärän ja kvootin erotus.

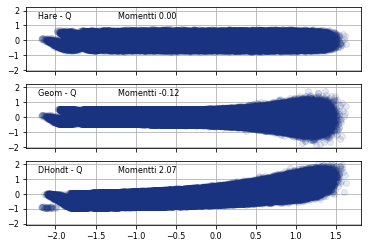
Ylimpänä Hare-Niemeyer pysyttelee tiukasti alle yhden äänen päässä kvootista, kuten teorian mukaan kuuluukin. Keskellä geometrinen menetelmä, suhteellisuuden pakottamana, levittäytyy suurten puolueiden päässä laajemmalle hoikentuen vastaavasti pienten puolueiden kohdalla. D’Hondtin menetelmän tuottama epäsymmetrinen “vihannes” käyristyy UNECE FFV-15 -luokitusrajoja [4] koetellen.

Kuvasta selvästi havaitaan, että D’Hondtin menetelmä suosii suuria puolueita pienten kustannuksella. Havainto voidaan vahvistaa laskennallisesti työkalulla, joka saa ideansa fysiikasta. Kysymyksessä on momentti, kaikkien vipuvaikutusten äiti:

\[\begin{split} &\text{Mom}(\mathbf{\Delta S};\mathbf{V}) := \mathbf{\Delta S}\,\mathbf{\cdot}\ln\frac{\mathbf{V}}{\text{GM}(\mathbf{V})} \\ &\phantom{xxxx}= \sum_{p=1}^P (\Delta S)_p\,\ln\frac{V_p}{\text{GM}(\mathbf{V})} \\ &\phantom{xxxx}= \sum_{p=1}^P (\Delta S)_p\,\ln V_p = \mathbf{\Delta S}\mathbf{\cdot}\ln\mathbf{V}. \end{split}\]

Tässä $\mathbf{\Delta S}=\mathbf{S}-\mathbf{Q}$. Toisessa ja viimeisessä lausekkeessa piste $\mathbf{\cdot}$ tarkoittaa vektorien pistetuloa⁸:

\[\mathbf{u}\mathbf{\cdot}\mathbf{v} = u_1v_1+\ldots+u_nv_n = \sum_{k=1}^n u_kv_k.\]

Toiseksi viimeinen yhtälö johtuu logaritmien laskusäännöistä ja siitä, että kelvollisille paikkajaoille

\[(\Delta S)_1+\ldots +(\Delta S)_P=0.\]

Kun kaikille kolmelle momentille, joista kustakin on $100\,000$ toteutumaa, lasketaan aritmeettinen keskiarvo AM, saadaan seuraava taulukko:

Taulukon perusteella D’Hondtin menetelmä pyrkii “kiertämään” suhteellisuusperiaatteen mukaista paikkajakoa positiiviseen kiertosuuntaan niin, että suurten puolueiden paikkamäärät kasvavat pienten kustannuksella. Sama ilmiö toistuu lähes samoilla momenteilla, kun äänisaalisvektori $\widehat{V}$ peilataan päinvastaiseen järjestykseen (engl. flip) ja arvotaan uudet äänestystulokset, ihan vaan tarkistuksen vuoksi.

Mistähän D’Hondtin puoluetuki suurille puolueille johtuu? Vastauksen miettiminen jätetään lukijalle. Vihjeenä muistutetaan, että äänissä mitattu D’Hondtin hinta paikalle on yleensä pienempi kuin $V/\Sigma$, äänten kokonaismäärä jaettuna paikkojen kokonaismäärällä.

Yhteenveto

Vaalien suhteellisuudella tarkoitetaan sitä, että edustajapaikat jakaantuvat puolueille samoin kuin vaaleissa saadut äänet. Suomen eduskuntavaaleissa suhteellisuus toteutuu heikosti: eräät pienet puolueet menettävät jopa useita paikkoja suurille puolueille vaalijärjestelmän takia. Perustuslain edellyttämälle suhteelliselle vaalitavalle pahin este on perustuslain niin ikään edellyttämä vaalipiirijako. Suhteellisuuden vinoumaa suurten puolueiden eduksi kärjistää vaalipiirien paikkajaossa käytetty D’Hondtin menetelmä.

Eduskuntavaaleja simuloitiin ilman vaalipiirijakoa. Simulaatiossa tutkittiin suhteellisen vaalitavan toteutumista vertaamalla keskenään kolmea laskentamenetelmää: Hare-Niemeyerin menetelmä, geometrinen menetelmä ja D’Hondtin menetelmä. Näistä keskimmäisessä minimoidaan suoraan suhteellisuuden virhettä. Siksi ei ole yllättävää, että geometrinen menetelmä osoittautui suhteellisuusmielessä parhaimmaksi. D’Hondt selvästi suosi suuria puolueita, monesti jopa kahdella ylimääräisellä paikalla.

Artikkelissa tarkasteltiin vaaleja puhtaasti matemaattiselta kannalta — muutamia sivuhuomautuksia ehkä lukuunottamatta. Matematiikan ohella vaaleihin liittyy lukuisia puolue- ja yhteiskuntapoliittisia näkökohtia ja muita aspekteja.

Viitteet

[1] Alestalo, Pekka: Alabaman paradoksi.
https://matematiikkalehtisolmu.fi/2007/2/alestalo.pdf

[2] Finlex: Suomen perustuslaki.
https://www.finlex.fi/fi/laki/ajantasa/1999/19990731

[3] Finlex: Vaalilaki.
https://www.finlex.fi/fi/laki/ajantasa/1998/19980714

[4] United Nations Economic Commission for Europe:
Fresh Fruit and Vegetables - Standards.
FFV-15, Cucumbers.
https://unece.org/trade/wp7/FFV-Standards

[5] Yle: Eduskuntavaalit 2019. Tulospalvelu. Puolueet.
https://vaalit.yle.fi/ev2019/fi/parties

Alaviitteet

Yksinkertaisuuden vuoksi tässä artikkelissa kutsutaan puolueiksi vaaliliittoja, vaaliliittojen ulkopuolisia puolueita, yhteislistoja ja yhteislistoihin kuulumattomia valitsijayhdistyksiä.↩︎
D’Hondt-sukunimen kirjoitusasu on varmistettu Kotimaisten kielten keskukselta.↩︎
Aluevaaleissa kunkin hyvinvointialueen aluevaltuustopaikat jaetaan D’Hondtin menetelmällä (vaalilaki [3], 143 l §, 88–91 §). Menetelmä on käytössä niin ikään kunta- ja europarlamenttivaaleissa (vaalilaki [3], 91 §, 179 §).↩︎
Oikeusministeriön julkaisuissa käytetään tätä määritelmää kvootille. Termin merkityssisältö vaihtelee kirjallisuudessa.↩︎
Valtakunnan jakoa maantieteellisiin vaalipiireihin eduskuntavaaleissa voidaan kritisoida. Eduskunta on pääasiassa valtakunnallisia lakeja säätävä ja eräitä muita valtakunnallisia ja kansainvälisiä tehtäviä hoitava elin. Alue- ja kuntavaaleilla valitaan henkilöitä paikallisiin luottamustoimiin. Ahvenanmaalla on eduskuntavaaleissa erityisasema. Tässä artikkelissa tuota erityisasemaa ei oteta huomioon.↩︎
Nolla ajatellaan tässä samanmerkkiseksi kaikkien lukujen kanssa.↩︎
Kvoottivyöksi kutsuttu joukko on itse asiassa $P$-ulotteisen avaruuden ${\mathbb R}^P$ yksikkökuutio, joten yhtä hyvin voitaisiin puhua kvoottikuutiosta.↩︎
Kaavassa esiintyvä pistetulo saattaa hämätä fyysikoita. Kysymyksessä on itse asiassa momenttien summa samalla tavalla kuin jäykän kappaleen tasapainoehdossa.↩︎