Tuntiselostuksissa on yritetty tuoda esille luokassa
käytyä keskustelua.
Opettaja: Márta Oravecz
Taso: 1. luokka, oppilaat 6-7 vuotiaita
Aihe: lukujen havainnollistaminen
Aiheen käsittely aloitetaan värisauvoilla. Opettaja kiinnittää taululle punaisia sauvoja 6 kpl ja kysyy lukumäärää. Mietitään, miten se voidaan laskea eri tavoilla. Joukossa on 3 vähän vaaleampaa, joku käyttää tätä apuna 6 = 3 + 3. Sauvoja katsomalla seurataan laskemista lähtien yhdestä. Sitten tehdään sama vihreillä -- pidemmillä -- sauvoilla. Kuusi punaista sauvaa mitataan nauhalla. Tehdään sama vihreille. Opettaja kehottaa jokaista tekemään saman kuin taululla ja varmistaa, että kaikki tietävät, mitä tehdään. Valmiit viittaavat, opettaja kiertää ja neuvoo, jos on tarpeen. Jos tämän vaalensinisen sauvan pituus on yksi, niin minkä pituus on kaksi? Paljonko on vihreän pituus? Neljä. Kaikilla lapsilla on paperiliuska. Opettaja kysyy: Voinko sanoa, että tämän paperiliuskan pituus on 6? Oppilas perustelee: Voi, jos asetan 6 vaaleansinistä peräkkäin, se riittää juuri täsmälleen, siis se on 6.
Oppilaiden tehtävänä oli tuoda kouluun jotain, mitä on kuusi kappaletta. Oppilas: Toin 6 lusikkaa. Miksi niitä on kuusi? Yleensä ostetaan 6 haarukkaa, lusikkaa ja veistä. Toin 6 tussikynää. Jollain on Rubikin kuutio, siinä on 6 sivutahkoa. Joku on tuonut palapelin, jossa on 6 osaa, joku tietää, että leppäkertulla on 6 täplää. Eräs lapsi kertoo, ettei hän tuonut mitään, mutta Jumala loi maailman kuudessa päivässä ja lepäsi seitsemäntenä. Jonkun kotona on kylpyhuoneessa 6 kaappia, jollain on kengässä 6 reikää, jollain hiuksissa 6 kukkaa. Löytyykö vaatteista jotain 6 kappaletta, kysyy opettaja. Lapsella on 4 nappia takissa. Opettaja kysyy, montako puuttuu, jotta olisi 6. Opettaja näyttää syntymäpäiväkakun kuvaa, siinä on kynttilöitä. Kuinka monta? Kuka on 6 vuotta? Kenellä on lähellä 7. syntymäpäivä? Katsokaa ympärillenne, mitä on 6? Erään lapsen syntymäpäivä on 6.3. Laatikossa on lukusuora helmistä. Näyttäkää, missä on 6. helmi. Montako on kädessä, kun näytätte 6. helmen? Yksi, se 6.
Lattialla on lukusuora, johon oppilas merkitsee 0-kohdan. Kukkapurkki asetetaan 6:n kohdalle. Nollan paikkaa vaihdetaan nyt; joku lapsista näyttää, missä on 0 ja kaikki miettivät, mihin tulee 8. (Tämä on lapulla oleva talon kuva, jossa on numero 8). Miten voi tarkistaa, onko oikein? Oppilaat antavat ohjeet tarkistukselle: 6:sta kaksi (lukusuoran yksikön pituista) askelta oikealle. Sitten asetetaan 7 ja 5 paikoilleen. Jokaisella on oma lukusuora (helminauha). Opettaja kysyy: Voiko merkitä viidennen, vai onko tehtävä jotain sitä ennen? Mitä on tehtävä ensin? Ensin on valittava 0, sitten 5:n paikka. Mikä on 5:n suurempi, mikä pienempi naapuri? Mitkä ovat 4:n naapurit? Mitkä 6:n naapurit? Tehdään vastaava yhdessä: opettajalla on naru, jossa on pyykkipoikia tasaisin välein. Ensin valitaan 0, sitten asetetaan 5, 6 ja 7 paikalleen. (Kiinnitetään lappuja, joissa on numerot 5, 6 ja 7). Opettaja kysyy, missä on 6:n paikka. Joku saattaa huomata, että se riippuu siitä, kummasta suunnasta laskeminen aloitetaan. Opettaja tekee tahallaan virheen. Sen jälkeen hän kysyy, onko oikein. Asia korjataan ja laskemalla tarkistetaan lopuksi, että tuli oikein.
Opettaja kiinnittää taululle kuvan, jossa on 6 teepussia. Hän pyytää
kertomaan kuvasta. Toisessa kuvassa on yksi teepussi. Niiden väliin
merkitään nuoli muutosta merkitsemään. Lapset keksivät tarinan muutoksesta.
Merkitään muutos taululle lapulla, jossa on ![]() . Lopuksi se sanotaan
matematiikan kielellä:
. Lopuksi se sanotaan
matematiikan kielellä: ![]() . ("Kuudesta pois viisi, jää yksi.")
. ("Kuudesta pois viisi, jää yksi.")
Opettaja pyytää lapsia sulkemaan silmät. Kun he avaavat silmät, he kertovat, mikä muutos on tapahtunut. Kuvat on vaihdettu toiseen järjestykseen. Taas tehdään tarina. Ajattele, että olet keittiössä, ensin oli 1 teepussi, sitten ostit 5 lisää. Muutos merkitään taululle lapulla, jossa on +5. Matematiikan kielellä 1 ja 5 on 6, 1 + 5 = 6.
Pidättekö teestä? Mistä muusta juomasta pidätte? Kuka pitää maidosta, teestä, kaakaosta, appelsiinimehusta? Taululle kiinnitetään näiden kuvat ja jokainen käy pistämässä napin (tytöt punaisen, pojat sinisen) mieluisen juomamerkin yläpuolelle (katso kuva ). Näin saadaan tilasto, jota tarkastellaan. Useimmat pitävät kaakaosta, harvat maidosta, teestä pitää 9, kuinka monta oppilasta enemmän pitää kaakaosta kuin teestä? 3 pitää appelsiinimehusta (1 tyttö ja 2 poikaa).
Taas suljetaan silmät, opettaja pistää oman nappulansa maidon kohdalle. Mitä
muuttui? Nyt maidosta pitää 3, 11 kaakaosta. Miksi opettajalla on suurempi
punainen nappula? Koska hän on opettaja ja suurempi ja nainen. Kotitehtäväksi
tulee kirjoittaa vihkoon ![]() , piirtää tästä tarina ja kertoa se. Tehtävä
luetaan ''6:sta pois 2 on 4''.
, piirtää tästä tarina ja kertoa se. Tehtävä
luetaan ''6:sta pois 2 on 4''.
Opettaja: Márta Oravecz
Taso: 1. luokka, oppilaat 6-7 vuotiaita
Aihe: luvun 6 hajoitelmat
Tunnin aihe on hankkia kokemuksia lukuun 6 liittyen. Tunnin alussa opettaja tarkistaa, onko kaikilla tarvittavat välineet. Kullakin oppilaalla on kangaspussi, näitä on neljää eri kangasta (ja samanlaisissa pusseissa on samanlainen sisältö). Pyöreästä pahvikotelosta on tehty laite; kotelon kanteen on liimattu tornimainen lisä ja kotelon sisus on jaettu neljään yhtäsuureen sektoriin pahviristillä. Kotelon “tornista” voidaan pudottaa pieniä esineitä, jotka pudotessaan joutuvat johonkin näistä neljästä sektorista. Kansi avaamalla voidaan tarkastella, miten jakautuminen on tapahtunut.
Tarkistetaan riveittäin, montako oppilasta on. Ensimmäisessä rivissä on 2 + 2 + 2, siis 6 oppilasta. Löytyykö toista samanlaista riviä? Yhdessä rivissä on 5, siis 6 – 1 oppilasta, viimeisessä 6 + 2 eli 8 oppilasta. Oppilaat sanovat nämä asiat. Edellisen tunnin harjoitus oli nopea laskutoimitus kuvasta. Nyt sama tehdään muistista, kääntyen selin piirtoheittimeen, jolla näytetään aikaisempi kuva. Kuvan ruuduissa on 1 – 6 esinettä, sormia, puun lehtiä, nappula, jossa on 6 pistettä, karkkeja. Mitä on 6? Mitkä kuvassa voidaan jakaa kahteen yhtäsuureen osaan (tämä pohjustaa parillisuutta)?
Jokaisella oppilaalla on helminauha, jossa on 10 helmeä. Jokainen laskee helmet. Sitten helminauha laitetaan selän taakse ja lasketaan helmet sormin tunnustelemalla. Näyttäkää 10 – 1, laskekaa 3 + 3 sormin selän takana, samoin yhtä suurempi kuin 6, kahta suurempi kuin 4, laskekaa sormin selän takana 1 + 2 + 3. Näyttäkää kuudes helmi. Tunnista on nyt kulunut n. 10 minuuttia.
Kangaspusseja on neljää erilaista. Kaikissa on helmiä. Lasketaan helmet tunnustelemalla.Ne, joiden pussissa on 10 helmeä, ottavat tulitikkulaatikkoon niistä 4, 9:n pussista otetaan 3, 8:n pussista 2, 7:n helmen pussista 1 helmi. Onko nyt jokaisessa pussissa 6 helmeä? Helmet otetaan ulos ja tarkistetaan. Jos joltakulta on hävinnyt helmiä, opettaja antaa tilalle. Taululle piirretään neljä pussia, jotka ovat samanlaisia kuin oppilaiden pussit. Niiden alle kiinnitetään (vastaaville kohdille) laput 8 – 2, 7 – 1, 9 – 3, 10 – 4.

Ensimmäisen tyyppisistä pusseista otetaan vasempaan käteen 2, oikeaan 4 helmeä. Toisesta pussista 1 ja 5, kolmannesta 3 ja 3, neljännestä 4 ja 2. Tähän toimintaan käytettiin n. 10 minuuttia.
Oppilaat ovat pareittain. Kullakin parilla on alussamainittu pyöreä kotelo. Toinen parista pudottaa yläaukosta sisään 6 helmeä. Mitä tapahtui? Toistetaan. Tuleeko sama tulos? Tämä tehdään parityönä ja oppilaat ovat innostuneita. Miten kerrotaan, että johonkin lokeroon ei tullut yhtään helmeä? Nolla helmeä. Toinen oppilas kirjaa tuloksia, esim. 2 + 0 + 0 + 4, 2 + 3 + 1 + 0. Vastaavaa on tehty aikaisemmin sini-punakiekoilla. Kuka on saanut kaikki eri tulokset? Kenellä on enemmän kuin 4 erilaista tulosta? Tämä tullaan tekemään myöhemmin uudelleen. Toimintaan kului n. 15 min. Inostuneen luokan rauhoittamiseksi opettaja sanoo, että kuudennella taputuksella jokainen menee hiljaa paikalleen.
Nyt aletaan katsella tulitikkulaatikoita. Montako helmeä siellä on? Niitä on yhdestä neljään, taululta näkee, montako pitäisi olla, koska eri pussit ovat näkyvissä. Montako on lisättävä, jotta saadaan 6? Näytä kädellä. Mitä tämä olisi matematiikan kielellä? Opettaja lisää pussien kuvien alle 2 + 4, 1 + 5, 3 + 3, 4 + 2. Nyt huomataan, että kaikki taulun hajoitelmat ovat 6. Aikaa on vielä 5 minuuttia, otetaan harjoituskirja esiin ja tehdään 6:n hajoitelmiin liittyviä tehtäviä, joissa osassa on myös kuvat, tehtävät on täydennettävä niin, että tulokseksi saadaan 6. Loput jätetään kotitehtäväksi. Onko kysymyksiä? Tehtävien tarkastusta tehdään myös pareittain.
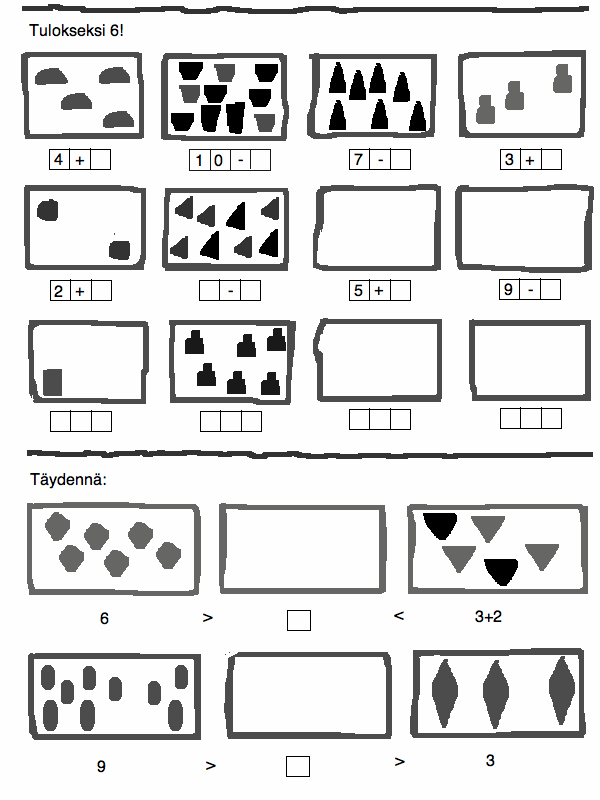
(Kuva kirjasta: C. Neményi Eszter ja Sz. Oravecz Márta: Matematika Munkafüzet általános iskola 1. osztály)
Parityöskentelyn aloitus on tärkeää, sitten 3. luokalla tätä tehdään enemmänkin. Jos joku on valmis, joko opettaja tarkistaa tai tarkistus tehdään parin kanssa. On helpompaa, jos virhe huomataan vain parin kanssa kahden. Lopuksi opettaja kehuu, että yhteistyö meni hyvin ja tarkistaa, että kaikki ymmärtävät, mikä on kotityö. Kotityö voidaan tarkistaa koulussa pareittain. Lopuksi oppilaat tekevät 6 kumarrusta luokassa vierailevalle.
Opettaja: Márta Oravecz
Taso: 1. luokka, oppilaat 6-7 vuotiaita, tukiopetus
Opettaja kysyy lapsilta: Montako teitä on? Miten teidät voitaisiin jaotella ryhmiin? Osaatte sanoa sen jo matematiikankin kielellä. Antakaa esimerkkejä. Lapset sanovat esimerkiksi: 1 + 6, 1 poika ja 6 tyttöä, 3 + 4, 3 vaaleatukkaista ja 4 ruskeatukkaista lasta, 3 + 4 sama päinvastoin, 6 + 1, 6 tyttöä ja 1 poika.
Opettaja: Entä 5 + 2? Mikä voisi olla näin? Yrittäkää keksiä. Osaatko antaa esimerkin?
(Lapset kääntyvät ja tarkastavat laskutoimituksen) Opettaja: - Menkää nyt jonoon, leikitään niin, että jotkut teistä menevät ensin ulos ja tulevat sitten takaisin. Sisään tultaessa on keksittävä, mitä luokassa on muuttunut. Ne voivat mennä ensin ulos, joilla on koulutakki päällä. Tulkaa takaisin, kun koputan. Mutta tarkistetaan ensin, kuinka monta meitä on. (Lapset laskevat että luokassa on 7 oppilasta, joista 4 menee ulos.) Opettaja: - Osaatteko kertoa, millainen muutos täällä luokassa tapahtui? (sanoilla) Montako lasta luokassa oli? 7. Sano se kokonaisella lauseella! Luokassa oli 7 oppilasta, joista 4 meni ulos, luokkaan jäi 3. Osaatko kertoa tämän saman asian matematiikan kielellä? 7 - 4 on 3.
Opettaja koputtaa.
Opettaja: - Osaatteko kertoa, mitä nyt tapahtui? Ensiksi sanoilla.
Luokassa oli ensin 3 lasta, sitten 4 tuli vielä lisää.
Montako lasta luokassa nyt on?
7.
Osaatko kertoa tämän matematiikan kielellä?
3 + 4 on 7.
Jatketaanko vielä?
Kyllä.
Nyt voisivat mennä ulos, ne joilla on vaaleapunainen pusero päällä. Tule sitten takaisin, kun
koputan oveen. (1 lapsi menee ulos)
Opettaja: - Kertokaa matematiikan kielellä, mitä äsken tapahtui.
Luokassa oli 7 lasta, 1 meni ulos ja luokkaan jäi 6.
Haluaisin, että sanoisit tämän nyt matematiikan kielellä.
7 - 1 on 6.
Hyvä.
Opettaja koputtaa ja vaaleanpunapuseroinen tyttö tulee sisään.
- Kerro (sanoilla) mitä tapahtui, kun Zsófi tuli sisään.
6 + 1 on 7.
Hyvä. Sanoitkin asian heti matematiikan kielellä.
Miettikääpäs nyt sitä, että Zsófi meni ensin ulos ja tuli sitten takaisin. Osaatteko sanoa nämä molemmat asiat matematiikan kielellä?
7 - 1 on 6.
Kyllä, mutta hän tuli sitten takaisin.
6 + 1 on 7.
Oikein hyvä.
Opettaja: - Nyt annan kaikille erilaiset tehtävät.
Muistipeli autokorteilla
Opettaja: Tehän tunnette säännöt. Yhdistäkää kortit pareittain sen mukaan, meneekö auto oikealle vai
vasemmalle.
Pikkukorttipeli
Opettaja: - Muistatteko tämän pelin? Osaatteko kertoa sen säännöt?
Kortit laitetaan pöydälle kuvapuoli alaspäin. Käännetään yksi kortti ja sen päälle etsitään
sellaista korttia, joka on samanvärinen tai jossa on sama luku.
Domino
- Keksitte varmasti tämän pelin säännöt. Jos ette, autan kyllä, mutta toivoisin, että keksisitte
säännöt itse.
Seitsemäs lapsikin saa tehtävän:
Opettaja: - Haluaisin että sinä valmistelisit toisille lukusuoran. Mistähän olen alkanut sitä mittaamaan?
Opettaja tarkistaa, ovatko lapset ymmärtäneet pelit.
Opettaja: - Mihin suuntaan auto kulkee?
- Vasemmalle.
- Kumpi on sinun vasen kätesi? Näytä!
Opettaja: - Miten teidän pelinne sujuu. Mitä te etsitte?
- Vihreää tai kuutosta.
Opettaja: - Mihin suuntaan kulkee se, jota nyt etsitään?
- Oikealle.
Opettaja:- Jatketaan vähän eri tavalla. Jatketaan niin, että voit nostaa 5 korttia ja jos niiden joukossa
on sopiva, voit pitää sen itselläsi. (Opettaja näyttää.)- No niin. Tälle ei nyt löytynyt paria. Nyt
on sinun vuorosi. Voitte jatkaa. Onnistuuko?
Ensimmäinen lukusuora on jo valmis, opettaja antaa lukusuoratehtävän myös toiselle lapselle.
1, 2, 3, 4, 5, 6
Opettaja: Hyvää. Jätä leppäkerttu sinne. Tuoli on pikku mökki. Tuo se tänne.- 7 on pensas. Missä 5
on? Hyvä. Laita se sinne.- Nyt liikut leppäkertun kanssa.
(Opettaja auttaa tarvittaessa.)
Opettaja: - Astu 8 askelta. Montako askelta leppäkerttu on astunut, ja missä se on nyt? Missä pensas on?
Seitsemässä.
- Ja missä leppäkerttu on nyt?
- Kahdeksikossa.
Osaatko kertoa myös matematiikan kielellä, mitä on tapahtunut? Missä leppäkerttu ensin oli, montako
askelta se meni eteenpäin? Kerro.
7 ja 1 on 8.
Opettaja: - Nyt leppäkerttu astuu 1 askeleen taaksepäin. Osaatko kertoa tämän matematiikan kielellä?
8 - 1 on 7.
Hyvä. Mene nyt etsimään pöydältä jotain sellaista, jota on 6.
Opettaja kysyy toisilta, miten peli etenee.
Opettaja: - Kun peli loppuu, menkää etsimään pöydältä jotain sellaista, mitä on 6.
Myöhemmin opettaja kysyy: - Mitä löysitte?
- Hyvä. Pikkuleipiä.
- Tämäkin on hyvä, eläimellä on 6 jalkaa. Vie se sinne taulun viereen.
- Voitte mennä omaan luokkaan, Bea voi jäädä tänne.
Bea saa lukusuoratehtävän.
Opettaja: - Leppäkerttu kulkee nyt pensaan luokse. Se lähtee tästä pikku mökistä. Kerro nyt tämä sama
asia myös matematiikan kielellä.
Montako askelta oli pensaaseen asti?
Laskutoimitus ei onnistu, opettaja auttaa.
Opettaja: - Aloitetaanpa uudelleen, niin nähdään. 0 1 2 3 4 5 6 7
Se lähtee tästä. Muistatko, mikä se oli? Lasketaan. 0 1 2 3 4 5
Montako askelta se otti, kun se meni pensaan luokse?
2
- Kyllä. Osaatko kertoa sen matematiikan kielellä?
5 + 3
- Katso! 1, 2
5 + 2 on 7.
Opettaja: - Voiko se leppäkerttu mennä nyt takaisin pikku mökkiin?
- Kyllä. 1, 2
- Osaatko kertoa tämän asian matematiikan kielellä? Mistä se lähti kulkemaan takaisin?
7 - 2 on 5.
- Oikein hyvä. Voit istua sinne.
Seuraava tehtävä suoritetaan kahdella erilaisella välineellä. Toinen on sini-punainen kiekko ja toinen
on paperinauha. Kaksi tyttöä tekee samaa tehtävää, mutta erilaisilla välineillä.
Opettaja: - Voit katsoa, mitä hän tekee ja yrittää tehdä saman asian tällä toisella välineellä.
Opettaja: - Montako punaista ja montako sinistä tässä on?
Ei yhtään punaista, mutta 6 sinistä.
Käännä niistä yksi toisin päin. Kerro matematiikan kielellä mitä nyt näet.
(Toinen tytöistä tekee samaa tehtävää paperinauhalla, hän taittelee nauhaa.)
1 + 5 on 6.
Opettaja sanoo toiselle tytölle:
- Sinäkin osaat nyt sanoa, mitä olet tehnyt. Kerro matematiikan kielellä.
1 + 5 on 6.
Opettaja: - Käännä 2 kiekkoa toisin päin.
Kerro matematiikan kielellä.
2 + 4 on 6.
Opettaja toiselle tytölle:
- Kerro sinäkin, mitä teit.
2 + 4 on 6.
- Osaatteko jatkaa tehtävää?
Tytöt jatkavat tehtävää.
Opettaja: - Oikein hyvä. Kerro sinä nyt ensiksi.
3 + 3 on 6.
Osaatteko jatkaa?
4 + 2 on 6.
5 + 1 on 6.
6 + 0 on 6.
Toinen lapsista lähtee, toinen saa "kiekkotehtävän".
1 + 5 on 6.
2 + 4 on 6.
3 + 3 on 6.
4 + 2 on 6.
5 + 1 on 6.
6 + 0 on 6.
Opettaja: Osaatko kertoa tämän nyt silmät kiinni sillä tavalla, että vain kuvittelet sen? Voit
näyttää kädellä.
Oppilas tekee tehtävän.
- Oikein hyvä. Keksitkö sen heti?
- Kyllä.
Näytä nyt sormilla paljonko on 6.
Opettaja näyttää sormilla 2, oppilas näyttää 4, jne.
Seuraavat tehtävät tehdään värisauvoilla.
Opettaja: Etsi sauva, jonka voi mitata kahdella vaaleanpunaisella.
Oppilaan vastaus on väärä ja opettaja kysyy siten, että lapsi itse keksii oikean ratkaisun.
Tämä on 4 ja tämä toinenkin on 4. Kumpi näistä on perusyksikkö neljään kertaan?
Seuraava värisauvatehtävä on "maton kutominen" erilaisista värisauvoista.
Matto on vihreän mittainen. Muistatko, mikä on tämän nimi, jos perusmittana on vaaleanpunainen?
Opettaja: Onko vielä sellaisia sauvoja, että niistä saa kokonaisen rivin?
Opettaja auttaa ja aloittaa rivin, oppilas jatkaa.
Opettaja valmistelee tehtävää siten, että hän panee pöydälle myös vaaleanpunaisia sauvoja.
Opettaja: - Katsotaanpa tätä. Ensiksi sanoilla, sitten matematiikan kielellä.
Luokan eteen kerätään ne, joilla on koulutakki. Kuka on jossain suhteessa
erilainen? (Opettajalla on mielessä jotain, joka oppilaiden tulee arvata.)
Kahdella oppilaalla oli saappaat jalassa.
Luokan eteen kerätään 5 tyttöä. Heistä tehdään tosia lauseita. Kaikki ovat
tyttöjä, kaikilla on poninhäntä. Mikä väite heistä ei ole totta? He eivät ole
poikia. Opettaja haluaa jakaa heidät jotenkin kahteen ryhmään. Hän ottaa
erikseen kaksi tyttöä. Mikä oli peruste? Ne, joilla on hiusnauha, valittiin. Kuka
luokasta tulisi vielä tähän joukkoon? Kuka heistä on erilainen? Yhdellä on
valkoinen hiusnauha, muilla punainen. Miten voitte esittää piirroksella tätä
ryhmää? Minkä merkin voisitte antaa sille? Joka on valmis, näyttää koko
luokalle. Ovatko piirrokset samanlaisia? Sopivatko ne kaikki hiusnauhallisten
ryhmän merkiksi? Miten saisi kaikille yhteisen merkin? Punainen ei sovi
kaikille. Sellainen merkki, josta näkyy vain että on kyseessä hiusnauha kelpaa
kaikille, ilman väriä.
Opettajalla on suuri kori, jossa on kaikenlaisia tavaroita (lankakerä, muki,
taulusieni, hiusharja, sakset, pullo, ankkalelu). Päättelyä: onko näissä eläviä
olentoja? Onko ankkalelu elävä? Osaako se puhua? Vastaus: vain, jos oppilas
puhuu lelun puolesta. Kasvaako se suureksi ankaksi? Opettaja valikoi tavaroita ja
kysyy, osaako joku jatkaa samalla periaattella. Esim. kaikki valitut tavarat ovat
vihreitä. Luokitteluja jatketaan, jokainen tuo esineen, joka ei ole vihreä.
Symboleilla näytetään, mitä halutaan. Esimerkiksi vihreä ruutu tarkoittaa, että
halutaan vihreää väriä, yliviivattuna samanlainen ruutu, että halutaan esineitä,
jotka eivät ole vihreitä. Opettajalla on piilossa kuva, kysymyksillä
selvitetään, mitä siinä on. Näytetään kyllä (tosi) lappuja ja ei (epätosi)
lappuja, kun opettaja tekee kysymyksiä. Oppilaat tekevät omia lauseita.
Taululla on isoja lukudominoita, esim. 728 999 ja 542 300 + 76. Pulpetit on järjestetty 4:n oppilaan ryhmiin, kummallakin laidalla 2 oppilasta. He ottavat matematiikkalaatikot esiin. Leikitään lukudominoilla. Opettaja on kiinnittänyt niitä taululle. Lapuissa on lukuja erilaisissa muodoissa. Etsikää taululta 802. Dominoita jatketaan lattialla. Jotkut ovat muodossa 4 5k 0t (eli 54) tai 50k – 1 (eli 499). Ratkaisut myös luetaan. Tähän kuluu 10 minuuttia.
Etsikää näin paljon rahaa: lapulla lukee 33 sataa ja 3. Pussissa on itse tehtyjä leikkirahoja. Samoin jatketaan. Sitten opettaja ottaa ison pallon ja heittää sen jollekulle, ensin lähdetään luvusta 57 ja jokainen pallon saaja lisää yhden ja sanoo luvun ääneen. Sitten aletaan luvusta 370 ja tehdään samoin. Sitten lähdetään luvusta 70 edeten 10:n lisäyksillä, sitten 170:stä kymmenen lisäyksin, pallo heitetään opettajalle joka toinen kerta. Lähdetään 370:stä, 10:n lisäyksin, sitten 320:stä 10:n vähennyksin. Tätä tehdään 15 minuuttia, josta pallolla heittelyä 5 minuuttia.
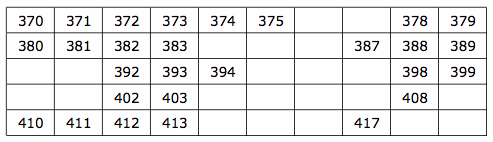
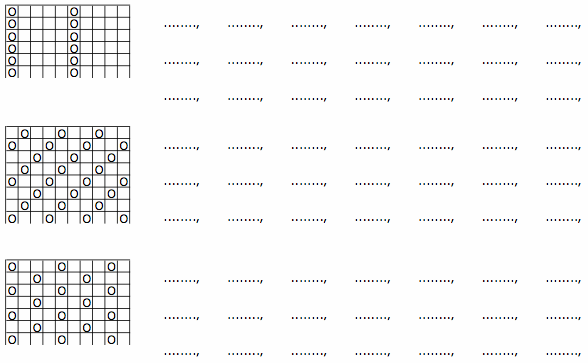
Otetaan harjoituskirja ja tehdään täydennystehtäviä, jokainen täydentää kuvaa ja opettaja kiertää luokassa.
Taulukkoon väritetään ne luvut, joissa on 6 ykköstä, ne, joissa on 8 kymmentä. Kuka on valmis? Piirtoheittimellä tarkistetaan sama harjoitus, opettaja täyttää, kun oppilas lukee tuloksia. Kenellä on oikein? Missä ovat ne luvut, jotka ovat etäisyydellä 10 tästä luvusta (opettaja näyttää luvun kohtaa)? Tarkistetaan kalvolta. Kalvolla on ruudukko, johon opettaja merkitsee oppilaiden ehdotusten mukaan merkittyihin kohtiin lukuja, kun ensimmäinen on 370. Luvut luetaan, tehdään uusia tehtäviä pistämällä kalvolle nappuloita. Täydennetään taulukkoa erilliselle lukuarkille, johon on merkitty osa luvuista. Tehdään samaa arkille, johon on merkitty vain lukujen paikkoja erilaisina kuvioina, kuten edellä. Piirtoheittimelle asetetaan nappuloita ja oppilaat kertovat, mitä lukuja niihin paikkoihin kuuluu.
(Kuvat kirjasta: C. Neményi Eszter ja Wéber Anikó: Matematika Munkafüzet általános iskola 3. osztály)
Opettaja antaa lompakkotehtävän: On kolme erilaista lompakkoa, yhdessä on 200 forinttia, toisessa 500 forinttia ja kolmannessa 750 forinttia. Nahkaisessa lompakossa on vain yksi seteli. Vetoketjullisessa on kolme rahaa. Kolmannessa lompakossa jokainen raha on suurempi kuin 100 forinttia ja tässä kukkarossa on vähemmän rahaa kuin nahkaisessa. Mitkä rahat ovat missäkin kukkarossa? Käytettävissä olevat rahat ovat: setelit: 200, 500, 1000, kolikot: 1, 2, 5, 10, 20, 50, 100, 200.
Opettaja jakaa apuvälineitä: riisiä, hiekkaa, eri muotoisia paperinpaloja.
Lopuksi hän varmistaa, että kaikilla on tehtävää, jokaisen tulisi muodostaa
neljännes saamastaan materiaalista. Kaksi oppilasta saa litran vettä ja
heidän tehtävänään on jakaa se neljään yhtä suureen osaan. Heillä on laseja
apuna. Hiekkakasan saaneet jakavat sen ensin kahtia ja sitten vielä kahtia.
Valmiit oppilaat viittaavat. Kun melkein kaikki ovat valmiita, oppilaat
selvittävät, miten he ratkaisivat tehtävän. Oppilas kertoo leikanneensa
omenan ensin puoliksi ja sitten puolikkaat vielä puoliksi. Näin tulee neljä
osaa, jotka ovat suunnilleen saman kokoisia. Mikä tämä yksi pieni osa on?
Osaatko sanoa sen? Neljäs osa. Oikein hyvä. Montako neljäsosaa on kokonainen?
Mitä tapahtui riisille? Ensin yritimme jakaa sen kahtia ja sitten vielä osat
kahtia, näistä osista tuli suunnilleen saman suuruisia. Osaatko näyttää, mikä
näistä on neljäsosa? Onko tämä ainoa neljäsosa? Tämäkin on neljäsosa. Toinenkin
on neljäsosa ja neljäskin on.
Miten hiekan kanssa kävi? Miten työskentelitte? Jaoimme sen ensin kahtia ja
sitten vielä kahtia, näin syntyi 4 samanlaista osaa. Näytä, mikä on yksi
neljäsosa. Tämä ja nämä kaikki ovat neljäsosia.
Mitä välineitä vielä oli? Kenellä oli lankaa? Taitoin langan kahtia ja sitten vielä
kahtia. Tämä on siis neljäsosa. Montako osaa täytyy tehdä, jotta saamme
neljäsosia? Mikä on yhden osan nimi? Neljäsosa. Jollakin oli
ympyränmuotoinen paperinpala. Tämä on myös neljäsosa, ympyrän neljäsosa.
Moneksiko osaksi hän jakoi sen? Neljäksi. Miksi näitä osia sanotaan? Näytä
minulle neljäsosa.
Oliko vielä muita tehtäviä? Paljonko vettä oli tässä astiassa? Yksi litra. Mitä
sille tehtiin? Yritettiin kaataa kaikkiin laseihin yhtä paljon vettä ja kun sitä
jäi jäljelle, kaadettiin vielä lisää ja siitä, jossa oli enemmän, kaadettiin
muihin. Näin kaikkiin tuli suunnilleen yhtä paljon. Paljonko vettä on
yhdessä lasissa? Oppilas vastaa 250 dl. Jos jaamme litran vettä, on 250 dl
liian paljon. Toinen vastaa 2 ja puoli desilitraa. Juuri niin, voimmeko
mitata tämän? Mitataan tällaisella mitta-astialla. Minkä takia kaadoitte
neljään lasiin eikä kolmeen tai viiteen? Koska näin oli helpointa jakaa se
neljään osaan.
Kenellä oli paperiliuska? Tämä oli aika pitkä paperinpala. Taitoin sen
kahtia ja sitten taitoin vielä kahtia. Siis yksi kokonainen paperiliuska on
montako neljäsosaa?
Tällä välin on tarkistusmittaus valmistunut, mitta-astian mukaan vettä oli
2 ja puoli dl.
Miten tämä toinen (neliapila, jossa on varsi) paperinpala onnistui?
Piirtäkää vihkoihinne ja kokeilkaa. Ei onnistunut. Osat eivät olleet saman
suuruisia. Tässä oli pieni osa, josta oli vain yksi kappale.
Yrittäkää keksiä, montako tällaista pientä kantaa siinä pitäisi olla, jotta
sen voisi jakaa täsmälleen neljään osaan. Joku ehdottaa: mutta sen voisi leikata
poiskin. Sen voi kyllä puolittaa, mutta pitäisi laskea, mistä kohdasta se
pitäisi taittaa, niin että jäisi yhtä paljon paperia molempiin osiin. Sen
voisi kyllä jakaa neljään osaan, mutta pitäisi laskea kauan ja monimutkaisesti.
Sen voisi jakaa, mutta pinta-ala olisi hyvin monimutkainen.
Mitä taululla on? 1 t, 1 l, 1 km, 1 kg. Nämä pitäisi nyt jakaa neljään
osaan. Tunnista neljäsosa on neljännestunti, se on 15 minuuttia, litran
neljäsosa on kaksi ja puoli desilitraa, kilometrin neljäsosa on 250 metriä
ja kilon neljäsosa 250 gr tai 25 dekagrammaa. Nämä ovat siis yhtä
suuria, 250 gr ja kaksi ja puoli dekagrammaa. Voidaan käyttää kumpaa tahansa.
Opettaja: Nyt näytän taululla jotain. Pyysin lapsia tuomaan minulle
neljäsosan jostain paperista. Nämä paperit taululla ovat niitä. Mitkä
näistä ovat neljäsosia?
Oppilas vastaa: kaikki. Voivatko ne kaikki olla neljäsosia, ne ovat eri kokoisia?
Ovatko kaikki neljäsosia jostain paperista? Nehän ovat kaikki erilaisia. Kaikkien
pitäisi olla jonkinlaisia neljäsosia. Voivatko ne olla? Vastaus: esim. kolmioon
voisi lisätä kolme samanlaista kolmiota ja siitä tulisi paperi, jonka neljäsosa
se kolmio on. Se olisi vain erilainen paperi. Meidän tulisi löytää niiden toiset
osat. Siis mihin verrattuna nämä ovat neljäsosia? Onko jossain se loppupaperikin,
siis nämä ovat neljäsosia vain jos niitä verrataan johonkin kokonaisuuteen. Tässä
on suuri paperi. Jos tämä on kokonainen, niin mikä on tämän neljäsosa tuolla
taululla? Aivan oikein. Onko tämä oikea neljäsosa? Montako kertaa tämä mahtuu
tämän paperin päälle? Kahdestiko? Monestiko sen pitäisi mahtua siihen? Neljästi.
No niin, se sopii siihen 4 kertaa.
Tässä on toinen paperi. Mikä on tämän neljäsosa? Kuinka monta kertaa tämä
paperiliuska mahtuu tuohon paperille? Sen pitäisi mahtua neljästi.
Laskekaa, kuinka monesti se mahtuu siihen. Kolmesti ja vielä neljännenkin
kerran. Tämäkin oli siis oikea ratkaisu. Mikä tämän neljäsosa olisi?
Tämäkin sopii neljästi. Mitä näille lopuille tapahtuu? Kuka löytäisi
pöydältä sellaisen paperin, joka on näiden nelinkertainen määrä? Minusta
nämä sopivat yhteen. Yritetään mitata. Miksi tämä ei sovi? Oppilas: Tämä ei
mahdu neljä kertaa tälle paperille. Hän pani sen siihen kahdesti, mutta siihen jäi
liikaa tilaa jäljelle. Se paperi mahtuu tälle paperille 8 kertaa. Tämä on siis
kahdeksasosa, tämän suuren paperin 8. osa. Tämä paperi taas on siitä juuri
puolet. Tämä on puolet, siihen mahtuisi täsmälleen 4 kertaa se paperi. Mikä tämä
pieni paperi on, joka jäi jäljelle? Mittaapa tällä paperin palalla. Se on
4. osa. Nyt löysimme kokonaisen. Onko tämä pieni paperi näinkin päin sen 4. osa?
Kahdesti se mahtuu näinkin päin, entäs vielä? Mahtuuko se 3. kerran? Näin se ei
mahdu, mutta reunasta jää kuitenkin vielä lisää paperia. Se on näinkin 4. osa. Onko
se 4. osa? Onko se näinkin 4. osa? On, mutta se pitää panna siihen toisin päin.
Mutta jos tämä pieni paperi asetetaan siihen pystyasennossa, niin se mahtuu
siihen 4 kertaa. Sen täytyy siis olla 4. osa. Mutta, entä jos paperi
asetetaan makuuasennossa, eikö se silloin ole 4. osa? Otetaan esimerkiksi tämä
omena. Katsotaan tätä 4. osaa. Jos otan sen pois ja leikkaan sen pieniksi
paloiksi, onko se silloinkin neljännes omena, siinä hedelmäsalaatissa pieneksi
leikattuna? Onko sekin 4. osa? Oppilas: On se edelleenkin.
Kuka voisi leikata tämän pienen paperin sillä tavalla osiin, että se mahtuisi
neljä kertaa tälle suurelle paperille? Kaksi tyttöä alkaa miettiä tätä tunnin
loppuun saakka.
Haluaisin, että kaikki ottavat tämän pienen sauvan eteensä, eikä pulpetilla
ole mitään muuta. Ottakaa esiin tällainen punainen sauva. Etsikää sen 4.
osa. Mitatkaa siitä 4. osa. Piilottakaa 4. osa kämmeneenne ja näyttäkää se
sitten. Kaikki ottivat vaaleanpunaisen sauvan. Mistä voitte tietää,
että tämä vaaleanpunainen on 4. osa punaisesta? Koska vaaleanpunaisia saa
panna 4 kpl sen päälle. Millaisia osia nämä vaaleanpunaiset ovat? Ne ovat
samanlaisia, yhtäsuuria ja niitä mahtuu 4 kpl. Ota nyt käteesi 3 neljäsosaa.
Näyttäkää minulle kolme neljäsosaa. Montako vaaleanpunaista sauvaa tässä on?
Kolme. Kuinka paljon tämä on enemmän kuin neljäsosa? Kaksi neljäsosaa enemmän.
Etsikää nyt puolta tästä punaisesta. Näyttäkää nyt yhtä aikaa. No niin,
kaikki löysivät tämän. Mikä on toiselta nimeltä tämä puolet? Kahdesosa.
Mikä sen nimi voisi vielä olla? Kaksi neljäsosaa. Miksi yksi kahdesosa ja
kaksi neljäsosaa on yhtä paljon? Koska 2 vaaleanpunaista sauvaa on yhtä
pitkä kuin tämä pidempi. Ja jos tämä vaalenpunainen on yksi neljäsosa, se
on ehkä 2 cm, mutta sitä nimitetään nyt yhdeksi neljäsosaksi. Mihin
verrattuna tämä oli yksi neljäsosa? Tähän viininpunaiseen sauvaan
verrattuna. Ja jos vaalenpunaiset ovat neljäsosia, mikä on viininpunaisen
nimi? Yksi kokonainen, yksikkö. Mikä se on numeroina ilmaistuna? Jos
vaalenpunainen on yksi neljäsosa, se on yksi.
Valitkaa vielä yksi sauva. Vaaleansininen on neljäsosa jostain muusta.
Mikä on se, joka on 4 kertaa vaaleansinisen pituinen? Ottakaa se
käteenne ja näyttäkää sitten, kun sanon. Nyt näyttäkää! Kaikki löysivät
vihreän. Mutta jos vaalensininen on neljäsosa, mikä on vihreän nimi?
Vihreän nimi on yksi, yksikkö.
Etsikää sellainen, joka on 4 kertaa punaisen pituinen, josta punainen on
neljäsosa. Minkä löysitte? Mikä on siis tämä ruskea sauva, jos punainen on
yksi neljäsosa? Ruskea on siis yksi kokonainen yksikkö.
Pistäkää värisauvat pois ja ottakaa esille eilinen paperista taiteltu kuvio.
Eilen siis taittelimme tämän paperin palan. Ensiksi puoliksi, mitä osia
syntyi silloin? Puolikkaita. Siis 2 puolikasta. Mutta sitten taiteltiin se
vielä kahtia ja taas saimme saman kokoisia paloja ja mikä niiden nimi voisi
olla? Ne ovat 4. osia. Ja sitten taiteltiin vielä. Mikä osan nimi voisi
olla nyt? Joku sanoi, että ne ovat 6. osia, joku, että 8. osia. Mitähän ne
ovat? Minusta 8. osia, aloitimme puolesta ja tuli 4. osia, siis 2 kertaa 2.
Sekin taitettiin kahtia, tuli vielä 2 kertaa enemmän, 8. osia. Siis jos 4.
osa kerrotaan kahdella, tulee 8. osa. Onko tämä totta? Siitähän tulisi
isompi, jos se kerrotaan kahdella. Katsokaa tänne. Kuinka monta osaa tässä
paperissa on? 4 samanlaista osaa. Mikä tämän pienen osan nimi on? 4. osa.
Jos se kerrotaan kahdella, tulee puolikas, eli yksi kahdesosa.
Tuliko siitä suurempi vai pienempi? Suurempi. Mutta mitä tässä äsken
haluttiin sanoa, mitä niille tapahtuu, jos paperi jaetaan edellen? Tulee 8.
osa. Tuleeko se pienemmäksi vai suuremmaksi? Pienemmäksi.
Avatkaa paperi, jota eilen taittelimme. Laskekaa siitä nämä pienet osat.
Kuinka monta samanlaista osaa tässä on? 8. Ja mikä on yhden osan nimi? 8.
osa. Taitellaan taas paperi pieneksi. Mitä tapahtuu, jos tämä taitetaan
vielä kahtia? Mitähän siitä syntyy? Kuudestoistaosia. Niin minustakin.
Ajattelevatko kaikki 16:ta? Taittakaa vielä kahtia. Avatkaa paperinpala.
Sanoitte, että siihen tulisi 16 osaa. Laskekaa nämä osat. Montako osaa
tässä paperissa on? 16 samanlaista osaa. Mikä yhden mini on? 16. osa.
Mitähän seuraavaksi tulee? 32. osa. Avatkaa edelleen taitettu paperi.
Montako osaa tässä on? Montako samanlaista osaa tässä on? 32. Mikä niiden
nimi siis on? 32. osa. Taittakaa uudelleen paperi pieneksi, pankaa
kynäkoteloon. Kotitehtävänä on taittaa vielä eteenpäin ja miettiä,
millaisia osia sitten tulee. Joka haluaa, voi taittaa vielä kahtia.
Ottakaa työvihko, sivu 109, tehtävä numero 1. Värittäkää ruudukosta sopivat
osat punaisella kynällä. Jos asetatte suuruusjärjestykseen nämä pienet
osat, mikä niistä on suurin ja mikä kaikkein pienin? Tunnista on jäljellä 5
minuuttia ja kaikki alkavat tehdä kotitehtävää.
On selitettävä ilman katsomista, miksi saatiin 8 samanlaista osaa taittamalla
paperi kolmesti. Kotitehtäväksi: kirjoita vihkoon suuruusjärjestyksessä
neljäsosa, kolmasosa, puolet, kahdeksasosa, kuudesosa, kahdestoistaosa.
Opettaja antaa vetää kaksi lukukorttia (4 ja 5) ja lasketaan niiden summa,
9. Ensin varmistetaan, että jokainen ymmärtää seuraavan tehtävän:
jos kahdella lukukortilla saadaan summaksi 9, voisivatko ne olla muitakin
kuin 4 ja 5? Voivat, 6 ja 3 tai 2 ja 7. Voiko olla sama luku kaksi kertaa?
Onko muita mahdollisuuksia? 4 ja 5 tai 5 ja 4. Onko parempi kokeilla vai ajatella?
Lasten mielestä on parempi ajatella. Eräs tyttö kysyy, pistetäänkö numerokortit
takaisin. Ei. Tässä siis otetaan pois.
Lapsille annetaan ratkaistavaksi seuraava tehtävä. Viisi lasta leikkii luvuilla.
Lukukortit ovat 1-10, yksi kutakin, ne pistetään laukkuun. Kukin lapsi nostaa
kaksi korttia ja kertoo muille vain summan. Agi: 11, Eva: 4, Peti: 7, Zoli: 16,
András: 17. Mitkä kortit he nostivat? Kirjataan taululle ratkaisuja.
Toinen tehtävä: 7 tyhjää, 7 täyttä, 7 puoliksi täyttä säkkiä viinirypäleitä
lastataan kolmeen autoon niin, että jokaiseen tulee tasan 7 säkkiä ja
viinirypälemäärät ovat samat. Ensin keskustellaan tehtävästä, jotta
varmistuu, että lapset ovat ymmärtäneet tehtävän. Piirretään taululle 3
autoa ja säkit. Oppilaat tekevät itsenäisesti 5 minuuttia, opettaja kiertää
ja korjaa väärinkäsityksiä. Hän pyytää tehtävän jo ratkaisseen oppilaan tarkastamaan
vastauksen. Lopuksi käydään läpi tehtävä taululla yhdessä. Oppilas tekee
ratkaisua taululla, tarvittaessa toinen jatkaa. Toisetkin ideat esitetään.
Tarkistus tehdään aina lopuksi.
Opettaja kysyy, miten tehtävä olisi voitu ratkaista toisella tavalla.
Käytetään lappuja, joissa on 0, 1/2 ja 1. 0 merkitsee tyhjää säkkiä, 1/2
puoliksi täyttä, 1 täyttä. Mikä on lappujen summa? Puolikkaat yhdistetään
pareiksi, niistä saadaan 3 ja 1/2, siis yhteensä 10 1/2. Tämä jaetaan
kolmella, tulee 3 1/2. Tehtävä tehdään loppuun taululla ja tarkistetaan.
Kotitehtävä: Tamás pitää vadelmakarkista. Auta häntä löytämään se allaolevista
kuudesta karkista. Pilkullinen ei ole sitruunan makuinen. Raidallisen maku ei ole
ananas eikä suklaa. Parittomissa ei ole omenanmakua eikä mansikanmakua.
Parillisissa ei ole ananaksen eikä sitruunan makua. Ensimmäisessä rivissä
ei ole vadelmakarkkia, mutta on suklaa. Toisessa rivissä suklaakarkin
oikealla puolella oleva on mansikanmakuinen.
Oppitunnin alussa tervehditään ja kerrotaan, ketkä ovat poissa.
Luokassa on 25 oppilasta. Opettaja näyttää aluksi erilaisia kuvia ja
taulukkoja. Niistä keskustellaan ja yritetään päätellä, mitkä niistä voivat
esittää tilastollista aineistoa. Keskustelun jälkeen siirrytään
yksityiskohtaisempaan työskentelyyn.
Kuvassa on eri väristä mustetta sisältäviä kyniä. Väriä on jäljellä
erilaisia määriä. Mitä kynistä on käytetty eniten? Perustelu?
Entä vähiten? Perustelu? Jos kynät olisivat sinun, mikä niistä olisi (värin
takia) suosikkisi?
Näytetään kuva, josta näkyy, kuinka moni tyttö ja poika juo aamulla
kaakaota tai maitoa. Kummasta pidetään enemmän? Asia esitetään kaakaokupeilla ja
maitolaseilla. Jos kaakaokuppeja on enemmän, se merkitsee, että useammat
lapset juovat aamulla kaakaota kuin maitoa.
Opettaja ottaa esiin vihkopinot. Tehtävät on korjattu ja vihkot on
järjestetty tehtyjen virheiden lukumäärän mukaan. Hyvät tulokset,
keskimääräiset ja vähemmän hyvät on luokiteltu virheiden lukumäärän
0, 1, 2, 3, 4 mukaan. Näistä tehdään yhdessä taulukko, jossa esitetään tulokset
tason mukaan.
Kolmannessa kuvassa on esitettynä erilaisia tapoja, miten lapset tulivat
kouluun (jalan, polkupyörällä, bussilla, raitiovaunulla, metrolla), yksikkö ja
kullakin tavalla tulevien lukumäärä annetaan janana. Arvioidaan lukumäärät
kuviosta mittaamalla eri janojen pituudet. Lasketaan kokonaislukumäärä, se
on 25. Onko taulukko tästä luokasta? Miksi? Kuvion mukaan 3 oppilasta tulee
henkilöautolla, voiko olla tästä luokasta? Oppilaat huomauttavat, että on
muitakin samankokoisia luokkia, joten ei ole varmaa, onko taulukko tästä luokasta.
Keskustellaan lempiaineiden esittämisestä kiekkokuviona. Opettaja kertoo,
että matematiikka vastaa punaista, ympäristöoppi vihreää, äidinkieli
valkoista ja näyttää kiekkokuvan, jossa on valkoista, vihreää, punaista,
Hän kysyy, mikä on kunkin oppilaan lempiaine. Jokainen kertoo
vastauksen. Miten tämä tieto voidaan esittää kiekkomallilla? Opettaja antaa
jokaiselle sektoripalan, jossa ei ole väriä. Oppilas antaa ohjeet: jos
pidät eniten matematiikasta, värjäät punaiseksi. Nämä väritetään
lempiaineen värillä. Kun oppilaat ovat valmiit, he nostavat kätensä. Sitten
kerätään palat väreittäin, punaiset ensin, lasketaan lukumäärä. Saadaan 14
matematiikkaa, 10 ympäristöoppia, 1 äidinkieli. Tehdään tästä aineistosta
huomioita. Huomataan esimerkiksi, että tämän luokan useimpien oppilaiden
lempiaine on matematiikka. Kerätään palat kiekkokuvioon ja tarkistetaan
laskemalla palat.
Opettaja kysyy, kuka pitää jäätelöstä. Kaikki vastaavat yhtäaikaa. Sitten
hän kysyy, kuka pitää eniten mansikkajäätelöstä, vaniljajäätelöstä,
suklaajäätelöstä. Oppilaat vastaavat ryhmänä. Opettaja ottaa pahviset
jäätelön kuvat, suklaa, mansikka, vanilja ja antaa kunkin jollekin
oppilaalle, joka pitää juuri tästä jäätelöstä eniten. Kaikki oppilaat
ryhmittyvät riviin lempijäätelönsä taakse. Ryhmiksi tulee 9 vanilja, 7
suklaa, 5 mansikka, 4 jää erikseen. Nämä 4 oppilasta eivät pidä
jäätelöstä. Mitä havaintoja voidaan tehdä nyt? Esimerkiksi, että tytöistä
enemmistö pitää eniten vaniljajäätelöstä. Poikien joukossa on suklaa
suosituin. Nyt halutaan esittää tulokset niin, että tytöt ja pojat
esitetään erikseen. Miten tämän voi tehdä? Opettaja kirjaa taululle luvut,
oppilaat ehdottavat. Saadaan taulukko:
Opettaja kysyy: Miten voit esittää tämän yhdellä kuvalla? Asiasta
keskustellaan, kerätään ideat. Löytyy ongelma: miten voidaan esittää myös
ne, jotka eivät pidä lainkaan jäätelöstä? Oppilaiden ratkaisuja on useita, yksi
niistä on: punainen kiekko vastaa tyttöä, sininen kiekko poikaa, jäätelön laatu
esitetään väritangolla. Väritankojen alle kerätään punaisia ja sinisiä kiekkoja
edellisen taulukon mukaisesti. Joku ehdottaa, että värin tummuudella voidaan erotella
tytöt ja pojat. Jokainen piirtää oman ratkaisunsa, jossa koko luokka esitetään
yhdellä kuvalla. Toinen ratkaisu on pylväät, joissa väritetään tyttöjen ja
poikien lukumääriä vastaten eri päät väreillä. Opettaja kiertää luokassa ja kommentoi
eri ratkaisuja ja kyselee, mitä kuvioista näkyy tarkistaen näin, että jokainen lapsi
on ymmärtänyt asian. Montako poikaa yhteensä, mikä esittää poikaa, mitä tämä
tarkoittaa? Montako lasta on yhteensä? Jos joku ei ole vielä valmis tunnin
päättyessä, jää tehtävän lopettaminen koti- tai iltapäivätehtäväksi. Kotitehtäväksi
jaetaan kaikille uusi kuva ja tehtävänä on siinä esitetyn tilastollista aineistoa
esittävän taulukon tulkinta. Tunnin lopussa noustaan ylös ja sanotaan meille
vierailijoille näkemiin.
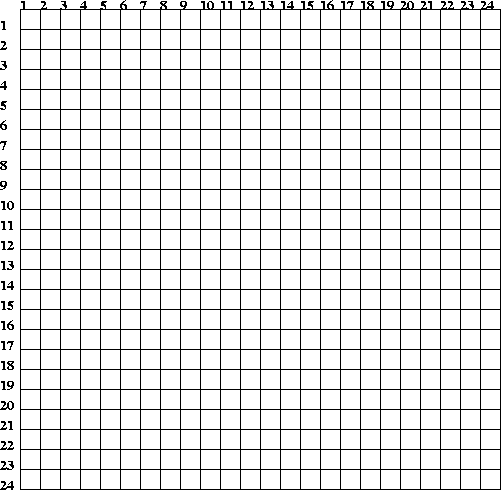
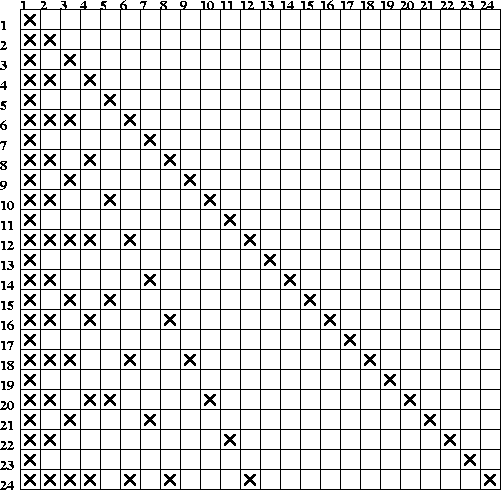
Opettaja on tehnyt kalvolle ruudukon
Oppilailla on samanlainen paperiruudukko. Ruudukkoon merkitään
lukujen 1 - 24 jakajat ristillä tätä lukua vastaavalle vaakariville.
Alku tehdään yhdessä, sitten oppilaat jatkavat itsenäisesti. Opettaja
johdattelee kysymyksillä, joihin oppilaat vastaavat. Milloin luku on
toisen jakaja? Onko 1 on 2:n jakaja? Miksi? Entä onko 2 on 2:n
jakaja? Miksi? Mikä on jakojäännös? Miksi kysyn jakojäännöksestä?
Jakojäännös 0 on sama asia, kuin että kyseessä on luvun jakaja
(tekijä). 3 on 3:n tekijä, 3 sisältyy kerran 3:een ja jakojäännös on
0. Mitkä ovat 5:n tekijät? Kokeillaan lukuja 1,2,3,4,5. Onko minkään
luvun kohdalla merkitty koko riviä lävistäjälle asti? Ykköselle on.
Miksi? Onko lävistäjällä aina risti? Miksi? Etsitään yhdessä luvun 7
tekijät, sitten luvun 11. Jatketaan itsenäisesti. Joku oppilaista käy
tekemässä merkinnät kalvolle. Nimitystä "alkuluku" ei käytetä vielä
tässä vaiheessa, nyt vain hankitaan siitä kokemuksia myöhempää
varten. Näkyykö jossain rivissä jotain mielenkiintoista? Oppilas: 2:n
rivissä on risti joka toisessa ruudussa, 3:n joka kolmannessa, 4:n
joka 4:ssä. Tästä keskustellaan hetki. Mitä on 16:n kohdalla? Kynien
avulla tarkstellaan esille tullutta mallia, kynä 1:n kohdalle
pystysarakkelle, toinen lävistäjälle. Etsitään lisää suoria, joihin
asetetaan kyniä. Mitä yhteistä näillä on? Oppilas: kynät ovat kuin
auringon säteet. Tähän on kulunut tunnista n. 20 minuuttia. Jatketaan
itsenäisesti suurempien lukujen, kuten 24 tekijöiden etsimistä ja
merkitsemistä, joku oppilaista tekee tämän kalvolle. Oppilaat
tarkastavat oman työnsä ja kalvolla olevat ristit. Mitä jäi
huomaamatta? Montako askelta on kussakin pylväässä x:ien välissä?
Oliko malli oikein? Millä luvuilla on vähiten jakajia? Vastaus:
ykkösellä. Miksi? 1:n jakaa vain 1. Onko sellaisia lukuja, joilla on
tasan kaksi jakajaa? Onko niitä monta vai vähän? Löytyy 1 ja 5.
Väritetään värikynällä ne rivit, joilla on vain 2 jakajaa. Tämä
tehdään itsenäisesti, väri valitaan itse, mutta ei kovin tummaa.
Millä riveillä on 2 x:ää, miten ne sijoittuvat riville? Tarkastetaan
värjätyt rivit. Mitkä ne ovat? Oppilaat vastaavat ja opettaja
merkitsee kalvolle niitä, löytyy 3,7. Kerätään ne kaikki kalvolle.
Minne x:t sijoittuvat? Luku itse ja 1. Miksi ääripäät ovat l ja
lävistäjä? Löytyykö esimerkkiä luvusta, joka on jaollinen 1:llä ja
itsellään? Onko 2 7:n tekijä?
Onko 24:ää suurempia lukuja, joilla on vain 1 ja luku itse tekijänä?
Vastaus: 41, se sisältää 41:n kerran ja 1:n 41 kertaa. Onko sillä
muita tekijöitä? Ei ole. Oppitunnista on nyt kulunut 30 minuuttia.
Tehdään uuteen taulukkoon parityönä niiden lukujen väritys, jotka
ovat 4:n monikertoja.
Tarkastetaan tulos. Joku oppilaista kertoo, mitä on merkinnyt. Oliko
virheitä? 0 ei ollut mukana. Miksi 4 on 0:n tekijä? Onko
jakojäännöstä, kun 0 jaetaan 4:llä? Tarkastetaan kyseinen kohta
oppikirjasta. Kirjassa on esimerkki 0
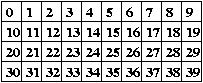
Leikataan ruudut irti paperista, saadaan lukukortit. Joku on vielä
epävarma, pitikö 0 värjätä. Kun oppilaat ovat valmiita, he nostavat
kätensä. Opettaja auttaa tarvittaessa. Tunnista on jäljellä 5
minuuttia. Oppilaat tekevät tilaa pulpetille. Ikkunan puoleinen
oppilas kustakin parista ottakoon ne kortit, joissa oleva luku on
24:n tekijä, toinen 32:n tekijät ja kerätköön ne erilleen. Taululle
kirjoitetaan 24 ja 32. Opettaja: Nostakaa käsi ylös, jos olette
valmiita.
Parit alkavat kiistellä yhteisistä tekijöistä. Onko sellaisia,
pareja, joissa toisella on kaikki 24:n ja toisella kaikki 32:n
tekijät? Oppilas: Tuolla toisella on tarvitsemiani tekijöitä!
Opettaja antaa kotitehtävän ja tarkastaa, että kaikki ymmärtävät,
mitä tulee tehdä. Lukusuoralle on merkittävä 24:n tekijät ja on
tehtävä joukkokaavio 24:n ja 36:n tekijöistä. Opettaja: Miettikää,
onko 0 mukana.
Opettajan kommentteja: lukukorttien leikkaaminen voi näyttää ajan
haaskaukselta, mutta se on vaihtelua ja leikkausjoukko tullaan
muistamaan. Jaollisuuteen liittyviä vaikeuksia: 0:n rooli, milloin
jaetaan, milloin kerrotaan, 1 ja alkuluvut, tässä kuva auttaa.
1 jakaa jokaisen luvun, myös itsensä. Tässä tapauksessa se on ainoa
tekijä.
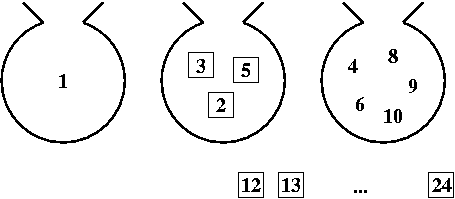
Taululla on valmiina kuva ja keltaisilla liimautuvilla
lapuilla lukuja 1 - 24, yksi kullakin lapulla. Samanlaisia lappuja
on useita päällekkäin. Minne sijoitetaan 7? Toiseen ryhmään. Minne 11? Toiseen. Minne 12?
Muistatteko viime tunnin kuvan? Otetaan esiin kalvo. Opettaja pyytää
ehdotuksia. Toiseen ryhmään tulevat vain ne luvut, jotka ovat jaollisia 1:llä
ja itsellään. Esimerkiksi 2:lla on 2 jakajaa (tekijää). Millaiset luvut
tulevat 3. ryhmään? Minne 13 sijoitetaan? Toiseen. Miksi? Oppilaat
käyvät taululla sijoittamassa keltaiset laput ryhmiin. 3. ryhmään ne,
joilla on enemmän kuin 2 jakajaa. Luetellaan lukujen jakajia.
Asetellaan uusia lappuja paikoilleen. Mitkä ovat 18:n jakajat?
Jatketaan lappujen sijoittelua. Tuleeko ryhmään 1 uusia lukuja? Ei,
vain 1 on kaikkien lukujen jakaja. Onko tämä oikein? Mikä nimi tulee
1. ryhmälle? 1:n jakajat. Voidaanko jokainen 3. ryhmän luku saada
täsmälleen kahden 2. ryhmän luvun tulona? Taululle kirjoitetaan tuloksia ja
sijoitellaan lappuja. Joku ehdottaa 24 = 3
(nimitykset alkuluku, yhdistetty luku tulevat vasta 5. luokalla, nyt
vain kerätään kokemuksia) Mitä saadaan, jos käytetään kaikkia näistä
luvuista? Tuleeko eri tulos, jos käyttää toista tai ensimmäistä
kakkosta? Ei. Mitä lukuja löysitte? 36 = 2
72 = 3
ja viitata, kun ovat valmiita. Opettaja kysyy, näyttävätkö luvut
tutuilta. Mistä alkutunnin joukosta ne ovat? Tehdään ensimmäinen
pylväs yhdessä ja tarkastetaan samalla. Etsitään vaiheittain lukuja,
esim. 12. Opettaja kehottaa menemään 24:ään useammalla kuin yhdellä
tavalla. Reitti merkitään värikynällä harjoituskirjaan. Taululla
näytetään reittejä. Seuraavaksi mennään lukuun 72. Montako kertaa
käytetään lukuja 2 ja 3? Vastaus: 2 3 kertaa,3 2 kertaa. Oliko
oikein? Lasketaan eri tavoilla. Vasemmalla kädellä lasketaan, montako
lukua 2, oikealla, montako lukua 3. Luetaan laskutoimituksia samalla,
kun liikutaan kuviossa. Löydättekö kaikki 72:n tekijät, jos katsotte
kuvaa? Kyllä. Etsikää kaksi lukua, jotka kertomalla saadaan 72. Ne voivat olla 8
ja 9 tai 2 ja 36 tai 24 ja 3. Ovatko myös nämä tekijöitä? Ovat.
Saadaanko samoin 6
Jos on käytössä monta lukua 2 ja 3, saadaan kertomalla paljon lukuja.
Voidaanko 72 jakaa osiin? Miten se jaetaan kahden luvun tuloksi?
Esimerkiksi 72 = 72
Jatketaan tekijöihin jakoa.
Samalla keskustellaan: Voidaanko 2 jakaa kahteen osaan? Ei. Entä 36?
Jatkakaa itsenäisesti. Etsikää suurin ja pienin tekijä. Entä 9? Joku
ehdottaa tekijäksi lukua 4. Entä, jos kerrotaan 2
Eräitä tunnilla tehtyjä harjoituksia: miten moneen järjestykseen voidaan
kirjoittaa kolme eri kirjainta? Miksi? Luokalla tehdään arpajaiset vetämällä
lakista arpalippuja.
Viisi oppilasta valitaan kättelemään kukin toisiaan, montako eri kättelyä
tulee? Opettajan johdolla yritetään selvittää asia.
Opettaja kertoo, että tällä tunnilla tulee uusi asia, joka ei kuitenkaan ole
kokonaan uutta. Luonnolliset luvut tunnetaan jo, nyt laajennetaan lukualuetta.
Opettaja kirjoittaa taululle 53 + 17 ja kysyy, millaisilla lausekkeilla voidaan
esittää sitä viidellä pienempi luku. Oppilaat ehdottelevat erilaisia lausekkeita:
Keskustellaan siitä, missä negatiivisia lukuja tavataan: säätiedoituksissa,
esim. jos on pakkasta
Mikä on negatiivisten lukujen yhteys lukusuoraan?
Opettaja piirtää suoran, merkitsee 0:n ja kysyy, mitä muuta tarvitaan.
Yksikkö. Opettaja toistaa: tarvitaan 0 ja yksikkö. Hän kysyy, mikä on
kasvava suunta ja piirtää näkyviin positiivisia kokonaislukuja sekä
kirjoittaa niiden alle ''positiiviset kokonaisluvut''. Onko 0 positiivinen?
Mikä on positiivisten kokonaislukujen ja nollan nimitys? Hän lisää niiden
alle ''luonnolliset luvut''. Nyt pitäisi sijoittaa negatiiviset luvut
lukusuoralle. Minne tulee 3:n vastaluku
Nyt tulee vaikea kysymys: minkä vastaluku on 5? Havainnollistus: 5 askelta
vastapäiseen suuntaan 0:sta kuin 5. Mikä on
Yhteenveto: Positiivisten ja negatiivisten lukujen läheinen yhteys; positiiviset
luvut, 0, negatiiviset luvut. Lukusuora, 0, yksikkö. Merkitään vastalukujen
pareja. Mitä havaitaan? Ne ovat eri puolilla ja yhtä kaukana 0:sta. Toinen on
positiivinen, toinen negatiivinen (nolla!). Vastaluvut ovat 0:sta yhtä etäällä.
Opettaja merkitsee lukusuoralle luvut 1 ja
Minkä luvun itseisarvo on -5:n itseisarvo?
Koko tunnin ajan opettaja ja luokka ovat tiiviissä yhteistyössä, ideat tulevat
lapsilta, opettaja kertaa ne. Hän tekee lyhyitä hyppäyksiä muuhun (lämpimät/kylmät
värit, maantiede, ...) mutta palaa hyvin pian ja täsmälleen lähtökohtaan.
Luokan alussa oppilaat (joille on kerrottu, että tuntia seuraavat henkilöt
ovat tulleet Suomesta) lähettävät suomeksi terveisiä joulupukille (joulu on
pian tulossa). Kotitehtävänä on ollut selvittää, onko annetussa kuviossa
peilaussymmetriaa. Kuviossa on janoja siroteltuna tasoon. Opettaja käyttää
kalvoja ja taittamalla kalvon ehdotetun symmetria-akselin kohdalta
tarkistaa, menevätkö kuviot päällekkäin. Symmetria-akselit voivat olla eri
suuntaisia. (Oppilaat käyttävät kaksipuolista peiliä symmetrian opetteluun
jo ensimmäisestä luokasta lähtien.)
Kotitehtävänä on ollut myös tarkastella kuvia, joihin on kätketty symmetrinen kuva
(katso kuva ).
Tunnilla tarkastellaan ensin arvaamalla, voidaanko erilaisia kolmioita
(tasasivuinen, suorakulmainen, tasakylkinen, ei mitenkään säännöllinen
kolmio) käyttämällä peittää yhdensuuntaisten suorien välinen tason osa.
Arvaukset merkitään taulukkoon, viimeiseen kohtaan (ei säännöllinen kolmio)
tulee kysymysmerkki. Arvauksia tarkistetaan kokeilemalla ja oppilaat esittävät
taululla ratkaisunsa. Luokassa on erilaisia mielipiteitä. Oppilailla on omat
muoviset kolmionsa, joilla he voivat kokeilla itse.
Opettaja piirtää myös yhdensuuntaisvyön jaon suunnikkaisiin ja kysyy,
voidaanko peittäminen tehdä kolmioilla. Kolmioiden lisäksi tarkastellaan
myös muita monikulmioita. Säännöllisillä kuusikulmioilla voidaan peittää
yhdensuuntaisvyö, millaisia kolmiojakoja tähän liittyy? Montako tapaa on peittää
yhdensuuntaisvyö tasasivuisilla kolmioilla? Entä suorakulmaisilla? Oppilaat
esittävät ratkaisunsa tai perustelevat, ettei ratkaisua ole. Tällöin päädytään
laskemaan kulmia. Oppilaat eriytetään, toiset hakevat kokeellisesti mahdollisimman
monta tapaa, toiset yrittävät todistaa tuloksia.
Symmetristä pisarakuviota peilataan erisuuntaisten suorien suhteen.
Aloitetaan yhdensuuntaisten suorien tapauksesta.
Mitä tapahtuu?
Käytetään kahta peilausta. Mikä on lopputuloksessa olevien kuvien
lukumäärä, jos lähdetään pisara (tai kukan terälehti) kuviosta? Tuleeko
aina 4-lehtinen kukka (joka on lopputulos, jos lähtökuvio on keskellä
ensimmäistä koordinaattineljännestä -- akselit peilausakseleina). Tuleeko aina
parillinen lukumäärä terälehtiä? Onko pariton lukumäärä terälehtiä
mahdotonta saada muuttelemalla peilien asemaa?
Entä peilaus, jossa kuvio peilautuu itselleen? Miten voidaan saada lopputulokseksi
kolme terälehteä? Millainen kulma peilaussuorien väliin tulee? Entä 5 terälehteä?
Mitä tapahtuu, jos peilaussuorien välinen kulma on
Tutkitaan peilin avulla kuvaa
Lopuksi tarkastellaan lyhyiden tikkukirjaimilla kirjoitettujen sanojen ja
niiden kirjainten symmetriaominaisuuksia. Sanoja ovat BIBE, BEOE, DODI sekä
pystysuuntaan kirjoitetut OTTO, MOHA, HIT. Kotitehtävänä on koota lisää
sanoja ja kuvioita, joissa on symmetriaa.
Opettaja: Kovácz
Opettaja on kätkenyt pienen merkin erään kiekon alle, hän näyttää kalvolla kuvan.
Kyselemällä on löydettävä sen kiekon keskipisteen koordinaatit, jonka alla
merkki on. Vastaukset ovat vain kyllä/ei. Oppilaat kyselevät ja käyvät
sitten poistamassa turhat kiekot. Onko ensimmäinen koordinaatti pienempi
kuin 2? Ei. Onko ensimmäinen koordinaatti suurempi kuin 0 ja pienempi kuin
4? Ei. Onko jälkimmäinen koordinaatti pienempi kuin 3? Ei. Onko
jälkimmäinen koordinaatti suurempi kuin 3 ja pienempi kuin 5? On. Nyt on
jäljellä enää kaksi mahdolisuutta (4,4) ja (5,4). Onko ensimmäinen
koordinaatti suurempi kuin 5? Onko tämä hyvä kysymys, kysyy opettaja. Ei
ole, todetaan. Onko ensimmäinen koordinaatti suurempi kuin jälkimmäinen?
Ei. Nyt merkki löytyy kohdalta (4,4).
Toistetaan vastaava niin, ettei saa käyttää koordinaattien numeroarvoja ja
koordinaatit ovat väliltä 0-4. Oppilas kysyy: Onko ensimmäinen koordinaatti
suurempi kuin jälkimmäinen? Vapaaehtoisena valittu toinen oppilas vastaa
nyt kysymyksiin. Poistaessaan turhia kiekkoja oppilas epäröi, jolloin opettaja
tulee apuun ja kysyy erikseen tiettyjä kiekkoja. Onko tämä poistettava? Jäävätkö
muut varmasti? Uusi kysymys: onko jälkimmäinen koordinaatti parillinen?
Oppilaat ovat piirtäneet vaakunoita. Opettaja ajattelee niistä yhtä, oppilaiden
saatava kyselemällä selville, mikä on kyseessä. Vastaukset ovat jälleen
vain kyllä/ei. Käytetään symmetria-akseleiden olemassaoloa ja suuntaa,
pyörityssymmetrian olemassaoloa, värejä. Joskus opettaja kysyy, oliko turha
kysymys, erotteliko kysymys kuvat, ja pyytää perustelun. Kaksi kuvista ei ole
symmetristä, mitkä ne ovat?
Opettaja näyttää kalvon ja kertoo, että voimme ajatella, että siinä on
kylän kartta ja yksikkönä sentti. Poliisiasema on merkitty pisteellä P, sairaala
pisteellä S. Sairaala on kauempana kuin 4 cm P:stä. Todellisuudessa etäisyys olisi
paljon suurempi, mutta nyt puhutaan kartasta ja senttimetrin etäisyys sentin
kartalla vastaa todellisuudessa kilometriä. Tie kulkee niiden välissä, kumpikaan
pisteistä ei ole tiellä. Roisto (tai koulu, kumpaa haluatte ajatella) on yhden
sentin etäisyydellä tiestä ja 4 cm etäisyydellä poliisiasemasta.
Ensin etsitään, missä ovat ne pisteet, jotka ovat sentin etäisyydellä
tiestä. Montako ratkaisua? Saadaan kaksi tien suuntaista suoraan. Seuraava
tieto on, että etsitty piste (missä roisto on) on neljän sentin päässä
poliisiasemasta. Missä nämä pisteet ovat kartalla? Montako ratkaisua olisi
nyt? Minne poliisiasema tulisi siirtää, jottei tulisi yhtään ratkaisua? Yli
5 sentin päähän tiestä. Entä jos se on tasan 5 sentin etäisyydellä? Lisäksi
tiedetään, että roisto ei voi olla kauempana sairaalasta kuin 3 cm. Kalvolle
asetetaan punainen kiekko, jonka säde on 3 yksikköä. Opettaja liikuttelee
kiekkoa ja tutkitaan, montako ratkaisua milloinkin on. Oppilaat piirtävät kuvia
eri tilanteista.
Opettaja antaa uuden tehtävän. Kaksi kaupunkia on merkitty sinisellä ja vihreällä.
Huono tie ei kulje kummankaan kaupungin kautta. Kumpikin kaupunki maksaa tien
korjauksesta itseään lähimmän osan edestä. Kuka maksaa minkäkin osan korjauksen?
Ratkaisu värjätään sinisellä ja vihreällä. Miten löysitte pisteen, joka erottaa
sinisen ja vihreän viivan osan? Kyseessä on kahden pisteen välisen janan
keskinormaali. Nämä pisteet ovat yhtä kaukana molemmista. Nyt tulee mukaan myös
punainen kaupunki, joka haluaa osallistua samoin ehdoin. Miten saadaan selville
heille maksettavaksi tuleva tien osa? Värjätään punaiseksi ne pisteet, jotka
lähinnä punaista kaupunkia.
Otetaan esille paperi, johon merkitään kaksi pistettä esittämään kahta
ihmistä, heitä merkitään A:lla ja P:llä. A:n sukulaiset asuvat lähempänä
A:ta, P:n P:tä. Miten paperin voi taittaa niin, että nähdään, missä
kummankin sukulaiset asuvat? Mitä pitää tehdä taululla, jota ei voi
taittaa? Mukaan tulee kolmas henkilö, B. Käytetään värejä, punainen,
sininen ja vihreä. Kuvioon tulee keskelle kolmio, jota ei osata värittää.
Missä on virhe? Todetaan, että suorat leikkaavat yhdessä pisteessä, eikä
kolmiota tulekaan.
Kotitehtäväksi tulee vastaava tehtävä: neliö, jonka kulmissa on 4 ''henkilöä'',
ja valitaan johonkin sisäpisteeseen viides. Tehtävä ratkaistaan taittelulla
ja värittämällä. Mitä tapahtuu, jos viides piste on lähellä kärkipistettä? On
tutkittava, mitä tapahtuu, jos piste valitaan eri tavoin neliön sisältä.
7. luokasta lähtien voi olla 6-8 tuntia matematiikkaa viikossa. Ryhmässä
oli 18 oppilasta, voidaan myös jakaa ryhmä. Geometriassa käsitellään esim.
inversio, analyysiä, kuten derivaatta, integraali, sarjat, jonot ja raja-arvot.
Oppilaiden kotitöitä kerätään kirjallisina ja arvioidaan. Kotityöt ovat
pakollisia, oppilaat saavat numeroita ja pisteitä.
Aiheina on myös analyyttistä geometriaa, esimerkiksi tasossa suoran yhtälö
käyttäen pistetuloa, pisteen etäisyys suorasta jne.
Opettaja: - Tämä vaaleanpunainen on perusyksikkö. Mikä tämän nimi sitten olisi? (punainen)
2
Etsi, mikä sauva vastaa kolmosta.
Oppilas etsii sen laatikosta.
- Näytä, että todella se on 3. Oppilas mittaa sauvan.
Mikä on sitten 5 ?
Onkohan varmasti, todista se! Oppilas todistaa sen mittauksella.
Entä mikä tämän nimi voisi olla?
Mittaa se!
- Minkä nimen haluat antaa tälle?
4.
Tummanpunainen.
Opettaja: - Etsi laatikosta sellaisia sauvoja, joita jo on pöydällä.
Tehdään niistä matto. Olemme tehneet sellaisen jo aikaisemminkin, muistatko?
6.
Opettaja: Joka riville tehdään erilainen yhdistelmä palikoista. Mikä on ensimmäinen?
Oppilas tekee yhdistelmän.
Opettaja: - Keksi vielä uusia yhdistelmiä!
- Saisiko sinusta kokonaisen rivin vaaleanpunaisista?
Kyllä.
Näytä sitten.
Saisiko kokonaisen rivin violeteista?
Kyllä.
Kokeile.
- Punaiset.
- Tarkista, toimiiko?
Opettaja: - Minä aloitan, jatka sinä sitten. Osaatko sanoa, mikä voisi olla seuraava?
- Punainen.
- Näytä.
- Oikein hyvä. Matto on jo aika suuri, luetaan siitä nyt.
Muistatko, mikä tämän nimi oli? (vaaleanpunainen)
1
- Entä tämän?
2
Opettaja: - Otetaan tänne vielä vaaleanpunaisia sauvoja, sitten voit lukea matosta helpommin.
Kuinka monta sauvaa minun pitäisi panna tänne, että sinä voisit mitata kaikki sauvat?
6
Opettaja: - Lue matosta näin:
Vihreä sauva on yhtä pitkä kuin vaaleanpunainen ja tummanpunainen ja vaaleanpunainen yhteensä.
Osaatko toistaa?
Oppilas toistaa.
Opettaja: - Osaatko kertoa saman asian myös matematiikan kielellä?
6 on 1 + 4 + 1.
Sano vielä kerran.
6 on 1 + 4 + 1.
Oikein hyvä.
- Vihreä on yhtä pitkä, kuin punainen ja violetti ja oranssi.
Lapsi sanoo oranssi, mutta sauva onkin vaaleanpunainen.
Opettaja: - Katso, tämä on oranssi.
- Niin, vaaleanpunainen eikä oranssi.
- Kerro nyt vain luvuilla!
6 on 2 + 3 + 1
Opettaja: - Osaatko kertoa tällä tavalla ? 6 on yhtä pitkä, kuin 1 ja 2 ja 3 yhteensä
Opettaja: - Mitä tästä voisi rakentaa?
Portaat.
Kerro sillä tavalla.
6 on yhtä paljon kuin 1 + 2 + 3.
Opettaja: - Kerro vain näistä riveistä.
6 on yhtä paljon kuin 3 + 3.
6 on yhtä paljon kuin 2 + 2 + 2.
Oikein hyvä. Kiitos ja pyydä nyt Doraa tulemaan tänne.
Uusi oppilas, Dora, tulee. Hänkin saa värisauvatehtävän.
Opettaja: 1 2 3 4 5 6
Etsi saman pituinen sauva. Jos vaaleanpunaisen nimi on 1, mikä vihreän nimi on?
Etsi sauva, jonka nimi on 3.
Hyvä. Pane sen viereen sellainen sauva, että ne ovat yhteensä samanpituisia kuin 6.
Tehdään niistä matto.
Oppilas rakentaa maton.
- Oikein hyvä. Mikä violetin nimi voisi olla?
3
Etsi sauva, jonka nimi on 4.
Lisää sauva siten, että ne ovat yhteensä samanpituisia kuin vihreä.
Hyvä. Mikä 5 on?
- Voitko todistaa minulle, että niistä todellakin tulee 5.
1 2 3 4 5
Hyvä, olet aivan oikeassa.
Miten voisit rakentaa siten, että ne yhteensä olisivat yhtä pitkiä kuin vihreä?
- Voidaan vielä jatkaa, mutta nyt haluaisin tietää, osaatko lukea tästä.
Opettaja: - Minä kerron ensiksi. Vihreä on yhtä pitkä kuin vaaleanpunainen ja
vaaleanpunainen ja vaaleanpunainen ja vaaleanpunainen ja vaaleanpunainen ja vaaleanpunainen.
6 on yhtä paljon kuin ? kerro luvuilla!
Oppilas: 1 + 1 + 1 + 1 + 1 + 1.
Opettaja: - Luetaan vielä. Vihreä on yhtä pitkä kuin
2 violettia.
Niin, tai voi sanoa että violetti ja violetti.
6 on yhtä monta kuin 3 + 3.
Seuraava.
6 on yhtä monta kuin ?
Oppilas ei osaa jatkaa.
Opettaja: - Voit mitata, jos haluat. Oppilas mittaa sen.
Oppilas: - yhtä monta kuin 4 + 2.
Oppilas: - 6 on monta kuin 1 + 5.
- Oikein hyvä. Kerro nyt, mitä minä teen.
6 on yhtä monta kuin 3 + 3.
6 on yhtä monta kuin 5 + 1.
6 on yhtä monta kuin 2 + 4.
Opettaja: Márta Oravecz
Taso: 1. luokka, oppilaat n. 6-7 vuotiaita
Opettaja Agnes Kivovics.
Taso: 3. luokka, oppilaat n. 9 vuotiaita
Aihe: Harjoituksia luvuilla
Opettaja: Agnes Kivovicz
Taso: 3. luokka, oppilaat n. 9 vuotiaita
Aihe: murtoluvut
Opettaja: Agnes Kivovics
Taso: 3. luokka, oppilaat n. 9 vuotiaita, erityislahjakkaat
summa
mahdolliset kortit
11
1 + 10
2 + 9
3 + 6
4 + 7
5 + 6
4
1 + 3
2 + 2 (ei käy)
7
2 + 5
3 + 4
1 + 6 (ei käy)
![\includegraphics[width=0.8\textwidth]{video9.eps}](img28.png)
Opettaja: Agnes Kivovics
Taso: 3. luokka, oppilaat n. 9 vuotiaita
Aihe: tilastollisen aineiston esittäminen
pojat
tytöt
yhteensä
vanilja
0
9
9
suklaa
3
4
7
mansikka
2
3
5
ei mitään
2
2
4
Opettaja: Agnes Kivovics
Taso: 4. luokka
Aihe: jaollisuus, oppitunnin pituus 45 min.
 13 = 0, siis jako menee
tasan, ei ole jakojäännöstä. Pitikö 0 värjätä? Kyllä. Värjätään
toisella värillä luvut, jotka voidaan jakaa vain 1:llä ja luvulla
itsellään. Opettaja kiertää luokassa tämän itsenäisen työn aikana ja
neuvoo tarvittaessa. Eräs pari kiistelee siitä, onko 2 värjättävä vai
ei. Mitkä luvut on värjätty? Katsotaan myös edellistä kalvoa. Saadaan
lukuja..., 17,..., 23, 31. Onko kahden viimeisen välillä tällaisia
lukuja? Oppilas ehdottaa lukua 27. Onko tämä oikein? Ei, sillä 3
jakaa 27:n ja 9 myös.
13 = 0, siis jako menee
tasan, ei ole jakojäännöstä. Pitikö 0 värjätä? Kyllä. Värjätään
toisella värillä luvut, jotka voidaan jakaa vain 1:llä ja luvulla
itsellään. Opettaja kiertää luokassa tämän itsenäisen työn aikana ja
neuvoo tarvittaessa. Eräs pari kiistelee siitä, onko 2 värjättävä vai
ei. Mitkä luvut on värjätty? Katsotaan myös edellistä kalvoa. Saadaan
lukuja..., 17,..., 23, 31. Onko kahden viimeisen välillä tällaisia
lukuja? Oppilas ehdottaa lukua 27. Onko tämä oikein? Ei, sillä 3
jakaa 27:n ja 9 myös.
Opettaja: Agnes Kivovics
Taso: 4. luokka
Aihe: jaollisuus, edellistä seuraava tunti
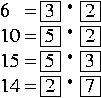
 8, häntä täytyy korjata, koska vain 2. ryhmän
lukuja saa nyt käyttää. Joku ehdottaa 24 = 3(3+5). Tämäkään ei
kelpaa, koska saa käyttää vain tuloja. Joku ehdottaa 2
8, häntä täytyy korjata, koska vain 2. ryhmän
lukuja saa nyt käyttää. Joku ehdottaa 24 = 3(3+5). Tämäkään ei
kelpaa, koska saa käyttää vain tuloja. Joku ehdottaa 2
 11, mutta
tämä on 22, ei käy. Samaa lukua voi nyt käyttää useamman kerran.
Oppilaille annetaan parin minuutin itsenäinen työ täydentää 24 = 3
11, mutta
tämä on 22, ei käy. Samaa lukua voi nyt käyttää useamman kerran.
Oppilaille annetaan parin minuutin itsenäinen työ täydentää 24 = 3

![[ ]](box.gif) . Vastaukseksi tulee 24 = 3
. Vastaukseksi tulee 24 = 3  2
2  2
2  2.
Tulokset tarkastetaan. Oppilaat saavat valita jäljelläolevista
lukuista jonkin ja tehdä sille vastaavasti. Opettaja kehottaa heitä
tekemään kaikille jäljelläoleville samoin. esimerkiksi 12 = 2
2.
Tulokset tarkastetaan. Oppilaat saavat valita jäljelläolevista
lukuista jonkin ja tehdä sille vastaavasti. Opettaja kehottaa heitä
tekemään kaikille jäljelläoleville samoin. esimerkiksi 12 = 2  3
3  2, 18 = 2
2, 18 = 2
 3
3
 3, 16 = 2
3, 16 = 2
 2
2
 2
2
 2 Onko oikein? Tarkastetaan
ketomalla. Oppilaita kehotetaan tekemään sama 22:lle.
Uusi tehtävä: Nyt on käytettävissä vain 3 kappaletta lukuja 2 ja 2
kappaletta lukuja 3, näitä saadaan vain kertoa. Mitä lukuja saadaan?
Tämä tehdään itsenäisesti ja vastauksia kirjoitetaan, nyt siis
saadaan käyttää enintään näitä lukuja.
2 Onko oikein? Tarkastetaan
ketomalla. Oppilaita kehotetaan tekemään sama 22:lle.
Uusi tehtävä: Nyt on käytettävissä vain 3 kappaletta lukuja 2 ja 2
kappaletta lukuja 3, näitä saadaan vain kertoa. Mitä lukuja saadaan?
Tämä tehdään itsenäisesti ja vastauksia kirjoitetaan, nyt siis
saadaan käyttää enintään näitä lukuja.
 2
2
 3
3
 3. Kuka sai
tämän? Entä muita?
3. Kuka sai
tämän? Entä muita? 3
3
 2
2
 2
2
 2. Oppilas ehdottaa 54 = 3
2. Oppilas ehdottaa 54 = 3  3
3
 2
2
 3. Opettaja
toteaa, että ehto voi unohtua, varsinkin, kun on kuuma päivä. Tässä
on liikaa lukuja 3. Oppials ehdottaa 48 = 2
3. Opettaja
toteaa, että ehto voi unohtua, varsinkin, kun on kuuma päivä. Tässä
on liikaa lukuja 3. Oppials ehdottaa 48 = 2
 2
2
 2
2
 3
3
 3. Joku
huomauttaa, ettei se voi olla oikein, tämä olisi sama kuin 72. Lukua
ehdottanut oppilas korjaa virheensä laskemalla.
Seuraavaksi tehdään itsenäinen työ: Oppilaiden tulee täydentää kuvio
3. Joku
huomauttaa, ettei se voi olla oikein, tämä olisi sama kuin 72. Lukua
ehdottanut oppilas korjaa virheensä laskemalla.
Seuraavaksi tehdään itsenäinen työ: Oppilaiden tulee täydentää kuvio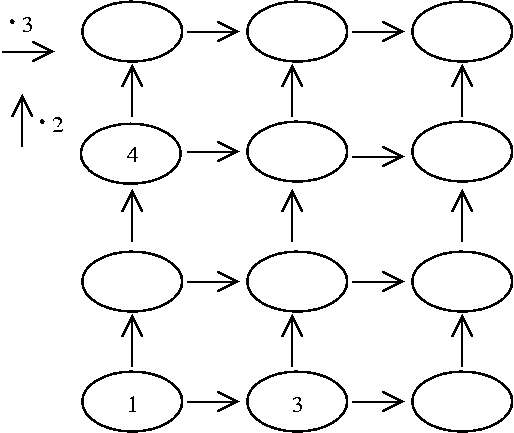
 12 = 72? Miten se saadaan? Jos jaetaan 24 2:lla
ja 3 kerrotaan 2:lla.
12 = 72? Miten se saadaan? Jos jaetaan 24 2:lla
ja 3 kerrotaan 2:lla. 1. Pitääkö luku 1 kirjoittaa tähän?
Tarkoittavatko nämä samaa 72 ja 72
1. Pitääkö luku 1 kirjoittaa tähän?
Tarkoittavatko nämä samaa 72 ja 72
 1? tarvitaanko sulkuja?
1? tarvitaanko sulkuja?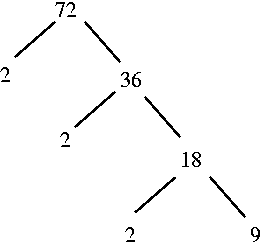
 4? Saadaankin 8.
Todetaan, että 3
4? Saadaankin 8.
Todetaan, että 3
 3 = 9. Nyt muodostetaan luku 72 tästä ketjusta eri
tavoin. Ketjussa nähdään 2. ryhmän lukuja, joilla on 2 tekijää.
Lopuksi annetaan kotitehtävät.
3 = 9. Nyt muodostetaan luku 72 tästä ketjusta eri
tavoin. Ketjussa nähdään 2. ryhmän lukuja, joilla on 2 tekijää.
Lopuksi annetaan kotitehtävät.
Opettaja: Rubóczky
Taso: 5. luokka, oppilaat n. 11 vuotiaita
Aihe: kombinatoriikka
Opettaja: Paróczai
Taso: 5. luokka, oppilaat n. 11 vuotiaita
Aihe: negatiiviset luvut (ensimmäinen oppitunti, jolloin puhutaan
negatiivisista luvuista, kaksoistunnista ensimmäinen)
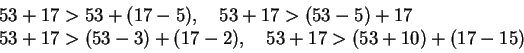
Opettaja kysyy: Mitä tapahtuu, jos ensimmäisessä sulkulausekkeessa suurennetaan
jälkimmäistä lukua, 10:n sijasta lisätäänkin 20. Miten se vaikuttaa
jälkimmäiseen?
![]() . Viimeisen lausekkeen alle
opettaja piirtää kysymysmerkin ja toteaa, että tällaista lukua ei ole
näkynyt aikaisemmin. Onko tällainen olemassa? Käydään läpi vielä toinen
samantapainen esimerkki ja päädytään yhtälailla (negatiiviseen)
lausekkeeseen, jonka alle opettaja piirtää kysymysmerkin. Nämä eivät ole
posiitivisia lukuja, tietääkö joku niiden nimen? Joku tietää: negatiiviset
luvut. Opettaja kirjoittaa sen taululle ja sanoo, että tällä ja seuraavilla
tunneilla tutustutaan näihin enemmän. Aloitetaan keskustelulla. Opettaja
kysyy: Mitä sinulle merkitsee negatiivinen luku? Missä jokapäiväisen elämän
tilanteissa niitä tavataan?
. Viimeisen lausekkeen alle
opettaja piirtää kysymysmerkin ja toteaa, että tällaista lukua ei ole
näkynyt aikaisemmin. Onko tällainen olemassa? Käydään läpi vielä toinen
samantapainen esimerkki ja päädytään yhtälailla (negatiiviseen)
lausekkeeseen, jonka alle opettaja piirtää kysymysmerkin. Nämä eivät ole
posiitivisia lukuja, tietääkö joku niiden nimen? Joku tietää: negatiiviset
luvut. Opettaja kirjoittaa sen taululle ja sanoo, että tällä ja seuraavilla
tunneilla tutustutaan näihin enemmän. Aloitetaan keskustelulla. Opettaja
kysyy: Mitä sinulle merkitsee negatiivinen luku? Missä jokapäiväisen elämän
tilanteissa niitä tavataan?
![]() , on hyvin kylmä. Opettaja kertoo, että tässä
tilanteessa negatiivinen luku ei merkitse hänelle, että luku on outo, vaan
, on hyvin kylmä. Opettaja kertoo, että tässä
tilanteessa negatiivinen luku ei merkitse hänelle, että luku on outo, vaan
![]() merkitsee, että hän tarvitsee paljon vaatteita, hän hytisee kertoessaan
tätä. Lämpötila on siis nollan alapuolella 13:lla asteella. Lukusuora on
toinen yhteys, missä on alusta alkaen nähty negatiivisia lukuja (mutta niihin ei
ole kiinnitetty huomiota). Opettaja kysyy: tiedättekö, mikä on pankkikortti
ja mitä sillä voi tehdä? Pankkitilille voi tulla rahaa, mutta laskujen
maksaminen vie pois rahaa. Tulot ovat positiivisia ja maksettavat menot
negatiivisia, pankkitili on esimerkki, jossa voidaan joutua negatiiviselle
puolelle. Pankista voidaan myös ottaa laina, tällöin ollaan negatiivisella
puolella. Hintojen alennukset, esim. 20% ale, pörssikurssien alamäki ovat
esimerkkejä. Opettaja kertoo leikkineensä pienenä kartoilla. Tällöin hän
löysi negatiivisia lukuja. Karttaan oli merkitty meren syvyyttä väreillä.
Meren syvyys on negatiivinen nollatasoon verrattuna. Esimerkiksi
Hollannissa on merenpinnan alla olevaa maata. Missä Hollanti onkaan? Mitkä
ovat Hollannin naapurimaat? Kotitehtäväksi tulee: tarkastele kartan avulla
Panaman kanavaa, Panaman kanava yhdistää eri korkeudella olevat meret.
Miten tämä on
mahdollista? Oppilaiden tulee hakea eri syvyydet, jotka on
merkitty karttaan. Opettaja kertoilee, että negatiiviset luvut ovat
matematiikan historiassa aika uusia. Aikaisemmin pelättiin negatiivisia
lukuja ja ajateltiin, että negatiiviset luvut ovat absurdeja -- tiedättekö,
mitä sana absurdi tarkoittaa? Negatiivisia lukuja pidetiin kuviteltuina,
ei todellisina. Nyt niitä tarvitaan jokapäiväisessä elämässä.
merkitsee, että hän tarvitsee paljon vaatteita, hän hytisee kertoessaan
tätä. Lämpötila on siis nollan alapuolella 13:lla asteella. Lukusuora on
toinen yhteys, missä on alusta alkaen nähty negatiivisia lukuja (mutta niihin ei
ole kiinnitetty huomiota). Opettaja kysyy: tiedättekö, mikä on pankkikortti
ja mitä sillä voi tehdä? Pankkitilille voi tulla rahaa, mutta laskujen
maksaminen vie pois rahaa. Tulot ovat positiivisia ja maksettavat menot
negatiivisia, pankkitili on esimerkki, jossa voidaan joutua negatiiviselle
puolelle. Pankista voidaan myös ottaa laina, tällöin ollaan negatiivisella
puolella. Hintojen alennukset, esim. 20% ale, pörssikurssien alamäki ovat
esimerkkejä. Opettaja kertoo leikkineensä pienenä kartoilla. Tällöin hän
löysi negatiivisia lukuja. Karttaan oli merkitty meren syvyyttä väreillä.
Meren syvyys on negatiivinen nollatasoon verrattuna. Esimerkiksi
Hollannissa on merenpinnan alla olevaa maata. Missä Hollanti onkaan? Mitkä
ovat Hollannin naapurimaat? Kotitehtäväksi tulee: tarkastele kartan avulla
Panaman kanavaa, Panaman kanava yhdistää eri korkeudella olevat meret.
Miten tämä on
mahdollista? Oppilaiden tulee hakea eri syvyydet, jotka on
merkitty karttaan. Opettaja kertoilee, että negatiiviset luvut ovat
matematiikan historiassa aika uusia. Aikaisemmin pelättiin negatiivisia
lukuja ja ajateltiin, että negatiiviset luvut ovat absurdeja -- tiedättekö,
mitä sana absurdi tarkoittaa? Negatiivisia lukuja pidetiin kuviteltuina,
ei todellisina. Nyt niitä tarvitaan jokapäiväisessä elämässä.
![]() ? Lapset ehdottavat: Otetaan 3
(yksikön pituista) askelta nollasta eri suuntaan kuin positiiviset luvut.
Oppilaat etsivät
? Lapset ehdottavat: Otetaan 3
(yksikön pituista) askelta nollasta eri suuntaan kuin positiiviset luvut.
Oppilaat etsivät ![]() :n paikan lukusuoralta. Opettaja käyttää koko ajan
nimitystä ''vastaluku''. Keskustellaan lämpimistä ja kylmistä väreistä,
lukusuorassa negatiivinen puoli on sininen (kylmä) ja positiivinen punainen
(lämmin). Mikä luku on
:n paikan lukusuoralta. Opettaja käyttää koko ajan
nimitystä ''vastaluku''. Keskustellaan lämpimistä ja kylmistä väreistä,
lukusuorassa negatiivinen puoli on sininen (kylmä) ja positiivinen punainen
(lämmin). Mikä luku on ![]() :n vastaluku? Keskustellaan etumerkeistä.
Huomataan, ettei positiivisen luvun eteen tarvitse merkitä +:aa.
Negatiivinen merkitään, joten ellei ole etumerkkiä, on luku positiivinen. Näin
säästetään energiaa. Tarvitseeko 0 etumerkkiä? Mikä on 0:n vastaluku?
Mietitään askelilla lukusuoralla. Ei yhtään askelta. 0:n vastaluku on
:n vastaluku? Keskustellaan etumerkeistä.
Huomataan, ettei positiivisen luvun eteen tarvitse merkitä +:aa.
Negatiivinen merkitään, joten ellei ole etumerkkiä, on luku positiivinen. Näin
säästetään energiaa. Tarvitseeko 0 etumerkkiä? Mikä on 0:n vastaluku?
Mietitään askelilla lukusuoralla. Ei yhtään askelta. 0:n vastaluku on ![]() ,
tämän sijasta kirjoitetaan 0, sillä on vain yksi 0.
,
tämän sijasta kirjoitetaan 0, sillä on vain yksi 0.
![]() :n vastaluku? Selitetään
kaava
:n vastaluku? Selitetään
kaava ![]() . Kaksi miinusta kumoaa toisensa. Opettaja tuo mukaan
logiikan: kyllän vastakohta on ei ja ei:n kyllä. Verrataan kahta miinusta logiikan
kaksoisnegaatioon: ''Ei ole totta, ettei sada'' on sama, kuin että ''sataa''.
Jossain vaiheessa oppilas ehdottaa värien käyttöä negatiivisten lukujen
suhteen ja opettaja toteaa, ettei se auta, sillä voi olla tapaus, jossa on
vain yksi väri käytössä.
. Kaksi miinusta kumoaa toisensa. Opettaja tuo mukaan
logiikan: kyllän vastakohta on ei ja ei:n kyllä. Verrataan kahta miinusta logiikan
kaksoisnegaatioon: ''Ei ole totta, ettei sada'' on sama, kuin että ''sataa''.
Jossain vaiheessa oppilas ehdottaa värien käyttöä negatiivisten lukujen
suhteen ja opettaja toteaa, ettei se auta, sillä voi olla tapaus, jossa on
vain yksi väri käytössä.
![]() . Mitä yhteistä näillä on?
Hän lisää lukuja, 3 ja
. Mitä yhteistä näillä on?
Hän lisää lukuja, 3 ja ![]() . Miten ne näkyvät lukusuoralla, havainnollistetaan
askelilla 0:sta. Uusi käsite: itseisarvo. Mitä se tarkoittaa? Opettaja antaa
itseisarvon merkinnän. Se on etäisyys 0:sta, 0:sta tarvittavien ''askelten
määrä''. Luvut, joilla on sama itseisarvo, ovat yhtä kaukana 0:sta. Mitä tarkoittaa
. Miten ne näkyvät lukusuoralla, havainnollistetaan
askelilla 0:sta. Uusi käsite: itseisarvo. Mitä se tarkoittaa? Opettaja antaa
itseisarvon merkinnän. Se on etäisyys 0:sta, 0:sta tarvittavien ''askelten
määrä''. Luvut, joilla on sama itseisarvo, ovat yhtä kaukana 0:sta. Mitä tarkoittaa
![]() ? Se tarkoittaa, että 1:n ja
? Se tarkoittaa, että 1:n ja ![]() :n etäisyys nollasta on sama, 1
''askel''.
:n etäisyys nollasta on sama, 1
''askel''.
![]() . Mikä on
. Mikä on ![]() ? Mikä on 0:n itseisarvo? Montako
''askelta'' 0:sta? Joku lapsi huomaa, ettei itseisarvo voi olla negatiivinen. Tämä
kirjoitetaan taululle. Minkä luvun itseisarvo on 12? Montako ratkaisua? 12 on
ratkaisu,
? Mikä on 0:n itseisarvo? Montako
''askelta'' 0:sta? Joku lapsi huomaa, ettei itseisarvo voi olla negatiivinen. Tämä
kirjoitetaan taululle. Minkä luvun itseisarvo on 12? Montako ratkaisua? 12 on
ratkaisu, ![]() kelpaa myös. Onko enemmän ratkaisuja? Miksi? Vain kaksi suuntaa 0:sta.
kelpaa myös. Onko enemmän ratkaisuja? Miksi? Vain kaksi suuntaa 0:sta.
![]() ,
, ![]() , onko muita
ratkaisuja?
, onko muita
ratkaisuja? ![]() . Onko tällaista lukua? Lapsi ehdottaa lukua 3. Muistutetaan,
että itseisarvo on aina ei-negatiivinen ja kerrataan vielä ''askeleet'' 0:sta.
Lopuksi opettaja kertaa, mitä nyt tiedetään, ja mitä ei vielä tiedetä: voiko
negatiivisia lukuja käyttää laskutoimituksiin? Tämä selviää seuraavalla tunnilla.
Näkemiin.
. Onko tällaista lukua? Lapsi ehdottaa lukua 3. Muistutetaan,
että itseisarvo on aina ei-negatiivinen ja kerrataan vielä ''askeleet'' 0:sta.
Lopuksi opettaja kertaa, mitä nyt tiedetään, ja mitä ei vielä tiedetä: voiko
negatiivisia lukuja käyttää laskutoimituksiin? Tämä selviää seuraavalla tunnilla.
Näkemiin.
Opettaja: Jakucs
Taso: 6. luokka, oppilaat n. 12 vuotiaita
Geometrian tunti, aiheena peilaus ja symmetria.
![]() ?
?
Taso: 6. luokka, oppilaat n. 12 vuotiaita
Aihe: geometria
Opettaja: János Pataki
Taso: 11. luokka, oppilaat n. 17 vuotiaita, matematiikan erityisryhmä
Solmun toimitus
2002-12-20