
Virpi Kauko
Assistentti
Matematiikan ja tilastotieteen laitos, Jyväskylän yliopisto
Monitahokas tarkoittaa tasomonikulmioiden rajaamaa kolmiulotteista joukkoa, tai myös tällaisista monikulmioista koostuvaa pintaa. (Tarvittaessa täsmennetään tarkoitetaanko kulloinkin umpinaista kappaletta vai sen onttoa kuorta.)
Monikulmio puolestaan on tasokuvio, jota reunustaa itseään leikkaamaton murtoviiva eli äärellinen määrä peräkkäin silmukaksi liitettyjä janoja (tai myös tällaisen tasoalueen reunaviiva).
Monitahokkaita voidaan luokitella erilaisten säännöllisyys- ym. ominaisuuksien perusteella, mutta on myös olemassa kaikille monitahokkaille yhteisiä ominaisuuksia.
Jokaisella tahokkaalla on tietty määrä kärkiä (![]() ),
kärkiä toisiinsa yhdistäviä särmiä (
),
kärkiä toisiinsa yhdistäviä särmiä (![]() ) ja särmien
reunustamia tahkoja eli monikulmioita (
) ja särmien
reunustamia tahkoja eli monikulmioita (![]() ).
Vierekkäisten tahkojen tasot leikkaavat toisensa särmiä pitkin.
Näiden kolmen suureen avulla määritellään monitahokkaan
Eulerin karakteristika
).
Vierekkäisten tahkojen tasot leikkaavat toisensa särmiä pitkin.
Näiden kolmen suureen avulla määritellään monitahokkaan
Eulerin karakteristika ![]() , jota on tapana merkitä
lyhyesti kreikkalaisella khi-kirjaimella
, jota on tapana merkitä
lyhyesti kreikkalaisella khi-kirjaimella ![]() . Esimerkiksi kuutiolla
(kuva a) on
. Esimerkiksi kuutiolla
(kuva a) on
![]() ja siten
ja siten
![]() .
.
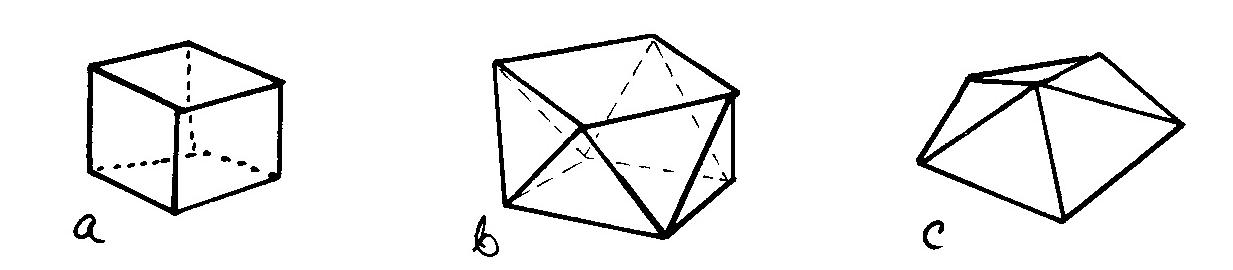
1. Tehtäviä. (a) Laske Eulerin karakteristika muille oheisen kuvan monitahokkaille ja keksi itse lisää esimerkkejä.
(b) Monikulmio tai monitahokas on kupera eli konveksi, jos sen kärkiä yhdistävät janat eivät joudu joukon ulkopuolelle. Mitkä oheisen kuvan monitahokkaista ovat kuperia?
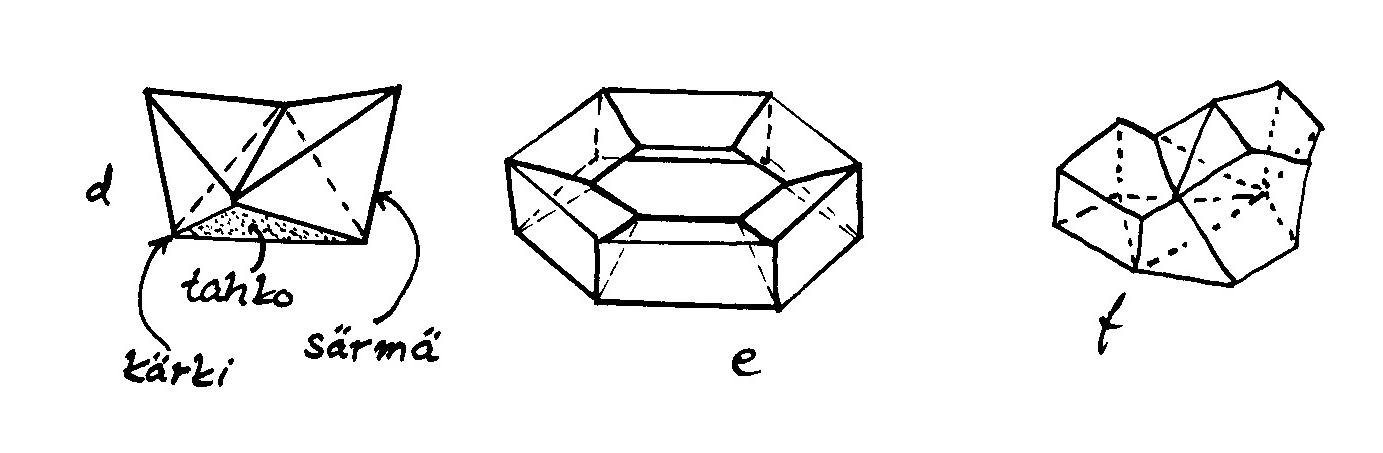
(c) Monitahokasta sanotaan deltaedriksi, jos sen kaikki tahkot ovat tasasivuisia kolmioita. Yksi sellainen on kuvassa d. Montako erilaista deltaedriä on olemassa? Entä montako kuperaa deltaedriä?
Tehtävän 1.c ehdot täyttäviä monitahokkaita voi etsiä ilman mitään lisätietoja, piirtämällä ja/tai leikkaamalla ja liimaamalla pahvikolmioita reunoistaan yhteen. Mutta mistä tiedetään, milloin kaikki ovat löytyneet? Etsintää voi helpottaa huomaamalla muutaman yleisen säännönmukaisuuden.
Tehtävän 1.a tehtyämme huomaamme, että ![]() ainakin kaikille kuvan tahokkaille, paitsi mutterimaiselle kappaleelle
(kuva e). Mahtaako tämä tulos päteä yleisemminkin? Miksi mutteri poikkeaa
muista - voimmekohan todistaa teoreeman, jonka mukaan
ainakin kaikille kuvan tahokkaille, paitsi mutterimaiselle kappaleelle
(kuva e). Mahtaako tämä tulos päteä yleisemminkin? Miksi mutteri poikkeaa
muista - voimmekohan todistaa teoreeman, jonka mukaan ![]() kaikille ''epämutterimaisille'' monitahokkaille? Tai toisaalta,
mitä yhteistä on niillä tahokkailla, joille mainittu kaava pätee?
kaikille ''epämutterimaisille'' monitahokkaille? Tai toisaalta,
mitä yhteistä on niillä tahokkailla, joille mainittu kaava pätee?
2. Lause.
Jokaiselle kuperalle monitahokkaalle pätee ![]() .
.
Tämä on klassinen Eulerin monitahokaslause. Itse asiassa kuperuus ei ole tässä välttämätön ehto, sillä väite pätee myös esimerkiksi kuvissa d ja f oleville ''lommoisille'' tahokkaille. Etsimmekin toisentyyppisen luonnehdinnan, jonka avulla tulos on myös helpompi todistaa.
Tavoittelemamme monitahokkaat ovat tietyllä tavalla ''pallomaisia''. Määrittelemme tämän ominaisuuden tarkemmin kohta, mutta ensin selitämme idean: jos monitahokas ajatellaan valmistetun jäykän pahvin sijasta jostakin venyvästä ja taipuisasta materiaalista, sen voi pullistaa pyöreäksi. Mutteri pullistuu tällöin uimarenkaan muotoiseksi pinnaksi, torukseksi, kun taas kuvan muut tahokkaat muuttuvat palloksi. Pallo on kupera, torus ei. Palloa ei voi muuttaa torukseksi (eikä torusta palloksi) leikkaamatta siihen ensin reikiä.
Jos kärjet ja särmät on merkitty tahokkaan muusta pinnasta poikkeavalla värillä, ne jäävät näkyviin pullistettuun pintaan verkoksi. Niiden lukumäärä ei selvästikään moisessa pullistelussa muutu, joten myöskään Eulerin karakteristika ei riipu siitä onko kyseessä teräväsärmäinen monitahokas vai sileällä pinnalla oleva verkko - tai siitäkään onko tahokas kupera vai lommoinen. Sillä sen sijaan on väliä, onko verkko pallon vai toruksen pinnalla, kuten mutteriesimerkki osoittaa.
Laajemmassa mielessä verkko eli graafi on mikä tahansa kuvio, joka koostuu kärki- eli solmupisteistä ja niitä yhdistävistä, toisiaan leikkaamattomista särmistä. Palloverkoksi nimitetään tässä sellaista äärellistä ja yhtenäistä verkkoa, jonka kärjet ja särmät ovat pallopinnalla ja siis jakavat pallon ''tilkkuihin'' eli tahkoihin. Äärellisyys tarkoittaa, että kärkiä, särmiä ja tahkoja on vain äärellisen monta kappaletta. Yhtenäisyys taas tarkoittaa, että verkon jokaisesta kärjestä pääsee särmiä myöten mihin tahansa muuhun kärkeen.
Puhkaisemalla palloverkon yhteen tahkoon reiän ja venyttämällä sitä verkon voi ''litistää'' tasoon ilman että verkon kärkien ja niissä kohtaavien särmien ja tahkojen määrät muuttuvat.
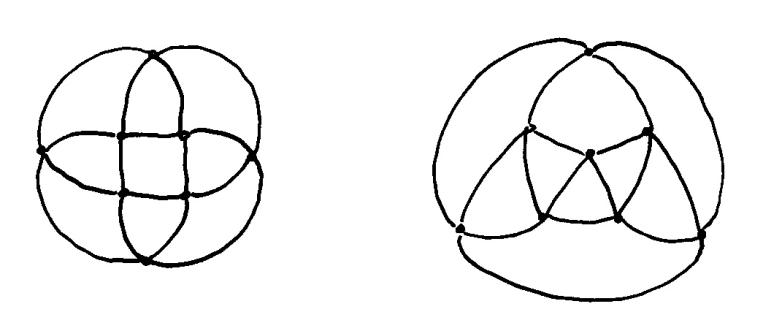
3. Tehtäviä. (a) Yllä on eräs monitahokas - neliöpohjainen vinoprisma - levitetty auki tasograafiksi kahdella eri tavalla. Piirrä tai rakenna siitä kolmiulotteinen malli.
(b) Rakenna erilaisia palloverkkoja solmimalla lankaa paperimassa- tms. askartelupallon ympärille.
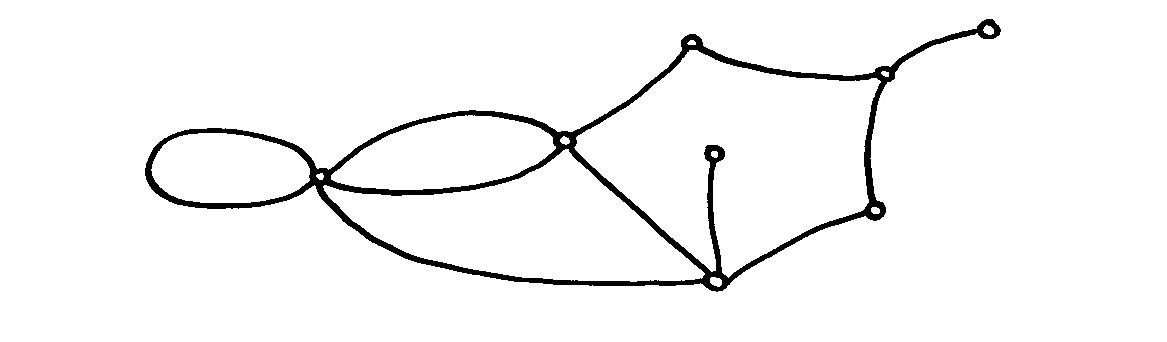
Jokaista kuperaa monitahokasta siis vastaa jokin palloverkko, mutta on myös sellaisia palloverkkoja joita ei vastaa mikään monitahokas. Palloverkossa nimittäin voi olla ''halkioita'', ''irtopäitä'' ja ''yksi- ja kaksikulmioita'', toisin kuin monitahokkaassa. Nyt osaamme muotoilla väitteen, jonka haluamme todistaa:
4. Lause.
Palloverkolle pätee ![]() .
.
Todistus.
Teemme eräänlaisen induktiopäättelyn: todistamme väitteen ensin
mahdollisimman yksinkertaiselle palloverkolle, ja sitten osoitamme
ettei ![]() muutu vaikka kärkiä tai särmiä lisättäisiin.
muutu vaikka kärkiä tai särmiä lisättäisiin.
Otetaan ensin pallolta vain yksi kärkipiste, jolloin loppuosa on
yhtä tahkoa. Tässä yksinkertaisimmassa palloverkossa on
![]() ;
väite siis pätee ainakin tässä erikoistapauksessa.
;
väite siis pätee ainakin tässä erikoistapauksessa.
Oletetaan sitten, että pallo on verkotettu millä tahansa tavalla, kunhan
vain
![]() . (Näin voidaan olettaa, koska olemme jo löytäneet
ainakin yhden palloverkon, joka tämän toteuttaa.)
. (Näin voidaan olettaa, koska olemme jo löytäneet
ainakin yhden palloverkon, joka tämän toteuttaa.)
Muodostetaan nyt uusi verkko lisäämällä uusi särmä jo ennestään
olevien kärkien välille, jolloin yksi tahko tulee jaetuksi kahtia.
Näin kärkien määrä ei muutu, mutta särmät ja tahkot lisääntyvät molemmat
yhdellä, joten uuden verkon Eulerin karakteristika on
![]()
Uusi verkko voidaan muodostaa myös siten, että lisätään kärkipiste
ja yhdistetään se uudella särmällä johonkin ennestään olleeseen
kärkipisteeseen. Tällöin kärjet ja särmät lisääntyvät kumpikin yhdellä
ja tahkojen määrä pysyy ennallaan, joten ![]() ei nytkään muutu.
ei nytkään muutu.
Uusia palloverkkoja voidaan rakentaa lisää äärettömän monta toistamalla näitä kahta operaatiota. Toisaalta mikä tahansa palloverkko saadaan aikaan tällä tavoin: annetun palloverkon voi purkaa poistamalla siitä yksi kerrallaan särmiä ja yhden särmän varaan jääneitä kärkipisteitä, siten että verkko pysyy joka vaiheessa yhtenäisenä (lukija keksiköön säännön, jolla moinen onnistuu!). Kun tämä prosessi sitten tehdään takaperin, alkuperäinen verkko tulee rakennetuksi mainittuja operaatioita käyttäen.
Koska kyseiset operaatiot siis eivät muuta Eulerin karakteristikaa,
se on vakio kaikille palloverkoille. Ja koska ![]() yhdelle
palloverkolle (sille jossa on vain yksi kärki ja yksi tahko),
tämä vakio on
yhdelle
palloverkolle (sille jossa on vain yksi kärki ja yksi tahko),
tämä vakio on ![]() .
. ![]()
Tämä tulos pätee siis kaikille palloverkoille - erityisesti sellaisille jotka vastaavat jotakin monitahokasta. Niinpä tulimme samalla todistaneeksi Eulerin monitahokaslauseen 2.
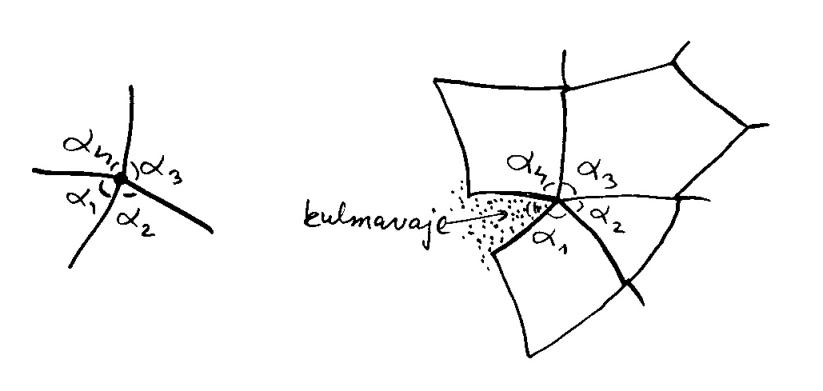
Monitahokkaan jokaisessa kärkipisteessä ![]() kohtaa jokin määrä
kohtaa jokin määrä ![]() särmiä ja saman verran tahkoja. Kaksi vierekkäistä särmää ovat jonkin
tasomonikulmion sivuja, ja niiden välinen kulma
särmiä ja saman verran tahkoja. Kaksi vierekkäistä särmää ovat jonkin
tasomonikulmion sivuja, ja niiden välinen kulma ![]() voidaan mitata
tai laskea.
Kun lasketaan nämä kaikkien kulmien
voidaan mitata
tai laskea.
Kun lasketaan nämä kaikkien kulmien
![]() asteluvut yhteen, saadaan luku, joka kertoo jotakin kyseisen
kärkipisteen luonteesta. Mikäli kulmien summa sattuu olemaan tasan
asteluvut yhteen, saadaan luku, joka kertoo jotakin kyseisen
kärkipisteen luonteesta. Mikäli kulmien summa sattuu olemaan tasan
![]() , monikulmiot voi latoa samaan tasoon pisteen ympärille.
Kulmasumman poikkeama täydestä kulmasta määritellään kärkipisteen
, monikulmiot voi latoa samaan tasoon pisteen ympärille.
Kulmasumman poikkeama täydestä kulmasta määritellään kärkipisteen ![]() kulmavajeeksi:
kulmavajeeksi:
5. Tehtäviä. (a) Leikkaa paperista monikulmioita. Liittele niitä yhteen ja mieti, voiko jonkin kärkipisteen kulmavaje olla negatiivinen? Miltä sellainen kärkipiste näyttäisi? Miten kulmavajeen ja kuperuuden käsitteet liittyvät toisiinsa?
(b) Rakenna paperimonikulmioista (mielellään säännöllisistä, jottei mene turhan vaikeaksi) mieleisesi monitahokas. Laske kunkin kärkipisteen kulmavaje ja kaikkien kärkien kulmavajeiden summa. Tee sama tarkastelu ainakin kahdelle erilaiselle tahokkaalle.
Monitahokkaan kaikkien kärkien (joita on ![]() kappaletta) kulmavajeiden
summaa
kappaletta) kulmavajeiden
summaa
![]() merkitään kreikkalaisella
isolla delta-kirjaimella. Itse asiassa pätee yleisestikin:
merkitään kreikkalaisella
isolla delta-kirjaimella. Itse asiassa pätee yleisestikin:
6. Lause.
Kuperan monitahokkaan kärkien kulmavajeiden summa on
![]() .
.
Todistus.
(a) Oletetaan aluksi jokainen tahko kolmioksi. Silloin monitahokkaassa on
kolme särmää jokaista tahkoa kohti; toisaalta jokainen särmä on kahdelle
tahkolle yhteinen, joten ![]() . Sijoittamalla tämä yhtälö Eulerin
monitahokaslauseeseen 2 saadaan
. Sijoittamalla tämä yhtälö Eulerin
monitahokaslauseeseen 2 saadaan ![]() . Kaikkien
kärkien kulmavajeiden summa on
. Kaikkien
kärkien kulmavajeiden summa on
Koska kolmion kulmien summa on ![]() (tätä tulosta ei todisteta
nyt, mutta asiaan ehkä palataan Solmussa joskus myöhemmin) ja koska
tahkoja on
(tätä tulosta ei todisteta
nyt, mutta asiaan ehkä palataan Solmussa joskus myöhemmin) ja koska
tahkoja on ![]() kappaletta, summaksi tulee
kappaletta, summaksi tulee
![]()
(b) Jos monitahokkaan tahkoina on muitakin monikulmioita kuin kolmioita,
tahkot voidaan jakaa lävistäjillä kolmioiksi. Nyt tälle pelkistä
kolmioista koostuvalle ''monitahokkaalle'' pätee (a)-kohdan päättely
siitä huolimatta, että vierekkäiset ''tahkot'' saattavat olla samassa
tasossa. ''Särmien'' lisääminen ei muuta kulmien suuruuksia, joten
myös tässä tapauksessa kulmavajesumma on ![]() .
. ![]()
Huomaa, että emme todistuksessa oikeastaan käyttäneet oletusta monitahokkaan kuperuudesta. Käytimme vain sitä tietoa, että sille pätee Eulerin monitahokaslause - ja kuten totesimme, tämä pätee aina kun tahokas voidaan pullistaa palloverkoksi. Kuperuus ei siis tällekään lauseelle ole välttämätön ehto (siis väite on totta kuperille tahokkaille, mutta myös joillekin muille).
Tämä tulos on itse asiassa aika hämmästyttävä. Onhan kulmien mittaaminen luonteeltaan erilaista kuin kärkien, särmien ja tahkojen lukumäärien laskeminen: tahokasta ei voi noin vain korvata pyöreällä pallolla kuten teimme monitahokaslauseen todistuksessa, koska venyttely ja pullistelu tietenkin muuttaa kulmia. Mutta silti myös kulmavajelause pätee riippumatta tahokkaan tarkemmasta muodosta, kunhan siinä ei ole ''reikää'' kuten toruksessa ja mutterissa.
Kuperien deltaedrien etsinnässä (1.c) voi nyt käyttää apuna
juuri todistettuja lauseita 4 ja 6.
Laske ensin sellaisen kärjen kulmavaje, jossa kohtaa ![]() tasasivuista
kolmiota, ja mieti miten suuri kokonaisluku
tasasivuista
kolmiota, ja mieti miten suuri kokonaisluku ![]() voi olla.
Em. lauseet antavat välttämättömän ehdon etsitynlaisten tahokkaiden
kärkien lukumäärille, joten
''yrityksen ja erehdyksen menetelmää'' ei tarvitse jatkaa loputtomiin.
(Tehtävään annetaan ratkaisu seuraavassa Solmussa.)
voi olla.
Em. lauseet antavat välttämättömän ehdon etsitynlaisten tahokkaiden
kärkien lukumäärille, joten
''yrityksen ja erehdyksen menetelmää'' ei tarvitse jatkaa loputtomiin.
(Tehtävään annetaan ratkaisu seuraavassa Solmussa.)
Monikulmioita ja -tahokkaita tarkastellaan usein geometrisina olioina. Geometria on matematiikan ala, jossa ''mitataan'' tai oikeastaan lasketaan etäisyyksiä ja kulmien suuruuksia; itse sanakin on johdettu kreikan maanmittausta tarkoittavasta sanasta. Tuttu esimerkki geometrisesta tuloksesta on Pythagoraan lause, joka koskee suorakulmaisen kolmion sivujen pituuksia.
Edellä kuitenkin tarkastelimme monitahokkaita hiukan eri kannalta: Eulerin lauseessa ei puhuta mitään pituuksista eikä kulmista. Eulerin karakteristika on monitahokkaan geometrisesta muodosta riippumaton vakio.
Joukon muotoa voivat muuttaa niissä määritellyt
kuvaukset eli funktiot. Esimerkiksi kuvaus
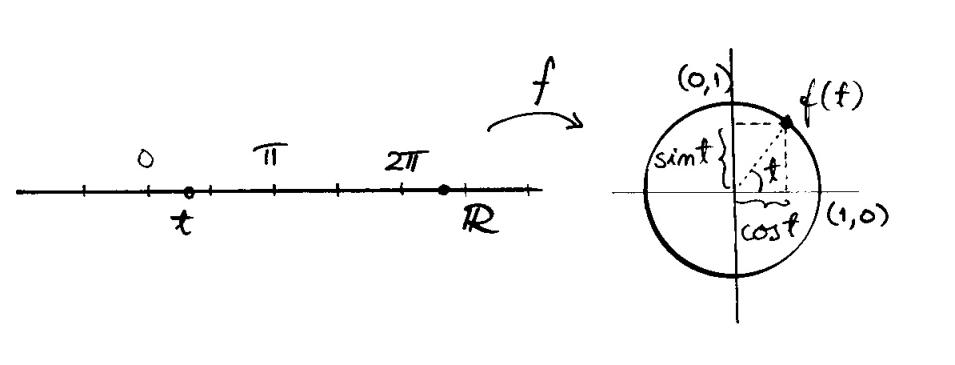
Jokaista reaalilukua ![]() vastaa siten yksi (ympyrän kehällä oleva)
tason piste
vastaa siten yksi (ympyrän kehällä oleva)
tason piste ![]() , mutta jokaista ympyrän pistettä vastaa
äärettömän monta reaalilukua: esimerkiksi pistettä
, mutta jokaista ympyrän pistettä vastaa
äärettömän monta reaalilukua: esimerkiksi pistettä ![]() vastaavat
luvut
vastaavat
luvut
![]() (radiaania). Toisaalta muita tason pisteitä kuin ympyrällä olevia
ei kuvauksessa
(radiaania). Toisaalta muita tason pisteitä kuin ympyrällä olevia
ei kuvauksessa ![]() vastaa mikään reaaliluku.
vastaa mikään reaaliluku.
Kuvauksia voidaan luokitella erinäisten ominaisuuksien perusteella.
Kaksi joukkoa ![]() ja
ja ![]() ovat topologisesti ekvivalentit,
mikäli niiden välillä on topologinen kuvaus eli
homeomorfismi. Havainnollisesti tämä tarkoittaa, että
ovat topologisesti ekvivalentit,
mikäli niiden välillä on topologinen kuvaus eli
homeomorfismi. Havainnollisesti tämä tarkoittaa, että

Ominaisuuksia ja vakioita, jotka säilyvät topologisessa kuvauksessa, sanotaan topologisiksi. Esimerkiksi Eulerin karakteristika on topologinen vakio, ja yhtenäisyys on topologinen ominaisuus.
Toisin kuin Eulerin lauseessa, kulmavajelauseessa puhutaan kulmien asteluvuista - siis geometriasta! - mutta lauseen sisältö on että näistä laskettu tietty lauseke on topologinen vakio. Topologia ja geometria kietoutuvatkin monin tavoin yhteen, mutta ne eivät ole sama asia.
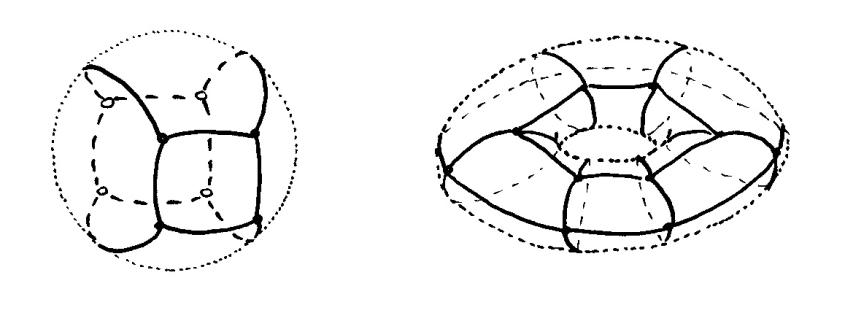
Ominaisuus, joka erottaa ratkaisevasti pallomaiset pinnat torusmaisista, on myös luonteeltaan topologinen. Huomaamme, että toruksen voi leikata auki sopivasti valittua silmukkaa myöten (sylinteriputkeksi) niin että se pysyy yhtenä kappaleena. Pallolle tämä ei onnistu: leikkasipa sitä millaista silmukkaa pitkin tahansa, siitä aina irtoaa pala. Toisaalta torustakaan ei voi leikata enää toista silmukkaa pitkin: joko putken kylkeen tulee reikä tai putken päästä irtoaa rengas. Kuvassa oikealla olevan pinnan voi avata peräti neljää erillistä silmukkaa pitkin halkaisematta sitä kahtia.
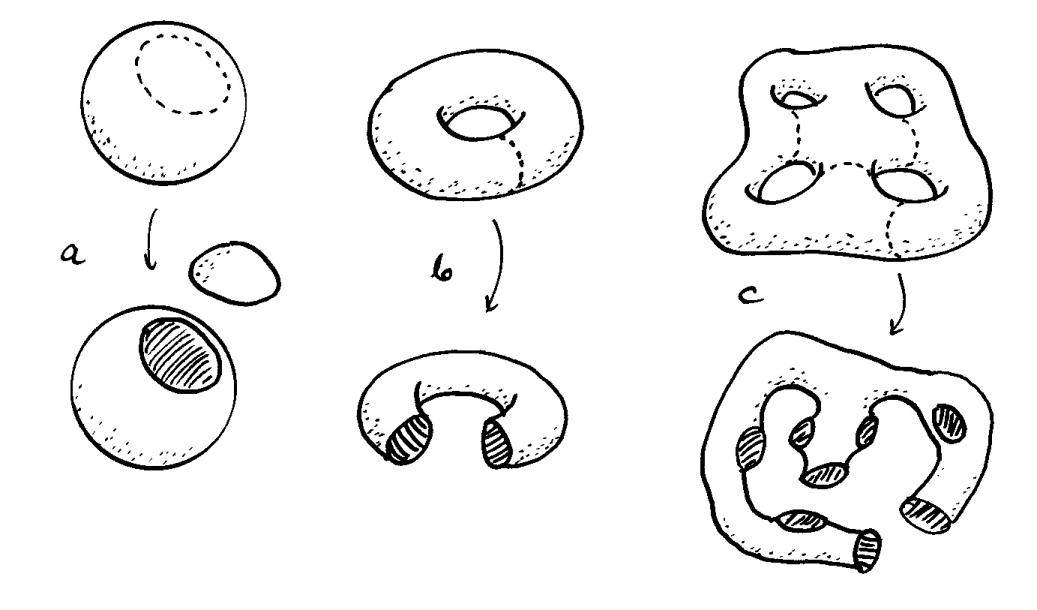
Pinta tarkoittaa tässä yhtenäistä, kaksiulotteista, suljettua ja reunatonta joukkoa. Yhtenäisyys merkitsee, että mitkä tahansa kaksi pistettä voidaan yhdistää toisiinsa jollakin pintaa pitkin kulkevalla käyrällä; 2-ulotteisuus taas sitä, että pinnasta leikattu pieni pala ''näyttää samalta'' kuin tasosta leikattu pala (tarkemmin sanoen pinta on paikallisesti topologisesti ekvivalentti tason kanssa). Erityisesti monitahokkaat ovat sellaisia. Nyt voimme määritellä tärkeän topologisen käsitteen:
Pinnan genus on kokonaisluku ![]() , joka kertoo montako
erillistä silmukkaa myöten pinnan voi leikata auki niin että se pysyy
yhtenäisenä.
, joka kertoo montako
erillistä silmukkaa myöten pinnan voi leikata auki niin että se pysyy
yhtenäisenä.
Siispä pallon, kuution, pyramidin jne. genus on ![]() ; toruksen,
uimarenkaan, mutterinpinnan jne. genus on puolestaan
; toruksen,
uimarenkaan, mutterinpinnan jne. genus on puolestaan ![]() .
Genus on toisin ilmaistuna ''pujotusreikien'' tai ''kahvojen'' lukumäärä.
.
Genus on toisin ilmaistuna ''pujotusreikien'' tai ''kahvojen'' lukumäärä.
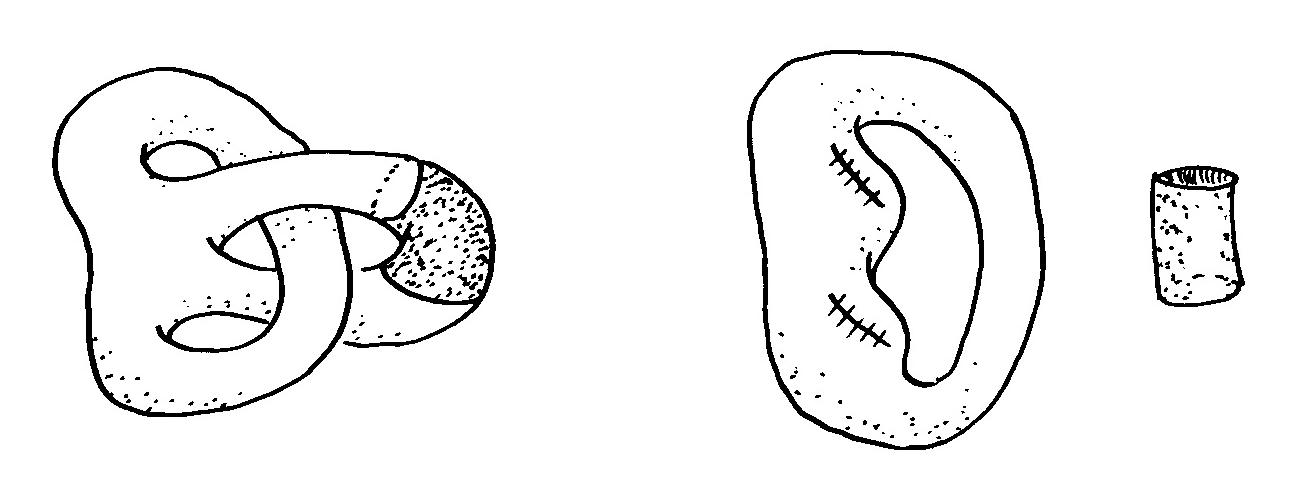
7. Lause. (a) Pinnan genus kasvaa yhdellä, jos siihen tehdään kaksi viiltoa ja liitetään näihin sylinteriputki päistään kahvaksi.
(b) Jos pinnan genus on vähintään yksi, niin siitä voidaan poistaa kahva leikkaamalla kahta silmukkaa myöten ja sulkemalla syntyneet reiät. Tällöin pinnan genus vähenee yhdellä.
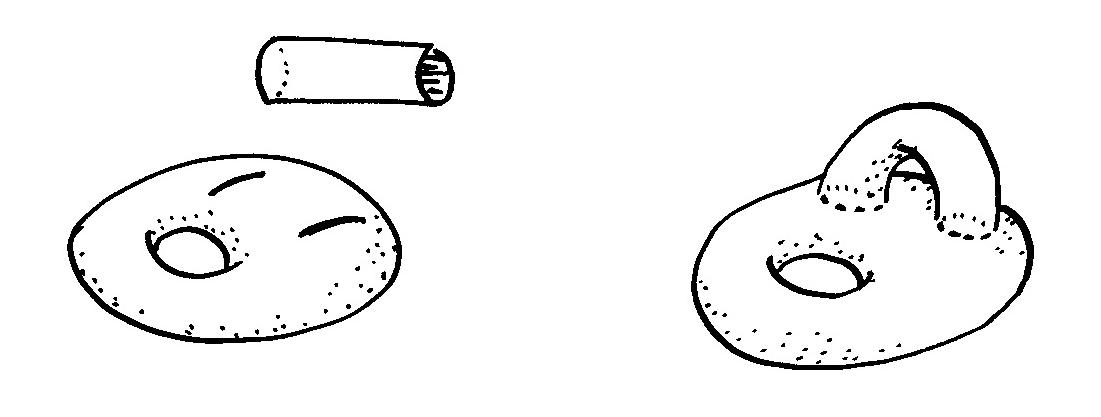
Todistus.
(a) Olkoon ![]() pinta ja
pinta ja ![]() sen genus.
Viiltämällä
sen genus.
Viiltämällä ![]() kahdesta kohtaa auki ja liittämällä reikiin
putki päistään kahvaksi syntyy uusi pinta
kahdesta kohtaa auki ja liittämällä reikiin
putki päistään kahvaksi syntyy uusi pinta ![]() . Nyt kahvan voi
taas irrottaa toisesta päästään leikkaamalla silmukkaa myöten.
Näin ollen sellaisia silmukoita, joita pitkin pinnan voi leikata
auki irrottamatta siitä palaa, löytyy
. Nyt kahvan voi
taas irrottaa toisesta päästään leikkaamalla silmukkaa myöten.
Näin ollen sellaisia silmukoita, joita pitkin pinnan voi leikata
auki irrottamatta siitä palaa, löytyy ![]() :lta yksi enemmän kuin
:lta yksi enemmän kuin
![]() :ltä;
:ltä; ![]() :n genus on siis
:n genus on siis ![]() .
.
(b) Olkoon ![]() pinta ja
pinta ja ![]() sen genus, jolloin sillä määritelmän
mukaan on
sen genus, jolloin sillä määritelmän
mukaan on ![]() eri silmukkaa
eri silmukkaa
![]() , joita myöten sen voi
leikata auki irrottamatta paloja. Leikataan
, joita myöten sen voi
leikata auki irrottamatta paloja. Leikataan ![]() auki yhtä tällaista
silmukkaa
auki yhtä tällaista
silmukkaa ![]() pitkin, jolloin pinta siis jää yhtenäiseksi ja siihen
tulee kaksi silmukanmuotoista reikää.
pitkin, jolloin pinta siis jää yhtenäiseksi ja siihen
tulee kaksi silmukanmuotoista reikää.
Sitten leikataan pinta auki syntyneen reiän reunan läheltä kulkevaa
silmukkaa pitkin. Tällöin irtoaa sylinteriputken muotoinen pala,
joten kyseinen silmukka ei voinut olla mikään edellämainituista
![]() :stä silmukasta.
Ommellaan sitten pintaan jääneet kaksi reikää umpeen, jolloin syntyy
uusi pinta
:stä silmukasta.
Ommellaan sitten pintaan jääneet kaksi reikää umpeen, jolloin syntyy
uusi pinta ![]() . Nyt pinnalla
. Nyt pinnalla ![]() on edelleen
on edelleen ![]() erillistä
silmukkaa, joita pitkin auki leikattuna se pysyisi yhtenäisenä:
erillistä
silmukkaa, joita pitkin auki leikattuna se pysyisi yhtenäisenä:
![]() . Niinpä
. Niinpä ![]() :n genus on
:n genus on ![]() , ja
operaatiosta jäi yli yksi sylinterinmuotoinen kahva.
, ja
operaatiosta jäi yli yksi sylinterinmuotoinen kahva. ![]()
Mutterille ja muille positiivisen genuksen omaaville monitahokkaille pätee Eulerin monitahokaslausetta (4) ja kulmavajelausetta (6) vastaavat tulokset; niissä vain esiintyy eri vakiot. Todistaaksemme nämä tulokset käytämme jälleen apuna verkkoja.
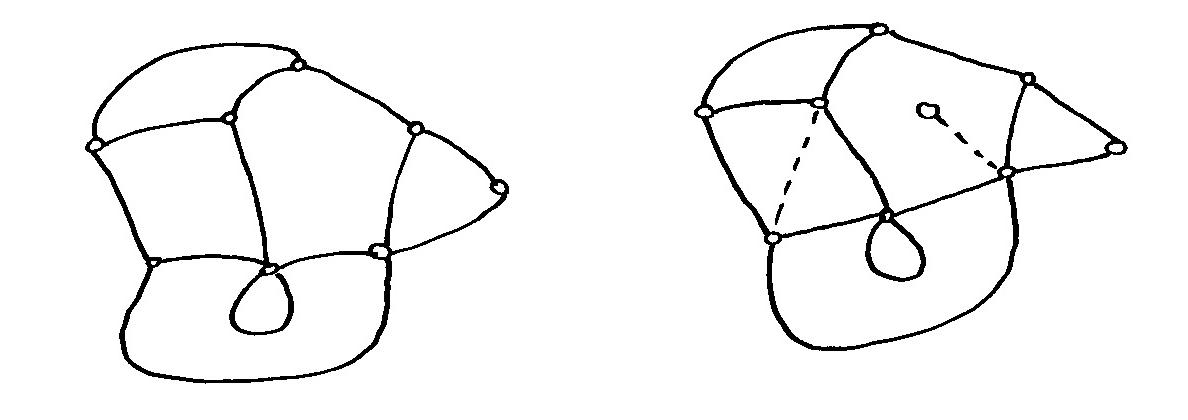
Mikä tahansa pinta voidaan ''verkottaa'' samaan tapaan kuin pallo. Mielivaltaisesti valitut kärjet ja särmät jakavat pinnan alueisiin, mutta tässä tarvitsemme lisäehdon. Jokaisen alueen reuna saa koostua vain yhdestä (murtoviiva)silmukasta - toisin sanoen vaadimme, että alue on monikulmion kanssa topologisesti ekvivalentti. (Tämä ehto sulkee pois rengasmaiset tai reiälliset alueet.)
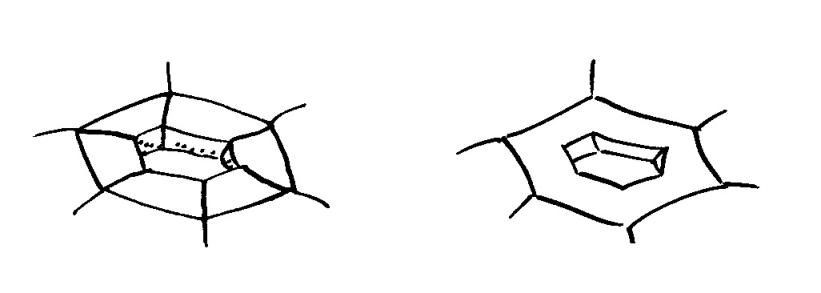
Esimerkiksi toruksen voi verkottaa siten, että saadaan edellä esiintyneen mutterin ''pyöristetty'' vastine - mutta jos tästä verkosta poistetaan tietyt kuusi viivaa, saadaan toinen verkko, jonka yksi alue on renkaan muotoinen.
Nimitämme pintaverkoksi äärellistä ja yhtenäistä verkkoa, joka jakaa jonkin pinnan topologisiin monikulmioihin. Edellisen kuvan vasemmanpuoleinen verkko on pintaverkko, oikeanpuoleinen ei. (Aiemmin määritelty palloverkko on siis pintaverkon erikoistapaus.)
8. Tehtäviä. (a) Piirrä tai rakenna monitahokas, jonka genus on vähintään yksi ja jossa on ainakin yksi rengasmainen ''tahko''. Laske sen Eulerin karakteristika. Lisää sitten kärkiä tai särmiä siten, että rengasalue jakautuu tavallisiksi monikulmioiksi, ja laske tämän uuden tahokkaan karakteristika.
(b) Vertaa ylläolevaa pintaverkon määritelmää palloverkon määritelmään. Palloverkon määritelmä ei kieltänyt rengasalueita - siinä vaadittiin vain että verkon pitää olla yhtenäinen. Voiko palloverkossa olla rengasalueita? Mieti miksi rengasalueet pitää kieltää erikseen suurempigenuksisilta pintaverkoilta.
(c)
Voiko ![]() -genuksista monitahokasta (tai pintaverkkoa) esittää
tasograafina (vrt. tehtävä 3.a)?
-genuksista monitahokasta (tai pintaverkkoa) esittää
tasograafina (vrt. tehtävä 3.a)?
Nyt yleistämme äsken nollagenuksisille monitahokkaille todistamamme kaksi lausetta isompigenuksisillekin tahokkaille.
9. Lause.
Jos pinnan genus on ![]() , niin sen jokaisen pintaverkon
Eulerin karakteristika on
, niin sen jokaisen pintaverkon
Eulerin karakteristika on ![]() .
.
Todistus.
Käytämme jälleen induktiotyyppistä päättelyä. Pallon tapauksessa ![]() ja
ja
![]() , jo todistetun tavallisen Eulerin lauseen nojalla.
Oletetaan sitten väitteen pätevän jollakin luonnollisella
luvulla
, jo todistetun tavallisen Eulerin lauseen nojalla.
Oletetaan sitten väitteen pätevän jollakin luonnollisella
luvulla ![]() , eli että (minkä tahansa)
, eli että (minkä tahansa) ![]() -genuksisen pintaverkon
-genuksisen pintaverkon ![]() karakteristika on
karakteristika on ![]() .
.
Eulerin lauseen perusteella ![]() ei riipu pinnan eikä verkon geometriasta.
On osoitettava, että tällöin minkä tahansa
ei riipu pinnan eikä verkon geometriasta.
On osoitettava, että tällöin minkä tahansa ![]() -genuksisen pintaverkon
karakteristika on
-genuksisen pintaverkon
karakteristika on
![]() . Koska
. Koska
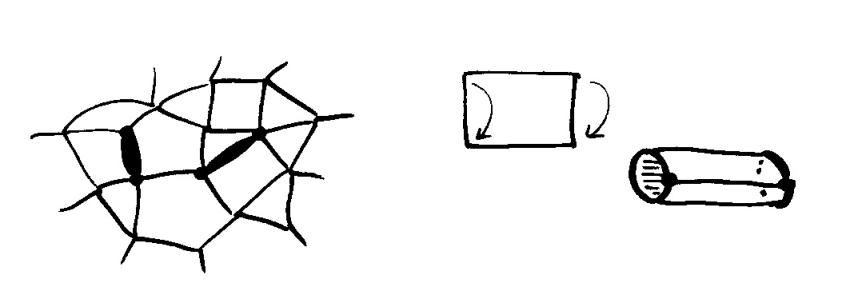
Leikataan pintaverkko ![]() auki kahta erillistä särmää myöten. Kahvaksi
liitettävän putken voi tehdä vaikkapa yhdestä topologisesta neliöstä,
jonka vastakkaiset sivut yhdistetään uudeksi särmäksi. Operaation jälkeen
meillä on uusi pintaverkko
auki kahta erillistä särmää myöten. Kahvaksi
liitettävän putken voi tehdä vaikkapa yhdestä topologisesta neliöstä,
jonka vastakkaiset sivut yhdistetään uudeksi särmäksi. Operaation jälkeen
meillä on uusi pintaverkko ![]() , jonka genus on
, jonka genus on ![]() ja jossa on kärkiä
saman verran kuin
ja jossa on kärkiä
saman verran kuin ![]() :ssä, särmiä kolme enemmän ja tahkoja yksi enemmän.
Siten verkon
:ssä, särmiä kolme enemmän ja tahkoja yksi enemmän.
Siten verkon ![]() Eulerin karakteristika on
Eulerin karakteristika on
![]()
kuten väitettiin. Vielä todetaan tavallisen Eulerin lauseen perusteella,
ettei ![]() :n karakteristika riipu valitusta pintaverkosta eikä
siten myöskään tavasta jolla kahvan lisäys tehtiin, joten todistuskin
pätee näistä valinnoista riippumatta.
:n karakteristika riipu valitusta pintaverkosta eikä
siten myöskään tavasta jolla kahvan lisäys tehtiin, joten todistuskin
pätee näistä valinnoista riippumatta. ![]()
Jokaista monitahokasta vastaa sen kanssa topologisesti ekvivalentti pintaverkko, joten lauseesta 9 seuraa yleistetty Eulerin monitahokaslause:
10. Lause.
Jos monitahokkaan genus on ![]() , niin sen Eulerin karakteristika on
, niin sen Eulerin karakteristika on
![]() .
.
Todistamme vielä yleistetyn kulmavajelauseen:
11. Lause.
Jos monitahokkaan Eulerin karakteristika on ![]() , niin sen
kaikkien kärkien kulmavajeiden summa on
, niin sen
kaikkien kärkien kulmavajeiden summa on
![]() .
.
Todistus.
Lauseen 6 todistus yleistyy melko suoraan;
ainoa ero on, että (a)-kohdassa yhtälöä ![]() ei sijoiteta Eulerin
monitahokaslauseeseen
ei sijoiteta Eulerin
monitahokaslauseeseen ![]() , vaan Eulerin karakteristikan
määritelmään
, vaan Eulerin karakteristikan
määritelmään ![]() .
.
Tällöin saadaan
![]() ja kaikkien kulmavajeiden summaksi
ja kaikkien kulmavajeiden summaksi
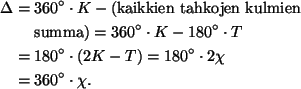
(b)-kohdan päättely toimii sellaisenaan. ![]()
Nämä tulokset osoittavat, että Eulerin karakteristika ![]() ja
kulmavajeiden summa
ja
kulmavajeiden summa ![]() kertovat (verkotetusta) pinnasta tasan
saman asian kuin genus
kertovat (verkotetusta) pinnasta tasan
saman asian kuin genus ![]() . Jos siis yksi näistä luvuista tiedetään,
voidaan laskea myös muut. Kaikki (yhtenäiset, kaksiulotteiset, suljetut
ja reunattomat) pinnat voidaan luokitella tämän ominaisuuden perusteella
topologisiin luokkiin.
. Jos siis yksi näistä luvuista tiedetään,
voidaan laskea myös muut. Kaikki (yhtenäiset, kaksiulotteiset, suljetut
ja reunattomat) pinnat voidaan luokitella tämän ominaisuuden perusteella
topologisiin luokkiin.
12. Tehtävä.
Piirrä tai rakenna erigenuksisia monitahokkaita ja laske niiden
![]() ja
ja ![]() .
.
Tämän artikkelin tarkoitus oli esitellä havainnollisten esimerkkien avulla millaisia asioita tutkii topologiaksi kutsuttu matematiikan ala ja todistaa muutama topologinen lause. Muodollisia määritelmiä esitettiin mahdollisimman vähän, mutta kiinnostunut lukija löytää niitä helposti lisää oppikirjoista.
Topologisen kuvauksen eli homeomorfismin oikea määritelmä on 'jatkuva bijektio, jonka käänteiskuvauskin on jatkuva'. Sana topologia on peräisin kreikasta (kuten moni muukin matematiikan termi). Se on matematiikan ala, jossa avoimet joukot ja jatkuvat kuvaukset ovat keskeisiä käsitteitä.
Oletimme (erikseen mainitsematta) kaikki pinnat suunnistuviksi, eli että niillä on sekä sisä- että ulkopuoli. On olemassa myös suunnistumattomia pintoja kuten Kleinin pullo, joita tämä tarkastelu siis ei koske. Nollagenuksisen monitahokkaan ja pallo(verko)n topologista ekvivalenssia perustelimme edellä vain intuitioon vedoten: monitahokkaan voi ''pullistaa'' palloksi. Tämä voitaisiin todistaa täsmällisesti määrittelemällä kuvaus, joka kuvaa monitahokkaan särmineen palloksi, ja osoittamalla kyseinen kuvaus homeomorfismiksi. Muutkin nyt perustelematta esitetyt väitteet (kuten 'yhtenäisyys on topologinen ominaisuus' ja 'ympyrän ja suoran välillä ei ole homeomorfismia') ovat helposti todistettavissa lyhyehkön topologian perusteisiin tutustumisen jälkeen.
Lisätehtävä. Sen sijaan että verkotetaan valmiita pintoja, kuten edellä tehtiin, voitaisiin aluksi rakentaa pelkkä verkko kärjistä ja särmistä. (Tällöin ei kuitenkaan välttämättä synny pintaverkkoa; totea tämä rakentamalla sopiva esimerkkiverkko.) Mutta jos verkko on jonkin monitahokkaan ''luuranko'', onko kyseinen monitahokas yksikäsitteinen? Löydätkö verkon, johon voi pingottaa tahkoja kahdella eri tavalla siten, että syntyy eri genuksiset monitahokkaat? (Tämä on vaikea - älä masennu vaikka et löytäisi tällaista verkkoa!)