PDF

Otsikkokuva

Sattuman matematiikkaa I - klassinen todennäköisyys

Mika Koskenoja
Assistentti
Matematiikan laitos, Helsingin yliopisto


Johdanto

Aloitan todennäköisyyslaskennasta kertovan kirjoitussarjan, jonka toinen osa ilmestynee seuraavassa Solmussa syksyllä. Inspiraation aiheesta kirjoittamiseen olen saanut kahdeltakin taholta. Ensinnäkin, Ilta-Sanomien toimittaja soitti minulle muutama kuukausi sitten ja pyysi kommentoimaan Veijo Wirénin vasta ilmestynyttä kirjaa Näin voitan lotossa? (Gummerus, 2002). Kirjassa esitetyt menetelmät ''todennäköisten'' lottorivien löytämisestä on helppo osoittaa hölynpölyksi klassisen todennäköisyyslaskennan avulla (Ilta-Sanomat, 9.2.2002). Kirjan kirjoittaja intoutui kuitenkin vielä arvostelemaan toimittajaa - ja siinä samalla minuakin - kirjansa teilaamisesta Ilta-Sanomien yleisönosastolla 16.2.2002. Hänen mielestään ''kaavamainen'' matematiikka ei lainkaan sovi yhteen hänen luovan ajattelunsa kanssa; siitä on toki helppo olla samaa mieltä hänen kanssaan.

Toinen ja edellistä tärkeämpi syy todennäköisyyslaskennasta kirjoittamiseen on Solmun lukijoilta tullut toivomus. Erityisesti on toivottu Bertrandin paradoksin käsittelyä, johon palaankin myöhemmin. Se on esimerkki klassisen (geometrisen) todennäköisyyslaskennan tunnetusta ongelmasta.

Tässä kirjoitussarjan ensimmäisessä osassa käsittelen todennäköisyyslaskennan historiaa sekä klassista todennäköisyyttä ja tämän laajennuksena geometrista todennäköisyyttä. Näihin liittyen esitän jo mainitsemieni loton ja Bertrandin paradoksin lisäksi muutamia varsin yksinkertaisia esimerkkejä. Seuraavissa kirjoitussarjan osissa Solmun lukijat on aikomus tutustuttaa todennäköisyyden aksioomiin ja perusominaisuuksiin, satunnaismuuuttujiin sekä erilaisiin jakaumiin, jotka mahdollistavat satunnaisilmiöiden kuvaamisen klassisia menetelmiä huomattavasti tehokkaammin. Erityisen ilahduttavaa uskoisin lukijoille olevan, että lukiomatematiikka - suurelta osin jopa hyvin hallittu peruskoulumatematiikka - riittää vallan mainiosti esitedoiksi kirjoitussarjan seuraamiseen.


Historiaa

Todennäköisyyslaskennan katsotaan saaneen alkunsa 1600-luvun puolivälissä siitä, kun Chevalier de Mérén nimellä tunnettu ranskalainen aatelismies Antoine Gombaud (1607-1684) esitti maanmiehelleen Blaise Pascalille (1623-1662) uhkapeleihin liittyneet kaksi kysymystä. Näistä ensimmäinen koski peliä, joka koostuu pelieristä, joiden voittamiseen kummallakin pelaajalla on samat mahdollisuudet. Jos ensimmäisenä kuusi erää voittanut saa pelipanoksen, mutta peli keskeytetään tilanteessa, jossa toinen pelaaja on voittanut viisi ja toinen kolme erää, niin mikä on oikeudenmukainen tapa jakaa pelipanos? Pascal ja Pierre de Fermat (1601-1665, hänkin Pascalin tavoin ranskalainen matematiikan historian suuri nimi) käsittelivät ongelmaa kirjeenvaihdossaan ja päätyivät samaan ratkaisuun $7:1$. Toinen de Mérén kysymys koski nopanheittoa, ja siihen palaan tarkemmin klassista todennäköisyyttä koskevassa luvussa.

Pascal Fermat

Pascalin ja Fermat'n lisäksi klassisen todennäköisyyden käsitteen yksi ensimmäisiä kehittäjiä oli 1600-luvun puolivälissä hollantilainen Christiaan Huygens (1629-1695), joka vuonna 1657 ilmestyneessä kirjasessaan tarkasteli de Mérén nopanheittoon liittynyttä kysymystä. Koska todennäköisyyslaskennan ensimmäiset ongelmat versoivat juuri uhkapeleistä, niin teoreettinen tarkastelu perustuikin aluksi lähes yksinomaan aritmetiikkaan ja kombinatoriikkaan. Muutamaa vuosikymmentä myöhemmin saksalainen Jakob Bernoulli (1654-1705) toi tilastollisen todennäköisyyden käsitteen mukaan teorian piiriin. Bernoullin Ars Conjectandi (1713) laajensi todennäköisyyskäsitystä uhkapeleistä arkitodellisuuteen.

Huygens Bernoulli

Vaikka analyysin ensiaskeleita jo otettiinkin 1600-luvulla, niin todennäköisyyslaskennan varhaisvaiheiden aikaan analyysi vielä odotteli todellista läpimurtoaan luonnontieteissä. Kuitenkin jo 1700-luvun puolivälissä analyysi muodostui luonnontieteiden ja samalla myös todennäköisyyslaskennan edistyksen perustaksi. Suurimman paineen analyysin kehitykselle loivat fysikaalisten tieteiden tarpeet. Todennäköisyyslaskennan puolella analyysin voimakas kehitys vauhditti erityisesti normaalijakauman käyttöönottoa, joka loi pohjan mm. havaintovirheiden analysoinnille ja väestötieteelle.

de Moivre Laplace

Tärkeimmät tuon ajan matemaatikot, joiden nimet monen muun luonnontieteiden alan lisäksi liitetään myös todennäköisyyslaskentaan, olivat ranskalainen, jo nuorena Englantiin muuttanut Abraham de Moivre (1667-1745), ranskalaiset Pierre Laplace (1749-1827) ja Siméon Poisson (1781-1840) sekä saksalainen Carl Friedrich Gauss (1777-1855).

Poisson Gauss

Todennäköisyysteorian itsenäinen kehitys alkoi 1800-luvun puolivälissä. Venäläisen koulukunnan johdolla - etunenässä Pafnuti Tšebyšev (1821-1894) - se eli kulta-aikaansa aina 1930-luvulle asti. Satunnaismuuttujan ja odotusarvon käsitteiden katsotaan olevan peräisin juuri Tšebyševiltä.

Tšebyšev Markov

Teorian kehitykseen 1900-luvun vaihteessa vaikuttaneista venäläisistä matemaatikoista mainittakoon Andrej Markov (1856-1922), jonka ansioksi luetaan stokastisten prosessien tutkimuksen aloittaminen ns. Markovin ketjujen muodossa. Todennäköisyyslaskennan yleisen teorian loivat vähän myöhemmin 1930-luvulla venäläiset Andrej Kolmogorov (1903-1987) ja Aleksander Hintšin (1894-1959). Koko teorian perustana pidetään Kolmogorovin vuonna 1933 julkaisemaa aksiomatiikkaa.

Kolmogorov Hintšin

Täydellisempi esitys todennäköisyyslaskennan historiasta löytyy Matti Lehtisen kirjoittamasta Matematiikan historiasta, http://matematiikkalehtisolmu.fi/2000/mathist/. Seuraava klassisen todennäköisyyden esitys perustuu Pekka Tuomisen ja Pekka Norlamon 2-osaiseen kirjaan Todennäköisyyslaskenta, jossa käsitellään jonkin verran myös todennäköisyyslaskennan historiaa.


Klassinen todennäköisyys

Klassinen todennäköisyys voidaan määritellä käyttäen useaa toisistaan hieman poikkeavaa lähestymistapaa. Määritelmän on kuitenkin toteutettava muutamia perusperiaatteita lähestymistavasta riippumatta. Tärkein näistä on yhtä todennäköisen periaate, jota voidaan pitää klassisen todennäköisyyden tunnusmerkkinä.

Tilannetta tai ilmiötä, jossa esiintyy satunnaisuutta, kutsutaan satunnaiskokeeksi. Klassisessa todennäköisyydessä on voitava olettaa, että koe on mahdollista toistaa samoissa olosuhteissa rajattoman monta kertaa toistojen ollessa riippumattomia. Tämä ei aivan kirjaimellisesti ottaen ole tietenkään ikinä mahdollista muuten kuin periaatteena.

Satunnaiskokeen erilaisia tulosmahdollisuuksia kutsutaan alkeistapauksiksi. Klassisessa todennäköisyydessä alkeistapauksia on aina äärellinen määrä. Lisäksi oletetaan, että kaikki alkeistapaukset ovat yhtä mahdollisia eli yhtä todennäköisiä. Tämä olettamus lausutaan tavallisesti sanomalla, että alkeistapaukset ovat symmetrisiä. Esimerkiksi kolikonheitossa on kaksi symmetristä alkeistapausta, kruuna ja klaava, ja nopanheitossa on kuusi symmetristä alkeistapausta, pisteluvut $1,2,\ldots,6$.

Tapahtumalla tarkoitamme mielivaltaista alkeistapausten joukkoa, erityisesti se voi olla tyhjä tai kaikkien alkeistapausten joukko. Tapahtumia on tapana merkitä isoilla aakkosilla $A$, $B$, $C$, jne. Esimerkiksi nopanheitossa tapahtuma $A$ voisi olla ''nopanheiton tulos on vähintään neljä'', siis $A=\{4,5,6\}$. Tapahtuman sanotaan olevan varma, jos se sattuu välttämättä jokaisessa satunnaiskokeessa, ja tapahtuma on mahdoton, jos se ei voi sattua yhdessäkään kokeessa. Nopanheitossa tapahtuma $B$ = ''pisteluku on vähintään yksi'' on varma, kun sen sijaan tapahtuma $C$ = $\emptyset$ eli ''pisteluvuksi ei tule mitään'' on mahdoton.

Merkitsemme kaikkien alkeistapausten lukumäärää $n$:llä ja joukon $A$ alkioiden lukumäärää $n(A)$:lla, jota on tässä yhteydessä tapana kutsua $A$:lle suotuisien alkeistapausten lukumääräksi. Tapahtuman $A$ klassinen todennäköisyys määritellään nyt lukuna 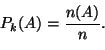\begin{equation*} P_k(A)=\frac{n(A)}{n}. \end{equation*} Merkinnässä $P_k$ kirjain $P$ tulee englannin kielen sanasta ''probability'' eli ''todennäköisyys'' ja alaindeksi $k$ osoittaa, että kyseessä on ''klassinen'' todennäköisyys. 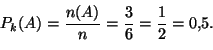Tämän määritelmän perusteella edellä esitetyn tapahtuman $A$ = ''nopanheiton tulos on vähintään neljä'' todennäköisyys on \begin{equation*} P_k(A)=\frac{n(A)}{n}=\frac{3}{6}=\frac{1}{2}=0{,}5. \end{equation*} Vastaus on tapana antaa desimaalilukuna kahden tai kolmen merkitsevän numeron tarkkuudella, mutta myös murtolukuna erityisesti silloin, kun desimaalilukuarvo on likiarvo tarkalle murtolukuarvolle.

Alkeistapausten symmetrisyyttä ei voi perustella pelkästään matemaattisesti, vaan sen tueksi tarvitaan havainnollinen käsite ''umpimähkäinen valinta''. Mistä yleensä ottaen edes tiedämme, mitkä tarkasteltavana olevassa ilmiössä ovat symmetrisiä alkeistapauksia? Pulman voisi yrittää ratkaista johtamalla alkeistapausten symmetrisyys fysikaalisesta symmetriasta. Esimerkiksi kolikonheitossa kruuna ja klaava ovat symmetrisiä alkeistapauksia edellyttäen, että kolikkoa ei ole mitenkään painotettu. Symmetriaa ei tässä voi kuitenkaan perustella sillä, että kolikko olisi fysikaalisesti täysin symmetrinen; silloinhan kruunaa ja klaavaa ei voisi erottaa toisistaan. Fysikaalisesta symmetriasta voi siis olla hyötyä intuitiivisessa tarkastelussa, mutta on selvää, että sitä ei voi sisällyttää klassisen todennäköisyyden määritelmään.


Frekvenssitulkinta

Klassisen todennäköisyyden merkitystä voidaan havainnollistaa frekvenssitulkinnan avulla. Itse asiassa tilastollisen todennäköisyyden käsite perustuu juuri frekvenssitulkintaan. Tarkastelemme satunnaiskoetta, jota voidaan toistaa samanlaisissa olosuhteissa rajattomasti. Olkoon $A$ tähän kokeeseen liittyvä tapahtuma ja $F_n(A)$ tapahtuman $A$ esiintymiskertojen lukumäärä $n$:ssä toistossa. Määrittelemme $A$:n suhteellisen frekvenssin lukuna 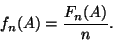\begin{equation*} f_n(A)=\frac{F_n(A)}{n}. \end{equation*} Kokeellisesti on havaittu, että toistojen lukumäärän $n$ kasvaessa suhteellinen frekvenssi $f_n(A)$ näyttää yhä varmemmin keskittyvän tietyn luvun läheisyyteen. Frekvenssitulkinnan mukaan tapahtuman $A$ todennäköisyys on juuri kyseinen luku, jota $A$:n suhteellinen frekvenssi näyttää lähestyvän toistojen lukumäärän kasvaessa. Toteamme kuitenkin, että frekvenssitulkinta ei voi olla todennäköisyyden määritelmä matemaattisessa mielessä. Ensinnäkin, kyseinen ''raja-arvo'' ei ole raja-arvo matemaattisen analyysin mielessä, ja toiseksi, äärettömiä toistosarjoja on mahdoton realisoida.


de Mérén ongelma

Chevalier de Méré oli havainnut kokeellisesti seuraavaa:

Havainto 1. Kannattaa lyödä vetoa siitä, että heitettäessä neljä kertaa noppaa saadaan ainakin yksi kuutonen.

Havainto 2. Ei kannata lyödä vetoa siitä, että heitettäessä kahta noppaa 24 kertaa saadaan ainakin yksi kuutospari.

Hän ei kuitenkaan kyennyt osoittamaan havaintojaan teoreettisesti, joten hän kääntyi Pascalin puoleen noin vuonna 1650.

Ratkaisu. de Mérén ensimmäisen havainnon selittävän satunnaiskokeen symmetrisiksi alkeistapauksiksi voidaan valita 4-jonot \begin{equation*} (x_1,x_2,x_2,x_4),\quad x_i\in\{1,2,\ldots,6\}. \end{equation*} Jokainen $x_i$ ilmoittaa siis $i$:nnen heiton pisteluvun, yksi mahdollinen tulos on esimerkiksi 4-jono $(5,1,3,5)$. Kaikkien mahdollisten alkeistapausten lukumäärä on \begin{equation*} n=6^4=1\,296. \end{equation*} Jos $A$ on tapahtuma ''saadaan ainakin yksi kuutonen'', niin $A$:lle suotuisien tapahtumien lukumäärä on \begin{equation*} n(A)=6^4-5^4=1\,296-625=671, \end{equation*} sillä $A$:lle epäsuotuisia tapauksia on $5^4$. 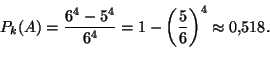Näin ollen \begin{equation*} P_k(A)=\frac{6^4-5^4}{6^4}=1-\left(\frac{5}{6} \right)^4\approx 0{,}518. \end{equation*}

Kahden nopan heiton symmetrisiksi alkeistapauksiksi valitsemme järjestetyt parit \begin{equation*} (1,1),\ (1,2),\ (1,3),\ldots,(6,6), \end{equation*} joiden lukumäärä on $6^2=36$. Koska tarkastelemme järjestettyjä pareja, niin esimerkiksi tapahtuma $(1,2)$ on eri tapahtuma kuin $(2,1)$. Tämä merkitsee, että on eri asia saada ensin ykkönen ja sitten kakkonen kuin saada ensin kakkonen ja sitten ykkönen. Näin ollen de Mérén toisen havainnon selittävässä satunnaiskokeessa on yhteensä $n=36^{24}$ erilaista alkeistapausta. Näistä tapauksia, joissa ei ole yhtään kuutosparia, on $35^{24}$. 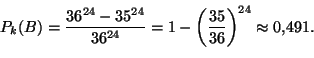Jos $B$ on tapahtuma ''saadaan ainakin yksi kuutospari'', niin \begin{equation*} P_k(B)=\frac{36^{24}-35^{24}}{36^{24}}=1-\left( \frac{35}{36}\right)^{24}\approx 0{,}491. \end{equation*}

Havaitsemme, että $P_k(A)>0{,}5$, joten $A$:n puolesta kannattaa lyödä vetoa. Sen sijaan $P_k(B)<0{,}5$, joten $B$:n puolesta ei kannata lyödä vetoa. Toki kysymystä siitä, milloin jonkin asian puolesta kannattaa lyödä vetoa, voi pohtia syvällisemminkin, mutta puhtaasti klassisen todennäköisyyden kannalta kysymys ei ole tämän monimutkaisempi.


Lotto

Meidän suomalaisten parhaiten tuntema ja eniten pelaama rahapeli on epäilemättä lotto. Luultavasti jokainen meistä on ainakin itse mielessään pohtinut loton täysosuman todennäköisyyttä. Laskemmekin tämän seuraavaksi klassisen todennäköisyyden keinoin.

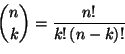
Tarkastelemme ensin hieman kombinatoriikkaa tarvitsemassamme laajuudessa. Jos $E$ on $n$-alkioinen joukko ja $k$ on kokonaisluku, jolle pätee $1\le k\le n$, niin $E$:n $k$-kombinaatio on $E$:n $k$-alkioinen osajoukko. Alkioiden järjestyksellä kombinaatioissa ei siis ole merkityssä. On varsin helposti osoitettavissa, että $n$-alkioisella joukolla $E$ on \begin{equation*} \binom{n}{k}=\frac{n!}{k!\,(n-k)!} \end{equation*} $k$-kombinaatiota. Edellä merkintä $n!$ tarkoittaa $n$:n kertomaa, joka määritellään positiiviselle kokonaisluvulle \begin{equation*} n!=1\cdot 2\cdot 3\cdots n. \end{equation*} Lukuja $\binom{n}{k}$ kutsutaan binomikertoimiksi, ja merkintä luetaan ''$n$ alle $k$'' (tai ''$n$ yli $k$'').

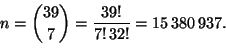Lotossa joukon $E$ muodostavat kaikki arvottavat numerot, siis \begin{equation*} E=\{1,2,3,\ldots,39\}. \end{equation*} Koska (varsinaisia) numeroita arvotaan 7 kappaletta, niin tutkimme $E$:n 7-kombinaatioita, jotka voimme valita loton symmetrisiksi alkeistapauksiksi. Näiden lukumäärä on edellä olevan perusteella \begin{equation*} n=\binom{39}{7}=\frac{39!}{7!\,32!}=15\,380\,937. \end{equation*} Kaikista mahdollisista riveistä vain yksi on kulloisenkin kierroksen täysosumarivi, joten tämän klassinen todennäköisyys on \begin{equation*} P_k(\text{''7 oikein''})=\frac{1}{15\,380\,937}\approx 6{,}5\cdot 10^{-8}. \end{equation*}

On syytä huomauttaa, että loton muiden - erityisesti lisänumeroja sisältävien - voittoluokkien todennäköisyyksien määrääminen on jonkin verran edellä esitettyä hankalampaa. Näiden laskeminen jää tässä yhteydessä kuitenkin lukijoiden oman mielenkiinnon varaan. Voitte miettiä mahdollisia ratkaisumalleja ja lähettää ne Solmun toimitukseen; parhaat ehdotukset julkaistaan kirjoitussarjan seuraavissa osissa.


Geometrinen todennäköisyys

Heti todennäköisyyslaskennan varhaiskehitysvaiheessa huomattiin, että symmetrisiin yhtä todennäköisiin tapahtumiin perustuva todennäköisyyden klassinen määritelmä oli riittämätön. Yksi ensimmäisistä yrityksistä laajentaa määritelmää oli geometrisen todennäköisyyden idea. Tässäkin lähestymistavassa yhtä todennäköisen käsite oli vielä keskeisessä roolissa, mutta geometrista todennäköisyyttä voidaan kuitenkin hyvällä syyllä pitää klassisen todennäköisyyden yleistyksenä; esimerkiksi alkeistapauksia geometrisessa todennäköisyydessä on rajaton määrä.

Geometrista todennäköisyyttä on mahdollista soveltaa tilanteissa, joissa satunnaiskokeen tulos voidaan havainnollistaa geometrisella kuviolla ja kiinnostuksen kohteena oleva tapahtuma $A$ tämän osakuviona. Tällaisia kuvioita ja niiden osakuvioita voivat olla esimerkiksi yksiulotteinen jana, kaksiulotteinen tasoalue tai kolmiulotteinen kappale. Tilanteen on oltava siinä mielessä symmetrinen, että $A$:n mahdollisuus esiintyä riippuu vain $A$:n geometrisesta mitasta (janalla pituus, tasoalueella pinta-ala ja kappaleella tilavuus), eikä lainkaan $A$:n muodosta ja sijainnista. Tällöin voimme määritellä $A$:n geometrisen todennäköisyyden lukuna 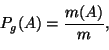\begin{equation*} P_g(A)=\frac{m(A)}{m}, \end{equation*} missä $m(A)$ edustaa osakuvion $A$ ja $m$ koko kuvion geometrista mittaa; lisäksi oletetaan, että koko kuvion mitalle pätee $0<m<\infty$. Kyseisen määritelmän täsmentäminen vaatisi tiettyjä rajoituksia koko kuviolle ja sen osakuviolle $A$, mutta se johtaisi euklidisen avaruuden mitan määrittelyyn, ja tyydymmekin tässä yhteydessä pelkästään havainnolliseen käsittelyyn.

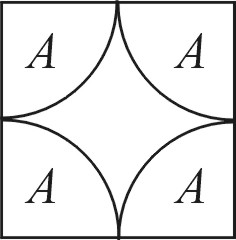
Esimerkki. Huoneen lattialla on neliöruudukko, jossa neliön sivu = kolikon halkaisija = $2r$. Millä todennäköisyydellä lattialle heitetty kolikko peittää neliön kärjen?

Ratkaisu. Tutkimme kysytyn geometrisen todennäköisyyden selvittämiseksi kolikon keskipisteen sijaintia neliöruudukossa. Koska eri neliöt ovat toisiinsa nähden samassa asemassa, voimme tarkastella yhtä neliötä. Sen pinta-ala on $m=(2r)^2=4r^2$. Tarkastelemme tapahtumaa $A$ = ''lattialle heitetty kolikko peittää neliön kärjen'', jota mallissamme edustaa kolikon keskipisteen sijainti neliössä. Suotuisissa tapauksissa kolikon keskipisteen etäisyys neliön kärjestä on pienempi kuin $r$ (katso kuva). 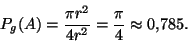Näin ollen $A$:n pinta-ala on $m(A)=4\cdot \frac{\pi r^2}{4}=\pi r^2$, ja kysytty geometrinen todennäköisyys on siten \begin{equation*} P_g(A)=\frac{\pi r^2}{4 r^2}=\frac{\pi}{4}\approx 0{,}785. \end{equation*}

On selvää, että geometrisen todennäköisyyden määrittelyyn liittyy aivan samoja periaatteellisia ongelmia kuin klassisenkin todennäköisyyden määrittelyyn. Vakavin puute kummassakin määritelmässä on, että ne kattavat vain hyvin suppean osan niistä satunnaiskokeista, joista olemme kiinnostuneet. Kummankaan määritelmän pohjalta on mahdotonta konstruoida alkeistapauksia, joiden avulla voisimme johtaa todennäköisyyden, että syntyvä lapsi on tyttö tai että tietyn radioaktiivisen atomin elinikä on suurempi kuin 1000 vuotta.


Bertrandin paradoksi

Ranskalainen matemaatikko Joseph Bertrand (1822-1900) esitti todennäköisyyslaskennan kursseillaan useita geometriseen todennäköisyyteen liittyviä ongelmia, joissa tulos riippui ongelman ratkaisutavasta. Bertrandin esittämistä ongelmista tunnetuin lienee seuraava paradoksi, jonka käsittely perustuu venäläisen Boris Gnedenkon (1912-1995) todennäköisyysteorian klassisen teoksen The Theory of Probability esitykseen.

Bertrand Gnedenko

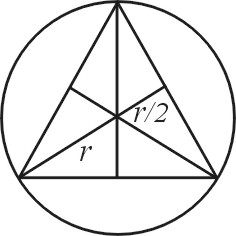
Bertrandin paradoksi. Annettuun ympyrään piirretään umpimähkään jänne. Mikä on todennäköisyys, että jänne on pidempi kuin ympyrän sisään piirretyn tasasivuisen kolmion sivu?

Merkitään totuttuun tapaan kysyttyä tapahtumaa $A$:lla. Ympyrän sisään piirretyn tasasivuisen kolmion kulmanpuolittajat leikkaavat toisensa samassa pisteessä suhteessa $1:2$. Näin ollen ympyrän keskipisteen etäisyys kolmion sivuista on $\frac{r}{2}$ (katso kuva).

Ratkaisu 1. Oletetaan, että jänteen keskipisteen ja ympyrän keskipisteen etäisyys valitaan umpimähkään väliltä $]0,r[$, missä $r$ on ympyrän säde. Tällöin geometrinen mitta $m=r$. Tapahtumalle $A$ suotuisissa tapauksissa jänteen ja ympyrän keskipisteiden välinen etäisyys kuuluu välille $]0,\frac{r}{2}[$, joten $m(A)=\frac{r}{2}$. Näin ollen kysytty geometrinen todennäköisyys on \begin{equation*} P_g(A)=\frac{\frac{r}{2}}{r}=\frac{1}{2}=0{,}5. \end{equation*}

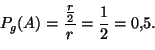
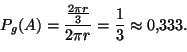
Ratkaisu 2. Oletetaan, että jänteen toinen päätepiste ajatellaan kiinteäksi ja toinen valitaan umpimähkään ympyrän kehältä. Kehän pituus on $m=2\pi r$. Tapahtumalle $A$ suotuisissa tapauksissa jänteen toinen päätepiste kuuluu ympyrän kaareen, jonka pituus on $m(A)=\frac{2\pi r}{3}$. Näin ollen kysytty geometrinen todennäköisyys on \begin{equation*} P_g(A)=\frac{\frac{2\pi r}{3}}{2\pi r}=\frac{1}{3}\approx 0{,}333. \end{equation*}

Ratkaisu 3. Oletetaan, että jänteen keskipiste valitaan umpimähkään ympyrän sisältä eli kiekosta \begin{equation*} \{(x,y)\in\mathbb{R}^2:x^2+y^2<r^2\}. \end{equation*} Tämän $r$-säteisen kiekon pinta-ala on tunnetusti $\pi r^2$, siis tämä on $m$. Tapahtumalle $A$ suotuisissa tapauksissa jänteen keskipiste kuuluu kiekkoon \begin{equation*} \{(x,y)\in\mathbb{R}^2:x^2+y^2<\left(\frac{r}{2}\right)^2\}, \end{equation*} jonka pinta-ala on \begin{equation*} m(A)=\pi\left(\frac{r}{2}\right)^2=\frac{\pi}{4}r^2. 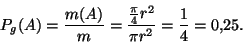\end{equation*} Näin ollen kysytty geometrinen todennäköisyys on \begin{equation*} P_g(A)=\frac{m(A)}{m}=\frac{\frac{\pi}{4}r^2}{\pi r^2}=\frac{1}{4} =0{,}25. \end{equation*}

Saimme esitettyyn ongelmaan kolme erilaista vastausta, ja seuraava tehtävämme onkin yrittää selvittää, miksei ongelman ratkaisu ole yksikäsitteinen. Onko syy mahdollisesti jokin perustavaa laatua oleva mahdottomuus määrittää todennäköisyys yksikäsitteisesti tilanteissa, joissa on ääretön määrä mahdollisia tuloksia (jännehän voidaan piirtää ympyrän sisään äärettömän monella eri tavalla)? Vai johtuuko havaintomme kenties joistakin vääristä alkuoletuksista ongelman kolmessa eri ratkaisussa?

On selvää, että edellä esitetyt ratkaisut ovat yhden ja saman ongelman kolme erilaista ratkaisua, sillä ongelman asettelu ei määrittele tapaa, jolla jänne tulee satunnaisesti piirtää ympyrän sisälle.

Ensimmäisessä ratkaisussa voidaan ajatella, että vähintään lävistäjän pituinen tanko (ympyrän sisään jäävä osa vastaa jännettä) ''vierii'' kohtisuorasti yhtä lävistäjää (siis kahta peräkkäin asetettua samansuuntaista sädettä) pitkin. Kaikki mahdolliset tangon keskipisteen pysähtymiskohdat muodostavat janan $AB$ (katso kuva), jonka pituus on sama kuin lävistäjänkin. Yhtä todennäköisiä ovat tällöin ne tapahtumat, jotka koostuvat tangon pysähtymiskohdista $h$:n pituisella janalla riippumatta siitä, missä kyseinen jana sijaitsee lävistäjällä.

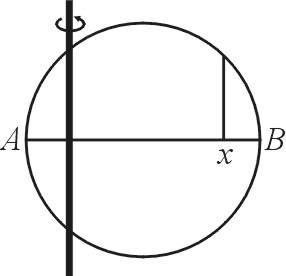
Ratkaisun 1 kuva.

Toisessa ratkaisussa voidaan ajatella, että vastaava tanko on kiinnitetty yhteen pisteeseen ympyrän kehällä, ja tankoa on mahdollista käännellä korkeintaan $180^\circ$ siten, että se leikkaa aina ympyrän kehää (katso kuva). Tangon liikkumista rajoittaa siis kiinnityspisteeseen ympyrälle piirretty tangentti. Nyt oletetaan, että tangon pysähtymiskohta $h$:n pituisella ympyrän kaarella riippuu kaaren pituudesta mutta ei riipu kaaren paikasta ympyrän kehällä. Näin ollen yhtä todennäköisiä tapahtumia ovat tangon pysähtymiskohdat kaarilla, joiden pituudet ovat samat.

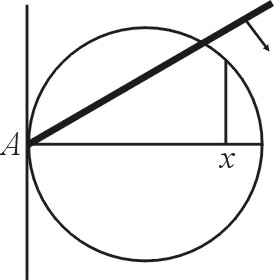
Ratkaisun 2 kuva.

Näiden tarkastelujen jälkeen on varsin selvää, että geometrisen todennäköisyyden määritelmät ensimmäisessä ja toisessa ratkaisussa ovat ristiriidassa keskenään. Ensimmäisen ratkaisun mukaan todennäköisyys, että jana pysähtyy välille $]A,x[$, on $\frac{x}{2r}$. 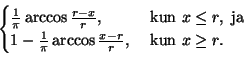Todennäköisyys sille, että janan ja ympyrän kehän leikkauspisteen kohtisuora projektio lävistäjälle toisessa ratkaisussa osuu samalle välille, on alkeellisen geometrisen tarkastelun nojalla \begin{equation*} \begin{cases} \frac{1}{\pi}\arccos\frac{r-x}{r},\ &\text{kun}\... ...ac{1}{\pi}\arccos\frac{x-r}{r},\ &\text{kun}\ x\ge r. \end{cases}\end{equation*}

Kolmannessa ratkaisussa ''heitämme'' jänteen keskipisteen umpimähkään ympyrän sisälle. Tällöin yhtä todennäköisiä tapahtumia ovat pinta-alaltaan samansuuruiset ympyrän sisällä sijaitsevat tasoalueet. Kysytty todennäköisyys saadaan siitä, että keskipiste putoaa tiettyyn pienempään samankeskiseen ympyrään (katso kuva). Erilaiset lopputulokset esittämissämme kolmessa eri ratkaisussa ovat tämän jälkeen varsin ilmeisiä.

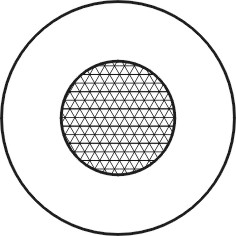
Ratkaisun 3 kuva.


Lähteet

Elfving, Gustav, ja Tuominen, Pekka: Todennäköisyyslaskenta II, Limes ry, Helsinki, 1990.

Gnedenko, Boris: The Theory of Probability, Mir Publishers, Moscow, 1976.

Lehtinen, Matti: Matematiikan historia,
http://matematiikkalehtisolmu.fi/2000/mathist/.

Tuominen, Pekka: Todennäköisyyslaskenta I, Limes ry, Helsinki, 2000.

Tuominen, Pekka, ja Norlamo, Pekka: Todennäköisyyslaskenta, osa 1, Limes ry, Helsinki, 1985.

Tuominen, Pekka, ja Norlamo, Pekka: Todennäköisyyslaskenta, osa 2, Limes ry, Helsinki, 1988.

The MacTutor History of Mathematics archive,
http://turnbull.dcs.st-and.ac.uk/history/.

Solmun toimitus
11.6.2002