
PDF
- PS
Esimerkki ääriarvo-ongelmasta, joka
voidaan ratkaista alkeellisilla tavoilla
Prof. István Hortobágyi
Usein halutaan määrittää funktion suurin (maksimi)
tai pienin (minimi) arvo sen
määrittelyjoukossa. Tällaisia tehtäviä kutsutaan
ääriarvo-ongelmiksi. Yleensä ne
ratkaistaan differentiaalilaskennan keinoin.
Jos differentiaalilaskentaa ei käytetä
tehtävän ratkaisussa, sanotaan, että kyseessä on
alkeellinen ratkaisu. Tässä käsitellään vain yhtä
ongelmaa, ja annetaan sille useita ratkaisuja.
Halutaan rakentaa suorakulmainen puutarha, joka ympäröidään 100 metrin pituisella aidalla.
Miten pitkiä tulee suorakulmion sivujen olla, jotta puutarhan
ala olisi mahdollisimman suuri?
Merkitään suorakulmion kahta sivua 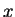 ja
ja 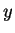 . Koska
. Koska 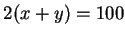 , niin
, niin 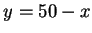 . Suorakulmion
pinta-alaa kuvaa seuraava toisen asteen yhtälö:
. Suorakulmion
pinta-alaa kuvaa seuraava toisen asteen yhtälö:
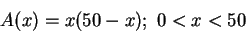
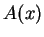 :n kuvaajasta (kuva 2) huomataan helposti, että suurin mahdollinen suorakulmion
ala on
:n kuvaajasta (kuva 2) huomataan helposti, että suurin mahdollinen suorakulmion
ala on 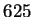 m
m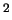 , ja tämä tulos saadaan, kun
, ja tämä tulos saadaan, kun 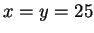 .
.
Kun täydennetään 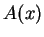 neliöksi, saadaan
neliöksi, saadaan
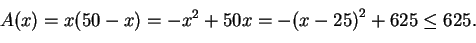 Tässä epäyhtälössä yhtäsuuruus on voimassa jos ja vain jos
Tässä epäyhtälössä yhtäsuuruus on voimassa jos ja vain jos 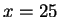 . Ratkaisuna on siis
neliö. Ratkaisusta voidaan nähdä seuraava idea:
Kyse on ekstremaalitehtävästä, joka ratkaistaan arvioimalla funktion
ylärajoja ja löytämällä niistä pienin, joka on tässä tapauksessa
myös funktion saama arvo, funktion maksimiarvo.
Samoin funktion pienin arvo voidaan
määrittää löytämällä vakio, joka on
funktion saavuttama alaraja (siis funktion saama arvo).
Tätä ratkaisutapaa kutsutaan
estimoinniksi. Ala- ja ylärajojen löytämiseksi on useita
mahdollisuuksia.
. Ratkaisuna on siis
neliö. Ratkaisusta voidaan nähdä seuraava idea:
Kyse on ekstremaalitehtävästä, joka ratkaistaan arvioimalla funktion
ylärajoja ja löytämällä niistä pienin, joka on tässä tapauksessa
myös funktion saama arvo, funktion maksimiarvo.
Samoin funktion pienin arvo voidaan
määrittää löytämällä vakio, joka on
funktion saavuttama alaraja (siis funktion saama arvo).
Tätä ratkaisutapaa kutsutaan
estimoinniksi. Ala- ja ylärajojen löytämiseksi on useita
mahdollisuuksia.
Tunnemme seuraavan epäyhtälön aritmeettisen ja geometrisen
keskiarvon välillä:
Jos 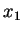 ja
ja 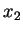 ovat kaksi positiivista lukua, niin
ovat kaksi positiivista lukua, niin
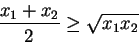 Yhtäsuuruus on voimassa jos ja vain jos
Yhtäsuuruus on voimassa jos ja vain jos 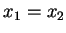 .
Käytetään tätä epäyhtälöä, kun
.
Käytetään tätä epäyhtälöä, kun 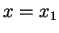 ja
ja 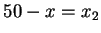 . Tällöin
. Tällöin
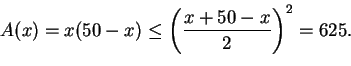 Yhtäsuuruus on voimassa, jos
Yhtäsuuruus on voimassa, jos 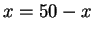 , joten
, joten 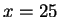 .
.
Johdetaan alueen pinta-alalle saavutettava yläraja
käyttäen uutta muuttujaa 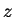 .
Koska
.
Koska 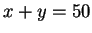 ,
, 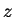 voidaan kirjoittaa
voidaan kirjoittaa
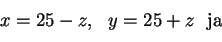
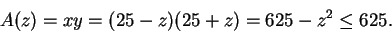 Yhtäsuuruus on voimassa, jos
Yhtäsuuruus on voimassa, jos 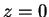 . Tässä tapauksessa
. Tässä tapauksessa 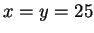 , joten ratkaisu on neliö.
, joten ratkaisu on neliö.
Johdetaan alueen pinta-alalle saavutettava yläraja geometrian keinoin.
Otetaan neljä samanlaista, mielivaltaista
suorakulmiota, joiden piirin pituus on 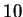 m ja ala
m ja ala 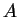 . Asetetaan ne kuvan 4 osoittamalla tavalla.
Huomataan, että kaikissa tapauksissa suorakulmiot ovat
. Asetetaan ne kuvan 4 osoittamalla tavalla.
Huomataan, että kaikissa tapauksissa suorakulmiot ovat 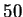 m
m
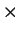
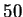 m neliön
sisällä. Tästä seuraa, että
m neliön
sisällä. Tästä seuraa, että
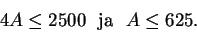 Yhtäsuuruus on voimassa kun neliön sisään ei jää
"tyhjää tilaa". Tällöin
suorakulmio on neliö, jonka sivun pituus on
Yhtäsuuruus on voimassa kun neliön sisään ei jää
"tyhjää tilaa". Tällöin
suorakulmio on neliö, jonka sivun pituus on 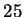 m.
m.
Kuvaa 5 apuna käyttäen verrataan neliön 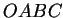 alaa (sivut
alaa (sivut 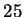 m) mielivaltaisen
suorakulmion
m) mielivaltaisen
suorakulmion 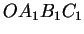 alaan (sivut
alaan (sivut 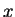 ja
ja 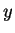 ).
Merkitään sivujen
).
Merkitään sivujen 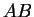 ja
ja 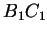 leikkauspistettä
leikkauspistettä 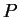 :llä ja
suorakulmioiden
:llä ja
suorakulmioiden 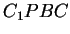 ja
ja 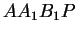 aloja
aloja 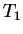 :llä ja
:llä ja 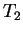 :lla.
:lla.
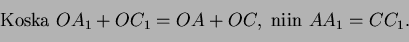 Lisäksi
Lisäksi 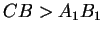 , joten
, joten 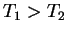 . Kun lisätään OABC:n
ja OA1B1C1:n
leikkauksen
. Kun lisätään OABC:n
ja OA1B1C1:n
leikkauksen 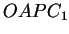 ala
ala 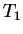 :n ja
:n ja 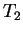 :n alaan, niin huomataan,
että neliön ala on suurempi kuin suorakulmion ala.
:n alaan, niin huomataan,
että neliön ala on suurempi kuin suorakulmion ala.
Solmun etusivu
15.12.2001
![\includegraphics[width=0.35\textwidth]{kuva1.eps}](img1.png)

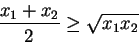 Yhtäsuuruus on voimassa jos ja vain jos
Yhtäsuuruus on voimassa jos ja vain jos 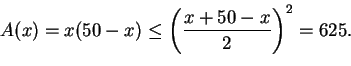 Yhtäsuuruus on voimassa, jos
Yhtäsuuruus on voimassa, jos