Diofantoksen yhtälöt

Katariina Hemmo

Tämä osa lukuteoriasta kuuluu matematiikan laajan oppimäärän valinnaisiin kursseihin. Kurssi käsittelee matemaattisen logiikan ja lukuteorian perusteita.

Esimerkki. Jos sinulla on kaksi tikkua, joiden pituudet ovat 5 m ja 3 m, niin kuinka voit mitata 1 m pituuden?

I: $\hspace{1cm}\text{5 m}\qquad\qquad\text{5 m}$
$\rule{2.5cm}{1.5mm}\,\rule{2.5cm}{1.5mm}$
$\text{3 m}\qquad\text{3 m}\qquad\text{3 m}$ $2\cdot 5-3\cdot 3=1.$
$\rule{1.5cm}{1.5mm}\,\rule{1.5cm}{1.5mm}\,\rule{1.5cm}{1.5mm}$
II: $\hspace{0.5cm}\text{3 m}\qquad\text{3 m}$
$\rule{1.5cm}{1.5mm}\,\rule{1.5cm}{1.5mm}$
$\text{5 m}$ $2\cdot 3-1\cdot 5=1.$
$\rule{2.5cm}{1.5mm}$

Harjoitus. Entä jos sinulla on tikut, joiden pituudet ovat

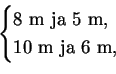
$\begin{displaymath} \begin{cases} 8\ \text{m ja}\ 5\ \text{m},\\ 10\ \text{m ja}\ 6\ \text{m}, \end{cases}\end{displaymath}$

voitko mitata 2 m pituuden samoilla tikuilla? Mitä pituuksia voit mitata?

Ratkaisu. Oletetaan, että on käytössä kpl 8 m tikkuja ja kpl 5 m tikkuja. Onko seuraavilla yhtälöllä ratkaisuja?

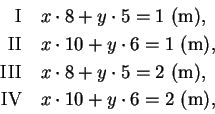
$\begin{displaymath} \begin{split} \text{I}\quad &x\cdot 8+y\cdot 5= 1\ \text{(m)... ... \text{IV}\quad &x\cdot 10+y\cdot 6= 2\ \text{(m),} \end{split}\end{displaymath}$

missä $x,y\in\Z$ .

Yhtälötyyppiä kutsutaan Diofantoksen yhtälöksi, ja se on nimetty kreikkalaisen matemaatikon Diofantoksen mukaan. Hän tutki yhtälöiden ratkaisumenetelmiä ja oli ensimmäinen, joka käytti algebrallisia merkkejä. Hän ei kuitenkaan tutkinut Diofantoksen yhtälöitä.

I

$x\cdot 8+y\cdot 5= 1.$ Suurin yhteinen tekijä

. Eukleideen algoritmilla

jaettava jakaja

$1\cdot 5+3$

$1\cdot 3+2$

$1\cdot 2+1$ jakojäännös

$1\cdot 2$ suurin yhteinen tekijä .

Kääntäen:

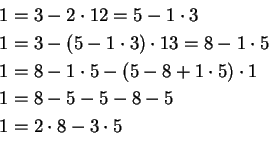
$\begin{displaymath} \begin{split} 1 &= 3-2\cdot 1 \vspace{2cm} 2=5-1\cdot 3\\ 1... ...\cdot 1\\ 1 &= 8-5-5-8-5\\ 1 &= 2\cdot 8-3\cdot 5 \end{split}\end{displaymath}$

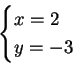
$\begin{displaymath} \begin{cases} x =2\\ y =-3 \end{cases}\end{displaymath}$

III

$x\cdot 8+y\cdot 5= 2.$ Käyttämällä hyväksi I yhtälöä saadaan

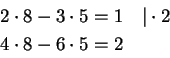
$\begin{displaymath} \begin{split} &2\cdot 8-3\cdot 5=1\quad \vert\cdot 2\\ &4\cdot 8-6\cdot 5=2 \end{split}\end{displaymath}$

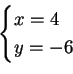
$\begin{displaymath} \begin{cases} x =4\\ y =-6 \end{cases}\end{displaymath}$

II

$x\cdot 10+y\cdot 6= 1.$ Suurin yhteinen tekijä

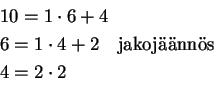
$\begin{displaymath} \begin{split} &10=1\cdot 6+4\\ &6=1\cdot 4+2\quad\text{jakojäännös}\\ &4=2\cdot 2 \end{split}\end{displaymath}$

tai

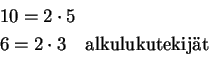
$\begin{displaymath} \begin{split} &10=2\cdot 5\\ &6=2\cdot 3\quad\text{alkulukutekijät} \end{split}\end{displaymath}$

Kääntäen:

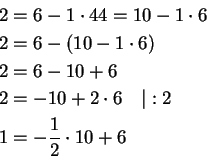
$\begin{displaymath} \begin{split} 2 &=6-1\cdot 4\vspace{1.5cm} 4=10-1\cdot 6\\ ... ...2\cdot 6\quad \vert:2\\ 1 &=-\frac{1}{2}\cdot 10+6 \end{split}\end{displaymath}$

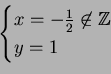
$\begin{displaymath} \begin{cases} x =-\frac{1}{2}\not\in\Z\\ y =1 \end{cases}\end{displaymath}$

Ei ole olemassa ratkaisua $x,y\in\Z$ .

IV

$x\cdot 10+y\cdot 6= 2.$ Tämä tapaus on selvä vertaamalla edellä olevaan ratkaisuun (yhtälö II):

$\begin{displaymath} -10+2\cdot 6=2 \end{displaymath}$

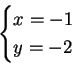
$\begin{displaymath} \begin{cases} x =-1\\ y =-2 \end{cases}\end{displaymath}$

Edelliset ratkaisut olivat yksittäisiä. Yleiset ratkaisut ovat:

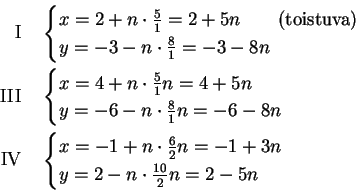
$\begin{displaymath} \begin{split} \text{I}\quad &\begin{cases} x=2+n\cdot\frac{5... ...}n=-1+3n\\ y=2-n\cdot\frac{10}{2}n=2-5n \end{cases}\end{split}\end{displaymath}$

Pituudet, jotka voit mitata:

I: $x\cdot 10+y\cdot 5= 1\ \text{(m)}.$ Kaikki kokonaislukupituudet voidaan mitata.
II: Ei ratkaisuja.
IV: $x\cdot 10+y\cdot 6=2$ . Voidaan mitata kaikki kokonaislukupituudet, jotka ovat kahdella jaollisia.

Harjoitus. Perttu osti muutaman omenan ja appelsiinin, ja ne maksoivat yhteensä 16,80. Kuinka monta omenaa ja appelsiinia hän osti, jos yksi omena maksoi 1,40 ja yksi appelsiini maksoi 1,20?

Ratkaisu. $1{,}40\,x+1{,}20\,y=16{,}80\quad \vert\cdot 10$

$\begin{displaymath} \begin{cases} x = \text{omenoiden lukumäärä}\\ y = \text{appelsiinien lukumäärä} \end{cases}\end{displaymath}$

$\begin{displaymath} 14{,}0\,x+12{,}0\,y=168{,}0 \end{displaymath}$

		$1\cdot 12+2$
		$6\cdot 2$
		$14-1\cdot 12\qquad \vert\cdot 84$
		$84\cdot 14-84\cdot 12$

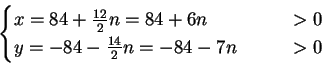
$\begin{displaymath} \begin{cases} x=84+\frac{12}{2}n=84+6n\qquad &>0\\ y=-84-\frac{14}{2}n=-84-7n\qquad &>0 \end{cases}\end{displaymath}$

	$\wedge$

$x=84+6\cdot(-13)=6$		$y=-84-7\cdot(-13)=7$

Vastaus:

$\begin{displaymath} \begin{cases} x =6=\text{omenoiden lukumäärä}\\ y =7=\text{appelsiinien lukumäärä} \end{cases}\end{displaymath}$

Harjoitus. Kasper, Jesper ja Joonatan olivat varastaneet keksejä, jotka on pakattu 14 ja 21 kappaleen laatikoihin. Pojat jäivät kiinni, ja heiltä löytyi 295 keksiä. He väittivät, etteivät olleet syöneet yhtään keksiä. Etsivä Marvola tiesi heti, että pojat valehtelivat. Miten hän tiesi tämän?

Ratkaisu.

$\begin{displaymath} 14\,x+21\,y=295 \end{displaymath}$

Onko tällä yhtälöllä ratkaisua?

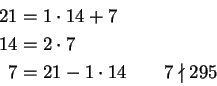
$\begin{displaymath} \begin{split} 21 &= 1\cdot 14+7\\ 14 &=2\cdot 7\\ 7 &=21-1\cdot 14\qquad 7\nmid 295 \end{split}\end{displaymath}$

Seuraus: Pikkuleipiä puuttui.

Solmun etusivu
8.12.2001

jaettava	jakaja
	$1\cdot 5+3$
	$1\cdot 3+2$
	$1\cdot 2+1$	jakojäännös
	$1\cdot 2$	suurin yhteinen tekijä .