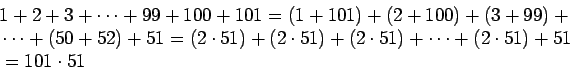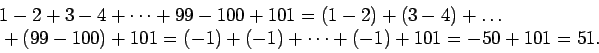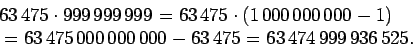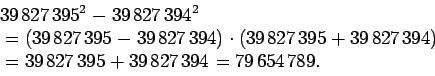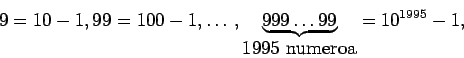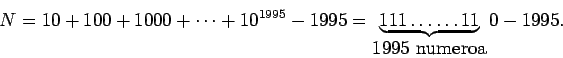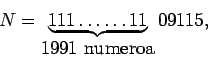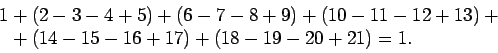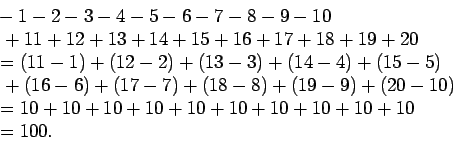1.
Summa on nolla, sillä luvut muodostavat vastalukuparit:
2.
Nolla, koska kerrotaan nollalla.
3.
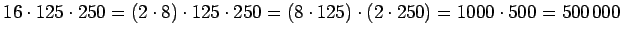 .
.
4.
Yksi mahdollinen ratkaisu:
5.
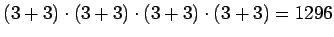 .
.
6.
Summa
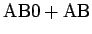 päättyy numeroihin 27,
joten
päättyy numeroihin 27,
joten
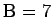 .
Edelleen summasta
.
Edelleen summasta
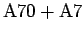 ratkeaa
ratkeaa
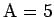 .
Kysytyt kaksi lukua ovat 570 ja 57.
.
Kysytyt kaksi lukua ovat 570 ja 57.
7.
Ratkaisun etsimistä helpottaa tieto siitä, että kerrottavassa on kaksi
nollaa vierekkäin. Välittömästi nollien vasemmalla puolella ei voi
missään tapauksessa esiintyä muistinumeroa.
Kun toinen tekijä kerrotaan luvulla 7, tulos päättyy numeroon
5; siksi haettu kertoja voi olla vain 5.
8.
Ratkaisu näkyy alla vasemmalla olevassa kuvassa.
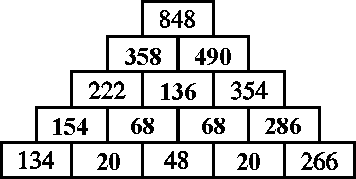
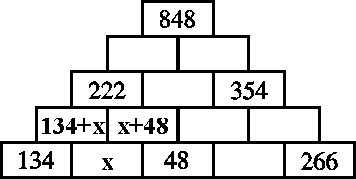
Tehtävää ratkaistaessa tarkastellaan ensin taulukon vasenta alakulmaa
(kuva yllä oikealla). Alimmalta riviltä puuttuvaa lukua merkitään x:llä.
Silloin sen
yläpuolella oleviin tyhjiin ruutuihin tulevat luvut 134+x ja x+48.
Saadaan yhtälö
(134+x)+(x+48)=222; siis
182+2x=222, 2x=40,
x=20. Samalla tavalla voidaan laskea alkuperäisen taulukon alimman
rivin toinen puuttuva luku, joka on myös 20.
Tämän jälkeen onkin taulukon muiden tyhjien ruutujen
täyttäminen helppoa.
9.
Esimerkkinä toimivan taulukon luvut voidaan laskea kätevästi yhteen, kun
käännetään taulukossa sekä rivien että sarakkeiden järjestys
päinvastaiseksi (toisin sanoen uuden taulukon ensimmäiselle riville
tulevat alkuperäisen taulukon viimeisen rivin alkiot takaperoisessa
järjestyksessä, toiselle riville toiseksi viimeisen rivin alkiot
takaperin jne.) ja verrataan sitten näin
saatua taulukkoa alkuperäiseen. Huomataan, että toistensa kanssa kohdakkain
osuvien lukujen summa on kaikkialla 8. Yhteensä kahdessa taulukossa
esiintyvien lukujen summa on 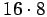 ,
jolloin yhden taulukon lukujen
summa on
,
jolloin yhden taulukon lukujen
summa on
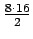 .
Vastaavasti
.
Vastaavasti
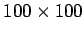 -ruutuisen
taulukon lukujen summa on
-ruutuisen
taulukon lukujen summa on
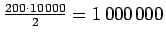 .
.
10.
Koska tulo päättyy nollaan, niin b=5. Kirjoitetaan kertolasku totuttuun
tapaan ja merkitään luvulla 5 tapahtuva osa kertolaskusta:
| | |
1 | 1 | 8 |
5 | 1 | 8 |
4 |
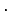 | | |
| |
| |
a | 5 |
| - | - | - |
- | - | - |
- | - | - |
| | |
5 | 9 | 2 |
5 | 9 | 2 |
0 |
| + | |
| |
| |
| |
x |
| - | - | - |
- | - | - |
- | - | - |
| | c |
c | c |
c | c |
c | 0 |
0 |
Tästä nähdään, että x=8, jolloin a=2 tai a=7. Tapauksessa a=2
kertolaskun ensimmäisen vaiheen jälkeen voidaan havaita, ettei haluttuun
lopputulokseen päästä. Oikea ratkaisu on a=7, ab=75 ja
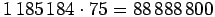 .
.
11.
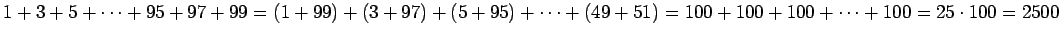 .
.
12.
ja
Näin ollen
13.
14.
Pekan ja isän ikäero on 23 vuotta. Kun isä on kaksi kertaa Pekan ikäinen,
ikäero on sama kuin Pekan ikä. Pekka on siis 23-vuotias.
15.
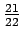 on suurempi:
on suurempi:
16.
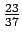 on suurempi. Lavennetaan murtoluku
on suurempi. Lavennetaan murtoluku
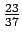 viidellä:
viidellä:
17.
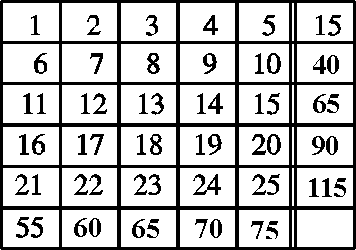
Toisella rivillä jokainen luku on 5 suurempi kuin sen yläpuolella oleva
luku. Toisen rivin numeroiden summa on siis
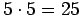 suurempi kuin
ensimmäisen rivin numeroiden summa. Muidenkin rivien summat ovat
laskettavissa samalla tavalla: seuraavan rivin summa on aina 25
suurempi kuin edellisen.
Toisen sarakkeen jokainen numero on 1 suurempi kuin edellinen, joten
toisen sarakkeen numeroiden summa on
suurempi kuin
ensimmäisen rivin numeroiden summa. Muidenkin rivien summat ovat
laskettavissa samalla tavalla: seuraavan rivin summa on aina 25
suurempi kuin edellisen.
Toisen sarakkeen jokainen numero on 1 suurempi kuin edellinen, joten
toisen sarakkeen numeroiden summa on
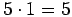 suurempi kuin ensimmäisen
sarakkeen. Muidenkin sarakkeiden summat ovat laskettavissa samalla
tavalla: seuraavan sarakkeen lukujen summa on aina 5 suurempi kuin
edellisen.
Näiden havaintojen jälkeen taulukko on helppo täyttää.
suurempi kuin ensimmäisen
sarakkeen. Muidenkin sarakkeiden summat ovat laskettavissa samalla
tavalla: seuraavan sarakkeen lukujen summa on aina 5 suurempi kuin
edellisen.
Näiden havaintojen jälkeen taulukko on helppo täyttää.
18.
Koska
1+2+3+4+5+6+7+8+9+10+11+12+13=91, oikea vastaus saadaan, kun
13 vaihdetaan 14:ksi. Kysytyt luvut ovat siis 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, 11, 12 ja 14:
1+2+3+4+5+6+7+8+9+10+11+12+14=92.
19.
Tytöistä
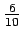 ratkaisi vähintään 2 tehtävää oikein. Tyttöjä voi olla
vain 5 kilpailussa mukana, sillä
ratkaisi vähintään 2 tehtävää oikein. Tyttöjä voi olla
vain 5 kilpailussa mukana, sillä
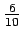 muista mahdollisista
lukumääristä (1-8) ei ole kokonaisluku. Finaalissa oli siis mukana
5 tyttöä ja 4 poikaa.
muista mahdollisista
lukumääristä (1-8) ei ole kokonaisluku. Finaalissa oli siis mukana
5 tyttöä ja 4 poikaa.
20.
Oletetaan, että kauppiaalla oli 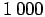 taaleria. Ensimmäisen oston jälkeen
hänellä oli hevonen ja 400 taaleria, myytyään hevosen hänellä oli
taaleria. Ensimmäisen oston jälkeen
hänellä oli hevonen ja 400 taaleria, myytyään hevosen hänellä oli
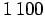 taaleria taskussaan. Sitten kauppias osti hevosen uudelleen ja
taskuun jäi 300 taaleria. Kun kauppias oli myynyt hevosen 900 taalerilla,
hänellä oli
taaleria taskussaan. Sitten kauppias osti hevosen uudelleen ja
taskuun jäi 300 taaleria. Kun kauppias oli myynyt hevosen 900 taalerilla,
hänellä oli 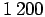 taaleria. Kauppias siis sai 200 taaleria voittoa.
taaleria. Kauppias siis sai 200 taaleria voittoa.
21.
Tulo on nolla, koska kerrotaan nollalla:
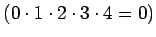 .
.
22.
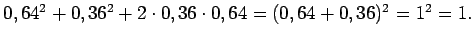
23.
Käytetään apuna tuntematonta x:
jolloin
Sijoitetaan nämä yhtälöön abc=576:
Täten
24.
a2 - b2 = (a -
b)(a + b), minkä perusteella
25.
Jos lähdetään ajatuksesta, että
niin luku N voidaan kirjoittaa muotoon
Vähennyslaskun jälkeen
Kymmenjärjestelmää käytettäessä numero 1 siis esiintyy 1993 kertaa.
26.
a = b2(b2 + c2), joten 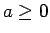 .
Jos olisi a = 0, niin b
tai sekä b että c olisivat myös nollia. Siis a > 0. Niinpä
.
Jos olisi a = 0, niin b
tai sekä b että c olisivat myös nollia. Siis a > 0. Niinpä
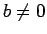 ,
joten b < 0 ja c = 0.
,
joten b < 0 ja c = 0.
27.
101 - 102 = 1.
Toinen ratkaisu:
101 - 10 = 21. Yhtälö on paikkansapitävä, mikäli käytetään
3-järjestelmää.
28.
Mikäli a + b = 1, niin
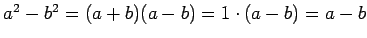 .
Jos siis
a:n ja b:n summa on 1, niiden erotus ja niiden neliöiden erotus ovat
yhtä suuret.
.
Jos siis
a:n ja b:n summa on 1, niiden erotus ja niiden neliöiden erotus ovat
yhtä suuret.
29.
Merkitään mainittuja lukuja a:lla ja b:llä.
a + b = 1000. Näiden
kahden luvun neliöt päättyvät kolmeen samaan numeroon, mikäli niiden
erotus on jaollinen tuhannella. Tämä todellakin toteutuu, koska
30.
a + b + 1 = (a - b) + 2b + 1 = b2 + 2b + 1 = (b + 1)2.
31.
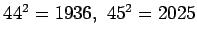 .
Niinpä 2000:ta pienempiä neliölukuja ovat
.
Niinpä 2000:ta pienempiä neliölukuja ovat
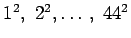 .
(Jos hyväksymme myös nollan neliöluvuksi,
2000:a pienempiä neliölukuja on 45.)
.
(Jos hyväksymme myös nollan neliöluvuksi,
2000:a pienempiä neliölukuja on 45.)
32.
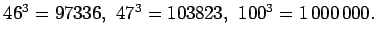 Siispä 6-numeroisia
kuutiolukuja ovat
Siispä 6-numeroisia
kuutiolukuja ovat
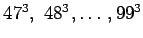 .
Yhteensä lukuja on 53.
.
Yhteensä lukuja on 53.
33.
Oikea vastaus on (D) 6, sillä
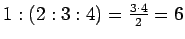 .
Täten
vastaus (E) on virheellinen, eikä myöskään (C) ole oikein, koska 5 on jaoton
luku eikä se siten voi olla murtolausekkeessa yhtenä tekijänä. Ratkaisu (A)
ei sekään ole oikein, sillä siinä tapauksessa luvut 2 ja 4 kumoaisivat
murtolausekkeessa toisensa, mikä ei käy päinsä. Samaten myös (B)
on vastauksena mahdoton, sillä silloin taas 2 ja 3 kumoaisivat toisensa.
.
Täten
vastaus (E) on virheellinen, eikä myöskään (C) ole oikein, koska 5 on jaoton
luku eikä se siten voi olla murtolausekkeessa yhtenä tekijänä. Ratkaisu (A)
ei sekään ole oikein, sillä siinä tapauksessa luvut 2 ja 4 kumoaisivat
murtolausekkeessa toisensa, mikä ei käy päinsä. Samaten myös (B)
on vastauksena mahdoton, sillä silloin taas 2 ja 3 kumoaisivat toisensa.
34.
Murtolausekkeen vastaus ei voi olla (E) 24, koska silloin murtolausekkeen
tekijät muodostaisivat tulon
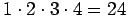 .
Niinpä kaikkien
tekijöiden pitäisi olla osoittajassa, mutta luku 2 on aina nimittäjässä. Muut
vastausmahdollisuudet toteutuvat.
.
Niinpä kaikkien
tekijöiden pitäisi olla osoittajassa, mutta luku 2 on aina nimittäjässä. Muut
vastausmahdollisuudet toteutuvat.
(A)
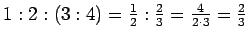 .
.
(B)
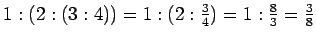 .
.
(C)
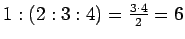 .
.
(D)
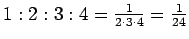 .
.
35.
Oikea vastaus on (D) 5, sillä
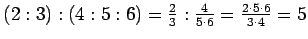 .
Siksi vastaus (E) on väärin. Vastaukset (A), (B) ja (C) ovat myöskin väärin,
sillä tekijä 5 on murtolausekkeessa aina joko
osoittajassa tai nimittäjässä eikä lukua 5 sisältäviä tekijöitä ole
murtolausekkeessa kuin yksi.
.
Siksi vastaus (E) on väärin. Vastaukset (A), (B) ja (C) ovat myöskin väärin,
sillä tekijä 5 on murtolausekkeessa aina joko
osoittajassa tai nimittäjässä eikä lukua 5 sisältäviä tekijöitä ole
murtolausekkeessa kuin yksi.
36.
Murtolausekkeen tulos ei voi olla (D)
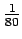 ,
sillä
,
sillä
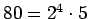 .
Sen vuoksi jokaisen tekijöistä 2, 4 ja 6 täytyy olla nimittäjässä,
jotta 24:ssä olisi 4 kappaletta lukua 2. Kuitenkin
ensimmäinen tekijä 2 on aina osoittajassa. Muut vastausmahdollisuudet
toteutuvat.
.
Sen vuoksi jokaisen tekijöistä 2, 4 ja 6 täytyy olla nimittäjässä,
jotta 24:ssä olisi 4 kappaletta lukua 2. Kuitenkin
ensimmäinen tekijä 2 on aina osoittajassa. Muut vastausmahdollisuudet
toteutuvat.
(A)
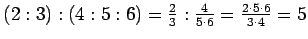 .
.
(B)
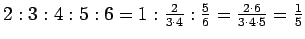 .
.
(C)
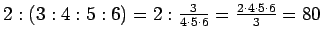 .
.
(E)
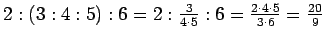 .
.
37.
Oikea vastaus on (B) 7. Koska
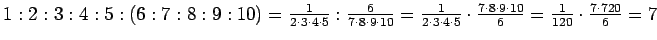 ,
niin
vastaus (E) on väärin. Vastaukset (A), (C) ja (D) eivät myöskään ole oikein,
sillä tekijä 7 on murtolausekkeessa aina joko osoittajassa tai
nimittäjässä eikä lukua 7 sisältäviä tekijöitä ole
murtolausekkeessa kuin yksi.
,
niin
vastaus (E) on väärin. Vastaukset (A), (C) ja (D) eivät myöskään ole oikein,
sillä tekijä 7 on murtolausekkeessa aina joko osoittajassa tai
nimittäjässä eikä lukua 7 sisältäviä tekijöitä ole
murtolausekkeessa kuin yksi.
38.
Lukua (E)
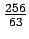 ei voi saada vastaukseksi, sillä 256 = 28.
Siten jokaisen tekijöistä 2, 4, 6, 8 ja 10 täytyy olla osoittajassa,
jotta 28 olisi 8 kappaletta lukua 2. Kuitenkin luku 2 on
aina nimittäjässä. Muut vastausmahdollisuudet toteutuvat.
ei voi saada vastaukseksi, sillä 256 = 28.
Siten jokaisen tekijöistä 2, 4, 6, 8 ja 10 täytyy olla osoittajassa,
jotta 28 olisi 8 kappaletta lukua 2. Kuitenkin luku 2 on
aina nimittäjässä. Muut vastausmahdollisuudet toteutuvat.
(A)
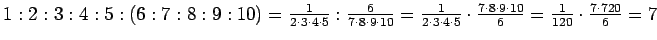 .
.
(B)
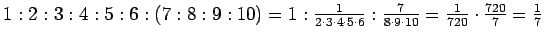 .
.
(C)
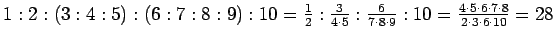 .
.
(D)
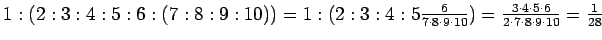 .
.
39.
Sadan ensimmäisen alkuluvun joukossa on yksi parillinen luku,
loput 99 ovat parittomia. 99 parittoman ja 1 parillisen luvun summa
on pariton.
40.
Sadan ensimmäisen neliöluvun joukossa on 50 parillista ja 50 paritonta
lukua. 50 parillisen ja 50 parittoman luvun summa on parillinen.
Summa
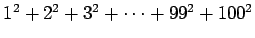 on parillinen.
on parillinen.
41.
Yhtälö ei toteudu koskaan, sillä sen vasemman puolen arvo on aina
parillinen, koska kuuden parittoman luvun summa on aina parillinen.
42.
Yhtälö toteutuu esim. seuraavalla tavalla:
43.
Summan
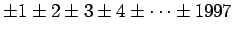 pienin positiivinen arvo on 1.
Se saadaan esim. seuraavalla tavalla:
pienin positiivinen arvo on 1.
Se saadaan esim. seuraavalla tavalla:
Suluissa olevien neljän luvun summa on aina 0.
44.
Ensimmäisestä 20 luvusta saadaan halutulla tavalla summa 100 esim.
seuraavasti:
Ensimmäisestä 18 luvusta ei saa summa 100 millään tavalla, sillä näiden
18 luvun joukossa on 9 parillista ja 9 paritonta lukua ja siksi
etumerkeistä riippumatta niiden summa on aina pariton.
45.
Ei voida, sillä lukua 100 ei voi esittää viiden parittoman luvun summana.
(5 parittoman luvun summa on aina pariton.)
46.
Jos neljän kokonaisluvun tulo päättyy numeroon 1, tulo on pariton
ja kaikki 4 lukua ovat parittomia. Kuitenkin 4 parittoman luvun summa
on aina parillinen. Tämän takia ei ole olemassa neljää sellaista
kokonaislukua, että niiden summa olisi 1997 ja tulo päättyisi numeroon 1.
47.
Ei voi. Jos voisi, lukujen
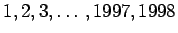 summa olisi parillinen.
Summa on kuitenkin pariton, sillä se muodostuu 999 parillisesta ja
999 parittomasta yhteenlaskettavasta.
summa olisi parillinen.
Summa on kuitenkin pariton, sillä se muodostuu 999 parillisesta ja
999 parittomasta yhteenlaskettavasta.
48.
Ei voi. Jos voisi, lukujen
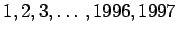 summa olisi
parillinen. Summa on kuitenkin pariton, sillä se on 999 parittoman ja
998 parillisen luvun summa.
summa olisi
parillinen. Summa on kuitenkin pariton, sillä se on 999 parittoman ja
998 parillisen luvun summa.
49.
Luku
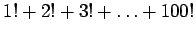 on pariton, sillä sen ensimmäinen
yhteenlaskettava on pariton ja loput parillisia. Kahdesta
peräkkäisestä luvusta toinen on pariton ja toinen parillinen,
joten niiden tulo on parillinen.
Tämän takia luku
on pariton, sillä sen ensimmäinen
yhteenlaskettava on pariton ja loput parillisia. Kahdesta
peräkkäisestä luvusta toinen on pariton ja toinen parillinen,
joten niiden tulo on parillinen.
Tämän takia luku
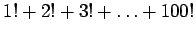 ei voi olla kahden peräkkäisen
kokonaisluvun tulo.
ei voi olla kahden peräkkäisen
kokonaisluvun tulo.
50.
Kun kakku leikataan yhden reunan suuntaisesti a kertaa, kakku jakautuu
a+1 palaan. Kun kakku leikataan vielä b kertaa kohtisuoraan edellisiin
viiltoihin nähden, kakku on leikattu
(a+1)(b+1) palaseen.
(a+1)(b+1)=1995,
joten a+1 on pariton, kuten myös b+1, mutta näin ollen sekä a että b
ovat parillisia, kuten myös a+b, jolloin a+b on eri suuri kuin 111.
Tämän takia kakkua ei voi leikata 111 viillolla 1995 palaseen.
51. Lukujen 1, 2, 3, 4, 5, 6,
7, 8, 9 ja 10 joukossa on 5 parillista ja 5 paritonta lukua, joten
niiden summa on pariton. Jos haluttu jako voidaan suorittaa, joukkojen lukujen
yhteenlaskun jälkeen saadaan kaikkien lukujen summa laskemalla joukkojen summat
yhteen. Tällöin saadaan parillinen luku, koska kaikkien lukujen summa on sama
kuin yhden joukon lukujen summa kerrottuna kahdella. Kaikkien lukujen summa on
kuitenkin pariton, joten lukuja 1, 2, 3, 4, 5, 6, 7, 8, 9 ja
10 ei voida jakaa kahteen joukkoon
niin, että joukoissa lukujen summat olisivat yhtäsuuret.
52.
Kahteen joukkoon jaon jälkeen siinä joukossa, jossa luku 7 on,
lukujen tulo on jaollinen 7:llä, kun taas toisen joukon lukujen
tulo ei ole (koska 7 on alkuluku
ja muut tekijät eivät ole jaollisia 7:llä). Näin ollen nämä kaksi
tuloa eivät voi olla yhtäsuuret.
53.
Viiden peräkkäisen luvun joukossa on tasan yksi viidellä jaollinen luku.
Kahteen joukkoon jakamisen jälkeen sen joukon, jossa luku 5 on, tulo on
jaollinen viidellä, kun taas toisen ei (koska 5 on
alkuluku). Näin ollen näiden kahden joukon tulot eivät voi olla yhtäsuuret.
54.
Kuudesta peräkkäisestä luvusta kolme on parittomia, joista kaksi
päätyy joko kolmen ensimmäisen tai kolmen viimeisen luvun joukkoon, jolloin
kyseisen joukon lukujen summa on parillinen. Tästä syystä tulo
on parillinen eikä voi olla
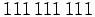 .
.
55.
Mikäli summalle annetaan yhteinen
nimittäjä, osoittajan kaikki yhteenlaskettavat ovat parittomia ja osoittaja
on siis parillinen
(100 parittoman luvun summa). Nimittäjä puolestaan on pariton. Näin ollen
osoittaja (parillinen luku) ei voi olla yhtä suuri nimittäjän (pariton
luku) kanssa. Täten tämä murtoluku (100 parittoman luvun käänteislukujen
summa) ei voi olla yksi.
56.
Jos summalle annetaan yhteinen
nimittäjä, osoittajan ensimmäinen jäsen on pariton, muut parillisia, joten
osoittaja on pariton (1 parillisen ja 99 parittoman luvun summa). Nimittäjä
puolestaan on parillinen.
Näin ollen tämä murtoluku (100 ensimmäisen alkuluvun käänteislukujen
summa) ei ole kokonaisluku.
57.
abcd - a = 1997 ja
a(bcd -1) = 1997,
joten a on jaollinen 1997:lla, jolloin a on pariton luku. Samalla tavoin
saadaan selville että b, c ja d ovat parittomia lukuja. Tällöin yhtälö
abcd - a = 19997 ei voi pitää paikaansa, koska abcd on pariton, jolloin
erotus abcd - a on parillinen, jolloin se ei voi olla 1997. Yhtälöryhmälle ei
löydy ratkaisua kokonaislukujen joukosta.
58.
Alkuluvut.
59.
Tasan kolmella luvulla jaolliset
luvut ovat muotoa p2, missä p on alkuluku. Lukua 100 pienemmistä
luvuista löytyy neljä sellaista lukua: 4, 9, 25 ja 49.
60.
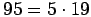 ,
joten 19x +
95y on aina jaollinen 19:llä. 2000 ei ole jaollinen 19:llä. Siispä yhtälön
19x + 95y = 2000 puolet eivät ole yhtäsuuret. Yhtälölle ei löydy ratkaisua
kokonaisluvuista.
,
joten 19x +
95y on aina jaollinen 19:llä. 2000 ei ole jaollinen 19:llä. Siispä yhtälön
19x + 95y = 2000 puolet eivät ole yhtäsuuret. Yhtälölle ei löydy ratkaisua
kokonaisluvuista.
Matematiikkalehti Solmu
2000-01-31


![]() ,
jolloin yhden taulukon lukujen
summa on
,
jolloin yhden taulukon lukujen
summa on
![]() .
Vastaavasti
.
Vastaavasti
![]() -ruutuisen
taulukon lukujen summa on
-ruutuisen
taulukon lukujen summa on
![]() .
.