Valintakuulustelujen matematiikan koe 28.5.1997; Ratkaisut

HTKK, TTKK, LTKK, OY, ÅA/Insinööriosastot
Valintakuulustelujen matematiikan koe 28.5.1997
Ratkaisut

1. Merkitään $\bar{a}=\bar{a_1}+\bar{a_2}$ , missä $\bar{a_1}$ on vektorin $\bar{b}$ suuntainen ja $\bar{a_2}$ vektoria $\bar{b}$ vastaan kohtisuorassa. On olemassa luku $\bar{t}\in R$ siten, että $\bar{a_1} = t\bar{b}.$ Tälloin $\bar{a_2}=\bar{a}-t\bar{b}$ . Kohtisuuruuden perusteella on

$\begin{displaymath}\bar{a}\cdot\bar{b}=(\bar{a}-t\bar{b})\cdot \bar{b}=0, \end{displaymath}$

mistä

$\begin{displaymath}t=\frac{\bar{a}\cdot \bar{b}}{\bar{b}\cdot \bar{b}}. \end{displaymath}$

Koska $\bar{a}\cdot \bar{b}=24$ ja $\bar{b}\cdot \bar{b}=6$ , on t=4. Tällöin kysytyt komponentit ovat $\bar{a_1}=4(\bar{i-j+2k})$ ja $\bar{a_2}=2(\bar{-i+3j+2k})$

2. Olkoon $D=(x,y), \sphericalangle DAB=\alpha$ ja $\sphericalangle DBA=\beta$ . Tällöin

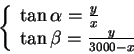
$\begin{displaymath}\left\{ \begin{array}{ll} \tan \alpha = \frac{y}{x}\\ \tan \beta = \frac{y}{3000-x} \end{array} \right. \end{displaymath}$

Ratkaisemalla x ja y saadaan

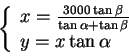
$\begin{displaymath}\left\{ \begin{array}{ll} x = \frac{3000\tan\beta}{\tan\alpha +\tan\beta }\\ y = x\tan\alpha \end{array} \right. \end{displaymath}$

Koska $\alpha$ = $32,8^\circ$ ja $\beta$ = $64,1^\circ$ , on D=(2280,1470). Jos merkitään $\sphericalangle DAE = \phi$ , räjähdyspatsaan korkeudelle hpätee, että

$\begin{displaymath}\tan\phi = h/\sqrt{x^2 + y^2}, \end{displaymath}$

missä x ja y ovat pisteen D koordinaatit. Tällöin $h=\sqrt{x^2+y^2}\tan\phi$ . Koska $\phi=3,5^\circ$ ja D=(2280,1470), on h=170m.

3. Erotusfunktion

$\begin{displaymath}u(R)=u_1(R)-u_2(R)=\frac{ER}{R-81}-\frac{ER}{R-2025}\qquad (R\geq 0) \end{displaymath}$

derivaatta on

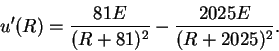
$\begin{displaymath}u'(R)=\frac{81E}{(R+81)^2}-\frac{2025E}{(R+2025)^2}. \end{displaymath}$

Yhtälön u'(R)=0 ratkaisu antaa paikalliseksi ääriarvokohdaksi ehdolle vastuksen arvon $R=\sqrt{81\cdot 2025}=9\cdot 45=405.$ Derivaatan u'(R) merkin vaihtumisen perusteella erotusfunktio u(R) saavuttaa paikallisen maksimin tällä arvolla. Koska u'(R)>0 joukossa $\lbrack 0,450 \rbrack, u(R)$ on kasvava arvoa R=450 pienemmillä vastuksen arvoilla. Vastaavasti u'(R) on vähenevä suuremmilla arvoilla. Siten erotusfunktio u(R)saavuttaa suurimman arvonsa, kun $R=450\Omega$ . Ilmeisesti suurin arvo on $u(450)=\frac{2}{3}E$ .

4. Olkoon X kelvottomien rasioiden lukumäärä otoksessa(100kpl). Tällöin X on binomijakautunut satunnaismuuttuja parametrein n=100 ja p=0,025. Erä hyväksytään, jos $X\le 1$ . Hyväksymistodennäköisyys on

$\begin{displaymath}P(X\le 1)=P(X=0)+P(X=1)\, \end{displaymath}$

$\begin{displaymath}=(1-p)^n+np(1-p)^n-1% =0,28=28\%.\, \end{displaymath}$

5. Käyrien $x=y^\frac{1}{2}+1$ ja $x=\frac{-1}{3}+\frac{13}{3}$ leikkauspisteeksi tulee (3,4). Säiliön tilavuus on

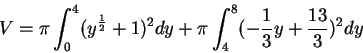
$\begin{displaymath}V=\pi\int_{0}^{4}(y^\frac{1}{2}+1)^2dy+\pi\int_{4}^{8}(-\frac{1}{3}y+\frac{13}{3})^2dy \end{displaymath}$

$\begin{displaymath}=\pi/_{0}^{4}\frac{1}{2}y^2+\frac{4}{3}y^\frac{3}{2}+y+\frac{\pi}{9}/_{4}^{8}-\frac{1}{3}(-y+13)^3 \end{displaymath}$

$\begin{displaymath}=22\frac{2}{3}\pi+22\frac{10}{27}\pi=45\frac{1}{27}\pi\approx 141,5m^2. \end{displaymath}$

Koska $65<\frac{2}{3}\pi$ , on löydettävä korkeus h, jolle on

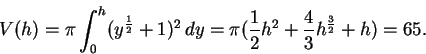
$\begin{displaymath}V(h)=\pi\int_{0}^{h}(y^\frac{1}{2}+1)^2\,dy=\pi(\frac{1}{2}h^2+\frac{4}{3}h^\frac{3}{2}+h)=65. \end{displaymath}$

Esimerkiksi haarukointimenetelmällä $h\approx3,8m.$

6. Bakteereja tappajasolujen istuttamisen hetkellä eli välittomästi bakteerien n:nnen jakaantumisen jälkeen oli 2ⁿ kpl. Olkoon k=0 hetki, jolloin bakteerien n:s jakaantuminen tapahtuu, ja olkoon x_k bakteerien (vast. y_k tappajasolujen) lukumäärä hetkellä k=0,1,2,... (juuri syömisen ja jakaantumisen jälkeen). Siten