PDF

17. Matematiikkaa Suomessa

Suomi oli pitkään matematiikan periferiaa. Matemaattiset innovaatiot tulivat tänne useiden vuosikymmenien viipeellä. Eräillä matematiikan osa-alueilla suomalainen matematiikka on kuitenkin ajoittain ollut ehdotonta maailmankärkeä.

17.1 Varhaisvaiheet

Korkeamman opetuksen ja tieteenharjoituksen katsotaan Suomessa alkavan Turun akatemian perustamisesta vuonna 1640. Akatemian vähälukuiseen opettajakuntaan määrättiin kuuluvaksi myös matematiikan professori. Professuurin opetusalaan, joka määriteltiin sanalla mathesis, kuului myös tähtitiede. Viran ensimmäinen haltija oli ruotsalaissyntyinen, Upsalassa opiskellut Simon Kexlerus (1602-69). Kexleruksen, samoin kuin hänen seuraajiensakin, edustaman tietämyksen ja opetuksen taso oli melko alhainen. (Kexlerus esimerkiksi omisti paljon vaivaa ptolemaiolaisen maailmankuvan puolustamiseen kopernikaanista vastaan.) Uuden ajan alkuvuosisatojen merkittävistä uusista keksinnöistä ei Suomessa tunnuttu vielä tiedettävän mitään. Opetus rajoittui seksagesimaali- ja kymmenjärjestelmän aritmetiikkaan sekä trigonometrian ja geometrian alkeisiin. Infinitesimaalilaskenta alkoi tehdä tuloaan Suomeen vasta 1700-luvun puolivälissä, yli 50 vuotta syntyaikojensa jälkeen.

1700-luvun turkulaismatemaatikoista voi mainita Martin Johan Walleniuksen (1731-73), joka 1766 julkaisi täydellisen todistuksen Hippokrateen kuunsirppiongelman yleistykselle säännöllisen monikulmion sivuihin liittyvien ympyränkaarien tapauksessa. Wallenius pani myös alulle differentiaali- ja integraalilaskennan opetuksen Turussa.

Ensimmäinen eurooppalaiselle tasolle päässyt suomalainen matemaatikko oli Turussa syntynyt ja opiskellut Anders Lexell (1740-84), joka kuitenkin toimi melkein yksinomaan Pietarissa, aluksi sokean Eulerin assistenttina ja puhtaaksikirjoittajana, myöhemmin myös vähän aikaa Eulerin seuraaja-akateemikkona. Lexell suoritti merkittäviä tähtitieteellisiä laskuja ja tutki differentiaaliyhtälöitä. Hän piti hallussaan matematiikan professuuria Turussa muutaman vuoden. Hän oli kuitenkin koko ajan virkavapaana ja toimi edelleen Pietarissa. Matemaattista jälkikasvua Lexelliltä ei jäänyt.

Turun akatemia siirtyi Turun palon jälkeen vuonna 1828 Helsinkiin ja muuttui samalla Keisarilliseksi Aleksanterin-yliopistoksi. Vähittäinen kehitys kohti Manner-Euroopan tieteen tasoa alkoi; tuon ajan ensimmäinen matematiikan professori Nathanael af Schultén (1794-1860) oli sen eturintamasta vielä varsin kaukana. Hänen tuotannossaan vilahtelee kuitenkin selvästi ajankohtaisia aiheita: interpolointi trigonometristen funktioiden avulla suunnilleen Fourier'n aikoihin, irrationaalilukujen olemus, ketjumurtoluvut ja differentiaalilaskennan perusteet.

Schulténia seurasi matematiikan oppituolissa Lorenz Lindelöf (1827-1908). Lindelöf oli merkittävä variaatiolaskennan tutkija; vaikka hän ei tällä alalla mitään vallankumouksellista uutta luonutkaan, oli hänen 1861 Pariisissa julkaistu ranskankielinen variaatiolaskennan oppikirjansa Leçons de calcul des variations laajalti käytössä. - Lindelöf oli kiinnostunut yhteiskunnallisista asioista. Hän siirtyi 1874 professuuristaan Kouluylihallituksen johtajaksi (ja jäi eläkkeelle vasta 1902), ehti olla säätyvaltiopäivillä niin pappis-, porvaris- kuin aatelissäätyjenkin edustajana ja oli joitakin vuosia Helsingin kaupunginvaltuuston puheenjohtajana. Professorivuosinaan Lindelöf toimi myös yliopiston rehtorina.

17.2 Kansainväliset yhteydet avautuvat

Vuonna 1877 Lorenz Lindelöfiä seurasi matematiikan professuurissa kiivaan kieliriidan jälkeen ruotsinmaalainen Gösta Mittag-Leffler (1846-1927), Weierstrassin oppilas. Hänen kilpahakijansa oli Ernst Bonsdorff (1842-1936), etevä invarianttiteorian tutkija. Mittag-Leffler oli huomattava funktioteorian tutkija ja myöhemmin, Ruotsissa toimiessaan, matematiikan kansainvälisen tieteellisen yhteistoiminnan keskeisiä organisoijia. - Mittag-Lefflerin Tukholman liepeillä sijaitseva koti on nykyisin matemaattinen tutkimuslaitos, Institut Mittag-Leffler; tutkimuslaitoksen pohjana oleva suuri omaisuus on huomattavalta osalta peräisin Suomesta, Mittag-Lefflerin varakkaalta suomalaiselta vaimolta Signe Lindforsilta.

Mittag-Leffler aloitti Suomessa funktioteoreettisen tutkimussuunnan, joka on historiallisesti merkittävin suomalaisen matematiikan panos matematiikan yleiseen kehitykseen. Mittag-Leffler ehti nelivuotisen Helsingin-kautensa aikana kouluttaa muutamia oppilaita, joista ensimmäinen on Hjalmar Mellin (1854-1933). Myös Mellin opiskeli jonkin aikaa Weierstrassin johdolla Berliinissä. Gammafunktiota ja hypergeometrista funktiota tutkiessaan hän johtui integraalimuunnokseen $F(z)=\int_0^{\infty}\Phi(x)x^{z-1}dx$ käänteismuunnoksineen. Tämä muunnos tunnetaan kansainvälisesti Mellinin transformaationa. - Vanhemmilla päivillään Mellin otti päätehtäväkseen Einsteinin suhteellisuusteorian vastustamisen: hän kirjoitti useita artikkeleita, joissa suhteellisuusteoria kumottiin terveen järjen perusteluin.

Mittag-Lefflerin seuraaja matematiikan professuurissa oli Edvard Neovius (1851-1917), Suomen johtavan matemaattisen suvun Neovius-Nevanlinnan edustaja. Neovius oli opiskellut Zürichin teknillisessä korkeakoulussa Weierstrassin oppilaan ja työtoverin Hermann Amandus Schwarzin (1843-1921) johdolla; Schwarz tunnetaan funktioteorian Schwarzin lemmasta ja Schwarzin epäyhtälöstä, joka kuitenkin on peräisin Cauchylta. Neovius tutki projektiivista geometriaa ja Riemannin ja Weierstrassin alulle panemaa minimipintojen teoriaa, kysymyksiä kiinteässä reunassa olevista pinta-alaltaan mahdollisimman pienistä pinnoista. Yliopistosta Neovius siirtyi vuonna 1900 senaattoriksi, mutta joutui vuoden 1905 tapahtumien jälkeen vetäytymään syrjään politiikasta. Viimeiset elinvuotensa hän vietti vaimonsa kotimaassa Tanskassa.

Neovius oli osaltaan vaikuttamassa Suomen korkeamman tekniikanopetuksen aseman vakiinnuttamiseen 1800-luvun lopulla. Vuonna 1849 perustettu Teknillinen reaalikoulu muutettiin 1879 Polyteknilliseksi opistoksi ja 1908 Teknilliseksi korkeakouluksi. Korkeakoulun ensimmäinen matematiikan professori oli Mellin.

17.3 Ernst Lindelöf ja hänen oppilaansa

Suomalainen funktioteoreettinen koulukunta sai varsinaisesti hahmonsa Lorenz Lindelöfin pojan Ernst Lindelöfin (1870-1946) pitkäaikaisen opettajan- ja tutkijantyön ansiosta. Ernst Lindelöf oli Helsingin yliopiston matematiikan professori 1903-1938. Lindelöfin pääyhteydet kohdistuivat Ranskaan, ja myös suurin osa hänen tutkimuksistaan on kirjoitettu ranskaksi. Funktioteoriassa Lindelöf tutki mm. kokonaisia (so. ei napoja eli äärettömyyskohtia omaavia) analyyttisiä funktioita, residylaskentaa ja konformikuvausten teoriaa. Kokonaisia funktioita koskevat työt ennakoivat arvojenjakautumisteorian tuloa Suomeen. Residylaskennasta eli kompleksisten viivaintegraalien teorian hyödyntämistä reaalifunktioiden integroinnissa Lindelöf kirjoitti suositun ranskankielisen oppikirjan. Tunnettu on Lindelöfin yhteistyö ruotsalaisen E. Phragménin (1863-1937) kanssa. Phragménin-Lindelöfin lause koskee analyyttisen funktion käyttäytymistä äärettömyyteen ulottuvan sektorin muotoisessa alueessa.

Lindelöfin kiinnostus suuntautui myös muihin matematiikan aloihin. Hän toi lisiä differentiaaliyhtälöiden ratkaisujen olemassaolotuloksiin ja pistejoukkojen topologiassa todisti tunnetulle Heinen-Borelin lauseelle sukua olevan Lindelöfin peitelauseen. Myöhempinä vuosinaan Lindelöf keskittyi opetukseen ja kirjoitti mm. merkittävät oppikirjat Johdatus korkeampaan analyysiin ja Differentiaali- ja integraalilasku ja sen sovellutukset I-IV. Jälkimmäisen teoksen neljäs osa on omistettu variaatiolaskennalle, kunnianosoitukseksi isä-Lindelöfin harrastuksille.

Etupäässä funktioteorian alalla toimineita Ernst Lindelöfin työtovereita ja oppilaita ovat mm. Severin Johansson (1879-1929), Felix Iversen (1887-1973), Pekka Myrberg (1892-1976) sekä veljekset Rolf Nevanlinna (1895-1980) ja Frithiof Nevanlinna (1894-1977).

Severin Johansson, vuonna 1918 perustetun Åbo akademin ensimmäinen matematiikan professori ja sen toinen rehtori, pani alulle automorfifunktioiden tutkimuksen Suomessa. (Ernst Lindelöfin mielestä automorfifunktiot olivat niin vaikeita, että hän ei uskaltanut niihin puuttua.) Felix Iversenin alaa olivat meromorfifunktioiden singulariteetit; hän tuli tunnetuksi myös filantrooppina ja pasifistina sekä 40-vuotisesta toiminnastaan ylioppilastutkintolautakunnan sihteerinä. Pekka Juhana Myrberg oli kansainvälisesti arvostettu automorfifunktioiden tutkija, Teknillisen korkeakoulun ja Helsingin yliopiston professori ja lopulta Helsingin yliopiston kansleri. - Kuuluisaksi tuli Myrbergin osallistuminen saksalaisen Jablonowski-seuran kilpailuun 1922: kilpailutehtävänä tutkia algebrallisen yhteenlaskuteoreeman (kuten f(x+y)=f(x)+f(y)) toteuttavia funktioita, ja kilpailuaikaa oli neljä vuotta. Myrberg sai tiedon kilpailusta viimeisen kilpailuvuoden kuluessa, kirjoitti tutkimuksen ja voitti kilpailun. Myrbergin vanhemmilla päivillään kirjoittamat rationaalifunktioiden iterointia koskeneet tutkimukset ovat osoittautuneet aikaansa edellä olleiksi: mm. viimeaikaisen fraktaalitutkimuksen yhteydessä on tullut esiin Myrbergin tutkimia ongelmia.

Kaikki Lindelöfin oppilaat ja työtoverit eivät olleet funktioteoreetikkoja. Monipuolinen ja itsenäinen Jarl Lindeberg (1876-1932) tutki mm. potentiaaliteoriaa, variaatiolaskentaa, todennäköisyyslaskentaa ja matemaattista tilastotiedettä. Lindebergin todistus todennäköisyyslaskennan keskeiselle raja-arvolauseelle (jonka mukaan lähes mielivaltaisesti jakautuneiden satunnaismuuttujien summa noudattaa likimain normaalijakaumaa, kun yhteenlaskettavia on paljon) on kuuluisa. Nils Pipping (1890-1982), Severin Johanssonin seuraaja Åbo akademissa, tutki lukuteoriaa ja Kalle Väisälä (1893-1968), Turun yliopiston ensimmäinen matematiikan professori ja sittemmin pitkään vastaavan viran haltija Teknillisessä korkeakoulussa, algebraa ja algebrallista lukuteoriaa. Turkuun onkin aikaa myöten kehittynyt huomattava algebrallis-lukuteoreettinen koulukunta, jonka merkittävä edustaja on mm. Kustaa Inkeri (1908-1997). Turun matematiikka on tästä edelleen kehittynyt mm. automaatien teorian ja koodausteorian suuntaan. Seuraavan Turun-sukupolven merkittävin edustaja on Arto Salomaa (1934-), kansainvälisesti arvostettu automaattien teorian tutkija. - Kalle Väisälän merkitys matematiikan kouluopetuksen kehittäjänä on huomattava. Hänen oppikirjansa olivat 1950- ja 60-luvuilla oppikoulun vakio-oppimateriaalia. Väisälä paneutui oppikirjantekoon tunnollisesti. Hän rupesi koulunopettajaksi ja testasi materiaalinsa ensin omassa käytössään.

17.4 Rolf Nevanlinna ja arvojenjakautumisteoria

Neovius-Nevanlinnan suvussa on poikkeuksellisen paljon matemaatikkoja. Rolf Nevanlinnan isoisä oli Haminan kadettikoulun matematiikan opettaja, sittemmin kenraalimajuri Edvard Neovius, Rolf ja Frithiof Nevanlinnan isä Otto Nevanlinna normaalilyseon matematiikan yliopettaja, setä Edvard Neovius matematiikan professori, toinen setä Lars opettaja ja matematiikan oppikirjojen tekijä. Frithiof Nevanlinnan poika Veikko Nevanlinna (1920-) on Jyväskylän yliopiston matematiikan professori. Oulun yliopiston matematiikan emeritusprofessori Heikki Haahti (1929-) on Rolfin ja Frithiofin sisarenpoika, Teknillisen korkeakoulun matematiikan professori Olavi Nevanlinna Frithiofin pojanpoika.

Rolf Nevanlinnaa pidetään yleisesti merkittävimpänä suomalaisena matemaatikkona. Nevanlinnan maine perustuu ennen muuta 1925 syntyneeseen meromorfifunktioiden yleiseen arvojenjakautumisoppiin. (Kompleksimuuttujan z funktio f on analyyttinen eli holomorfinen, jos se on jokaisessa määrittelypisteessään derivoituva. Tällöin se voidaan jokaisessa määrittelyjoukon pisteessä kehittää Taylorin sarjaksi. Jos määrittelyjoukko vielä on koko kompleksitaso, funktiota sanotaankokonaiseksi. Funktio on meromorfinen, jos sen saamien arvojen joukkoon sallitaan $\infty$, mutta jos sillä kuitenkin jokaisessa määrittelyjoukon pisteessä on Laurent-sarja, joka on muotoa

$$f(z)=\sum_{k=-n}^{\infty}a_k(z-z_0)^k.$$

Tämä voidaan ilmaista myös sanomalla, että funktion singulariteetit ovat enintään n:nnen kertaluvun napoja.) Arvojenjakautumisteorian lähtökohtana oli ranskalaisen Emile Picardin (1856-1941) jo vuonna 1879 todistama tulos, jonka mukaan koko kompleksitasossa määritelty kokonainen analyyttinen funktio saa enintään yhtä poikkeusta lukuun ottamatta kaikki kompleksilukuarvot. Tällainen poikkeusarvo voi kuitenkin esiintyä: esim. e^z ei missään ole 0.

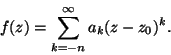
Picardin tulosta oli parantanut mm. Borel, mutta Nevanlinnan 1920-luvun puolivälissä julkaisemat tutkimukset, jotka koskivat paljon laajempaa yleisten meromorfisten funktioiden luokkaa, laajensivat teorian kokonaan uudelle tasolle. Nevanlinnan tulokset tunnetaan Nevanlinnan teorian ensimmäisenä ja toisena päälauseena. Niiden olennainen sisältö on, että meromorfifunktio saa kaikki arvot suunnilleen yhtä monesti. Jos jokin arvo esiintyy muita harvemmin funktionarvojen joukossa, niin funktio tulee toisaalta lähelle tällaista arvoa "useammin" kuin muita. - Arvojenjakautumisteoria on osaksi Nevanlinnan veljesten yhteistyötä. Siitä on tullut yksi kompleksianalyysin kestäviä tutkimuskohteita. Yleistyksiä on tehty eri suuntiin. Frithiof Nevanlinna teki elämäntyönsä pääosan vakuutusjohtajana. Hän ehti kuitenkin olla muutaman vuoden Helsingin yliopiston matematiikan professorina 1950-luvulla.

Rolf Nevanlinna oli aktiivinen monilla matematiikan aloilla; näihin kuuluvat Riemannin pintojen teoria, funktionaalianalyysi ja geometrian aksiomatiikka. Myös Nevanlinna ehti sotavuosina toimia yliopiston rehtorina. Nevanlinna oli osittain sukulaisuussuhteidenkin takia melko voimakkaasti Saksaan suuntautunut. Sodan aikana hän oli tekemisissä suomalaisen SS-pataljoonan kanssa. Sodan jälkeen hän ei ymmärrettävästi voinut toimia yliopiston hallinnossa. Kun ns. vanha Suomen Akatemia perustettiin 1948, Nevanlinnasta tuli sen ensimmäinen (ja ainoa) matemaatikkojäsen. Nevanlinna hoiti pitkään osa-aikaista professuuria Zürichin yliopistossa. Tästä yhteistyöstä juurtavat alkunsa edelleen säännöllisin väliajoin suomalais-sveitsiläisin voimin järjestettävät Rolf Nevanlinna -kollokviot. Suomen Akatemian perustaminen sodan jälkeisissä oloissa oli mitä suurimmassa määrin silloisen maisteri Leo Sarion (1916-) tarmokkuuden ansiota. Sario oli myös Nevanlinnan oppilas. Hän toimi pitkään professorina Kalifornian yliopistossa ja tutki Riemannin pintojen teoriaa.

Rolf Nevanlinnan monista oppilaista ensimmäinen ajallisesti ja asiallisesti on Lars V. Ahlfors (1907-1996), monipuolinen kompleksianalyysin tutkija ja ainoa suomalainen Fieldsin mitalin saaja; suurimman osan elämäntyöstään Ahlfors teki ulkomailla, vuodesta 1946 alkaen Harvardin yliopistossa. Ahlfors saavutti huomiota varsin nuorena ratkaistuaan ällistyttävän nopeasti ranskalaisen Arnaud Denjoyn (1884-1974) jo huomattavasti aikaisemmin esittämän ongelman. Myöhemmin Ahlfors kehitti Nevanlinnan arvojenjakautumisteoriasta geometrisemman version, peitepintojen teorian, ja oli ensimmäinen saksalaisen Oswald Teichmüllerin (1913-1943) tutkimusten arvon ymmärtäjiä ja niiden tulkitsijoita. Näin Ahlforsista tuli sittemmin Suomessakin menestyksellisesti harjoitetun kvasikonformikuvausten teorian perustajia.

Kvasikonformikuvauksia ja Teichmüllerin avaruuksia Suomessa tutkineista matemaatikosta huomattavimpia on Olli Lehto (1925-), myöskin Rolf Nevanlinnan oppilas. Lehtokin oli aikanaan Helsingin yliopiston rehtori ja kansleri.

Alkuun - Etusivu - Edellinen - Seuraava