
Nämä tehtävät on poimittu vuonna 1999 julkaistusta kirjasta Century of Kömal 1994-1997. Lisää tietoa unkarilaisesta matematiikanopetuksesta löytyy mm. internetistä osoitteesta http://komal.elte.hu.
Tehtävä 1. Bob suunnitteli labyrintin ruutupaperille. Labyrintin seinät seurasivat ruutujen sivuja. Bob aloitti piirtämällä ensin suuren neliön ja sitten sen sisään väliseiniä. Väliseinien piirtämiseen Bob käytti yhteensä 400 seinän palasta.
Kun Bob oli valmis, hän huomasi, että hänen labyrintissaan oli mistä tahansa ruudusta toiseen täsmälleen yksi sellainen reitti, joka ei palaa samaan ruutuun. Mikä oli suuren neliön sivujen pituus?
Ratkaisu 1. Olkoon Bobin ensin piirtämä suuri neliö kooltaan
n x n, ja ajatellaan siinä kaikkien vierekkäisten ruutujen
keskipisteet yhdistetyiksi viivoilla. Silloin joka rivillä on
n-1vaakasuoraa yhdysviivaa ja näin ollen n:llä rivillä on yhteensä
n(n-1) vaakasuoraa yhdysviivaa. Pystysuoria viivoja on samaten
n(n-1) kappaletta ja täten saamme yhteensä 2n(n-1) kappaletta
viivoja, jotka yhdistävät kaikkien n2:n ruudun keskipisteitä.
Kun Bob piirtää yhden osan väliseinää, hänen täytyy leikata matkalla tasan yksi yhdysviiva; vaakasuora, kun hänen seinänsä kulkee pystysuunnassa, ja pystysuora muutoin. Poistetaan nyt ne yhdysviivat, jotka Bob joutuu leikkaamaan piirtäessään seiniä. Silloin labyrintissä tulee olemaan tasan 2n(n-1)-400 yhdysviivaa jäljellä; nämä seuraavat labyrintin polkuja.
Muodostetaan nyt uusi verkko (graafi), missä labyrintin ruutujen
keskipisteet ovat kärkinä ja jäljelle jääneet yhdysviivat särminä.
Tässä verkossa on n2 kärkeä ja
2n(n-1)-400 särmää. Tiedämme,
että verkko on yhtenäinen (eli voimme saavuttaa jokaisen kärjen mistä
tahansa kärjestä), koska labyrintti kulkee jokaisen ruudun kautta.
Lisäksi tiedämme, että verkko on silmukaton (eli se ei sisällä umpinaisia
polkuja), koska labyrintissä on vain yksi tie kulkea ruudusta
toiseen. Täten voimme päätellä, että verkko on puu ja että siinä on
siten tasan yksi kärki enemmän kuin siinä on särmiä. Tästä saamme
yhtälön
Tehtävä 2. Matemaatikkojen julisteet oli kiinnitetty pyöreisiin mainospylväisiin, joiden halkaisija oli 1,5 metriä. Julisteiden kiinnittäjät huomasivat, että lukijat seisoivat kolmen metrin päässä pylvään keskipisteestä. He halusivat asettaa julisteet siten, että mistä tahansa suunnasta olisi ainakin yksi niistä kokonaan näkyvissä. Kuinka leveitä tulisi julisteiden tällöin enintään olla?
Ratkaisu 2. Jokainen kolmen metrin päässä mainospylvään keskuksesta seisova näkee sen osuuden pylväästä, joka on esitettynä vasemmalla kuvassa 1. Koko pylvään asemasta on siten riittävää tarkastella kuvan leikkausympyrää.
Kuvaan 1 merkityssä pisteessä M seisova ihminen näkee
ympyränkaaren E1E2. Merkitään nyt tämän ympyräkaaren pituutta
s:llä ja kulmaa E1OE2 ![]() :llä. Tällöin
vasemmanpuoleisesta kolmiosta E1OM saadaan
:llä. Tällöin
vasemmanpuoleisesta kolmiosta E1OM saadaan
![]() ja edelleen
ja edelleen
![]() .
.
Ympyräkaaren s pituus saadaan nyt laskettua seuraavasti.
Jos nyt merkitsemme julisteen leveyttä d:llä, niin täytyy olla
![]() ,
koska jos
,
koska jos
![]() ,
niin silloin olisi
mahdollista, että kaksi julistetta koskettaisivat toisiaan s:n
pituisen ympyräkaaren keskellä, ja tällöin kumpikaan julisteista ei
näkyisi kokonaan pisteeseen M. (Katso kuva 1.)
,
niin silloin olisi
mahdollista, että kaksi julistetta koskettaisivat toisiaan s:n
pituisen ympyräkaaren keskellä, ja tällöin kumpikaan julisteista ei
näkyisi kokonaan pisteeseen M. (Katso kuva 1.)
Koska etsimme suurinta mahdollista leveyttä, voimme olettaa, että
julisteet peittävät pylvään kokonaan; tällöin pylvään ympärysmitta on
jokin kokonaisluku n kertaa julisteen leveys. Jos meillä on siis
n julistetta, niin on oltava voimassa, että
![]() .
Tästä epäyhtälöstä saadaan ratkaisuksi
.
Tästä epäyhtälöstä saadaan ratkaisuksi
![]() .
.
Pienin julisteiden määrä, jolla julisteet näkyvät kaikkiin
suuntiin, on siis 5. Ja yhden julisteen leveys on tällöin
Tehtävä 3. Yhdysvalloissa yliopistojen välinen lentopallomestaruus ratkaistaan seuraavasti. Joukkueet jaetaan ensin lohkoihin, joissa on viisi tai kuusi joukkuetta. Lohkoittain joukkueet pelaavat ns. round robin -järjestelmän mukaan, jossa jokainen joukkue pelaa ainakin kerran jokaista muuta joukkuetta vastaan. Joukkueet, jotka häviävät enintään kerran pääsevät jatkoon lohkostaan. Kuinka monta joukkuetta voi enintään päästä jatkoon yhdestä alkulohkosta?
Ratkaisu 3. Voimme lähestyä kysymystä yleisemmin. Ajatellaan, että yksi lohko koostuu k:sta joukkueesta ja että joukkueet, joilla on enintään m tappiota, lunastavat paikan jatkossa. Ja kysymys on edelleen sama: kuinka monta joukkuetta voi selvitä jatkoon yhdestä lohkosta?
Jos ![]() ,
niin selvästi jokainen joukkue pääsee jatkoon.
Oletetaan nyt, että
,
niin selvästi jokainen joukkue pääsee jatkoon.
Oletetaan nyt, että ![]() ja siis
ja siis ![]() .
.
Merkitään jatkoon pääsevien joukkueiden lukumäärää t:llä, ja
tutkitaan ensin niitä otteluita, jotka nämä joukkueet pelaavat
keskenään. Niitä on
![]() kappaletta, koska jokainen
joukkue pelaa (t-1):n joukkueen kanssa, eli yhteensä t(t-1)ottelua, kun jokainen lasketaan kahdesti. Joka ottelussa on
myös häviäjäjoukkue; täten jatkoon päässeet t joukkuetta kärsivät
yhteensä vähintään
kappaletta, koska jokainen
joukkue pelaa (t-1):n joukkueen kanssa, eli yhteensä t(t-1)ottelua, kun jokainen lasketaan kahdesti. Joka ottelussa on
myös häviäjäjoukkue; täten jatkoon päässeet t joukkuetta kärsivät
yhteensä vähintään
![]() tappiota. Mitään näistä jatkoon
menevistä joukkueista ei voitettu enempää kuin m kertaa, joten
saadaan epäyhtälö
tappiota. Mitään näistä jatkoon
menevistä joukkueista ei voitettu enempää kuin m kertaa, joten
saadaan epäyhtälö
Seuraavaksi käsittelemme samaan tapaan niitä otteluita, jotka
pelattiin pudonneiden joukkueiden kesken. Jokainen näistä on hävinnyt
enintään t:lle jatkoon selviytyneelle joukkueelle, ja koska jokainen
kärsi vähintään m+1 tappiota kaiken kaikkiaan, seuraa tästä, että
jokaisen pudonneen joukkueen voitti vähintään m+1-t muuta pudonnutta
joukkuetta. Tästä taas seuraa, että pudonneet joukkueet hävisivät
yhteensä vähintään
(k-t)(m+1-t) ottelua keskinäisissä
otteluissaan. Tämä luku ei voi kuitenkaan olla suurempi kuin kaikkien
pudonneiden joukkueiden keskenään pelaamien otteluiden lukumäärä, eli
epäyhtälönä
Yhteenvetona saadaan siis, että mahdolliset t:n arvot ovat välillä
Tutkitaan sitten niitä otteluita, jotka pelataan jatkoon menevien joukkueiden välillä. Oletetaan ensin, että t=2m+1. Ajatellaan joukkueet sijoitetuiksi ympyrän kehälle jossakin järjestyksessä. Sovitaan, että jokainen joukkue voittaa ne m joukkuetta, jotka ovat sen oikealla puolella, ja vastaavasti tietenkin häviää vasemmalla puolellaan oleville m:lle joukkueelle. Tällä tavalla kaikkien otteluiden tulos on valittu ja nämä t joukkuetta todella pääsevät jatkoon.
Tapauksessa t<2m+1 voidaan toimia seuraavasti: Siirretään tilapäisesti putoavia joukkueita jatkoon pääsevien seuraan kunnes lukumäärä on 2m+1, ja valitaan tulokset yllä esitetyllä tavalla. Lopuksi palautetaan mukaan otetut putoavat joukkueet taas omaan ryhmäänsä ja muutetaan niiden mahdolliset voitot jatkoon valituista joukkueista tappioiksi. Tällöin yksikään t:stä alunperin jatkoon tarkoitetusta joukkueesta ei häviä useammin kuin m kertaa ja todella pääsee siis jatkoon.
Seuraavaksi tarkastellaan putoaviksi jätettyjen joukkueiden pelaamia otteluita. Olkoon tällä kertaa aluksi t=2m-k+3. Tällöin on siis k-(2m-k+3)=2k-2m-3 putoavaa joukkuetta. Edellä esitettyyn tapaan voimme järjestää myös nämä joukkueet ympyrän kehälle ja valita tulokset niin, että jokainen putoava joukkue häviää k-m-2 kertaa muille jatkosta putoaville joukkueille (ja samoin voittaa k-m-2 niistä). Lisäksi niiden pitää hävitä myös jatkoon pääseville joukkueille; ne kärsivät siten yhteensä (k-m-2)+(2m-k+3)=m+1 tappiota ja siksi siis putoavat.
Suuremmilla t:n arvoilla putoavia joukkueita tulee olemaan vähemmän. Lainaamalla joukkueita jatkoon pääsevien joukosta voimme kasvattaa ryhmän lukumäärän tilapäisesti arvoon 2k-2m-3 ja sopia tulokset samalla tavoin kuin edellä. Tämän jälkeen palautetaan jatkoon pääseville joukkueille jo aikaisemmin valitut tulokset sekä keskinäisiin että putoavien kanssa käytäviin otteluihin. Silloin putoaviksi tarkoitetut k-t joukkuetta häviävät edelleen vähintään m+1 kertaa ja aiemmin määritellyt jatkoon menevien tulokset eivät ole muuttuneet.
Lähempi tarkastelu osoittaa, että pieni korjaus on paikallaan. On
näet mahdollista, että 2m+1>k tai 2m-k+3<0, jolloin t ei voi
saavuttaa vastaavia arvoja. Täten enintään seuraavat epäyhtälöt
pätevät
Jos tarvitsemme tilapäisesti useampia joukkueita kuin mitä todellisuudessa on, niin voimme käyttää lisäksi kuvitteellisia ''haamujoukkueita''. Asetetaan tällöin ensin tulokset samalla tavoin kuin edellä on tehty ja jätetään sitten kokonaan ''haamujoukkueet'' sekä niiden pelaamat ottelut pois. Tämä menettely ei suurenna jatkoon meneviksi valittujen t:n joukkueen tappioiden lukumäärää eikä se kasvata myöskään putoavien joukkueiden voittojen lukumäärää. Toisin sanoen, valitsemamme t joukkuetta kärsivät edelleen enintään m tappiota, ja muut k-t joukkuetta voittavat enintään k-m-2=(k-1)-(m+1) ottelua. Tämän johdosta annetut tjoukkuetta pääsevät jatkoon, kun taas muut joukkueet putoavat.
Täten saimme tuloksen jokaisella epäyhtälöiden sallimalla t:n
arvolla, ja näin ongelmamme myös ratkeaa. Annetuilla arvoilla k=5,
m=1 ja k=6, m=1 jatkoon menevien joukkueiden lukumäärä ttoteuttaa epäyhtälöt
VASTAUS: Ei yhtään, yksi, kaksi tai kolme joukkuetta voi päästä jatkoon yhdestä lohkosta.
Tehtävä 4. Vertaile lukuja 200! ja 100200 käyttämättä taskulaskinta tai logaritmitauluja.
Ratkaisu 4. Kirjoitetaan annetut luvut tuloiksi
Ratkaisu 4, yleinen tapaus. Olkoon n positiivinen
kokonaisluku. Vertaillaan lukuja (2n)! ja n2n, joissa
kummassakin on 2n tekijää. Tällöin huomaamme heti, että
(2n)!>n2n, kun n=1 tai n=2. Oletetaan siis jatkossa, että ![]() .
Tutkitaan nyt osamäärää
.
Tutkitaan nyt osamäärää
![]() kirjoittamalla se tuloksi, jonka tekijöinä on 2n-1 murtolukua
kirjoittamalla se tuloksi, jonka tekijöinä on 2n-1 murtolukua
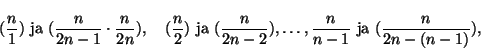
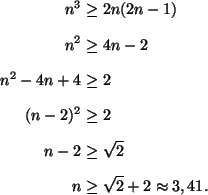
Tehtävä 5. On helppoa peittää taso samankokoisilla säännöllisillä kuusikulmioilla. Mutta onko mahdollista peittää tasoa kahdenlaisilla säännöllisillä kuusikulmioilla, jotka ovat eri kokoisia ja joita molempia pitää käyttää ainakin kerran?
Ratkaisu 5. Näytämme, ettei laatoitus onnistu. Oletetaan,
että olisimme onnistuneet laatoittamaan tason siten, että
kummankinlaisia kuusikulmioita on käytetty ainakin kerran. Tällöin
siis jossain on oltava kaksi eri kokoista kuusikulmiota, jotka
koskettavat toisiaan pitkin joitakin sivujaan.
Tehtävä 6. Kahdella teräväkulmaisella, tasakylkisellä kolmiolla on yhtä pitkät kyljet. Myös kolmioiden sisään piirrettyjen ympyröiden säteet ovat yhtä pitkät. Ovatko kolmiot välttämättä yhtenevät?
Ratkaisu 6. Osoitetaan, että on olemassa kaksi erilaista tasakylkistä kolmiota, joilla on yhtä pitkät kyljet ja joiden sisään piirrettyjen ympyröiden säteet ovat samat.
Olkoon F tasakylkisen kolmion ABC kannan BC keskipiste. (Katso
kuva 3.) Olkoon kolmion sisään piirretyn ympyrän säde r ja edelleen
![]() =
=
![]() .
Kolmio on
teräväkulmainen, jos ja vain jos
.
Kolmio on
teräväkulmainen, jos ja vain jos
![]() .
Ongelmamme on
yhtäpitävä kysymyksen ''Määrääkö lukujen AB ja r suhde
yksikäsitteisesti kulman
.
Ongelmamme on
yhtäpitävä kysymyksen ''Määrääkö lukujen AB ja r suhde
yksikäsitteisesti kulman ![]() ?'' kanssa.
?'' kanssa.
Ilmaistaan aluksi suhde
![]() luvun
luvun ![]() avulla. Kolmio
ABF on suorakulmainen; täten
avulla. Kolmio
ABF on suorakulmainen; täten
![]() ja
ja
![]() .
Jos merkitsemme kolmion ABC alaa T:llä, niin
.
Jos merkitsemme kolmion ABC alaa T:llä, niin
![]() .
Voimme ilmaista
kyseisen alan myös sisään piirretyn ympyrän avulla seuraavasti
.
Voimme ilmaista
kyseisen alan myös sisään piirretyn ympyrän avulla seuraavasti
| (1) |
Täten funktio ei ole monotoninen. (Tämä voitaisiin näyttää myös ilman
likiarvotarkasteluja derivaatan avulla.) Siis, jos esimerkiksi
![]() ,
niin on mahdollista löytää ainakin kaksi ehdon
(1) täyttävää eri
,
niin on mahdollista löytää ainakin kaksi ehdon
(1) täyttävää eri ![]() :n arvoa; toinen väliltä
:n arvoa; toinen väliltä
![]() ja toinen väliltä
ja toinen väliltä
![]() .
.
Olemme siis näyttäneet, että kaksi tasakylkistä kolmiota eivät ole
välttämättä yhtenevät, vaikka niiden kyljet olisivatkin yhtä pitkät ja
niiden sisään piirretyt ympyrät samankokoiset. ![]()
Tehtävä 7. Rengasmaisen kilparadan pituus on yksi kilometri. Kaksi moottoripyöräilijää ajaa rataa vastakkaisiin suuntiin. Molemmat moottoripyöräilijät lähtevät pisteestä A. Toinen ajaa koko ajan vakionopeudella, toinen taas kiihdyttää tasaisesti. Moottoripyöräilijät kohtaavat ensimmäisen kerran pisteessä B ja sitten uudelleen lähtöpisteessä A. Kuinka pitkän matkan oli vakionopeudella ajanut moottoripyöräilijä ehtinyt ajaa saapuessaan pisteeseen B?
Ratkaisu 7. Olkoon ensimmäisen ajajan nopeus v (km/h)
ja olkoon toisen ajajan kiihtyvyys a (km/h2). Koska molemmat
kulkevat saman yhden kilometrin matkan saman ajan t kuluessa, seuraa
tästä, että
at2/2=vt=1 eli
![]() ja
ja
![]() .
.
Merkitään T:llä sitä aikaa, joka ajajilta kuluu, kun he ajavat
pisteestä A pisteeseen B. Tiedämme, että molempien moottoripyörien
tänä aikana yhteensä kulkema matka on yksi kilometri ja näin ollen
Tehtävä 8.
Etsi ne positiiviset kokonaisluvut a,b,c, jotka toteuttavat yhtälön
Ratkaisu 8. Koska yhtälö on symmetrinen lukujen a, b ja csuhteen, voimme olettaa, että
![]() .
Permutoimalla tällaisia
ratkaisuja, saamme lopulta kaikki alkuperäisen yhtälön ratkaisut.
.
Permutoimalla tällaisia
ratkaisuja, saamme lopulta kaikki alkuperäisen yhtälön ratkaisut.
Tarkastellaan ensin pienintä lukua a. Jos a=1, niin
Tapauksessa a=2 saadaan
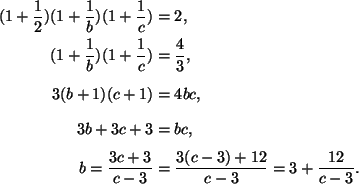
Koska b on kokonaisluku ja ![]() ,
niin nimittäjän c-3mahdolliset arvot ovat ne luvun 12 tekijät, jotka eivät ole
pienempiä kuin -1, eli luvut
-1,2,3,4,6,12, ja vastaavat parit
(b,c) ovat (-9,2), (15,4), (9,5), (7,6), (6,7), (5,9),
(1,15). Näistä vain parit (6,7), (5,9) ja (4,15) täyttävät ehdon
,
niin nimittäjän c-3mahdolliset arvot ovat ne luvun 12 tekijät, jotka eivät ole
pienempiä kuin -1, eli luvut
-1,2,3,4,6,12, ja vastaavat parit
(b,c) ovat (-9,2), (15,4), (9,5), (7,6), (6,7), (5,9),
(1,15). Näistä vain parit (6,7), (5,9) ja (4,15) täyttävät ehdon
![]() ,
ja ne myös ovat tarkastellun yhtälön ratkaisuja.
,
ja ne myös ovat tarkastellun yhtälön ratkaisuja.
Tapauksessa a=3 saadaan taas
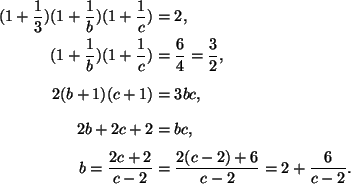
VASTAUS: Alkuperäisen yhtälön kaikki lukukolmikkoratkaisut (a,b,c) ovat (2,4,15), (2,5,9), (2,6,7), (3,3,8), (3,4,5) sekä kaikki näiden kolmikoiden eri permutaatiot (Esom. ratkaisun (2,4,15) permutaatiot ovat (2,4,15), (2,15,4), (15,2,4), (15,4,2), (4,2,15) ja (4,15,2)), joita on yhteensä 6+6+6+3+6=27 kappaletta.
Tehtävä 9. Suorakulmainen suuntaissärmiö leikataan ensin
kahteen, sitten neljään ja sitten vielä kahdeksaan yhtäsuureen osaan
kolmella toisiaan vastaan kohtisuoralla viillolla. Näin syntyneiden
suuntaissärmiöiden yhteenlaskettu pinta-ala kasvaa samassa suhteessa
joka leikkauksella. Osoita, että alkuperäisen suuntaissärmiön tilavuus
on kaksi kertaa suurimman sen sisään mahtuvan kuution tilavuus.
Ratkaisu 9. Merkitään särmiön sivuja symboleilla a, b,
c ja sen alaa S:llä. Koska kolmen leikkauksen jälkeen
alkuperäinen pinta-ala kaksinkertaistuu (meidän tulee leikata
jokaisen tahkon suuntaan yhden kerran, jotta saisimme 8 pientä
särmiötä), alueen pitää siis kasvaa
![]() -kertaiseksi
alkuperäisestä arvostaan joka leikkauksella. Kolmessa leikkauksessa
tämä johtaa yhtälöihin
-kertaiseksi
alkuperäisestä arvostaan joka leikkauksella. Kolmessa leikkauksessa
tämä johtaa yhtälöihin
![\begin{align*}\sqrt[3]{2}S&=S+2bc,\\
\sqrt[3]{2}(S+2bc)&=S+2bc+2ac,\\
\sqrt[3]{2}(S+2bc+2ac)&=S+2bc+2ac+3ab.\\
\end{align*}](img84.gif)
Tehtävä 10. Onko mahdollista kääriä laatikko, jonka sivujen
pituudet ovat a, b ja c, neliönmuotoiseen käärepaperiarkkiin,
jonka sivun pituus on
![]() ? (Paperia ei saa
leikata ja paperin pitää peittää kuutio täydellisesti.)
? (Paperia ei saa
leikata ja paperin pitää peittää kuutio täydellisesti.)
Ratkaisu 10. Kääriminen on mahdollista. Todistamme tämän
''avaamalla'' laatikon, levittämällä sen tasoon (Katso kuva 4.) ja
sitten peittämällä näin syntyneen monikulmion neliöllä, jonka sivun
pituus on vaadittu
Valitaan ensin toinen suorakulmaisen suuntaissärmiön tahkoista, jonka
sivujen pituudet ovat a ja b, ja liitetään sen viereen neljä muuta
sivutahkoa kuten kuvassa 4 vasemmalla on tehty. Sen jälkeen
yhdistetään liitettyjen c-sivuisten tahkojen kärjet janoilla kuten
kuvassa 4 oikealla (kärjet E ja G, H ja I, K ja L sekä Mja N). Näiden janojen jatkeet määrittävät nyt nelikulmion
ABCD. Koska kolmio EFG (kuten myös muut tummennetut kolmiot
kuvassa 4) on tasakylkinen ja suorakulmainen, seuraa tästä, että
ABCD on myös suorakulmainen. Edelleen,
Nyt meidän täytyy enää näyttää, että särmiön kuudes sivutahko
(sivuinaan a ja b) peittyy myös neliön ABCD alle. Olkoot
kuudennen tahkon kärkinä pisteet P, R, S ja T ja sen kulmien
puolittajien leikkauspisteet V, Z, X ja Y. (Katso kuva 5.)
Täten jakamalla kuudes särmiön tahko neljään osaan (tapauksessa
VASTAUS: Kääriminen on mahdollista.
Tehtävä 11. Äärellisestä joukosta on valittu seitsemän
kolmialkioista osajoukkoa niin, että mitkä tahansa kaksi joukon
alkiota kuuluvat tasan yhteen osajoukoista.
Ratkaisu 11. a) Merkitään joukon alkioiden lukumäärää
n:llä. Tällöin niiden osajoukkojen lukumäärä, joissa on tasan
kaksi alkiota on
b) Jos merkitsemme joukon alkioita symboleilla 1, 2, 3, 4, 5, 6 ja 7,
niin mahdolliset ehdokkaat seitsemäksi osajoukoiksi ovat
esim.
Seuraavaksi meidän tulee näyttää, että enintään neljä osajoukkoa
voidaan valita siten, että millään kolmella niistä ei ole yhteisiä
alkioita. Jos valitsemme viisi osajoukkoa, niin silloin niillä on
yhteensä
Siis: joukossa on seitsemän alkiota ja voimme aina valita enintään
neljä osajoukkoa siten, että missään kolmessa näistä osajoukoista
ei ole yhteistä alkiota.
VASTAUS: Osajoukoista voidaan valita neljä siten,
ettei millään kolmella niistä ole yhteisiä alkioita.
Ratkaisu 12. Merkitään kuution kärkiä symboleilla
A,B,C,D,E,F,G,H kuten kuvassa 12.
Olkoot kärkeä F vastassa olevien tahkojen keskipisteet K, L, ja
M. Olkoon edelleen suoran KM keskipiste R. Tetraedrissä KLMFsuorat KM, ML, ja LK ovat kaikki pituudeltaan
![]() .
.
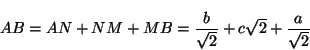
ja
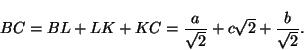
Siten ABCD on neliö, jonka sivun pituus on
![]() .
.
Jos a=b niin nämä neljä pistettä yhtyvät. Koska kulmien puolittajat
leikkaavat toisensa kohtisuoraan, PRY, RSV, STZ ja TPX ovat
suorakulmaisia tasakylkisiä kolmioita ja
![]() ja
ja
![]() .
.
![]() kolmioihin RSV ja TPX sekä kolmi- tai nelikulmioihin PRVX ja
STXV) ja sitten asettamalla joka palanen vastaavan sivutahkon
jatkoksi kuten kuvassa 5 saadaan koko särmiö peitetyksi neliöllä,
jonka sivun pituus on
kolmioihin RSV ja TPX sekä kolmi- tai nelikulmioihin PRVX ja
STXV) ja sitten asettamalla joka palanen vastaavan sivutahkon
jatkoksi kuten kuvassa 5 saadaan koko särmiö peitetyksi neliöllä,
jonka sivun pituus on
![]() .
.
a) Kuinka monta alkiota joukossa on?
b) Kuinka monta annetuista
osajoukoista voidaan valita siten, että millään kolmella niistä ei
ole yhteistä alkiota.
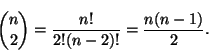
Jokainen kolmialkioinen osajoukko sisältää tasan kolme
kaksialkioista osajoukkoa, ja siksi, tehtävänannosta johtuen,
seitsemän kolmialkioista osajoukkoa yhdessä sisältää
![]() eri kaksialkioista osajoukkoa. Täten
eri kaksialkioista osajoukkoa. Täten
![]() ,
josta saamme yhtälön
n2-n-42=0 ja edelleen ratkaisuksi n=7.
,
josta saamme yhtälön
n2-n-42=0 ja edelleen ratkaisuksi n=7.
VASTAUS: Joukossa on 7 alkiota.
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
Sama esimerkki on kuvattuna seuraavassa
kuviossa, missä joukon alkiot on kuvattu pisteillä ja merkitty
numeroilla ja missä annetut osajoukot on kuvattu suorilla ja
ympyrällä.
.
Sama esimerkki on kuvattuna seuraavassa
kuviossa, missä joukon alkiot on kuvattu pisteillä ja merkitty
numeroilla ja missä annetut osajoukot on kuvattu suorilla ja
ympyrällä.
![]() alkiota (kun alkion jokainen esiintymä
lasketaan erikseen). Koska
alkiota (kun alkion jokainen esiintymä
lasketaan erikseen). Koska
![]() ,
niin on siis ainakin
yksi alkio, joka esiintyy (vähintään) kolme kertaa; ts. näiden viiden
osajoukon joukossa on kolme osajoukkoa, joissa on sama
alkio. Toisaalta on kuitenkin mahdollista valita neljä osajoukkoa
siten, että millään kolmella niistä ei ole yhteistä alkiota. Tätä
varten valitaan jokin joukon alkio, esim. 1. Ehtojen mukaisesti tämä
alkio sisältyy tasan
,
niin on siis ainakin
yksi alkio, joka esiintyy (vähintään) kolme kertaa; ts. näiden viiden
osajoukon joukossa on kolme osajoukkoa, joissa on sama
alkio. Toisaalta on kuitenkin mahdollista valita neljä osajoukkoa
siten, että millään kolmella niistä ei ole yhteistä alkiota. Tätä
varten valitaan jokin joukon alkio, esim. 1. Ehtojen mukaisesti tämä
alkio sisältyy tasan
![]() eli kolmeen annettuun
osajoukkoon. Näytetään nyt, etteivät mitkään lopuista 7-3=4osajoukosta sisällä samaa alkiota. Jos meillä on kolme osajoukkoa,
joissa on kaikissa sama alkio, niin silloin loppujen näiden kolmen
osajoukon 3(3-1)=6 eli kuudesta alkiosta täytyy kaikkien olla eri
alkioita ja niin niiden täytyy sisältää myös alkio 1, mikä on
mahdotonta. (Nämä neljä osajoukkoa, edellisessä esimerkissä ovat
eli kolmeen annettuun
osajoukkoon. Näytetään nyt, etteivät mitkään lopuista 7-3=4osajoukosta sisällä samaa alkiota. Jos meillä on kolme osajoukkoa,
joissa on kaikissa sama alkio, niin silloin loppujen näiden kolmen
osajoukon 3(3-1)=6 eli kuudesta alkiosta täytyy kaikkien olla eri
alkioita ja niin niiden täytyy sisältää myös alkio 1, mikä on
mahdotonta. (Nämä neljä osajoukkoa, edellisessä esimerkissä ovat
![]() ,
,
![]() ,
,
![]() ja
ja ![]() .)
.)
Tehtävä 12. Annetun kuution särmän pituus on a. Eräs kärki
ja kolmen sitä vastassa olevan sivutahkon keskipisteet
yhdistetään. Laske näin muodostuvan tetraedrin pinta-ala.
![]() ,
koska nämä suorat ovat keskijanoja tasasivuisessa
kolmiossa ACH, jonka sivun pituudet ovat
,
koska nämä suorat ovat keskijanoja tasasivuisessa
kolmiossa ACH, jonka sivun pituudet ovat ![]() .
Edelleen,
KF=LF=MF, koska jokainen yhdistää yhden kuution sivun keskipisteen
toiseen sen vastakkaisista kärjistä. Voimme laskea näiden janojen
pituudet käyttämällä Pythagoraan lausetta:
.
Edelleen,
KF=LF=MF, koska jokainen yhdistää yhden kuution sivun keskipisteen
toiseen sen vastakkaisista kärjistä. Voimme laskea näiden janojen
pituudet käyttämällä Pythagoraan lausetta:
![]()
![]()
Kolmiot KMF,LMF ja LKF ovat yhteneviä, koska niiden vastinsivut
ovat pareittain samat. Käyttämällä uudelleen Pythagoraan lausetta
saadaan
![]()
ja koska kolmion KMF ala on
![]()
ja tasasivuisen kolmion KLM ala on
![]()
saadaan täten tetraedrin kokonaisalaksi
![]()
VASTAUS:
Tetraedrin pinta-ala on noin 1,46a2.
Matematiikkalehti Solmu
2000-09-12