
Márta Oravecs ja Ágnes Kivovics
Tehtäväsivut: 1/A - 1/B - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12/A - 12/B - 13 - 14 - 15/A - 15/B - 16 - 17 - 18/A - 18/B - 19 - 20 - 21/A - 21/B - 21/C - 22 - 23 - 24/A - 24B - 25 - 26 - 27 - 28 - 29 - 30 - 31 - 32 - 33/A - 33/B - 33/C - 34 - 35 - 36 - 37 - 38 - 39 - 40 - 41 - 42 - 43 - 44 - 45/A - 45/B - 46 - 47 - 48 - 49 - 50 - 51 - 52 - 53 - 54/A - 54/B - 55 - 56 - 57 - 58 - 59 - 60 - 61 - 62
Tulosta tehtäväsivut ilman sivun ylä- ja alatunnisteita (dokumentin nimi, sivu, www-osoite ja päivämäärä), näin ne eivät ole mukana oppilaillekaan kopioimissasi arkeissa. Tunnisteet on poistettavissa selaimen valikosta Tiedosto - Sivun asetukset.
Mikäli sivut tulostuvat liian pienenä A4-sivulle, voit suurentaa sivujen kokoa kopioidessasi niitä kopiokoneella. Tarkoitus on, että sivut mahtuvat tulostettaessa yhdelle A4-sivulle. Ellei näin käy, voit kopioida sivuilla olevat GIF-kuvat itsellesi ja käsitellä niitä grafiikkaohjelmilla niin, että tulostus yhdelle A4-sivulle onnistuu. Kuvien kopioiminen tapahtuu osoittamalla kuvia hiirellä ja klikkaamalla hiiren oikeaa näppäintä. Tämän jälkeen valitaan Tallenna kuva... ja annetaan kuville nimet.
1-10 -- 11-20 -- 21-30 -- 31-40 -- 41-50 -- 51-60 -- 61-62
Tehtäväsivut 1/A ja 1/B: Kuvia voi käyttää valikointiharjoituksiin. Teiden alussa oleviin tienviittoihin sijoitetaan sopivat ominaisuuskortit, joiden perustella kuvia tai loogisia nappuloita erotellaan ryhmiin. Olemme piirtäneet valmiiksi joitakin ominaisuuskortteja, jotka voidaan leikata irti ja asettaa tienviittoihin. Lapset ja opettaja voivat myös piirtää lisää kortteja, jotka sopivat muidenkin asioiden kuin loogisten nappuloiden erotteluun. Oppilaat voivat itse värittää ne ominaisuuskortit, jotka kuvaavat värejä.
Kahden tien tapauksessa (sivu 1/A) erottelun perusteena voi olla: suuri-pieni, reiällinen-reiätön, sininen-punainen, vihreä-punainen, silmälasipäinen-silmälasiton, vaaleatukkainen-tummatukkainen, poika-tyttö..., kolmen tien tapauksessa (1/B) pitää omenasta-päärynästä-banaanista, henkilöauto-kuorma-auto-kilpa-auto..., yms.
Suosittelemme, että ennen tehtäväsivun käyttöä tienviittojen mukaista liikkumista harjoitellaan luokan edessä.
2. tehtäväsivu: Kortit leikataan aluksi irti toisistaan. Niillä voidaan sitten pelata
3. tehtäväsivu: Avoimia lauseita koskevat tehtävät on ensin tarkoitus ratkoa opettajan avustuksella; kun oppilaat osaavat lukea, he voivat ratkaista tehtäviä itsekin. Ennen tehtävien ratkaisua oppilaat saavat leikkiä keskenään suullisilla avoimilla lauseilla. Esim: Pöydällä on ... (pallo, kirja, avain, yms.) Avoimet lauseet voidaan täydentää 2. tehtäväsivusta leikattujen kuvien paikalleenasettamisella ja koko lauseen ääneen sanomisella.
4. tehtäväsivu: Sivun kuvat on tarkoitettu vertailujen harjoittelemiseen. Lapset voivat etsiä esimerkiksi suhteita vanhempi-nuorempi, pitempi-lyhyempi, laihempi-lihavampi, vaaleampi-tummempi (kuvia voidaan ensin värittää)...
Tehtäväksi voidaan antaa nuolen piirtäminen esim. aina kohti vanhempaa, nuorempaa, laihempaa jne. Jos nuolet piirretään erillisille paperinpaloille tai käytetään vaikkapa tulitikkuja, samaa tehtäväsivua voi käyttää monta kertaa.
Voimme myös esittää kuvista väitteitä, joista oppilaat saavat miettiä, ovatko ne tosia vai epätosia. Esim: Jokaisella on jokin raidallinen vaatekappale. Joukossa ei ole pikkuvauvaa. Pikkutyttö kohottaa vasenta kättään.
Oppilaat voivat keksiä tosia ja epätosia väitteitä myös itsestään ja toisistaan.
5. tehtäväsivu: Sivulle piirrettyjen viivojen pituuksia voidaan vertailla vain jonkin mittavälineen (narun, langan, väritangon) avulla. Tehtävän voi hyvin teettää monessa pienessä osassa, sillä vertailuja voi tehdä paljon. Jos lapset värittävät ensin kuvan opettajan ohjeen mukaan, on helpompi puhua eri viivoista. Vertaillessa voidaan vastata seuraavanlaisiin kysymyksiin:
Ennen tehtäväsivun käyttöä on hyvä tehdä yhdessä kokovertailuja. Opettaja voi esim. pyytää kaksi oppilasta luokan eteen. Sitten katsotaan, kumpi on pitempi. Lyhyempi oppilas osoittakoon pitempää. Saman voi tehdä kolmen oppilaan kanssa. Oppilaat voivat myös pitää käsissään paperisia nuolia tai kiinnittää sellaisen sinitarralla sormeensa. Esineitä voi vertailla samaan tapaan: kumpi tuoli on kapeampi, kumpi leveämpi, jne.
Muita vertailtaviksi sopivia esineitä ovat lelut, kirjat, kodinkoneet, huonekalut. Lapset voivat mittailla esineitä kotona narulla ja sitten vertailla koulussa narujen pituuksia. Myös erilaisten astioiden (tölkkien, lusikoiden, kuppien, mukien...) vetoisuuksia on hyvä harjoitella vertailemaan.
6. tehtäväsivu: Käsitteiden niin ja niin paljon enemmän kuin ja yhtä paljon kuin esitteleminen pitäisi aloittaa tekemisellä (kasojen, palikkatornien rakentamisella), äänillä, liikkeillä, sitten jatkaa piirtämällä. Neljään osaan taitetun tyhjän arkin yhteen osaan voidaan vaikkapa piirtää 6 lehteä, sen viereen tätä vähemmän hedelmiä, alapuolelle yhtä monta vihannesta, viimeiseen osaan edellistä vähemmän leivoksia. Sitten voidaan antaa lapsille tehtäväksi 6. arkin ensimmäinen harjoitus. Opettaja voi tarpeen mukaan piirtää samanlaisia tehtäviä lisää.
Vertailumerkkien < ja > käytön johdatuksena lapset voivat itse esittää kettutarinan. Pyydetään luokan eteen 3 oppilasta hanhiksi, 7 oppilasta kanoiksi. Yksi oppilas saa olla kettu ja nosta kätensä suunsa eteen isoksi kidaksi. Ketulta kysytään, kummalta puolelta hänen kannattaa saalistaa ja miksi. Hän tietysti valitsee kanat, koska niitä on enemmän. Tämä mielikuva auttaa oppilaita varmasti muistamaan, mitä vertailumerkki tarkoittaa.
Sitten itse kukin oppilas voi esittää tarinan omalla pulpetillaan. Jotkin hedelmät tai pähkinät voivat olla kanoja, jokin muu hanhia. Ketun kidan voi tehdä vaikkapa tulitikuista. Tämän jälkeen käydään pohtimaan 6. tehtäväsivun tehtävää 2.
7. tehtäväsivu: Tehtäväsivu harjoittaa nuolten käyttöä, joka esiteltiin jo 4. tehtäväarkissa.
8. tehtäväsivu: Tässä lapset valikoivat jo lukumääriä merkkien mukaan. Tehtävää tarkistettaessa voidaan huomata, että oikeita ratkaisuja on useita.
Tehtäväsivut 9. ja 10: Sivuissa harjoitellaan lukumäärien vertailua käyttämällä jotakin apuvälinettä. On tärkeää, että aluksi tehdään todella konkreettista pareiksi yhdistelemistä, esim. haarukka-lusikka, lautasliina-lautanen tms.
9. sivun tehtävässä 1 viivan piirtäminen merkitsee pariksi yhdistämistä.
Muissa tehtävissä yhdistetään viivalla pareiksi täpliä ja kuvioita.
11. tehtäväsivu: Tällä sivulla harjoitellaan lukumäärien ilmaisemista erilaisten symbolien avulla.
Käsien pystyssä olevat sormet vastaavat jotain lukua. Lasten täytyy etsiä käsien alla olevista joukoista ne, joissa on sormien osoittama määrä alkioita, ja ympyröidä nämä joukot. Kannattaa edelleen etsiä muualta luokasta viiden, seitsemän ja yhdeksän alkion joukkoja ja asettaa niihin, sekä asettaa kuvien päälle, vastaavat lukukortit.
Antakaa lapsille sarja lukukortteja, muutamasta numerosta useampi kuin yksi kappale. Jos kortteja ei ole valmiina saatavilla, niitä voi piirtää ja leikata itse. Lukukortteja voi käyttää useamman kerran. Numeroiden lisäksi kannattaa tehdä myös symbolit +, -, =, <, >.
Tehtäväsivut 12/A ja 12/B: Tämä tehtäväsivu on oikeastaan vain kokoelma värillisiä kiekkoja. Valmiit kiekot ovat toiselta puolelta punaisia, toiselta sinisiä tai vastaavasti keltaisia ja vihreitä.
Kiekkojen valmistustapa: Värittäkää ensin ympyröiden kehät, lapset värittävät kiekot loppuun mallin mukaan. Kun kaikki kiekot on väritetty, asettakaa kiekot värittömältä puoleltaan toinen toisiaan vasten, laittakaa kiekkojen väliin pala kartonkia tai muuta taipumatonta materiaalia. Liimatkaa kerrokset yhteen.
Alussa kiekkoja voi käyttää hyväksi lukumäärän havainnollistamisessa, aivan kuin nappeja tai tulitikkuja. Myöhemmin kiekoista voi tarkastella lukujen esityksiä summamuodossa. Esimerkki: Heitetään 7 kiekkoa ilmaan, pöydälle putoaa 3 punaista ja 4 sinistä kiekkoa eli matematiikan kielellä 3+4. Tai 2 punaista, 3 keltaista ja 1 vihreä eli matematiikan kielellä 2+3+1.
Kiekkoja voi käyttää hyväksi laskutoimitusten havainnollistamisessa myöhemmin. Otamme tämän puheeksi tuonnempana, laskutoimitusten opettamisen yhteydessä.
Edelleen kiekkoja voi käyttää kombinatoriikan tehtävien ratkaisuun sekä tietyn suuruisten pinta-alojen peittämiseen.
13. tehtäväsivu: Olemme vieläkin opettelemassa lukujen ja merkkien välistä yhteyttä, mutta tällä tehtävällä pohjustetaan jo lukujen esittämistä summamuodossa. Ennen kuin käydään käsiksi itse tehtäväsivuin, perehdytään hyvin johonkin lukuun. Taputetaan esim. neljä kertaa, ja sitten laitetaan esille yhtä monta kiekkoa, nappia, tulitikkua jne. Todetaan, että luku 4 kuuluu neljään kiekkoon, nappiin, tulitikkuun jne. Tämän jälkeen lapset voivat värittää oman mielen mukaan tehtäväarkilla olevat kortit. Sitten kerätään taululle "yhtä monet". Etsitään niihin kuuluvat luvut, ja kiinnitetään nekin taululle. Vahvistetaan sitä ajatusta, että yhtä moniin kuuluu sama luku, ja sitten luetaan matematiikan kielellä. Esimerkiksi koon perusteella voidaan ensimmäisestä kuvasta lukea muodot 3+1, 1+2+1, 1+3, 2+1+1. Oppilas voi lukea kuvasta muitakin ositettuja muotoja oman värityksensä perusteella.
14. tehtäväsivu: Kun lukujen ja merkkien yhteys on pohjustettu hyvin, lapset osaavat helposti ratkaista ensimmäisen tehtävän. Pohjustetaan toista tehtävää lyhyellä toiminnalla. Esitetään summamuotoja esineillä tai lapsilla ja vertaillaan, mitä on enemmän, mitä vähemmän. Merkitään vertailumerkkikin.
Tehtäväsivut 15/A ja 15/B: Sarjan nimi on värilliset kortit. Niitä voidaan käyttää koko oppivuoden ajan, vieläpä toisella luokallakin, erilaisissa matemaattisissa teemoissa. Lapset värittävät mustavalkoiset kuviot sarakkeittain ylle kirjoitetun värin mukaisesti. Värityksen lomassa on heillä mahdollisuus tutustua kortteihin perusteellisesti. Korteista voi tehdä kestävämpiä, jos ne liimataan pahville ennen irti leikkaamista.
Tehtäviä:
Etsitään yhteen kuuluvat. Etsitään värillisille korteille parit niihin kuuluvista lukukorteista (yhdestä tai useammasta). Jos lapsi näkee jossakin kuvassa sellaisen vaihtoehdon, jota ei ole kirjoitettu, annetaan hänelle tyhjä kortti, johon hän voi kirjoittaa näkemyksensä. Jos hän ei osaa vielä kirjoittaa lukuja helposti, voi hän sanella ehdotuksensa opettajalle, joka kirjoittaa sen korttiin.
Käytetään hyväksi, että meillä on summamuotojen kortteja. Ei vain lueta niitä matematiikan kielellä, vaan laitetaan myös esille kortteja vastaavia lukumääriä. Esimerkiksi lukukortissa on 6+1, jolloin lapsi laittaa esille kiekoista 6 punaista ja 1 sinisen. Voidaan tietenkin käyttää myös muun värisiä kiekkoja, tai laitetaan saman värisiä kiekkoja 6 ylös, 1 alas.
Pelejä:
16. tehtäväsivu: Ennen tehtävän ratkaisua voi pienen ryhmän lapsia pyytää luokan eteen. Lapset asettuvat erilaisiin muodostelmiin ja toiset miettivät, miten heidän lukumääränsä voitaisiin ilmaista summalausekkeena. Tämän jälkeen siirrytään paperilla oleviin tehtäviin.
Ratkaisu: Ensimmäisessä kuvassa on neljä lasta 2+2-muodostelmassa (2 ylhäällä, 2 alhaalla). Ei haittaa, vaikka joku tulkitsisi kuvan toisella tavalla, mutta muita tähän kuvaan sopivia lukukortteja ei ole. Seuraavaan kuvaan liittyy sekä kortti 5+3 että 1+2+5. Yksi lukukorteista (1+2+4) ei liity mihinkään kuvaan, pyytäkää lapsia piirtämään tähän korttiin sopiva kuva.
17. tehtäväsivu: Luonnollisesti ennen tehtäväsivun ratkaisemista pohjustetaan summamuotojen vertailua toiminnalla. Verrataan toisiinsa oppilasryhmiä, sisustuksessa käytettyjä esineitä. Käytetään omia välineitä hyväksi ja otetaan niitä esille, kerrotaan niistä matematiikan kielellä. Esitetään lukuja summamuodoissa. Asetetaan väliin pienempi kuin, suurempi kuin tai yhtä suuri kuin -merkki. On tärkeää, että tehdyt muodostelmat ovat paikkansa pitäviä vertailumerkkien kanssa.
Tällä tehtäväsivulla vertaillaan jo summamuotoja. 1. tehtävässä tämä tehdään kuvien avulla. Asiaa helpottaa se, että samantyyppisten lelujen määrät on merkitty yksinkertaisilla merkeillä (2 palloa on sama lukumäärä kuin 2 tyhjää ympyrää, 3 pikkuautoa on sama lukumäärä kuin 3 väritettyä ympyrää). Ne on merkitty myös luvuilla (2 + 3).
Luonnollisestikin tätä voidaan myös leikkiä jotenkin, taputuksin, askelin jne. Lasten tehtävänä on piirtää kuvien väliseen tyhjään neliöön pienempi, suurempi tai yhtä suuri kuin -merkki.
2. tehtävässä piirretään dominolaattaan täplät vertailumerkin mukaisesti. Viimeisen kahden laattaparin kohdalla voi syntyä monia ratkaisuja, kunhan oppilas vain huomioi vertailumerkin.
Tehtävän ratkaisemisen jälkeen luetaan matematiikan kielellä kaikki eri summalausekkeet dominoista.
Hyväksytään kaikki matemaattisesti oikeat ratkaisut, mutta kiinnitetään huomio siihen, että täpliä voidaan piirtää vain sillä lailla kuin dominotehtaassakin oikeisiin laattoihin: Esimerkiksi jos ensimmäisen dominoparin kohdalla vasemmanpuoleiseen tyhjään kenttään ei piirretä mitään, on ratkaisu silloinkin matemaattisesti oikein. Neljännen dominoparin kohdalla on 0 = 0 ratkaisukin oikea. 18 on täplien enimmäismäärä yhden dominon ala- ja yläkentissä yhteensä. 9:ää täplää enempää ei voi sisällyttää yhteen kenttään, ei edes vaikka se olisi matemaattisesti oikein.
Tehtäväsivut 18/A ja 18/B: Todellisuudessa tehtäväsivun harjoitukset pohjustavat 18/B-tehtäväsivun viimeistä harjoitusta, luvun summamuotojen tunnistamista myös mittaluvuilla. Aloitetaan teeman käsittely ensin konkreettisella harjoituksella. Lasten täytyy tuntea hyvin väritangot, niiden väliset suhteet, värien tarkat nimet, mittayksiköllä tapahtuva mittaaminen. Käydään käsiksi siihen tietoiseen työhön, jolla pohjustetaan yksikön käsitettä ja joka mahdollistaa yksikön vaihtamisen.
Mittaillaan tankoja valitulla yksiköllä: olkoon vaaleansininen yksi (vaaleansininen = 1). Monellako vaaleansinisellä tangolla mittasit tummansinisen? Mittasin tummansinisen kolmella vaaleansinisellä tangolla. Minkä niminen tulee tummansinisestä tangosta, jos vaaleansininen on 1? Tummansinisen tangon nimi on 3, jos vaaleansininen on yksi. Mittaa myös lila tanko vaaleansinisellä! Monellako vaaleansinisellä mittasit sen? Mikä on lilan tangon nimi, jos vaaleansininen on 1? Etsi, mikä tangoista on 4, jos vaaleansininen on 1! (Vihreä, koska se voidaan mitata neljällä vaaleansinisellä tangolla.) Toistetaan tätä harjoitusta useita kertoja niin, että valitaan aina eri tanko mittayksiköksi. Olkoon 1 vaaleanpunainen, valkoinen tai vaikka sitruunankeltainen. Pidempää tankoa ei kannata ottaa yksiköksi, koska mitattavia tankoja löytyy aina vähemmän, mutta suuremmalla yksiköllä voi mittailla myös pöydän leveyttä tai oppikirjan korkeutta. Tällöin sanotaan, että oppikirjan korkeus on 4 viininpunaista tankoa. Ei sallita lasten nimetä tankoja pelkästään luvuilla ilman määrättyä mittayksikköä. Opettajienkaan ei tule sanoa seuraavanlaisesti: ykköstanko, nelostanko tai nyt kakkostangosta tulee ykkönen. Ei yritetä yhdistää tiettyyn tankoon aina yhtä lukua pysyvästi, sillä myöhemmin oppilas ei mittaa, vaan nimeää tangot luvuilla muististaan. Kun mittayksikön vaihtamisen ideasta tulee luonnollinen, voidaan tankoja käyttää edelleen myöhempinä vuosina, 3.-4. luokalla, myös kertolaskun, lukualueen laajentamisen tai murtoluvun käsitteen muodostamisessa. Esim. olkoon vaaleanpunainen tanko 100. Mikä tangoista on 400, 1000 jne.? Tai olkoon lila 1. Mikä tangoista on puolikas, kolmasosa, kuudesosa, kaksi kolmasosaa jne.?18/A-tehtäväsivu, tehtävä 1: Aseta sopivat tangot mallipiirrokselle. Kuvasta nähdään, että viininpunaisen tangon voi muodostaa 4:llä vaaleanpunaisella. Tämän vuoksi on viininpunaisen tangon nimi 4. Toistetaan sama muiden kuvien kohdalla ensin sanoin ja sitten värittämällä kuvat tankojen mukaan. Näin varmennetaan vielä, mikä tangoista oli sopiva, montako kertaa väritettiin vaaleanpunaisella, minkä värinen tanko oli yhtä pitkä kuin vaaleanpunaisilla täytetty alue. Varmennukseksi piirretään yhtä monta täplää kuin monellako vaaleanpunaisella tangolla mitattiin pidempi tanko.
18/A, tehtävä 2: Lähes sama kuin edellinen tehtävä, mutta oppilaat saavat työskennellä itsenäisemmin. Heidän on etsittävä mittayksikkö itse, nimettävä mitattu tanko sekä kirjoitettava sama luvuin tankojen viivoille.
18/B, tehtävä 1: Tehtävä on helppo. Opettaja pyytää oppilaita värittämään tyhjät kentät niiden tankojen värisiksi jotka hän haluaa mittauttaa. Merkitään ne myös luvuin. Sitten etsitään lukuihin sopivan väriset tangot. Esimerkiksi: Mittaa sitruunankeltainen tanko! Sen nimi on 5. Mittaa musta tanko! Sen nimi on 7. Kolmen mittaisen tangon väri on vaaleansininen, kuuden mittaisen lila. Väritetään tyhjät kentät näillä väreillä. Kun kahteen ylempään kenttään voi värittää mitä vain, voi sitä vastoin alemmissa kentissä olla ratkaisuna vain vaaleansininen ja lila, sillä jos valkoinen on 1, voi 3 olla ainoastaan vaaleansinisen tangon nimi.
18/B, tehtävä 2: Tehtävässä tutustutaan tulevaisuudessa hyvin paljon esiintyvään toimintaan. Voimme nimittää sitä peitteen (tai maton) tekemiseksi. Tämä on välttämättömän tärkeä harjoitustyyppi ositettumuotoisten lukujen opetuksessa, sillä se muokkaa ja vahvistaa lukukäsitettä mittaluvun ominaisuudessa. Kun 17. harjoitusarkissa ajateltiin lukuja kappalelukuina (2 palloa ja 3 autoa on 5 lelua), niin tässä voikin lilan tangon mitata 1 valkoisella, 1 vaaleanpunaisella ja 1 vaaleansinisellä tangolla, tai 1 vaaleanpunaisella ja 1 punaisella, tai jollakin toisella lailla. Ensin selvitetään leveys mallipiirroksesta. Nyt valmistetaan lilan tangon levyinen peite. Jokaisen rivin tulee olla yhtä leveä kuin lila tanko. Laitetaankin sopivat tangot piirroksen päälle. Värittäminen ei ole nyt tärkeää - on parempi, jos oppilas asettelee tankoja. Painopiste on matematiikan kielellä lukemisessa. Jos oppilas onnistuu nyt asettelussa, pystyy hän tuota pikaa tekemään peitteen ilman mallipiirrostakin ja kertomaan siitä matematiikan kielellä. Kiinnitetään oppilaan huomio siihen, että nyt valkoinen tanko on 1. Vaaditaan oppilasta kertomaan kuvasta ensin selkeällä pitkällä lauseella ja vasta sitten matematiikan kielellä. Malli löytyy tehtäväsivusta.
19. tehtäväsivu: Seuraavaa tehtävätyyppiä on hyvä harjoitella usein lukukauden aikana. Tässä on taulukko, joka soveltuu erilaisten kysymys - vastaus -pelien, sääntöpelien tai konepelien piirtämiseen. Idea on, että oppilas näkee esillepanot taulukkoon järjestettynä. Leikataan alla olevat kortit irti ja laitetaan ne kirjekuoreen, jotta niitä voidaan käyttää toistekin. Opettaja voi myös suunnitella toisenlaisia korttipareja. Ilmaisemme säännön panemalla kortteja taulukon yläreunassa olevaan kehykseen.
Mikä onkaan kysymys - vastaus -peli? Siinä etsitään yhteenkuuluvuuksia esineiden ja lukujen kesken. Tällä pohjustetaan funktiopelejä. Ensin harjoitellaan vain toiminnalla. Esimerkki: Oppilas taputtaa kolme kertaa, koska opettaja pyytää häntä taputtamaan jonkin verran. Opettaja koputtaa yhtä monta kertaa. Oppilaan taputtaessa 5 kertaa opettaja koputtaa 5 kertaa, 6 taputuksen jälkeen 6 kertaa. Sitten vaihdetaan osia. Opettaja taputtaa ja oppilas koputtaa. Oppilaan tulee arvata sääntö. Muutama idea leikkeihin: kyykätään x kertaa, taputetaan kahta enemmän. Laitetaan esille x tulitikkua, viereen pannaan 3 tikkua vähemmän. Värillisillä korteillakin voi pelata, kuten myös millä tahansa loogisella sarjalla. Otetaan esille esimerkiksi samanlainen looginen nappula, mutta reiällisenä. Tai valitaan aina vain keltainen vastaukseksi kaikista nappuloista.
Käytetään myöhemmin tähän tarkoitukseen tehtäväsivun taulukkoa. Nyt laitetaan kysymys- ja vastaussanoja taulukon yläreunassa olevaan kehykseen. Kysymys on esimerkiksi 3 nappia, vastaus yksi enemmän. Kysymys on 8 nappia, vastaus 9 nappia. Kysymys on 5 nappia, vastaus 6 nappia. Mitä voi kysyä, jos vastaus on 10 nappia?
Voidaan kysyä myös väritangoilla. Vihreä, punainen, vaaleanpunainen, vaaleansininen. Vastaus on vihreä. Yhdestä tapauksesta ei vielä voi päätellä sääntöä, mutta arvailla voi jo. Seuraava kysymys: keltainen, valkoinen, lila, musta. Vastaus: keltainen, lila ja musta. Voidaan otaksua, että vastauksen tulee olla pidempi kuin punainen tanko. Mutta edes kaksi esimerkkiä ei ole tarpeeksi. Autetaan säännön arvaamista esittämällä useita kysymyksiä ja vastauksia. Kun oppilas tietää jo säännön, voi hänkin esittää kysymyksiä ja vastauksia. Voi olla myös kysymyksiä, joihin ei ole vastausta. Esimerkki: kysytään vain sellaisilla tangoilla, jotka ovat lyhyempiä kuin punainen tanko.
Konepelit ovat periaatteeltaan samanlaisia kuin kysymys - vastaus -pelit, mutta näissä pelataan automaattikoneella, joka on "ohjelmoitu" tietyn säännön mukaan. Kysytään lapsilta, mitä kone tekee. "Mitä kone tekee?" -kysymys suuntaa huomion sääntöön. Kannattaa valmistaa laatikosta sellainen pelikone, jossa on ylhäällä ja alhaalla SISÄÄN ja ULOS -aukot. Laitetaan sisään reiätön looginen nappula, jolloin ulos tulee muuten samanlainen, mutta reiällinen nappula. Oppilas pystyy konkreettisesti määrittelemään, että kone rei'itti nappulan. Tai kone haukkasi palan sisään laitetusta keksistä. Tai se antoi yhdellä markalla yhden suklaapalan, kahdella markalla kaksi jne. Eli kone antaa aina yhtä monta suklaapalaa kuin sisään laitettujen markkojen määrä.
Voidaan myös valita jo leikityistä kysymys - vastaus -peleistä jokin ja toteuttaa se uudestaan koneella. Käytetään taulukkoa siihen, että oppilas voi laittaa esille asiat, jotka pantiin Sisään koneeseen ja jotka tulivat sieltä Ulos.
Korttien joukossa on vielä kolmion, puoliympyrän ja nelikulmion merkit, mutta niitä käytetään vasta myöhemmin ilmaisemaan käsitettä "jonkin verran". Mainittakoon tässä, että myöhemmin pelataan myös lukukorteilla tai lukumäärillä. Esimerkki: Laitetaan koneeseen viisi, ulos tulee 7. Laitetaan sisään 3, ulos tulee 5. Laitetaan sisään 8, ulos tulee 10. Sääntö: kone antaa ulos aina kahta suuremman luvun. Sisään laitetaan kaksi vähemmän kuin mitä tulee ulos.
Lukuihin 5-10 tutustumista varten ei tehdä erikseen tehtäväsivuja, koska tähän on jo annettu mallit lukujen 1-4 kohdalla. Muistin virkistämiseksi: leikit, esillepanot, piirrokset, kuvasta kertominen, luetteloiden tekeminen auttaa tutustumaan lukuihin lähemmin ja perusteellisesti sekä muodostamaan lukukäsitystä.
20. tehtäväsivu:
Tehtäväsivut 21/A ja 21/B ovat irti leikattavia pelikortteja.
Tehtäväsivu 21/C on itse piirrettäviä pelikortteja.
22. tehtäväsivu: Jokaisen luvun (5-10) kohdalla tulee käsitellä erikseen lukujen osittamista kahteen osaan. Tärkeintä on usein toistuva esillepano, taittelu. Esillepano: kutakin lukua käsiteltäessä otetaan esiin vastaava määrä lasten värittämiä kaksivärisiä kiekkoja. Asetetaan kiekot toistensa viereen punainen puoli ylöspäin. Konkreettinen kysymys kuuluu: Kuinka monta sinistä ja punaista kiekkoa oppilas näkee edessään? Vastaus: hänen edessään on 0 sinistä ja 5 punaista kiekkoa. Sanotaan sama myös matematiikan kielellä: 0 + 5. Tämän jälkeen käännetään ensimmäinen kiekko toisin päin. Kysytään jälleen sama kysymys. Nyt nähdään 1 sininen ja 4 punaista kiekkoa, matematiikan kielellä 1 + 4. Toistetaan sama kiekkorivin loppuun asti. Viimeinen näkymä on 5 + 0. Kiekonkääntöpeli voidaan aloittaa alusta siten, että nyt 0 punaista ja 5 sinistä näkyy ensin. Ahkera harjoittelu voi auttaa ositettujen muotojen muistamisessa. Usean harjoittelukerran jälkeen voidaan pyytää oppilaita sanomaan esillepanot myös suljetuin silmin muististaan. Tämän jälkeen voidaan alkaa värittää ja kirjoittaa muistiin. Tätä voi harjoitella millä tahansa luvulla harjoitusarkilla olevan mallin mukaisesti. 2. tehtävässä oppilas näkee toisenlaisia kuvioita. Nämä muistuttavat häntä taiteltavasta paperista.
Taiteltava paperi: Taiteltava paperi voidaan valmistaa leikkaamalla paperiarkista suikale ja jakamalla se kuuteen yhtä suureen osaan. (Tämä on piirretty tehtäväarkille pienennettynä.) Jotta papereiden taittelu sujuisi oppilaalta helpommin, "teroitetaan" taittoreunoja molemmin puolin useita kertoja ennen niiden käyttöönottoa. Harjoituksen kulku: oppilas sanoo ensin, mitä näkee edessään. 0 + 6. Tämän jälkeen hän taittaa paperista yhden osan taakse ja kertoo: 1 takana ja 5 edessä, eli matematiikan kielellä 1 + 5. Ja niin edelleen. Harjoitellaan tätäkin useita kertoja, jotta se painuisi oppilaan mieleen. Nytkin huolehditaan siitä, että tehtäväsivun värittäminen ja matematiikan kielellä muistiin merkitseminen tehdään vasta konkreettisen harjoittelun jälkeen!
Kunkin luvun harjoittelemiseen käytetään useampi oppitunti. Ei missään tapauksessa yritetä tutustua perusteellisesti sekä viitoseen että kuutoseen yhden oppitunnin aikana, eli tätä tehtäväsivua ei ratkaista kokonaan yhdellä tunnilla. Opettaja voi tehdä monisteita lukuihin tutustumista varten, tai oppilaat voivat työskennellä vihkoihin. Mallia voi ottaa edellisistä ja tästä harjoitusarkista.
Tehtäväsivut 23-24/A-B pohjustavat lukusuoran käsitettä ja auttavat järjestyslukujen tunnistamisessa sekä käsitteiden "pari" ja "kappale" erottamisessa.
23. tehtäväsivu, tehtävä 2: Oppilaalle annetaan harjoituksessa ohje "väritä". Opettajan täytyy sanoa, monesko pikkuauto, lapsi tai helmi väritetään. Luonnollisesti tätäkin harjoitellaan ensin leikkimällä, esille panemalla. Esim. pyydetään rivin toista tyttöä astumaan esiin. Pyydetään rivin viidettä oppilasta ottamaan korvistaan kiinni. Kuka seisoo ensimmäisenä? Kuka viimeisenä? Monesko hän on? Asetetaan lapset ongelman eteen. Esim. kuka on keskimmäinen? (Keskimmäinen löydetään vain, jos oppilaita on pariton määrä.) Tai kerrotaan rivistä käänteisessä järjestyksessä. Pyydetään lapsia seisomaan myös peräkkäin, ei pelkästään rinnakkain.
23. tehtäväsivu, tehtävä 3: Harjoituksen tarkoituksena on, että lapset oppisivat erottamaan käsitteet montako ja monesko. Helmiä on 7 kappaletta, joista kolmas (3.) on tumma. Legojen kohdalla täytyy sopia myöskin se, lasketaanko alhaalta ylös vai ylhäältä alaspäin.
24/A tehtäväsivu: Askelmatehtävien ratkaisemista pohjustetaan askeltamalla oikeasti tikkailla. Ensin oppilaat voivat kiivetä tikkaille, ja sitten he pysähtyvät opettajan ohjeiden mukaisesti toiselle, neljännelle askelmalle jne. Pyydetään oppilaita kertomaan, monennelleko askelmalle he seisahtuivat. Luetellaan askelmat myös yksitellen: ensimmäinen, toinen, kolmas jne. Takaisin päin astellen voidaan päästä nollaan. Kysytään ensimmäisen askelman jälkeen, mikä sitten seuraa. Vahvistukseksi laitetaan seisovien tikkaiden eteen paperi, jolle oppilas astuu. Pysäytetään oppilas ja piirretään paperille ympyrä hänen jalkojensa ympäri. Paperilta voidaan lukea luku nolla. Laitetaan tikkaat makaamaan. Leikitään niillä näinkin, ja kerrotaan samaan tapaan. Merkitään askelmat lapuin. Selvitetään, miksi kutakin askelmaa nimitetään. Kolmannesta askelmasta tulee kolmonen, toisesta kakkonen, ensimmäisestä ykkönen, ja lopuksi tulee nolla. Ratkaistaan tehtäväsivun harjoitukset vasta konkreettisen harjoittelun jälkeen. 24/A-tehtäväsivu, tehtävässä 1 a) ensimmäinen kuva on illustraatio. Analysoidaan kuvaa puhumalla siitä. Sen jälkeen täydennetään toiseen kuvaan puuttuvat luvut.
b)-tehtävä on samantyyppinen kuin a), mutta oppilas voi työskennellä itsenäisemmin. Lasten on huomattava, että vaikka makaavien tikkaiden viidennellä askelmalla ei ole ruutua järjestysluvulle, on viides askelma silti olemassa. Ratkaisu on siis: 0, 3, 6, 7.
24/B tehtäväsivu, tehtävä 1: Lukusuoraa voi harjoitella myös talorivistön avulla. Puu kuvaa nollan paikkaa, mutta ei puhuta siitä. Lasten tulee täydentää puuttuvat talojen numerot.
24/B tehtäväsivu, tehtävä 2: sammakko, jänis ja etana lähtevät liikkeelle puun luota. Lasten tulee keksiä se, että START:iin täytyy kirjoittaa 0. Tehtävää käsiteltäessä keskustellaan samalla yksiköiden suuruuksista. Jäniksen loikka on pidempi kuin sammakon jne.
Annetaan lapsille tehtäväksi valmistaa lukusuora. Siihen voidaan käyttää yhtä pitkiä juomapillin pätkiä tai tulitikkuja. He voivat tehdä lankaan solmuja yhtä pitkin välimatkoin tai yhdistellä ketjuja hakaneuloista ja paperiliittimistä. Varmistetaan aina 0:n paikka.
Aina lukusuoraa piirrettäessä piirretään myös nollaa edeltävä sekä viimeisen merkityn luvun jälkeinen osa. Näin tehdään myöskin, vaikka ei käytettäisi tai nimettäisi siellä olevia lukuja. Ei herätetä lapsessa luuloa, ettei nollaa ennen olisi lukuja.
25. tehtäväsivu: Tähän asti ollaan käsitelty lukujen summamuotoja. Nyt tutustutaan lukujen erotusmuotoihin. Lähdetään liikkeelle tavan mukaan konkreettisella tekemisellä. Analysoidaan näkymää, ei opeteta yhtälöä. Erotusmuodot voidaan havainnollistaa parhaiten puutteella, vajauksella. Näytetään kolmihaaraista kynttilänjalkaa, jossa on kaksi kynttilää. Kuuden kananmunan pakkauksesta puuttuu 3 munaa. Kuuden värikynän laatikossa on kaksi tyhjää paikkaa. Neljän hengen pöydässä istuu kaksi henkilöä. Lapsi kertokoon näkymästä, kuvasta. Esimerkki konkreettisesta kertomisesta: Minulle tulee mieleen näistä kahdesta kynttilästä se, että kolmesta puuttuu yksi. Matematiikan kielellä: 3-1. Mitä sinulle tulee mieleen näistä kolmesta kananmunasta? Kuudesta munasta puuttuu kolme. 6-3. tehtäväsivun tehtävässä 1 on värikynien lukumäärä 6-1. Vesivärejä on 6-3, tarroja 8-3, hyllyllä on 6-2 hillopurkkia, kynttilöiden määrä on 4-1. Lukukorttiin 8-5 ei voi yhdistää mitään. Tästä voi oppilas vaikkapa piirtää kuvan vihkoonsa.
Tehtävä 2: Oppilaiden tulee itsenäisesti kirjoittaa näkymä luvuilla.
26. tehtäväsivu: Sekä summa- että erotusmuoto esiintyvät samassa tehtävässä sekä myös lukusuoralla. Lukusuorien kohdalla luetaan ensin ositetut muodot. Tämän jälkeen tutustutaan niihin liittyviin piirroksiin. Sitten yhdistetään ne oikeisiin kohtiin lukusuoralla. On tärkeää, että lapset huomaavat, kuinka yhteen lukuun voi liittyä myös useampia summa- ja erotusmuotoja. Erotusmuodon kohdalla merkittiin vajaus nyt vetämällä viiva yli. Runsaan konkreettisen tekemisen jälkeen lapset ymmärtävät tämän asian hyvin, ja heille voi antaa sellaisenkin tehtävän, jossa tietylle luvulle pitää kerätä useita summa- ja erotusmuotoja.
27. tehtäväsivu: Yhteen- ja vähennyslaskun laskutoimitus esiintyy ensimmäisen kerran tehtäväsivulla. Tähän mennessä oppilaat ovat tutustuneet lukujen moniin nimiin, summa- ja erotusmuotoihin. Laskutoimitus on eri asia kuin lukujen summa- ja erotusmuoto. Laskutoimitukset merkitsevät jonkinlaista tapahtumaa, jonka voi leikkiä, panna esille, kuvitella.
Yhteen- ja vähennyslaskun laskutoimitusta käsitellään 1. luokalla kolmella tavalla (lisääminen-vähentäminen, joukkojen yhdistäminen-osajoukkojen ilmaiseminen, vertailu). Aloitetaan helpoimmasta. Tämä on lisääminen, vähentäminen. Annetaan lasten aloittaa tehtäväarkilla olevien tehtävien ratkaiseminen vasta konkreettisen tekemisen jälkeen. Esimerkiksi taulun edessä on 4 oppilasta. Pyydetään sinne vielä 3 lisää. Taulun edessä seisoo jo 7 oppilasta (4 + 3 = 7). Lähetetään 3 oppilasta takaisin paikoilleen (7 - 3 = 4). Kerrotaan tapahtumat ensin sanoilla ja sitten matematiikan kielellä. Muistiin merkitseminen tapahtuu myöhemmin.
28. tehtäväsivu: 1. tehtävä on vaikea siksi, että nuoli tarkoittaa + 3:a, mutta kuitenkin 8:sta pitää ottaa pois 3. Lapsi osaa laskea helpommin täydentämällä: __ + 3 = 8.
2. tehtävässä voidaan sanoa myös "kääntäen" kuvista ilmenevä tapahtuma.
3. tehtävä: Ei piirretä heti! Keksitään ensin samaan lukutehtävään toinen tarina. Tehtävä on siksi vaikea, että nyt haetaan konkreettista esimerkkiä abstraktista asiasta. On hyvä, jos oppilaat tekevät paljon tällaisia tehtäviä paperille tai vihkoon.
29. tehtäväsivu: Tämän sivun käsittelemisen voi aloittaa, kun on harjoiteltu paljon konkreettisesti, leikitty, pantu esille ja piirretty. Tässä on jo piirrettynä vain toinen kuva, lasten täytyy itse keksiä tarina. On edelleen hyvin tärkeää, että pyydetään lapsia kertomaan tarinat.
Oppilaiden on helpompi keksiä tarinoita, jos autamme heitä keräämällä sanoja. "Ynnä"-merkkiin, plussaan, voi liittää sellaisia ilmaisuja kuin lensi sinne, ompeli siihen, sai, osti, kiinnitti vielä, laittoi sinne, tuli jne. "Pois"-merkkiä, miinusta, voivat kuvata sellaiset ilmaisut kuin lensi pois, juoksi pois, antoi, myi, sammutti, otti siitä pois, söi, puhkesi, rikkoi.
Tällä arkilla lapsi jo tunnistaa aikaisemmin erotuslauseketta (esimerkiksi: takin napit) tai summalauseketta (5 + 3 ilmapalloa) havainnollistaneet kuvat, mutta hän ei enää muodosta "valmiista" kuvasta lukua, vaan hän muodostaa tarinan kuvan syntymisestä. Jos vähentämistä ei voi havainnollistaa omenan siemenkodilla tai langanpätkillä, merkitään sitä ylivetämisellä.
Annetaan lapsille sanallisia tehtäviä. Pyydetään niiden täydennykseksi esille panoja tai piirroksia. Esimerkiksi: Minulla oli 9 markkaa. Tuhlasin 3 markkaa suklaaseen, 2 tarroihin. Monellako markalla voisin vielä tehdä ostoksia? Ei käytetä vielä sulkuja. 2:n ja 3:n voi vähentää joko erikseen tai yhdessä (9 - 3 - 2 tai 9 - 5), mutta tehtävän voi ratkaista myös kahdessa osassa: 9 - 3 = 6, 6 - 2 = 4. Esille pano tai piirros johdattaa oppilaan helposti tehtävän ratkaisuun.
1 1 1 1 1 1 1 1 1
Yhteen- ja vähennyslaskun toinen käsittelytapa on huomattavasti vaikeampi kuin ensimmäinen. Nyt asiaa lähestytään joukkojen yhdistämisen ja osajoukkojen erottamisen näkökulmasta. Nyt voi nähdä, kuinka vuoden alussa tehdyistä ryhmittelyistä on hyötyä.
Nytkin voidaan puhua tarinoista, vieläpä siten, että esitetään tarina, kuinka jokin tähän asti summa- tai erotuslausekkeena nähty kuva muodostuu. Esimerkiksi: Laitoin koriin 3 päärynää ja 2 omenaa. Montako hedelmää korissa on?
Matemaattisesti tapahtuu niin, että yhdistetään päärynöiden 3-alkioinen joukko ja omenien 2-alkioinen joukko. Vaihtamalla päärynöiden ja omenoiden järjestys voidaan havainnollistaa yhteenlaskun vaihdannaisuutta. Jos kysyttäisiin, montako päärynää on 5:stä hedelmästä, niin silloin hedelmien joukosta täytyy poistaa omenien osajoukko, jotta päärynöiden osajoukko jäisi jäljelle. Jos taas täytyy ilmaista omenien määrä, niin silloin vähennetään se osajoukko, joka ei ole omenien.
Ei puhuta oppilaille joukoista, osajoukoista. Nimetään asiat niiden omien nimien mukaan. Käytetään ryhmäkäsitteitä: omenat, päärynät - hedelmät, tulppaani, päivänkakkara - kukat, pojat, tytöt - lapset. Nämä sijoitetaan viivalla ympäröinnin sijasta hedelmämaljaan, puutarhaan, luokkaan, hyllyyn tai huoneeseen.
Ennen tehtävien ratkaisemista voidaan tehdä seuraavanlaisia asioita: pyydän eteen yhdellä kertaa 2 poikaa ja 3 tyttöä. Kutsuin heidät synttäreilleni. Montako lasta kutsuin? 2 + 3 = 5. Kutsuin 5 lasta. Menen seisomaan poikien eteen ja peitän heidät käsilläni ja vartalollani. Kysyn, montako tyttöä tässä on kaikista lapsista. Sanotaan, että 3. Matematiikan kielellä 5 - 2 = 3. Tässä on 3 tyttöä. Tehdään sama toisin päin. 5 - 3 = 2, poikien määrä on 2.
Lapsetkin voivat tehdä vähennyksiä parilla kolmella luonnontuotteella (pavuilla, maissinjyvillä). Peitetään kämmenellä, läpinäkyvällä astialla tai laatikolla "pois ottaen" se osa, joka pitää vähentää kaikista, jotta voidaan ilmaista haluttu osa.
30. tehtäväsivu: Esineitä on yhteensä 7, ja ne muodostuvat 4 napista ja 3 helmestä. Kaikki voidaan siis kirjoittaa muistiin laskutoimituksella 4 + 3 = 7 tai 3 + 4 = 7. Leikataan irti 33/C-tehtäväsivulla oleva käsi. Tällä voidaan peittää napit, jos halutaan puhua helmistä, ja toisin päin. Lapset voivat peittää kuvia myös omilla kämmenillään. Läpinäkyvällä kalvolla peittäminen auttaa heikompia oppilaita, koska näin he näkevät, paljonko pitää ottaa pois. Tällä harjoitussivulla on ainoana tehtävänä pelkästään tekeminen. Muistiin merkitseminen on malli lapselle, opettajalle ja vanhemmalle.
31. tehtäväsivu, tehtävä 1: Pujotetaan ketjuun tummia ja vaaleita helmiä. Tehtävän ratkaisemista helpottaa se, että summa, tehtävässä kysytty luku, on kirjoitettu laskutoimituksen alkuun.
2. tehtävä: Luonnollisestikaan ei yhdistellä aina vain kahdenlaisia asioita. Tällä vadillakin on useammanlaisia hedelmiä. Kaikki yhteensä (2 omenaa, 3 luumua, 1 sitruuna) voidaan ilmaista 2 + 1 + 3 = 6, 1 + 2 + 3 = 6, 2 + 3 + 1 = 6 jne., mutta voi olla, että summaksi tulee niiden makujen perusteella 1 hapan ja 5 makeaa, 1 + 5 tai 5 + 1. Etsitään useita eri merkitsemisvaihtoehtoja.
Kukatkin voi merkitä monella tapaa: tulppaanit - orvokit 4 + 2 = 6, 2 + 4 = 6. Lehdelliset - lehdettömät 3 + 3 = 6, mutta myös riveittäin voi lukea: 3 + 2 + 1 = 6.
Osista kannattaa kirjoittaa siten, että aina rivin alkuun merkitään, mistä halutaan kirjoittaa. Esimerkiksi: (tummat) 6 - 5 = 1 (vaaleat) 6 - 1 = 5.
Lasta täytyy auttaa alinomaa tämäntyyppisten tehtävien ratkaisemisessa. Vain hyvin harvat oppilaat pystyvät heti itsenäiseen työskentelyyn. Näytetään malliksi peittämistä tai piilottamista. Myös kirjalliset harjoitukset tehdään opettajan opastuksella. Aina on oppilaita, jotka tulevat ymmärtämään tämän laskutoimitusten käsittelytavan vasta myöhemmin.
32. tehtäväsivu, tehtävä 1: Ennen tehtävän tekemistä harjoitellaan leikkimällä. Leikitään väritangoilla. Muodostetaan jokin tangoista kahdella muulla tangolla, mutta näytetään lapsille vain toinen näistä. Lasten tulee keksiä puuttuvan tangon väri. Lapset voivat harjoitella myös pareittain. Harjoitusarkilla merkitään leikki muistiin myös täydentämällä ja vähentämällä. 10 = 6 + 4, 4 = 10 - 6.
2. tehtävä: Tehtävät vaativat lapsilta jo opittujen asioiden soveltamista. Esille paneminen, piirtäminen on välttämätöntä. Nyt voidaan nähdä, kuka ratkaisee tehtävän itsenäisesti, kuka tarvitsee vielä apua. 9 - 6 = 3 sekä 6 + 3 = 9 ovat yhtä lailla oikeita ratkaisuja. Totutetaan lapset siihen, että he kirjoittavat tehtävän ratkaisuna olevan luvun värikynällä. (Kysymykseen vastaavan luvun.)
b)-tehtävässä voi odottaa seuraavanlaisia ratkaisuja: 2 + 3 + 3 = 8, 8 - 2 - 3 = 3, 8 - 2 = 6, 6 - 3 = 3.
33/A tehtäväsivun kortit on tehty ennen kaikkea tätä laskutoimituksen käsittelyä varten. Leikataan kuvat irti. Asian ymmärtämistä helpottaa se, jos tarinat ilmaistaan aluksi kahdella kuvalla. Tämä kuvastaa hyvin sitä, kuinka tarinan tapahtumat tulevat ajallisesti toistensa jälkeen. 33/A-tehtäväsivun kuvien kaveriksi voidaan valmistaa paperista nuoli, jonka voi laittaa kahden kuvan väliin. Nuoli havainnollistaa muutosta. Esimerkiksi: minulla oli 4 pikkuautoa, joista annoin yhden kaverilleni. Nyt minulla on 3 autoa, 4 - 1 = 3. Se, että kuvien toisin päin vaihtamisella tai nuolen kääntämisellä voi muuttaa myös laskutoimituksen suunnan, havainnollistaa hyvin yhteen- ja vähennyslaskun suhdetta. Näin ensimmäinen esimerkki muuttuu seuraavanlaiseksi: minulla on 3 pikkuautoa. Sain lahjaksi yhden lisää. Nyt minulla on jo 4 pikkuautoa, 3 + 1 = 4.
Myös 27. tehtäväsivun 2. tehtävään voidaan käyttää 33/A-tehtäväsivun irti leikattuja kuvia.
Pidetään huolta siitä, että lapset vastaavat aina "tarinoissa" esiin tuleviin kysymyksiin. Tällä voidaan hyvin pohjustaa sanallisten tehtävien ratkaisemista.
33/B tehtäväsivu: tämä on tarkoitettu yhteen- ja vähennyslaskun suhteen syventämiseksi. Sivua voi käyttää useaan otteeseen lukuvuoden aikana, koska todellisen laskutoimituksen tekemisen lisäksi sillä voi vahvistaa myös lukukäsitettä, kun harjoitellaan sen avulla johonkin lukuun (esim. kymmeneen) asti täydentämistä.
Oppilaat tarvitsevat harjoitteluun myös oikeita tulitikkuja ja nappeja.
Laitetaan kuvien päälle ensin yksi tai kaksi, myöhemmin vaikkapa useampi tulitikku/nappi yksi kerrallaan. Tämän jälkeen toistetaan yhteenlaskut ääneen: 2 + 1 = 3, 4 + 1 = 5, 1 + 1 = 2 jne.
Sitten otetaan tulitikut/napit pois kuvien päältä. Toistetaan ääneen vähennyslaskutkin: 3 - 1 = 2, 5 - 1 = 4, 2 - 1 = 1 jne.
Yhteen- ja vähennyslaskun suhdetta voi havainnollistaa vielä selkeämmin, jos lisääminen ja pois ottaminen tapahtuvat saman kuvan päällä välittömästi peräkkäin: 2 + 1 = 3, 3 - 1 = 2.
34. tehtäväsivu: Tehtäväsivulla siirrytään yhteen- ja vähennyslaskun kolmanteen merkitykseen. Aluksi lapset suorittavat vertailuja ympärillään. Joku on päätä pidempi toista, torni on kolme palikkaa matalampi kuin toinen, tikku on pidempi tai lyhyempi kuin toinen, nappeja on vähemmän...
Tehtäväsivun 1a, 1b ja 1c -tehtävät ovat suullisia avoimia lauseita. Lasten tulee täydentää lausekkeet kuvien perusteella. Antti on päätä lyhyempi kuin Pekka. Vasemmanpuoleinen torni on kolme palikkaa matalampi kuin oikeanpuoleinen. Oikeanpuoleinen on kolme palikkaa korkeampi kuin vasemmanpuoleinen. Raidallinen nauha on lyhyempi kuin valkoinen nauha. Valkoinen nauha on pidempi kuin raidallinen. Ennen 2a-tehtävään siirtymistä lapset rakentavat kiekoista lautaspinon, jossa on 5 lautasta ja viereen pinon, jossa on yksi lautanen vähemmän. Laskeminen aloitetaan alhaalta ja verrataan vieressä olevaan pinoon. Rakentamisen jälkeen siirrytään tehtäväsivun piirroksiin.
35. tehtäväsivu: Tehtävän tarkoituksena on selvittää lapselle, että määrien vertailua voi oppia myös täydentämällä yhtä suuriksi. Jos haluan saada johonkin kaksi enemmän, se voi tapahtua siten, että aluksi panen kumpaankin pinoon yhtä monta ja lopuksi toiseen kaksi enemmän. Kaksi vähemmän saadaan taas siten, että otan yhtä suurista pinoista toisesta kaksi pois. Tehtävää voi hyvin harjoitella tehtäväsivu 38 pylväillä. A-tehtävän kumpikin pylväs leikataan irti, niitä voidaan käyttää apuna hyvin monella tavalla. Pylväät pannaan vierekkäin ja toisesta käännetään osa pois. Näin voidaan verrata esimerkiksi lukuja 19 ja 16. Verrata voidaan myös lukuja 18 (käännetään alas 1 ruutu) ja 15 (käännetään alas 4 ruutua) Pylväillä voi leikkiä myös taivuttelematta. Pylvään ruutuihin voidaan panna nappeja tai siemeniä. Esimerkiksi vasemmanpuoleiseen 4, oikeanpuoleiseen 8. Näin voidaan havainnollistaa, kummassa on enemmän ja kuinka paljon enemmän. B-tehtävän pylväät on varapylväitä, jos taivuttelussa innostutaan.
36. tehtäväsivu: Tällä tehtäväsivulla on jo numeromerkintöjä, siksi se onkin vaativampi. Numeroratkaisuihin siirtymistä voidaan toki aina siirtää myöhemmäksikin. Tulitikkuja voidaan käyttää vertailuissa todellisuudessakin. Tehtävään suositellaan toimimista pareittain. Kumpikin lapsi saa 10 tai 12 tulitikkua ja peliin tarvitaan myös arpakuutio. Toinen lapsista heittää esim. 5, toinen 3. Kumpikin panee eteensä niin monta tulitikkua kuin arpaluku on osoittanut.
Lapset vertaavat tulitikkuja ja huomaavat, kumpi on heittänyt pienemmän luvun. Se lapsista, joka on heittänyt vähemmän voi nyt ottaa enemmän heittäneen esille asettamista tikuista niin monta tulitikkua itselleen, montako enemmän toinen ensimmäisellä kierroksella heitti. Peliä jatketaan. Se pelaajista voittaa, jonka tikut ensin loppuvat. Pelin aikana lapset saavat jatkuvasti havaintoja yhtä suureksi täydentämisestä. Jos kumpikin heittää saman luvun, peliä jatketaan uudella heitolla, koska toinen pylväs ei nyt kasva toista korkeammaksi.
37. tehtäväsivu: Tätä pelilautaa voidaan käyttää useampaan eri leikkiin, tarvitaan vain arpakuutio ja pelinappulat. Aluksi lapset voivat pelata kukin yksinään siten, että opettaja heittää arpakuutiota ja lapset siirtyvät nopan osoittaman luvun eteenpäin. Lasten tulee kertoa, kuinka monta ruutua on vielä maaliin eli ruutuun 10. Opettaja voi myös heittää useamman kerran peräkkäin ja lasten tulee kertoa, montako ruutua mennään heittojen jälkeen eteenpäin. Nytkin lasketaan, montako ruutua on vielä maaliin. Esimerkiksi 2 + 3 + 4 ja enää on vain yksi ruutu maaliin.
Myös parin kanssa pelattava peli on samantapainen. Aluksi valitaan, monellako (1, 2 tai 3) heitolla aiotaan päästä maaliin. Kun kumpikin lapsista on tehnyt valintansa ja heittänyt, verrataan, kumpi on päässyt lähemmäksi maalia. Jos toinen lapsista pääsi ruutuun 8 ja toinen ruutuun 11, on jälkimmäinen voittanut, koska ruudussa 8 olevalla nappulalla on maaliin vielä 2 ruutua, kun taas ruudussa 11 olevalla vain 1 ruutu. Voitosta saa yhden pisteen ja peli jatkuu. Eniten pisteitä saanut on voittanut koko pelin.
Peliin voi luonnollisesti keksiä muitakin sääntöjä, onhan tämä yksinkertainen seurapelilauta. Nappuloita eteen ja taakse siirtämällä lapset saavat kuitenkin paljon arvokkaita kokemuksia luvuista.
Huomautus: Tarvittaessa on aina palattava takaisin laskutoimitusten selvittämiseen ja otettava avuksi toimintaan kannustavia leikkejä. Lapsille on syytä antaa paljon sanallisia tehtäviä, niiden ratkaisuun ei tarvita edes tehtäväsivuja, tarvittaessa paperiarkki tai vihko voidaan ottaa avuksi. Lasten on hyvä piirtää paljon, omat piirrokset auttavat havainnoinnissa.
Tässä ei ole annettu erikseen tehtäviä 10:tä suuremmista luvuista, mutta edellä kuvattuja tehtäviä voidaan soveltaa myös suurempiin lukuihin. Laskutoimitusten perusominaisuudet on kerrattava 10:tä suurempiin lukuihin siirryttäessä. Voidaan leikkiä esim. sääntöleikkejä ja nyt voidaan käyttää jo numerokortteja ja itse numeroita.
38. tehtäväsivu: Tehtävässä 35 käytettäviä pylväitä.
Tehtäväsivut 39-51: Tehtävien avulla tutkitaan lukujen erilaisia ominaisuuksia (lukujen suuruus, parillinen vai pariton, lukujen purkaminen tasasuuruisiin osiin, neliöluvut, "porrasluvut", yksinumeroiset ja kaksinumeroiset luvut, lukujen suuruus, lukujen muodostuminen laskutoimitusten tuloksena jne.).
Lukujen ominaisuuksia voidaan havainnollistaa niillä leikkimällä, lukuja kokoamalla, kuvasta kertomalla tai piirtämällä.
Lukujen ominaisuuksien oivaltamiseen etsitään kuhunkin ominaisuuteen parhaiten sopivat luvut, tavallisesti käytetään lukuja 20:een asti.
39. tehtäväsivu: Lapset leikkaavat itse rahat ja ruudut. Nämä tulevat olemaan hyödyllisiä apuvälineitä, niitä voidaan käyttää uudelleen ja uudelleen tämän aihepiirin käsittelyssä. "Satumaan" rahoista voidaan erotella parilliset ja parittomat luvut, 10:tä suuremmat luvut, pelkillä viitosilla kuvattavat luvut jne. Rahoilla voidaan leikkiä kauppaa, ostajat maksavat ostokset leikkirahoilla (ostokset esim. tehtäväsivulta 50).
Rahoilla tai numerokorteilla voidaan leikkiä myös leikkiä "kakkosen ja viitosen kolikko". Tätä leikkiä varten tarvitaan paljon kakkosen ja viitosen kolikoita. Lapsia kehotetaan modostamaan erilaisia lukuja kakkosilla ja viitosilla. Lapset kuvaavat helposti lukua 10 kahdella viitosella (5 + 5) tai viidellä kakkosella (2 + 2 + 2 + 2 + 2), mutta lukujen 11 ja 13 kuvaaminen ei enää olekaan niin helppoa. Monet lapset luulevat, ettei se edes ole mahdollista. Kehotetaan lapsia yrittämään! Jonkin ajan kuluttua lapset huomaavatkin, että 6 + 5 on 11 ja että tehtävän ratkaisuun tarvitaan 3 kakkosen ja yksi viitosen kolikko. Tämän jälkeen kannattaakin kysyä, voidaanko kaikki luvut kuvata kakkosen ja viitosen kolikoilla. Ennen pitkää lapset huomaavat, että jos 5:stä otetaan pois 2, jäljelle jää 3. Jos 5:stä otetaan pois kaksi kakkosta, jäljelle jää yksi. Lapsille annetaan käteen paljon viitosen ja kakkosen numerokortteja sekä miinus- ja pluskortteja ja yritetään kerätä kaikki tapaukset yhdestä 20:een. Porrasluvut taas on helppo havainnollistaa ruutulapuilla (matematiikassa ne esiintyvät kolmiolukuina):
1 1 + 2 1 + 2 + 3 1 + 2 + 3 + 4 jne.
Ruutulapuilla saadaan havainnollistettua myös neliöluvut:
1 2 x 2 3 x 3 4 x 4 jne.
Tehtäväsivut 40 ja 41: Ennen tehtäväsivujen käyttöönottoa tutkitaan erikokoisten lapsiryhmien avulla, löytyykö kaikille pari ja voidaanko muodostaa kaksi samankokoista ryhmää. 11 lasta on pariton lukumäärä, koska yhdelle lapsista ei löydy paria. Parittomuus näkyy siitäkin, että jaettaessa luokkaa kahdeksi joukkueeksi olisi toisessa joukkueessa yksi lapsi enemmän kuin toisessa. Oranssin väritangon pituus (10 cm) saadaan rakennettua 2 cm:n vaaleanpunaisista, mutta se voidaan rakentaa myös kahdesta samanlaisesta keltaisesta (5 cm) tangosta. Tehtäväsivulla olevia janoja voidaan tutkia samalla periaatteella.
42. tehtäväsivu: Pareihin tai kahteen samankokoiseen ryhmään jakautumista voidaan tutkia kiekoilla, valkoisilla kuutioilla, siemenillä tai kolikoilla. Jäljentäminen ja paperille piirtäminen ovat tämän saman toiminnon abstrakteja ilmenemiä. Lapset saavat näiden avulla paljon tietoa parillisen ja parittoman luvun käsitteistä. Voimme myös kaksinkertaistaa parillisten ja parittomien esineiden määrät peilillä. Kolme nappia on pariton määrä, peiliin kurkistettaessa nähdään 6 nappia ja se onkin parillinen luku. 8 nappia on kaksinkertaistettuna 16, joten parillisuus säilyy kaksinkertaistettunakin. Monen peiliin kurkistuksen jälkeen lapset huomaavat, että peilin avulla saadaan vain parillisia lukuja.
Seuraavaksi tutkitaan, mitä tapahtuu kun parilliseen lukuun lisätään pariton luku (tai päinvastoin) tai mitä tapahtuu, kun parillisesta luvusta vähennetään pariton luku. Tätä voidaan hyvin havainnollistaa lapsiryhmiä kokoamalla tai niitä jakamalla. (Esim. yhdessä pulpettirivissä istuu parillinen määrä lapsia, toisessa pariton määrä. Jos nämä kaikki lapset kootaan yhteen, lapset huomaavat, että uusi ryhmä on pariton. Jos oppilasmäärältään parillisesta luokasta erotetaan parillinen määrä oppilaita, onko jäljelle jäävä lapsimäärä parillinen vai pariton?)
43. tehtäväsivu: Myös tämäntyyppiset tehtävät tukevat edelläkuvattua aihepiiriä. Yhtä monta sormea kummassakin kädessä samaan aikaan esiin nostettuna antavat yhteenlaskettuna lopputulokseksi parillisen luvun. Jos toinen käsi laitetaan selän taakse, jää jäljelle alunperin yhdellä kädellä näytetty luku.
Lähdettäessä symmetrisestä tilanteesta päädytään parittomaan lukuun, kun toisella kädellä näytetään yksi sormi enemmän kuin alunperin.
Myöhemmin toimintaan otetaan mukaan laskeminen (Jos 7 + 7 = 14, niin 7 + 8 on yhtä enemmän.)
Hieman epätavallinen, mutta hyvin havainnollinen tapa on ottaa laskuihin mukaan myös varpaat. Viittä suuremmat luvut voidaan näyttää siten, että lukua 6 vastaa oikean jalan 5 varvasta sekä oikean käden yksi sormi. Lopputulosta laskettaessa on helpompi laskea ensin 5 varvasta ja vasta sitten yksi sormi.
44. tehtäväsivu: Näillä pikalukusivuilla voidaan tarkistaa, tunnistavatko lapset käsitteen parillinen ja käyttävätkö he hyväksi oppimiaan matemaattisia kokemuksia. Esineitä on tarkoituksella enemmän kuin 20, sillä tarkoituksena on, etteivät lapset ryhtyisi laskemaan, vaan tunnistaisivat parillisuuden, peilikuvan, samansuuruiset ryhmät ja parilliseen lisätyn parittoman. Tällaisia tehtäviä lapset voivat ratkaista myös taululle tai piirtoheittimelle asetetuista kuvista. Opettaja voi helposti itse piirtää lisää erilaisia kuvia.
Tehtäväsivut 45/A ja 45/B: Tarkoitus on leikkiä tehtäväsivun "ihmekoneella". Syötän ihmekoneeseen lukukortteja ja kone lajittelee erilleen parilliset ja parittomat. Koneen kuva monistetaan ja lapset voivat leikkiä numerokorteilla: koneeseen pudotetaan lukukortit 5, 7, ja 8, kone sylkäisee toisesta aukosta kortit 5 ja 7, toisesta taas kortin 8.
Konetta voidaan käyttää koko vuoden ajan, sillä voidaan harjoitella yhteenkuuluvuuksia, kysymys-vastaus -leikkejä, sääntöjä, laskutoimitusten suorittamisia, käänteisiä laskutoimituksia, avoimien lausekkeiden muodostamista jne.
Yksinkertaisemmassa koneessa (45/A) on vain yksi sisäänmenoaukko. Paperia käännettäessä kone toimii päinvastoin. +:sta tulee -, pienentämisestä tulee suurentaminen jne. Koneeseen voidaan esim. pudottaa pienikokoinen looginen pala ja se sylkäisee ulos samanlaisen, mutta suuremman. Sääntö: Kone suurentaa. Jos käännän koneen ylösalaisin, suuresta loogisesta palasta tulee pieni ja kone siis pienentää. Koneen sääntö voi olla myös sellainen, että sisään pannaan tietty määrä ja kone sylkäisee ulos tietyn verran suuremman luvun. Koneella voidaan leikkiä myös siten, että se antaa ulos tietyllä määrällä vähemmän kuin mitä sinne on pantu. Opettajan mielikuvituksella ei tässä suhteessa ole rajoja.
Toisessa koneessa on kaksi sisäänmenoaukkoa ja yksi ulostuloaukko (45/B), mutta myös tämä kone voidaan kääntää toisinpäin. Jos sisään pannaan esim. 3 kiekkoa toisesta ja 2 kiekkoa toisesta aukosta, koneen alaosasta tulee ulos 5 kiekkoa. Päinvastoin käytettynä kone jakaa sisään pudotetut 5 kiekkoa kolmeen ja kahteen kiekkoon. Koneeseen voidaan pudottaa myös esim. kaksi eriväristä tikkua ja alaosasta putoaa ulos lyhyempi, jolloin kone on siis valinnut kahdesta pienemmän. Kun kone on suorittanut useamman tehtävän, lapset helposti oivaltavat koneen käyttösäännön.
46. tehtäväsivu: Kolmella jaollisuutta voidaan tutkia samalla tavoin kuin kahdella jakamista. (Vrt. Parillisten lukujen tutkiminen) Tällainen abstrakti määritelmä on kuitenkin lapsille vaikea, sen sijaan heiltä kysytään, osaavatko he muodostaa luvun pelkillä kolmosilla (esittää luvun pelkkien kolmosten summana), osaavatko he muodostaa sen kolmesta samanlaisesta luvusta (esittää kolmen yhtä suuren luvun summana).
Pikkulautasille laitetaan kullekin 3 helmeä, sen jälkeen kolmelle lautaselle kullekin yhtä monta helmeä. Yhtä lukua voidaan näin tarkastella kahdesta eri näkökulmasta.
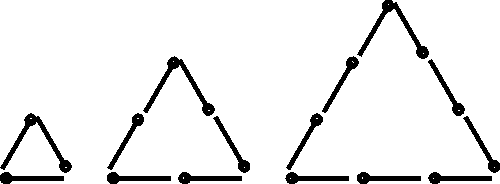
Tulitikuista kootaan kolmioita, joiden jokainen sivu muodostuu yhtä monesta tulitikusta. Tämän jälkeen lasketaan yhdessä, montako tulitikkua on tarvittu yhden kolmion rakentamiseen (3, 6, 9...)

47. tehtäväsivu: Lapset tekevät tehtävää annettujen ohjeiden mukaan. Apuna voidaan käyttää myös sivun 45/A konetta. Tehtävä voidaan suorittaa myös siten, että koneeseen syötetään yksi tikku tai siemen ja alhaalta tulee ulos kolme tikkua tai siementä. Jos koneeseen syötetään 4 siementä, alhaalta tulee ulos 12 siementä. Tämä kone antaa siis ulos kolme kertaa niin paljon kuin siihen on syötetty. Ekaluokkalainen ei varmasti vielä osaa muotoilla sääntöä näin selvästi, mutta se ei ole ongelma, sillä säännön muotoilun aika tuleekin vasta myöhemmin.
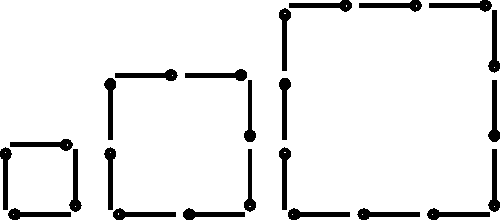
48. tehtäväsivu: Tämän sivun avulla harjoitellaan neljällä jaollisuutta ilman, että ekaluokkalaiset vielä muotoilisivat säännön näin selkeästi. Ennen tehtäväsivun aloittamista voidaan tulitikuilla koota neliön sivuja siten, että tehtävään tarvitut tulitikut yhteenlaskemalla saadaan aina neljällä jaollisia lukuja. Käytetyistä tulitikuista voidaan koota taulukko.
| Sivu | 1 | 2 | 3 | 4 | |
| Neliö yhteensä | 4 | 8 | 20 |
49. tehtäväsivu: Tehtäväsivulla on Lottoa varten tarvittava taulukko. Lapset voivat pelin aikana hyvin tarkkailla lukujen suuruuksia ja tämän lisäksi lapset saavat aimo annoksen todennäköisyyslaskennan perusteita.
Pelin säännöt: Valitaan luvut, joilla peliä pelataan (esimerkiksi yhdestä 20:een). Numerokortit pannaan sekoitettuna hattuun tai jumppapussiin. Vedetään yksitellen 5 korttia. Ensimmäinen numero pannaan sen suuruuden mukaan johonkin viidestä ruudusta. Tarkoituksena on, että viiden vedetyn numeron jälkeen numerot sijaitsevat 5 ruudussa suurusjärjestyksessä. Jos esim. ensimmäisenä vedetään numero 10, se pannaan kolmanteen ruutuun, koska ajatellaan, että myöhemmin vedettävien numeroiden joukossa tulee olemaan sekä 10:tä pienempiä että suurempia lukuja. Jos toinen vedettävä numero on 4, se voidaan panna joko ensimmäiseen tai toiseen ruutuun, koska se on kymmentä pienempi - päätetään panna kortti ensimmäiseen ruutuun. Meillä on onnea, jos tämän jälkeen vedetään kortti 7, sillä toinen ruutu on vielä vapaana. 7 kuuluu 4:n ja 10:n väliin. Nyt on jäljellä enää kaksi tyhjää ruutua. Sinne voidaan panna vain 10:tä isompia kortteja. Jos vedettävien numeroiden joukossa ei tällaista tule, käyttämättä jäänyt numero kirjoitetaan käsin viivalle. Jos viimeinenkään vedettävä numero ei sovi ruudukkoon, on meillä lotossa tulos kolme oikein.
Lapset oppivat pelisäännöt muutaman harjoituspelin jälkeen. Lapsista on hauska taktikoida ja arvioida. 5 oikein saanut on syystäkin iloinen. Jos ruudukot loppuvat, lapset voivat piirtää niitä lisää vihkoon. Tyhjiä ruudukoita on tietysti myös helppo monistaa.
50. tehtäväsivu: Tätä tehtäväsivua voidaan käyttää moneen eri tarkoitukseen. Lukujen ominaisuuksien vertailun lisäksi tehtäväsivua voidaan käyttää myös mm. laskutoimitusten harjoitteluun. Tehtäväsivulla on tavaratalon näyteikkuna. Lapsille voidaan esittää kysymyksiä: Mikä lelu on kallein? Mikä maksaa vähiten? Mikä maksaa vähemmän kuin kymmenen (markkaa/euroa/taaleria)? Mikä maksaa tasan kymmenen? Paljonko maksaa 2, 3 tai 4 leppäkerttua, kynää tai nallea? Rahayksikkönä voidaan käyttää todellista rahayksikköä (markkaa). Tässä tapauksessa on huolehdittava siitä, että esitetyt luvut ovat ainakin lähellä todellisia hintoja. Toisaalta voidaan sanoa, että Satumaassa ostokset maksetaan taalereilla. Tarkoituksena on, että lapset huomaavat suhteet: pieni marmorikuulapussi maksaa puolet suuren marmorikuulapussin hinnasta. Yksi kynä maksaa 1 taalerin, 6 kynää 6 taaleria. Pelle maksaa yhtä paljon kuin kaksi autoa ja värikynät yhteensä. Lapset voivat tehdä leikkirahoilla ostoksia: Sinulla on 20 taaleria (markkaa). Tee ostoksia niin, että saat takaisin alle 10 taaleria. Mitä voit silloin ostaa? Opettaja voi keksiä kuvasta paljon tehtäviä.
51. tehtäväsivu: Tehtäväsivulla on noppapelin pelilauta. Pelilautaa ei tarkoituksella ole numeroitu, jotta lapset laskisivat pelilaudan siirrot. Tässä pelissä voidaan harjoitella lukujen suuruutta, parillisuutta, moninkertaisuutta jne.
Joka toinen luku on parillinen, niiden välissä olevat luvut ovat parittomia. Pelilaudalla voidaan kulkea myös taaksepäin. Tärkeää on huomata, että myös 0 on parillinen luku. Jos peliä pelataan siten, että astutaan 3 askelta eteenpäin, tarkkaillaan 3:n kerrannaisia. Tarkkaillaan, mitkä näistä ovat parillisia.
Joka viides pelilaudan paikka on tipanmuotoinen, joka kymmenes taas vahvennettu. Kun pelilaudalla on jonkin aikaa liikuttu eteen ja taaksepäin, lapsia voidaan pyytää kirjoittamaan paikkoihin myös numerot.
Paikat voidaan myös värittää. Parilliset paikat ovat punaisia, parittomat saavat jäädä valkoisiksi. Joka kolmas paikka voi olla pallollinen, joka kuudes raidallinen. Joka neljännestä paikasta väritetään reunat. Näin esim. luvusta 12:sta voidaan sanoa, että se on parillinen ja siihen päästään siirtymään kahdella, neljällä, kolmella ja kuudella edettäessä. Se on myös 10:tä isompi ja 20:ta pienempi.
Tätä peliä kannattaa pelata monta kertaa. Lapset ryhtyvät hyvin pian kilpailemaan keskenään, kuka tietää numeroista eniten.
Vaikka kaikista lukujen ominaisuuksista ei ole tehty erillisiä tehtäviä, ei niitäkään ominaisuuksia tule unohtaa. Voidaan esim. tarkastella, mitkä luvut kirjoitetaan yhdellä numerolla, mitkä kahdella. Tarkastellaan myös lukujen ulkoasua: 11 kirjoitetaan kahdella samanlaisella numerolla, joista kumpikin on pariton. Lukujen summa on 2, niiden erotus on 0.
Voimme etsiä myös lukupareja, joiden jäsenten erotus on suurempi kuin 5: 1 ja 12, 2 ja 13, 3 ja 14, 4 ja 15.
Luvuilla voidaan leikkiä myös arvausleikkiä. Numerokortti pannaan pöydälle kuvapuoli alaspäin. Toiset tekevät kysymyksiä ja yrittävät arvata, mikä numero kortissa on. Esim. Onko se yksinumeroinen? Onko se parillinen? Onko se porrasnumero? Onko se suurempi kuin 15? Opettaja vastaa vain sanoilla kyllä tai ei. Myöhemmin myös lapset itse voivat olla vastaajan roolissa. Kysymyksissä kannattaa välttää turhaa toistoa. Jos numerosta jo tiedetään, että se on suurempi kuin 15, ei kannata turhaan kysyä, onko se suurempi kuin 11. Lapset oppivat helposti tarkkailemaan myös muiden kysymyksiä, mikä on kasvatuksen kannalta tärkeä ominaisuus.
Lapset voivat leikkiä myös lukukilpailua: Kuka ehtii annetun ajan sisällä antaa yhdelle luvulle eniten summa- ja erotusmuotoja. 15:n summa- ja erotusmuodot ovat esim. 10 + 5, 5 + 5 + 5, 20 - 5, 16 - 1 jne.
Käytännöllisten laskumenetelmien opettelu aloitetaan nyt, jotta
laskutoimitusten suorittamiseen saadaan varmuutta. Samanaikaisesti
pyritään kiinnittämään huomiota erilaisiin yhtäläisyyksiin ja kehitetään
myös analogista ajattelua.
52. tehtäväsivu: Kirjallisia harjoituksia valmistellaan suullisesti. Lukuihin lisätään tai niistä vähennetään 1, 2, 3 tai 4 laskemalla eteen- tai taaksepäin tai lukujonoja luettelemalla. Leikitään esim. vastausleikkiä: minä sanon luvun, sano sinä nopeasti yhtä suurempi (tai pienempi) luku, kahta suurempi (tai pienempi) luku. Kun lukuun lisätään kolme tai siitä vähennetään kolme, on syytä ottaa sormet avuksi ja näyttää, missä vaiheessa ollaan menossa. Sanotaan: 15 plus 3 on 16, 17 ja 18, 19 miinus 3 on 18, 17 ja 16. Painotetaan analogiaa: 5 + 3 = 8, 15 + 3 = 18, 7 - 3 = 4, 17 - 3 = 14 jne.
4:n lisääminen on helpompaa, jos se tapahtuu kahdessa vaiheessa. Tässä auttaa tehtäväsivun tehtävä 2. 2:n lisäämistä ja vähentämistä havainnollistaa tehtävä 1. Tehtävän 3 avulla voidaan näyttää, miten naapurilukujen etsiminen tapahtuu lisäämällä tai vähentämällä 1.
53. tehtäväsivu: Tehtäväsivun piirustukset tukevat ryhmittäin tapahtuvaa laskemista. Ensin lasten annetaan laskea ryhmittäin tikkuja, vihkoja, pelikortteja jne. 20 pelikorttia voidaan laskea esim. 2, 6, 10, 13, 16, 18, 20, mutta muitakin vaihtoehtoja tietysti on. On kuitenkin pidettävä huolta siitä, etteivät lapset aloita laskemista alusta vaan lisäämällä aina viimeksi laskettuun summaan. Kuvan lukemista helpottaa, jos peitämme kuvan aluksi paperilla ja kuvia näytetään paperia pikkuhiljaa siirtämällä. Kahdelle ensimmäiselle riville on tietoisesti valittu käsitteellisiä ryhmiä, jotta laskemista voidaan tukea suullisesti: ensimmäisellä rivillä on 6 henkilöautoa, 10 autoa, 13 maakulkuneuvoa, 16 liikennevälinettä. Toisella rivillä on 10 isoa palloa, 16 palloa, 18 lelua.
Kolmas rivi voidaan lukea vasemmalta oikealle ja sitten oikealta vasemmalle ja näin voidaan lasten huomiota kiinnittää siten, että loppusumma pysyy samana. Pienet kappalemäärät helpottavat laskemista, ja tässä ovat tukena myös vuoden aikana läpikäydyt pikalaskuharjoitukset.
Samansuuruisten lukujen lisääminen ja vähentäminen Emme ole valmistaneet erillistä tehtäväsivua, sillä jo 43. tehtäväsivulla olemme esitelleet tehtävään sopivia harjoituksia. Näitä kannattaa kerrata. Kannattaa muistuttaa, että jos näytän toisella kädellä yhtä enemmän (tai vähemmän), on koko summa yhtä enemmän (tai vähemmän). 8 + 7 voidaan laskea näin: 8 + 8 - 1, mutta myös näin: 7 + 7 + 1. Tämä on lapsille uusi asia. Laskutoimituksista lisää tehtäväsivulla 58, jossa on myös esimerkkejä yhtäsuurten lukujen lisäämisestä; näitä voidaan verrata viereisiin viistoriveihin. Samassa yhteydessä on esimerkkejä myös em. 1, 2, 3, 4:llä lisäämisestä.
Tehtäväsivut 54/A ja 54/B: Ennen kuin opetamme toiselle kymmenelle siirtyvän perinteisen laskutavan (8 + 7 = 8 + 2 + 5), on syytä esitellä oma menetelmä lukujen 9 ja 8 lisäämiselle tai vähentämiselle. Tehtäväsivun kuvat esittävät munakennoja. Ne leikataan irti. Ennen kuvien käyttöä lasten annetaan leikkiä oikeilla munakennoilla. Täytetään yksi munakenno konkreettisilla "munilla" (esim. Kinder-munien muovikoteloilla) ja lisätään vielä esim. 4 munaa. 10 + 4 = 14. Otetaan sitten pois 4 munaa: 14 - 4 = 10. Kokeillaan tämän jälkeen muidenkin lukujen lisäämistä ja vähentämistä. Annetaan lasten huomata, ettei näissä tapauksissa munakennon muniin tarvitse lainkaan koskea. Tämän jälkeen voidaankin siirtyä jo käyttämään tehtäväsivun munakennoja. Tehtäväsivun 54/a tummennetut ympyrät tarkoittavat sitä, että kenno on täynnä munia. Kiekkoja kuvan päälle panemalla voidaan havainnollistaa kananmunien lisäämistä. 10:n rinnalle asetettujen alle kymmenen kiekon poistamisella voidaan havainnollistaa vähennyslaskua. Vasta tämän jälkeen ryhdytään opettamaan 9:ään, 8:aan lisäämistä tai niistä vähentämistä. (Tehtävät 54/a, 54/b, 54/c). Jos kymmenen kananmunan kennosta puuttuu yksi muna, voidaan yhteenlasku suorittaa aivan kuin ensimmäinen yhteenlaskettava olisi 10; vasta lopputuloksesta vähennetään yksi puuttunut kananmuna. 9 + 7 = 10 + 7 - 1, kahdeksan tapauksessa 8 + 5 = 10 + 5 - 2. Luokassa on varmasti oppilaita, jotka ehdottavat ryhmittelyä. Yhteenlaskun 9 + 7 tapauksessa 7 kiekosta siirretään yksi yhdeksän joukkoon, näin siihen saadaan 10. Näin 9 + 7 = 9 + 1 + 6 = 10 + 6. 8 + 5 = 8 + 2 + 3 = 10 + 3. Jos alle 10 kananmunaan halutaan lisätä 9 tai 8 kananmunaa, voidaan sekin tehdä siten, että lukuun lisätään 10 ja lopuksi summasta vähennetään 1 tai 2. Esimerkiksi 4 + 8 = 4 + 10 - 2. Kun alle 20 suuruisesta kaksinumeroisesta luvusta vähennetään 9 tai 8, voi menetelmä jälleen olla se, että vähennämme 10 ja lopuksi lisäämme erotukseen 1 tai 2. Tämäntyyppiseen vähennyslaskuun sopii havaintovälineeksi myös raha. Monien esimerkkien jälkeen annetaan lapsille laskutehtäviä, joiden ratkaisemisessa sallitaan myös apuvälineiden käyttö niille, jotka niitä vielä kaipaavat; ne, jotka osaavat jo laskea päässään, voivat niin tehdä.
Tehtäväsivun 54/B tyhjillä kuvioilla voidaan havainnollistaa toiselle kymmenelle siirtymisen perinteistä mallia. Esimerkiksi otetaan 6 + 7, lapset laittavat eteensä rinnakkain kaksi tyhjää munakennoa. 6 punaista kiekkoa pannaan ylhäältä alaspäin vasemmanpuoleiseen munakennoon. Tähän summaan lisätään nyt kananmunia. Otan käteeni 7 sinistä kiekkoa, täydennän aluksi 4 kiekolla vasemmanpuoleisen munakotelon tyhjän tilan, jäljelle jääneet 3 kiekkoa pannaan toiseen munakoteloon. Lapset huomaavat: 6 punaista ja 4 sinistä on yhteensä 10 kiekkoa ja toisessa kotelossa 3 sinistä, yhteensä 13 kiekkoa. Luetaan: 6 + 7 on yhtä paljon kuin 6 + 4 + 3 on yhtä paljon kuin 10 + 3 on yhtä paljon kuin 13. Kirjoitetaan numeroin.
Vähentämistä harjoitellaan samalla tavoin. Esim. 14 - 6. Punaiset kiekot pannaan kahteen koteloon, toiseen 10 ja toiseen 4. Aluksi otan pois 4, sitten toisesta kotelosta vielä 2. Matematiikan kielellä 14 - 6 = 14 - 4 - 2 = 10 - 2 = 8.
Vuoden lopussa voidaan harjoitella 21:stä ja 22:stä vähentämistä ja niihin lisäämistä, siksi tehtäväsivulla onkin 3 koteloa.
55. tehtäväsivu: Tällä tehtäväsivulla siirrytään pelinappulalla eteenpäin ja taaksepäin saman periaatteen mukaan kuin edellisellä tehtäväsivulla. Luvun jakamista kahteen osaan on syytä kerrata, jotta lapset oivaltaisivat, miksi tehtävässä 8 plus 7 jaan luvun seitsemän lukuihin 2 + 5. Tästä on kyse harjoituksessa 2. Asiaa voidaan havainnollistaa helmitaulullakin.
56. tehtäväsivu: Vähentäminen kahdessa vaiheessa
57. tehtäväsivu: Jos kaksinumeroisesta luvusta vähennetään kaksinumeroinen luku, tehtävä kannattaa suorittaa vertailulla. Ennen tehtäväsivun ratkaisemista suoritetaan vertailuja väritangoilla. Ruskea väritanko on 4 valkoista kuutiota pidempi kuin vihreä tanko. Vihreä väritanko on 4 valkoista kuutiota lyhempi. Niiden erotus on 4 valkoista kuutiota. 16 cm - 12 cm = 4 cm. Kun tehtävää on valmisteltu puuhastelulla, lasten annetaan toimia itsenäisesti ohjeiden mukaan.
Tehtävässä 2 vertailu tapahtuu lukusuoralla. Kynä pannaan 19:n kohdalle ja sormi 17:n kohdalle ja katsotaan, paljonko on näiden lukujen erotus.
58. tehtäväsivu: Tämä on yhteenlaskutaulukko. Taulukkoa ei tule täyttää kerralla, vaan jos esim. harjoitellaan lisäämistä 10:een, täytetään ensin mustalla nuolella osoitettu pystyrivi (10 + 1, 10 + 2, 10 + 3 jne.) Tämän jälkeen täytetään sen viereiset rivit (lisääminen 9:ään, 8:aan jne.) Kysytään lapsilta, mitä huomioita he tekivät.
Laskutapoja on monenlaisia, ne kannattaa koota yhteen. Lapsille on syytä antaa myös laskutehtäviä, ja he voivat itse kertoa, miten laskeminen oli "helppoa". Lapset oppivat paljon myös toisiltaan. Esim. summa 7 + 12 on helpompi laskea muodossa 12 + 7. Lukua 7 ei tarvitse laskea suoraan yhteen 12:n kanssa, vaan lasku voidaan suorittaa vaiheittain. Tehtävässä 6 + 11 + 4 kannattaa etsiä luku 10 ja lisätä se lukuun 11 jne. On hyvä kerrata myös yhteenlaskun ja vähennyslaskun merkitys joukkojen yhdistämisenä ja erottamisena (esim. tehtäväsivut 30, 31, 32, 33/c), sillä luvun täydentäminen kymmeneen on myös hyvä keino. Tehtävän __ - 8 = 7 ratkaisu on helppo: jos koko summasta vähennetään 8 ja jää jäljelle 7, niin 7:ään on lisättävä takaisin 8, jotta koko summa olisi taas edessäni. Lapset voivat löytää monia yhteyksiä. Jotkut oivaltavat yhteen- ja vähennyslaskun tämän konkreettisen merkityksen vasta nyt.
Ensimmäisellä luokalla ei opeteta geometriaa, mutta voimme antaa lapsille monipuolisia kokemuksia asiasta. Aina on syytä lähteä tilasta. Työ aloitetaan aina tilan rakentamisella. Tähän sopivia havaintovälineitä ovat legopalikat, rakennuspalikat, sokeripalat, tulitikkulaatikot, väritangot jne. Mittatikuilla leikitään aluksi vapaasti, vasta myöhemmin leikkiin lisätään erilaisia näkökulmia. Rakenna samanlainen. Rakenna samanlainen vain sinisistä väritangoista. Tee ikkunallinen talo. Tee monikerroksinen talo. Jne.
59. tehtäväsivu: Tässä tehtävässä on rakennettava valkoisista kuutioista pohjapiirustuksen mukaan. Lapsia on autettava, sillä muuten he eivät ehkä oivalla, että luvun 3 päälle on pantava 3 valkoista kuutiota päällekkäin. Käytetään hyväksi tehtävän tarjoamia mahdollisuuksia. Väritangon voi vaihtaa toiseksi, rakennelmaa voi katsoa peilistä. Samanlainen rakennus voidaan tehdä pulpetille. Rakennelman asentoa voidaan muuttaa. Tutkitaan rakennelman joka sivua peilin avulla. Rakennetaan peilikuvatalo. Tehtävässä 2 peilikuvan rakentaminen onkin tehtävänä. Annetaan lasten rakentaa vapaasti käyttäen 10 kuutiota. Kiinnitetään lasten huomiota siihen, että samanlaisen pohjapiirroksen päälle voidaan laatia monenlaisia rakennelmia. Näillekin tehdään peilirakennelmat. Lasten työn etenemistä kannattaa valvoa ja auttaa, missä tarvitaan. Myös lasten kommentteja tulee kuunnella.
Tilatyöskentelyn jälkeen siirrytään tasotyöskentelyyn. Leikitään nyt suuntaleikkiä: edetään alas, ylös, eteenpäin, taaksepäin esim. käytävän kaakelilaatoilla. Tämän jälkeen sama leikki siirretään ruutupaperille. Sanellaan piirustuksia, jossa edetään ruudun mitan verran eteenpäin. Leikin johtaja määrää suunnan ylös, alas, oikealle tai vasemmalle. Lipputanko voidaan piirtää esim. näin: ylös - ylös - ylös - ylös - oikealle - oikealle - oikealle - ylös - ylös - ylös - vasemmalle - vasemmalle - vasemmalle - alas - - alas - alas. Nuolet voidaan myöhemmin korvata sanoin. Lapsista on hauska tutkia valmiiksi saamaansa piirrosta.
Tasotyöskentelyssä on tärkeä tunnistaa erilaiset tasokuviot. Valitaan erilaisista esineistä esim. seuraavien periaatteiden mukaan: kappaleet - tasot. Seuraava valintaperiaate voi olla tasokuvioiden erottelu "kulmikkaat" ja "kaarevareunaiset". Lasten annetaan etsiä tunnustelemalla kolmikulmaisia, nelikulmaisia, viisikulmaisia ja kuusikulmaisia tasokappaleita. Tämän jälkeen sidotaan pillinpaloja nauhaan. Nauhan päät yhteensolmimalla saadaan aikaan monikulmio, jossa on yhtä monta kulmaa ja sivua kuin montako pillinpalaa työhön käytettiin. Tikut ja muovailuvahakin sopivat tehtävään. Tehtävässä 3 pyydetään lapsia tekemään vastaavia monikulmioita. Lapset voivat hyvin tehdä muitakin kuvioita kuin mitä tehtäväsivulla on kuvattu. Lasten pyydetään kiinnittämään huomiota käytettyjen tikkujen ja muovailuvahapallojen määrään. Lasten annetaan itse tehdä havainto tikkujen ja pallojen määrän suhteesta. Tämän havainnon teossa auttaa taulukko. Ei tuputeta lapsille valmista vastausta, vaan annetaan heidän itse kokea keksimisen ilo.
60. tehtäväsivu: Tätä tehtävää ennen tutustutaan symmetrisiin liikkeisiin, esineiden siirtoon molemmin käsin, peilikuvarakennelmien tekemiseen sekä tasokuvioiden tutkimiseen peilin avulla. Lasten annetaan kaikessa rauhassa tutustua tehtäväsivun mustavalkoiseen sydämeen peilin avulla, niin että heillä on riittävästi aikaa oivaltaa asioita. Vasta viimeisessä tehtävässä pyydetään lapsia piirtämään, mutta tässäkään tapauksessa ei pidä vielä odottaa heiltä tarkkaa, huoliteltua piirrosta. Lopputulos tarkistetaan peilin avulla.
61. tehtäväsivu: Tehtäväsivu on ohjeellinen, opettaja voi itse keksiä vastaavanlaisia tehtäviä. Tilastointi on tärkeä osa matematiikkaa; nykyajan ihmisiltä vaaditaan lukujen yhteyksien ymmärrystä. Lasten tulee hankkia kokemusta tietojen keruusta ja kirjaamisesta, samoin niiden systemaattisesta esittämisestä.
Lapset keräävät tosia lauseitä taulukosta. Useimmat joivat kaakaota. Yhtä moni lapsi pitää teestä kuin hedelmämehusta. 4 lasta vähemmän joi maitoa kuin kaakaota. Luokan lasten lukumäärä on 26.
62. tehtäväsivu: Tehtäväsivulla on kaksi kombinatorista (yhdistelemiseen liittyvää) tehtävää. Lasten annetaan ensin leikkiä: 3 lasta lähetetään luokasta käytävälle ja muut yrittävät arvata, missä järjestyksessä he tulevat sisään. Tehtävä toistetaan useamman kerran. Peliä voidaan pelata myös kasvojen ilmeillä: iloinen, tavallinen, surullinen. Tämän jälkeen lapset siirtyvät piirrostehtävään. Tämänikäisiltä ei voi vielä vaatia järjestelmällisyyttä, siihen he ovat liian pieniä. Edellytetään heiltä vain sitä, ettei heidän piirroksissaan esiinny samaa järjestystä kahteen kertaan. Korjauksia saa tehdä. Dominotehtävässä huomautetaan, että tyhjä ruutukin on yksi vaihtoehdoista.
Keksitään lisää vastaavia tehtäviä. Lapset voivat värittää useammalla eri tavalla vaatteita tai lippuja, he voivat yhdistellä kirjaimia tai muodostaa kaksinumeroisia lukuja.
Viimeisillä tehtäväsivuilla halutaan muistuttaa, että opetuksessa on koko vuoden ajan esiinnyttävä useampia matemaattisia aiheita, matematiikka ei ole vain aritmetiikkaa. 62 tehtäväsivua eivät korvaa kirjaa ja harjoituskirjaa, vaan niillä pyritään antamaan ideoita ja laajentamaan opettajien keinovalikoimaa. Olemme pyrkineet herättämään kollegoissamme luovalle opettajalle ominaisen terveellisen tunteen: "Tuollaisia minäkin osaan keksiä." Työn iloa ja paljon uusia ideoita!
Terveisin
Márta Oravecz ja Ágnes Kivovics
Lukijalle: Tehtäväsivujen käännöksiä tarkistetaan vielä. Jos löydätte painovirheitä tai muita ongelmallisia kohtia, ilmoittakaa siitä esim. sähköpostilla osoitteeseen toimitus@matematiikkalehtisolmu.fi.
Katsokaa myös http://www.polvijarvi.fi/koulut/ruvaslahti/.