Useimmat differentiaali- ja integraalilaskennan keskeiset ideat olivat olemassa jo 1600-luvun puoliväliin mennessä. Kuitenkin vasta Isaac Newton (1642-1727) ja Gottfried Wilhelm Leibniz (1646-1716) oivalsivat pinta-alanmääritys- ja tangenttitehtävien yhteyden sekä kehittivät aiemmin yksittäisiin tehtäviin sovelletuista keinoista yhtenäisen laskennallisen metodin, kalkyylin. Aikanaan väiteltiin paljon siitä, olivatko keksijät itsenäisiä vai jäljittelikö Leibniz Newtonia (toiseen suuntaan tapahtunutta plagiointia ei liene epäilty). Tarkempien todisteiden puutteessa on varminta olettaa, että Newton ja Leibniz kehittivät oppirakennelmansa toisistaan riippumatta.
Newton kiinnostui matematiikasta vasta opiskeluvuosinaan Cambridgessä, jossa matematiikkaa opetti Isaac Barrow. Suurimmat tieteelliset keksintönsä binomisarjan, differentiaali- ja integraalilaskennan sekä yleisen painovoimalain, hän teki vuosina 1665-66, vielä opiskelijana, kun yliopisto oli suljettuna kulkutautiepidemian vuoksi. Kuten Newton itse vanhana kirjoitti:
''All this was in the two plague years 1665 & 1666 for in those days I was in the prime of my age for invention and minded Mathematics and Philosophy more than at any time since.''
Binomikaava oli positiivisten kokonaislukueksponenttien tapauksessa vanhastaan tunnettu (Pascalin kolmio). Newton ei kuitenkaan johtunut binomisarjaan suoraan binomikaavaa yleistämällä. Tosiasiassa hän tutki Wallisin määrittämiä käyrien y= (1-x2)n/2 alle jääviä pinta-aloja, jotka parillisilla n:n arvoilla ovat x:n polynomeja. Parittomia n:n arvoja vastaavat alat Wallis sai parillisista tietyllä interpolointimenettelyllä. Newtonin keskeinen huomio oli, että myös itse (1- x2)n/2 voitiin parittomilla n:n arvoilla interpoloida tunnetuista parillisten arvojen lausekkeista pinta-alakaavojen kanssa yhteensopivalla tavalla. Tämä interpoloimalla saatu kaava oli sitten yleistettävissä mielivaltaisille eksponenteille.
Newtonin binomisarja tuli julkisuuteen 1676. Binomisarja, vaikkakin ilman suppenemistarkasteluja, antoi matematiikan käyttöön erittäin tärkeän uuden työkalun, mahdollisuuden esittää funktioita äärettömien prosessien avulla, ei ainoastaan approksimaatioina vaan tarkasti.
Newtonin ensimmäinen differentiaali- ja
integraalilaskentaa käsittelevä käsikirjoitus on vuodelta
1666, ja vuonna 1669 kirjoitettu De analysi per æquationes
numero terminorum infinitas liikkui käsikirjoituksena
Englannissa. Newtonin differentiaalilaskennan perustana oli
fysikaalinen analogia: käyrän voi ajatella syntyvän kahdella
akselilla liikkuvien pisteiden liikkeiden yhdistämisestä. Jos
x ja y ovat ajan funktioita, Newtonin sanastossa fluentteja,
niin ne saavat lyhyenä aikana o lisäykset
po ja qo. Käyrän f(x,y)=0 tangentin kulmakerroin on
![]() eli y:n ja x:n hetkellisten muutosten suhde.
Tämän suureen laskemiseksi Newton käytti binomisarjaa.
Esim. käyrän yn=xm kulmakertoimen määrittämiseksi
lasketaan binomisarjasta ja yhtälöstä
(y+oq)n=(x+op)m ja
o:lla jakaen ja sen jälkeen o-termit unohtaen
eli y:n ja x:n hetkellisten muutosten suhde.
Tämän suureen laskemiseksi Newton käytti binomisarjaa.
Esim. käyrän yn=xm kulmakertoimen määrittämiseksi
lasketaan binomisarjasta ja yhtälöstä
(y+oq)n=(x+op)m ja
o:lla jakaen ja sen jälkeen o-termit unohtaen
Differentiaali- ja integraalilaskennan kehityksen
ratkaiseva askel oli derivointi- ja integrointioperaatioiden
käänteisyyden havaitseminen. Tämän huomion Newton teki
tarkastellessaan käyrän y = f(x) alle jäävää
pinta-alaa: jos kyseinen ala on esim.
Newton nimitti fluenttiensa eli funktioidensa x ja y''aikaderivaattoja'' p ja q fluksioiksi; niiden
merkinnät olivat ![]() ,
,
![]() .
Vastaavasti fluentteja,
joiden fluksiot ovat x, y merkittiin
.
Vastaavasti fluentteja,
joiden fluksiot ovat x, y merkittiin ![]() ,
,
![]() .
Nämä merkinnät säilyivät Brittein saarilla viime
vuosisadan lopulle asti, ja mekaniikassa niitä käytetään
vielä nykyäänkin. Fluksiolaskennan piiriin kuului
kahdenlaisia tehtäviä: fluenttien välisistä relaatioista
johdettiin fluenttien ja niiden fluksioiden välisiä
relaatioita tai fluenttien ja fluksioiden välisistä
relaatioista pelkkien fluenttien relaatioita. Edellinen
tehtävä vastaa derivointia ja jälkimmäinen
differentiaaliyhtälön ratkaisemista.
.
Nämä merkinnät säilyivät Brittein saarilla viime
vuosisadan lopulle asti, ja mekaniikassa niitä käytetään
vielä nykyäänkin. Fluksiolaskennan piiriin kuului
kahdenlaisia tehtäviä: fluenttien välisistä relaatioista
johdettiin fluenttien ja niiden fluksioiden välisiä
relaatioita tai fluenttien ja fluksioiden välisistä
relaatioista pelkkien fluenttien relaatioita. Edellinen
tehtävä vastaa derivointia ja jälkimmäinen
differentiaaliyhtälön ratkaisemista.
Analyysin perusteiden kannalta olennainen raja-arvon
käsite ei ollut Newtonille aivan selvä. ''Pienet lisäykset''
ovat tarpeen mukaan tasan nollia, jolloin ne voidaan pyyhkiä
pois, tai pieniä nollasta eroavia lukuja, jolloin niillä voi
supistaa. Derivaattaa määritellessään Newton käyttää
puhetapaa häviävien suureiden viimeinen suhde tai
syntyvien suureiden ensimmäinen suhde, silloin kun
nykymatematiikka tarkastelee raja-arvoa
Newtonin pääteos on monumentaalinen Philosophiæ Naturalis Principia Mathematica (1687), mekaniikan ja gravitaation yleisesitys. Principian matemaattiset metodit ovat lähes kauttaaltaan traditionaalisia. On arveltu, että Newton olisi johtanut Principian tulokset differentiaali- ja integraalilaskennan avulla ja pukenut sitten todistukset euklidiseen asuun. Tätä väitettä ei ole voitu todentaa. Newton ei juuri julkaissut elinaikanaan puhtaasti matemaattisia töitä. Ensimmäinen painettu versio hänen differentiaali- ja integraalilaskennastaan oli 1704 ilmestyneen Opticks-teoksen liitteenä julkaistu De quadratura curvarum, ja hänen tärkein matemaattinen tutkielmansa oli Methodus fluxionum et serierum infinitorum, joka kirjoitettiin 1671, mutta julkaistiin vasta 1736.
Viimeksi mainitussa teoksessa Newton esittää myös
sittemmin Newtonin menetelmän nimellä tunnetun
likimääräisen menetelmän yhtälön ratkaisemiseksi.
Tämä menetelmä perustuu funktion kuvaajan korvaamiseen
funktion tangentilla. Newton kuitenkin johti menetelmän
binomisarjan avulla. Jos ratkaistavana on yhtälö
Approksimaatiomenetelmäänsä Newton käytti uusien
sarjakehitelmien muodostamiseen. Esimerkiksi
Nicolaus Mercatorin (1620-87)
(joka on eri henkilö kuin
Mercatorin projektion esittäjä
Gerhardus Mercator
(1512-94)) ja Newtonin itsensä johtamasta käyrän y(1+x)=1ja x-akselin väliin jäävän alueen pinta-alan (eli
![]() :n) sarjasta
:n) sarjasta
![]() Newton ratkaisi
Newton ratkaisi
![]() ,
eli sai eksponenttifunktion
ez-1 sarjan. Samoin Newtonin binokaavan johdon yhteydessä
saama integraalin
,
eli sai eksponenttifunktion
ez-1 sarjan. Samoin Newtonin binokaavan johdon yhteydessä
saama integraalin
Newtonin panos analyyttisen geometrian kehitykselle on myös merkittävä. Hän suoritti kolmannen asteen käyrien luokittelun, jota pidetään ensimmäisenä täysin uutena analyyttisen geometrian avulla saavutettuna tuloksena - aikaisemmin oli vain johdettu uudelleen mm. Apollonioksen jo tuntemia totuuksia.
Newton toimi 30 vuotta Cambridgen yliopiston professorina - tähän asemaan hän pääsi Barrowin luovuttua 1669 vapaaehtoisesti oppituolistaan lahjakkaan oppilaansa hyväksi - ja myöhemmin Englannin rahapajan johtajana. Newtonin toiminta yliopistonopettajana ei juuri jättänyt pysyviä jälkiä. Huomattavan osan tieteellisistä ponnisteluistaan Newton omisti alkemistisille yrityksille muuttaa halpoja metalleja kullaksi sekä teologialle - Newton oli erityisen kiinnostunut varhaiskristillisyydestä ja aikoinaan kolminaisuusopille hävinneestä areiolaisuudesta.
Filosofi ja yleisnero Leibniz oli kotoisin Leipzigista. Hän oli poikkeava lahjakkuus jo nuorena: Leipzigin yliopiston kateelliset professorit hylkäsivät hänen filosofian alaan kuuluneen loistavan väitöskirjansa, koska tekijä oli liian nuori, vain 20-vuotias. (Tohtorinarvonsa Leibniz toki sai seuraavana vuonna Nürnbergin yliopistosta, juridiikan opetusta käsittelevällä työllä, jonka hän oli kirjoittanut matkalla Leipzigista Nürnbergiin.) Leibnizin leipätyönä olivat diplomaattiset ja hallintotehtävät ensin Mainzin arkkipiispan ja sitten Hannoverin vaaliruhtinaan palveluksessa. Leibnizin aikaansaannokset ulottuvat filosofian ja matematiikan lisäksi ainakin juridiikan, politiikan, teologian, historian, geologian ja fysiikan aloille. Matemaatikkona Leibniz oli itseoppinut ja joutui itseoppineiden tapaan keksimään uudelleen monia jo tunnettuja asioita.
Matematiikan historiassa Leibniz muistetaan paitsi differentiaali- ja integraalilaskennan toisena keksijänä myös symbolisen logiikan ja mekaanisen laskennan edelläkävijänä. Hän kaavaili universaalikalkyylia, jota käyttäen kaikki filosofian ongelmat voitaisiin yksiselitteisesti ratkaista laskemalla. Leibniz rakensi laskukoneita ja ennusti niille tulevaisuutta: ''Ei ole järkevää, että viisaat miehet kuluttavat orjien tavoin tuntikausia laskutoimituksiin, jotka kuka tahansa voisi helposti suorittaa koneiden avulla.''
Newtonin tavoin myös Leibniz sai ensimmäiset
herätteet differentiaali- ja integraalilaskentaan
päättymättömistä sarjoista. Sarjateoriassa Leibnizin
oivallus oli tarkastella sarjan termejä jonkin lukujonon
peräkkäisten termien erotuksena. Näin hän esim. pystyi
laskemaan summan
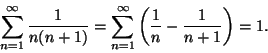
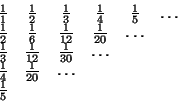
Toisesta rivistä alkaen kunkin vaakarivin alkioiden summa on välittömästi yläpuolella olevan rivin ensimmäinen alkio. Tälle ilmiölle on sukua funktion kuvaajan alle jäävän pinta-alan lausuminen toisaalta funktion integraalifunktion ''viereisten arvojen'' erotuksien summana, toisaalta alkuperäisen funktion arvojen summana.
Vuonna 1673 Leibniz tutustui aikaisemmin mainittuun
Pascalin sinifunktiota käsittelevään tutkimukseen.
Tällöin hänelle valkeni ''karakteristisen kolmion''
![]() yleinen käyttökelpoisuus; yksinkertainen
geometrinen tarkastelu johti pinta-alanmäärityksen,
''integroimisen'', tehtäväksi, jossa on konstruoitava käyrä,
kun sen tangentit tunnetaan. Pascal oli tarkastellut vain
r-säteisen ympyränkehän erikoistapausta, ja päätynyt
karakteristisen kolmion ja kolmion, jonka kärjet ovat ympyrän
keskipiste, kehän piste ja sen projektio x-akselilla,
yhdenmuotoisuudesta olennaisesti relaatioon
yleinen käyttökelpoisuus; yksinkertainen
geometrinen tarkastelu johti pinta-alanmäärityksen,
''integroimisen'', tehtäväksi, jossa on konstruoitava käyrä,
kun sen tangentit tunnetaan. Pascal oli tarkastellut vain
r-säteisen ympyränkehän erikoistapausta, ja päätynyt
karakteristisen kolmion ja kolmion, jonka kärjet ovat ympyrän
keskipiste, kehän piste ja sen projektio x-akselilla,
yhdenmuotoisuudesta olennaisesti relaatioon
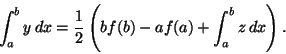
Leibniz alkoi 1684 julkaista differentiaalilaskentaansa koskevia tiedonantoja toimittamassaan Acta Eruditorum Lipsienium (Leipzigin oppineiden toimituksia) -nimisessä aikakauskirjassa. Ensimmäiseen, kuusisivuiseen julkaisuun sisältyi myös ensimmäinen uuden analyysin fysikaalinen sovellus: valon taittumista kahden väliaineen rajapinnassa koskevan Snellin lain johto ''kuin taikatempulla''. - 1600-luvun oppineitten lähes ainoa keino kertoa suhteellisen nopeasti tuloksistaan oli kirjeenvaihto; tieteellisten aikakauslehtien syntyminen vilkastutti merkittävästi tiedonvälitystä.
Leibnizin käyttämät symbolit olivat onnistuneita.
Vaikka dx:n ja dy:n täsmällistä merkitystä ei
määritelläkään, niillä operoiminen on intuitiivisesti
selvää ja johtaa oikeisiin tuloksiin. ''Ketjusääntö''
''
![]() '' on ymmärrettävä muodossa
'' on ymmärrettävä muodossa
Alkuun - Etusivu - Edellinen - Seuraava