Toisen asteen yhtälön ratkaiseminen

Keskustelupalstalla oli http://matematiikkalehtisolmu.fi/palautteet/2001/syys2001.html Tomi Tukiaisen kysymys toisen asteen yhtälön ratkaisukaavan johtamisesta. Hieman hämmästelin, että sitä ei koulussa ole esitetty, mutta uskottavahan se on.

Kysyjä viittaa Eero Saksmanin mainioon kirjoitukseen kolmannen asteen yhtälöstä, jossa käytetään toisen asteen yhtälön ratkaisukaavaa. http://matematiikkalehtisolmu.fi/2000/2/saksman/

Kuten Saksman mainitsee, toisen asteen yhtälön ratkaisukaavan johtaminen on olennaisesti yksinkertaisempaa kuin kolmannen. Ainoa ``syvällisempi'' piirre liittyy kompleksilukuihin, jotka myös tässä toisen asteen yhtälön tapauksessa astuvat luontevasti näyttämölle.

Reaaliluvuissa pitäytyvää lukijaa ajatellen voidaan kysymys asettaa myös puhtaasti niitä koskevana, jolloin ratkaisukaava antaa kaksi, yksi tai ei yhtään reaalijuurta.

Yksinkertainen erikoistapaus

Toisen asteen yhtälöä voidaan lähestyä vaiheittain aloittamalla ensin kaikkein yksinkertaisimmasta. Olkoon yhtälömme aluksi vaikkapa x²=3, jonka ratkaisut ovat $x_1=\sqrt{3}$ ja $x_2=-\sqrt{3}$ . Kirjoitamme yhtälön muotoon

x² -3 = 0.

(1)

Seuraavaksi siirrämme yhtälön vasenta puolta kuvaavan paraabelin huipun pisteeseen x=2, ts. katsomme vaikkapa yhtälöä

(x-2)²-3 = 0.

(2)

Ratkaisun voimme kirjoittaa taas suoraan:

$\displaystyle (x-2)=\pm \sqrt{3}, \textrm{eli} \ \ x_1=2+\sqrt{3},\ \ x_2=2-\sqrt{3} .$

(3)

Erikoistapauksesta yleiseen

Toisen asteen yhtälön yleinen muoto on

ax²+bx+c=0,

josta jakamalla kertoimella a saadaan muoto

x² + px +q =0

(Jakaminen on luvallista, koska $a\ne 0$ , muutenhan kyseessä ei olisi toisen asteen yhtälö).

Peruskaava, johon koko ajan nojaamme, on binomin neliön kaava:

(a+b)² = a² + 2ab + b²

Tämän mukaan auki kerrottuna yhtälö (2) tulee muotoon

x² -4 x +4 = 3

(4)

Kysymys on nyt siitä, miten pääsemme tästä muodosta takaisin edelliseen muotoon (2). Tässä tapauksessa meidän tarvitsee vain osata lukea binomin neliön kaavaa takaperin. Vasemmalla on lukujen x ja -2 neliöt ja niiden kaksinkertainen tulo (-4x), siitä saamme binomin neliön (x-2)².

Yleinen päättely esimerkin avulla

Entä, jos yhtälömme olisikin esimerkiksi

x² +3 x +1 =0

(5)

Tällöin yritämme järjestää vasemmalle puolelle binomin neliön. Meillä on neliö: x², joten toinen luku on x. Kaksinkertainen tulo on 3 x, joten toisen luvun on oltava $\frac{3}{2}$ , jonka neliö on $\frac{9}{4}$ . Siispä lisäämme tämän luvun yhtälöön puolittain ja siirrämme ylimääräisen termin 1 oikealle puolelle, jolloin saamme:

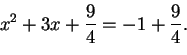
$\begin{displaymath}x^2 +3 x + \frac{9}{4} = -1 + \frac{9}{4}. \end{displaymath}$

Järjestimme näin vasemman puolen binomin neliöksi $(x+\frac{3}{2})^2$ , joten olemme muokanneet yhtälön muotoon

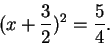
$\begin{displaymath}(x+\frac{3}{2})^2 =\frac{5}{4}. \end{displaymath}$

Tästä saamme ratkaisut neliöjuuren otolla, kuten edellä:

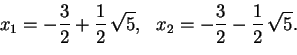
$\begin{displaymath}x_1=-\frac{3}{2}+\frac{1}{2}\,\sqrt {5},\ \ x_2=-\frac{3}{2}-\frac{1}{2}\,\sqrt {5} .\end{displaymath}$

Yllä olevassa esimerkissä käyttämämme menettely on nimeltään neliöksi täydentäminen. Sen voimme yhtä hyvin tehdä mielivaltaisten kertoimien tapauksessa.

Ratkaisualgoritmimme on nyt periaatteessa valmis, voimme aina tehdä yllä kuvatun neliöksi täydentämisen ja saamme tehtävän palautumaan neliöjuuren ottoon.

Voisimmeko siis lopettaa tähän? Muuten kyllä, mutta entä jos yhtälön oikea puoli on negatiivinen? Jos haluamme rajoittua reaalilukuihin, voimme todeta, että silloin yhtälöllä ei ole ratkaisuja, eihän minkään luvun neliö ole negatiivinen.

Kompleksijuurista

Palatkaamme ensimmäiseen yhtälöömme muuttaen sen oikea puoli -1:ksi. Siis x² =-1, eli

x²+1=0.

Vasemman puolen kuvaaja sijaitsee kokonaan x-akselin yläpuolella joten leikkauspisteitä x-akselin kanssa ei ole.

Reaalista ratkaisua ei ole, mutta nytpä voimmekin laajentaa lukualuetta, jolta ratkaisua etsimme. Voi tuntua epäreilulta sääntöjen muuttamiselta kesken pelin, mutta tällaiset katsantokannan laajentamiset ovat hyvin usein matematiikassa osoittautuneet erinomaisen hedelmällisiksi.

Otamme käyttöön kompleksiluvut, jotka voidaan määritellä reaalilukujen pareina ja havainnollistaa lukusuoran sijasta tason pistejoukkona. Lyhyt katsaus kompleksilukujen perusominaisuuksiin on http://matematiikkalehtisolmu.fi/2000/2/saksman/ Saksmanin kirjoituksen lopussa.

Kompleksialueella voidaan ottaa neliöjuuri myös negatiivisista luvuista, tapana on merkitä $i=\sqrt{-1}$ . Tason pisteenä i=(0,1), eli y-akselin yksikköpiste.

Palaamme yleistä tilannetta kuvaavaan yhtälöömme (5) lisäämällä vasemman puolen vakiotermin riittävän suureksi, jotta kuvaaja on kokonaan x-akselin yläpuolella, esimerkiksi

x² + 3 x + 3=0 .

(6)

Kompleksiluvuilla lasketaan muodollisesti samoin kuin reaaliluvuilla, kunhan käytetään sääntöä $\sqrt{-1}=i.$ Ottamalla tämä huomioon ja menettelemällä muuten yllä esitetyllä tavalla, saadaan

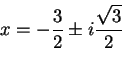
$\begin{displaymath}x=-\frac{3}{2}\pm i\frac{\sqrt{3}}{2} \end{displaymath}$

Yleinen muoto

Nyt voimmekin esittää yleisen menetelmän yhtälön

x² + p x + q =0

ratkaisemiseksi. Jotta saamme binomin neliön vasemmalle, on lisättävä puolittain luku $(\frac{p}{2})^2$

$x^2 + p x + q =0 \iff x^2 + p x + (\frac{p}{2})^2 +q =(\frac{p}{2})^2$ $\iff (x+\frac{p}{2})^2 = (\frac{p}{2})^2-q$ .

Nyt vain otamme neliöjuuren. Lopullinen kaava on siten:

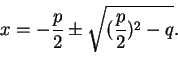
$\begin{displaymath}x=-\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} .\end{displaymath}$

Juurrettavana olevaa lauseketta $(\frac{p}{2})^2-q$ kutsutaan diskriminantiksi, merkittäköön sitä D:llä. Ratkaisujen lukumäärän suhteen näemme kaavasta, että reaalisia ratkaisuja on 2, jos D > 0 ja yksi, jos D = 0. Tapauksessa D <0ei reaalisia ratkaisuja ole, kompleksitasossa niitä on kaksi ja ne saadaan kirjoittamalla juurrettavaksi -D ja ottamalla i eteen tekijäksi.

Jääköön lukijalle harjoitustehtäväksi lausua kertoimet p ja qyhtälön ax² + bx + c = 0 kertoimien a,b,c avulla ja johtaa näin kaavan toinen yleisesti käytetty muoto.

8.10.2001, Heikki Apiola

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

Paluu palautepalstan lokakuun viesteihin

Matematiikkalehti Solmu
2001-10-08