Rekonstruktiokonjektuuri verkkoteoriassa
Milo Orlich
Matematiikan ja systeemianalyysin laitos, Aalto-yliopisto
milo.orlich@aalto.fi
Vapaasti kuvailtuna verkko (tai graafi) on jotakin, joka näyttää tältä:

Verkko koostuu siis solmuista (“paksuista pisteistä”) ja kaarista (“viivoista”). Kaksi solmua voi liittyä toisiinsa kaarella tai ei. Joissakin tilanteissa verkossa voi olla “silmukka”, eli jokin solmu voi yhdistyä itseensä, tai kahden solmun välillä voi olla enemmän kuin yksi kaari, tai jokaisella kaarella voi olla suunta, esimerkiksi näin:
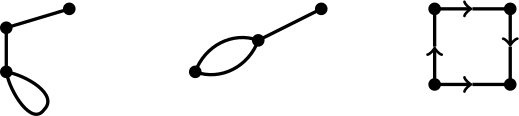
Emme ota huomioon näitä mahdollisuuksia tässä kirjoituksessa.
Esimerkki 1. Koska verkon käsite on niin yksinkertainen ja abstrakti, sitä käytetään monella matematiikan alalla ja muissa tieteissä. Verkkojen avulla voi mallintaa monimutkaisilta näyttäviä tosielämän tilanteita:
Facebookin käyttäjät ovat ison verkon solmut, ja kaksi käyttäjää yhdistyy kaarella, jos he ovat Facebook-kavereita.
Kaikki maailman asukkaat ovat vielä isomman verkon solmut, ja kaksi ihmistä yhdistyy kaarella, jos he ovat jossakin vaiheessa kätelleet.
Kartassa olevat valtiot ovat verkon solmut, ja kaksi valtiota yhdistyy kaarella, jos niillä on yhteistä rajaa:
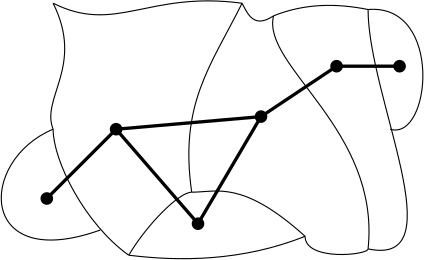
Seuraavaksi esitetään verkon määritelmä.
Määritelmä 2. Verkko \(V\) on järjestetty pari \((S_V,K_V)\), jossa \(S_V\) on äärellinen joukko, jonka alkioita kutsutaan verkon \(V\) solmuiksi, ja \(K_V\) on joukko joukkoja, jotka koostuvat tarkalleen kahdesta solmusta ja joita kutsutaan verkon \(V\) kaariksi.
Esimerkki 3. Jos \(V\) on ensimmäisessä kuvassa oleva verkko, niin \[\begin{align*} S_V&=\{a,b,c,d,e,f\},\\ K_V&=\Big\{\{a,b\},\,\{a,c\},\,\{a,d\},\,\{b,d\},\,\{d,e\},\,\{e,f\}\Big\}. \end{align*}\]
Tämä vaivalloinen verkon määritelmä voi vaikuttaa hankalalta ja epäselvältä, mutta sen avulla suurien verkkojen tutkiminen on mahdollista tietokoneella, ja se on täsmällisempi kuin “piirustus” matemaatikon näkökulmasta. On tärkeää huomata, että piirustus on vain visuaalinen apu. Esimerkiksi nämä kaksi piirustusta esittävät samaa verkkoa:

Syy on se, että “kunnon” verkko \(V\) on pari \((S_V,K_V)\).
Viitteet: Verkoista kirjoitettiin mm. Solmun artikkeleissa [2] ja [3]. Hyvä kirja on esimerkiksi [1], jota käytetään Aalto-yliopiston verkkoteorian kurssilla oppikirjana.
Kun tutustuu uuteen matemaattiseen käsitteeseen, voi olla hyödyllistä ajatella sitä kombinatorisesti, eli kysyä “Kuinka monta …?” -kysymyksiä.
Esimerkki 4.
On olemassa vain yksi verkko, jolla on tarkalleen yksi solmu \(a\):
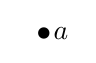
Tällä verkolla ei ole kaarta. (Mutta on olemassa äärettömän monta yksisolmuista verkkoa, koska on olemassa äärettömän monta yksiötä! Solmujoukko voi olla \(\{a\}\), \(\{b\}\), \(\{c\},\dots,\{1\}\), \(\{2\}\), \(\{3\},\dots,\) \(\{\text{Helsinki}\}\), \(\{\text{Uranus}\}\), \(\{\text{Teräsmies}\}\), jne.)
On olemassa kaksi verkkoa, joiden solmujoukko on \(S=\{a,b\}\); toisella ei ole kaarta, ja toisella on tarkalleen yksi kaari:

On olemassa kahdeksan verkkoa, joiden solmujoukko on \(S=\{a,b,c\}\):
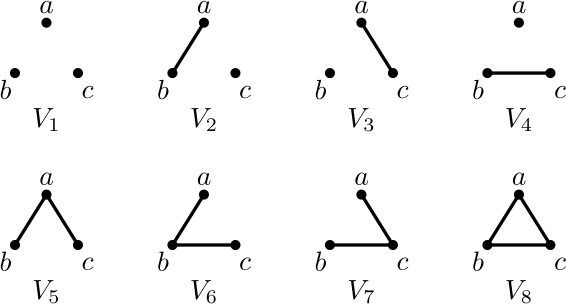
Entä, jos \(S=\{a,b,c,d\}\)?
Tehtävä 5. Kuinka monta kaarta voi korkeintaan olla verkossa, jossa on \(n\) solmua?
Tehtävä 6. Kuinka monta erilaista verkkoa on olemassa, jos solmujoukko on \(S=\{s_1,\dots,s_n\}\)?
Isomorfiset verkot
Kaksi verkkoa voi “näyttää samalta”, jos solmujen nimet unohdetaan. Esimerkin 4.3 verkot \(V_2\), \(V_3\) ja \(V_4\) ovat samannäköisiä: jokaisella on yksi kaari ja erillinen solmu. Verkot \(V_5\), \(V_6\) ja \(V_7\) näyttävät kaikki V-kirjaimelta. Kuten jo huomattiin, on itse asiassa olemassa äärettömän monta verkkoa, jotka näyttävät samalta, kun solmujen nimet unohdetaan!
Tämän koko tarinan tarkka nimi on verkkojen isomorfismi. (Isomorfismin täsmällinen määritelmä on alla. Muuten sana “isomorfismi” tulee kreikasta: “isomorfinen” on kirjaimellisesti “samanmuotoinen”.)
Esimerkki 7.
Kaikki yksisolmuiset verkot ovat keskenään isomorfisia. Toisin sanoen, jos solmun nimi unohdetaan, niin ainoa yksisolmuinen verkko näyttää tältä:

Jokainen kaksisolmuinen verkko on isomorfinen joko ensimmäisen tai toisen seuraavassa kuvassa olevan verkon kanssa:

Jos siis solmujen nimet unohdetaan, on olemassa vain kaksi kaksisolmuista verkkoa.
Jos solmujen nimet unohdetaan, on olemassa vain neljä kolmisolmuista verkkoa:

Tehtävä 8. Kun solmujen nimet unohdetaan, kuinka monta nelisolmuista verkkoa on olemassa? (Voit myös tutkia tapausta, jossa solmujoukko koostuu viidestä solmusta, mutta vastaus on \(>30\).)
Kuten verkon käsite itse, verkkojen isomorfismi on melko intuitiivinen asia. Se on valitettavasti vielä liian epämääräinen: tietokone ei voisi tehdä mitään “epämääräisen, mutta intuitiivisen” idean avulla, ja verkkojen piirtämisestä tulee nopeasti liian vaikeaa ihmisille, joten tarvitaan tietokonetta ja täsmällistä määritelmää.
Muista, että bijektio \(\varphi\colon A\to B\), missä \(A\) ja \(B\) ovat joukkoja, on sekä injektio että surjektio, eli bijektio on sellainen funktio, että:
jos \(a\ne a'\), niin \(\varphi(a)\ne\varphi(a')\),
jokaisella alkiolla \(b\in B\) on olemassa sellainen \(a\in A\), että \(\varphi(a)=b\).
Määritelmä 9. Verkkoja \(V\) ja \(W\) kutsutaan isomorfisiksi, jos on olemassa sellainen bijektio \(\varphi\colon S_V\to S_W\), että kaikilla solmuilla \(s,s'\in S_V\) pätee \[\{s,s'\}\in K_V\quad\Leftrightarrow\quad\{\varphi(s),\varphi(s')\}\in K_W.\] Tällaista bijektiota kutsutaan verkkojen \(V\) ja \(W\) isomorfismiksi. Jos isomorfismi on olemassa, niin kirjoitetaan \(V\cong W\). Jos ei, niin kirjoitetaan \(V\not\cong W\). Joukko, joka koostuu kaikista verkon \(V\) kanssa isomorfisista verkoista, on verkon \(V\) isomorfialuokka.
Esimerkki 10. Verkoille

on olemassa kaksi erilaista isomorfismia: \[\begin{array}{rcl} a&\leftrightarrow&1\\ b&\leftrightarrow&2 \end{array}\qquad\text{ja}\qquad \begin{array}{rcl} a&\leftrightarrow&2\\ b&\leftrightarrow&1. \end{array}\]
Tehtävä 11. Kirjoita eksplisiittisesti edellisen esimerkin tapaan isomorfismi \[a\leftrightarrow \varphi(a),\qquad b\leftrightarrow \varphi(b),\qquad c\leftrightarrow \varphi(c),\] \[d\leftrightarrow \varphi(d),\qquad e\leftrightarrow \varphi(e)\] seuraaville kahdelle verkolle:
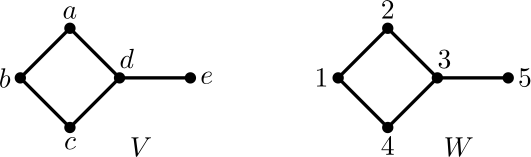
Kuinka monta erilaista isomorfismia on olemassa?
Entä, jos otetaan verkot

niin kuinka monta erilaista isomorfismia on olemassa?
Invariantit
Vaikka verkkojen isomorfismi määritellään huolellisesti, ongelma on se, että on vaikeaa saada selville, onko olemassa kahden annetun verkon isomorfismi vai ei. Joku voisi periaatteessa testata jokaisen mahdollisen bijektion ja tarkistaa, onko se isomorfismi, mutta tämä on todella hidas algoritmi. Siksi verkkoteoreetikot tutkivat mahdollisesti auttavia “invariantteja”. Verkon invariantti on suure tai ominaisuus \(\varphi\), joka on sama isomorfisille verkoille. Eli jos \(V\cong W\), niin \(\varphi(V)=\varphi(W)\). Esimerkiksi solmujen tai kaarten määrät ovat invariantteja:
Jos verkot \(V\) ja \(W\) ovat isomorfisia, niin niillä on sama solmujen määrä ja sama kaarten määrä.
Päinvastainen lause ei pidä paikkaansa:
Tehtävä 12. Etsi kaksi sellaista verkkoa \(V\) ja \(W\), joilla on sama solmujen määrä ja sama kaarten määrä, mutta \(V\) ja \(W\) eivät ole isomorfisia.
Määritelmä 13. Olkoon \(s\) verkon \(V\) solmu. Solmun \(s\) asteluku \(al(s)\) on solmuun \(s\) liittyvien solmujen lukumäärä. Verkon astelukujen jono koostuu kaikista asteluvuista, suurimmasta pienimpään.
Esimerkki 14. Alla olevassa verkossa, \(al(d)=3\), \(al(a)=al(b)=al(c)=2\) ja \(al(e)=1\).
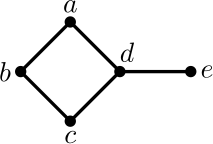
Astelukujen jono on siten \((3,2,2,2,1)\).
Huomaa, että:
asteluvuista voi laskea kaarten lukumäärän: \[\frac12\sum_{s\in{S_V}}al(s)=|K_V|,\]
jos \(V\cong W\), niin verkkojen \(V\) ja \(W\) astelukujen jonot ovat samat.
Tehtävä 15. Etsi kaksi verkkoa, joilla on sama solmujen määrä ja sama kaarten määrä, mutta eri astelukujen jonot.
Tehtävä 16. Etsi sellaiset verkot \(V\) ja \(W\), joiden astelukujen jonot ovat samat, mutta \(V\not\cong W\).
Verkon pakka ja konjektuuri
Multijoukko on sellainen joukon yleistys, jossa jokaisella alkiolla on oma “toistoluku”, joka voi olla suurempi kuin \(1\). Jokainen alkio voi siis esiintyä multijoukossa enemmän kuin yhden kerran.
Määritelmä 17. Jokaiselle solmulle \(s_i\in S_V=\{s_1,\dots,s_n\}\) määritellään verkko \(V-s_i\) poistamalla solmu \(s_i\) ja kaikki solmuun \(s_i\) liittyvät kaaret. Multijoukko, joka koostuu verkkojen \(V-s_1,\dots,V-s_n\) isomorfialuokista, on verkon \(V\) pakka, ja sitä merkitään symbolilla \(P(V)\). Pakan alkioita kutsutaan korteiksi.
Esimerkki 18. Jos \(V\) on esimerkissä [14] oleva verkko, niin saadaan
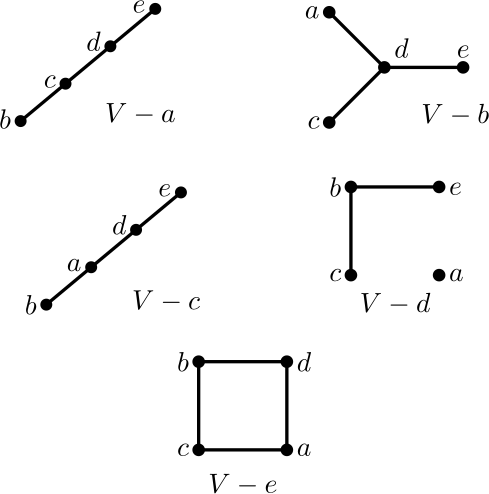
Siten verkon \(V\) pakka \(P(V)\) on multijoukko
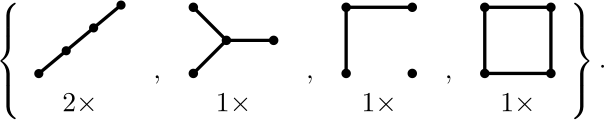
On tärkeää muistaa, että jokaiselle verkolle \(V-s_i\) laitamme pakkaan vain sen isomorfialuokan, eli emme tiedä, minkä solmun poistamalla saimme tämän kortin.
Verkon pakka muistaa kuitenkin joitakin alkuperäisen verkon tietoja. Esimerkiksi verkon \(V\) solmujen määrä on sama kuin korttien määrä, tai myös jokaisen kortin solmujen määrä plus \(1\).
Tehtävä 19. Todista, että:
jos \(k_i\) on verkon \(V-s_i\) kaarten määrä, niin \[|K_V|=\frac1{n-2}\sum_{i=1}^nk_i,\]
verkon pakasta voi laskea sen astelukujen jonon,
\(V\cong W\Rightarrow P(V)=P(W)\), eli pakka on verkon invariantti.
Seuraavaksi esitetään vanha konjektuuri, eli avoin ongelma, jota verkkoteoreetikot ovat yrittäneet todistaa jo 70 vuotta!
Konjektuuri 20 (Kelly, Ulam). Jos \(n\ge3\), niin \(P(V)=P(W)\ \Rightarrow\ V\cong W\).
Sanallisesti ilmaistuna konjektuuri sanoo, että pakka määrää verkon isomorfialuokan: ei ole olemassa epäisomorfisia verkkoja, joilla on sama pakka. Tämä on siksi tunnettu myös “rekonstruktiokonjektuurina”.
Esimerkki 21. Osoitetaan eksplisiittisesti, että konjektuurissa oleva implikaatio pätee, jos \(n=3\). Kaikki mahdolliset kolmisolmuisten verkkojen pakat ovat
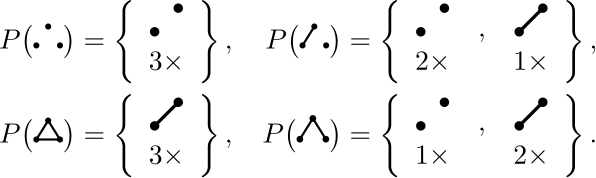
Selvästi pätee: jos \(V\not\cong W\), niin \(P(V)\ne P(W)\).
Tehtävä 22. Tarkista samalla tavalla, että konjektuurissa oleva implikaatio pätee, jos \(n=4\), mutta ei päde, jos \(n=2\).
Implikaation pätevyys on tarkistettu tietokoneella, kun \(3\le n\le13\). Konjektuuri on todistettu myös muutamassa erikoistapauksessa, eli kun \(V\) ja \(W\) kuuluvat joihinkin tiettyihin verkkoperheisiin. Jos esimerkiksi \(V\) ja \(W\) ovat niin sanottuja “puita”, tai jos jokaisella solmulla on sama asteluku, niin konjektuurin implikaatio pitää paikkansa. Aiheesta voi lukea lisää verkkosivulta [4].
Suuri kiitos arvokkaista kommenteista Pekka Alestalolle, Tuomas Kelomäelle ja Teemu Lundströmille!
Viitteet
[1] R. Diestel, Graph Theory, Springer-Verlag, Heidelberg, Graduate Texts in Mathematics, Volume 173.
[2] V. Romanov, Verkkojen teoriaa Königsbergistä internetiin (Solmu 3/2016),
https://matematiikkalehtisolmu.fi/2016/3/verkkojen_teoriaa.pdf
[3] E. V. Vesalainen, Tasograafit ja väritykset (Solmu 1/2016),
https://matematiikkalehtisolmu.fi/2016/1/varityksia.pdf
[4] Wikipedia: Reconstruction conjecture
https://en.wikipedia.org/wiki/Reconstruction_conjecture