Tarinoita polynomeista (osa 4)

Jukka Tuomela
Itä-Suomen yliopisto, Joensuu
jukka.tuomela@uef.fi

Kertaus

Jatketaan aiempien kirjoitusten polynomiteemaa [6, 7, 8]. Laskuissa viitataan jakolaskuun, jonka algoritmi on esitetty kirjoituksessa [6]. Lukijalta oletetaan, että hän tietää, mitä tarkoittaa polynomien yhteen- ja kertolasku.

Erinomainen kirja polynomeista kiinnostuneille on [3], ja erityisesti tämän kirjoituksen asioista löytyy lisätietoa kirjasta [2]. wxMaxima, jonka avulla esimerkkejä voi helposti laskea, on vapaasti saatavilla oleva symbolisen laskennan ohjelmisto.¹

Myös Sage on ilmainen ohjelmisto, jolla voi laskea sekä symbolisesti että numeerisesti [1].² Jäljempänä olevat tehtävät voi helposti laskea myös Sagen avulla. Samoin Wolfram Alphalla voi kätevästi laskea polynomeilla.³

Esimerkkeinä on taas käytetty matematiikkakilpailusivun tehtäviä.⁴

Epäyhtälöt

Aiemmissa kirjoituksissa on analysoitu polynomiyhtälöitä, ja on havaittu, että muuttujien eliminointi, tekijöihinjako ja jakolaskualgoritmi ovat työkaluja, joita jatkuvasti on hyödyllistä käyttää. Katsotaan tässä epäyhtälöitä. Havaitaan, että jakolasku on edelleen jopa yllättävän hyödyllinen, mutta epäyhtälötehtävät johtavat myös aivan uudenlaisiin ideoihin.

Koska tehtävien polynomit ovat usein homogeenisia ja/tai symmetrisiä, niin palautetaan ensin mieleen, mitä näillä tarkoitetaan.

Funktio $g$ on homogeeninen astetta $k$, jos pätee

\[g(tx_1,\dots,tx_n)=t^kg(x_1,\dots,x_n).\]

Esimerkiksi jos $x$, $y$ ja $z$ ovat kolmion sivut ja $A$ on pinta-ala, niin selvästi

\[A(tx,ty,tz)=t^2A(x,y,z),\]

kun $t>0$. $A$ ei kuitenkaan ole polynomi, mutta kuten kohta nähdään, niin $A^2$ on polynomi. Sen täytyy siis olla homogeeninen neljännen asteen polynomi.

Geometrian tehtävät usein johtavat homogeenisiin polynomeihin, koska klassisessa geometriassa ei ole mitään valittua skaalaa. Muistetaan myös viime kerralta [8], että klassisen geometrian tehtävät voidaan aina muotoilla polynomitehtävinä.

Tarkastellaan symmetriaa vain kahden ja kolmen muuttujan tapauksessa. Kahden muuttujan funktio $f$ on symmetrinen, jos $f(x,y)=f(y,x)$. Kolmen muuttujan tapauksessa tulee erilaisia symmetrian asteita. Olkoon $f$ muuttujien $x$, $y$ ja $z$ funktio. Muuttujilla on kuusi permutaatiota:

\[\begin{align*} &(x, y, z), \quad (z, x, y), \quad (y, z, x)\\ &(y, x, z), \quad (x, z, y), \quad (z, y, x). \end{align*}\]

Määritellään nyt

$f$ on symmetrinen, jos

\[\begin{align*} & f(x,y,z)=f(z,x,y)=f(y,z,x)=\\ &f(y,x,z)=f(x,z,y)=f(z,y,x). \end{align*}\]
$f$ on syklisesti symmetrinen, jos

\[f(x,y,z)=f(z,x,y)=f(y,z,x).\]

Myös symmetriaa esiintyy usein geometrian tehtävissä, koska tyypillisesti geometrisesti mielekkäät asiat eivät voi riippua siitä, miten eri asioita, kuten kolmion sivuja, nimetään.

Esimerkki 1. Äsken jo huomattiin, että $A$ on homogeeninen; sen täytyy olla myös symmetrinen, koska pinta-ala ei voi riippua siitä, miten sivut on nimetty. Edelleen pinta-ala on nolla, jos $x+y=z$, joten polynomin

\[g=(x+y-z)(x+z-y)(y+z-x)\]

täytyy olla $A^2$:n tekijä. Siis

\[A^2=c(x+y+z)g\]

jollekin $c$. Kutsutaan näin saatua polynomia Heronin polynomiksi:⁵

\[\begin{align*} h_A &=(x+y+z)g\\ &=2(x^2y^2+x^2z^2+y^2z^2)-x^4-y^4-z^4\\ &= (x^2+y^2+z^2)^2-2(x^4+y^4+z^4). \end{align*}\]

Koska tiedetään, että $A^2=1/4$, kun $x=y=1$ ja $z=\sqrt{2}$, niin $c=1/16$, joten $A^2=h_A/16$. Huomaa, että $h_A$ ei ole positiivinen kaikilla muuttujien arvoilla. $\Box$

Esimerkki 2. Olkoot $x$, $y$ ja $z$ kolmion sivut ja $A$ kolmion pinta-ala. Osoita, että⁶

\[x^2+y^2+z^2\ge 4\sqrt{3}A.\]

Tämä oli IMOn matematiikkakilpailuissa vuonna 61. Matematiikkavalmennuksen 15. tehtävä kesällä 2022 oli muuten sama, mutta vakion $4\sqrt{3}$ tilalla oli $6$.

Heronin polynomin avulla nähdään, että

\[\begin{align*} f &=\tfrac{1}{2}\Big((x^2+y^2+z^2)^2-3h_A\Big)\\ &= 3(x^4+y^4+z^4)-(x^2+y^2+z^2)^2\\ &=(x^2-y^2)^2+(x^2-z^2)^2+(y^2-z^2)^2\ge0. \end{align*}\] Selvästi yhtäsuuruus pätee vain, jos $x=y=z$. $\Box$

Esimerkin ratkaisussa tuli ilmi eräs tärkeä strategia: pyritään kirjoittamaan polynomi summana, jonka jokainen termi on jotenkin selvästi positiivinen. On osoittautunut, että tuo neliöllinen tapaus on niin tärkeä, että sille on annettu oma nimi:

$f$ on sos-polynomi (sum of squares), jos on olemassa polynomit $q_j$ siten, että

\[f=\sum_{j=1}^m q_j^2.\]

Käytännön laskuissa on kätevämpi välttää neliöjuuria ja kirjoittaa $c_jq_j^2$, missä $c_j>0$.

Joskus epäyhtälö ikään kuin ratkeaa itsestään, koska annettu polynomi on valmiiksi neliö; esimerkiksi IMOn 2. tehtävässä vuonna 2008 piti osoittaa, että

\[(x^2y^2-3xy+x+y)^2\ge0.\]

Samoin matematiikkavalmennuksen 16. tehtävässä syyskuussa 2022 piti osoittaa, että $h^2>0$, kun $x$, $y$ ja $z$ ovat erisuuria, missä

\[h=xyz-(x+y-z)(x+z-y)(y+z-x).\]

Esa Vesalaisen tehtäväkokoelmassa 20. tehtävässä puolestaan piti osoittaa, että

\[(x^2 - 2x - 1)(x^2 - 2)(2x-1)^2\ge0,\]

kun $0\le x\le 1$. Tietenkin nämä kaikki tehtävät oli muotoiltu niin, ettei ratkaisua heti nähnyt.

Epäyhtälötehtävissä on usein joitain lisärajoituksia. Esimerkiksi voitaisiin haluta osoittaa, että $f\ge0$, kun lisäksi oletetaan, että $g_1=0$ ja/tai $g_2\ge0$. Tässä tapauksessa strategiana olisi etsiä esitysmuotoa

\[f=r+q_1g_1+q_2g_2. \tag{1}\]

Jos $r\ge0$ ja $q_2\ge0$, niin tämä todistaa väitteen. Huomaa, että tavallaan $r$ on jakojäännös ja $q_j$ ovat osamääriä, joten varmaankin jakolaskualgoritmi on tässä hyödyllinen.

Esimerkki 3. Osoitetaan ideaa (1) käyttäen, että

\[h=xyz-(x+y-z)(x+z-y)(y+z-x)\ge0,\]

kun $x\ge0$, $y\ge0$ ja $z\ge0$.⁷ Koska $h$ on selvästi symmetrinen, voidaan olettaa, että $z\ge x\ge y$. Jaetaan ensin polynomilla $z-x$:

\[\begin{align*} h &=q(z-x)+y(x-y)^2,\\ q &=z(z-y)-(x-y)^2. \end{align*}\]

Jakojäännös on positiivinen; jaetaan sitten osamäärä polynomilla $x-y$:

\[q=(y+z-x)(x-y)+z(z-x).\]

Siis osamääräkin on positiivinen, joten $h\ge0$.

Jos $x$, $y$ ja $z$ ovat jonkin kolmion sivujen pituuksia, niin jakamalla polynomilla $g=(z-x)(z-y)$ saadaan yhdellä jakolaskulla

\[h=z\,g+(x-y)^2(x+y-z)\ge 0.\]

Toisaalta tämän voi todistaa tavallaan ilman mitään laskuja järjestämällä $h$:n termit uudelleen:

\[h=(z-x)(z(z-y)-x(x-y))+y(z-y)(x-y).\]

Selvästi $h\ge0$, kun $z\ge x\ge y$.

Tämän avulla voidaan ratkaista pohjoismaitten matematiikkakilpailuissa vuonna 2004 ollut geometrian tehtävä. Siinä piti osoittaa, että jos $x$, $y$ ja $z$ ovat kolmion sivut ja $r$ on kolmion kärkien kautta kulkevan ympyrän säde, niin

\[f=(x + y + z)r^2 - xyz\ge 0.\]

Muistetaan geometriasta, että⁸

\[4Ar=xyz,\]

missä $A$ on kolmion pinta-ala. Käytetään taas Heronin polynomia $h_A$ ja sitä, että $h_A\ge 0$, kun $x$, $y$ ja $z$ on kolmion sivut. Tästä saadaan

\[\begin{align*} h_Af &=xyz\Big((x+y+z)xyz-h_A\Big)\\ &=xyz(x+y+z)h\ge 0. \end{align*}\]

Epäyhtälö $h\ge0$ ratkaisee myös IMOn toisen tehtävän vuodelta 2000 ja pohjoismaisen matematiikkakilpailun toisen tehtävän vuodelta 2005. $\Box$

Esimerkki 4. IMOn tehtävä vuodelta 1983. Oletetaan, että $x$, $y$ ja $z$ ovat kolmion sivut; osoita, että

\[f =yx^2(x-y)+zy^2(y-z)+xz^2(z-x)\ge0. \tag{2}\]

$f$ on syklisesti symmetrinen, joten riittää tarkastella kahta tapausta: (i) $z\ge x\ge y$ ja (ii) $y\ge x\ge z$.

Tapauksessa (i) jaetaan käyttämällä tuttua polynomia $g=(z-x)(z-y)$:

\[f= (xz+y(x-y))g+xy(x-y)^2.\]

Tämä on selvästi positiivinen. Tässä ei siis tarvittu sitä tietoa, että kyseessä on kolmion sivut. Tapauksessa (ii) jaetaan polynomilla $x+z-y$, jolloin saadaan

\[f=q(x+z-y)+2x(y-x)^3.\]

Siis jakojäännös on positiivinen. Jaetaan sitten osamäärä polynomilla $x-z$, mistä saadaan

\[q=\big(y(y-x)+x(x-z)\big)(x-z)+x(y-x)^2\ge0,\]

joten $f\ge0$ tässäkin tapauksessa. $\Box$

Esimerkki 5. Pohjoismaitten matematiikkakilpailuissa vuonna 1987 piti osoittaa, että

\[f= x^2y^4+y^2z^4+z^2x^4-xyz(xy^2+yz^2+zx^2)\ge0,\]

kun muuttujat ovat positiivisia. $f$ on syklisesti symmetrinen, joten periaatteessa pitäisi tarkastella kahta tapausta: (1) $z\ge x\ge y$ ja (2) $z\ge y\ge x$. Kuitenkin molemmissa tapauksissa ongelma ratkeaa, kun jaetaan polynomilla $g=(z-x)(z-y)$:

\[\begin{align*} f&=qg+r,\\ q&=y^2z(z+y)+y^4-x^3y+x^4,\\ r&=(x-y)^2(y^2+xy+x^2)(yz+xz-xy). \end{align*}\]

Selvästi $q\ge0$ ja $r\ge0$.

Myös IMOn 4. tehtävä vuodelta 1963, Baltian tie kilpailun 5. tehtävä vuodelta 1991 ja Vesalaisen tehtävät 17, 27, 28 ja 49 ratkeavat jakamalla polynomilla $g=(z-x)(z-y)$.

$f$ voidaan symmetrisoida sijoituksella $\hat x^3=xy^2$, $\hat y^3=yz^2$ ja $\hat z^3=zx^2$, jolloin saadaan symmetrinen polynomi

\[\hat f=\hat x^6+\hat y^6+\hat z^6-\hat x\hat y\hat z(\hat x^3+\hat y^3+\hat z^3).\]

Vesalaisen tehtävässä 27 puolestaan piti osoittaa, että

\[f_0= x^4+y^4+z^4-xyz(x+y+z)\ge 0.\]

Itse asiassa $\hat f$ ja $f_0$ ovat sos-polynomeja, joten ne ovat positiivisia kaikilla arvoilla. Katsotaan tätä kohta. $\Box$

Tuntuu siltä, että yleispolynomi $g=(z-x)(z-y)$ ratkaisee monet ongelmat. Tämä oli minullekin yllätys: ajattelin, että laskemalla kuten kaavassa (1) voisi ratkaista joitain tehtäviä; kuten edellä nähtiin, niin osoittautui kuitenkin, että monet kilpailutehtävät ratkeavat näin. Lisäksi ei ollut mitenkään vaikea keksiä millä polynomilla jakaa; päinvastoin voisi sanoa, että nuo käytetyt polynomit ovat sellaisia, mitkä ensimmäisenä tulevat mieleen.

Päällisin puolin ei näytä olevan mitään selkeää syytä sille, että jakojäännös ja osamäärä osoittautuivat positiiviseksi. Periaatteessahan voisi yhtä hyvin käydä, että osamäärä (jakojäännös) on sopivasti positiivinen, kun jakojäännös (osamäärä) on negativiinen. Jos siis lähtee laskemaan käyttäen jakolaskua ja yhtälöä (1), niin tietääkseni ei ole mitään lausetta tai edes jotain ideaa, miksi tämä välttämättä johtaisi ratkaisuun. Kuitenkin näin tuntuu usein käyvän, enkä osaa edes muotoilla täsmällisesti, mikä lause tässä pitäisi todistaa.

Luonnollisesti ideaa (1) voidaan systemaattisesti soveltaa; tätä on tarkemmin kuvattu kirjassa [2, section 3.4].

Epäyhtälöt ja optimointi

Jos halutaan osoittaa, että $f\ge 0$ joko koko avaruudessa tai jossain sen osajoukossa, niin tämähän on oikeastaan optimointitehtävä, koska halutaan osoittaa, että $f$:n minimi on einegatiivinen halutussa joukossa. Ottamalla sitten käyttöön tietyt differentiaalilaskennan työkalut tehtävä voidaan joskus näppärästi ratkaista tätä kautta. Tietenkin kilpailutehtävissä tehtävät on muotoiltu niin, että ne ratkeavat muutenkin, mutta yleisesti ottaen kannattaa muistaa tämäkin näkökulma. Jätänkin harjoitustehtävksi seuraavan:

Olkoon $h$ esimerkissä 3 ollut polynomi. Osoita differentiaalilaskennan avulla, että $h\ge0$, kun $x\ge0$, $y\ge0$ ja $z\ge0$. Ohje: käytä hyväksi sitä, että $h$ on homogeeninen.

SOS-polynomit

Palataan sitten algebrallisiin menetelmiin ja tarkastellaan tässä vain tapausta, jossa haluttaisiin osoittaa, että polynomi $f\ge0$ kaikilla muuttujien arvoilla. Eräs idea olisi etsiä $f$:lle sos-esitystä. Mutta onko jokainen positiivinen polynomi sos-polynomi? Valitettavasti näin ei ole kuin muutamassa tapauksessa.

Lause 1. Olkoon $n$ polynomin muuttujien määrä ja $d$ polynomin aste. Positiiviset polynomit ovat aina sos-polynomeja vain seuraavissa tapauksissa:

$n=1$ ja $d$ on mielivaltainen parillinen luku,
$d=2$ ja $n$ mielivaltainen,
$n=2$ ja $d=4$.

Kohdat 1 ja 2 ovat varsin selkeitä tapauksia. Katsotaan kohta 1 tässä esimerkin avulla ja palataan kohtaan 2 myöhemmin.

Esimerkki 6. Jos $f$ on positiivinen yhden muuttujan polynomi, jolla on vain reaalisia nollakohtia, niin se on jo valmiiksi neliö. Katsotaan siis vain kompleksinen tapaus esimerkin avulla. Muistetaan identiteetti

\[(a^2+b^2)(c^2+d^2)=(ac+bd)^2 +(ad-bc)^2. \tag{3}\]

Tämän avulla saadaan

\[\begin{align*} f &=x^4 + 6x^3 + 39x^2 + 66x + 58\\ &=(x^2 + 2x + 2)(x^2 + 4x + 29)\\ &=\big((x+1)^2+1\big)\big((x+2)^2+25\big)\\ &=(x^2 + 3x + 7)^2+(4x+3)^2. \end{align*}\]

Siis soveltamalla identiteettiä (3) rekursiivisesti nähdään, että mikä tahansa positiivinen yhden muuttujan polynomi voidaan esittää korkeintaan kahden polynomin neliön summana.⁹ $\Box$

Sen sijaan lauseen kohta 3, ja se, että nämä todella ovat ainoat tapaukset, ei ole mitenkään selvää. Hilbert todisti tämän 1800-luvun lopussa, mutta konkreettinen esimerkki positiivisesta polynomista, joka ei ole sos-polynomi löydettiin vasta paljon myöhemmin. Helpoin esimerkki löytyy tapauksessa $n=2$ ja $d=6$; tämä on kuuluisa Motzkinin polynomi:

\[f_m=x^4y^2+x^2y^4-3x^2y^2+1. \tag{4}\]

Katsotaan kohta, miksi tämä ei voi olla sos-polynomi, ja osoitetaan sitten, että $f_m\ge0$ kuitenkin pätee.

Vaikka siis kaikki positiiviset polynomit eivät ole sos-polynomeja, niin tilanne on kuitenkin parempi kuin tuon lauseen perusteella voisi kuvitella. Katsotaan kuitenkin ensin, miten sos-esitysmuotoa voisi systemaattisesti etsiä.

Esimerkki 7. Äskeisessä esimerkissä polynomin

\[f=x^4 + 6x^3 + 39x^2 + 66x + 58\]

sos-muoto löydettiin, koska nollakohdat tunnettiin. Tyypillisesti nollakohtia ei tunneta, joten miten silloin voisi edetä? Tässä tarvitaan joitain matriisilaskun käsitteitä ja merkintöjä, jotka on esitelty kirjoituksen lopussa.

Jos $f=\sum_j q_j^2$, niin $q_j$:t ovat toisen asteen polynomeja. Olkoot $v=(1,x,x^2)$ ja $A$ symmetrinen $3\times 3$ matriisi. Yritetään esittää $f$ muodossa

\[f=\langle v,Av\rangle.\]

Koska $A$:ssa on 6 vapaata parametria ja $f$:ssä on 5 kerrointa, niin voisi kuvitella, että yksi parametri voidaan valita vapaasti. Kertomalla auki ja vertaamalla kertoimia nähdäänkin, että

\[A=\begin{pmatrix} 58&33&(39-c)/2\\33&c&3\\(39-c)/2&3&1 \end{pmatrix}.\]

Nyt pitäisi valita $c$ siten, että $A$ olisi psd (positiivisemidefiniitti). Lauseen 2 ja kriteerin (6) perusteella on järkevää valita parametri niin, että lävistäjäalkiot olisivat mahdollisimman isoja ja lävistäjän ulkopuoliset alkiot itseisarvoltaan mahdollisimman pieniä. Tuntuisi siis luonnolliselta kokeilla arvoa $c=39$.¹⁰ Saadaan siis

\[A=\begin{pmatrix} 58&33&0\\33&39&3\\0&3&1 \end{pmatrix}.\]

Lasketaan sitten $A$:n LDL-hajotelma $A=LDL^T$ (määritelmä 1 ja lause 3). Tämän voi laskea Sagessa seuraavasti. Ensin määritellään

A = matrix(QQ, [[58,33,0],[33,39,3],[0,3,1]])

Tämän jälkeen hajotelma saadaan komennolla

[P,L,D] = A.block_ldlt()

missä $P$, $L$ ja $D$ ovat kuten lauseessa 3. Tämä antaa $P=I$, $D=\mathsf{diag}(58,1173/58,217/391)$ ja

\[L=\begin{pmatrix} 1 & 0 & 0\\ 33/58 & 1 & 0\\ 0 & 58/391 & 1 \end{pmatrix}.\]

Matlabissa¹¹ sama hajotelma saadaan numeerisesti komennoilla

A = [58,33,0;33,39,3;0,3,1]
[L,D,P] = ldl(A)

Määritellään nyt $L^Tv=q$, minkä jälkeen

\[\begin{align*} f &=\langle v,Av\rangle= \langle v,LDL^Tv\rangle\\ &=\langle L^Tv,DL^Tv\rangle=58q_1^2+\tfrac{1173}{58}\,q_2^2+ \tfrac{217}{391}\,q_3^2\\ &=58(1+33x/58)^2+\tfrac{1173}{58}\,(x-58x^2/391)^2 +\tfrac{217}{391}\,x^4. \end{align*}\]

Kolmas yhtäsuuruus seuraa siis kaavasta (5). Huomataan, että saatiin aivan erilainen sos-muoto kuin äsken. Tämä onkin tyypillistä: sos-esitys ei ole yksikäsitteinen. $\Box$

Tässä jo nähtiin, miten sos-esitystä voisi etsiä yleisessä tapauksessa:

Laitetaan tarvittavat monomit vektoriin $v$.
Esitetään annettu polynomi $f$ muodossa

\[f=\langle v,Av\rangle,\]

missä $A$ on symmetrinen.
Tyypillisesti joitain $A$:n alkioita voi valita vapaasti. Pyritään valitsemaan nämä siten, että $A$ on psd.
Lasketaan LDL-hajotelma $A=LDL^T$ ja asetetaan $q=L^Tv$. Tästä saadaan

\[f=\sum_i d_{ii}q_i^2.\]

Jos $A$ on psd, niin $d_{ii}\ge 0$.

Tämän avulla voidaankin helposti todistaa äskeisen lauseen kohta 2. Jos $x=(x_1,\dots, x_n)$ ja $f$ on muuttujien $x_j$ toisen asteen homogeeninen polynomi, niin on olemassa symmetrinen $A$ siten, että $f=\langle x,Ax\rangle$. Jos $f\ge 0$, niin $A$ on psd ja sos-muoto saadaan kuten yllä kohdassa 4.

Newton ja Motzkin

Äskeisen menetelmän kohdassa 1 puhuttiin tarvittavista monomeista. Jos $f$ on vaikkapa 8. asteen polynomi, niin yleisesti ottaen polynomit $q_j$ ovat yleisiä 4. asteen polynomeja. Jos muuttujia on $n$, niin astetta $d$ olevassa polynomissa on $\binom{n+d}{d}$ eri monomia, joten monomien määrä kasvaa varsin nopeasti sekä $d$:n että $n$:n suhteen. Joskus kuitenkin pärjätään paljon pienemmällä määrällä. Katsotaan tämä vain kahden muuttujan tapauksessa, mutta idea yleistyy sellaisenaan $n$:n muuttujan tapaukseen.

Liitetään monomiin $x^iy^k$ tason piste $(i,k)$. Kahden muuttujan polynomiin $f$ voidaan siis liittää pisteet kaikista sen monomeista, ja Newtonin monikulmio $\mathcal{N}(f)$ on pienin konveksi monikulmio, joka sisältää kaikki $f$:n monomien pisteet. Jos nyt $g$ on jokin toinen polynomi, niin voidaan osoittaa, että

\[\mathcal{N}(fg)=\mathcal{N}(f)+\mathcal{N}(g).\]

Oikealla puolella olevaa summaa sanotaan Minkowskin summaksi. Jos siis $A$, $B\subset\mathbb{R}^n$, niin näitten Minkowskin summa on

\[A+B=\big\{p \in\mathbb{R}^n\,\big|\, p=a+b\ ,\ a\in A\,,\,b\in B\big\}.\]

Tätä hyväksi käyttäen voidaan edelleen osoittaa, että jos $f=\sum_j q_j^2$, niin

\[\mathcal{N}(q_j)\subset \frac{1}{2}\,\mathcal{N}(f).\]

Osoitetaan tämän avulla, että Motzkinin polynomi (4) ei ole sos-polynomi.

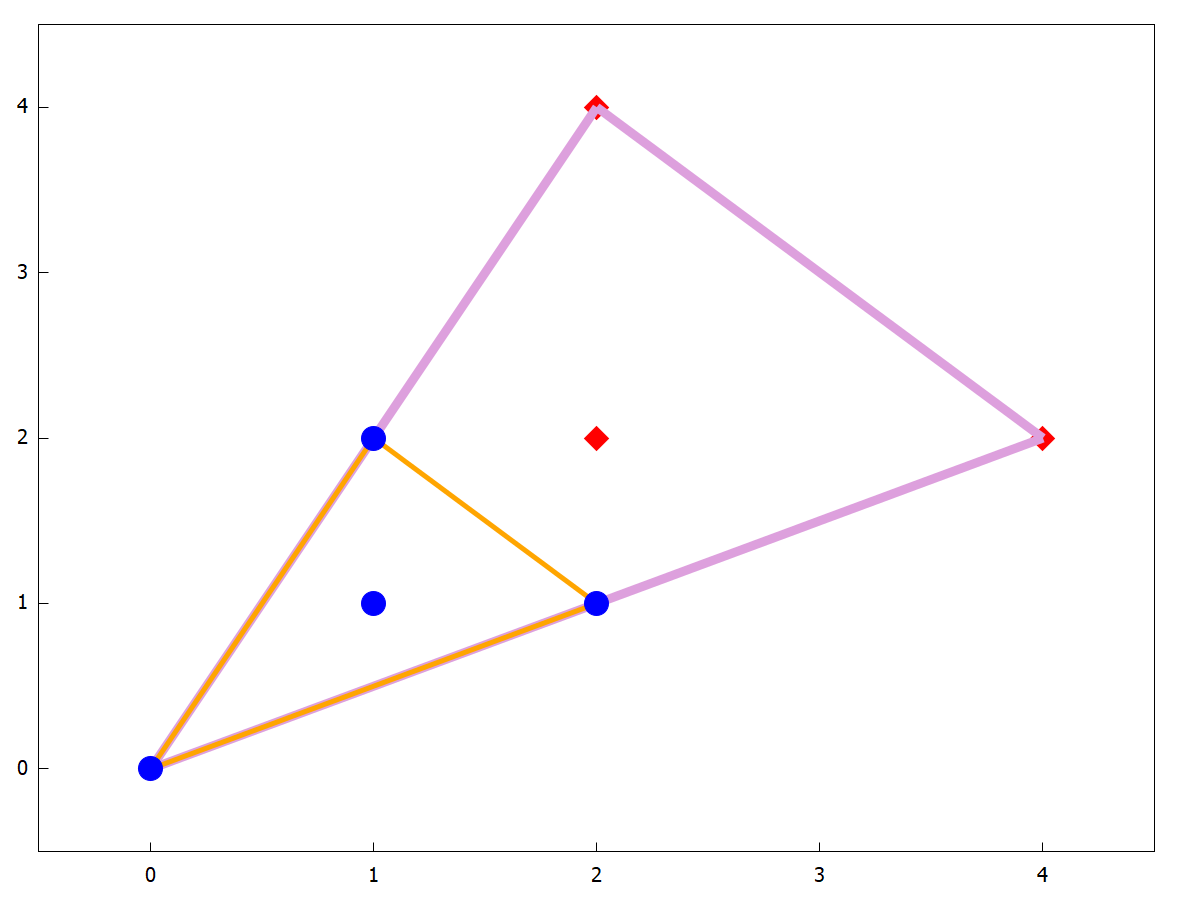
Kuvassa 1 on $\mathcal{N}(f_m)$ ja sen “puolikas”. Jos siis pätisi, että $f_m=\sum_j q_j^2$, niin $q_j$ olisi muotoa

\[q_j=c_{j,0}+c_{j,1}xy+c_{j,2}x^2y+c_{j,3}xy^2.\]

Huomaa, että $q_j$ on kolmannen asteen polynomi, joten periaatteessa siinä voisi olla 10 monomia ja siis 10 tuntematonta kerrointa. Newtonin monikulmion avulla kertoimien ja monomien määrä voidaan rajoittaa neljään, mikä on huomattava yksinkertaistus.

Mutta jos $q_j$ on edellä olevaa muotoa, niin

\[q_j^2=c_{j,1}^2x^2y^2+\dots,\]

mutta toisaalta $f_m=-3x^2y^2+\dots$, joten yhtäsuuruus on mahdoton.

Kuva 1: Motzkinin polynomin Newtonin monikulmio.

Kun Hilbert oli osoittanut, että yleensä positiiviset polynomit eivät ole sos-polynomeja, hän pohti, voisivatko kaikki positiiviset polynomit olla rationaalifunktioitten neliöitä. Hilbert selvästi piti tätä mielenkiintoisena kysymyksenä, koska tämä oli 17. ongelma, jonka hän esitti kuuluisassa esitelmässään vuonna 1900.¹² Parikymmentä vuotta myöhemmin Artin osoitti, että sopivat rationaalifunktiot aina löytyy. Artinin tulos voidaan muotoilla seuraavasti:

Jos $f\ge0$, niin on olemassa sos-polynomi $q$ siten, että $qf$ on sos-polynomi.

Artinin lauseen takia siis sos-tekniikat ovat paljon hyödyllisempiä kuin lauseen 1 perusteella voisi kuvitella. Nyt voitaisiinkin yrittää etsiä jotain sos-polynomia $q$ siten, että $qf_m$ olisi sos-polynomi. Jos tällainen $q$ löytyy, niin tästähän tietysti seuraa, että $f_m\ge0$.

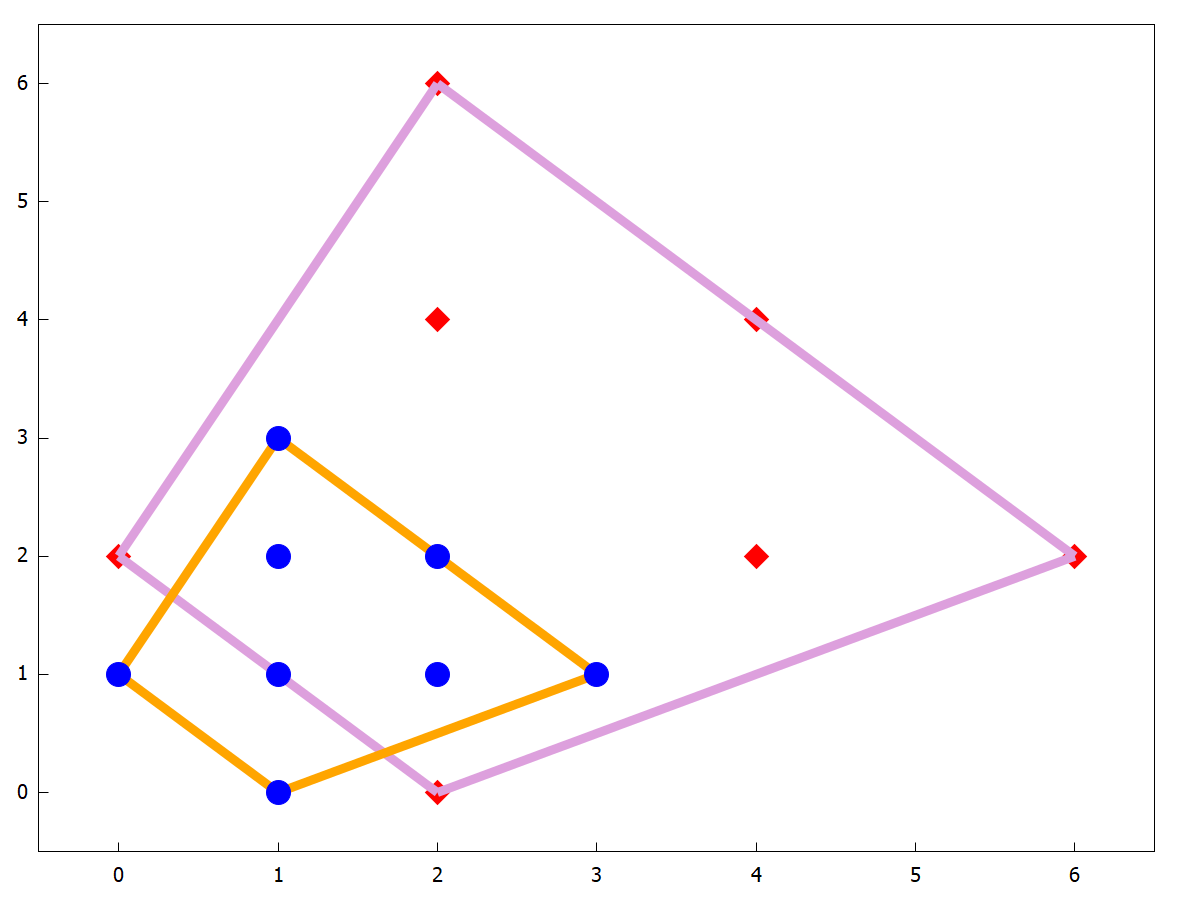
Nyt osoittautuu, että riittää valita $q=x^2+y^2$. Olkoon siis $\hat f_m=(x^2+y^2)f_m$. Kuvassa 2 on esitetty vastaavat Newtonin monikulmiot; tarvitaan siis monomivektori

\[v=\big(x,y,xy,x^2y,xy^2,x^3y,x^2y^2,xy^3\big).\]

Huomaa, että ilman Newtonin monikulmiota voisi luulla, että monomivektoriin pitää laittaa kaikki $\binom{6}{4}=15$ komponenttia.

Kuva 2: Polynomia $\hat f_m$ vastaava Newtonin monikulmio.

Yritetään nyt etsiä symmetrinen $A\in\mathbb{R}^{8\times 8}$ siten, että

\[\hat f_m=\langle v,Av\rangle.\]

Periaatteessa $A$:ssa on $36$ vapaata parametria. Symmetrian avulla voidaan kuitenkin heti pienentää parametrien määrää. Olkoon

\[\tilde v=\big(y,x,xy,y^2x,yx^2,y^3x,x^2y^2,yx^3\big).\]

Koska $f_m$ ja siis $\hat f_m$ ovat symmetrisiä, niin täytyy päteä

\[\langle v,Av\rangle=\langle \tilde v,A\tilde v\rangle.\]

Toisaalta $\tilde v=Pv$, missä

\[P=\begin{pmatrix} 0& 1& 0& 0& 0& 0& 0 &0\\ 1 &0 &0 &0 &0 &0 &0 &0\\ 0 &0& 1 &0 &0 &0 &0 &0\\ 0 &0 &0 &0& 1 &0 &0 &0\\ 0 &0 &0& 1 &0 &0 &0 &0\\ 0 &0 &0 &0 &0 &0 &0& 1\\ 0 &0 &0 &0 &0 &0& 1 &0\\ 0 &0 &0 &0 &0 &1 &0 &0 \end{pmatrix}.\]

Siispä kaavan (5) perusteella

\[\begin{align*} \langle \tilde v,A\tilde v\rangle &= \langle P v,A P v\rangle= \langle v,P^TAP v\rangle\\ &=\langle v,PAP v\rangle= \langle v,A v\rangle. \end{align*}\]

Täytyy siis päteä, että $A=PAP$. Vertaamalla matriiseja nähdään, että on enää 21 vapaata parametria:

\[A=\begin{pmatrix} a_{11} & a_{12} & a_{13}& a_{14}& a_{15} & a_{16}& a_{17}& a_{18}\\ a_{12}& a_{11} & a_{13}& a_{15} & a_{14}& a_{18}& a_{17}& a_{16}\\ a_{13} & a_{13}& a_{33}& a_{34}& a_{34}& a_{36}& a_{37}& a_{36}\\ a_{14} & a_{15}& a_{34}& a_{44}& a_{45}& a_{46}& a_{47}& a_{48}\\ a_{15} & a_{14}& a_{34}& a_{45}& a_{44}& a_{48}& a_{47}& a_{46}\\ a_{16}& a_{18}& a_{36}& a_{46}& a_{48}& a_{66}& a_{67}& a_{68}\\ a_{17}& a_{17}& a_{37}& a_{47}& a_{47}& a_{67}& a_{77}& a_{67}\\ a_{18}& a_{16}& a_{36}& a_{48}& a_{46}& a_{68}& a_{67}& a_{66} \end{pmatrix}.\]

Yhtälöstä $\hat f_m=\langle v,Av\rangle$ saadaan periaatteessa $24$ ehtoa, koska Newtonin monikulmiossa $\mathcal{N}(\hat f_m)$ on $24$ monomia vastaavaa pistettä. Symmetrian takia saadaan kuitenkin vain $14$ riippumatonta yhtälöä. Kun vain kertoo kaikki auki, niin havaitaan, että yhtälöt ovat lineaarisia ja vieläpä hyvin yksinkertaisia. Kun ratkaistaan nämä yhtälöt, niin jäljelle jää vielä $7$ parametria:

\[\begin{align*} A &=\Big(A_1\ ,\ A_2\Big),\\[6pt] A_1 &=\begin{pmatrix} 1 & 0 & 0& 0\\[3pt] 0& 1& 0& \dfrac{-a_{33}}{4}\\[6pt] 0 & 0& a_{33}& -a_{17}-a_{18}\\[6pt] 0& \dfrac{-a_{33}}{4}& -a_{17}-a_{18}& a_{44}\\[6pt] \dfrac{-a_{33}}{4} & 0& -a_{17}-a_{18}& -a_{37}\\[6pt] 0& a_{18}& \dfrac{-a_{44}}{2}-\dfrac{3}{2}& 0\\[8pt] a_{17}& a_{17}& a_{37}& a_{47}\\[6pt] a_{18}& 0& \dfrac{-a_{44}}{2}-\dfrac{3}{2}& -a_{47} \end{pmatrix},\\[6pt] A_2&=\begin{pmatrix} \dfrac{-a_{33}}{4} & 0& a_{17}& a_{18}\\[8pt] 0& a_{18}& a_{17}& 0\\[6pt] -a_{17}-a_{18}& \dfrac{-a_{44}}{2}-\dfrac{3}{2}& a_{37}& \dfrac{-a_{44}}{2}-\dfrac{3}{2}\\[8pt] -a_{37}& 0& a_{47}& -a_{47}\\[6pt] a_{44}& -a_{47}& a_{47}& 0\\[6pt] -a_{47}& 1& 0& 1-\dfrac{a_{77}}{2}\\[8pt] a_{47}& 0& a_{77}& 0\\[6pt] 0& 1-\dfrac{a_{77}}{2}& 0& 1 \end{pmatrix}. \end{align*}\]

Nyt muistetaan lause 2 ja pyritään laittamaan lävistäjän ulkopuoliset parametrit nollaksi, ja lävistäjäalkiot mahdollisimman isoiksi. Heti nähdään, että voidaan asettaa $a_{17}=a_{18}=a_{37}=a_{47}=0$. Tämän jälkeen 7. rivillä on enää vain $a_{77}$, joten valitaan sekin nollaksi. Nyt $A$:n ensimmäinen rivi toteuttaa ehdon (6), jos $a_{33}\le 4$, joten valitaan $a_{33}=4$. Lopuksi ehto (6) pätee neljännellä rivillä, jos $a_{44}\ge 1$, ja kolmannella rivillä, jos $0\le a_{44}\le 1$ joten valitaan $a_{44}=1$, jolloin

\[A=\begin{pmatrix} 1 & 0 & 0& 0&-1 & 0& 0& 0\\ 0& 1& 0& -1&0&0& 0& 0\\ 0 & 0& 4&0&0&-2&0&-2\\ 0&-1&0&1&0&0&0&0\\ -1&0&0&0&1&0&0&0\\ 0&0&-2&0&0&1&0&1\\ 0&0&0&0&0&0&0&0\\ 0&0&-2&0&0&1&0&1 \end{pmatrix}.\]

Kun nyt lasketaan hajotelma $A=LDL^T$, niin huomataan, että $D$:ssä on vain kolme nollasta poikkeavaa alkiota: $d_{11}=d_{22}=1$ ja $d_{33}=4$. Kun merkitään $q=L^Tv$, niin voidaan lopulta kirjoittaa \[\begin{align*} \hat f_m &=(x^2+y^2)f_m=q_1^2+q_2^2+4q_3^2,\\ q_1 &=y(1-x^2),\\ q_2 &=x(1-y^2),\\ q_3&=xy(x^2+y^2-2)/2. \end{align*}\]

Esimerkki 8. Esimerkissä 4 mainitussa Vesalaisen tehtävässä 27 piti osoittaa, että

\[f_0=x^4+y^4+z^4-xyz(x+y+z)\ge 0.\]

Näytetään, että tämä on sos-polynomi. Kyseessä on homogeeninen neljännen asteen polynomi, joten tarvitaan monomivektori

\[v=\big(x^2,xy,xz,y^2,yz,z^2\big).\]

Newtonin monikulmion avulla nähdään, että kaikkia näitä monomeja saatetaan tarvita. Nyt yhtälössä $f_0=\langle v,A_0v\rangle$ on periaatteessa 21 parametria, mutta symmetrian perusteella jäljelle jää vain 6 parametria:

\[A_0=\begin{pmatrix} c_{0} & c_{1} & c_{1} & c_{2} & c_{3} & c_{2} \\ c_{1} & c_{4} & c_{5} & c_{1} & c_{5} & c_{3} \\ c_{1} & c_{5} & c_{4} & c_{3} & c_{5} & c_{1} \\ c_{2} & c_{1} & c_{3} & c_{0} & c_{1} & c_{2} \\ c_{3} & c_{5} & c_{5} & c_{1} & c_{4} & c_{1} \\ c_{2} & c_{3} & c_{1} & c_{2} & c_{1} & c_{0} \end{pmatrix}.\]

Tämän jälkeen yhtälö $f_0=\langle v,A_0v\rangle$ kiinnittää 4 parametria, mistä saadaan $A_0 =$

\[\begin{pmatrix} 1 & 0 & 0 & -\frac{c_{4}}{2} & c_{3} & -\frac{c_{4}}{2} \\[2pt] 0 & c_{4} & -\frac{1}{2}-c_{3} & 0 & -\frac{1}{2}-c_{3} & c_{3} \\[2pt] 0 & -\frac{1}{2}-c_{3} & c_{4} & c_{3} & -\frac{1}{2}-c_{3} & 0 \\[2pt] -\frac{c_{4}}{2} & 0 & c_{3} & 1 & 0 & -\frac{c_{4}}{2} \\[2pt] c_{3} & -\frac{1}{2}-c_{3} & -\frac{1}{2}-c_{3} & 0 & c_{4} & 0 \\[2pt] -\frac{c_{4}}{2} & c_{3} & 0 & -\frac{c_{4}}{2} & 0 & 1 \end{pmatrix}.\]

Lopuksi valitaan lauseen 2 perusteella $c_4=1$ ja $c_3=0$, jolloin $A_0$ on psd:

\[A_0=\begin{pmatrix} 1 & 0 & 0 & -\frac{1}{2} & 0 & -\frac{1}{2} \\[2pt] 0 & 1 & -\frac{1}{2} & 0 & -\frac{1}{2} & 0 \\[2pt] 0 & -\frac{1}{2} & 1 & 0 & -\frac{1}{2} & 0 \\[2pt] -\frac{1}{2} & 0 & 0 & 1 & 0 & -\frac{1}{2} \\[2pt] 0 & -\frac{1}{2} & -\frac{1}{2} & 0 & 1 & 0 \\[2pt] -\frac{1}{2} & 0 & 0 & -\frac{1}{2} & 0 & 1 \end{pmatrix}.\]

Sitten lasketaan $A_0=LDL^T$, ja havaitaan, että $D$:ssä on 4 nollasta poikkeavaa alkiota, mistä lopulta saadaan

\[\begin{align*} f_0 &=q_1^2+q_2^2+\tfrac{3}{4}\,q_3^2+\tfrac{3}{4}\,q_4^2,\\ q_1 &=x^2 - y^2/2 - z^2/2,\\ q_2 &=xy - xz/2 - yz/2,\\ q_3 &=x(y-z),\\ q_4 &=y^2-z^2. \end{align*}\]

Aivan samoin voidaan osoittaa, että esimerkissä 3 ollut polynomi

\[f_1=x^6+y^6+z^6-xyz(x^3+y^3+z^3)\]

on sos-polynomi. Nyt tarvitaan monomivektori:

\[\begin{align*} v=\big(&x^3,x^2y,x^2z,xy^2,xyz,\\ & xz^2,y^3,y^2z,yz^2,z^3\big). \end{align*}\]

Yhtälön $f_1=\langle v,A_1v\rangle$ matriisilla $A_1$ on periaatteessa $55$ vapaata parametria, mutta symmetrian perusteella parametrien määrä onkin vain $13$. Yhtäsuuruus $f_1=\langle v,A_1v\rangle$ kiinnittää $7$ parametria. Loput $6$ parametria valitaan taas lauseen 2 mukaisesti. Kun valitaan lävistäjän ulkopuolella kaikki mahdolliset parametrit nolliksi, niin huomataan, että ehto (6) on voimassa. Kun sitten lasketaan $A_1=LDL^T$, niin nähdään, että $D$:n lävistäjällä on $8$ nollasta poikkeavaa alkiota, joten $f_1$ voidaan esittää kahdeksan polynomin neliön summana. $\Box$

Lopuksi

Sos-tekniikat eivät selvästikään sovellu käsin laskentaan, mutta yllä olevat laskut olivat helppoja sopivaa ohjelmaa käyttäen. Tarvittiin vain matriisien kertolaskua ja yksinkertaisten lineaaristen yhtälöitten ratkaisua. Lisäksi tietysti piti laskea LDL-hajotelma. Monissa sos-sovelluksissa on kuitenkin välttämätöntä käyttää numeerisia menetelmiä. Tähän on olemassa Matlabiin tehty paketti sostools [5].

Matriisit

Olkoot $x=(x_1,\dots,x_n)$ ja $y=(y_1,\dots,y_n)\in\mathbb{R}^n$ vektoreita ja asetetaan

\[\langle x,y\rangle=x_1y_1+\dots+x_ny_n.\]

Neliömatriisi $A$ on

\[A=\begin{pmatrix} a_{11}&\dots&a_{1n}\\ \vdots&\ddots&\vdots\\ a_{n1}&\dots&a_{nn} \end{pmatrix}\in \mathbb{R}^{n\times n}.\]

Matriisi määrittää lineaarikuvauksen, kun määritellään matriisin ja vektorin kertolasku:

\[\begin{align*} & A \colon \mathbb{R}^n\to\mathbb{R}^n,\\ & y=Ax\quad\longleftrightarrow\quad y_i= \sum_{j=1}^n a_{ij}x_j. \end{align*}\]

Matriisin $A$ transpoosi $A^T$ saadaan, kun indeksointia vaihdetaan: siis jos $A=\big(a_{ij}\big)$, niin $A^T=\big(a_{ji}\big)$. On helppo tarkistaa, että

\[\langle Ax,y\rangle=\langle x,A^Ty\rangle. \tag{5}\]

Matriisien $A$ ja $B$ kertolasku määritellään seuraavasti:

\[C=BA\quad\longleftrightarrow\quad c_{ij}= \sum_{\ell=1}^n b_{i\ell}a_{\ell j} .\]

Huomaa, että yleensä $AB\ne BA$. Seuraavat matriisiluokat ovat tässä oleellisia:

$A$ on lävistäjämatriisi, jos $a_{ij}=0$ kun $i\ne j$. Yksikkömatriisi $I$ on sellainen lävistäjämatriisi, jossa lävistäjäalkiot ovat ykkösiä. Huomaa, että $AI=IA=A$ kaikille $A$. Jos lävistäjäalkiot ovat $d_1,\dots,d_n$, niin voidaan merkitä $D=\mathsf{diag}(d_1,\dots,d_n)$.
$A$ on alakolmiomatriisi, jos $a_{ij}=0$, kun $i<j$.
$A$ on symmetrinen, jos $A=A^T$.
Symmetrinen matriisi $A$ on psd (positiivisemidefiniitti), jos

\[\langle x,Ax\rangle\ge 0\quad \mathrm{kaikilla}\ x\in\mathbb{R}^n.\]
$P$ on permutaatiomatriisi, jos jokaisella $P$:n rivillä ja sarakkeella on yksi alkio ykkönen ja muut alkiot nollia.¹³

Olkoon sitten $\mathsf{e}_j$ vektori, jonka $j$:s komponentti on $1$ ja muut nollia; tällöin

\[\langle \mathsf{e}_j, A\mathsf{e}_j\rangle=a_{jj}.\]

Saadaan siis välttämätön ehto:

jos $A$ on psd, niin $a_{jj}\ge0$ kaikilla $j$.

Tämä ei kuitenkaan ole riittävä ehto. Tarkastelemalla $2\times 2$ tapausta saadaan kuitenkin lisää käteviä välttämättömiä ehtoja:

Jos $A$ on psd, niin $a_{jj}a_{kk}-a_{jk}^2\ge0$ kaikilla $j$ ja $k$. Erityisesti jos $a_{kk}=0$, niin $a_{jk}=0$ kaikilla $j$.

Oletetaan sitten, että seuraava ehto pätee kaikilla $j$:

\[a_{jj}\ge \sum_{i\ne j}|a_{ij}|. \tag{6}\]

Tällöin on tapana sanoa, että $A$ on lävistäjävaltainen (diagonally dominant). Voidaan osoittaa:

Lause 2. $A$ on psd, jos ehto (6) pätee.

Tämä ehto ei puolestaan ole välttämätön. Eräs tunnettu esimerkki on Hilbertin matriisi $H$, jonka alkiot ovat $h_{ij}=1/(i+j-1)$. Baltian tie -matematiikkakilpailuissa vuonna 1990 piti osoittaa, että $H$ on psd.¹⁴ Olkoot

\[g=c_0+c_1x+\dots+c_nx^n\]

ja $c=(c_0,\dots,c_n)$. Nyt selvästi

\[\langle c,Hc\rangle=\int_0^1g^2dx\ge0.\]

Ehto (6) on silti erittäin hyödyllinen, koska se on niin helppo tarkistaa.

Tarvitaan vielä

Määritelmä 1. Olkoon $A$ on symmetrinen. $A$:n LDL-hajotelma on

\[A=LDL^T,\]

missä $D$ on lävistäjämatriisi ja $L$ on alakolmiomatriisi, ja lisäksi $l_{ii}=1$ kaikilla $i$.

Kaikilla symmetrisillä matriiseilla ei ihan ole juuri tällaista LDL-hajotelmaa. Yleisesti ottaen voidaan osoittaa:

Lause 3. Jos $A$ on symmetrinen, niin on olemassa $P$, $L$ ja $D$ siten, että

\[P^TAP=LDL^T,\]

missä $P$ on permutaatiomatriisi ja $L$ on alakolmiomatriisi, ja lisäksi $l_{ii}=1$ kaikilla $i$. $D$ on lohkolävistäjämatriisi, jossa lohkot ovat joko $1\times 1$ tai $2\times 2$.

Tarkka muotoilu löytyy Highamin kirjasta [4]. Vaikka kirjan nimessä on numerical algorithms, niin LDL-hajotelma on (myös) symbolinen algoritmi siinä mielessä, että jos $A$:n alkiot ovat rationaalilukuja, niin myös $L$:n ja $D$:n alkiot ovat rationaalilukuja.

Tätä yleistystä ei tässä kirjoituksessa tarvita, vaan kaikissa esimerkeissä $D$ on lävistäjämatriisi ja $P$ on yksikkömatriisi.

Viitteet

[1] G. V. Bard, Sage for undergraduates, 2nd ed., American Mathematical Society, 2022.

[2] G. Blekherman, P. A. Parrilo, and R. R. Thomas (eds.), Semidefinite optimization and convex algebraic geometry, MOS-SIAM Series on Optimization, vol. 13, SIAM, 2013.

[3] D. A. Cox, J. Little, and D. O’Shea, Ideals, varieties, and algorithms, 4th ed., Undergraduate Texts in Mathematics, Springer, Cham, 2015, An introduction to computational algebraic geometry and commutative algebra.

[4] N. Higham, Accuracy and stability of numerical algorithms, 2nd ed., SIAM, 2002.

[5] A. Papachristodoulou, J. Anderson, G. Valmorbida, S. Prajna, P. Seiler, and P. A. Parrilo, SOSTOOLS: Sum of squares optimization toolbox for MATLAB, http://arxiv.org/abs/1310.4716, 2013, Available from http://www.eng.ox.ac.uk/control/sostools, http://www.cds.caltech.edu/sostools and http://www.mit.edu/~parrilo/sostools.

[6] J. Tuomela, Tarinoita polynomeista (osa 1), Solmu (2022), no. 2.

[7] J. Tuomela, Tarinoita polynomeista (osa 2), Solmu (2022), no. 3.

[8] J. Tuomela, Tarinoita polynomeista (osa 3), Solmu (2023), no. 2.

Alaviitteet

https://wxmaxima-developers.github.io/wxmaxima/index.html↩︎
https://www.sagemath.org/index.html↩︎
https://www.wolframalpha.com/↩︎
https://matematiikkakilpailut.fi/aiheet/↩︎
https://www.wikiwand.com/en/Heron%27s_formula↩︎
Tämä tunnetaan Weitzenböckin epäyhtälönä.↩︎
Tämä on erikoistapaus Schurin epäyhtälöstä: https://www.wikiwand.com/en/Schur%27s_inequality↩︎
https://www.wikiwand.com/en/Circumscribed_circle↩︎
Tässä on yhdistetty kahta hyvin yleisesti käytettyä todistustekniikkaa: proof by example ja proof by omission.
https://www.math.utah.edu/$\sim$cherk/mathjokes.html↩︎
Jätän harjoitustehtäväksi sen tutkimisen mitä tapahtuu, kun $c=25$ tai $c=45$, ja miksi nämä arvot ovat mielenkiintoisia.↩︎
https://se.mathworks.com/help/matlab/ref/ldl.html↩︎
https://en.wikipedia.org/wiki/Hilbert%27s_problems↩︎
Shakin pelaajat huomaavat, että jokainen $8\times 8$ permutaatiomatriisi vastaa yhtä torniongelman ratkaisua. Torniongelmalla on siis $8!=40320$ ratkaisua. Harjoitustehtäväksi jätän sen pohtimisen, kuinka monta oleellisesti erilaista ratkaisua on, ja miten oleellinen erilaisuus pitäisi määritellä.↩︎
Hilbertin matriisi on erikoistapaus Gramin matriisista, jotka ovat aina psd. https://en.wikipedia.org/wiki/Gram_matrix↩︎